Круг косинусов синусов: Тригонометрический круг синус и косинус. Тригонометрический круг рисунок, картинка. Значениия тригонометриче…

Тригонометрический круг — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Центр образования « Школа здоровья» № 1099 « Ярославский».
Сенникова Наталья Викторовна,
учитель математики
г. Москва
Использованная литература: Мордкович А. Г., Тульчинская Е. Е. Тригонометрия –
М.: Издательский дом «Новый учебник» АО «Московский учебник», 1999.
«ШПАРГАЛКА», КОТОРАЯ
ВСЕГДА С ТОБОЙ.
Ось котангенсов
О
с
ь

с
и
н
у
с
о
в
ПОШАГОВОЕ
ПОСТРОЕНИЕ
О
с
ь
т
а
н
г
Ось косинусов е
н
с
о
в
УСКОРЕННЫЙ
ПОКАЗ
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
I четверть
Ось синусов
II четверть
p
2
1
p
+
0
-1
1
r=1
0
2p
Ось косинусов
-1
III четверть
3p
2
VI четверть
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
p
7p — 3
2
2
p
2
5p
2
9p
2
+
— 3p — p
0
p
p
3
5p
2p
p
— 2p — 4
4p
Ось косинусов
6p
5p
2
—
p
2
3p
2
7p
2
11p
2
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
p
2
Ось синусов
p
3
1
p
4
+
p
6
2
0
p
1
2
3p
2
2p
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
p
2
Ось синусов
p
3
3p
4
1
+
p
4 p
6
2
0
p
1
2p
2
5p
4
7p
4
3p
2
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
5p
6
p
2
p
3
1
+
p
4
p
6
2
0
p
1
2
7p
6
2p
11p
6
3p
2
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
p
2
Ось синусов
p
3
2p
3
1
+
p
4
p
6
2
0
p
1
2p
2
4p
3
3p
2
5p
3
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
p
2
Ось синусов
3p
4
p
3
2p
3
5p
6
p
4
1
1
2
3
2
2
2
+
p
6
2
0
p
1
2
2
2
3
2
2p
11p
6
7p
6
5p
4
4p
3
3p
2
5p
3
7p
4
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
p
2
Ось синусов
3p
4
p
3
2p
3
p
4
3
2
2
5p
6
2
1
+
p
6
2
0
p
—
3
2
—
2
2
—
1
1
2
2
—
7p
6
—
5p
4
4p
3
2
2
3
2
1
11p
2
2
2
—
2p
6
3
2
3p
2
5p
3
7p
4
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
3p
sin
=
4
2
3p
4
3p
cos
4
=-
p
2
Ось синусов
2
2p
3
p
3
p
4
3
2
2
5p
2
6
2
2
1
+
p
6
2
0
p
—
3
2
—
2
2
—
1
1
2
2
—
7p
6
—
5p
4
4p
3
2
2
3
2
1
11p
6
2
2
2
—
2p
3
2
3p
2
5p
3
7p
4
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
5p
cos
3
1
=
2
5p
3
sin
=3
2
p
2
Ось синусов
3p
4
p
3
2p
3
p
4
3
5p
6
p
6
2
2
+
2
1
2
0
p
—
3
2
—
2
2
—
1
1
2
2
—
7p
6
—
5p
4
4p
3
2
2
3
2
1
11p
2
2
2
—
2p
6
3
2
3p
2
5p
3
7p
4
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
p
sin
2
Ось синусов
=1
3p
4
p
cos
2
=0
1
2p
3
p
2
p
3
p
4
3
2
2
5p
6
2
1
+
p
6
2
0
p
—
3
2
—
2
2
—
1
2
—
7p
6
—
5p
4
4p
3
1
0
2
2
2
3
2
1
11p
6
2
2
2
—
2p
3
2
3p
2
5p
3
7p
4
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
4p
3
5p
4 3p
4
3p
2
2p
3
5p
3
p
4
2
2
1
6
-p
6
3p
4
— 2p
0
p
—
11p
6
p
2
2
5p
7p
4
p
3
3
5p
6
7p
6
p
2
—
3
2
—
2
2
—
1
1
2
2
—
7p
6
—
5p
4
2p
3
4p
3
2
2
3
2
11p
6
2
2
—
2p
1
2
3
2
p
3p 2
2
5p
3
7p
4
—
p
3
Ось косинусов
—
p
4
—
p
6
—
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
5p
4 3p
4
3
5p
3
p
1
6
3
0
2
—
6
3p
4
11p
6
p
2
p
2
2
—
1
1
2
2
—
7p
6
—
5p
4
2p
3
4p
3
2
2
3
2
1
—
3p
2
—
— 2p Ось косинусов
2p
11p
6
2
2
2
5p
3
cos( )=6
2
4
2
2
5p
7p
4
p
3
3
2
—
—
3p p
2 2
5p
6
7p
6
-p
4p
3
2p
5p
1
sin( )=6
2
3
7p
4
2
p
2
5p
3
—
p
3
—
p
4
p
6
—
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
-1
— 3
—
Ось тангенсов
p
2
2p
3
3p
4
Ось
котангенсов
3
3
3
3
p
3
5p
6
2
p
4
2
2
3
1
3
2
3
p
1
+
3
3
6
0
p
—
3
2
—
2
2
—
1
1
2
—
7p
6
—
5p
4
4p
3
2
2
2
2p
2
2
Ось косинусов
1
2
2
—
3p
2
3
3
2
p
2
—
p
3
—
p
4
—
p
—
3
3
6
-1
— 3
—
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
-1
— 3
—
Ось тангенсов
p
2
2p
3
3p
4
Ось
котангенсов
3
3
3
3
p
3
5p
6
2
p
4
2
2
3
1
3
2
3
p
1
+
3
3
6
0
p
—
3
2
—
2
2
—
1
1
2
2
—
7p
6
—
5p
4
4p
3
3
2
2p
2
2
Ось косинусов
1
2
2
—
3p
2
2
3
2
p
2
—
p
3
—
p
4
—
p
—
3
3
6
-1
— 3
—
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
-1
— 3
—
3p
Ось
котангенсов
Ось тангенсов
p
2
2p
3
3
3
p
3
p
4
2
2
p
1
2
6
p
—
3
2
—
2
2
—
1
1
2
—
7p
6
—
5p
4
4p
3
2
2
—
3p
2
2p
2
Ось косинусов
1
2
2
2
0
3
2
+
3
3
2
6
3
1
3
4
5p
7p
6
3
3
3
—
3
2
p
2
—
p
3
—
p
4
p
—
3
3
6
-1
— 3
11p
6
—
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
-1
— 3
—
Ось тангенсов
p
2
2p
3
113pp
44
Ось
котангенсов
3
3
3
3
2
2
5p
6
2
3
1
p5p
-3 p
3
4
3
2
3
p
1
+
3
3
6
0
p
—
3
2
—
2
—
1
1
2
—
4p
3
2
2
—
7p
6
p
5p
3
— 4
4
2
2p
2
2
Ось косинусов
1
2
2
—
3p
2
2
3
3
2
p
2
—
p
3
p
7p
44
—
p
—
3
3
6
-1
— 3
—
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
p
2
Ось синусов
3p
4
2p
3
p
3
p
4
3
2
2
5p
6
2
1
+
p
6
2
0
p
—
3
2
—
2
2
—
1
1
2
2
—
7p
6
—
5p
4
4p
3
2
2
3
2
1
11p
6
2
2
2
—
2p
3
2
3p
2
5p
3
7p
4
Ось косинусов
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось синусов
-1
— 3
—
Ось тангенсов
p
2
2p
3
3p
4
Ось
котангенсов
3
3
3
3
p
3
5p
6
2
p
4
2
2
3
1
3
2
3
p
1
+
3
3
6
0
p
—
3
2
—
2
2
—
1
1
2
—
7p
6
—
5p
4
4p
3
2
2
2
2p
2
2
Ось косинусов
1
2
2
—
3p
2
3
3
2
p
2
—
p
3
—
p
4
—
p
—
3
3
6
-1
— 3
—
Шаблон круга

English     Русский Правила

Теорема синусов.

Теорема косинусов

При решении прямоугольных треугольников используются только основные тригонометрические функции. Для решения же косоугольных треугольников потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим.

В дальнейшем мы будем пользоваться следующими обозначениями: a, b и c — стороны треугольника; А, В и С — противолежащие им углы; S — площадь; 2р — периметр; R — радиус описанного круга; r — радиус вписанного круга; h_а, l_а и m_а — высота, биссектриса и медиана, соответствующие стороне а.

Теорема синусов

Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов:

$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} $$

Доказательство. Опишем круг около данного треугольника ABC. Пусть R — радиус этого круга. Возьмём одну из вершин треугольника, например А; через одну из других вершин, например через В, проведём диаметр ВА’ описанного круга. Вспомогательный треугольник А’ВС прямоугольный, так как вписанный угол А’СВ опирается на диаметр. Из вспомогательного треугольника найдём:

а = 2Rsin A’.

Если угол А острый, то А = А’, так как вписанные углы A и A’ опираются на одну и ту же дугу.
Если угол А тупой, то угол А’ острый, измеряющийся половиной дуги ВАС:

$$ A’ = \frac{1}{2}\smile BAC = \frac{1}{2}(2\pi-\smile BA’C) = \pi — \frac{\smile BA’C}{2} = \pi-A $$

Итак, или A= А’, или A’ =\(\pi\) — A, в обоих случаях sin A’ = sin A, а потому

а = 2R sin A. (1)

Если угол Aпрямой, то а = 2R, sin A= 1 и равенство (1) также справедливо.

Аналогичные равенства найдём и для прочих углов В и С. Итак,

а =2R sin A; b =2R sin В; с = 2R sin С, откуда

$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R $$

Следствие.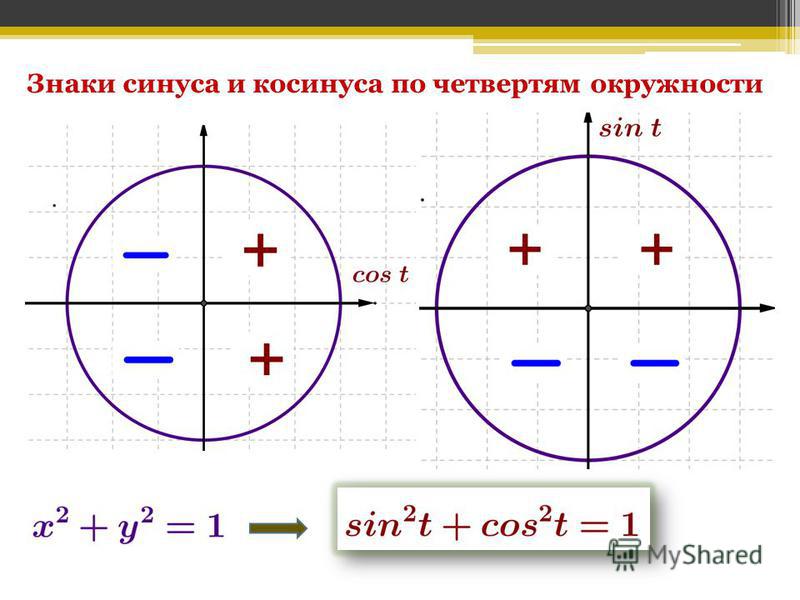 Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.

Теорема косинусов

Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:

а² =b² + с² — 2bccosА

b² =c² + a² — 2cacosB

c² =a² + b² — 2abcosC

Доказательство. Докажем первое равенство.

Случай 1. Угол A острый.

Пусть ВН — высота, опущенная из вершины В ; из геометрии известно, что
а² = b² + с²—2b · АН. (1)
Из прямоугольного треугольника АВН найдём
АН = с cos А; подставив в формулу (1), получим доказываемое равенство.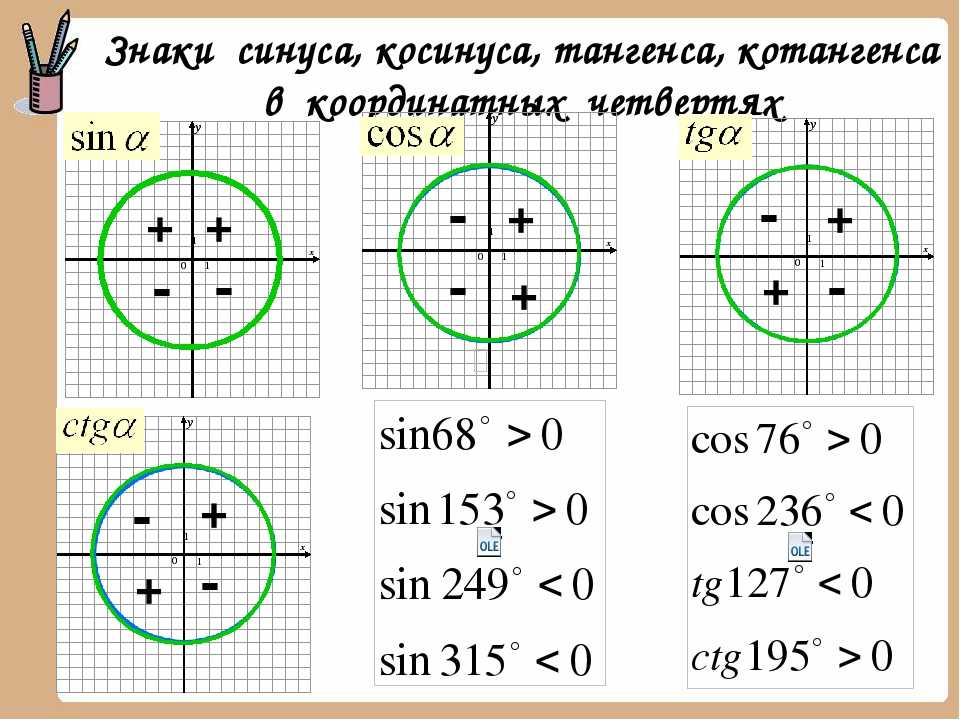

Случай 2. Угол A тупой.
В этом случае а² = b² + с² +2b · АН. (2)

Из треугольника АВН найдём:
АН = с cos∠BAH = с cos(\(\pi\) — A) = — с cosA.

Подставив в формулу (2), получим доказываемое равенство.

Случай 3. Угол А прямой.

В этом случае (по теореме Пифагора):

а² = b² + с²= b² + с² — 2bccosА

(так как cos А = 0).

Итак, во всех случаях

а² = b² + с² — 2bccosА

исчисление — Связь между синусом и косинусом в окружности

спросил

7 лет, 6 месяцев назад

Изменено 7 лет, 6 месяцев назад

Просмотрено 2к раз

$\begingroup$

Мой учитель сегодня задал нам этот вопрос: Какова связь между синусом и косинусом в окружности? На это ни у кого не было ответа. Может ли кто-нибудь просветить меня здесь?

• исчисление
• тригонометрия

$\endgroup$

4

$\begingroup$

Вот кое-что интересное: на этом графике показаны те отношения, которые вам нужны. Я думаю, что это самое простое, что вы можете получить с этим вопросом, если это то, что вы подразумеваете под отношениями между синусом, косинусом и окружностью.

Обратите внимание, как коричневая палочка движется по кругу, а золотые слитки, соответствующие синусоидальным и косинусным движениям, двигаются вверх и вниз и из стороны в сторону, как волнообразное образование! 92 = 1.$ пусть $t$ будет длиной дуги со знаком, отсчитываемой от точки $(1,0)$, при условии, что движение против часовой стрелки считается положительным.

теперь мы можем видеть $ x = \cos t, y = \sin t.$, то есть $cos t$ является проекцией $(x,y)$ на ось $x$. то же самое касается $\sin t.$

$\endgroup$

$\begingroup$

Связь между $\sin$ и $\cos$ прекрасно представлена ​​на следующем рисунке:

Другие алгебраические отношения являются просто представлением некоторых геометрических свойств. 9\circ$.

Косинус одного угла равен синусу дополнительного угла. Два острых угла в треугольнике дополняют друг друга, поэтому косинус любого из этих углов равен синусу другого.

Значение косинуса в любой точке пропорционально скорости изменения синуса в этой точке. Если, но только если используется радианная мера, константа пропорциональности равна $1$. Точно так же скорость изменения косинуса пропорциональна синусу, и если используются радианы, коэффициент пропорциональности равен $-1$.

Сумма квадратов синуса и косинуса всегда равна $1$.

Функции синуса и косинуса находятся под прямым углом друг к другу в скалярном произведении, относящемся к ряду Фурье.

Несомненно, можно сказать гораздо больше, чем вышеизложенное.

Возможно ли, что учитель задал вопрос в определенном контексте, который прояснил смысл таким образом, чтобы исключить все, кроме одного из вышеперечисленных пунктов?

$\endgroup$

Синусы, косинусы и тангенсы общих углов

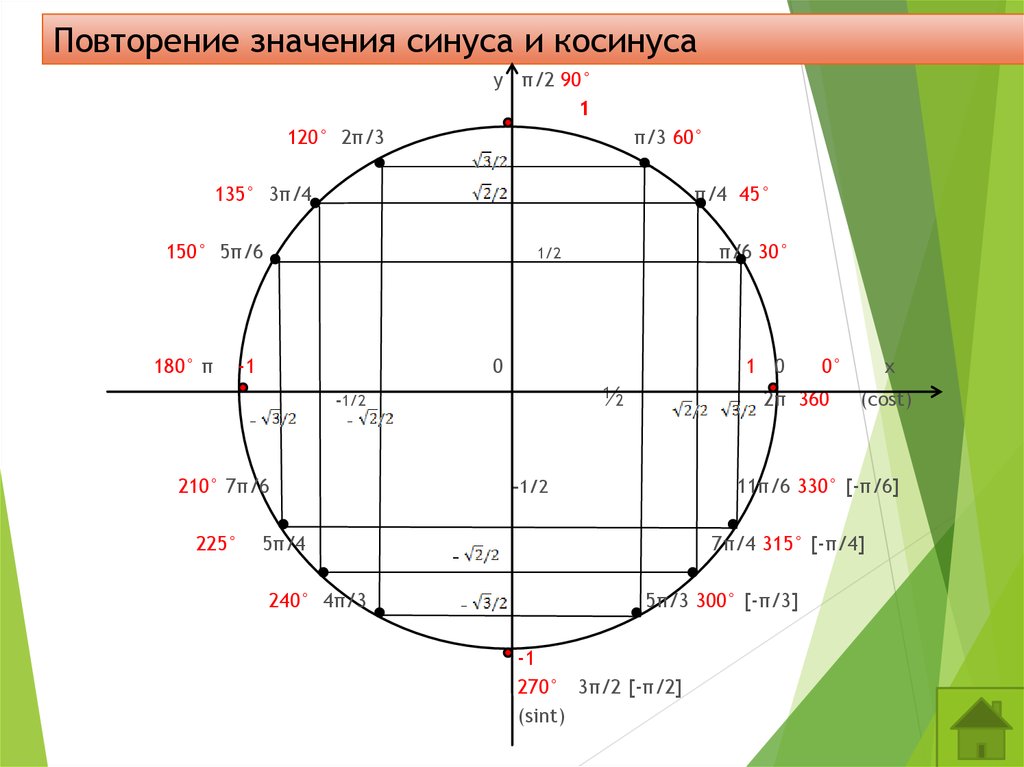
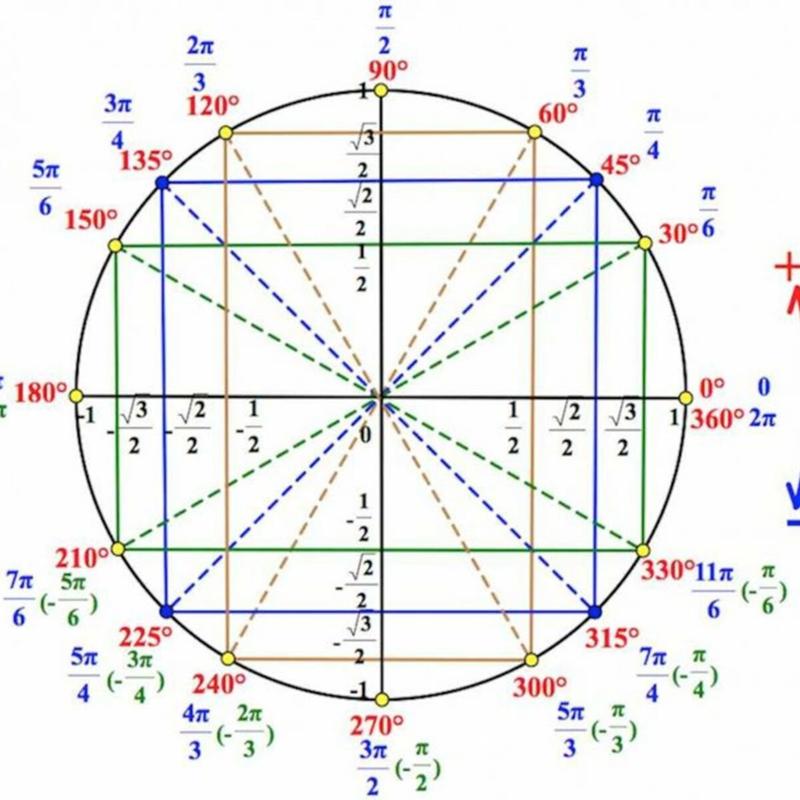
Введение

На этой странице перечислены значения синусов, косинусы и касательные общих (заслуживающих внимания) углов. На следующем рисунке показаны общие углы на единичной окружности (только для косинусов и синусов):

Таблица синусов, косинусов и тангентов

В следующей таблице показаны синусы и косинусы общих углов в радианах и градусах

Радиан	градусов	Косинус	Синус	Касательная
0	0	1	0	0
\( \frac{ \pi }{6} \)	30	\( \ гидроразрыва {\ sqrt {3}} {2} \)	\( \frac{1}{2} \)	\( \frac{ \sqrt{3}}{3} \)
\( \frac{ \pi }{4} \)	45	\( \ гидроразрыва {\ sqrt {2}} {2} \)	\( \ гидроразрыва {\ sqrt {2}} {2} \)	1
\( \frac{ \pi }{3} \)	60	\( \frac{1}{2} \)	\( \ гидроразрыва {\ sqrt {3}} {2} \)	\( \sqrt{3} \)
\( \frac{ \pi }{2} \)	90	0	1	—
\( \frac{ 2\pi }{3} \)	120	\( -\frac{1}{2} \)	\( \ гидроразрыва {\ sqrt {3}} {2} \)	\(-\sqrt{3} \)
\( \frac{ 3\pi }{4} \)	135	\( -\frac{\sqrt{2}}{2} \)	\( \ гидроразрыва {\ sqrt {2}} {2} \)	-1
\( \frac{ 5\pi }{6} \)	150	\( -\frac{\sqrt{3}}{2} \)	\( \frac{1}{2} \)	\( -\frac{ \sqrt{3}}{3} \)
\(\пи\)	180	-1	0	0
\( \frac{ 7\pi }{6} \)	210	\( -\frac{\sqrt{3}}{2} \)	\( -\frac{1}{2} \)	\( \frac{ \sqrt{3}}{3} \)
\( \frac{ 5\pi }{4} \)	225	\( -\frac{\sqrt{2}}{2} \)	\( -\frac{\sqrt{2}}{2} \)	1
\( \frac{ 4\pi }{3} \)	240	\( -\frac{1}{2} \)	\( -\frac{\sqrt{3}}{2} \)	\( \sqrt{3} \)
\( \frac{ 3\pi }{2} \)	270	0	-1	—
\( \frac{ 5\pi }{3} \)	300	\( \frac{1}{2} \)	\( -\frac{\sqrt{3}}{2} \)	\(-\sqrt{3} \)
\( \frac{ 7\pi }{4} \)	315 ​​	\( \ гидроразрыва {\ sqrt {2}} {2} \)	\( -\frac{\sqrt{2}}{2} \)	-1
\( \frac{ 11\pi }{6} \)	330	\( \ гидроразрыва {\ sqrt {3}} {2} \)	\( -\frac{1}{2} \)	\( -\frac{ \sqrt{3}}{3} \)
\( 2\пи \)	360	1	0	0

См.

также

• Расчет преобразования между двумя наборами точек
• Шлицы Catmull-Rom
• Проверить, является ли число простым онлайн
• Проверить, принадлежит ли точка отрезку
• Перекрестное произведение
• Общие правила деривативов
• Общие производные
• Скалярный продукт
• Как вычислить точки пересечения двух окружностей
• Как проверить, компланарны ли четыре точки?
• Общие интегралы (примитивные функции)
• Аппроксимация методом наименьших квадратов полиномом второй степени
• Аппроксимация кругов методом наименьших квадратов
• Фитинг сферы методом наименьших квадратов
• Математика PCA
• Онлайн-решатель квадратных уравнений
• Онлайн-упроститель квадратного корня
• Разложение по сингулярным числам (SVD) матрицы 2×2
• Отрезки касательных к окружностям
• Понимание ковариационных матриц
• Взвешенный PCA

---

Последнее обновление : 24.