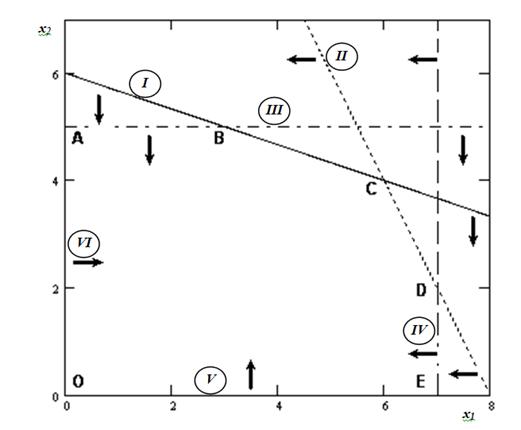
Вектор градиент целевой функции: Графический метод /qualihelpy

Вектор-градиент в некоторой точке определяется как вектор, компонентами которого являются частные производные первого порядка этой функции в точке

В задачах выпуклого программирования ограничения задают
 (*ответ*) выпуклое множество допустимых решений
 вогнутое множество допустимых решений
 несвязное множество допустимых решений
 дискретное множество допустимых решений
В задачах выпуклого программирования целевая функция является
 (*ответ*) выпуклой (при минимизации) или вогнутой (при максимизации)
 выпуклой (при максимизации) или вогнутой (при минимизации)
 квадратичной
 положительно определенной
В задачах квадратичного программирования целевая функция
 (*ответ*) квадратичная, а ограничения – линейны
 линейная, а ограничения – квадратичны
 И ограничения – линейны
 и ограничения – квадратичны
В задачах стохастического программирования
 (*ответ*) в целевой функции или в ограничениях содержатся случайные величины, которые подчиняются законам теории вероятностей
 только в целевой функции содержатся случайные величины, которые подчиняются законам теории вероятностей
 только в ограничениях содержатся случайные величины, которые подчиняются законам теории вероятностей
 в целевой функции и в ограничениях содержатся только целочисленные параметры
В задачах целочисленного программирования неизвестные параметры могут принимать
 (*ответ*) только целочисленные значения
 только положительные значения
 только отрицательные значения
 любые значения
В методах второго порядка при поиске экстремума целевой функции используются
 (*ответ*) значения ее вторых производных
 только значения ее первых производных
 только значения функции
 только значения функции и ее первых производных
В методах первого порядка при поиске экстремума целевой функции используются
 (*ответ*) значения ее первых производных
 значения ее вторых производных
 только значения функции
 значения функции и ее вторых производных
В методах прямого поиска при поиске экстремума целевой функции используются
 (*ответ*) только ее значения
 только значения ее производной
 только значения ее 2-й производной
 значения целевой функции и значения ее производной
В методе покоординатного спуска поочередно изменяют все переменные оптимизации так, чтобы по каждой из переменных достигалось
 (*ответ*) наименьшее (наибольшее) значение
 нулевое значение функции
 целое положительное значение функции
 целое отрицательное значение функции
В нелинейном программировании выделяют два основных типа задач
 (*ответ*) задачи выпуклого и задачи невыпуклого программирования
 детерминированные и недерминированные
 однопараметрические и многопараметрические
 условной и безусловной оптимизации
В постановках задач нелинейного программирования предполагается, что переменные оптимизации
 (*ответ*) непрерывны
 разрывны
 могут принимать только целочисленные значения
 могут принимать только положительные значения
В рамках нелинейного программирования задачу оптимизации называют классической, если предполагается известной аналитическая зависимость функции
 (*ответ*) от аргументов, а также существование обычных или частных производных до второго порядка включительно
 от аргументов, а также существование обычных или частных производных до первого порядка включительно
 от аргументов, а также существование обычных или частных производных до третьего порядка включительно
 от аргументов
Вектор-градиент в некоторой точке определяется как вектор, компонентами которого являются
 (*ответ*) частные производные первого порядка этой функции в точке
 частные производные второго порядка этой функции в точке
 частные производные третьего порядка этой функции в точке
 прямые производные этой функции в точке

Графическое решение задач линейного программирования

Похожие презентации:

Линейное программирование

Графическое решение задачи линейного программирования с двумя переменными

Методы оптимальных решений в линейном программировании

«Методы оптимальных решений» № 1. Задачи линейного программирования и графический метод решения

Графическое решение задач линейного программирования

Задачи линейного программирования

Геометрический метод решения задачи линейного программирования

Примеры задач линейного программирования

Методы и модели линейного программирования. Лекция 4

Задачи линейного программирования

1. Графическое решение задач линейного программирования

Графическое
решение задач
линейного
программирова
ния
Математическая модель
задачи.
f(X) = 2x -5x →max Целевая функция:
1
2
Ограничения:
3×1 + 2×2 ≥ 6
(1)
X1 ≤ 4
(2)
X2 ≤ 4
(3)
X1 + x2 ≤ 6
(4)
X1 ≥ 0 , x 2 ≥ 0
(5-6)
I.
Построение области допустимых планов
1) Построение границы 1:
3×1 + 2×2 = 6 – прямая линия
Решение неравенства 1:
x1
0
2
Подставляем координаты точки О(0;0) в неравенство: 3*0 +
x2 О не
3 принадлежит
0
2*0 ≥ 6-неверно, следовательно точка
области допустимых планов.
х2
3
0
2
х1
(1)
2) Построение границы 2: х1 = 4 –прямая линия
Решение неравенства 2: 0 ≤ 4 – верно
3) Построение границы 3: х2 = 4 – прямая линия
Решение неравенства 3: 0 ≤ 4 – верно
4)Построение границы 4: х1 + x2 = 6 – прямая линия
x1
0
6
x2
6
0
Решение неравенства 4: 0 + 0 ≤ 6 — верно
х2
(2)
6
(3)
4
A
B
3
F
C
4
Многоугольник ABCDEF является
областью допустимых планов.
Координаты любой точки
многоугольника, в том числе его
границ являются допустимым планом
задачи.
0
E
2
6
х1
D
(4)
Например точки (2;2), (3;2), (3;1)
Значение целевой функции
F(X)=2×1-5×2 в этих точках равны
соответственно -6, -4, 1.
(1)
II. Оптимизация целевой функции:
1) Построение линии уровня
целевой функции:
Линия, на которой функция принимает одно
и то же значение. (линия уровня)
f (X) = 0 => 2×1-5×2 = 0
x1
0
5
x2
0
2
II. Оптимизация целевой
функции:
2) Построение градиента:
g = (2; -5) – (коэффициенты при Х
в целевой функции)
Градиент — вектор, направление
которого показывает максимальную
скорость роста этой функции.
х2
(2)
6
(3)
4
A
B
3
F
C
4
0
E
2
6
х1
D
(4)
-5
g
(1)
х2
(2)
6
(3)
4
A
B
3
F
C
4
0
E
2
6
х1
D
(4)
-5
g
(1)
Передвигаем линию уровня в направлении
градиента (если задача на max), при этом
значение целевой функции возрастает.
Если задача на min, то — в направлении,
противоположном градиенту.
Последняя точка контакта линии уровня с
областью допустимых планов определяет
оптимальный план (Х*), на котором
целевая функция принимает max (или
min) значение.
х2
(2)
6
(3)
4
A
B
3
F
C
4
0
E
2
6
х1
D Х*
(4)
-5
g
(1)
Оптимальный план Х* совпадает с
точкой D.
Чтобы вычислить значения плана необходимо
вычислить координаты точки пересечения
соответствующих границ, где он находиться.
Х* (2) ∩ (5)
Х1 = 4
Х2 = 0
Координаты являются решением системы
уравнений, прямых в результате пересечения
которых получается точка Х*
Оптимальный план Х* = (4; 0)
Максимальное значение
целевой функции:
max f(X) = f(X*) = 2*4 – 5*0 = 8
• Непустое множество планов основной задачи
линейного программирования образует выпуклый
многогранник. Каждая вершина этого многогранника
определяет опорный план. В одной из вершин
многогранника решений (т. е. для одного из опорных
планов) значение целевой функции является
максимальным (при условии, что функция
ограничена сверху на множестве планов). Если
максимальное значение функция принимает более
чем в одной вершине, то это же значение она
принимает в любой точке, являющейся выпуклой
линейной комбинацией данных вершин.

Таким образом, исходная задача линейного программирования
состоит в нахождении такой точки многоугольника решений, в
которой целевая функция F принимает максимальное значение.
Эта точка существует тогда, когда многоугольник решений не
пуст и на нем целевая функция ограничена сверху. При
указанных условиях в одной из вершин многоугольника
решений целевая функция принимает максимальное значение.
Для определения данной вершины построим линию уровня,
проходящую через многоугольник решений, и будем
передвигать ее в направлении вектора до тех пор, пока она не
пройдет через ее последнюю общую точку с многоугольником
решений. Координаты указанной точки и определяют
оптимальный план данной задачи.
Стороны этого многоугольника лежат на прямых, уравнения
которых получаются из исходной системы ограничений заменой
знаков неравенств на знаки точных равенств.
При нахождении решения могут встретиться
случаи, изображенные на рис. 1 — 4.
Рис. 1 характеризует такой случай,
когда целевая функция принимает
максимальное значение в
единственной точке А (вершине
многоугольника).
Из рис. 2 видно, что максимальное
значение целевая функция принимает
в любой точке отрезка АВ.
•Если максимальное значение функция принимает
более чем в одной вершине, то это же значение она
принимает в любой точке, отрезка.
На рис. 3 изображен случай, когда целевая функция не
ограничена сверху на множестве допустимых решений.
На рис. 4 – случай, когда система ограничений задачи
несовместна.

19. Этапы графического решения задачи линейного программирования

1. Строят прямые, уравнения которых получаются в результате замены в
ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Находят многоугольник решений.
4. Строят вектор-градиент целевой функции .
5. Строят линию уровня целевой функции , проходящую через
многоугольник решений.
6. Передвигают прямую в направлении вектора , в результате чего-либо
находят точку (точки), в которой целевая функция принимает
максимальное значение, либо устанавливают неограниченность сверху
функции на множестве планов.
7. Определяют координаты точки максимума функции и вычисляют
значение целевой функции в этой точке.

20. Пример.

• Для производства двух видов изделий А и В предприятие использует три
вида сырья. Нормы расхода сырья каждого вида на изготовление единицы
продукции данного вида приведены в табл. В ней же указаны прибыль от
реализации одного изделия каждого вида и общее количество сырья
данного вида, которое может быть использовано предприятием.
• Определить оптимальный план выпуска продукции, при котором прибыль
будет максимальной.
Вид сырья
1
2
3
Прибыль от
реализации одного
изделия(руб)
Нормы расхода сырья (кг) на
одно изделие
А
В
12
4
3
30
4
4
12
40
Общее
количество
сырья (кг)
300
120
252
Учитывая, что изделия А и В могут производиться в любых соотношениях
(сбыт обеспечен), требуется составить такой план их выпуска, при
котором прибыль предприятия от реализации всех изделий является
максимальной,
Математическая модель задачи: среди всех неотрицательных решений
данной системы линейных неравенств требуется найти такое, при котором
функция F принимает максимальное значение.
12х1+4х2=300
30х1+40х2=1080
4х1+4х2=120
3х1+12х2=252

23. Задача составления рациона.

При откорме каждое животное ежедневно должно получать не
менее 9 ед. питательного вещества S1, не менее 8 ед. вещества
S2 и не менее 12 ед. вещества S3. Для составления рациона
используют два вида корма. Содержание количества единиц
питательных веществ в 1 кг каждого вида корма и стоимость 1 кг
корма приведены в таблице
Необходимо составить дневной рацион нужной питательности,
причем затраты на него должны быть минимальными.
Питательные вещества
Количество единиц
питательных веществ
в 1 кг корма.
Корм 1
Корм 2
S1(белки)
3
1
S2(жиры)
1
2
S3(углеводы)
1
6

24. Решение

Для составления математической модели обозначим через х1 и
х2 соответственно количество килограммов корма 1 и 2 в
дневном рационе. Принимая во внимание значения,
приведенные в таблице и условие, что дневной рацион
удовлетворяет требуемой питательности только в случае, если
количество единиц питательных веществ не меньше
предусмотренного, получаем систему ограничений
3х1 + х2>= 9
х1 + 2х2 >= 8
х1 + 6х2 >= 12
х1>= 0, х2 >= 0.
• Цель данной задачи – добиться минимальных затрат на
дневной рацион, поэтому общую стоимость рациона можно
выразить в виде линейной функции
• Z = 4х1 + 6х2 (ед.)
• Требуется найти такие х1 и х2, при которых функция Z принимает
минимальное значение.

Построим многоугольник решений. Для этого в системе координат х 1Ох2 на
плоскости изобразим граничные прямые
3х1 + х2 = 9 (L1)
х1 + 2х2 = 8 (L2)
х1 + 6х2 = 12 (L3)
х1 = 0, х2 = 0.
• Взяв какую-нибудь точку, например, начало координат, установим, какую
полуплоскость определяет соответствующее неравенство.
• В результате получим неограниченную многоугольную область с угловыми
точками А, В, С, D.
• Для построения прямой 4х1 + 6х2 = 0 строим радиус-вектор N = (4;6) и через
точку O проводим прямую, перпендикулярную ему. Построенную прямую Z = 0
перемещаем параллельно самой себе в направлении вектора N. Из риc.
следует, она впервые коснется многогранника решений и станет опорной по
отношению к нему в угловой точке В. Если прямую перемещать дальше в
направлении вектора N, то значения линейной функции на многограннике
решений возрастут, значит, в точке В линейная функция Z принимает
минимальное значение.
• Точка В лежит на пересечении прямых L1 и L2. Для определения ее координат
решим систему уравнений
3×1 + х2 = 9
х1 + 2х2 = 8
• Имеем: х1 = 2; х2 = 3. Подставляя значения х1 и х2 в линейную функцию,
получаем Zmin = 4 2 + 6 3 = 26.
• Таким образом, для того, чтобы обеспечить минимум затрат (26 ед. в день),
необходимо дневной рацион составить из 2 кг корма 1 и 3 кг корма 2.

26. Решите графически задачи

Ответ: F(1;2)=5
• 1
• 6
2
7
3
4
8
5
9
10

English     Русский Правила

Поведение векторного поля градиента

. Градиентный спуск — мощный инструмент для… | by Driss Boutat

Градиент всегда был важным средством в теме оптимизации, потому что многие другие алгоритмы полагаются на него для измерения «силы», которая ведет к минимуму. Градиентный спуск — это мощный инструмент для запуска алгоритма оптимизации всего, особенно с развитием машинного обучения, мощных компьютеров и огромных баз данных.

В этом посте я покажу, в чем заключается идея поведения градиента. Я хотел бы вернуться к выводу необходимого условия для того, чтобы точка была минимумом или максимумом. Моя цель состоит в том, чтобы объяснить эту идею геометрически. В терминах математики рассмотрим функцию

Целевая функция

Для достижения этой цели я ограничусь двумя следующими задачами.

Неограниченная задача : право на перемещение во всех направлениях рабочего пространства.

Неограниченная задача

Ограниченная задача : разрешено движение только в определенных заданных направлениях

Ограниченная задача

В этом случае направления движения касаются ограничения.

Когда можно нарисовать график, он показывает форму функции, особенно максимальное и минимальное значения функции.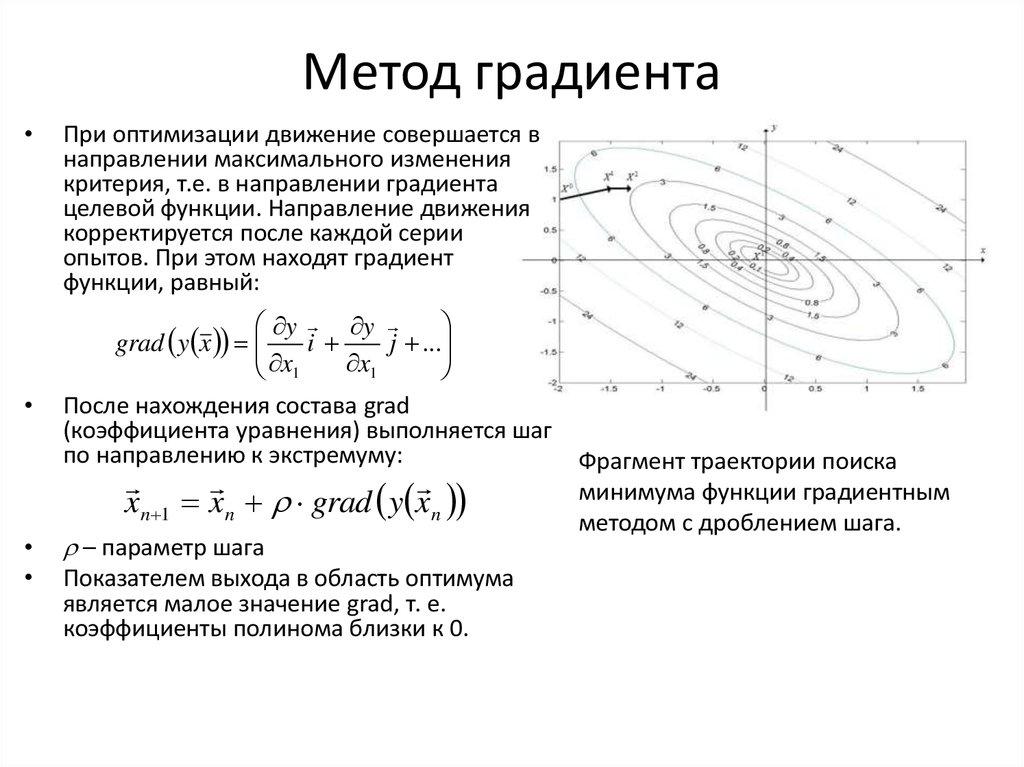 Но на практике целевые функции, с которыми мы имеем дело, включают несколько переменных, поэтому мы не можем их построить.

Рисунок 1: График целевой функции с двумя переменными.

Поле вектора градиента

Поле вектора градиента или, короче, градиент функции задается векторным полем, компоненты которого являются частными производными функции.

Градиент

Связывает вектор с каждой точкой функциональной области.

Поле вектора градиента исчезает в красной точке, а затем удаляется, но движется к синей точке, чтобы исчезнуть и там.

Думайте о целевой функции как о потенциальной энергии, а о точках в ее области — как о частицах, на которые действует сила, противоположная градиенту. Таким образом, эта сила, создаваемая этой потенциальной энергией, выглядит следующим образом:

Уравнение 1

Имея это в виду, точка равновесия — это точка, в которой градиент равен нулю. Если мы дадим ему небольшой толчок, и он вернется на свое место (устойчивую точку), то это минимум: он реализует локальное минимальное значение потенциальной энергии. С другой стороны, если он бежит под действием силы, противоположной градиенту, то это максимум (неустойчивая точка): он реализует локальное максимальное значение потенциальной энергии.

Как вы можете видеть на рисунке ниже, если точка находится в максимуме (максимальной потенциальной энергии) вверху, и если мы немного нажмем на нее, она убежит вниз. Однако, если он находится внизу в минимуме (минимальной потенциальной энергии) и мы подвергаем его небольшому давлению, то он снова опустится.

Рисунок 2

Кривые градиента и уровня принадлежат области определения целевой функции. Как видно из рисунка выше, градиент движется от минимума к максимуму (см. уравнение 1). Контуры кривых уровня замкнуты в окрестностях точек равновесия.

Говоря о градиенте функции, следует иметь в виду три вещи:

i) Кривая уровня: подмножество всего пространства, где целевая функция является постоянной:

Кривая уровня : подмножество Рисунок 3 : Кривые уровня на приведенном выше графике рис.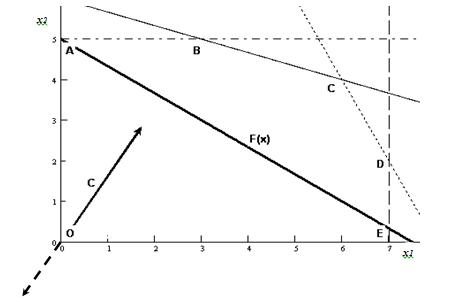 1. Они замкнуты в окрестности минимумов и максимумов.

ii) Ортогональность градиента к кривым уровня

гамма-кривая синего цвета.

Если мы движемся вдоль кривой уровня, мы не меняем значение уровня (потенциальная энергия остается постоянной), что означает, что градиент не оказывает никакого влияния как сила в касательном направлении к кривой уровня, поэтому это нормально к кривым уровня.

iii) Градиент направлен к самым высоким уровням.

Градиент движется от минимумов к максимумам: показаны самые высокие уровни. Даже максимальный уровень, который содержит только одну точку, является наибольшим уровнем на этом рисунке.

Понятие минимума является локальным, поэтому указанное выше свойство проверяется локально в малой окрестности точки.

Если рассматривать градиент в точке как силу, приложенную к этой точке (единственную силу). Следовательно, если вы планируете двигаться вдоль направления d в пространстве с помощью этой силы, сила, действующая на точку, равна (рисунок ниже)

Величина градиента, действующего на точку в направлении d

Если направление перпендикулярно градиенту, вы застрянете и не сможете двигаться вперед. На самом деле, согласно физике, сила, перпендикулярная направлению движения, не меняет скорости точки, к которой она приложена. Если эта величина отрицательна, то есть угол больше 90°, то направление d называется направлением спуска (оно направлено к нижним уровням) . Если угол равен 90°, точка неподвижна. Однако, если угол меньше 90°, направление d направлено в сторону более высоких уровней.

Минимум функции, снабженной ограничением, должен оставаться неподвижным где-то на ограничении под действием градиента функции. Следовательно, градиент напряжения должен вмешиваться, чтобы сбалансировать градиент критерия, который необходимо минимизировать.

x шляпа является стационарной точкой, потому что градиент ортогонален ограничению.

градиент целевой функции делится на ортогональную составляющую и касательную составляющую по напряжению.

Если вы используете градиент в качестве силы смещения для зависимости, оставаясь в зависимости, то единственный компонент, который выполняет работу, — это компонент градиента, касательный к зависимости. Как мы видим на рисунке, касательная часть удаляется от точки, где градиент ортогонален напряжению: т. е. эта точка представляет собой минимум целевой функции, ограниченный напряжением.

Таким образом, равнодействующая градиента целевой функции и величины градиента ограничения равна нулю в этой точке:

Результат двух градиентов

, где параметр лямбда выбирается таким образом, чтобы эти два градиента удовлетворяли приведенному выше уравнению. Этот параметр является так называемым множителем Лагранжа.

В литературе мы говорим о лагранжиане как о сумме целевой функции и лямбда, умноженной на функцию ограничений. Если мы рассмотрим их как две потенциальные энергии, то функция ограничения будет представлять собой потенциальную энергию, уравновешивающую целевую функцию.

Лагранжиан

Хорошо известное необходимое условие минимума приводит к

Первое уравнение является векторным уравнением и имеет несколько решений. Второй позволяет нам указать решение, которое принадлежит ограничению.

Эквивалентность приведенного выше уравнения

i) Это эквивалентно тому, что касательная составляющая градиента в точке равновесия равна нулю:

Касательная часть равна нулю.

ii) В равновесии x (минимум или максимум) градиент целевой функции ортогонален всем направлениям, которым разрешено движение по ограничению (на нашем рисунке у нас есть два противоположных направления: влево и вправо)

iii) Если нам разрешено двигаться во всех направлениях, ограничений нет, то точка является минимумом, если градиент равен нулю. В самом деле, в этой точке он должен быть ортогонален всем направлениям пространства, поэтому он должен быть нулевым вектором в этой точке, таким образом, приведенное выше уравнение принимает вид

В точке минимума без ограничений

В этом случае все пространство является пространством ограничений а касательная часть такая же, как и весь градиент.

Динамическая точка зрения . Далее мы увидим поведение -градиента как векторного поля, порождающего динамику: обозначим через точку x производную по времени от x(t):

В первом уравнении точка x обозначает производную по времени от x(t).

Давайте представим квадратичный случай

Метод наискорейшего спуска: алгоритм градиентного спуска

градиентный спуск

градиентный спуск — это широко используемый алгоритм оптимизации в машинном обучении (а также в других областях). Вообще говоря, градиентный спуск — это алгоритм, который минимизирует функции. Для заданной функции и начального входа значение к нему, градиентный спуск итеративно движется к входному значению, которое минимизирует функцию, т.е. оптимально алгоритм градиентного спуска завершится со значением, при котором рассматриваемая функция минимальна.

Алгоритм градиентного спуска интуитивно работает, всегда следуя самому крутому нисходящему «наклону», пока не «площадь уровня» — или достигнут минимум*. * К сожалению, полученный минимум может быть лишь одним из многих минимумов, т.е. гарантировать, что мы окажемся в глобальном минимуме, если будем жадно следовать по наикрутейшему спуску. Позже мы посмотрим в методы, которые могут быть использованы, чтобы смягчить это. Чтобы в полной мере оценить оптимизацию градиентного спуска, нам нужно погрузиться в кровавые математические детали градиента. Далее понятия вводятся в их общей, многомерной форме, но проиллюстрировано в 2-х и 3-х измерениях, что, как мы надеемся, дает лучшее представление о том, что происходит. 9{n}\), обозначаемый \(\nabla f(x)\), это:

$$\begin{уравнение} \label{eq:gradient_definition} \набла f(x) = \begin{bmatrix} \ гидроразрыв {\ парциальное е (х)} {\ парциальное х_1} \\ \vdots\\ \ гидроразрыв {\ парциальное е (х)} {\ парциальное х_п} \end{bmatrix} \end{уравнение}$$

т.е. градиент является \(n\)-мерным вектор, где \(i\)-й элемент является частной производной† от \(f(x)\) относительно \(x_i\), † A частная производная функции нескольких переменных является его производной по одной из этих переменных, а остальные остаются постоянными.

где \(x = (x_1, \ldots, x_n).\) Кроме того, \(f\) должен быть дифференцируемым, чтобы частные производные существовали.

Интуитивная интерпретация вектора градиента в определенной точке \(x\) состоит в том, что он указывает на направление наибольшего увеличения функции \(f\), так как каждый элемент градиента говорит вам, насколько быстро \(f(x)\) меняется по отношению к стандартная основа. Тогда можно задаться вопросом, может ли \(f\) меняться быстрее по отношению к в каком-то другом направлении, но действительно можно показать, что вектор градиента \(\nabla f(x)\) указывает направление наибольшего подъема‡. ‡ Доказательство можно найти здесь. Конечно, это также означает, что противоположное направление, \(−\nabla f(x)\), является направление наибольшего спуска.

Таким образом, градиент — это вектор, элементами которого являются наклон функции вдоль каждой из координатных осей, то есть это многомерное обобщение обычной производной одномерной функции действительной переменной. {2}\): 9{2} — 4xy \end{уравнение}$$

Где частные производные по \(x\) и \(y\) равны

$$\begin{уравнение} \label{eq:example_function_derivative_x} \frac{\partial f(x,y)}{\partial x} = 12x — 4y \notag \end{уравнение}$$

и

$$\begin{уравнение} \label{eq:example_function_derivative_y} \frac{\partial f(x,y)}{\partial y} = 8y — 4x \notag \end{уравнение}$$

Что согласно \eqref{eq:gradient_definition} дает нам вектор градиента

$$\begin{уравнение} \label{eq:example_function_gradient} \набла f(x,y) = \begin{bmatrix} 12х — 4у\ 8 лет — 4 раза \end{bmatrix} \end{уравнение}$$

На рис. 1 ниже показан график нашего примера функции, \eqref{eq:example_function}, построенный вместе с полем вектора градиента, заданным \eqref{eq:example_function_gradient}.

Рисунок 1: Пример функции и ее векторное поле градиента

Длина и направление векторов градиента соответствуют наклону функции в исходной точке каждого вектора. Можно видеть, что векторы затухают вокруг «дна» графика поверхности, достигая кульминации в нулевой градиент в (глобальном) минимуме, расположенном в точке \((x, y) = (0, 0)\).

При проецировании на плоскость \((x, y)\) вы также видите контуры функции, где контурные линии изолинии постоянного значения функции (т. е. все точки на данной линии контура имеют одинаковое значение функции). контуры функций можно сравнить с контурными линиями, известными из картографии — на карте эти линии соединяют точки равном возвышении (высоте) над заданным уровнем. Это означает, что если вы идете по контурной линии, наклон будет равен нулю. (вы будете следовать по склону долины), и если вы пойдете перпендикулярно контурным линиям на карте, склон может быть довольно крутым (поскольку вы направляетесь либо к дну долины, либо к вершине). И чем ближе контурные линии вместе, тем круче склон. Опять же, эта аналогия очень хорошо согласуется с нашим графиком функции, где длина градиента векторы увеличиваются по мере того, как контуры функций сближаются из-за более крутого наклона. Также направление г. векторы градиента ортогональны контурам функции, что указывает на то, что мы поднимаемся по склону.

Алгоритм градиентного спуска

Из приведенного выше обсуждения должно быть ясно, что, начиная с произвольного места, можно найти (потенциально локальный) минимум для дифференцируемой функции путем спуска в направлении, противоположном градиенту, то есть в направлении, заданном \(−\nabla f(x)\). Помимо знания того, в каком направлении искать дальше, нам также нужна размер шага, определяющий, как далеко мы продвинемся в этом конкретном направлении. Этот размер шага необходимо выбирать тщательно — если это слишком велико, мы могли бы на самом деле «отскочить» от нашего минимума, как мы увидим в примере ниже. Если, наоборот, размер нашего шага слишком мал, мы можем спускаться мучительно медленно. 9{(к)})) \end{уравнение}$$

Пока что предположим, что мы можем найти подходящий размер шага (не обязательно оптимальный, т.к. это может быть дорого в вычислительном отношении). Ниже мы рассмотрим несколько примеров, чтобы увидеть Эффект изменения размера шага.

Алгоритм

Когда функция минимальна, ее градиент исчезнет, ​​т.е. если мы будем продолжать повторять рекурсивное правило \eqref{eq:gradient_descent_recursive_rule}, пока градиент не станет достаточно малым, мы будем знать, что мы близки к минимуму.

Формально определяем градиентный спуск алгоритм, описанный ниже, где формализовано «достаточно малое» из предыдущего абзаца как желаемая точность \(\epsilon >

0.\) Как упоминалось выше, мы предполагаем, что можем чтобы найти допустимый размер шага \(t_k\).

Размер градиента задается векторная норма \(\lVert \nabla f(x) \rVert\) — пока достаточно подумать о норме как евклидова длина вектора градиента. 9{2} — 4xy\)). Мы начнем с \((x, y) = (-20, 0)\), вычислим градиент, указанный \eqref{eq:example_function_gradient}, и примените алгоритм градиентного спуска с фиксированным размером шага \(0,02\). Результаты первых нескольких итераций алгоритма приведены в таблице ниже.

\(к\)	\(\frac{\partial f(x,y)}{\partial x}\)	\(\frac{\partial f(x,y)}{\partial y}\)	\(х\)	\(у\)	\(е(х,у)\)
0	н/д	н/д	-20	0	2400
1	-240 \(=12\cdot(-20)-4\cdot0\)	80 \(=8\cdot0-4\cdot(-20)\)	-15,2 \(=-20-0,02\cdot(-240)\)	-1,6 \(=0-0,02\cdot80\)	1299,2
2	-176 \(=12\cdot(-15. 2)-4\cdot(-1.6)\)	48 \(=8\cdot(-1.6)-4\cdot(-15.2)\)	-11,68 \(=-15,2-0,02\cdot(-176)\)	-2,56 \(=-1,6-0,02\cdot48\)	725.146
3	-129,92	26,24	-9.0816	-3,0848	420.857
4	-96,64	11.648	-7.1488	-3.31776	255,79
5	-72,51456	2.05312	-5.69851	-3.35882	163.404

Цифры из таблицы наглядно проиллюстрированы на рис. 2, где красные точки в плоскости x, y соответствуют значениям x, y, рассчитанным для алгоритма градиентного спуска. выше, а красные «шарики» катятся по поверхности к минимуму функции представляют значения функции \(f\) для этих входных данных.

Рисунок 2: Пример градиентного спуска

Если мы продолжим применять алгоритм градиентного спуска к нашей примерной функции, в результате x,y-пары будут тяготеть к \((0,0)\), где расположен минимум функции. Это должно быть довольно очевидно из рисунка выше, но может быть лучше проиллюстрировано рис. 3, который избавляется от поверхности функции и фокусируется только на ее контурной карте. Функция и размер шага градиентного спуска одинаковы для обеих фигур.

Размер шага имеет значение

Как упоминалось выше, не всегда возможно применить оптимальный размер шага, так как это может быть дорогостоящим в вычислительном отношении. вычислить его. Но мы должны быть осторожны при выборе размера шага — если он будет слишком маленьким, наш прогресс может останавливаться, когда градиент сужается на плато, в то время как слишком большие размеры шага могут отбросить нас прямо мимо тот минимум, который мы ищем.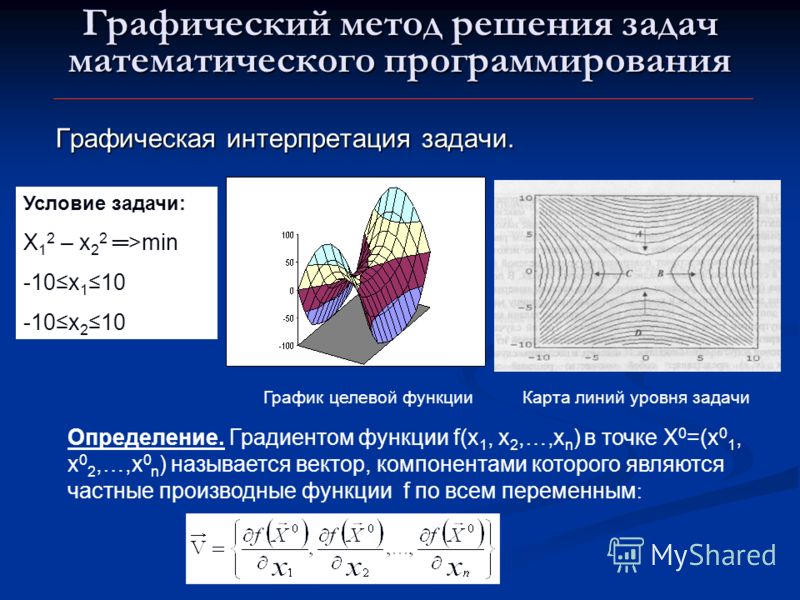 Это показано на рисунках ниже, на которых показана контурная карта для нашего пример функции \eqref{eq:example_function} вместе с путем, пройденным градиентным спуском с различными размерами шага.

Первый пример иллюстрирует градиентный спуск с небольшим размером шага. Этот спуск следует градиенту нашей тестовой поверхности очень близко, но также движется очень медленно, когда мы приближаемся к минимуму (если бы мы разрешено только повторять наш алгоритм спуска для заданного числа шагов, можно легко представить себе алгоритм заканчивая до того, как приблизиться к фактическому минимуму).

Рисунок 3: Градиентный спуск с небольшим шагом

В следующем примере показан путь, пройденный градиентным спуском с использованием размера шага, в 5 раз превышающего размер шага размер шага, использованный выше. Как мы видим, это приводит к гораздо более быстрому, но и более неустойчивому спуску. Все еще, поскольку спуск «захватывается» минимумом функции, шаги становятся меньше по мере того, как градиент стремится к \(0\) вокруг минимума.

Рисунок 4: Градиентный спуск с «эффективным» размером шага

Последний пример иллюстрирует градиентный спуск с использованием шага на 50% больше, чем в предыдущем примере. Неустойчивое поведение полностью вышло из-под контроля, швыряя «спуск» вперед и назад, перелетая через минимум, удаляясь от него все дальше.

Рисунок 5: Градиентный спуск со слишком большим шагом

Застревание на локальном минимуме

При работе с оптимизацией градиентного спуска вы должны знать, что нет никаких гарантий что алгоритм находит глобальный минимум — если у вашей функции несколько минимумов, градиентный спуск может также привести вас к локальному минимуму.

Рисунок 6: Функция с несколькими минимумами

Если вы рассмотрите функцию с несколькими минимумами, показанную выше, вы увидите этот градиент спуск не обязательно приведет вас к глобальному минимуму (расположенному примерно в \((0,-2)\)).