Формулы тригонометрии — Алгебра — Подготовка к ЕГЭ по математике
Основные тригонометрические формулы
Пример. Найти значение выражения:
Решение. Применяем основное тригонометрическое тождество в виде:
Пример. Найти значение выражения:
Решение. Из основного тригонометрического тождества следует:
Подставим в выражение:
Тригонометрические формулы суммы и разности двух углов
Пример. Вычислить
Решение.
Пример. .
Решение.
Тригонометрические формулы двойного угла
Пример. Найдите 2cos2?, если sin? = — 0,7.
Решение. Используем формулу косинуса двойного угла: cos2? = 1 – 2sin??.
Получаем: 2cos2? = 2·(1 – 2sin??) = 2·(1-2·(-0,7)2) = 2·(1-2·0,49) = 0,04.
Пример. Найдите значение выражения
Решение. Применяем формулу sin2? = 2sin?·cos?:
Формулы понижения степени
Пример. Найти значение выражения, если
Решение. Используем формулу понижения степени:
Применительно к углам 4x и 8x она будет выглядеть так:
Находим значение выражения:
Тригонометрические формулы произведения
Пример. Вычислить sin 20°·sin 40°, считать, что cos20° = 0,9
Решение. Заметим, что
Формулы суммы и разности тригонометрических функций
Формулы приведения
Формул приведения много, а точнее 32. И все формулы надо знать.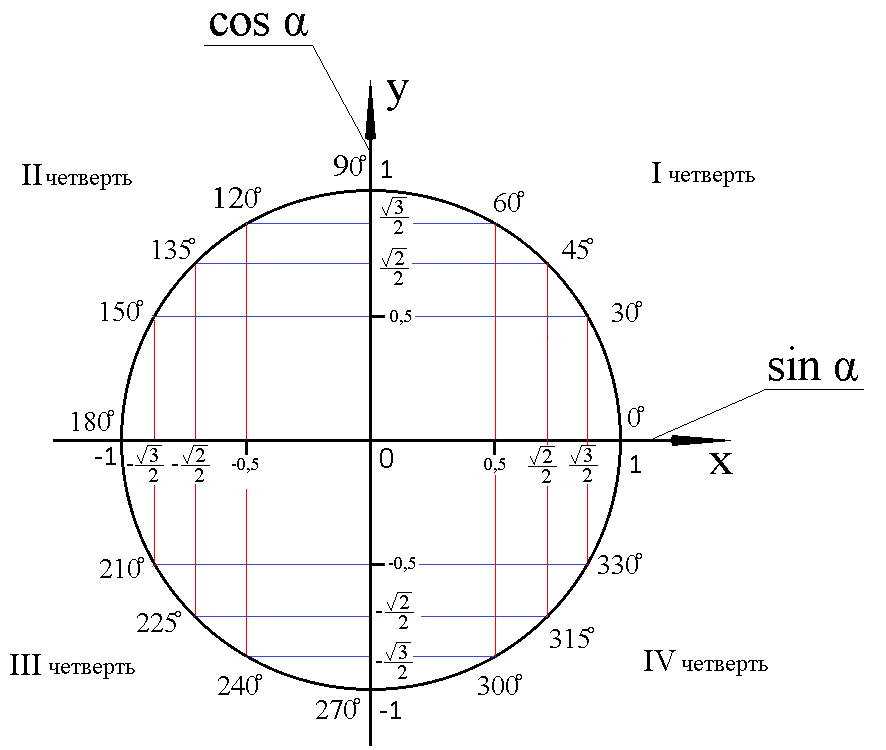 К счастью существует простое мнемоническое правило, позволяющее быстро воспроизвести любую формулу приведения.
К счастью существует простое мнемоническое правило, позволяющее быстро воспроизвести любую формулу приведения.
Каждая формула связывает между собой либо синус с косинусом, либо тангенс с котангенсом. Причём, первая функция либо меняется на вторую, либо нет.
1. В левой части формулы аргумент представляет собой сумму или разность одного из «основных координатных углов»:
, ?, , 2? и острого угла ?, а в правой части аргумент
2. В правой части знак перед функцией либо «плюс», либо «минус».
Мнемоническое правило
Достаточно задать себе два вопроса:
1. Меняется ли функция на кофункцию?
Ответ: Если в формуле присутствуют углы или — это углы вертикальной оси, киваем головой по вертикали и сами себе отвечаем: «Да», если же присутствуют углы горизонтальной оси ? или 2?, то киваем головой по горизонтали и получаем ответ: «Нет».
2. Какой знак надо поставить в правой части формулы?
Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части.
Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части.
Например, sin ( + ).
1) «Меняется функция или нет?»
— угол вертикальной оси, киваем головой по вертикали: «Да, меняется». Значит, в правой части будет cos?.
2) «Знак?»
Угол ( + ) попадает в IV четверть. Синус в IV четверти имеет знак «минус». Значит, в правой части ставим знак «минус».
Итак, получили формулу, sin( + ) = –cos?.
Пример. Найдите значение выражения .
Решение. Используем формулу приведения:
Пример. Найдите значение выражения 5tg17? · tg107?.
Решение. Используем формулу приведения:
5tg17? · tg107? = 5tg17?·tg(90? + 17?) = 5tg17?·(?ctg17?) = ?5(tg17?·ctg17?) = ?5·1 = ?5.
Тригонометрический круг
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Он заменяет десяток таблиц.
Сколько полезного на этом рисунке!
1. Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2? радиан.
2. Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси x, а значение синуса — на оси y.
3. И синус, и косинус принимают значения от –1 до 1.
Тригонометрический круг:
1. Значение тангенса угла ? тоже легко найти — поделив sin? на cos?. А чтобы найти котангенс — наоборот, косинус делим на синус.
2. Знаки синуса, косинуса, тангенса и котангенса.
3. Синус — функция нечётная, косинус — чётная.
4. Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен 2?.
Период равен 2?.
Графики тригонометрических функций
На рисунках приведены графики тригонометрических функций: y = sinx, y = cosx, y = tgx, y = ctgx.
1. График функции y = sinx
2. График функции y = cosx
3. График функции y = tgx
4. График функции y = ctgx
Видео-урок: Тригонометрические отношения на единичной окружности
Стенограмма видео
В этом видео мы научимся использовать тот факт, что квадрант, в котором лежит угол, определяет знак его тригонометрические функции синуса, косинуса и тангенса для решения уравнений. Начнем с размышлений о том, что мы знаем об углах на координатной плоскости.
На координатной плоскости центр
является источником. Для стандартных углов, измеренных в
координатная плоскость, положительная ось 𝑥 будет начальной стороной, начальной точкой
нашего измерения. Эта положительная 𝑥-ось и
начало представляет ноль градусов. К тому времени, когда мы доберемся до положительного
𝑦-ось, мы прошли 90 градусов. Отрицательная ось 𝑥 будет равна 180
градусов. Отрицательная 𝑦-ось будет 270
градусов. И весь обратный путь для
полный оборот 360 градусов. В радианах это будет ноль, 𝜋
больше двух, 𝜋, три 𝜋 больше двух, а затем два 𝜋.
Эта положительная 𝑥-ось и
начало представляет ноль градусов. К тому времени, когда мы доберемся до положительного
𝑦-ось, мы прошли 90 градусов. Отрицательная ось 𝑥 будет равна 180
градусов. Отрицательная 𝑦-ось будет 270
градусов. И весь обратный путь для
полный оборот 360 градусов. В радианах это будет ноль, 𝜋
больше двух, 𝜋, три 𝜋 больше двух, а затем два 𝜋.
Луч, представляющий, где мы
остановка измерения нашего угла называется конечной стороной. И угол и стандартное положение
будет располагаться между начальной и конечной сторонами. Но мы хотим специально
рассмотрим углы, лежащие на единичной окружности. Единичный круг имеет центр в
начало координат и имеет радиус в одну единицу. Для некоторой координаты 𝑥, 𝑦 в
первом квадранте длины 𝑥 и 𝑦 становятся катетами прямоугольного треугольника. А поскольку мы знаем, что радиус
этого круга один, гипотенуза этого прямоугольного треугольника будет один.
Если мы обозначим здесь длины сторон 𝑥 и 𝑦, мы можем взять теорему Пифагора, которая говорит нам 𝑎 в квадрате плюс 𝑏 в квадрате равно 𝑐 в квадрате, в единичном круге 𝑥 в квадрате плюс 𝑦 в квадрате равно один. Можно также сказать, что уравнение единичного круга должно быть 𝑥 в квадрате плюс 𝑦 в квадрате равно единице. Но то, что мы хотим сделать сейчас, это рассмотрим немного тригонометрии в отношении синуса единичной окружности, косинуса и касательная. Мы знаем синус угла представляет длину противоположной стороны по гипотенузе, косинус угла 𝜃 представляет длину прилегающей стороны по гипотенузе, а касательная Отношение угла — это отношение длины противоположной стороны к прилежащей стороне длина.
Для нашего угла 𝜃 внутри блока
круг, длина противоположной стороны всегда будет 𝑦-значением, это вертикаль
нога.
Прежде чем мы рассмотрим несколько примеров,
есть еще одна вещь, которую нам нужно рассмотреть. А это синус углов
квадранты. Если мы сохраним наш единичный круг, и мы
посмотрите на наши 𝑥, 𝑦 в первом квадранте, в первом квадранте все 𝑥-значения
положительный и все 𝑦-значения положительны. Это означает, что грех 𝜃 будет
положительна, так как 𝑦 положительна, то cos 𝜃 будет положительным, так как 𝑥
положительный, а поскольку 𝑥 и 𝑦 оба положительны, тангенс 𝜃 также будет
положительный.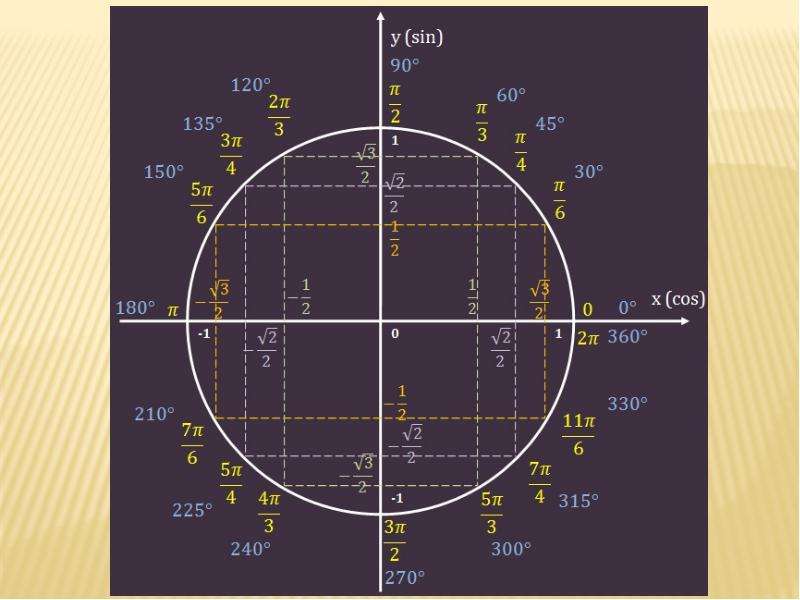
Но когда мы движемся ко второму квадранту и создадим прямой угол из точки отрицательный 𝑥, 𝑦, мы имеем дело с отрицательным 𝑥-значения и положительные 𝑦-значения. 𝑦-значение положительно в второй квадрант, делая значение синуса положительным. Но 𝑥-значение отрицательное. А это означает, что во втором квадранте косинус будет отрицательным. С положительным значением и отрицательное значение, тогда тангенс становится отрицательным. Итак, мы можем обобщить и сказать в во втором квадранте синус положительный, а косинус и тангенс отрицательные.
Переход к третьему квадранту, в
третий квадрант, значение 𝑥 и значение 𝑦 будут отрицательными. Это означает, что синус будет
отрицательный, косинус будет отрицательным. Однако с касательной отрицательное 𝑦
над отрицательным 𝑥 будет положительным.
Один из способов запомнить эти синусоидальных значений с помощью диаграммы CAST, которая выглядит следующим образом. Диаграмма CAST показывает, какие значение триггера будет положительным в каком квадранте. В первом квадранте все положительный. Во втором квадранте синус равен положительный. В третьем квадранте тангенс равен положительный. А в четвертом квадранте косинус равен положительный. Теперь мы готовы рассмотреть некоторые Примеры.
Найти грех 𝜃, если 𝜃 находится в
стандартное положение и его крайняя сторона проходит через точку три пятых,
отрицательные четыре пятых.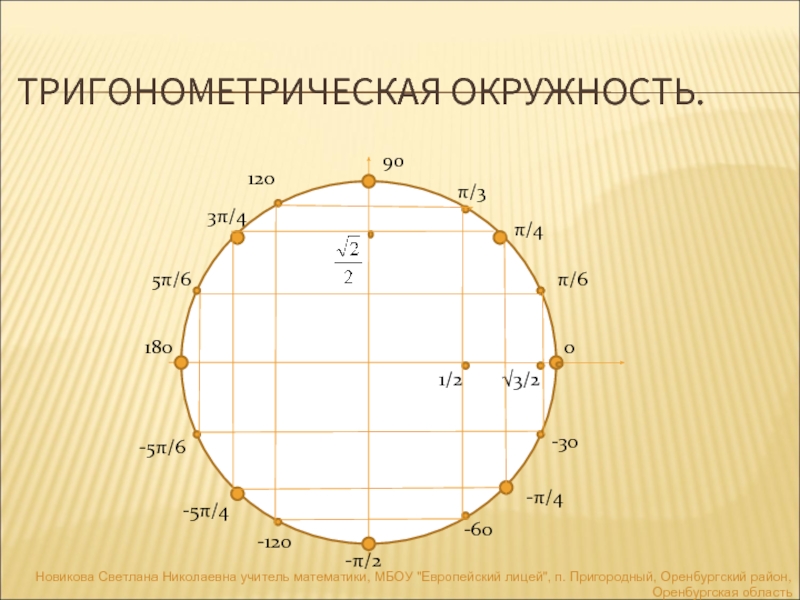
Возможно, здесь будет полезно нарисовать координатную плоскость. На этой координатной плоскости мы хотите построить точку три пятых, минус четыре пятых, которая здесь. Если мы знаем, что терминал сторона нашего угла проходит через эту точку и что наш угол находится в стандарте положение, то начальной стороной будет луч, который начинается в начале координат и проходит через положительную 𝑥-ось. Это означает, что мы интересует пространство от начальной стороны до конечной стороны. Однако для расчета этого мы образуем прямой угол с осью 𝑥.
Когда мы это делаем, мы получаем
прямоугольный треугольник. И мы будем использовать созданный угол
с осью 𝑥 для решения. Мы можем решить это, используя
тригонометрия прямоугольного треугольника, где у нас есть прямоугольный треугольник с длинами сторон
три пятых и четыре пятых. Мы помним, что грех 𝜃 будет
быть противоположным относительно гипотенузы. Однако в настоящее время мы не
знать гипотенузу. Мы не знаем расстояния от
начало координат до точки три пятых, минус четыре пятых. Мы можем использовать пифагорейскую
теорема, чтобы найти то, что означает три пятых в квадрате плюс четыре пятых в квадрате
равно 𝑐 в квадрате. Девять двадцать пятых плюс шестнадцать
двадцать пятых равно 𝑐 в квадрате. 25 больше 25 равно единице. И если 𝑐 в квадрате равно единице,
тогда 𝑐 должно быть равно единице.
Мы помним, что грех 𝜃 будет
быть противоположным относительно гипотенузы. Однако в настоящее время мы не
знать гипотенузу. Мы не знаем расстояния от
начало координат до точки три пятых, минус четыре пятых. Мы можем использовать пифагорейскую
теорема, чтобы найти то, что означает три пятых в квадрате плюс четыре пятых в квадрате
равно 𝑐 в квадрате. Девять двадцать пятых плюс шестнадцать
двадцать пятых равно 𝑐 в квадрате. 25 больше 25 равно единице. И если 𝑐 в квадрате равно единице,
тогда 𝑐 должно быть равно единице.
Теперь, когда мы знаем гипотенузу
равен единице, мы можем сказать кое-что еще об этом угле в нашей координате
самолет. И в этом наша точка
падает на единичную окружность. Единичный круг имеет свой центр
в начале координат и имеет радиус, равный единице. Мы ищем грех
𝜃. Это равносильно обратному
гипотенуза. Также в единичном круге грех
𝜃 равна его 𝑦-координате. 𝑦-координата для этого
точка минус четыре пятых. Итак, мы говорим, что грех
𝜃 равно отрицательным четырем пятым. И если бы мы хотели это проверить,
мы могли вспомнить, основываясь на нашей диаграмме CAST, что для углов, падающих в
в четвертом квадранте косинус положителен, но синус и тангенс будут
отрицательное, что подтверждает, что грех нашего угла 𝜃 равен отрицательному
четыре пятых.
Мы ищем грех
𝜃. Это равносильно обратному
гипотенуза. Также в единичном круге грех
𝜃 равна его 𝑦-координате. 𝑦-координата для этого
точка минус четыре пятых. Итак, мы говорим, что грех
𝜃 равно отрицательным четырем пятым. И если бы мы хотели это проверить,
мы могли вспомнить, основываясь на нашей диаграмме CAST, что для углов, падающих в
в четвертом квадранте косинус положителен, но синус и тангенс будут
отрицательное, что подтверждает, что грех нашего угла 𝜃 равен отрицательному
четыре пятых.
Рассмотрим другой пример.
Предположим, 𝑃 — точка на
единичный круг, соответствующий углу четыре 𝜋 больше трех. Есть ли еще один момент на
единичный круг, представляющий угол в интервале от нуля до двух 𝜋, который имеет
одинаковое значение тангенса? Если да, укажите угол.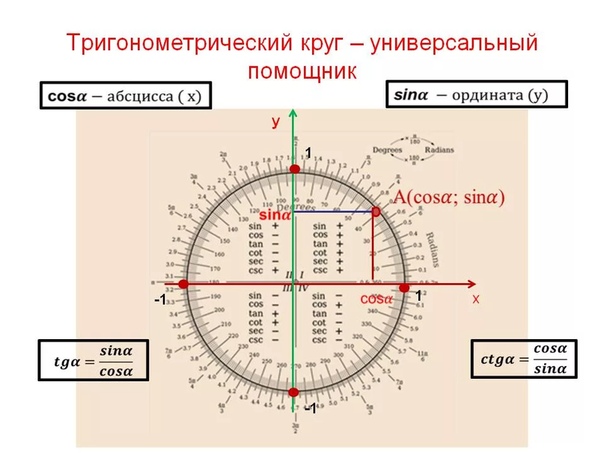
Во-первых, мы могли бы сделать набросок координатной плоскости, а затем добавьте единичный круг, который представляет собой круг с центром в начале координат и радиусом единицы. Оттуда мы также можем захотеть чтобы пометить нашу координатную плоскость радианами, начинающимися с нуля, 𝜋 более двух, 𝜋, три 𝜋 больше двух и два 𝜋. Потому что у нас есть интервал от нуля до двух 𝜋, мы знаем, что нас интересует только один полный оборот. Наша точка 𝑃 находится на единице окружности и соответствует углу четыре 𝜋 над тремя. Это означает, что наша первая задача состоит в том, чтобы узнайте, где приземлится угол четыре 𝜋 больше трех.
Я знаю, что 𝜋 больше трех
больше, чем 𝜋, но, вероятно, стоит сравнить, чтобы узнать, если четыре 𝜋 больше
три больше или меньше трех 𝜋 больше двух. Если дать этим дробям
общие знаменатели, четыре 𝜋 больше двух становится восемью 𝜋 больше шести и трех 𝜋
больше двух становится девятью 𝜋 больше шести.
Так как мы знаем, что наш угол попадает в третий квадрант, мы можем использовать диаграмму CAST, которая покажет нам что тангенс угла в третьей четверти будет положительным. Чтобы мы нашли другого точка внутри единичного круга, имеющая такое же значение касательной, мы будем искать для другого места, где значение тангенса может быть положительным. И это будет в первую квадрант. В первом квадранте все триггеры значения будут положительными.
Но для того, чтобы мы нашли
какое значение этого угла будет в первом квадранте, нам нужно разбить
наш угол четыре 𝜋 над тремя на более мелкие части.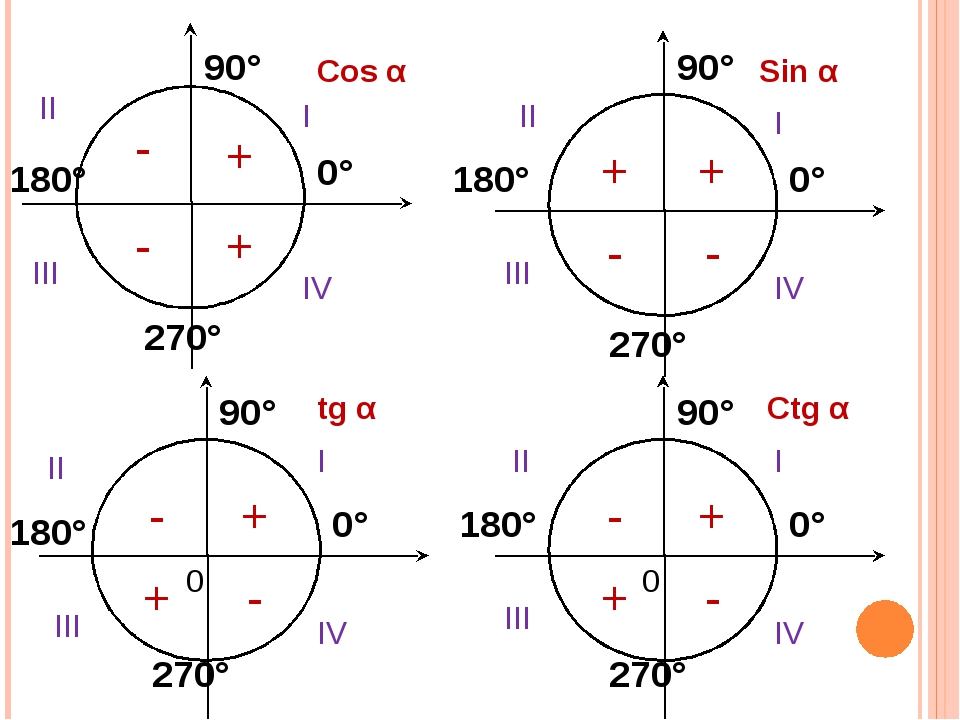 Можно сказать, что четыре 𝜋 более
три равно 𝜋 плюс 𝜋 на три, расстояние от нуля до 𝜋, а затем
дополнительный 𝜋 сверх трех. Создан прямоугольный треугольник
внутри единичного круга четыре 𝜋 больше трех в третьем квадранте будет выглядеть так
этот.
Можно сказать, что четыре 𝜋 более
три равно 𝜋 плюс 𝜋 на три, расстояние от нуля до 𝜋, а затем
дополнительный 𝜋 сверх трех. Создан прямоугольный треугольник
внутри единичного круга четыре 𝜋 больше трех в третьем квадранте будет выглядеть так
этот.
И в первом квадранте,
была бы некоторая точка, в которой мы имели бы дело с углом 𝜋
более трех. В первом квадранте это
будет иметь 𝑥, 𝑦 координаты. А в третьем квадранте это
будет иметь отрицательные 𝑥, отрицательные 𝑦 координаты. И мы знаем, что в единице
круг, тангенс 𝜃 будет равен 𝑦 над 𝑥. И мы бы сказали, что загар
из четырех третей 𝜋 равно отрицательному 𝑦 над отрицательным 𝑥 и тангенсом 𝜋
больше трех равно 𝑦 больше 𝑥. Но мы упрощаем отрицательное 𝑦
над отрицательным 𝑥 просто 𝑦 𝑥. Итак, мы показали, что да,
в этом интервале есть другой угол с таким же значением тангенса. И это угол 𝜋 закончился
три.
И это угол 𝜋 закончился
три.
В нашем следующем примере мы рассмотрим применение единичного круга.
Рассмотрим ветряную мельницу с лезвия длиной один метр. Положение вершины 𝑃 данная лопасть задается координатами 𝑎, 𝑏, которые зависят от угла 𝜃 как показано. Выразите 𝑎 и 𝑏 как функции меры угла 𝜃 в радианах. Если угол 𝜃 в определенный момент времени составляет пять третей 𝜋, какой она будет после того, как лезвие пройдет половину вращение?
Поскольку длина
лезвия составляют один метр, и на нашей диаграмме это представляет собой радиус
ветряная мельница, мы можем использовать наши знания об единичном круге, чтобы решить эту задачу.
проблема. Расстояние от центра г.
ветряная мельница в точку 𝑃 будет одной. И нам говорят, что суть
𝑃 находится по адресу 𝑎, 𝑏. Итак, мы можем создать право
треугольник с осью 𝑥 и говорят, что длины его сторон равны 𝑎 и 𝑏,
соответственно. Мы используем расстояние от
конечной стороной к оси 𝑥, чтобы вычислить угол 𝜃. Мы знаем, что в блоке
окружности, мы можем представить угол как отношение синуса и косинуса. Для нашего угла 𝜃 наоборот
длина стороны будет 𝑏, а ее гипотенуза равна одному метру, поэтому у нас есть грех 𝜃
равно 𝑏 больше единицы. И мы можем представить 𝑏 как грех
из 𝜃.
Итак, мы можем создать право
треугольник с осью 𝑥 и говорят, что длины его сторон равны 𝑎 и 𝑏,
соответственно. Мы используем расстояние от
конечной стороной к оси 𝑥, чтобы вычислить угол 𝜃. Мы знаем, что в блоке
окружности, мы можем представить угол как отношение синуса и косинуса. Для нашего угла 𝜃 наоборот
длина стороны будет 𝑏, а ее гипотенуза равна одному метру, поэтому у нас есть грех 𝜃
равно 𝑏 больше единицы. И мы можем представить 𝑏 как грех
из 𝜃.
Точно так же, если мы посмотрим на
косинус, мы получаем длину стороны 𝑎 больше единицы, что означает, что мы можем сказать, что
расстояние 𝑎 должно быть равно cos угла 𝜃. И без дополнительной информации,
это все, что мы можем сделать с этими двумя функциями. Мы можем сказать, что 𝑏 равно греху
𝜃 и 𝑎 равно потому что 𝜃.
Во второй части наших вопросов говорится если угол 𝜃 в определенный момент времени пять 𝜋 больше трех, то каким он будет после того, как лезвие совершило пол-оборота? Во-первых, мы уже нам сказали, что мы работаем в радианах, поэтому может быть полезно обозначить наша координатная плоскость. Начиная с оси 𝑥, ноль радиан, затем 𝜋 более двух радиан, 𝜋 радиан, три 𝜋 более двух радиан и полный оборот, что составляет два 𝜋 радиана. В такой системе полный очередь — два 𝜋. И, следовательно, пол-оборота будет равно 𝜋 радианам.
Если мы начнем с угла 𝜃
пять 𝜋 на три радиана, и мы добавляем половину оборота, мы добавляем 𝜋 к этому
угол. И так же, как добавление любого
дроби, нам нужен общий знаменатель. Мы можем написать 𝜋 как три 𝜋
более трех. Мы добавляем пять 𝜋 плюс три 𝜋 к
получить восемь 𝜋. И знаменатель не будет
изменять. Угол 𝜃 после половины
вращение будет восемь 𝜋 над тремя.
Мы добавляем пять 𝜋 плюс три 𝜋 к
получить восемь 𝜋. И знаменатель не будет
изменять. Угол 𝜃 после половины
вращение будет восемь 𝜋 над тремя.
Прежде чем мы закончим, давайте рассмотрим нашу ключевые моменты. Единичный круг — это круг с центр в начале координат и радиус в одну единицу. Для любой точки единичной окружности 𝑥, 𝑦, то грех угла 𝜃, образуемого этой точкой, будет равен 𝑦, а Кос угла 𝜃 будет равен 𝑥. Кроме того, 𝑥 в квадрате плюс 𝑦 квадрат должен быть равен единице. Мы также видели, что диаграмма CAST можно использовать для определения знаков тригонометрических функций в каждом квадранте.
Синусы без прямоугольных треугольников – The Math Doctors
(Новый вопрос недели)
Недавний вопрос касался явного конфликта между определением синусов и косинусов прямоугольным треугольником и определением единичного круга, относящимся к кратны 90° (углы на осях). Это дает возможность внимательно изучить взаимосвязь между этими двумя определениями.
Это дает возможность внимательно изучить взаимосвязь между этими двумя определениями.
Два определения
Вспомните, что определение прямоугольного треугольника синуса для острых углов есть «противоположный относительно гипотенузы»:
Определение единичной окружности синуса (которое применимо к любому углу) — это просто y -координата точки на единичной окружности:
Очевидно, что они совпадают для углов в первом квадранте .
Вот еще один прямоугольный треугольник, на этот раз во втором квадранте:
Здесь определение прямоугольного треугольника тесно связано с опорным углом, который в данном случае равен \(180°-\тета\). Но мы не можем нарисовать прямоугольный треугольник с тупым углом, поэтому это определение здесь неприменимо.
Как насчет точек на осях?
Вот вопрос, из середины марта:
На единичной окружности, как мы можем быть уверены что значения (x, y), лежащие на осях x и y, соответствуют значениям косинуса и синуса под таким углом?
Я имею в виду, что на единичной окружности есть упорядоченные пары (1, 0), (0, 1), (-1, 0) и (0, -1), которые, как и любая другая упорядоченная пара , соответствуют значениям косинуса и синуса угла, необходимого для достижения этой точки с x=косинусом и y=синусом.
Однако Чтобы доказать , что значения x и y равны значениям косинуса и синуса, необходимо построить прямоугольный треугольник , который использует значения x и y в качестве сторон треугольника и радиус 1 в качестве гипотенузы . Проблема в том, что это нельзя сделать, используя точки, которые я упомянул, поскольку они лежат на оси x или оси y, так как же мы можем быть уверены, что правило, которое мы доказали для всех других точек, работает для этих конкретных точек?
Сначала я подумал, что это следует из график триггерных функций, но график представляет собой отображение точек из единичного круга. Значения в этих точках все еще должны быть подтверждены, чтобы эти точки на графике были заполнены, так что это не может быть этим.
Например, точка (0, 1), соответствующая углу 90°, выглядит так, где «треугольник» не является треугольником:
Расширение определения
Доктор Рик ответил:
Привет, Марио.
Я полагаю, что в основе ваших вопросов лежит предположение о том, что тригонометрические функции определено через прямоугольные треугольники, и вся тригонометрия должна основываться на этих определениях. На самом деле это не так; если бы это было правдой, тригонометрические функции были бы определены только для углов 0 < θ < π/2. Что-то нужно добавить к определениям, верно? Эти определения сами по себе недостаточны.
Мы не знаем, как в классе Марио был представлен единичный круг; Я видел несколько очень разных подходов, и на самом деле есть учебники, названия которых включают что-то вроде «Прямоугольный подход к тригонометрии» или «Подход единичного круга», указывая, с каких определений они начинаются; и введение может предложить альтернативные пути через главы для учителей, которые хотят начать по-другому.
Предположительно, определение прямоугольного треугольника было представлено как исходное определение, а определения единичного круга были производными от них или, по крайней мере, обоснованными на этой основе.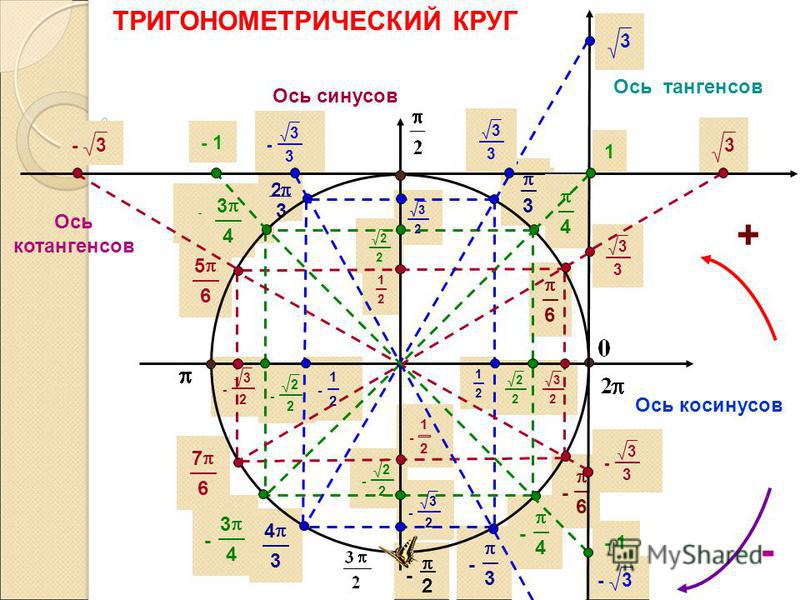 Марио, вероятно, неправильно понимает, о чем говорится в книге, потому что вы не можете на самом деле доказать факт для неострых углов из определения, которое к ним неприменимо. Доктор Рик предлагает лучший способ увидеть взаимосвязь:
Марио, вероятно, неправильно понимает, о чем говорится в книге, потому что вы не можете на самом деле доказать факт для неострых углов из определения, которое к ним неприменимо. Доктор Рик предлагает лучший способ увидеть взаимосвязь:
.0067 расширение определения триггерных функций для любого угла. Это немного похоже на то, как базовая концепция показателей степени , которая сначала применяется к показателям положительного целого числа (например, x 3 = x·x·x), представляет собой , расширенное , чтобы придать смысл отрицательным целым числам. степени, затем к рациональным силам и к силам вещественных чисел (и даже к комплексным силам).
Это распространено в математике, своего рода начальный подход; Я обсуждал эту идею в посте Что такое умножение… Правда? Такие понятия, как сложение, умножение или показатель степени, сначала рассматриваются в контексте целых чисел, а затем применяются к новым формам чисел по мере их изобретения.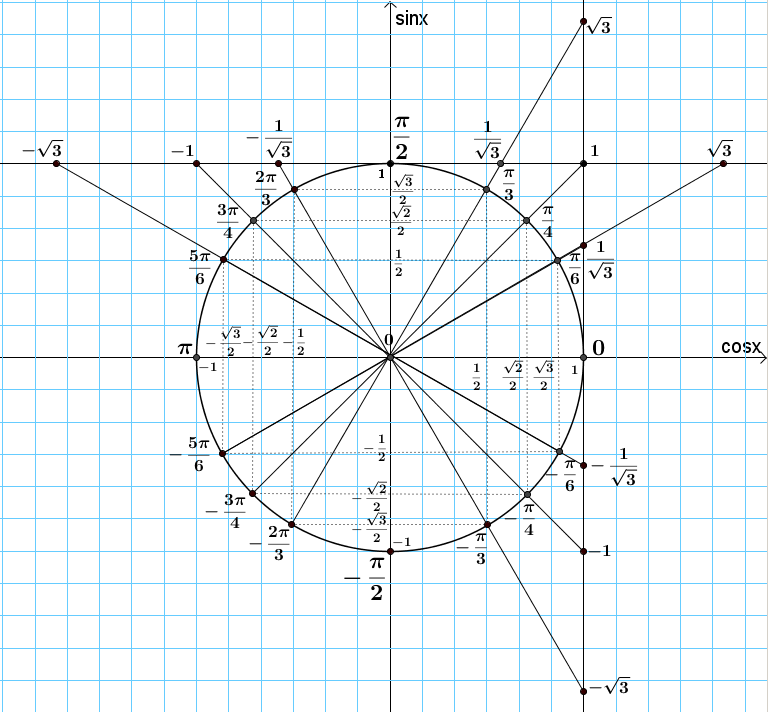 Здесь функции триггера сначала рассматриваются с точки зрения острых углов, а затем расширяются.
Здесь функции триггера сначала рассматриваются с точки зрения острых углов, а затем расширяются.
Другими словами, как только определение единичного круга установлено, оно заменяет определение прямоугольного треугольника в качестве основы для доказательства. Затем мы работаем в направлении, противоположном тому, что вы предложили: мы показываем, что в случае 0 < θ < π/2 определения прямоугольного треугольника следуют из определений единичного круга . Это делает определения единичных кругов совместимыми с определениями, которые они заменяют (можно сказать, что новые определения «обратно совместимы»).
Таким образом, вместо того, чтобы определения единичного круга были , доказано из определений прямоугольного треугольника (что невозможно сделать, потому что последние не определяют синус тупых углов в первую очередь), они вместо этого показано, что соответствует последнему, а затем может использоваться даже для острых углов. Точно так же новая версия программного обеспечения на вашем компьютере может быть установлена вместо старой, если она по-прежнему выполняет те же функции, что и старая, даже если теперь она может выполнять 9 операций.0075 больше . Вот что значит «обратная совместимость».
Точно так же новая версия программного обеспечения на вашем компьютере может быть установлена вместо старой, если она по-прежнему выполняет те же функции, что и старая, даже если теперь она может выполнять 9 операций.0075 больше . Вот что значит «обратная совместимость».
Есть ли что-то особенное в квадрантных углах?
Углы, о которых беспокоится Марио, называются квадрантными углами , что означает, что они лежат точно на осях, которые делят квадранты плоскости, и поэтому на самом деле не являются в каком-либо квадранте. (Я не совсем доволен этим термином, но я живу с ним. Я думаю об этом как о «четверть-оборотных углах».)
Я скажу немного больше на ваш конкретный вопрос о «квадрантных углах», хотя. Мы можем показать, что тригонометрические функции 0 радиан и π/2 радиан являются ограничивает триггерных функций, основанных на прямоугольных треугольниках, когда угол приближается к 0 или π/2 соответственно.
Например, если угол А прямоугольного треугольника очень мал, отношение противолежащего катета а к гипотенузе с очень мало; и по мере уменьшения угла это отношение (синус угла) становится меньше, приближаясь к 0 в пределе. Это согласуется с тем, что синусоидальная функция является непрерывной функцией. (С другой стороны, функция тангенса , а не непрерывна при θ = π/2, но это согласуется с наблюдением прямоугольного треугольника, когда угол A приближается к 90 градусов с фиксированной соседней стороной b, сторона a неограниченно увеличивается.)
Эти понятия (пределы, непрерывность) изучаются в математическом анализе, обычно после тригонометрии; но они должны иметь смысл, когда понимаются неформально. Вот изображение этой идеи, когда треугольник приближается к отрезку вдоль положительной оси x :
Катет a приближается к нулю, когда угол приближается к нулю, а гипотенуза c остается неизменной, поэтому синус стремится к нулю. Аналогично, нога b приближается к тому же значению, что и c , поэтому косинус приближается к 1.
Аналогично, нога b приближается к тому же значению, что и c , поэтому косинус приближается к 1.
Это показывает, что если мы хотим, чтобы наше расширенное определение синуса было непрерывным (неформально, без внезапных скачков), то синус 0 имеет быть равным 0, а косинус 0 должен быть равен 1. Это добавляет больше поддержки определению единичного круга, хотя последнее по-прежнему является определением , а не теоремой .
Объяснение преемственности на примере
Марио ответил:
Интересно. Так что, если бы я сказал это, если бы один из моих одноклассников задал мне тот же вопрос, что и я:
«Конечно, значения триггерных функций можно вычислить с помощью прямоугольного треугольника. Но помните, функции косинуса и синуса также представляют значения (x, y) периодического движения , например, положение тележки колеса обозрения по периметру колеса обозрения во время его работы. Периодическое движение существует в точках, в которых мы не можем нарисовать прямоугольный треугольник на единичной окружности.
Однако периодическое движение существует при этих значениях (x, y), и, поскольку тригонометрические функции описывают периодическое движение, тригонометрические функции могут иметь значения в этих точках».
Так ли это?
Это превращает идею непрерывной функции угла в непрерывную функцию времени, которую легче представить; если колесо обозрения движется плавно, то оно должно точно так же проходить через каждую показанную точку:
Нет ничего особенного ни в самом верху, ни в самой правой точке, ни в чем-то еще. Таким образом, в этих точках также будут значения синуса (высоты) и косинуса (горизонтальное положение). Правда, дело не столько в том, что функций периодические , так как они непрерывные , это важно. В нашем колесе обозрения нет резких рывков.
Доктор Рик ответил,
Я не вижу ничего плохого в том, что вы написали. Убедит ли это вашего гипотетического одноклассника? Возможно.
Позвольте мне применить новый подход и изучить этот пример с колесом обозрения .
Горизонтальное и вертикальное расстояния тележки от центра колеса вместе с радиусом до тележки образуют прямоугольный треугольник; отношение расстояния по вертикали (противоположная сторона треугольника) к радиусу равно синусу угла, образованного тележкой, центром и горизонталью.
Похоже, у вас нет проблем со случаями, когда прямоугольный треугольник не находится в первом квадранте — где косинус, или синус, или оба отрицательные. Вы выразили сомнение только по поводу квадрантных углов , когда горизонталь, вертикаль и радиус не образуют треугольника в обычном геометрическом смысле. Вместо этого они образуют вырожденный треугольник , в котором одна сторона имеет нулевую длину. Хотя треугольники в геометрии не могут иметь стороны нулевой длины, мы все еще можем говорить о них и применять «прямоугольные определения» триггерных функций , получая разумные результаты.

 Однако Чтобы доказать , что значения x и y равны значениям косинуса и синуса, необходимо построить прямоугольный треугольник , который использует значения x и y в качестве сторон треугольника и радиус 1 в качестве гипотенузы . Проблема в том, что это нельзя сделать, используя точки, которые я упомянул, поскольку они лежат на оси x или оси y, так как же мы можем быть уверены, что правило, которое мы доказали для всех других точек, работает для этих конкретных точек?
Однако Чтобы доказать , что значения x и y равны значениям косинуса и синуса, необходимо построить прямоугольный треугольник , который использует значения x и y в качестве сторон треугольника и радиус 1 в качестве гипотенузы . Проблема в том, что это нельзя сделать, используя точки, которые я упомянул, поскольку они лежат на оси x или оси y, так как же мы можем быть уверены, что правило, которое мы доказали для всех других точек, работает для этих конкретных точек?
 Например, если угол А прямоугольного треугольника очень мал, отношение противолежащего катета а к гипотенузе с очень мало; и по мере уменьшения угла это отношение (синус угла) становится меньше, приближаясь к 0 в пределе. Это согласуется с тем, что синусоидальная функция является непрерывной функцией. (С другой стороны, функция тангенса , а не непрерывна при θ = π/2, но это согласуется с наблюдением прямоугольного треугольника, когда угол A приближается к 90 градусов с фиксированной соседней стороной b, сторона a неограниченно увеличивается.)
Например, если угол А прямоугольного треугольника очень мал, отношение противолежащего катета а к гипотенузе с очень мало; и по мере уменьшения угла это отношение (синус угла) становится меньше, приближаясь к 0 в пределе. Это согласуется с тем, что синусоидальная функция является непрерывной функцией. (С другой стороны, функция тангенса , а не непрерывна при θ = π/2, но это согласуется с наблюдением прямоугольного треугольника, когда угол A приближается к 90 градусов с фиксированной соседней стороной b, сторона a неограниченно увеличивается.)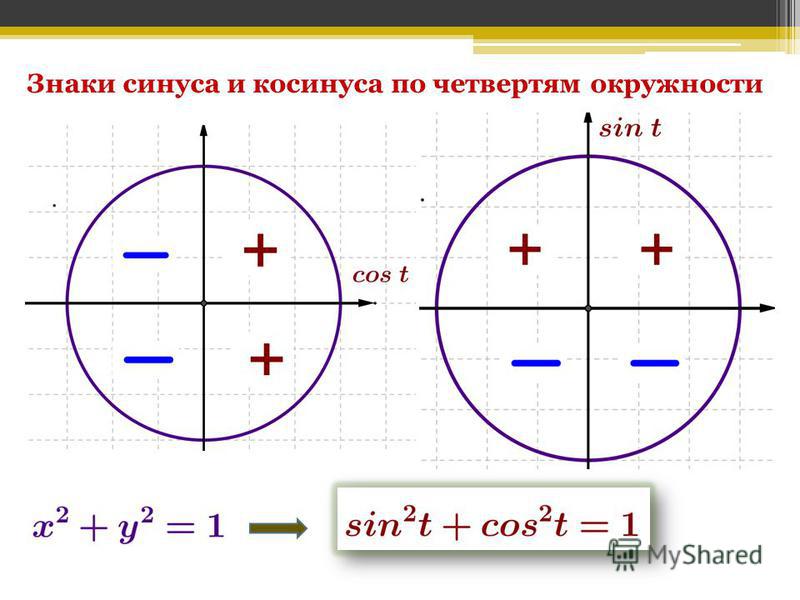 Однако периодическое движение существует при этих значениях (x, y), и, поскольку тригонометрические функции описывают периодическое движение, тригонометрические функции могут иметь значения в этих точках».
Однако периодическое движение существует при этих значениях (x, y), и, поскольку тригонометрические функции описывают периодическое движение, тригонометрические функции могут иметь значения в этих точках».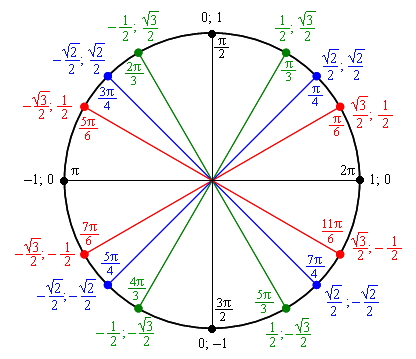 Горизонтальное и вертикальное расстояния тележки от центра колеса вместе с радиусом до тележки образуют прямоугольный треугольник; отношение расстояния по вертикали (противоположная сторона треугольника) к радиусу равно синусу угла, образованного тележкой, центром и горизонталью.
Горизонтальное и вертикальное расстояния тележки от центра колеса вместе с радиусом до тележки образуют прямоугольный треугольник; отношение расстояния по вертикали (противоположная сторона треугольника) к радиусу равно синусу угла, образованного тележкой, центром и горизонталью.