Окружность и круг — что это, определение и ответ
Окружность – это множество всех точек плоскости, равноудаленных от данной точки на плоскости.
Круг – это часть плоскости, ограниченная окружностью.
Окружность – это замкнутая линия, а круг – это площадь, находящаяся внутри окружности:
Длина окружности равна:
\(l = 2\pi R = \text{dπ}\)
где \(R\) – это радиус, а \(D\) – диаметр окружности
ЭЛЕМЕНТЫ ОКРУЖНОСТИ:
Центр окружности – точка O.
Радиус окружности – отрезок R, соединяющий точку окружности с центром. Все радиусы одной окружности равны.
Хорда – это отрезок АВ, соединяющий любые две точки окружности.
Диаметр – это хорда d, проходящая через центр окружности. Диаметр равен двум радиусам.
ДУГА И СЕКТОР:
Дуга – это часть окружности, заключенная между точками на ней. \circ}}\) показывает, какую часть от всей окружности занимает дуга
\circ}}\) показывает, какую часть от всей окружности занимает дуга
КАСАТЕЛЬНАЯ:
Касательная к окружности – это прямая, которая пересекается с окружностью в одной точке.
Свойства касательной:
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания:
\(a\bot OA,\ A \in a,\ OA = R\)
2. Отрезки касательных, проведенных из одной точки, равны до точек касания.
\(CA = CB,\ a,\ b\ –\ касательные\)
ЦЕНТРАЛЬНЫЕ И ВПИСАНЫЕ УГЛЫ:
С окружностью связано два вида углов – вписанные и центральные. Рассмотрим такую окружность:
На данном чертеже угол АОС является центральным, а угол АВС – вписанным.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны являются ее хордами.
Свойства вписанного угла:
1. Измеряется половиной дуги, на которую он опирается.
2. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
3. Вписанный угол, опирающийся на диаметр — прямой.
Центральный угол – угол, образованный двумя радиусами. Его вершина лежит на центре окружности.
Свойства центрального угла:
1. Измеряется дугой, на которую опирается;
2. Центральный угол в два раза больше вписанного, опирающегося на ту же дугу.
КОМБИНАЦИИ ХОРД, КАСАТЕЛЬНЫХ И СЕКУЩИХ:
Секущая – это прямая, которая пересекает окружность в двух точках.
ПЕРЕСЕЧЕНИЕ ХОРД
Хорды AB и CD пересекаются в точке M
1. Произведение длин отрезков пересекающихся хорд равны:
\(AM \bullet MB = CM \bullet MD\)
2. Угол между двумя пересекающихся хорд равен полусумме высекаемых ими дуг:
\(\angle AMD = \angle CMD = \frac{дуга\ AD + дуга\ \text{CB}\ }{2}\)
ХОРДА И КАСАТЕЛЬНАЯ
Прямая AB касается окружности в точке B, BC – хорда. {2}\)
{2}\)
2. Угол между секущей и касательной равен полуразности высекаемых ими дуг:
\(\angle DAC = \frac{дуга\ DC\ –\ дуга\ \text{CB}}{2}\)
УГОЛ МЕЖДУ СЕКУЩИМИ
AD и AE – секущие, выходящие из одной точки, пересекающие окружность в точках В и С соответственно.
Угол между секущими равен полуразности большей и меньшей высекаемых ими дуг:
\(\angle BAC = \frac{дуга\ \text{DE}\ –\ дуга\ \text{BC}}{2}\)
Шлифовальные круги для угловых шлифмашин. Статьи, обзоры, тесты оборудования
Шлифовальные круги представляют собой по большому счету очень толстый отрезной круг.
Назначение.
- Зачистка сварного шва
- Снятие фаски
- Удаление сварочных брызг
- Зачистка твердой окалины
- Разделка сварного шва
Особенности.
Часто они выполнены из аналогичных c отрезными кругами абразивных материалов, отличающихся только по размеру абразивного зерна.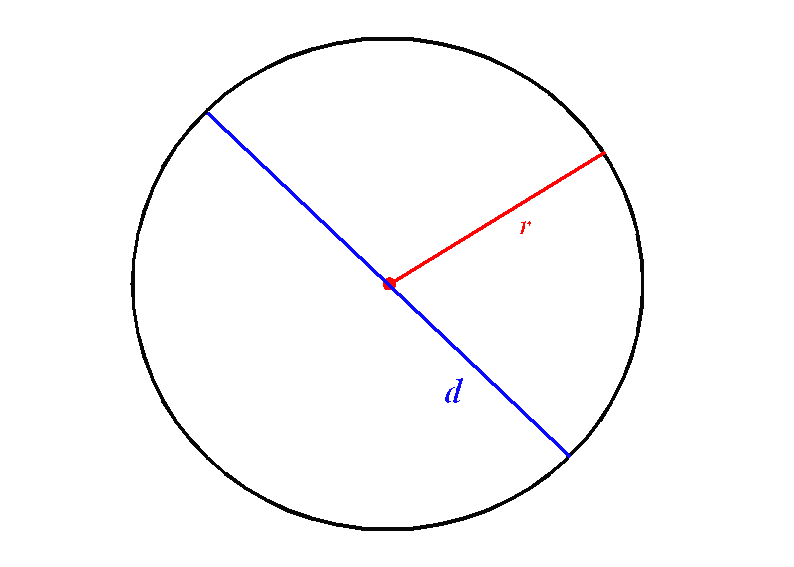
Например круги Сибо — отрезной и зачистной. Как видите, шлифовальный круг выполнен из того же материала, но с более грубым зерном.
Отличает такие круги помимо зерна форма круга, и его толщина.
Форма.
Шлифовальные круги, за исключением единичных случаев имеют форму с углублением. Чтобы гайка не мешала при работе под малыми углами.
Размеры. Толщина.
Диаметры шлифовальных кругов идентичны отрезным кругам — 115, 125, 150, 180 и 230 мм. В соответствии с используемой УШМ.
А толщина существенно больше. Самый распространенный размер — это 6–6,5 мм.
Реже встречаются круги толщиной 7 мм (Больше не бывает).
Или тоньше — 3,3, 4 или 5 мм. Это как правило специализированные круги.
Такая толщина обусловлена высокими требованиями к прочности круга на излом, так как в большинстве случаев принято такими кругами работать под углом 30–45 градусов к поверхности.
Об этом указывается на некоторых кругах.
Так же некоторых кругах указывается как рекомендуется выполнять работу.
Например этим кругом можно работать практически во всех положениях.
Но большинство кругов работают только под углом 30–45 градусов.
И не рекомендовано работать под другими углами. То же справедливо и отрезных кругов, обращайте внимание на инструкцию.
Почему зачистными кругами рекомендуется работать под углов 30–45 градусов?
При таком угле формируется правильная форма рабочей кромки круга.
Если мы будем держать круг под маленьким углом 10–15 градусов, как например фибровый круг, то это приведет к истончению рабочей кромки и преждевременному ее износу.
А вот с работой торцом круга все не так однозначно. Люди применяют такой способ для разделки корня сварного шва и подготовки пропила под новый шов.
И производители не пишут запрет на такое использование круга. Указывают только рекомендованное положение.
Указывают только рекомендованное положение.
На отрезном круге, например работа под малым углом приведет к излому круга и разрушению. Так как круг тонкий и имеет обычно одну армирующую сетку.
Конечно, есть специальные круги для работы торцом, например 3M™ Cubitron™ Круг зачистной Cubitron II Cut & Grind 125мм х 4.2мм х 22мм
Но такие круги дороги и имеют ограниченную толщину, так как в них заложено универсальное применение. А часто нужна максимальная толщина, чтобы качественно разделать кромку шва.
Материалы круга.
Сейчас шлифовальные круги изготавливаются чаще всего из Оксида Алюминия (А).
Iprix
Но становятся популярны и круги с керамическим абразивным зерном.
Rhodius
Или даже смешанные составы.
Cubitron 2 смесь
На фото круг 3М с зерном точной формы в составе.
Керамическое зерно имеет выше твердость и поэтому агрессивнее обрабатывает металл, снимает больше за тот же промежуток времени.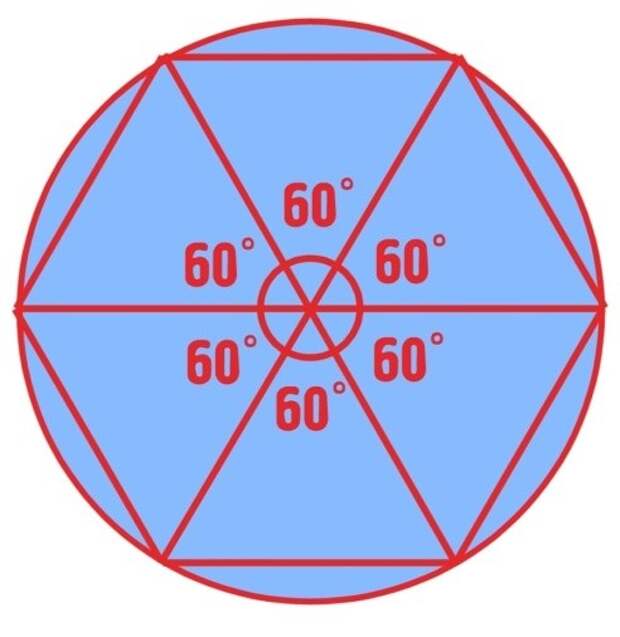
И соответственно имеет более высокую цену.
Существуют круги уменьшенной толщины с керамическим зерном.
Cubo Ceramax и Green Corps 3М
Такими кругами удобнее подбираться в более сложные места. Но как правило, производитель рекомендует использовать с ними небольшую опорную тарелку.
Инструкция к кругам Green Corps.
Таким образом, можно выбрать оптимальный круг для каждой задачи.
Преимущества зачистных кругов:
- Высокая агрессивность
- Высокий ресурс круга
- Возможность работать под разными углами, разделывать корень шва
Минусы:
- Высокий уровень шума и вибрации
- Повышенное пылеобразование
Самые актуальные новости в наших соцсетях и на нашем канале:
Круг в углу круга
Геометрия: круг в углу круга
Эта статья специально написана, чтобы ответить на вопрос геометрии: «Каков радиус круга, начерченного в пространстве между кругом радиуса 1 единица и углом окружающего его квадрата?» Чтобы лучше объяснить вопрос, а затем ответить на него, я нарисовал схему, показанную ниже.
Диаграмма не идеальна, но я лучше использую карандаш и циркуль, чем рисую геометрические фигуры в Photoshop. Больший круг имеет центр E, и DE = EF = 1 единица. Каков радиус меньшего круга с центром C (BC = CD = меньший радиус).
По симметрии угол при A = 45 градусов, поэтому треугольники ACG и AEH являются прямоугольными равнобедренными треугольниками.
AH и EH равны радиусу большего круга = 1 единица
По теореме Пифагора длина AE = √2
Длина AD = AE — DE = √2 -1
Однако длина AD не является диаметром меньшего круга. Диаметр меньшего круга равен BD, а не AD. Тем не менее, мы все еще делаем успехи.
Далее рассмотрим отношение длин AD:AF.
AD = √2 -1, как мы показали ранее
AF = AD + DF = (√2 -1) + 2 (диаметр круга) = √2 + 1
Таким образом, отношение AD:AF = √2 — 1 : √2 + 1
И дробь AD/AF = √2 -1 / √2 + 1
Каково оставшееся расстояние между окружностью и началом координат?
Посмотрите еще раз на больший круг и на отношение диаметра к расстоянию от угла до самой дальней точки круга?
Дробь AB/AD равна дроби AD/AF. Эта дробь описывает соотношение между диаметром круга и дополнительным расстоянием до угла окружающего его квадрата. Диаметр круга не важен, соотношение фиксированное.
Итак, мы можем разделить меньшую длину AD на отношение AD:AF, и это даст нам длину AB и (как мы уже знаем AD) диаметр меньшего круга BD. 92
BD — это диаметр меньшего круга, BD = 0,216… Сравнивая его с диаметром большего круга, который равен 2,00, мы видим, что меньший круг составляет около 10% от диаметра большего.
В будущих сообщениях я рассмотрю другие варианты расположения кругов в углах, в частности четверть круга в углу (который, как повторяющийся узор, приведет к тому, что меньший круг соприкасается с четырьмя большими кругами в виде квадрата). расположение) и треть круга в углу шестиугольника. Затем я сравню два устройства (с точки зрения заполненного пространства), а также сверюсь с любыми известными сплавами, посмотрев на соотношение диаметров, чтобы увидеть, смогу ли я найти применение в реальной жизни.
Новое сообщение Старый пост Главная
Подписаться на: Post Comment (Atom)
У круга всегда есть углы — Нариндер
Круг — это круглая фигура, похожая на колесо велосипеда или диск. Он непрерывен, плавно изгибается и соединяется с точкой, из которой он начался. Если провести ладонью по круглому краю, то не будет ни разрыва, ни угла. Значит ли это, что у круга нет угла? Наверное, сверху так кажется.
Для дальнейшего исследования материи требуется определение круга. Математика определяет круг как геометрическое место точки, которая движется таким образом, что ее расстояние от фиксированной точки всегда постоянно. Фиксированная точка называется центром, постоянное расстояние — радиусом. Проще говоря, это путь, прочерченный точкой, которая движется таким образом, что ее расстояние от фиксированной точки всегда постоянно. Если движущаяся точка (x’, y’) и постоянное расстояние, скажем, от фиксированной точки (0, 0) равно r, ее геометрическое место равно
, что является уравнением окружности .
Если зафиксировать один конец делителя, скажем, в точке О, а другой его конец повернуть, движущийся конец пересекает окружность с центром в О. Ясно, что такая круглая фигура не имеет острого изгиба или угла. Следовательно, это определение также приводит нас к мысли, что круг не имеет углов.
Также, если конус срезан плоскостью, параллельной горизонтальной плоскости, площадь поперечного сечения усеченного конуса представляет собой круг.
Правильный шестиугольник ABCDEF.
Теперь я возьму случай правильного многоугольника, скажем, правильного шестиугольника с шестью равными сторонами. Можно взять правильный многоугольник с любым количеством сторон. На рисунке ABCDEF показан правильный шестиугольник с внешним углом CBB’ = 2.pi/n и каждым внутренним углом = (1-2/n).pi, где n — количество сторон правильного многоугольника.
Площадь треугольника OAB = ½. перпендикуляр x основание
, где O точка пересечения диагоналей AD, BE, CF и OA = OB= OC = OD = OE = OF = r. 2x — внутренний угол, равный (1-2/n).pi.
Площадь правильного шестиугольника = количество треугольников, умноженное на площадь каждого треугольника будет стремиться к нулю, и правильный многоугольник точно примет форму круга.
Это приводит нас к выводу, что окружность, по сути, является правильным многоугольником с бесконечным числом сторон. Но как можно считать бесконечные стороны? Бесконечность не является конечной величиной или конечным числом, она постоянно увеличивается. Счет бесконечности * был объяснен в моей предыдущей статье, и образованный читатель может обратиться к ней, чтобы понять ее концепцию.
Счет бесконечности * был объяснен в моей предыдущей статье, и образованный читатель может обратиться к ней, чтобы понять ее концепцию.
В первых абзацах было упомянуто, что у круга нет сторон, а значит, нет и углов, но в последних абзацах упоминается, что он имеет бесконечные стороны и, следовательно, бесконечные углы. Какой из них верный, требует дальнейшего анализа. В предыдущих параграфах упоминалось , когда число сторон правильного многоугольника стремится к бесконечности, при этом 1/n или 2.pi/n стремится к нулю. Пожалуйста, прочтите между строк, что 2.pi/n стремится к нулю, но не равно нулю. Существует огромная разница между стремлением к нулю и нулем. Стремление к нулю бесконечно мало, настолько мало, что оно меньше наименьшего и стремится к нулевому значению. Или, другими словами, количество потеряет свою величину и станет равной нулю.
С другой стороны, ноль — это ничто или нуль, и он абсолютно лишен величины. Сама величина равна нулю, она не обязана достигать нуля.
Теперь допустим, круг имеет сторону нулевой длины (т.к. это означает отсутствие стороны), тогда 2.pi/n будет равно нулю, обратите внимание, в этом случае 2pi/n не стремится к нулю, как считалось ранее, здесь это идеальный ноль. В итоге (sin 2pi/n)/(2pi/n) будет 0/0**. Но деление нуля на ноль неопределенно. В этом случае площадь многоугольника будет неопределенной, но на практике площадь вычислима и конечна. Следовательно, наше предположение о том, что у окружности есть стороны нулевой длины или вообще нет сторон, неверно. 92. Следовательно, количество сторон правильного многоугольника должно быть бесконечным, а длина стороны стремится к нулю. Это доказывает, что у круга всегда бесконечные стороны, следовательно, бесконечные углы, и он никогда не бывает без углов.
Примечания:
1. Counting Infinity можно прочитать на https://narinderkw.wordpress.com/2017/03/12/counting-infinity/
2. 0/0** Решение деления нуля на ноль можно прочитать по адресу https://narinderkw.
