Коэффициент \(b\) означает симметричность относительно оси \(OY.\) Если \(b=0\), то вершина лежит оси \(OY.\)
Применение параболы
Радиоволны часто должна быть сконцентрирована в одной точке например, радиотелескопы, платные телевизионные тарелки, солнечные коллекторы.
Излучение должно передаваться из одной точки в широкий параллельный луч (например, отражатели фар).
Параллельные радиоволны собираются параболической антенной. Параллельные лучи отражаются от антенны и встречаются в точке F, называемой фокусом.
Часто задаваемые вопросы:
✅ Что такое парабола?
↪ Парабола — это геометрическое место точек, находящихся на равном расстоянии от фокуса и прямой, называемой директрисой.
✅ Каковы основные характеристики параболы?
↪ Основные характеристики параболы — вершина, фокус, директриса и ось симметрии. Вершина — точка наибольшего приподнятия параболы. Фокус — точка, находящаяся на оси симметрии и на расстоянии равном фокусному параметру от вершины параболы. Директриса — прямая, находящаяся на расстоянии фокусного параметра от вершины и перпендикулярная оси симметрии. Ось симметрии — линия, проходящая через вершину и перпендикулярная директрисе.
✅ Где используется парабола?
↪ Парабола находит применение в различных областях, например, в оптике для создания зеркал и антенн, в архитектуре для создания куполов и склонов крыш, в физике для моделирования траекторий движения тел, в математике для решения уравнений и графического представления данных.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Как построить параболу | Алгебра
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле
для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ=xₒ²+bxₒ+c. От вершины (хₒ; yₒ ) строим параболу y=x².
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
y=x²+2x-3
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
y= -x²+2x+8
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Примеры.
Построить график функции y=x²+5x+4.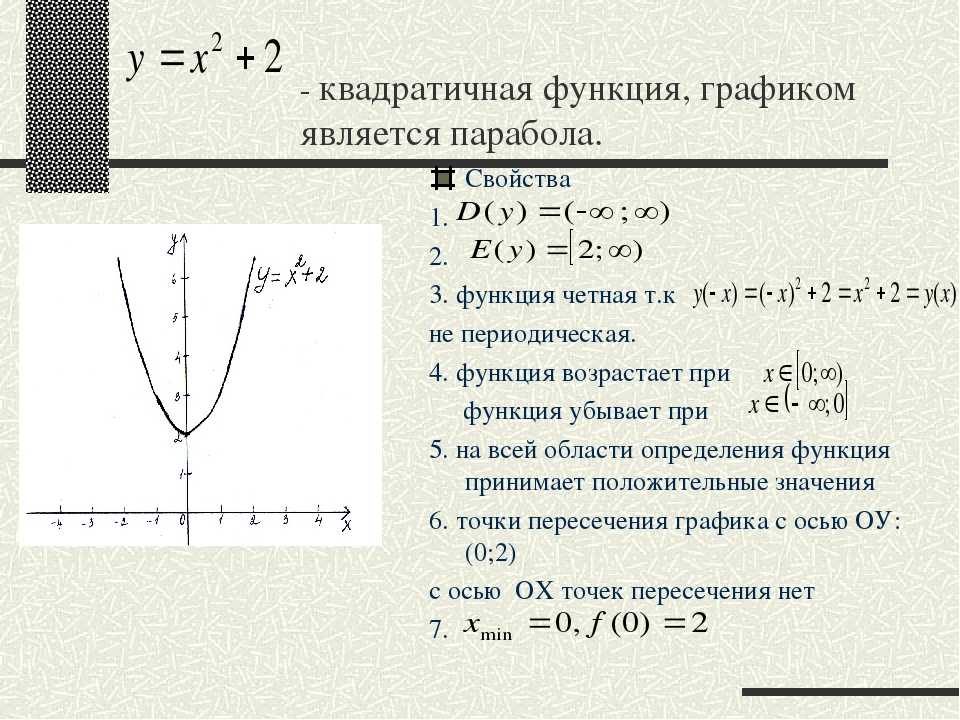
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
y=x²+5x+4
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
y= -x²-3x
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: Квадратичная функция | КомментарииПарабола — уравнение, свойства, примеры
Парабола — это график квадратичной функции. Паскаль утверждал, что парабола — это проекция окружности. Галилей объяснил, что снаряды, падающие под действием силы тяжести, следуют по траектории, называемой параболической траекторией. Многие физические движения тел следуют криволинейной траектории, имеющей форму параболы. Параболой в математике называют любую плоскую кривую, которая является зеркально-симметричной и обычно имеет приблизительно U-образную форму. Здесь мы будем стремиться понять вывод стандартной формулы параболы, различные стандартные формы параболы и свойства параболы.
Паскаль утверждал, что парабола — это проекция окружности. Галилей объяснил, что снаряды, падающие под действием силы тяжести, следуют по траектории, называемой параболической траекторией. Многие физические движения тел следуют криволинейной траектории, имеющей форму параболы. Параболой в математике называют любую плоскую кривую, которая является зеркально-симметричной и обычно имеет приблизительно U-образную форму. Здесь мы будем стремиться понять вывод стандартной формулы параболы, различные стандартные формы параболы и свойства параболы.
| 1. | Что такое парабола? |
| 2. | Стандартные уравнения параболы |
| 3. | Парабола Формула |
| 4. | График параболы |
| 5. | Вывод уравнения параболы |
| 6. | Свойства параболы |
| 7. | Часто задаваемые вопросы о Parabola |
Что такое парабола?
 Неподвижная точка называется фокусом параболы, а неподвижная линия — направляющей параболы. Также важно отметить, что фиксированная точка не лежит на фиксированной линии. Геометрическое место любой точки, равноудаленной от данной точки (фокуса) и данной прямой (направляющей), называется параболой. Парабола — важная кривая конических сечений координатной геометрии.
Неподвижная точка называется фокусом параболы, а неподвижная линия — направляющей параболы. Также важно отметить, что фиксированная точка не лежит на фиксированной линии. Геометрическое место любой точки, равноудаленной от данной точки (фокуса) и данной прямой (направляющей), называется параболой. Парабола — важная кривая конических сечений координатной геометрии.Уравнение параболы
Общее уравнение параболы: y = a(x-h) 2 + k или x = a(y-k) 2 +h, где (h,k) обозначает вершину. Стандартное уравнение правильной параболы: y 2 = 4ax.
Некоторые важные термины, приведенные ниже, помогут понять особенности и части параболы.
- Фокус: Точка (a, 0) является фокусом параболы
- Направляющая: Линия, проведенная параллельно оси Y и проходящая через точку (-a, 0), является направляющей параболы. Директриса перпендикулярна оси параболы.
- Фокусная хорда: Фокусная хорда параболы — это хорда, проходящая через фокус параболы.
 Фокальная хорда пересекает параболу в двух различных точках.
Фокальная хорда пересекает параболу в двух различных точках. - Фокусное расстояние: Расстояние точки \((x_1, y_1)\) на параболе от фокуса является фокусным расстоянием. Фокусное расстояние также равно перпендикулярному расстоянию этой точки от директрисы.
- Latus Rectum: Это фокальная хорда, перпендикулярная оси параболы и проходящая через фокус параболы. Длину широкой прямой кишки принимают LL’ = 4а. Концы широкой прямой кишки: (а, 2а), (а, -2а).
- Эксцентриситет: (e = 1). Это отношение расстояния точки от фокуса к расстоянию точки от директрисы. Эксцентриситет параболы равен 1,
Стандартные уравнения параболы
Есть четыре стандартных уравнения параболы. Четыре стандартные формы основаны на оси и ориентации параболы. Поперечная ось и сопряженная ось каждой из этих парабол различны. На изображении ниже представлены четыре стандартных уравнения и формы параболы.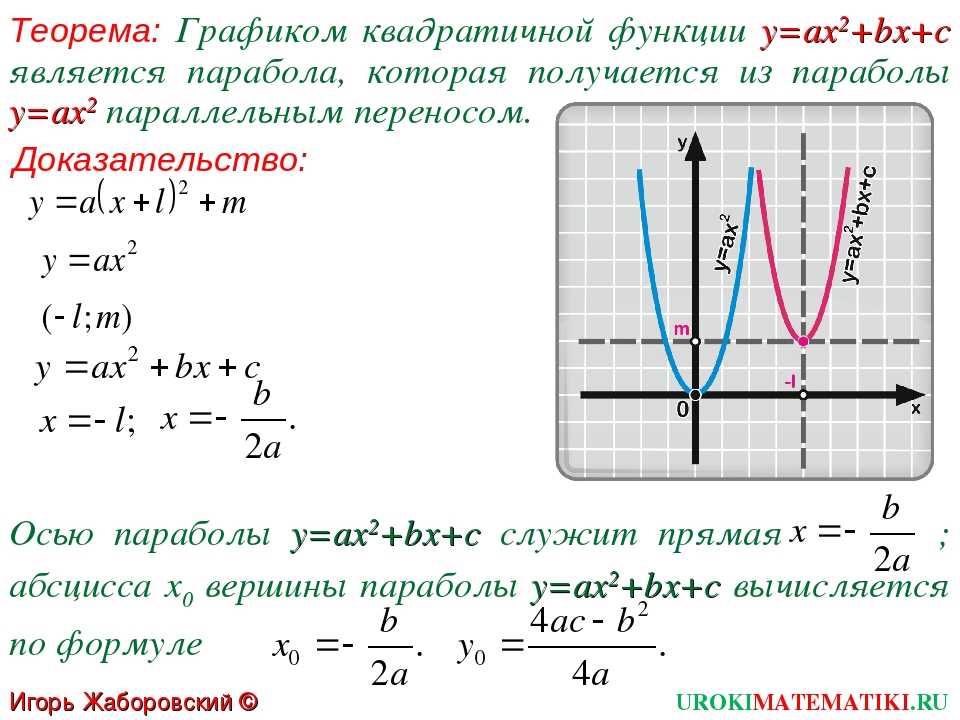
Следующие наблюдения сделаны из стандартной формы уравнений:
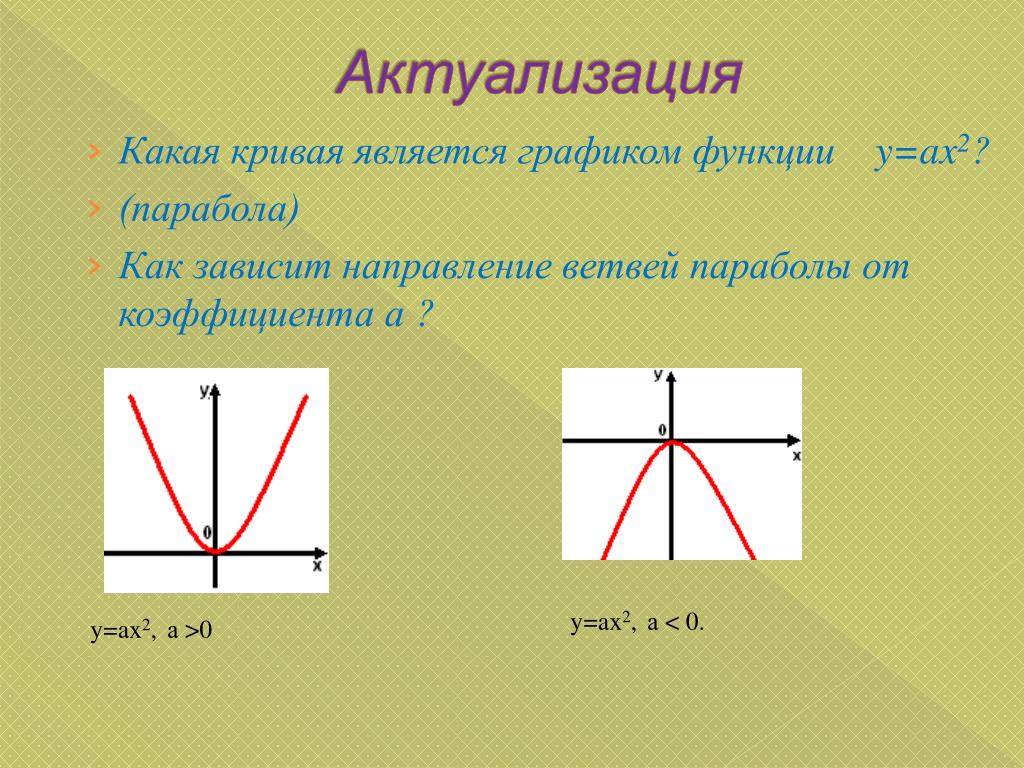
- Парабола симметрична относительно своей оси. Если в уравнении есть член с y 2 , то ось симметрии проходит по оси x, а если в уравнении есть член с x 2 , то ось симметрии проходит по оси y.
- Когда ось симметрии проходит вдоль оси x, парабола открывается вправо, если коэффициент x положительный, и открывается влево, если коэффициент x отрицателен.
- Когда ось симметрии проходит вдоль оси y, парабола открывается вверх, если коэффициент y положительный, и открывается вниз, если коэффициент y отрицателен.
Формула параболы
Формула параболы помогает представить общую форму параболического пути на плоскости. Ниже приведены формулы, которые используются для получения параметров параболы.
- Направление параболы определяется значением a.
- Вершина = (h,k), где h = -b/2a и k = f(h)
- Широкая прямая кишка = 4a
- Фокус: (h, k+ (1/4a))
- Директриса: y = k — 1/4a
График параболы
Рассмотрим уравнение y = 3x 2 — 6x + 5.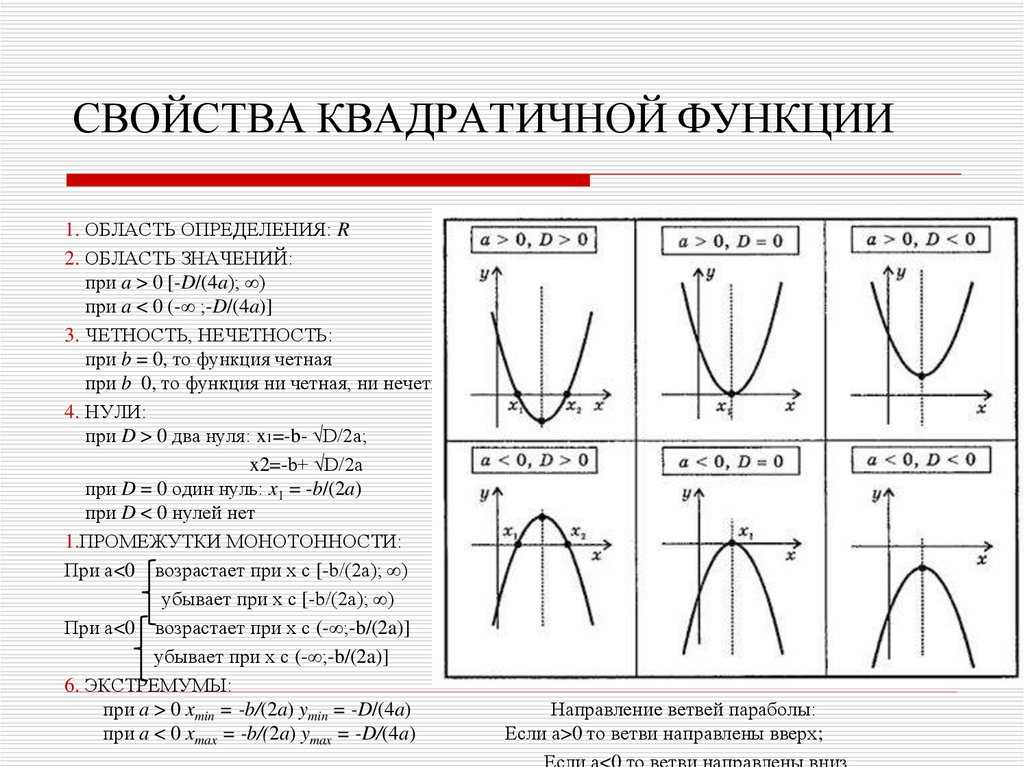 Для этой параболы a = 3, b = -6 и c = 5. Вот график данного квадратного уравнения, которое является параболой.
Для этой параболы a = 3, b = -6 и c = 5. Вот график данного квадратного уравнения, которое является параболой.
Направление: Здесь а положительно, поэтому парабола раскрывается.
Вершина: (h,k)
h = -b/2a
= 6/(2 × 3) = 1
k = f(h)
= f(1) = 3(1) 2 — 6 (1) + 5 = 2
Таким образом, вершина равна (1,2)
Широкая прямая кишка = 4a = 4 × 3 =12
Фокус: (h, k+ 1/4a) = (1,25 /12)
Ось симметрии x =1
Директриса: y = k-1/4a
y = 2 — 1/12 ⇒ y — 23/12 = 0
Вывод уравнения параболы
Рассмотрим точку P с координатами (x, y) на параболе. По определению параболы расстояние этой точки от фокуса F равно расстоянию этой точки P от директрисы. Здесь мы рассматриваем точку B на директрисе, а для расчетов берется перпендикулярное расстояние PB. 92}\)
Возведение уравнения в квадрат в обе стороны,
(х — а) 2 + у 2 = (х + а) 2
х 2 ах 2 5 9 + y 2 = x 2 + a 2 + 2ax
y 2 — 2ax = 2ax
y 2 = 4ax
3.
Точно так же мы можем вывести уравнения парабол как:
- (б): у 2 = – 4акс,
- (с): х 2 = 4ay,
- (г): х 2 = – 4ау.
Приведенные выше четыре уравнения являются стандартными уравнениями парабол.
Свойства параболы
Здесь мы постараемся понять некоторые важные свойства и термины, связанные с параболой.
Касательная: Касательная — это линия, касающаяся параболы. Уравнение касательной к параболе y 2 = 4ax в точке контакта \((x_1, y_1)\) равно \(yy_1 = 2a(x + x_1)\).
Нормаль: Линия, проведенная перпендикулярно касательной и проходящая через точку касания и фокус параболы, называется нормалью. Для параболы y 2 = 4ax уравнение нормали, проходящей через точку \((x_1, y_1)\) и имеющей наклон m = -y1/2a, уравнение нормали имеет вид \((y — y_1) = \dfrac{-y_1}{2a}(x — x_1)\)
Хорда контакта: Хорда, соединяющая точку касания касательных, проведенных из внешней точки к параболе, называется хордой касания. Для точки \((x_1, y_1)\) вне параболы уравнение хорды контакта имеет вид \(yy_1 = 2x(x + x_1)\).
Для точки \((x_1, y_1)\) вне параболы уравнение хорды контакта имеет вид \(yy_1 = 2x(x + x_1)\).
Полюс и поляра: Для точки, лежащей вне параболы, геометрическое место точек пересечения касательных, проведенных на концах хорд, проведенных из этой точки, называется полярой. И эта упомянутая точка называется полюсом. Для полюса с координатами \((x_1, y_1)\), для параболы y 2 =4ax, уравнение поляры: \(yy_1 = 2x(x + x_1)\).
Параметрические координаты: Параметрические координаты уравнения параболы y 2 = 4ax (at 2 , 2at). Параметрические координаты представляют собой все точки параболы.
☛ Также проверьте:
- Эллипс
- Гипербола
Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Примеры параболы
Пример 1: Уравнение параболы: y 2 = 24x. Найдите длину широкой прямой кишки, фокуса и вершины.
Решение:
Найти: Длину широкой прямой кишки, фокус и вершину параболы
Дано: Уравнение параболы: y 2 = 24x
Следовательно, 29 900/24 4 = 6
Теперь формула параболы для прямой кишки:
Длина широкой прямой кишки = 4a
= 4(6) = 24
Теперь, focus= (a,0) = (6,0)
Теперь, Vertex = (0,0)
Ответ: Длина широкой прямой кишки = 24, фокус = (6,0), вершина = (0,0)
Пример 2: Уравнение параболы: 2(y-3) 2 + 24 = x. Найдите длину широкой прямой кишки, фокуса и вершины.
Решение: Найти: длину широкой прямой кишки, фокус и вершину параболы
Дано: уравнение параболы: 2(y-3) 2 + 24 = x
Сравнивая его с общим уравнением параболы x = a(y-k) 2 + h, получаем
a = 2
(h, k) = (24, 3)
Теперь формула параболы для широкой прямой кишки: Длина широкой прямой кишки = 4a
= 4(2) = 8
Теперь фокус = (0, a) = (0,2)
Теперь Вершина = (24,3)
Ответ: Длина широкой прямой кишки = 8, фокус = (0, 2), Вершина = (24,3)
Пример 3.
 Какое уравнение описывает параболу с фокусом (0, 0) и направляющей y = 4?
Какое уравнение описывает параболу с фокусом (0, 0) и направляющей y = 4? Решение:
Учитывая, что Focus = (0, 0) и директриса y = 4
Предположим, что на параболе есть точка (x, y).
Его расстояние от точки фокусировки (0, 0) равно √((x − 0) 2 + (y — 0) 2 )
Его расстояние от направляющей y = 4 равно |y — 4|
Следовательно, уравнение будет таким:
√[(x − 0) 2 + (y — 0) 2 ] = |y — 4|
Квадрат с обеих сторон.
(x — 0) 2 + (y — 0) 2 = (Y — 4) 2
x 2 + Y 2 = Y 2 — 8Y + 16
x 2 + 8y — 16 = 0
Ответ: Следовательно, уравнение параболы с фокусом в точке (0, 0) и направляющей y = 4 равно x 2 + 8y — 16 = 0.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по параболе
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Parabola
Что такое парабола в коническом сечении?
Парабола — важная кривая конического сечения. Это геометрическое место точки, равноудаленной от фиксированной точки, называемой фокусом, а фиксированная линия называется направляющей. Многие движения в физическом мире следуют параболическим траекториям. Следовательно, изучение свойств и приложений параболы является основой для физиков.
Что такое уравнение параболы?
Стандартное уравнение параболы: y 2 = 4ax. Осью параболы является ось x, которая также является поперечной осью параболы. Фокус параболы есть F(a, 0), а уравнение директрисы этой параболы есть x + a = 0,
Что такое вершина параболы?
Вершина параболы — это точка пересечения параболы с осью.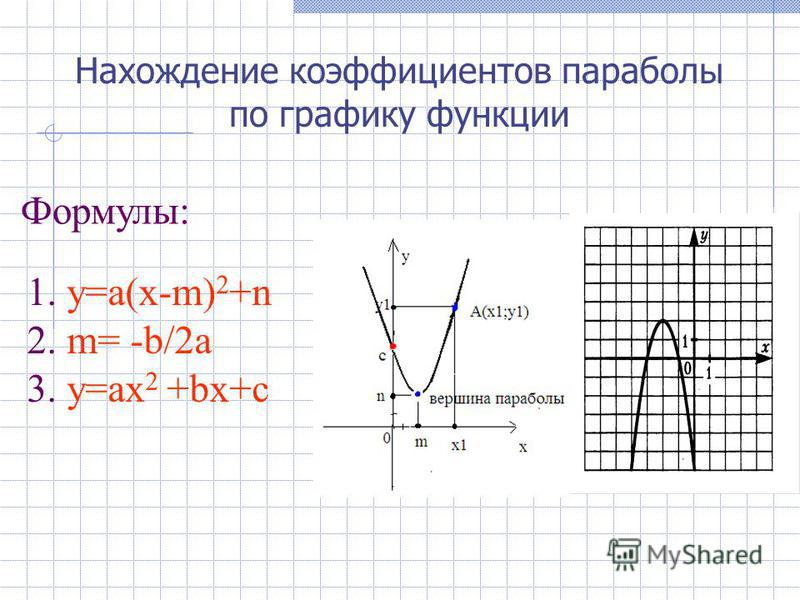 Вершина параболы, имеющей уравнение y 2 = 4ax, равна (0,0), так как она пересекает ось в начале координат.
Вершина параболы, имеющей уравнение y 2 = 4ax, равна (0,0), так как она пересекает ось в начале координат.
Как найти уравнение параболы?
Уравнение параболы можно вывести из основного определения параболы. Парабола — это геометрическое место точки, равноудаленной от фиксированной точки, называемой фокусом (F), а фиксированная линия называется директрисой (x + a = 0). Рассмотрим точку P(x, y) на параболе, и по формуле PF = PM можно найти уравнение параболы. Здесь точка «М» является основанием перпендикуляра из точки Р на директрисе. Следовательно, полученное стандартное уравнение параболы имеет вид y 2 = 4 оси.
Что такое эксцентриситет параболы?
Эксцентриситет параболы равен 1 (e = 1). Эксцентриситет параболы – это отношение расстояния точки от фокуса к расстоянию этой точки от директрисы параболы.
Что такое фокусы параболы?
Парабола имеет только один фокус. Для стандартного уравнения параболы y 2 = 4ax фокус параболы равен F(a, 0). Это точка, лежащая на оси абсцисс и на поперечной оси параболы.
Это точка, лежащая на оси абсцисс и на поперечной оси параболы.
Что такое сопряженная ось параболы?
Линия, перпендикулярная поперечной оси параболы и проходящая через вершину параболы, называется сопряженной осью параболы. Для параболы y 2 = 4ax сопряженной осью является ось y.
Что такое вершины параболы?
Точка на оси, где парабола пересекает ось, является вершиной параболы. Вершина параболы для стандартного уравнения параболы y 2 = 4ax равно (0, 0). Парабола пересекает ось x в начале координат.
Что такое стандартное уравнение параболы?
Стандартное уравнение параболы используется для алгебраического представления параболы в координатной плоскости. Общее уравнение параболы можно записать в виде y = a(x-h) 2 + k или x = a(y-k) 2 +h, где (h,k) обозначает вершину. Стандартное уравнение правильной параболы: y 2 = 4ax.
Как найти поперечную ось параболы?
Линия, проходящая через вершину и фокус параболы, является поперечной осью параболы.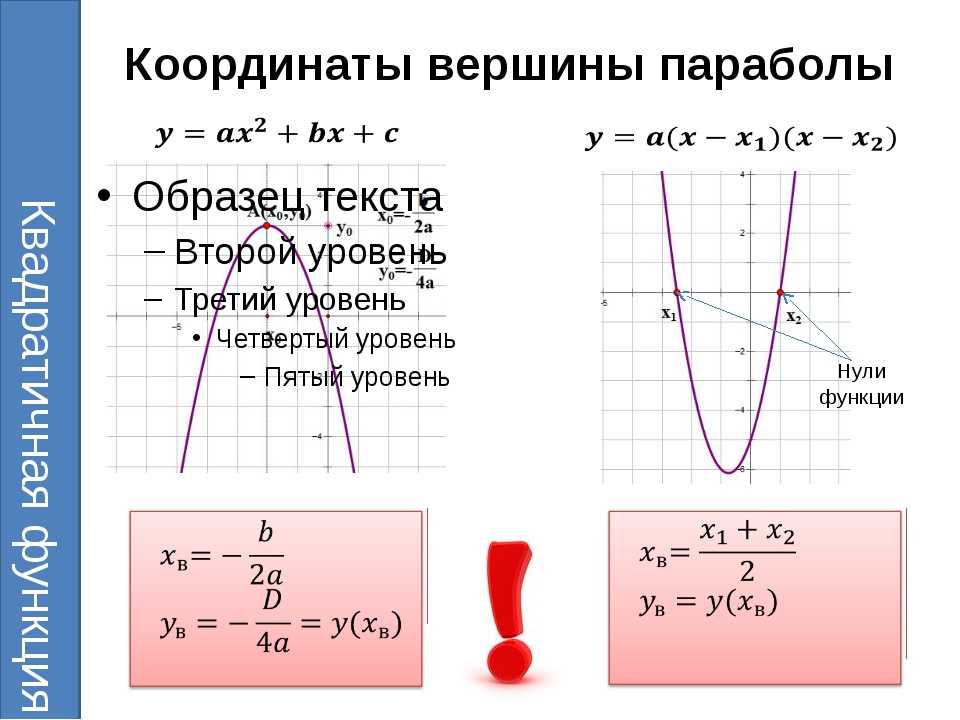 Стандартное уравнение параболы y 2 = 4ax имеет ось x в качестве оси параболы.
Стандартное уравнение параболы y 2 = 4ax имеет ось x в качестве оси параболы.
Общее уравнение параболы:
y = a(x — h) 2 + k (обычное)
x = a(y — k) 2 + h (боковое)
где,
(h,k) = вершина параболы
Где формула параболы используется в реальной жизни?
Параболы используются в физике и технике для траекторий баллистических ракет, конструкции отражателей автомобильных фар и т. д.
Как вы решаете задачи, используя формулу параболы?
Для решения задач на параболы используется общее уравнение параболы, оно имеет общий вид y = ax 2 + bx + c (вершинная форма y = a(x — h) 2 + k), где, (h,k) = вершина параболы.
Все ли формулы парабол представляют функцию?
Все параболы не обязательно являются функциями. Параболы, открывающиеся вверх или вниз, считаются функциями.
Парабола
Парабола определяется как совокупность точек, у которых расстояние до фиксированной точки (фокуса) и фиксированной прямой линии (директрисы) равны. Но, вероятно, его легче запомнить как U-образную изогнутую линию, созданную при построении квадратичного уравнения.
Но, вероятно, его легче запомнить как U-образную изогнутую линию, созданную при построении квадратичного уравнения.
Многие объекты реального мира движутся по параболе. Когда вы бросаете баскетбольный мяч, траектория мяча образует параболу.
Пример
Парабола, которая направлена вверх, имеет форму буквы «U», а парабола, направленная вниз, имеет форму перевернутой буквы U.
|
|
Парабола не обязательно должна быть вертикальной, но горизонтальные параболы не являются функциями (они не проходят тест вертикальной линии). Некоторые функции, которые вы видите, будут горизонтальными параболами с ограниченными областями (). Вы узнаете больше об этом, когда будете изучать коники.
Пример
|
|
Вершина параболы — это точка, в которой парабола меняет направление и где график наиболее изогнут. На графиках квадратичных чисел он находится в самом верху или в самом низу квадратичного уравнения. Вершина — это точка параболы на оси симметрии.
На графиках квадратичных чисел он находится в самом верху или в самом низу квадратичного уравнения. Вершина — это точка параболы на оси симметрии.
Для квадратичных уравнений стандартной формы ax 2 + bx + c ось симметрии можно найти с помощью уравнения x = . Чтобы найти координату y вершины, найдите ось симметрии и подставьте это значение x в исходное уравнение.
Пример
f(x) = x 2 + 6x + 11
a = 1; б = 6; c = 11
x = = -3
f(-3) = (-3) 2 + 6(-3) + 11
f(-3) = 9 — 18 + 11 = 2
Вершина в точке (-3,2)
Расчет фокуса и директрисы
Ниже приведен пример расчета фокуса и директрисы, который поможет лучше понять математическое определение параболы, приведенное выше:
Пример
Фокус — это точка, расположенная на одной линии с осью симметрии, а директриса — это линия, перпендикулярная оси симметрии. Для парабол фокус всегда находится внутри параболы, а директриса никогда не касается параболы.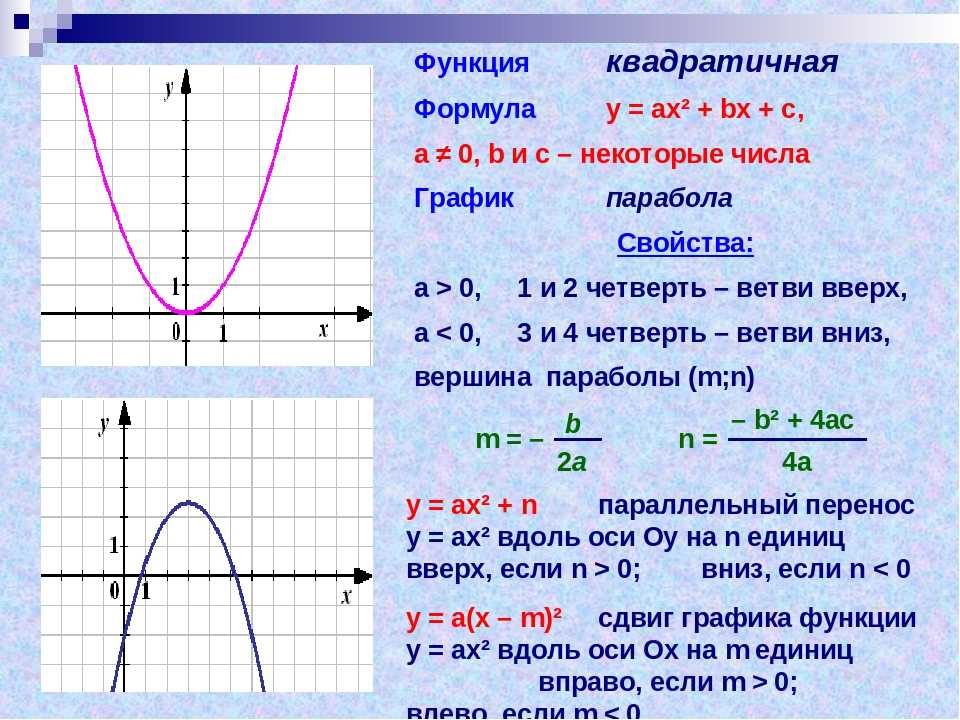 Поскольку вершина находится на одинаковом расстоянии от фокуса и директрисы, директриса находится прямо напротив фокуса.
Поскольку вершина находится на одинаковом расстоянии от фокуса и директрисы, директриса находится прямо напротив фокуса.
Для параболы в форме вершины y = a(x — h) 2 + k фокус расположен в точке (h, k + ), а направляющая расположена в точке y = k — .
Пример
y = (x — 3) 2 + 2
h = 3 ; к = 2; a =
Фокус: (3,2 + ) = (3,4)
Директриса: y = 2 — = 0
Для горизонтальных парабол вершина x = a(y — k) 2 + h , где (h,k) — вершина. Фокусы парабол в этой форме имеют фокус, расположенный в точке (h + , k), и направляющую в точке x = h — . Ось симметрии расположена в точке y = k.
Вершинная форма параболы
Вершинная форма параболы является другой формой квадратичной функции f(x) = ax 2 + бх + в. Вершинная форма параболы:
f(x) = a(x — h) 2 + k
А в вершинной форме параболы соответствует а в стандартной форме.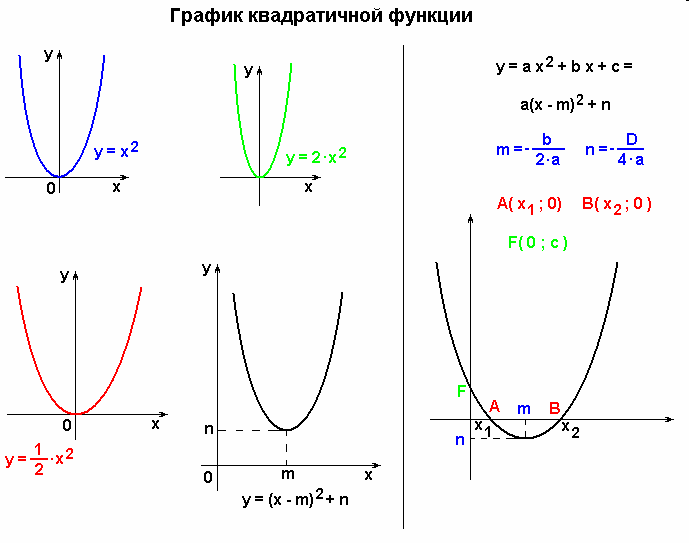 Если a положительно, парабола направлена вверх. Если а отрицательно, парабола направлена вниз.
Если a положительно, парабола направлена вверх. Если а отрицательно, парабола направлена вниз.
В вершинной форме (h,k) описывает вершину параболы, а парабола имеет линию симметрии x = h.
Форма вершины очень похожа на общее выражение для преобразований функций. Форма вершины значительно упрощает построение параболы, потому что она упрощает построение вершины.
Пример
f(x) = -(x — 1) 2 + 4
Из этого уравнения мы уже можем сказать, что вершина параболы находится в точке (1,4), а ось симметрии находится в точке x = 1. Теперь все, что нужно сделать, это подставить точки вокруг вершины, а затем построить график.
Вы можете использовать завершение квадрата для преобразования квадратного числа в стандартной форме в вершинную форму. Вы также можете преобразовать форму вершины, зная, что вершина лежит на оси симметрии.
Значение x вершины равно x = — , поэтому значение y равно y = f (-). Подставьте эти значения для h и k в уравнение формы вершины.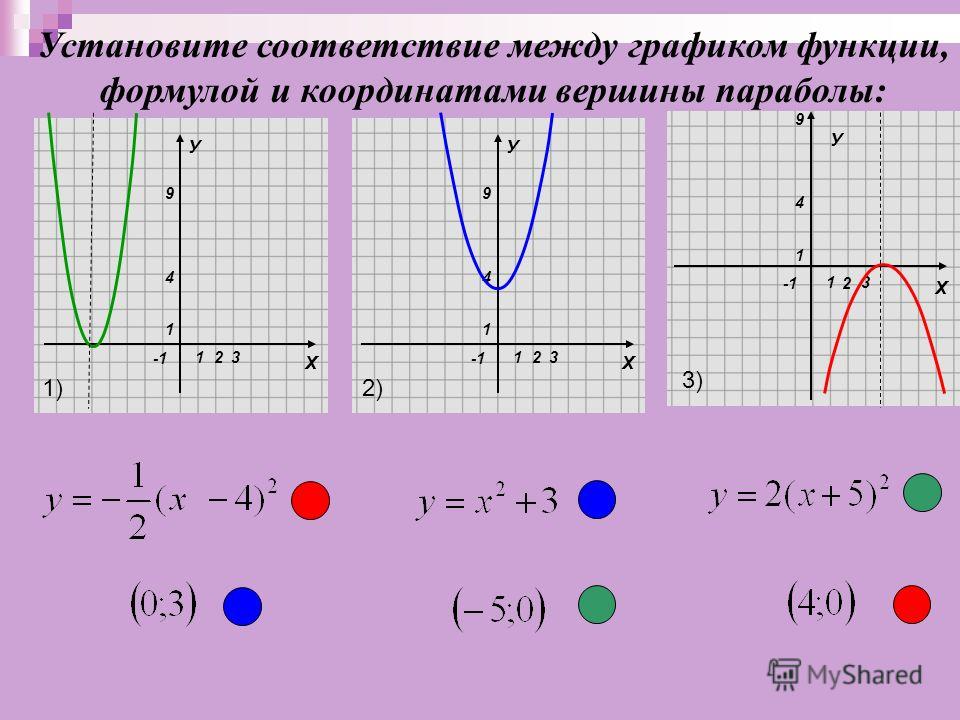

 Фокальная хорда пересекает параболу в двух различных точках.
Фокальная хорда пересекает параболу в двух различных точках.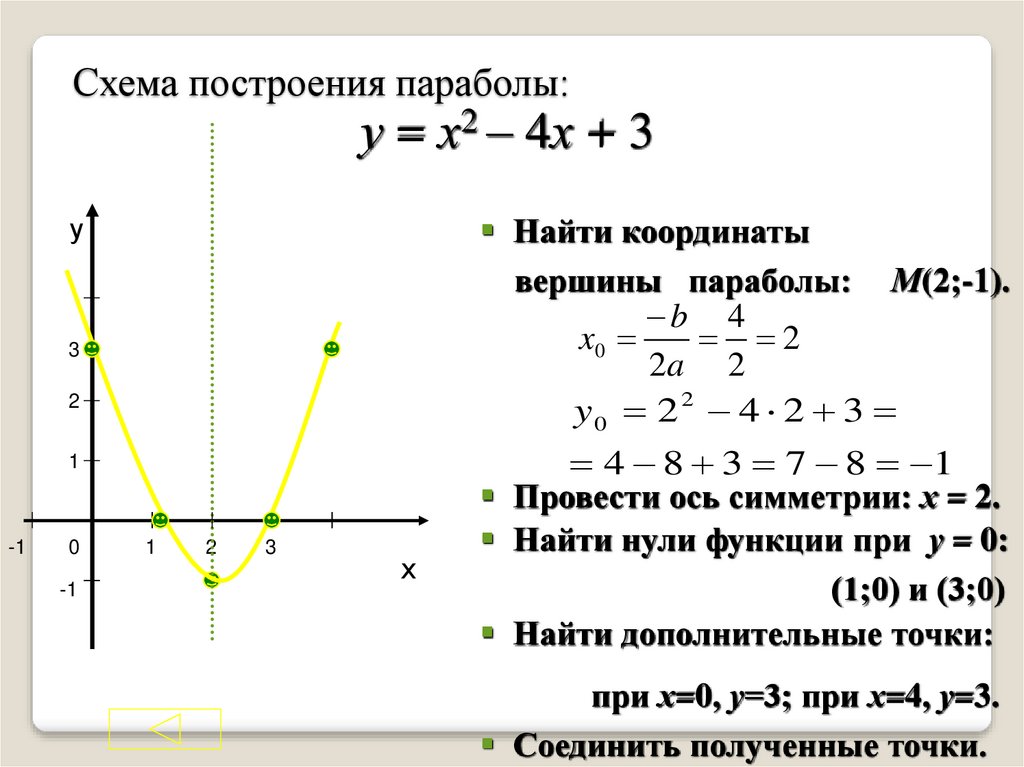 Какое уравнение описывает параболу с фокусом (0, 0) и направляющей y = 4?
Какое уравнение описывает параболу с фокусом (0, 0) и направляющей y = 4?