Тригонометрический круг — понятие, как им пользоваться онлайн
Общие сведения
Для правильного решения тригонометрических задач следует изучить основные понятия, формулы, а также методы нахождения основных величин. Раздел математики, изучающий функции косинуса, синуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса, называется тригонометрией. Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.
Значения функций, которые можно по ней находить, называются тригонометрическими. Однако существует множество способов нахождения их значений, но в некоторых ситуациях при использовании формул приведения решение затянется на продолжительное время, а вычисления будут громоздкими. Чтобы этого избежать, нужно использовать тригонометрический круг со всеми значениями. С его помощью также можно определить, является ли функция четной или нечетной.
youtube.com/embed/YpeV6t0nKxs»>Углы и их классификация
Перед тем как понять основное назначение тригонометрических функций, следует обратить внимание на классификацию углов. Она является важной для вычисления тригонометрических выражений. Углы в математических дисциплинах делятся на следующие типы:
- Острые.
- Прямые.
- Тупые.
- Развернутые.
- Выпуклые.
- Полные.
К первому типу относятся углы любой размерности градусной единицы измерения, которая не превышает 90 (а<90). Если значение соответствует 90, то он является прямым (а=90). Угол считается тупым, при выполнении следующего условия: 90<a<180. Если градусная размерность угла соответствует 180, то он является развернутым (а = 180). Выпуклым считается угол, когда выполняется такое условие: 180 < a < 360. Следует отметить, что он является смежным с острым углом. В случае, когда значение градусной размерности соответствует 360 градусам, то он является полным (а=360).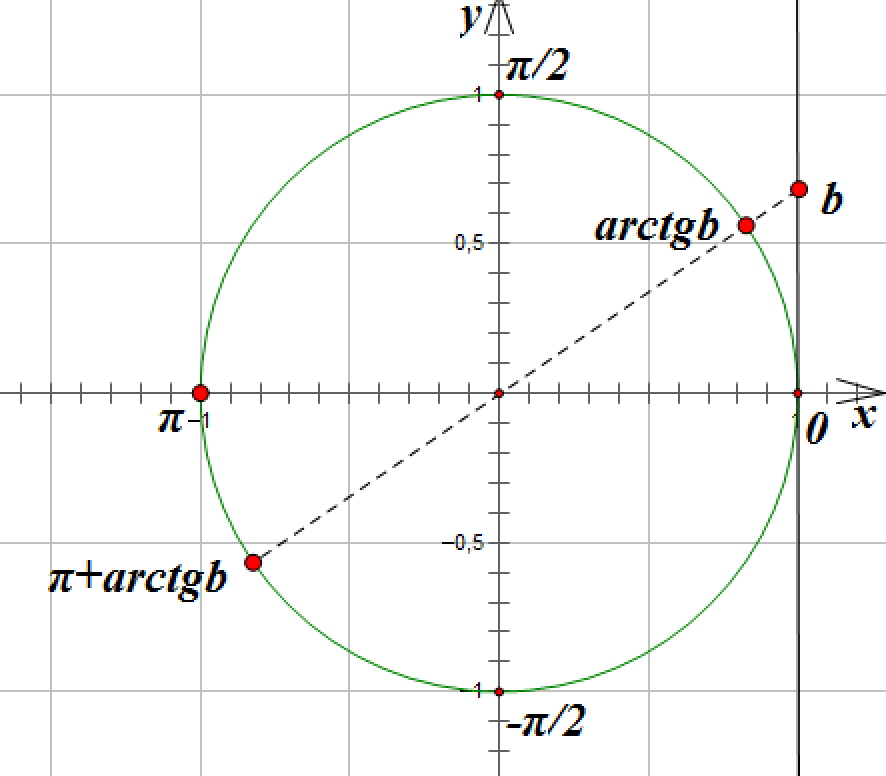
Однако углы измеряются не только в градусах, но и в радианах. Для решения тригонометрических задач оптимальным выбором градусной меры является радиан. Для соотношения между двумя единицами измерения применяется простая формула: 180 (град) = ПИ (рад). Из соотношения можно вывести формулу для перевода градусов в радианы: Pрад = (а * ПИ) / 180. Переменная «а» — значение величины градусной меры заданного угла. Обратное соотношение принимает следующий вид: а = (Ррад * 180) / ПИ.
Для быстрого перевода единиц измерения применяют такие инструменты: радианная табличка, программное обеспечение и тригонометрическая окружность. Однако для начала следует обратить внимание на тригонометрические функции, которые присутствуют в задачах физико-математического уклона.
Информация о функциях
Тригонометрических функций всего четыре вида: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.
Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.
Например, зависимость амплитуды напряжения переменного тока от времени описывается следующим законом: u = Um * cos (w*t) (графиком является косинусоида). Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.
Синусом угла называется величина, равная отношению противолежащего катета прямоугольного треугольника к его гипотенузе. Следовательно, косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение величины противолежащего катета к прилежащему. Котангенс является обратной функцией тангенсу, т. е. отношение прилежащего к противолежащему.
е. отношение прилежащего к противолежащему.
Функции arcsin, arccos, arctg, arcctg применяются в том случае, когда нужно найти значение угла в градусах или радианах. Вычисления выполняются по специальным таблицам Брадиса или с помощью программ. Также можно использовать тригонометрическую окружность.
Тригонометрический круг
Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, косинусе, тангенсе, котангенсе, системе координат и теореме Пифагора. Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.
Для решения задач различного типа применяется и теорема Пифагора. Она справедлива только для прямоугольного треугольника (один из углов — прямой). Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов. Следует также знать основные соотношения между функциями острых углов в заданном прямоугольном треугольнике:
Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов. Следует также знать основные соотношения между функциями острых углов в заданном прямоугольном треугольнике:
- a + b = 180.
- cos(a) = sin(b).
- cos(b) = sin(a).
- tg(a) = ctg(b).
- tg(b) = ctg(a).
- tg(a) = 1 / ctg(a).
- tg(b) = 1 / ctg(b).
Существуют и другие тригонометрические тождества, но для работы с кругом этого перечня будет достаточно.
Построение «инструмента»
Построить окружность, которая ускорит процесс решения задач, довольно просто. Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).
Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).
Окружность является единичной, но не стоит рисовать ее такой, поскольку работать будет неудобно. Этот прием называется масштабированием. Он широко применяется практически во всех сферах человеческой деятельности. Например, инженеры не чертят двигатель космического корабля в натуральную величину, поскольку с таким «рисунком» будет неудобно и невозможно работать. Они используют его макет.
Окружность пересекается с осями декартовой системы координат в 4 точках со следующими координатами: (1;0), (0;1), (-1;0) и (0;-1). Области, которые делят декартовую систему координат на 4 части, называются четвертями. Их четыре:
- Первая состоит из положительных координат по х и у.
- Вторая имеет по х отрицательные и положительные по у.
- Третья — только отрицательные значения.
- Четвертая — положительные значения по х и отрицательные по у.
Исходя из этих особенностей, определяется числовой знак функции, позволяющий определить ее четность и нечетность.
Готовый макет
Для решения задач специалисты рекомендуют иметь рабочий и готовый макеты тригонометрических окружностей. Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. д.).
Рисунок 1. Готовый макет тригонометрического круга синусов и косинусов.
Для нахождения необходимых значений объединяют две фигуры — единичную окружность и прямоугольный треугольник. Гипотенуза последнего равна 1 и соответствует радиусу окружности. Ось ОХ — косинусы, ОУ — синусы. С помощью этого «инструмента» определение синусов и косинусов становится намного проще. Для нахождения значения sin(30) необходимо воспользоваться следующим алгоритмом:
- Отметить угол на окружности и достроить его до прямоугольного треугольника.
 2] = sqrt(3) / 2.
2] = sqrt(3) / 2.Однако после всех вычислений следует выбрать знак функции. В данном случае угол находится в первой четверти. Следовательно, функция имеет положительный знак. Для нахождения тангенса и котангенса можно воспользоваться следующими формулами: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Подставив значения синуса и косинуса, можно определить значение tg: tg(30) = 0,5 / (sqrt(3) / 2) = 1 / sqrt(3) = sqrt(3) / 3. Тогда котангенс можно найти двумя способами:
- Через известный тангенс: ctg(30) = 1 / (1 / sqrt(3)) = sqrt(3).
- Использовать основное отношение: ctg(30) = (sqrt(3) / 2) / (1/2) = sqrt(3).
Вычислить значения синуса и косинуса для угла 60 градусов очень просто. Для этого нужно воспользоваться основными тождествами: sin(60) = сos(30) = sqrt(3) / 2, cos(60) = sin(30) = 1/2, tg(30) = ctg(60) = sqrt(3) / 3, tg(60) = ctg(30) = sqrt(3).
- Прямоугольный треугольник с углом 45 градусов является равносторонним (катеты равны).
 2 = 1.
2 = 1. - sin(45) + cos(45) = sqrt(2) / 2.
Тангенс и котангенс равен 1. Если угол равен 90, то необходимо внимательно посмотреть на рисунок 1. Следовательно, sin(90) = 1, cos(90) = 0, tg(90) = 1 и ctg(90) не существует. Линия тангенса на окружности не отображается. В этом случае нужно пользоваться основными тригонометрическими тождествами.
Правила использования
Инструмент позволяет легко и быстро находить значения тригонометрических функций любых углов. Если при решении задачи требуется найти sin(270), то нужно выполнить простые действия:
- Пройти против часовой стрелки (положительное направление) 180 градусов, а затем еще 90.
- На оси синусов значение составляет -1 (точка лежит на оси).
Существуют задачи, в которых угол представлен отрицательным значением. Например, нужно определить синус, косинус, тангенс и котангенс угла (-7ПИ/6).
 В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).
В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).Пример случая, когда нет необходимости переводить радианы в градусы, является следующим: нужно вычислить значения тригонометрических функций угла 5ПИ/4. Необходимо расписать значение угла таким образом: 5ПИ/4 = ПИ + ПИ/4. Против часовой стрелки следует пройти половину круга (ПИ), а затем его четвертую часть (ПИ/4). Далее нужно спроецировать координаты точки на ось синусов и косинусов. Это соответствует значению sqrt(2)/2. Тангенс и котангенс заданного угла будут равны 1.
Встречаются задачи, в которых значение угла превышает 360 градусов.
 Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.
Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.Таким образом, тригонометрический круг позволяет оптимизировать вычисления в дисциплинах с физико-математическим уклоном, в которых используются тригонометрические функции. Не имеет смысла устанавливать дополнительное программное обеспечение, пользоваться таблицами, поскольку это занимает некоторое время. При помощи этого «универсального инструмента» можно найти значение любого угла.
Тригонометрический круг презентация, доклад
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Тригонометрический круг, предмет презентации: Математика.
 Этот материал содержит 21 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Этот материал содержит 21 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!Слайд 1 Текст слайда: Центр образования « Школа здоровья» № 1099 « Ярославский».
Сенникова Наталья Викторовна, учитель математики
г. Москва
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ.
Использованная литература: Мордкович А. Г., Тульчинская Е. Е. Тригонометрия – М.: Издательский дом «Новый учебник» АО «Московский учебник», 1999.
Слайд 2 Текст слайда: «ШПАРГАЛКА», КОТОРАЯ
ВСЕГДА С ТОБОЙ.Ось косинусов
Ось
синусовОсь котангенсов
Ось
тангенс овПОШАГОВОЕ
ПОСТРОЕНИЕУСКОРЕННЫЙ
ПОКАЗСлайд 3 Текст слайда: r = 1
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
I четверть
II четверть
III четверть
VI четверть
Слайд 4 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
—
Слайд 5 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Слайд 6 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Слайд 7 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Слайд 8 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Слайд 9 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
1
2
3
2
2
2
+
Слайд 10 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Слайд 11 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Слайд 12 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Слайд 13 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
1
0
+
Слайд 14 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
—
Слайд 15 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
—
Слайд 16 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Ось тангенсов
—
Ось котангенсов
Слайд 17 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Ось тангенсов
—
Ось котангенсов
Слайд 18 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Ось тангенсов
—
Ось котангенсов
Слайд 19 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Ось тангенсов
—
Ось котангенсов
Слайд 20 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Слайд 21 Текст слайда: ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Ось косинусов
Ось синусов
+
Ось тангенсов
—
Ось котангенсов
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте.
 Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:Email: Нажмите что бы посмотреть
Что такое ThePresentation.ru?
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Урок 6 | Единичный круг и тригонометрические функции | 11 класс Математика
Цель
Определить и оценить тригонометрические функции тангенса, косеканса, секанса и котангенса.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Ф.ТФ.А.2 — Объясните, как единичный круг на координатной плоскости позволяет распространить тригонометрические функции на все действительные числа, интерпретируемые как радианные меры углов, пройденных против часовой стрелки вокруг единичного круга.

Ф.ТФ.А.3 — Используйте специальные треугольники, чтобы определить геометрически значения синуса, косинуса, тангенса для π/3, π/4 и π/6, и используйте единичный круг, чтобы выразить значения синуса, косинуса и тангенса для π-x, π +x и 2π-x через их значения для x, где x — любое действительное число.
Основополагающие стандарты
Основополагающие стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950G.SRT.C.6
Критерии успеха
Основные понятия, которые учащиеся должны продемонстрировать или понять для достижения цели урока.
- Вычислите все шесть тригонометрических функций по опорным углам.
- Этот демонстрационный инструмент с кругом единиц полезен для демонстрационных целей.

- «10 секретных триггерных функций, которым вас не учили учителя математики» Эвелин Лэмб на сайте ScientificAmerican.com предоставляет интересный контекст для различных тригонометрических функций.
- Открытый Средний Триггерные отношения
- Открытая середина Триггерные функции
- EngageNY Mathematics Algebra II > Модуль 2 > Тема A > Урок 7
- Иллюстративная математика Равносторонние треугольники и тригонометрические функции — Это дополнительная задача, в которой для получения тригонометрии используются некоторые геометрические понятия.
- Математические ошибки Если sin(x)/cos(x)=3/5, то 1/cos(x)=1/5 — Этот пост потрясающий. Он подходит к рассуждениям об отношениях и использует свойства слишком буквально, не помня, что они являются отношениями.
Советы учителям
Рекомендации учителям по проведению этого урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Проблемы с якорем
Задачи, предназначенные для изучения ключевых моментов урока, и наводящие вопросы, помогающие ученикам понять
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Проблема 1
Ниже приведены шесть различных тригонометрических соотношений, отмеченных на единичной окружности.
«$${\mathrm{sec}\theta}$$» — «секанс тета»
«$${\mathrm{cosec}\theta}$$» — «косекеканс тета» (также может быть записано как $${\mathrm{csc}\theta}$$)
«$${\mathrm{cot}\theta}$$» является «котангенсом тета»
Какая связь между синусом, косинусом и тангенсом и этими тремя новыми тригонометрическими функциями?
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Каталожные номера
GeoGebra Взаимные триггерные функции на единичном круге
Взаимные триггерные функции на единичном круге от mathsurgery.wikispaces предоставлены GeoGebra под лицензией CC BY-NC-SA 3.0. Авторское право © Международный институт GeoGebra, 2013. По состоянию на 26 февраля 2018 г., 13:00. 9\circ)}$$
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Проблема 3
На изображении ниже показаны положительные и отрицательные значения синуса и косинуса. Заполните аналогичное изображение для косеканса, секанса, тангенса и котангенса.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Набор проблем
Набор предлагаемых ресурсов или типов задач, которые учителя могут преобразовать в набор задач
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950 Следующие ресурсы включают проблемы и действия, связанные с целью
урок, который можно использовать для создания собственного набора задач.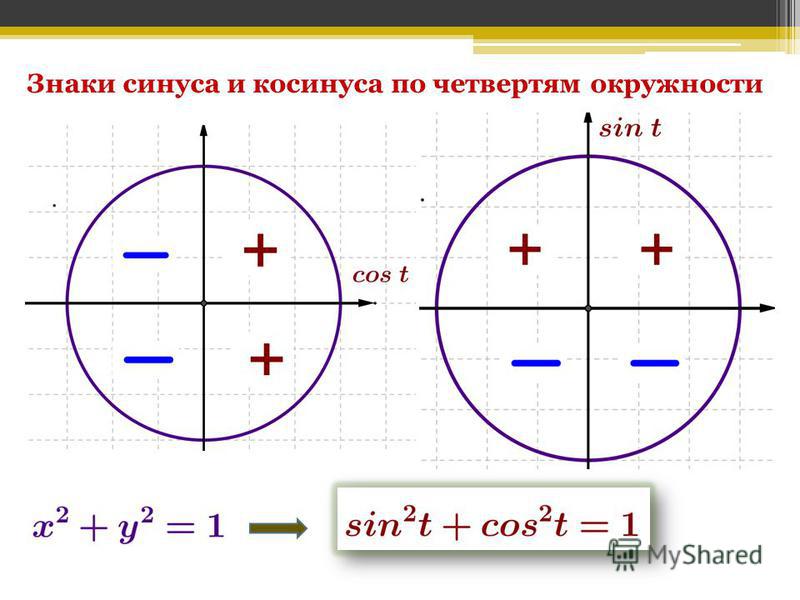
Целевая задача
Задача, которая представляет собой пик мышления урока — мастерство покажет, была ли достигнута цель 9\circ}$$
Проблема 2
Где значение $${\mathrm{sec}\theta}$$ не определено?
значок/стрелка/вправо/крупная копияУрок 5
значок/стрелка/вправо/большойУрок 7
Круговые функции
График уравнения окружность в прямоугольной системе координат.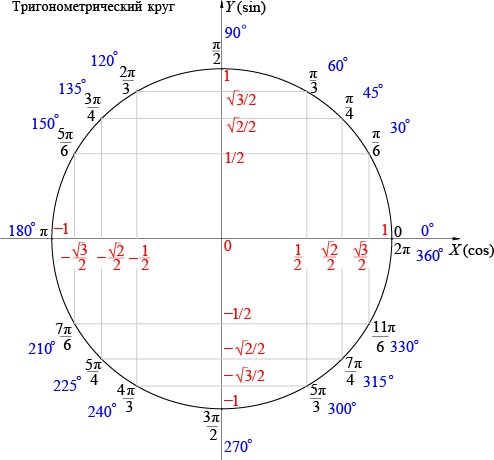 Этот график называется единичной окружностью , его центр находится в начале координат, а радиус равен 1 единице. Тригонометрические функции определяются так, что их домены — это наборы углов , а их диапазоны — это наборы действительных чисел. Круговые функции определены таким образом, что их областью определения являются наборы чисел , которые соответствуют мерам (в радианах) углов аналогичных тригонометрических функций. Диапазоны этих круговых функций, как и их аналогичные тригонометрические функции, представляют собой наборы действительных чисел. Эти функции называются круговыми, потому что радианные меры углов определяются длинами дуг окружностей. В частности, тригонометрические функции, определенные с помощью единичного круга, ведут непосредственно к этим круговым функциям.
Этот график называется единичной окружностью , его центр находится в начале координат, а радиус равен 1 единице. Тригонометрические функции определяются так, что их домены — это наборы углов , а их диапазоны — это наборы действительных чисел. Круговые функции определены таким образом, что их областью определения являются наборы чисел , которые соответствуют мерам (в радианах) углов аналогичных тригонометрических функций. Диапазоны этих круговых функций, как и их аналогичные тригонометрические функции, представляют собой наборы действительных чисел. Эти функции называются круговыми, потому что радианные меры углов определяются длинами дуг окружностей. В частности, тригонометрические функции, определенные с помощью единичного круга, ведут непосредственно к этим круговым функциям.
Начните с единичного круга x 2 + y 2 = 1, показанного на рисунке . Точка A (1,0) расположена на пересечении единичной окружности и оси x . Пусть q — любое действительное число. Начните с точки A и измерьте | q | единиц по единичной окружности против часовой стрелки, если q > 0, и по часовой стрелке, если q < 0, заканчивая точкой Р ( х, у ). Задайте синус и косинус q как координаты точки P . Другие круговые функции (тангенс, котангенс, секанс и косеканс) могут быть определены через синус и косинус.
Пусть q — любое действительное число. Начните с точки A и измерьте | q | единиц по единичной окружности против часовой стрелки, если q > 0, и по часовой стрелке, если q < 0, заканчивая точкой Р ( х, у ). Задайте синус и косинус q как координаты точки P . Другие круговые функции (тангенс, котангенс, секанс и косеканс) могут быть определены через синус и косинус.
Рисунок 1
Единица измерения окружности.
Sin q и cos q существуют для каждого действительного числа q , потому что (cos q , sin q ) — координаты точки P , расположенной на единичной окружности, что соответствует длине дуги | д |. Поскольку эта длина дуги может быть положительной (против часовой стрелки) или отрицательной (по часовой стрелке), домен каждой из этих круговых функций представляет собой набор действительных чисел. Диапазон более ограничен. Косинус и синус — это абсцисса и ордината точки, движущейся по единичной окружности, и они варьируются от −1 до 1. Следовательно, диапазон каждой из этих функций представляет собой набор действительных чисел z такое, что −1 ⩽ z ⩽ 1 (см. рис. 2).
Диапазон более ограничен. Косинус и синус — это абсцисса и ордината точки, движущейся по единичной окружности, и они варьируются от −1 до 1. Следовательно, диапазон каждой из этих функций представляет собой набор действительных чисел z такое, что −1 ⩽ z ⩽ 1 (см. рис. 2).
Рисунок 2
Диапазон значений триггерных функций.
Пример 1: Какие значения x в области синусоидальной функции между −2π и 2π имеют значение диапазона, равное 1 (рис. 3 )?
Рисунок 3
Чертеж для примера 1.
Значение диапазона sin x равно 1, когда точка P имеет координаты (0, 1). Это происходит, когда x = π/2 и x = −3π/2.
Пример 2: Какие значения x в области функции косинуса между −2π и 2π имеют значение диапазона −1 (рис. 4 )?
Рисунок 4
Чертеж для примера 2.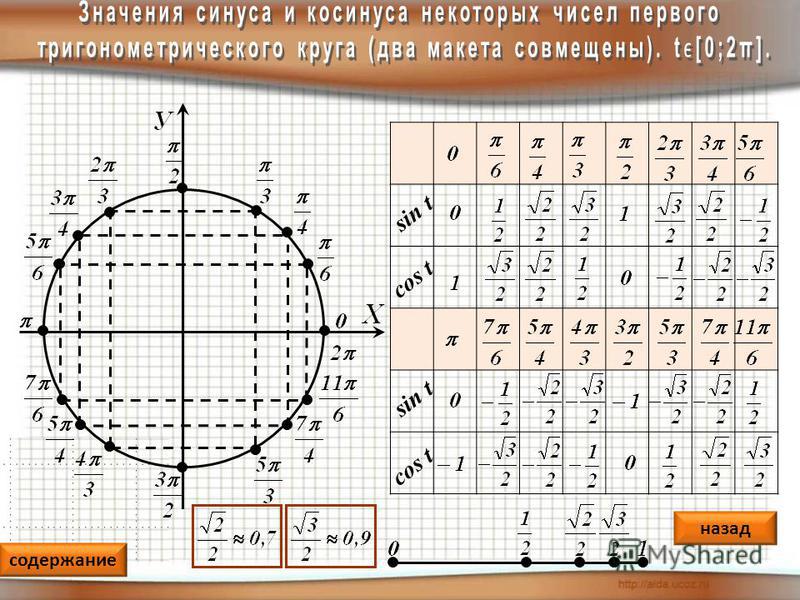

 2] = sqrt(3) / 2.
2] = sqrt(3) / 2.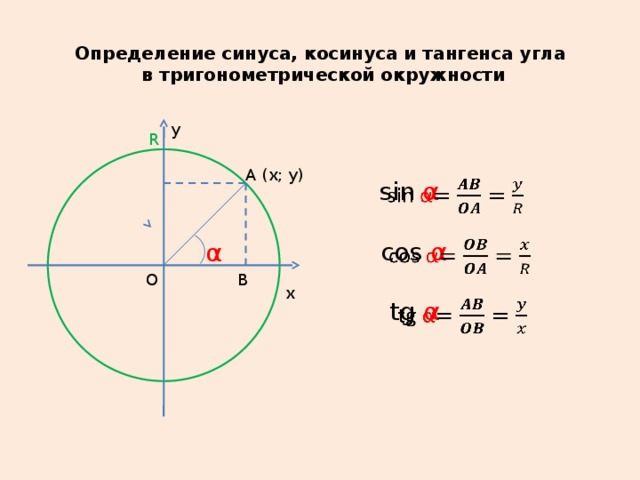 2 = 1.
2 = 1. В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).
В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).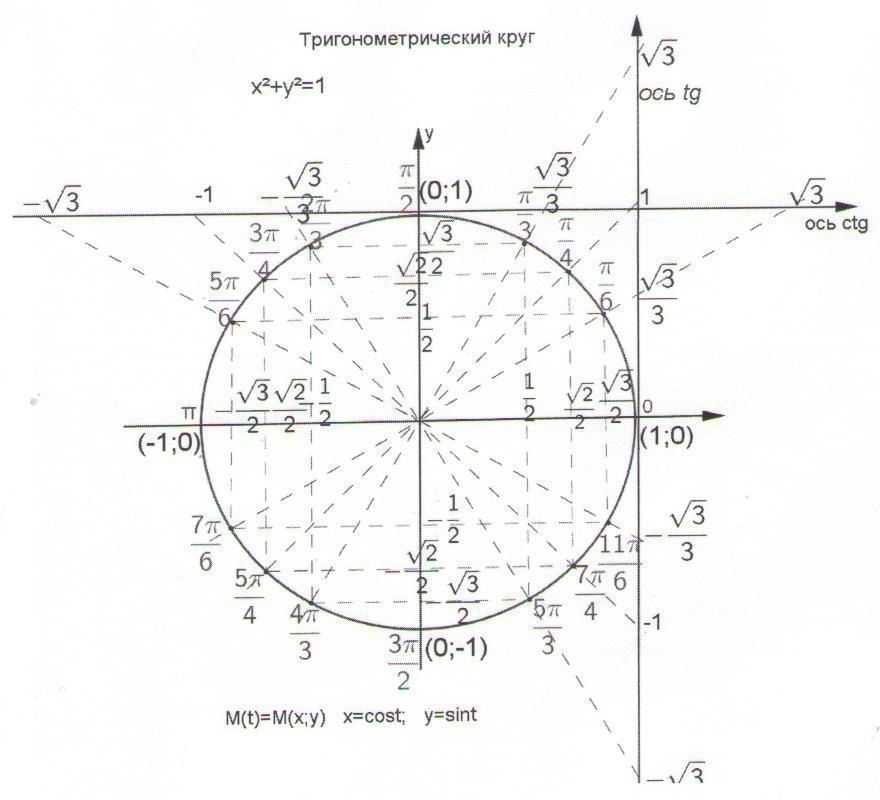 Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.
Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно. Этот материал содержит 21 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Этот материал содержит 21 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки! Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
