ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ — Без Сменки
30 июня, 2022
1 мин
Многие выражения, содержащие синусы и косинусы становятся значительно проще, если пользоваться надежным инструментом — тригонометрическим кругом. А для этого нужно три простых шага и запомнить их: один раз сделал, запомнил и заслуженная пара баллов в кармане.
💁🏼♀ Разделим тригонометрический круг на 4 четверти, или квадранта. Первая четверть соответствует интервалу углов 0<α<90, вторая четверть соответствует углам 90<α<180, третья четверть лежит в интервале 180<α<270, и, наконец, четвертая четверть находится в интервале 270<α<360.
✅ Знаки тригонометрических функций зависят от того, в какой четверти находится угол. Синус положительный в первой и второй, косинус в первой и четвертой, а тангенс и котангенс одинаково положительны в первой и третьей. На картинке указаны знаки тригонометрических функций, которые смело можно сохранять.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите 
Мы обязательно поправим!
Честно. Понятно. С душой.
45 подписчиков
+ Подписаться
Редакция Без Сменки01 июля, 2022
1 мин
Хим 🧪
Белки
❗️Полипептидная цепочка — это первичная структура белка.
Подробное рассмотрение структуры белка.
06 июня, 2022
1 мин
Англ 🇬🇧
Как читать на английском?Если тебе сложно заставить себя читать даже на русском, а на английском ты читал только вгоняющие в…
Редакция Без Сменки07 июня, 2022
1 мин
Англ 🇬🇧
Maybe, probably, perhaps, possiblyИтак, все эти слова, разумеется, являются синонимами, и переводятся как «вероятно», «возможно». Но…
03 июня, 2022
1 мин
Ист 🤴
Дворцовые перевороты
👉🏻 ПРИЧИНЫ ДВОРЦОВЫХ ПЕРЕВОРОТОВ:
— 1722 г.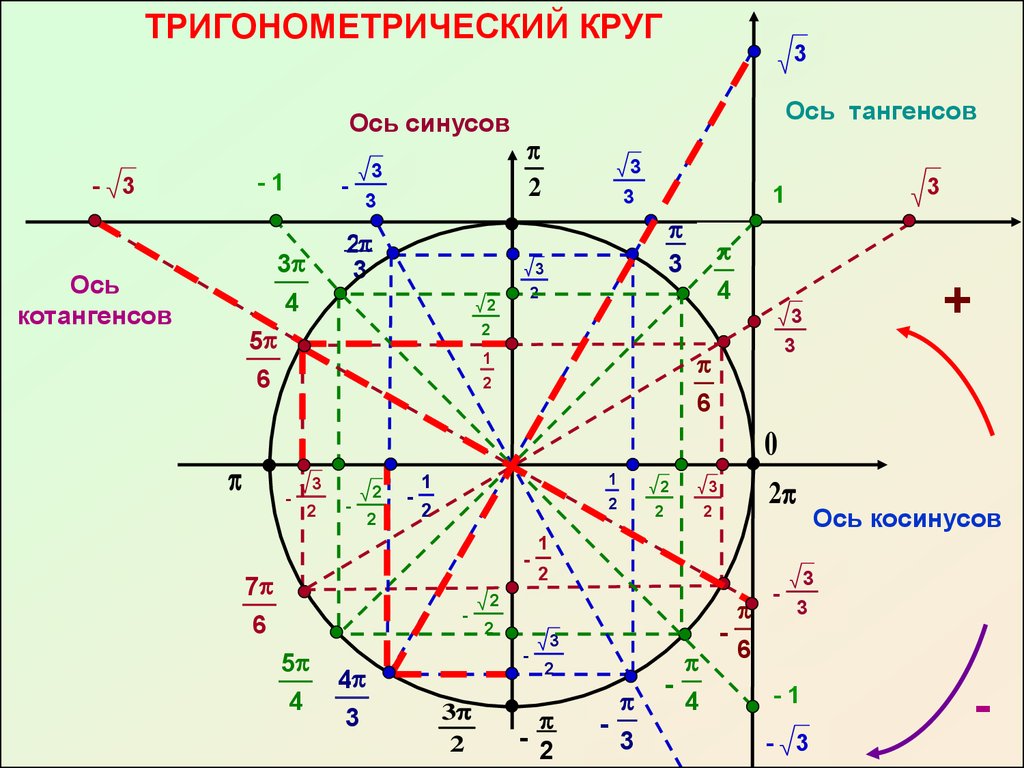
— указ Петра I о престолонаследии
— 1725 г. —…
10 класс. Алгебра. Тригонометрические функции. Тригонометрические функции числового аргумента. — Тангенс и котангенс.
Комментарии преподавателяТангенс и котангенс
На предыдущем уроке мы вспомнили определение синуса и косинуса. Дадим определение тангенса и котангенса.
Рассмотрим числовую окружность в координатной плоскости. Дано произвольное число Ему соответствует единственная точка на окружности. У точки есть две координаты (рис. 1).
Координату назвали косинусом числа координату синусом числа
Тангенсом числа называется отношение синуса к косинусу Котангенсом называется отношение косинуса к синусу .
Определим связь между тангенсом и котангенсом.
Линии синусов и косинусов – это координатные оси.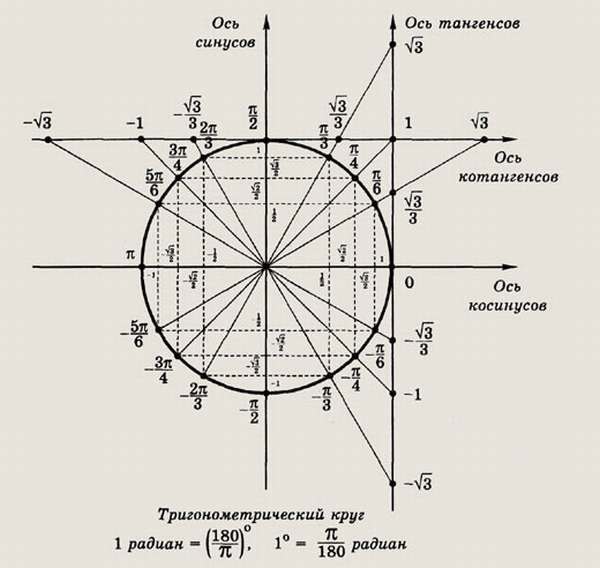
Линией тангенсов является касательная к окружности в точке A, параллельная оси y, линией котангенсов – касательная в точке B, параллельная оси x (рис. 2).
Вычислим тангенсы и котангенсы основных углов.
|
|
|
||||
|
1 |
|||||
|
1 |
0 |
Значения тангенса и котангенса угла найдем из прямоугольного равнобедренного треугольника (рис.
3):
Изобразим полученные значения тангенсов на числовой окружности (рис. 4).
Пример 1. Найти
Решение (рис. 5).
Пример 2. Решить уравнение
Решение:
Найдем на линии тангенсов точку проведём прямую через эту точку и начало координат и получим две точки пересечения с окружностью – (рис. 6).
Ответ:
Пример 3. Решить уравнение
Решение (рис. 7).
Ответ:
Мы рассмотрели функции тангенса и котангенса, стандартные задачи, составили таблицу значений тангенса и котангенса, решили простейшие тригонометрические уравнения.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/tangens-i-kotangens-2
http://www.