Решение задач с помощью дробных рациональных уравнений 8 класс онлайн-подготовка на Ростелеком Лицей
Решение задач с помощью дробных рациональных уравнений.
Напомним, что рациональные уравнения – это уравнения, у которых левая и правая части являются рациональными выражениями. Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называют дробным.
Очень часто решение задач сводится к решению дробных рациональных уравнений. Решим несколько задач, которые сводятся к решению таких уравнений.
Задача 1. Числитель дроби на 3 меньше её знаменателя. Сумма дроби и обратной ей дроби в 7,25 раза больше исходной дроби. Найти исходную дробь.
Решение: обозначим за хзнаменатель дроби. Тогда (х-3) – числитель этой дроби. Значит, исходная дробь имеет вид х-3х. Так как по условию задачи сумма дробих-3хи обратной ей дробихх-3 в 7,25 раза больше исходной дроби, то можем составить уравнение:
x-3x+xx-3=7,25x-3x
Представим 7,25 в виде неправильной дроби:
x-3x+xx-3=29(x-3)4x
Умножим обе части уравнения на 4x(x-3) при x≠0, x≠3, чтобы избавиться от знаменателей:
4x-3x-3+4×2=29(x-3)(x-3)
4×2-24x+36+4×2=29×2-174x+261
21×2-150x+225=0
D=(-150)2-4∙21∙225=3600
D=60
x1=—150-602∙21=9042=157 не соответствует условию задачи.
x2=—150+602∙21=21042=5
Значит, 5 – знаменатель, 5-3 = 2 – числитель.
Ответ: 25 – исходная дробь.
Задача 2. Велосипедисту надо проехать 30 км. Он выехал на полчаса позже намеченного срока и, чтобы приехать вовремя, увеличил скорость на 2 км/ч. С какой скоростью ехал велосипедист?
Пусть х (км/ч) – скорость велосипедиста. Тогда расстояние в 30 км велосипедист проедет за 30х часов. Если бы велосипедист выехал вовремя, то его скорость была бы равна (х-2) км/ч. И тогда расстояние в 30 км он проехал бы за 30х-2 часов. По условию задачи, велосипедист выехал на 30 минут позже намеченного срока, или, что тоже самое, на 3060=12 часа позже. Составим уравнение:
30x-2-30x=12
Умножим обе части уравнения на 2x(x-2) при x≠0, x≠2, чтобы избавиться от знаменателей:
30∙2x-30∙2x-2=x(x-2)
60x-60x+120=x2-2x
x2-2x-120=0
D=(-2)2-4∙1∙-120=4+480=484
D=484=22
x1=—2-222=-10 не соответствует условию задачи.
x2=—2+222=12
Ответ: 12 км/ч.
Задача 3. Лодка прошла вниз по реке 42 км, а затем 27 км против течения, затратив на весь путь 15 часов. Найти скорость течения реки, если скорость моторной лодки в стоячей воде равна 5 км/ч.
Пусть х (км/ч) – скорость течения реки. Тогда (5+х) км/ч скорость моторной лодки по течению реки и (5-х) км/ч скорость моторной лодки против течения. Известно, что моторная лодка прошла по течению реки 42 км, а значит, затратила на это расстояние 425+х часов. Затем против течения лодка прошла 27 км, затратив на это расстояние 275-х часов. По условию известно, что на весь путь моторная лодка затратила 15 часов. Составим уравнение:
425+x+275-x=15
Умножим обе части уравнения на (5+x)(5-x) при x≠-5, x≠5, чтобы избавиться от знаменателей:
425-x+275+x=15(5+x)(5-x)
210-42x+135+27x=375-15×2
5×2-5x-10=0
x2-x-2=0
По теореме Виета
x1+x2=1×1∙x2=-2
Следовательно, x1=-1; x2=2.
Ответ: 2 км/ч
Практика. Решение квадратных и дробно-рациональных уравнений 8 класс онлайн-подготовка на Ростелеком Лицей
Решение биквадратных уравнений
Математической моделью практических задач могут быть разные уравнения.
В школе мы чаще всего будем сталкиваться с линейными и квадратными уравнениями, которые уже умеем решать. Но иногда могут встречаться и более сложные уравнения. Существуют компьютерные алгоритмы, которые позволяют приближенно найти решение практически любого уравнения, а вот точное решение найти удастся не всегда. На этом уроке мы рассмотрим некоторые приемы, которые позволяют эквивалентными преобразованиями свести более сложные уравнения к тем, которые мы уже умеем решать, – линейным и квадратным.
Задание 1. Решить уравнение:
Решение.
Воспользуемся свойством степеней и перепишем уравнение в виде:
Обратим внимание, что неизвестная величина присутствует в уравнении только в составе «конструкции» . В таком случае применяют метод замены переменной.
Суть его состоит в том, что эту повторяющуюся конструкцию мы заменяем новой переменной:
Заменяя на , получаем уравнение:
Получили квадратное уравнение.
С его решением вы можете ознакомиться ниже.
Решение квадратного уравнения с помощью дискриминанта
Имеем следующее квадратное уравнение:
Решим уравнение с помощью дискриминанта. Коэффициенты из общего вида квадратного уравнения:
Тогда:
Найдем корни квадратного уравнения:
Ответ: .
Далее решения линейных и квадратных уравнений не будут разбираться подробно. Внимание будет сконцентрировано на том, как свести более сложное уравнение к линейному или квадратному. Если же у вас возникают проблемы при решении линейных или квадратных уравнений, пересмотрите соответствующие уроки:
- «Линейное уравнение с одной переменной (Г.Г. Гаицгори)»;
- «Квадратные уравнения».
Решаем уравнение, получаем корни:
Мы нашли значения . Но в исходном уравнении фигурировала переменная , и решить уравнение – значит, найти значения . Вернемся к замене:
Тогда:
Получили два квадратных уравнения.
Второе уравнение не имеет действительных корней.
Ответ: .
В процессе решения нам пришлось дважды решать квадратные уравнения: сначала для переменной , затем для переменной . Поэтому такие уравнения, в которых присутствуют только -я и -я степень неизвестной, а также свободный член, называются биквадратными уравнениями, т. е. «дважды квадратными»:
Решение дробно-рациональных уравнений
Теперь перейдем к решению дробно-рациональных уравнений. По названию понятно – это те уравнения, которые содержат в себе дробно-рациональные выражения. Если вы забыли, что это за выражения и как с ними работать, рекомендуем пересмотреть соответствующий видеоурок: «Дробно-рациональные выражения».
При решении дробно-рациональных уравнений важно:
- в самом начале найти ОДЗ выражений, которые встречаются в уравнении;
- после нахождения корней нужно проверить, входят ли они в ОДЗ.
Рассмотрим несколько примеров простейших дробно-рациональных уравнений.
Задание 2.Решить уравнение:
Решение.
Знаменатель дроби не должен равняться нулю, т. е. ОДЗ:
Поскольку , можем умножить обе части уравнения на , чтобы избавиться от дроби, тогда:
Получили линейное уравнение, решением которого является x = -3. Это решение входит в ОДЗ.
Ответ: -3.
Задание 3.Решить уравнение:
Решение.
Выпишем ОДЗ:
Чтобы избавиться от дроби, умножим обе части уравнения на . Мы это можем сделать, поскольку , тогда:
Раскроем скобки, перенесем все слагаемые в одну сторону, приведем подобные слагаемые. Получим квадратное уравнение:
Найдем корни этого уравнения:
Первый корень не входит в ОДЗ. Поэтому не является решением уравнения.
Ответ: .
Решение более сложных рациональных уравнений
Решим более сложные дробно-рациональные уравнения.
Задание 4. Решить уравнение:
Решение.
Выпишем ОДЗ:
Решим каждое из этих неравенств:
Можем объединить эти неравенства в одно:
Перенесем все слагаемые в одну сторону:
Выполним сложение дробей – для этого разложим знаменатели на множители:
Приведем все дроби к общему знаменателю :
Тогда:
Дробь равна , если ее числитель равен :
Раскрыв скобки и приведя подобные слагаемые, получаем квадратное уравнение:
Найдем корни квадратного уравнения:
Корень не входит в ОДЗ.
Ответ:
Отметим, что для решения дробно-рациональных уравнений можно использовать разные способы. Первый – это умножить обе части уравнения на некоторые выражения так, чтобы избавиться от дробей. Таким способом мы решили первые два примера с дробно-рациональными выражениями. Второй способ – перенести все слагаемые в одну сторону, преобразовать выражение и приравнять числитель полученной дроби к нулю.
Так мы решили последний пример. Вы можете выбрать тот способ, который вам удобнее и понятнее. Главное в каждом из них – не забывать про ОДЗ.
Задание 5. Решить уравнение:
Решение.
Выпишем ОДЗ:
Решим эти неравенства:
Обратим внимание, что неизвестная присутствует в уравнении в похожих конструкциях , которые являются взимнообратными выражениями. В таком случае можно применить метод замены переменной:
Тогда:
Исходное уравнение будет иметь вид:
Чтобы избавиться от дроби, умножим обе части уравнения на , при этом , поскольку :
Получили квадратное уравнение, решениями которого являются:
Вернемся к замене:
Решаем первое уравнение:
Решаем второе уравнение:
Полученные корни удовлетворяют ОДЗ.
Ответ:.
Задание 6. Решить уравнение:
Решение.
Выпишем ОДЗ:
В подобных уравнениях стандартной является замена:
Чтобы выразить через , произведем следующие действия:
После замены исходное уравнение будет иметь вид:
Преобразуя это выражение, получаем квадратное уравнение:
Найдем корни уравнения:
Вернемся к замене:
Поскольку , можем умножить обе части каждого из уравнений на и получить квадратные уравнения:
Первое уравнение имеет решения:
Оба решения удовлетворяют ОДЗ.
Второе уравнение не имеет вещественных корней.
Ответ: .
Решение иррациональных уравнений
Теперь перейдем к решению иррациональных уравнений. Так называются уравнения, которые содержат операцию извлечения корня из переменной.
Задание 7. Решить уравнение:
Решение.
Как мы знаем, выражение имеет смысл только для значения . Поэтому ОДЗ для данного уравнения будет следующей:
Чтобы привести иррациональное уравнение к линейному или квадратному, нужно избавиться от иррациональности. В данном случае – избавиться от квадратного корня. Для этого воспользуемся свойством корня:
Возведем обе части уравнения в квадрат:
Получили линейное уравнение, корнем которого является:
Полученное значение входит в ОДЗ:
При решении уравнения мы возвели обе части уравнения в квадрат, при этом могли возникнуть посторонние корни, т. е. те, которые не являются решением исходного уравнения.
Посторонние корни
Операция возведения в квадрат обеих частей равенства не является равносильным преобразованием. При применении этой операции можно получить из неправильного равенства правильное. Например, равенство очевидно неправильное. Но при возведении в квадрат получим правильное:
При этом из правильного равенства мы не получим неправильное, ведь если числа равны, то их квадраты также равны. Поэтому любой корень исходного уравнения является корнем уравнения, полученного после возведения в квадрат обеих частей. Но не все корни полученного уравнения являются корнями исходного. Могут возникнуть посторонние корни. Чтобы исключить их, проще всего выполнить проверку, подставив полученные значения в исходное уравнение.
Выполним проверку. Подставим полученный корень в исходное уравнение:
Мы получили правильное равенство, значит, является решением уравнения.
Ответ: .
Задание 8. Решить уравнение:
Решение.
Подкоренные выражения должны быть неотрицательными. Поэтому ОДЗ будет следующей:
Возведем обе части уравнения в квадрат:
После преобразования получим квадратное уравнение:
Найдем корни уравнения:
Проверим, входят ли корни в ОДЗ.
:
Неравенство неверное, значит, корень не входит в ОДЗ и не является решением исходного уравнения.
:
Корень входит в ОДЗ.
Теперь выполним проверку, подставив в исходное уравнение:
Получили правильное равенство, следовательно, исходное уравнение имеет один корень .
Ответ:.
Заключение
Итак, сегодня мы познакомились с некоторыми приемами, которые позволяют свести уравнения высших порядков, дробно-рациональные и иррациональные уравнения к квадратным и линейным уравнениям.
Список литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра, 8 класс. Учебник. – М.: ФГОС, издательство «Просвещение», 2018.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра, 8 класс. Учебник. – М.: «Просвещение», 2018.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б./Под ред. Теляковского С.А. Алгебра, 8 класс. Учебник. – М.: «Просвещение», 2018.
Учебник. – М.: ФГОС, издательство «Просвещение», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал youclever.org (Источник)
- Интернет-портал kontromat.ru (Источник)
Домашнее задание
1. Решить биквадратное уравнение:
2. Решить дробно-рациональное уравнение:
3. Решить иррациональное уравнение:
8.4 Решение уравнений с дробями или десятичными коэффициентами — Предварительная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Решение уравнений с дробными коэффициентами
- Решение уравнений с десятичными коэффициентами
Будь готов 8.
10Прежде чем начать, пройдите этот тест на готовность.
Умножить: 8·38,8·38.
Если вы пропустили эту проблему, просмотрите пример 4.28
Будь готов 8.11
Найдите ЖК-дисплей 56 и 14, 56 и 14.
Если вы пропустили эту проблему, просмотрите пример 4.63
Будь готов 8.12
Умножить: 4.784.78 на 100.100.
Если вы пропустили эту проблему, просмотрите пример 5.18
Решение уравнений с дробными коэффициентами
Давайте воспользуемся представленной ранее общей стратегией решения линейных уравнений, чтобы решить уравнение 18x+12=14,18x+12=14.
The next line says, “Change the constants to equivalent fractions with the LCD,” and shows one-eighth x equals one-fourth minus two-fourths. The next line says, “Subtract,” and shows one-eighth x equals negative one-fourth. The next line says, “Multiply both sides by the reciprocal of one-eighth,” and shows a red 8 over 1 times one-eighth x equals a red 8 over 1 times negative one-fourth. The next line says, “Divide,” and shows 12x over a red 12 equals 4.8 over a red 12. The last line says, “Simplify,” and shows x equals negative 2.» data-label=»»> 
Этот метод работал нормально, но многие ученики не чувствуют себя уверенно, когда видят все эти дроби. Итак, мы собираемся показать альтернативный метод решения уравнений с дробями. Этот альтернативный метод исключает дроби.
Мы применим свойство равенства умножения и умножим обе части уравнения на наименьший общий знаменатель всех дробей в уравнении. Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей. Этот процесс называется очистка уравнения дробей . Давайте снова решим то же уравнение, но на этот раз воспользуемся методом очистки дробей.
Пример 8,37
Решите: 18x+12=14,18x+12=14.
Решение
The next line says, “Multiply both sides of the equation by that LCD, 8. This clears the fractions,” and shows a red 8 times each side of the original equation. The next line says, “Use the Distributive Property. Simplify — and notice, no more fractions!” Beside that is 8 times one-eighth x plus 8 times one-half equals 8 and one-fourth, then x plus 4 equals 2. The next line says, “Solve using the General Strategy for Solving Linear Equations,” and shows x plus 4 minus a red 4 equals 2 minus a red 4. The last step says, “Check. Let x equal negative 2.” Beside that is the original equation followed by one-eighth times a red negative 2 plus one-half, equal sign with a question mark, one-fourth. Below that is negative 2 over 8 plus one-half, equal sign with a question mark, one-fourth. Below that is negative 2 over 8 plus 4 over 8, equal sign with a question mark, one-fourth. Below that is 2 over 8, equal sign with a question mark, one-fourth. The last line says one-fourth equals one-fourth.
Попробуй 8,73
Решите: 14x+12=58,14x+12=58.
Попробуй 8,74
Решите: 16y-13=16.16y-13=16.
Обратите внимание, что в примере 8.37, как только мы очистили уравнение дробей, оно стало таким же, как те, которые мы решали ранее в этой главе. Мы изменили задачу на ту, которую уже знали, как решить! Затем мы использовали общую стратегию решения линейных уравнений.
Как
Решите уравнения с дробными коэффициентами, очистив дроби.
- Шаг 1. Найдите наименьший общий знаменатель числа для всех дроби в уравнении.
- Шаг 2. Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает дроби.
- Шаг 3. Решите, используя общую стратегию решения линейных уравнений.
Пример 8,38
Решите: 7=12x+34x−23x.7=12x+34x−23x.
Решение
Мы хотим очистить дроби, умножив обе части уравнения на LCD всех дробей в уравнении.
The next line says, “Simplify — and notice, no more fractions!” Beside that is 84 equals 6x plus 9x minus 8x. The next line says, “Combine like terms,” and shows 84 equals 7x. The next line says, “Divide by 7,” and shows 84 over a red 7 equals 7x over a red 7. The next line says, “Simplify,” and shows 12 equals x. The last step says, “Check: Let x equal 12.” Beside that is the original equation. Below that is 7 followed by an equal sign with a question mark, then one-half times a red 12 plus three-fourths times a red 12 minus two-thirds times a red 12. Bellow that is 7 followed by an equal sign with a question mark, then 6 plus 9 minus 8. The last line says 7 equals 7, followed by a check mark.» data-label=»»>
Попробуй 8,75
Решите: 6=12v+25v−34v.6=12v+25v−34v.
Попробуй 8,76
Решите: −1=12u+14u−23u.−1=12u+14u−23u.
В следующем примере у нас будут переменные и дроби с обеих сторон уравнения.
Пример 8,39
Решите: x+13=16x−12.x+13=16x−12.
Решение
The next step says, “Simplify — no more fractions!” and shows 6x plus 2 equals x minus 3. The next line says, “Subtract x from both sides,” and shows 6x minus a red x plus 2 equals x minus a red x minus 3. The next line says, “Simplify,” and shows 5x plus 2 equals negative 3. The next line says, “Subtract 2 from both sides,” and shows 5x plus 2 minus a red 2 equals negative 3 minus a red 2. The next line says, “Simplify,” and shows 5x equals negative 5. The next line says, “Divide by 5,” and shows 5x over a red 5 equals negative 5 over a red 5. The next line says, “Simplify,” and shows x equals negative 1. The next line says, “Check,” and shows the original equation. The following line says, “Substitute x equals negative 1.” Beside that is a red negative 1 plus one-third followed by an equal sign with a question mark, then one-sixth times a red negative 1 minus one-half. Below that is negative 1 plus one-third followed by an equal sign with a question mark, then negative one-sixth minus one-half.
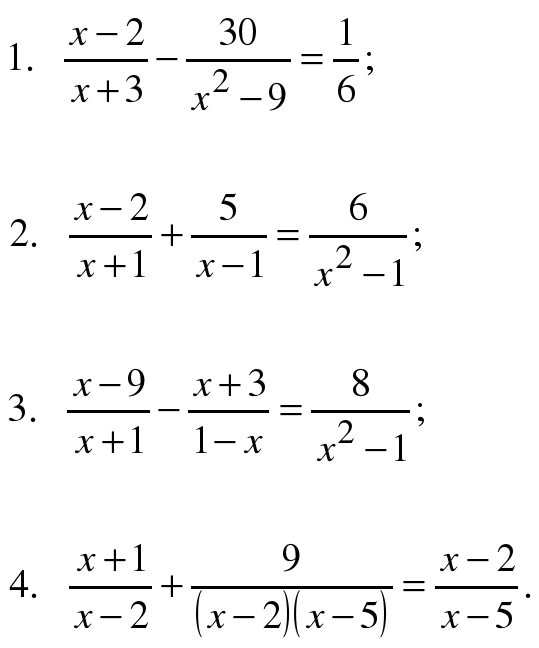Below that is negative 3 over 3 plus 1 over 3 followed by an equal sign with a question mark, then negative 1 over 6 minus 3 over 6. Below that is negative 2 over 3 followed by an equal sign with a question mark, then negative 4 over 6. The last line says negative 2 over 3 equals negative 2 over 3.» data-label=»»>Попробуй 8,77
Решите: a+34=38a−12.
a+34=38a−12.
Попробуй 8,78
Решите: c+34=12c−14.c+34=12c−14.
В примере 8.40 мы начнем с использования свойства Distribution. Этот шаг сразу очистит дроби!
Пример 8.40
Решить: 1=12(4x+2).1=12(4x+2).
Решение
Below that is 1 followed by an equal sign with a question mark, then one-half times parentheses 4 times a red 0 plus 2. Below that is 1 followed by an equal sign with a question mark, then one-half times 2. Below that is a 1 followed by an equal sign with a question mark, then 2 over 2. The last line says 1 equals 1.» data-label=»»>Попробуй 8,79
Решите: −11=12(6p+2).−11=12(6p+2).
Попробуй 8,80
Решите: 8=13(9q+6).8=13(9q+6).
Много раз, даже после распределения, все еще будут дроби.
Пример 8.41
Решите: 12(y−5)=14(y−1).12(y−5)=14(y−1).
Решение
The next line says, “Collect the constants to the right,” and shows y minus 10 plus a red 10 equals negative 1 plus a red 10. The next line says, “Simplify,” and shows y equals 9. The last step says, “Check. Substitute: 9 for y,” and shows the original equation. Below that is one-half times parentheses red 9 minus 5, equal sign with a question mark, one-fourth times parentheses red 9 minus 1. Below that is one-half times 4, equal sign with a question mark, one-fourth times 8, then 2 equals 2 followed by a check mark.» data-label=»»>
Попробуй 8,81
Решите: 15(n+3)=14(n+2).15(n+3)=14(n+2).
Попробуй 8,82
Решите: 12(м-3)=14(м-7).12(м-3)=14(м-7).
Решение уравнений с десятичными коэффициентами
В некоторых уравнениях есть десятичные дроби. Такое уравнение возникает, когда мы решаем задачи, связанные с деньгами и процентами. Но десятичные дроби — это еще один способ представления дробей. Например, 0,3=3100,3=310 и 0,17=17100,0,17=17100. Итак, когда у нас есть уравнение с десятичными дробями, мы можем использовать тот же процесс, который мы использовали для очистки дробей, — умножить обе части уравнения на наименьший общий знаменатель.
Пример 8,42
Решите: 0,8x−5=7,0,8x−5=7.
Решение
Единственный десятичный знак в уравнении — 0.
8.0.8. Поскольку 0,8=810, 0,8=810, ЖК-дисплей равен 10,10. Мы можем умножить обе части на 1010, чтобы очистить десятичную дробь.
Умножьте обе стороны на LCD. | |
| Распределить. | |
| Умножьте и обратите внимание, больше нет десятичных знаков! | |
| Добавьте 50, чтобы получить все константы справа. | |
| Упрощение. | |
| Разделите обе части на 8. | |
| Упрощение. | |
| Проверка: Пусть x=15.x=15. | |
Попробуй 8,83
Решите: 0,6x−1=11,0,6x−1=11.
Попробуй 8,84
Решите: 1,2x−3=9,1,2x−3=9.
Пример 8,43
Решите: 0,06x+0,02=0,25x−1,5.0,06x+0,02=0,25x−1,5.
Решение
Посмотрите на десятичные дроби и придумайте эквивалентные дроби.
0,06=6100,0,02=2100,0,25=25100,1,5=15100,06=6100,0,02=2100,0,25=25100,1,5=1510
Обратите внимание, на ЖК-дисплее 100,100.
Путем умножения на ЖК-дисплее мы очистим десятичные дроби.
The next line says, “Divide by 19,” and shows 152 over a red 19 equals 19x over a red 19. The next line says, “Simplify,” and shows 8 equals x. The last line says, “Check: Let x equal 8,” and shows 0.06 times a red 8 plus 0.02 equals 0.25 times a red 8 minus 1.5. Below that is 0.48 plus 0.02 equals 2.00 minus 1.5. The last line says 0.50 equals 0.50.» data-label=»»>Попробуй 8,85
Решите: 0,14ч+0,12=0,35ч-2,4.
0,14ч+0,12=0,35ч-2,4.
Попробуй 8,86
Решите: 0,65k−0,1=0,4k−0,35.0,65k−0,1=0,4k−0,35.
В следующем примере используется уравнение, типичное для тех, которые мы увидим в приложении к деньгам в следующей главе. Обратите внимание, что мы сначала распределим десятичную дробь, прежде чем очистим все десятичные дроби в уравнении.
Пример 8,44
Решите: 0,25x+0,05(x+3)=2,85.0,25x+0,05(x+3)=2,85.
Решение
The next line says, “Subtract 15 from both sides,” and shows 30x plus 15 minus a red 15 equals 285 minus a red 15. The next line says, “Simplify,” and shows 30x equals 270. The next line says, “Divide by 30,” and shows 30x over a red 30 equals 270 over a red 30. The next line says “Simplify” and shows x equals 9. The next line says, “Check,” and shows the original equation. Below that is “Let x equal 9” and 0.25 times a red 9 plus 0.05 times parentheses red 9 plus 3, equal sign with a question mark, 2.85. Below that is 2.25 plus 0.05 times 12, equal sign with a question mark, 2.85. Below that is 2.25 plus 0.60 followed by an equal sign with a question mark, then 2.85. The last line shows 2.85 equals 2.85.» data-label=»»>
Попробуй 8,87
Решите: 0,25n+0,05(n+5)=2,95.0,25n+0,05(n+5)=2,95.
Попробуй 8,88
Решите: 0,10d+0,05(d−5)=2,15.0,10d+0,05(d−5)=2,15.
Раздел 8.4 Упражнения
Практика ведет к совершенству
Решите уравнения с коэффициентами дробей
В следующих упражнениях решите уравнение, удалив дроби.
209.
14x−12=−3414x−12=−34
210.
34x−12=1434x−12=14
211.
56y−23=−3256y−23=−32
212.
56y−13=−7656y−13=−76
213.
12а+38=3412а+38=34
214.
58б+12=-3458б+12=-34
215.
2=13x−12x+23×2=13x−12x+23x
216.
2=35x−13x+25×2=35x−13x+25x
217.
14м-45м+12м=-114м-45м+12м=-1
218.
56n-14n-12n=-256n-14n-12n=-2
219.
х+12=23х-12х+12=23х-12
220.
х+34=12х-54х+34=12х-54
221.
13w+54=w−1413w+54=w−14
222.
32z+13=z−2332z+13=z−23
223.
12x−14=112x+1612x−14=112x+16
224.
12а-14=16а+11212а-14=16а+112
225.
13б+15=25б-3513б+15=25б-35
226.
13x+25=15x−2513x+25=15x−25
227.
1=16(12x−6)1=16(12x−6)
228.
1=15(15x−10)1=15(15x−10)
229.
14(р-7)=13(р+5)14(р-7)=13(р+5)
230.
15(q+3)=12(q−3)15(q+3)=12(q−3)
231.
12(х+4)=3412(х+4)=34
232.
13(х+5)=5613(х+5)=56
Решение уравнений с десятичными коэффициентами
В следующих упражнениях решите уравнение, очистив десятичные дроби.
233.
0,6г+3=90,6г+3=9
234.
0,4y−4=20,4y−4=2
235.
3,6j−2=5,23,6j−2=5,2
236.
2,1к+3=7,22,1к+3=7,2
237.
0,4х+0,6=0,5х-1,20,4х+0,6=0,5х-1,2
238.
0,7х+0,4=0,6х+2,40,7х+0,4=0,6х+2,4
239.
0,23х+1,47=0,37х-1,050,23х+1,47=0,37х-1,05
240.
0,48х+1,56=0,58х-0,640,48х+1,56=0,58х-0,64
241.
0,9x−1,25=0,75x+1,750,9x−1,25=0,75x+1,75
242.
1,2х-0,91=0,8х+2,291,2x−0,91=0,8x+2,29
243.
0,05n+0,10(n+8)=2,150,05n+0,10(n+8)=2,15
244.
0,05n+0,10(n+7)=3,550,05n+0,10(n+7)=3,55
245.
0,10d+0,25(d+5)=4,050,10d+0,25(d+5)=4,05
246.
0,10d+0,25(d+7)=5,250,10d+0,25(d+7)=5,25
247.
0,05(q-5)+0,25q=3,050,05(q-5)+0,25q=3,05
248.
0,05(q-8)+0,25q=4,100,05(q-8)+0,25q=4,10
Математика на каждый день
249.
Монеты У Тейлора есть $2,00$2,00 в десятицентовиках и пенни. Количество пенни на 22 больше, чем количество десятицентовиков. Решите уравнение 0,10d+0,01(d+2)=20,10d+0,01(d+2)=2 для d,d, количества десятицентовиков.
250.
Марки Трэвис купил на 9,45 долларов 9,45 долларов марок номиналом 49 центов49 центов и марок номиналом 21 цент21 цент. Количество марок номиналом 21 цент21 цент было на 55 меньше, чем количество марок номиналом 49 центов49 центов. Решите уравнение 0,49s+0,21(s−5)=9,450,49s+0,21(s−5)=9,45 для s,s, чтобы найти количество 49-центовых марок, купленных Трэвисом.
Письменные упражнения
251.
Объясните, как найти наименьший общий знаменатель чисел 38, 16 и 23.38, 16 и 23.
252.
Если уравнение состоит из нескольких дробей, как умножение обеих частей на ЖК-дисплей облегчает решение?
253.
Если в уравнении есть дроби только с одной стороны, зачем вам обе части уравнения умножать на LCD?
254.
В уравнении 0,35x+2,1=3,85,0,35x+2,1=3,85, что такое LCD? Откуда вы знаете?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ В целом, после просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующей главе? Почему или почему нет?
Решение линейных уравнений с дробями
Все основные арифметические ресурсы
6 диагностических тестов 75 практических тестов Вопрос дня Карточки Learn by Concept
Справка по основам арифметики » Фракции » Линейные уравнения с дробями » Решение линейных уравнений с дробями
Решить x
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с прибавления 10 к обеим сторонам.
Умножьте обе части на 9, чтобы избавиться от дроби.
Разделить на 5
Поскольку все варианты ответов содержат смешанные дроби, вам также потребуется сократить до смешанной дроби
Сообщить об ошибке
Решить для .
Возможные ответы:
Правильный ответ:
Объяснение:
Добавьте обе стороны по 9чтобы изолировать x на одной стороне.
Умножить обе стороны на 5.
Разделить обе стороны на 9.
Сообщить об ошибке
Решить для .
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала добавьте 10 к обеим сторонам, чтобы термин с буквой «z» был изолирован с одной стороны.
Чтобы избавиться от дроби, умножьте обе части на 3.
Разделить на 2.
Сообщить об ошибке
Решить для 005
Объяснение:
Начните с добавления терминов с помощью вместе. Найдите наименьший общий знаменатель двух дробей.
Теперь умножьте обе стороны на 10.
Затем разделите обе стороны на 23.
Сообщить об ошибке
Решить для .
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с добавления 9 к обеим сторонам.
Затем умножьте обе части на 3.
Наконец, разделите обе части на 2.
Сообщить об ошибке с:
Правильный ответ:
Пояснение:
Когда мы решаем уравнения, мы всегда должны помнить, что то, что в левой части, равно правой стороне.