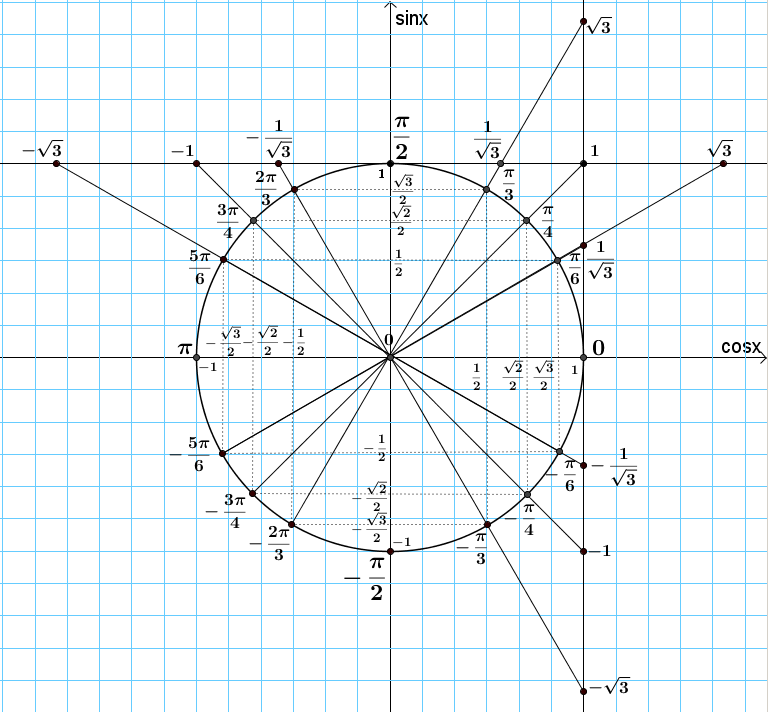
Тригонометрические функции любого угла — Математика в колледже
Тригонометрия > Тригонометрические функции любого углаОтправлено 11 февр. 2015 г., 06:49 пользователем Ksenya V
|
Тригонометрический круг презентация, доклад
Слайды и текст этой презентации
Слайд 1Тригонометрический круг
Радиус R = 1
1
1
Тригонометрический круг – это круг с радиусом
равным единице и с центром в начале координат.
(1;0)
(0;1)
(-1;0)
(0;-1)
180°
270°
Градусная мера углов
360°
Четверти круга
1
3
4
Слайд 3Углы на тригонометрическом круге
х
Угол на круге определяется поворотом радиуса
За
нулевое положение радиуса принято его положение на положительном направлении оси Х.
Угол поворота радиуса отсчитывается от положительного направления оси Х: с плюсом — против часовой стрелки, с минусом — по часовой стрелке.
х
х
Слайд 4Координаты положения радиуса
ордината
(х0;у0)
абсцисса
Слайд 5Радианная мера угла
Один радиан – это центральный угол, опирающийся на дугу
равную радиусу
Длина окружности 2πR
В окружности 2πR : R = 2π радиан
2π соответствуют 360°
2π ————— 360°
π ————— 180°
90° = 180° /2 = π /2
270° = 90°· 3 = 3π /2
0°
π /2
π
3π /2
Радианная мера углов в круге
2π
0°
1,57
3,14
4,71
6,28
Так как π = 3,14…, то
Слайд 6Перевод градусов в радианы
Перевести 120° в радианы.
Для
перевода в радианы удобно пользоваться пропорцией.
π ————— 180°
180°−−−−−−−−−−−− π
2
3
120° −−−−−−−−−−−− х
30° = π /6
45° = π /4
60° = π /3
Перевод радиан в градусы
Подставьте вместо π 180° и сократите
Перевести 3π /4 в градусы.
Слайд 7Определение тригонометрических функций
Повторение
α
ордината
О
А
В
Заметим, ОА = R = 1
Синусом угла α является
ордината точки А на круге,
Синус угла α – это ордината (у) угла α
sinα
Слайд 8Определение тригонометрических функций
Повторение
α
абсцисса
О
А
В
Заметим, ОА = R = 1
Косинусом угла α является
абсцисса точки А на круге,
получающаяся при повороте радиуса на угол α.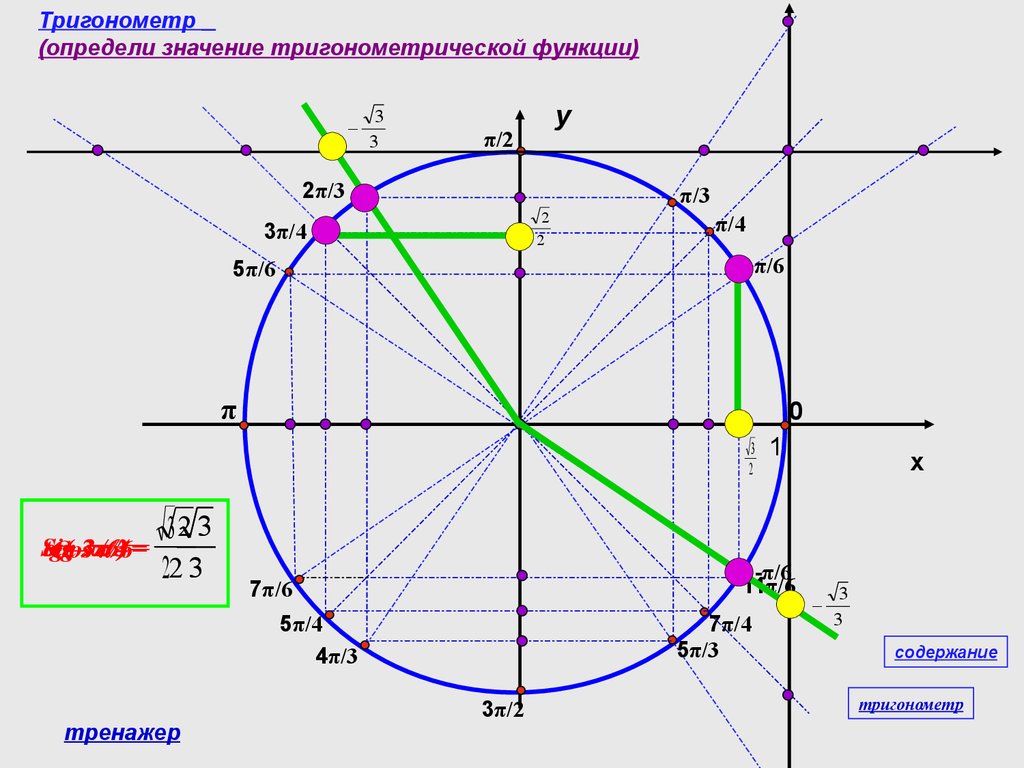
Косинус угла α – это абсцисса (х) угла α
cosα
Слайд 9Определение тригонометрических функций
Повторение
α
О
А
В
tgα, ctgα
Sin
M
Запомни! Синус – это ордината (y)
Слайд 11cosα
2) Косинусом угла α является абсцисса точки М на тригонометрическом круге,
получающаяся при повороте радиуса на угол α.
Абсцисса — cosα
cosα
cosα
M
Запомни! косинус – это абсцисса (x)
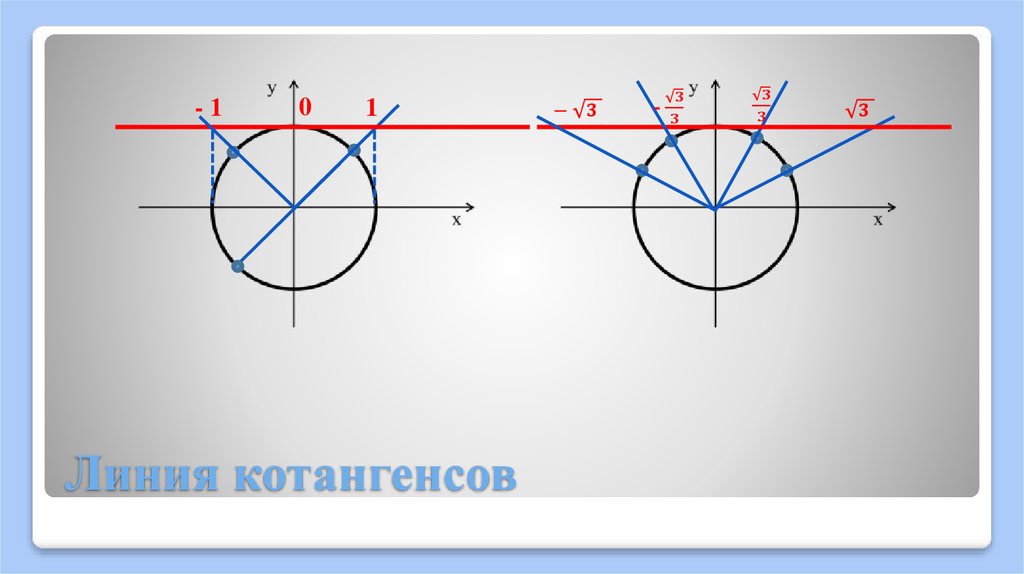
Слайд 133) Тангенсом угла α является ордината точки В на оси тангенсов
( х = 1 ), получающаяся при пересечении продолжения радиуса с осью тангенсов при повороте радиуса на угол α.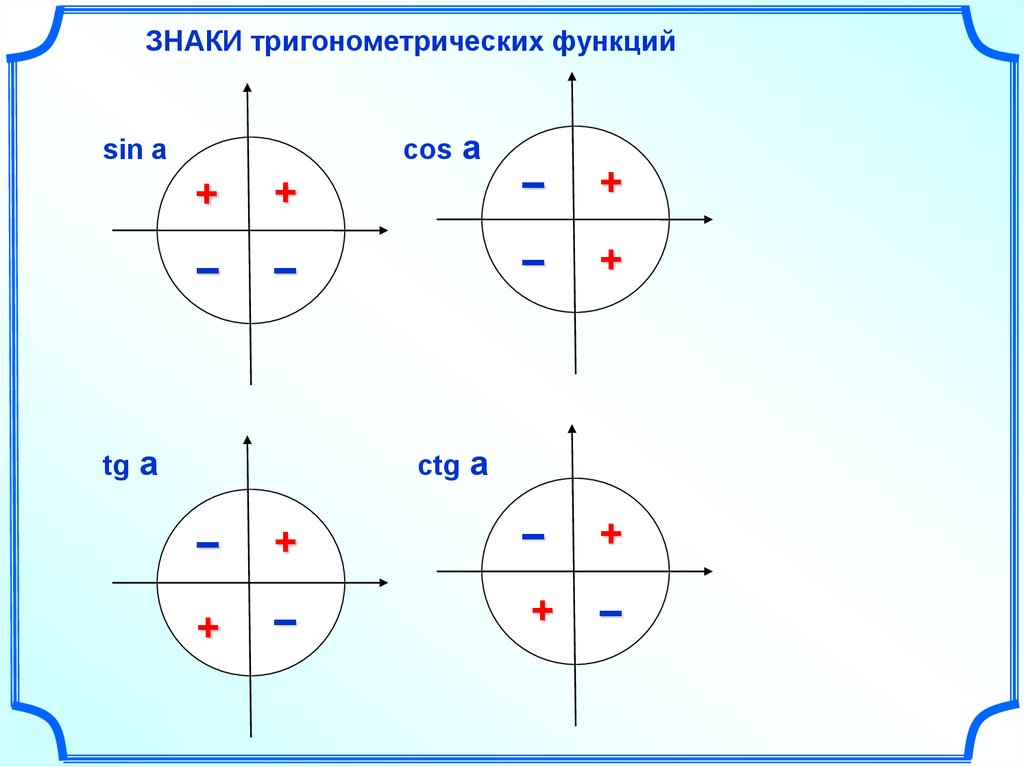
tgα
Ось тангенсов, х = 1
В
В
Слайд 144) Котангенсом угла α является абсцисса точки В на оси котангенсов
( у = 1 ), получающаяся при пересечении продолжения радиуса с осью котангенсов при повороте радиуса на угол α.
сtgα
Ось котангенсов, у = 1
В
В
0
π/2
π
3π/2
2π
3π/2
Красная линия — это плюс
Синяя – это минус
0
1
0
1
0
-1
-1
0
0
1
y
x
0 1
0 -1 0
1 0 -1 0 1
0 — 0 — 0
— 0 — 0 —
Значения тригонометрических функций
(1;0)
(0;1)
(-1;0)
(0;-1)
Диаметральные углы
Табличные значения
Значения тригонометрических функций
Ряд синуса
Запомни!
Для косинуса поменяйте крайние значения
Ряд тангенса
Для
Слайд 17Свойства триг.
 функций
функцийЗнать
Уметь
1. Знаки по четвертям
Синус: знаки соответствуют знакам по
оси У, косинус –по оси Х
Тангенс и котангенс в 1 четв.- плюс, далее знаки чередуются
1. Определять четверть нахождения угла; 2. Определить знак функции.
sin315º tg5π/6 cos2 11π/4 > 0, т.к Cos2
π/2
0
π/2
π
3π/2
2π
3π/2
Красная линия — это плюс
Синяя – это минус
Tg, ctg
+
—
+
—
+
—
+
—
+
—
+
—
Слайд 185. Множество значений функций
tgx € R, ctgx € R,
-1 ≤
sin х ≤ 1, или |sinx | ≤ 1,
-1 ≤ cos х ≤ 1, или |cosx | ≤ 1,
Уметь находить множество значений функции, выражения
y = 3 -2sinx.
sinx = -1, y = 3+2 = 5
sinx = 1, y = 3-2 = 1
π
3π/2
2π
3π/2
π/2
1
-1
1
-1
|sinx | ≤ 1
|cosx | ≤ 1
Слайд 19Период
Период – это число, при прибавлении которого к аргументу значение функции
не изменяется.
f(x +Т) = f(x)
Если Т – период, то Tn для n € Z тоже период. Считается Т – наименьший период
Так как f(x +Тn) = f(x), то Tn можно опустить
sin, cos Т = 2π
tg, ctg Т = π
Слайд 20Четность, нечетность
Синус, тангенс, котангенс – функции
нечетные.
Минус у угла можно вынести за знак функции
Примеры
1. sin ( – х) = — sin х
2. sin ( π/4 – х) = — sin ( х — π/4 )
4. cos (-7π/3)= cos 7π/3 = cos (2π + π/3) = cos π/3 = ½
5. cos (-β) = cos β
cos (-β) = cos β
6. ctg ( 2α — π/2) = — ctg (π/2 — 2α )
Косинус – функция
четная.
Минус у угла можно опустить
Слайд 21Область определения
Синус, косинус
D(y) =
R
Функции непрерывны на R
Tангенс
D(y) = R, x ≠ π/2 + πn
x = π/2 + πn – вертикальная асимптота
Котангенс
D(y) = R, x ≠ πn
x = πn – горизонтальная асимптота
tgx – определен при cosx ≠ 0
ctgx – определен при sinx ≠ 0
π/2
3π/2
0
π
Скачать презентацию
тригонометрия — Представление функции касательной к единичной окружности
спросил
Изменено 1 год, 7 месяцев назад
Просмотрено 2к раз
$\begingroup$
Я нашел интересный сайт в Google.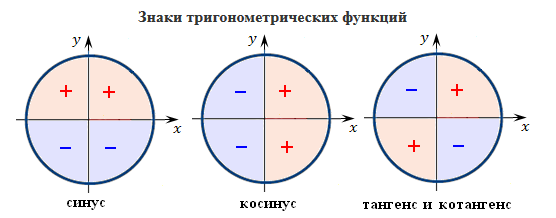 Он представляет функцию касательной определенного угла как длину касательной от точки, стягивающей угол. Я подумал, что это действительно удивительный результат. Но я не могу это переварить, потому что не знаю доказательств. Я пытался много раз, но неоднократно терпел неудачу. Помогите мне доказать этот факт
Он представляет функцию касательной определенного угла как длину касательной от точки, стягивающей угол. Я подумал, что это действительно удивительный результат. Но я не могу это переварить, потому что не знаю доказательств. Я пытался много раз, но неоднократно терпел неудачу. Помогите мне доказать этот факт
- тригонометрия
$\endgroup$
2
$\begingroup$
Два прямоугольных треугольника подобны (один с касательной, другой с синусом и косинусом). Рассмотрите две ноги и сделайте пропорцию.
П.С. Если вы продолжите линию касательной, вы получите котангенс (то же доказательство выше). Кроме того, вы видите, где эта линия пересекает оси x и y? Они секанс и косеканс!
$\endgroup$
2
$\begingroup$
На картинке много одинаковых треугольников. 2 \theta + 1} = \sin \theta \sec \theta = \tan \theta$$
2 \theta + 1} = \sin \theta \sec \theta = \tan \theta$$
$\endgroup$
$\begingroup$
Мне очень помогла эта картинка из курса Массачусетского технологического института «Исчисление с приложениями»:
Источник: нажмите здесь
Давайте назовем начало единичной окружности $F$.
$\sin\theta=\frac{\text{напротив}}{\text{гипотенуза}}=\frac{BD}{BF}=\frac{\sin\theta}{1}$ в $\треугольнике BDF$
$\cos\theta=\frac{\text{adjacent}}{\text{гипотенуза}}=\frac{BE}{BF}=\frac{\cos\theta}{1}$ в $ \треугольник BEF$
$\tan\theta=\frac{\text{напротив}}{\text{смежный}}=\frac{BC}{BF}=\frac{\tan\theta}{1}$ в $\треугольнике BCF$
$\csc\theta=\frac{\text{гипотенуза}}{\text{напротив}}=\frac{AF}{BF}=\frac{\csc\theta}{1}$ в $ \треугольник ABF$
$\sec\theta=\frac{\text{гипотенуза}}{\text{adjacent}}=\frac{CF}{BF}=\frac{\sec\theta}{1}$ в $\треугольнике BCF$
$\cot\theta=\frac{\text{смежный}}{\text{напротив}}=\frac{AB}{BF}=\frac{\cot\theta}{1 }$ в $\треугольнике ABF$
$\endgroup$
Тангенс единичной окружности и друзья
- Home /
- Pre-Calculus /
- Блок Круг /
- Темы /
- Блок Круг /
- Tangent and Friends
- БУДЕСТВЕННЫЙ КРУГ /
- TANGENT и Friends
- .

- Введение
- Темы
- Право-треугольник Обзор
- Блок Круг
- Радианы
- Кусочки круга
- Первые углы квадранта
- Соответствующие урагации . Стандартные углы
- В реальном мире
- Примеры
- Упражнения
- викторины
- Условия
- Раздаточный материал
- Лучшее из Интернета
- Содержание
- НАЗАД
- СЛЕДУЮЩИЙ
Знаете, что могло бы сделать нас по-настоящему счастливыми? Реактивные ранцы.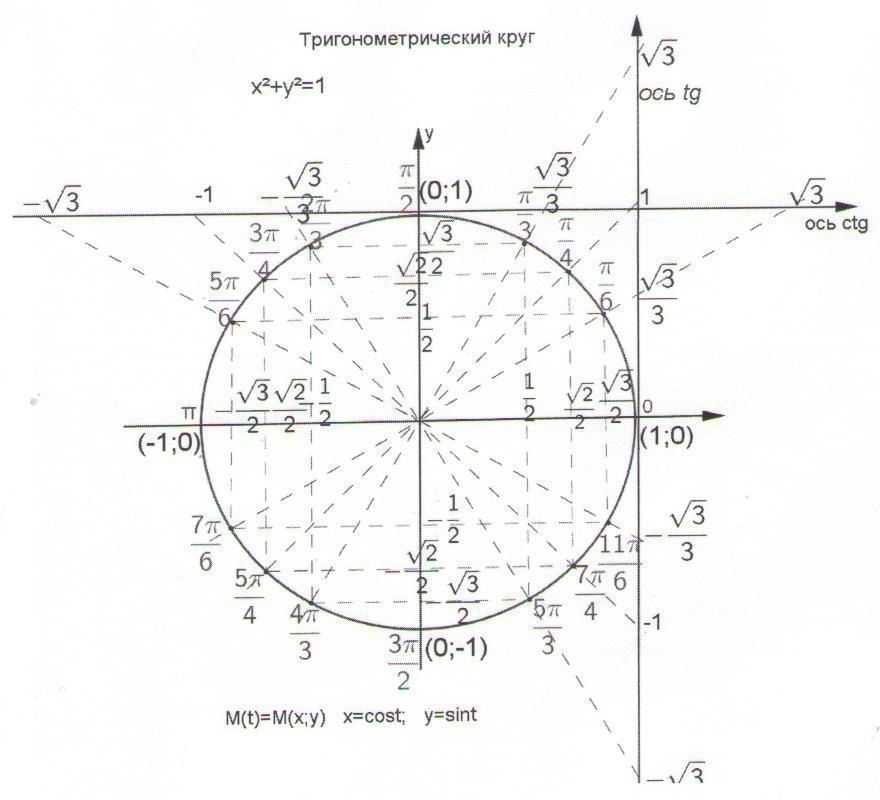 Мы летали, борясь с преступностью, медведями и медведями-преступниками. Вуш. Вроде супергерой, но Шмупьер.
Мы летали, борясь с преступностью, медведями и медведями-преступниками. Вуш. Вроде супергерой, но Шмупьер.
В любом случае, это довольно косвенно по отношению к тому, о чем мы здесь говорим, а именно касательной различных углов. У нас также есть косеканс, секанс и котангенс. К счастью, все они работают одинаково. Если бы они работали по-другому, это было бы в четыре раза больше работы, и мы бы честно выдохлись, прежде чем закончить.
Ключ к нахождению точек зрения на эти функции заключается в том, чтобы знать, что все они являются подделками под бренды содовой для синуса и косинуса кока-колы и пепси.
Как насчет решения проблемы? Мы думаем….
Угол немного меньше π, поэтому он во втором квадранте.
Это наш соответствующий острый угол. Нам нужно найти его котангенс. Оглядываясь на тот список, который мы составили всего минуту назад, мы видим, что:
Мы немного смотрим на свою левую руку и обнаруживаем, что cos есть и sin есть .
Это означает, что значение cot равно , но теперь нам нужен его знак. Мы делим косинус на синус, поэтому во втором квадранте мы делим минус (косинус) на плюс (синус). Если бы триггерные функции были магнитами, нам было бы трудно их разъединить. Однако это не так, поэтому вместо этого мы имеем:
Чтобы котангенс (или тангенс) был положительным, и косинус, и синус должны быть либо положительными, либо отрицательными вместе, как в квадрантах I и III. Квадранты II и IV отрицательные. Квадрант V существует за пределами нашего измерения и постоянно производит мороженое и вулканы. Они склонны уравновешивать друг друга.
Косеканс и секанс имеют тот же знак, что и синус и косинус соответственно. Нам не нужен совершенно новый язык жестов, чтобы работать с ними.
Существует опасность определения углов триггерных функций. Все четыре триггерные функции, кроме синуса и косинуса, включают в себя деление, так что существует риск всегда страшного деления на ноль.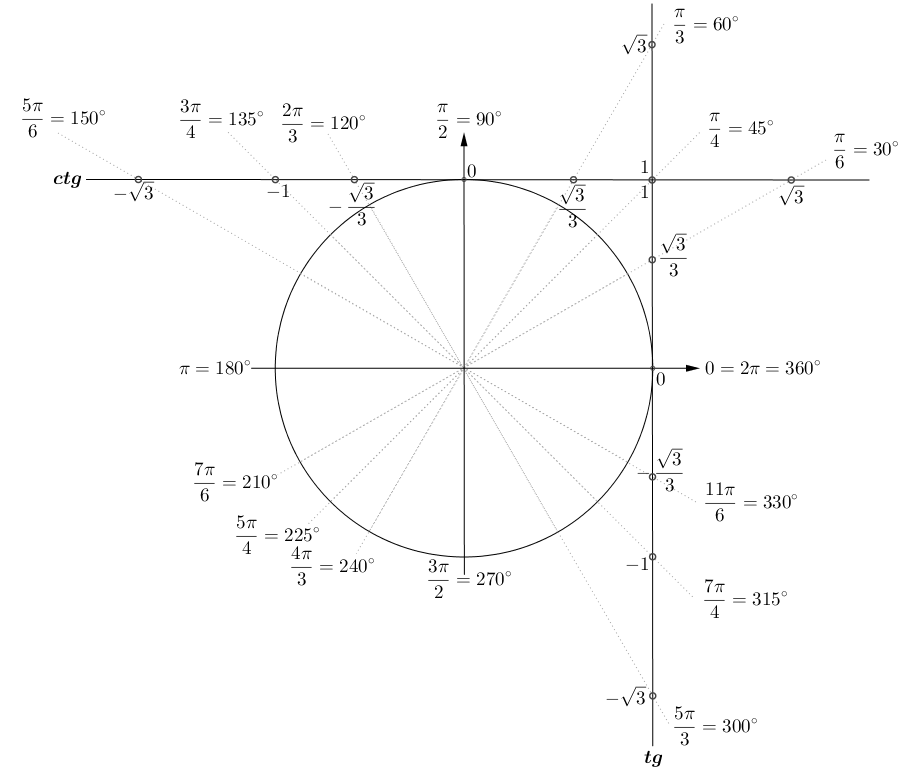


 Синус угла ( рис.4 ) – это отрезок OB на линии синуса, то есть проекция подвижного радиуса OK на линию синуса; косинус угла — отрезок OAлинии косинуса, то есть проекция подвижного радиуса OK на линию косинуса. Знаки синуса и косинуса в различных четвертях единичного круга показаны на рис.5 и рис.6.
Синус угла ( рис.4 ) – это отрезок OB на линии синуса, то есть проекция подвижного радиуса OK на линию синуса; косинус угла — отрезок OAлинии косинуса, то есть проекция подвижного радиуса OK на линию косинуса. Знаки синуса и косинуса в различных четвертях единичного круга показаны на рис.5 и рис.6.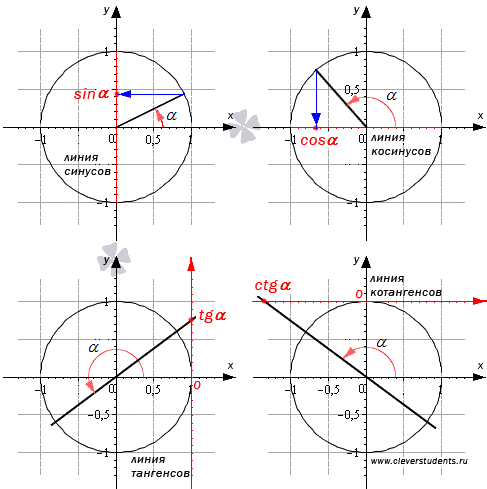 9.
9.