Круги эйлера квадрат ромб прямоугольник: становите отношения, в которых находятся пары понятий, изобразите отношения между объемами понятий при помощи кругов Эйлера:

Содержание

Четырехугольники — презентация онлайн

1. Из имеющихся четырёхугольников указать те, которые являются параллелограммами

3
2
1
6
4
5

2. Заполнить таблицу, отметив знаки «+» или «-»

Параллелогр
амм
Противоположные
стороны
параллельны и
равны
Все стороны равны
Противолежащие
углы равны, сумма
соседних углов
равна180
Все углы прямые
Диагонали
пересекаются и
точкой
пересечения
делятся пополам
Диагонали равны
Диагонали взаимно
перпендикулярны и
являются
биссектрисами
углов
Прямоугольник
Ромб
Квадрат

3. Ответы

№ Параллелограмм
Прямоугольник
Ромб
Квадрат
1
+
+
+
+
2
—
—
+
+
3
+
+
+
+
4
—
+
—
+
5
+
+
+
+
6
—
+
—
+
7
—
—
+
+

4.

Тест для капитана вариант 1 1.Любой прямоугольник является:
а)ромбом б) квадратом в)параллелограммом г)нет такого ответа
2.Если в четырёхугольнике диагонали перпендикулярны, то этот
четырёхугольник-…
а) ромб б)квадрат в) прямоугольник г) нет правильного ответа
3. Ромб- это четырёхугольник, в котором….
а)диагонали точкой пересечения делятся пополам и равны.
б)диагонали перпендикулярны и точкой пересечения делятся
пополам
в)противолежащие углы равны, а стороны параллельны
г) нет правильного ответа

5. Конкурс капитанов вариант 2

1.Любой ромб является :
а) квадратом б) прямоугольником в)параллелограммом г)нет
правильного ответа.
2.Если диагонали перпендикулярны, то это параллелограмм:
а)ромб б) квадрат в)прямоугольник в) нет правильного ответа
.Прямоугольник — это четырёхугольник, в котором :
а) противоположные стороны параллельны, а диагонали равны
б) диагонали точкой пересечения делятся пополам и являются
биссектрисами его углов
в)два угла прямые и две стороны равны
г) нет правильного ответа

6.

Устные задачи 1.Один из углов параллелограмма 40. Найти углы параллелограмма
2. Сумма двух углов параллелограмма равна 140. Найти углы

параллелограмма.
3.Одна из сторон параллелограмма в 2 раза больше другой, а Р=24см
Найти стороны параллелограмма.
4. Найти площадь треугольника ,если площадь параллелограмма 240 кв.см
Б
Е
С
АВСД параллелограмм
Найти: угол А, угол С
А
32
Д
В
В
В
В
АВСД ТРАПЕЦИЯ
НАЙТИ угол В.,угол Д
С
117
в
Д
36
А
В
С
АВСД прямоугольник
Найти АД
60
10
1
0
А
Д
В
А
6
6
60
С
р
м Д
АВСД ромб Найти МД+ДР
Леонард Эйлер, крупнейший
математик XVIII века, родился
в Швейцарии. В 1727г. по
приглашению Петербургской
академии наук он приехал в
Россию. Эйлер попал в круг
выдающихся математиков,
получил большие возможности
для создания и издания своих
трудов.

Он работал с
увлечением и вскоре стал, по
единодушному признанию
современников, первым
математиком мира.
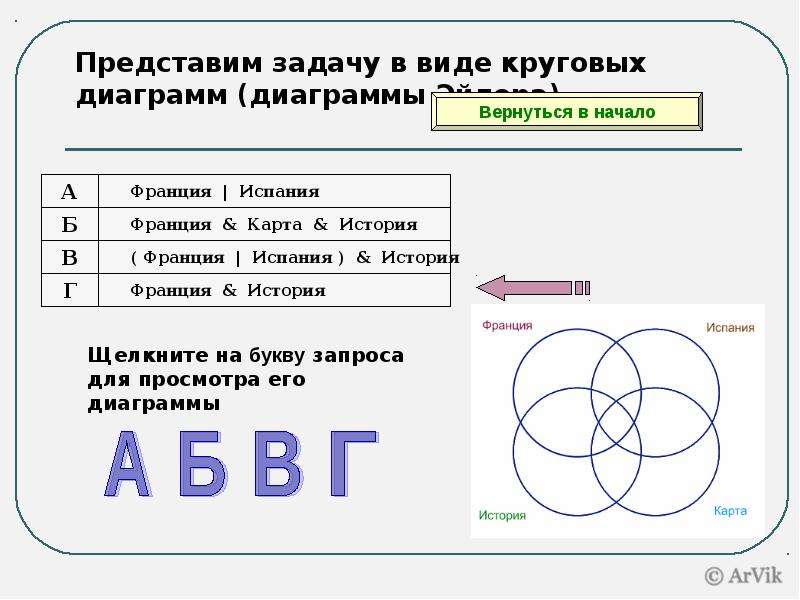
Круги ЭЙЛЕРА —
геометрическая схема,
с помощью которой
можно изобразить
отношения между
подмножествами, для
наглядного
представления
Множество всех действительных чисел Эйлер изобразил
с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вех действительных чисел.

Отношение рода и вида между понятиями

Во-первых, понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одному понятию и видовым по отношению к другому. Например, понятие «прямоугольник» – родовое по отношению к понятию «квадрат» и видовое по отношению к понятию «четырехугольник».

Во-вторых, для данного понятия часто можно указать несколько родовых понятий.

Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник».

Среди них можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм».

В–третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.

Так как объем понятия – множество, удобно, устанавливая отношения между объемами понятий, изображать их при помощи кругов Эйлера.

Установим, например, отношения между следующими парами понятий а и b, если:

1) а – «прямоугольник», b- «ромб»;

Объемы понятий пересекаются, но не одно множество не является подмножеством другого. Следовательно, можно утверждать, что данные понятия а и b не находятся в отношении рода и вида.

2) а – «многоугольник», b – «параллелограмм»;

Объемы данных понятий находятся в отношении включения, но не совпадают – всякий параллелограмм является многоугольником, но не наоборот. Следовательно, можно утверждать, что понятие «параллелограмм» — видовое по отношению к понятию «многоугольник», а понятие «многоугольник» – родовое по отношению к понятию «параллелограмм».

3) а — «прямая», b – «отрезок».

Объемы понятий не пересекаются, так как ни про один отрезок нельзя сказать, что он является прямой, и ни одна прямая не может быть названа отрезком. Следовательно, данные понятия не находятся в отношении рода и вида.

О понятиях «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок – часть прямой, а не ее вид.

Замечание.Если видовое понятие обладает всеми свойствами родового понятия, то часть не обязательно обладает всеми свойствами целого.

Например, отрезок не обладает такими свойствами прямой, как ее бесконечность.

3. Определение понятий

Появление в математике новых понятий, а значит, и новых терминов, обозначающих эти понятия, предполагает их определение.

Определением обычно называют предложение, разъясняющее суть нового термина (или обозначения). Как правило, делают это на основе ранее введенных понятий. Например, прямоугольник можно определить так: «Прямоугольником называется четырехугольник, у которого все углы прямые». В этом определении есть две части – определяемое понятие (прямоугольник) и определяющее понятие (четырехугольник, у которого все углы прямые). Если обозначить через а первое понятие, а через b – второе, то данное определение можно представить в таком виде:

а есть (по определению) b

Слова «есть (по определению)» обычно заменяют символом , и тогда определение выглядит так: а b

Читают: «а равносильно b по определению». Можно прочитать эту запись еще и так: «а тогда и только тогда, когда b».

Определения, имеющие такую структуру, называются явными. Рассмотрим их подробнее.

Обратимся опять к определению прямоугольника, вернее, к его второй части – определяющему понятию. В нем можно выделить:

1) понятие «четырехугольник», которое является родовым по отношению к понятию «прямоугольник»,

2) свойство «иметь все углы прямые», которое позволяет выделить из всевозможных четырехугольников один вид – прямоугольники; поэтому его называют видовым отличием.

Определение. Видовое отличие – это свойства (одно или несколько), которые позволяют выделять определяемые объекты из объема родового понятия.

Итоги нашего анализа можно представить в виде схемы

Определяемое понятие

Родовое понятие

видовое отличие

Определяющее понятие

Заметим, что в наглядном представлении структуры определения через род и видовое отличие мы допустили некоторые неточности. Во–первых, слова «родовое понятие» означают, что речь идет о родовом понятии по отношению к определяемому. Во-вторых, не совсем ясно, что означает знак «+», который, как известно, используется для обозначения сложения чисел. Смысл этого знака станет понятным немного позже, когда мы рассмотрим математический смысл союза «и». А пока познакомимся с еще одной возможностью наглядного представления определения через род и видовое отличие. Если определяемое понятие обозначить буквой

а, определяющее буквой b, родовое понятие (по отношению к определяемому) – буквой с, а видовое отличие – буквой Р, то определение через род и видовое отличие можно представить так:

Почему видовое отличие обозначено заглавной буквой, мы узнаем позже.

Нам известно, что любое понятие имеет объем. Если понятие а определено через род и видовое отличие, то о его объеме – множестве А – можно сказать, что в нем содержатся такие объекты, которые принадлежат множеству С (объему родового понятия с) и обладают свойством Р: А= { х | хÎ С и Р (х)}.

Например, если дано определение: «Острым углом называется угол, который меньше прямого», — то объем понятия «острый угол» – это подмножество множества всех углов плоскости, которые обладают свойством «быть меньше прямого».

Так как определение понятия через род и видовое отличие является по существу условным соглашением о введении нового термина для замены какой – либо совокупности известных терминов, то об определении нельзя сказать, верное оно или неверное; его не доказывают и не опровергают. Но, формулируя определения, придерживаются ряда правил. Назовем основные.

Требования к определению понятий

Определение должно быть соразмерным.

Это означает, что объемы определяемого и определяющего понятий должны совпадать. Это правило вытекает из того, что определяемое и определяющее понятия взаимозаменяемы.

Соразмерны, например, понятия «прямоугольник» и «четырехугольник, в котором все углы прямые». Если же объем определяющего понятия включает в себя объем понятия определяемого, то говорят об ошибке слишком широкого определения. Так, определение «Прямые

a и b называются параллельными, если они не имеют общих точек или совпадают» слишком широко, поскольку ему удовлетворяют и скрещивающие прямые.

Если же объем определяющего понятия уже объема определяемого понятия, то имеет место ошибка слишком узкого определения. Например, определение «Прямые a и b называются параллельными, если они не имеют общих точек» слишком узко, поскольку ему не удовлетворяют совпадающие прямые.

В определении (или их системе) не должно быть порочного круга.

Это означает, чтонельзя определять понятие через само себя (в определении не должно содержатся определяемого термина) или определять его через другое понятие, которое определяется через него.

Возьмем такие понятия начальной математики, как “умножение” и “произведение”, и дадим им следующие определения:

Умножением чисел называется действие, при помощи которого находят произведение этих чисел.

Произведением чисел называется результат их умножения.

Видим, что умножение определяется через понятие произведение, а произведение – через понятие умножения. Определения образовали, как говорят в математике, порочный круг. В результате цепочка последовательных определений, выстроенных в рамках курса, прерывается.

Порочный круг содержится и в таком определении: «Решением уравнения называется число, которое является его решением». Здесь понятие «решение уравнения» определяется, по сути дела, через решение уравнения.

Определение должно быть ясным.

Это на первый взгляд очевидное правило, но означает оно многое. Прежде всего, требуется, чтобы значения терминов, входящих в определяющее понятие, были известны к моменту введения определения нового понятия.

Например, нельзя определять прямоугольник как параллелограмм с прямым углом, если понятие «параллелограмм» еще не рассмотрено.

К условиям ясности определения относят также рекомендацию включать в видовое отличие лишь столько свойств, сколько необходимо и достаточно для выделения определяемых объектов из объема родового понятия.

Рассмотрим, например, такое определение прямоугольника: «Прямоугольником называется четырехугольник, у которого все углы прямые и противоположные стороны равны».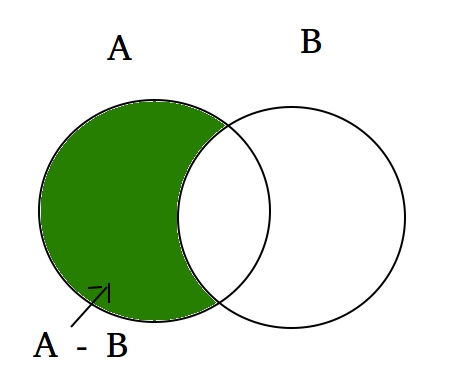

Нетрудно убедится в том, что это определение соразмерное и в нем нет порочного круга. Но можно показать, что включенное в определение свойство «в прямоугольнике противоположные стороны равны» вытекает из свойства «в прямоугольнике все углы прямые». В этом случае считают, что в данном определении прямоугольника второе свойство избыточное. Следовательно, правильнее определять прямоугольник таким образом: «Прямоугольником называется четырехугольник, у которого все углы прямые».

Замечание. Чтобы определение было ясным, желательно, чтобы оно не содержало избыточных свойств в определяющей части, т.е. таких свойств, которые могут быть выделены из других, включенных в это определение. Однако иногда для простаты изложения это правило нарушают.

Для обеспечения ясности определения важно также наличие понятия, родового по отношению к определяемому. Пропуск родового понятия делает определение несоразмерным. Неприемлемо, например, такое определение квадрата: «Квадрат – это когда все стороны равны».

К сказанному следует добавить, что, формулируя определение, надо стремиться в определяющем указать не просто родовое по отношению к определяемому понятие, а ближайшее.Это часто позволяет сократить количество свойств, включаемых в видовое отличие.

Например, если для определения квадрата в качестве родового выбрать понятие «четырехугольник», то тогда надо будет включать в видовое отличие два свойства: «иметь все прямые углы» и «иметь все равные стороны». В результате получим определение: «Квадратом называется четырехугольник, у которого все углы прямые и все стороны равны».

Если же в качестве родового выбрать ближайшее для квадрата родовое понятие – прямоугольник, то получим более короткое определение квадрата: «Квадратом называется прямоугольник, у которого все стороны равны».

Одно и то же понятие определить через род и видовое отличие, соблюдая сформулированные выше правила, можно по-разному.

Так, квадрат можно определить как:

а) прямоугольник, у которого соседние стороны равны;

б) прямоугольник, у которого есть прямой угол;

в) ромб, у которого есть прямой угол;

г) параллелограмм, у которого все стороны равны, а углы прямые.

Различные определения одного и того же понятия возможны потому, что из большего числа свойств, входящих в содержание понятия, в определение включаются только некоторые. И когда из возможных определений выбирают одно, исходят из того, какое из них проще и целесообразнее для дальнейшего построения теории.

Если же одному и тому же понятию даются, например, два различных определения, то необходимо доказывать их равносильность, т.е. убеждаться в том, что из свойств, включенных в одно определение, вытекают свойства, включенные в другое, и наоборот.

Завершая рассмотрение определений понятий через род и видовое отличие, назовем ту последовательность действий, которую мы должны соблюдать, если хотим воспроизвести определение знакомого понятия или построить определение нового:

1. Назвать определяемое понятие (термин).

2. Указать ближайшее родовое (по отношению к определяемому) понятие.

3. Перечислить свойства, выделяющие определяемые объекты из объема родового, т. е. сформулировать видовое отличие.

4. Проверить, выполнены ли правила определения понятия (соразмерно ли оно, нет ли порочного круга и т.д.).

Примеров явных родо-видовых отношений среди множества математических понятий, которые рассматриваются в начальных классах, не так уже и много. Но с учетом важности определения через род и видовой признак в дальнейшем обучении желательно добиваться понимания учениками сущности определения этого вида уже в начальных классах.

5. Неявные определения

При изучении математики в начальных классах определения через род и видовое отличие используются редко. Связано это как с особенностями курса, так и с возможностями детей. Но понятий в начальном курсе математики очень много – об этом мы говорили в начале лекции. Как же их определяют?

При изучении математики в начальной школе чаще всего используют так называемые неявныеопределения. В их структуре нельзя выделить определяемое и определяющее.

В обучении младших школьников особый интерес среди неявных определений составляют контекстуальные и остенсивныеопределения.

Вконтекстуальныхопределениях содержание нового понятияраскрывается через отрывок текста, через контекст, через анализ конкретнойситуации, описывающей смысл определяемого понятия с другими,известными, и тем самым косвенно раскрывается его содержание. Например, употребляя в работе с детьми такие выражения, как «найти значения выражения», «сравнить значение выражений 5 + а и (а — 3) × 2, если а = 7», «прочитать выражения, которые являются суммами», «прочитать выражения, и потом прочитать уравнения», мы раскрываем понятие «математическое выражение» как запись, которая складывается из чисел или переменных и знаков действий.

Или, примером контекстуального определения может быть определение уравнения и его решения, приведенного в учебнике математики для 3 класса. Здесь после записи ð + 6= 15 и перечня чисел 0,5,9,10 идет текст: «К какому числу надо прибавить 6, чтобы получилось 15? Обозначим неизвестное число латинской буквой х (икс):

Х + 6 = 15 – это уравнение.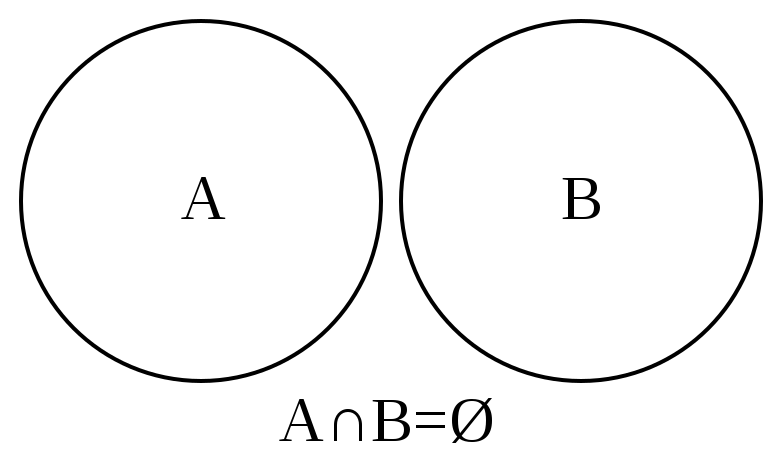

Решить уравнение – значит найти неизвестное число. В данном уравнении неизвестное число равно 9, так как 9+6=15.

Объясни, почему числа 0; 5 и 10 не подходят».

Из приведенного текста следует, что уравнение – это равенство, в котором есть неизвестное число. Оно может быть обозначено буквой х и это число надо найти. Кроме того, из этого текста следует, что решение уравнения – это число, которое при подстановке вместо х обращает уравнение в верное равенство.

Почти все определения, с которыми мы встречаемся в повседневной жизни — это контекстуальные определения. Услышав, неизвестное слово, мы стараемся сами установить его значение на основании всего сказанного.

Подобное имеет место и в обучении младших школьников. Много математических понятий в начальной школе определяются через контекст. Это, например, такие понятия, как «большой — маленький», «какой-нибудь», «любой», «один», «много», «число», «арифметическое действие», «уравнение», «задача» и т. д.

Контекстуальные определения остаются большей частью неполными и незавершенными. Они применяются в связи с неподготовленностью младшего школьника к усвоению полного и тем более научного определения.

Остенсивные определния — это определения путем демонстрации. Они напоминают обычные контекстуальные определения, но контекстом здесь есть не отрывок какого-либо текста, а ситуация, в которой оказывается объект, обозначенный понятием.

Например, учитель показывает квадрат (рисунок или бумажную модель) и говорит «Смотрите — это квадрат». Это типичное остенсивное определение.

Они используются также для введения терминов путем показа объектов, которые этими терминами обозначают. Например, таким способом можно определить в начальной школе понятия равенства и неравенства:

2 × 7 > 2 × 6 9×3 = 27

78- 9 < 78 6 × 4 = 4 × 6

37+ 6 > 37 17 — 5 = 8 + 4

В начальных классах остенсивные определения применяются при рассмотрении таких понятий как «красный (белый, черный и т. д.) цвет», «левый — правый», «слева направо», «цифра», «предшествующее и следующее число», «знаки арифметических действий», «знаки сравнения», «треугольник», «четырехугольник», «куб» и т.д.

На основе усвоения остенсивным путем значений слов есть возможность вводить в словарь ребенка уже вербальное значение новых слов и словосочетаний. Остенсивные определения — и только они — связывают слово с вещами. Без них язык — лишь словесное кружево, которое не имеет объективного, предметного содержания.

Остенсивные определения, как и контекстуальные, характеризуются некоторой незавершенностью. Действительно, определение посредством показа не выделяет понятие из других предложений, в нем не указываются свойства, характерные для данных понятий. Поэтому после контекстуального или остенсивного определения понятия необходимо дальнейшее изучение свойств так определенных объектов.

Заметим, что в начальных классах допустимые определения наподобие «Словом «пятиугольник» мы будем называть многоугольник с пятью сторонами». Это так называемое «номинальное определение».

Отдельные определения могут рассматривать понятие и по способу его образования или возникновения. Определение такого типа называют генетическими.

Примеры генетических определений: «Угол — это лучи, которые выходят с одной точки», «Диагональ прямоугольника — отрезок, который соединяет противоположные вершины прямоугольника». В начальных классах генетические определения применяют для таких понятий, как «отрезок», «ломаная», «прямой угол», «круг».

К генетическим понятиям можно отнести и определение через перечень.

Например, «Натуральный ряд чисел — это числа 1, 2, 3, 4 и т.д.».

Некоторые понятия в начальных классах вводят только через термин.

Например, единицы времени год, месяц, час, минута.

Есть в начальных классах понятия, которые подаются символическим языкомв виде равенства, например, а ×1 = а, а × 0 = 0

В начальных классах много математических понятий сначала усваиваются поверхностно, расплывчато. При первом ознакомлении школьники узнают только о некоторых свойствах понятий, очень узко представляют их объем. И это закономерно. Не все понятия легко усвоить. Но бесспорно, что понимание и своевременное использование учителем тех или других видов определений математических понятий — одна из условий формирования у учеников твердых знаний об этих понятиях.

Домашние задания по курсу логики

Здесь вы можете получить задачи по курсу логики, ссылка на страницу с решением приведена ниже.

Решения

Привести примеры нарушения законов логики

Привести примеры нарушения правил деления объема понятия.

Привести примеры нарушения правил определения понятия.

Изобразить на кругах Эйлера отношения между понятиями.

4.1. Студент, спортсмен, биатлонист, отец. 4.2. Мужчина, адвокат, юрист, прокурор.

4.3. Квадрат, прямоугольник, ромб, параллелограмм. 4.4. Деньги, валюта, доллары, банк.

4.5. Университет, вуз, академия, гимназия. 4.6. Пушка, пистолет, оружие, танк.

4.7. Кража, грабеж, разбой, мошенничество. 4.8. Искусство, эстрада, цирк, опера.

Обобщить понятие (три шага).

5.1. Учебник. 5.2. Лев. 5.3. Автомобиль. 5.4. Наука. 5.5. Цезарь. 5.6. Река. 5.7. Снег. 5.8. Береза.

Ограничить понятие (три шага).

6.1. Существо. 6.2. Искусство. 6.3. Животное. 6.4. Книга. 6.5. Река. 6.6. Поэма.

6.7. Средство связи. 6.8. Волейбол.

Дать определение, указав ближайший род и видовое отличие.

7.1. Свобода. 7.2. Преступление. 7.3. Философия. 7.4. Ответственность. 7.5. Долг.

7.6. Радость. 7.7. Любовь. 7.8. Совесть.

На основе логического квадрата, полагая исходное суждение сначала истинным, затем – ложным, выведите суждения, соотносимые с исходным, и установите их истинностные значения.

8.1. Коровы не летают. 8.2. Всяк кулик свое болото хвалит. 8.3. Услужливый дурак опаснее врага. 8.4. Насилие – спутник войны. 8.5. Не все сапожники в сапогах.

8.6. Рыбы живут в реках. 8.7. Наука на веру ничего не принимает. 8.8. Не все то золото, что блестит.

Осуществите превращение, обращение, противопоставление предикату.

9.1. Некоторые люди злые. 9.2. Доверчивый – беззащитен. 9.3. Утки не поют. 9.4. Дети любят шоколад. 9.5. Чиновники не любят работать. 9.6. Депутаты любят болтать.

9.7. Политики не следуют нормам морали. 9.8. Баскетболисты — люди высокорослые.

Приведите примеры умозаключений по схемам (модусам) условно-категорического силлогизма, а также – простой и сложной контрапозиции.

Подыщите средний термин и постройте силлогизм. Укажите фигуру и модус.

11.1. Железо – проводник тепла. 11.2. Декабрист — поэт. 11.3. Тигр – жвачное.

11.4. Певец – художник. 11.5. Композитор – ученый. 11.6. Собака – друг.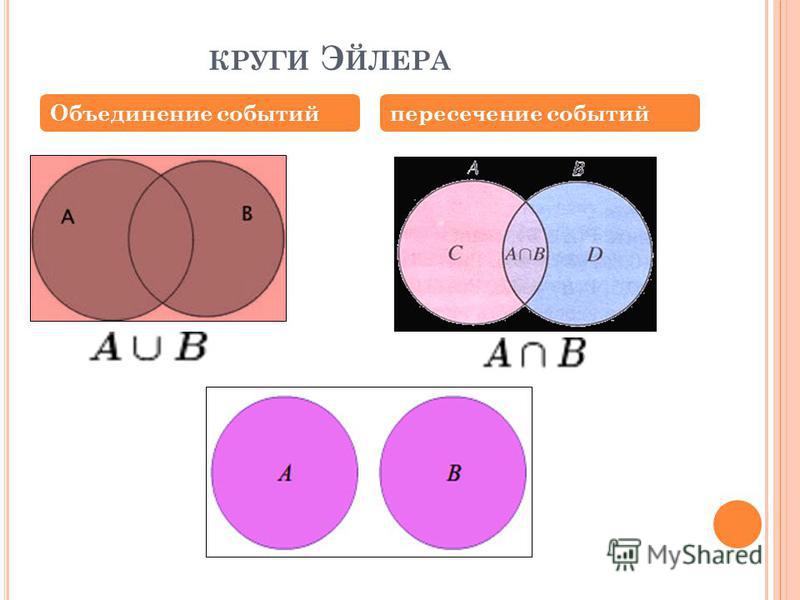 11.7. Кит – рыба. 11.8. Преступление – наказуемое действие.

Восстановите энтимему до полного силлогизма. Укажите фигуру и модус.

12.1 Они не больны, так как у них нет повышенной температуры. 12.2. Курица не птица, поскольку все птицы летают. 12.3. Металлы – химические элементы, так как все химические элементы – вещества. 12.4. Обвиняемый имеет право на защиту, Следовательно, М. имеет право на защиту. 12.5. Эта мысль ложна, ибо она не соответствует действительности. 12.6. Судья вправе задавать вопросы в любой момент допроса свидетеля, но вы не судья. 12.7. Наблюдение широко используется в оперативно- розыскной работе. Наблюдение – метод научного познания. 12.8. Все воспитатели должны быть хорошо воспитаны. Петров не является воспитателем.

Рекомендую посетить и эту страницу:

Аудио словарь латинского языка

И ИХ СТРУКТУРА

Математика И ИХ СТРУКТУРА

просмотров — 1204

МАТЕМАТИЧЕСКИЕ УТВЕРЖДЕНИЯ

Понятие. Виды понятий

Понятие — ϶ᴛᴏ форма мышления, в которой отражаются общие и существенные признаки предмета.

В языке понятия выражаются и закрепляются в словах и словосочетаниях, без которых невозможно ни формирование понятий, ни оперирование ими. К примеру, «треугольник», «дом», «добросовестный человек».

Понятия делятся на основные (неопределяемые) и определяемые (производные).

Основные понятия принимаются без определения. К примеру, в геометрии основными понятиями являются: точка, прямая, плоскость.

Определяемые (производные) понятия определяются через основные или ранее определенные. К примеру, луч – часть прямой, ограниченная с одной стороны точкой.

В понятии отражаются различные признаки предметов.

Признаком предмета принято называть то, в чем предметы сходны друг с другом или чем они друг от друга отличаются. Признаки могут выражаться в свойствах предмета͵ в форме отношения предмета к другим предметам.

Отличительные признаки — ϶ᴛᴏ признаки, которые принадлежат только одному предмету.

Общие признаки принадлежат нескольким предметам.

Признаки бываютсущественные и несущественные.

Существенным признаком какого-либо понятия принято называть такой признак, который принадлежит данному понятию при любых условиях, выражает его коренную сущность, с изменением которого меняется понятие.

К примеру, существенными признаками квадрата являются прямоугольность и равносторонность.

Несущественный признак не раскрывает сущность предмета͵ при изменении которого понятие о предмете не меняется.

Всякое понятие имеет содержание и объем.

Содержанием понятия принято называть совокупность существенных признаков предмета. Содержанием понятия «ромб» является совокупность двух существенных признаков: 1) быть параллелограммом и 2) иметь равные стороны.

Объемом понятия принято называть множество предметов, обладающих данными существенными признаками. К примеру, под объемом понятия «студент» подразумевается множество всех студентов, которые существуют сейчас, существовали ранее и будут существовать в будущем.

Связь между содержанием и объемом понятия выражается в законе обратного отношения между содержанием и объемом понятия: увеличение содержания понятия ведет к образованию понятия с меньшим объемом, и наоборот. Так, к примеру, если увеличить содержание понятия прямоугольник, добавив свойство равных сторон, то получится понятие с меньшим объемом – квадрат. В случае если же наоборот, убрать свойство прямоугольности в определении прямоугольника, то получится понятие с большим объемом – параллелограмм.

Способы определения понятий

При изучении понятий в любой науке им дают определения. Определить понятие – значит указать способ, с помощью которого можно отделять объекты или отношения, охватываемые данным понятием, от всех других объектов и отношений.

Для того чтобы определить понятие, нужно указать его место в ряду других понятий данной науки, выявить его связи, зависимости от других понятий. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, определяя понятие, приходится выполнять некоторую логическую операцию, в результате которой формулируется предложение, раскрывающее содержание понятия.

Определением (дефиницией) принято называть логическая операция, раскрывающая содержание понятия.

Понятие, содержание которого раскрывается в определении принято называть определяемым; понятие, раскрывающее содержание определяемого понятия, принято называть определяющим.

К примеру, квадрат — ϶ᴛᴏ прямоугольник, у которого все стороны равны. Квадрат – определяемое понятие, прямоугольник – определяющее понятие.

Для того, чтобы определения могли служить построению какой-либо научной теории, они должны удовлетворять определенным требованиям.

1. Требование соразмерности определения: объем определяемого понятия должен совпадать с объемом определяющего понятия.

К примеру, в определении «Биссектрисой угла принято называть луч, который делит угол пополам» объем определяющего понятия шире объема определяемого понятия (неполно видовое отличие – луч должен выходить из вершины угла).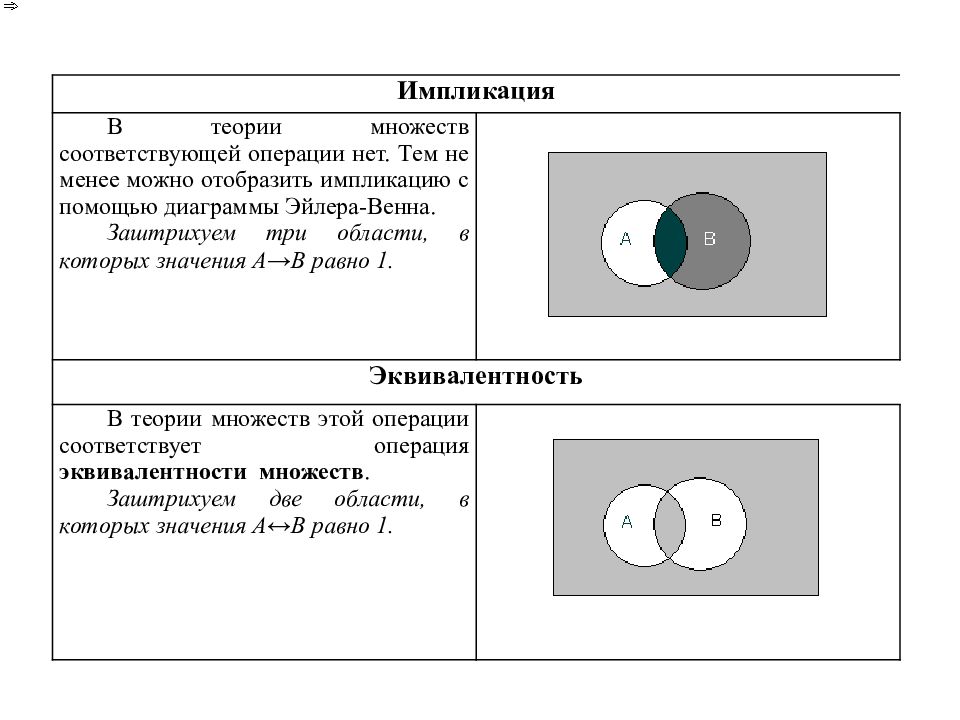

2. Отсутствие порочного круга: нельзя определить понятие через само себя или определить его через другое понятие, ĸᴏᴛᴏᴩᴏᴇ в свою очередь определяется через него.

К примеру, в определениях «Кругом принято называть часть плоскости, ограниченная окружностью. Окружностью принято называть граница круга» понятие круг определяется через окружность, а окружность – через круᴦ.

3. Отсутствие амонимии: каждый термин в качестве определяемого должен встречаться не более одного раза. При нарушении этого условия нарушается однозначность определения, один и тот же термин будет обозначать различные объекты или отношения.

К примеру, в математической литературе можно встретить следующую амонимию: термин «цифра» понимает как символ для записи числа и как соответствующее однозначное число.

4. Отсутствие лишних свойств: формулировка определения не должна содержать свойства, которые можно вывести из других свойств, указанных в этом же определении.

К примеру, в определении «Прямоугольник — ϶ᴛᴏ четырехугольник, у которого противоположные стороны равны и все углы прямые», условие «противоположные стороны равны» вытекает из свойства «все углы прямые».

В случае если определение удовлетворяет перечисленным требованиям, то его называют корректным.

Рассмотрим виды определений понятий.

Определения делятся на явные и неявные.

Явные определения раскрывают существенные признаки понятия. К неявным определениям относятся определения понятия путем непосредственной демонстрации объектов, охватываемых этим понятием, или приведение контекста͵ в котором содержится то или иное понятие.

Неявные определения используются на начальном этапе обучения математике. К примеру, данные определения используются при изучении геометрического материала. С помощью непосредственной демонстрации соответствующих моделей педагог знакомит детей с понятиями «круг», «треугольник», «многоугольник», «прямой угол» и др. Такие неявные определения называются остенсивными (от лат. показывать).

Отношения «больше», «меньше», «равно» в ДОУ и начальной школе определяются с помощью приведения контекста «равно — значит столько же». Такие неявные определения называются контекстуальными. Контекстуальное определение позволяет выяснить содержание определения незнакомого слова через контекст, не прибегая к словарю для перевода или толковому словарю.

В дальнейшем по мере накопления запаса знаний происходит накопление понятий, развивается язык и способность к обобщению. Все это дает возможность определять неизвестные понятия через известные. Таким образом появляются явные определения.

В явных определениях даны определяемое понятие и определяющее, объемы которых равны.

Рассмотрим некоторые способы явных определений.

1. Определение понятий через ближайший род и видовое отличие. Этот способ является наиболее распространенным.

К примеру, «Треугольник – многоугольник с тремя сторонами».

Признак, указывающий на тот круг предметов, из числа которых нужно выделить определяемое множество предметов, принято называть родовым признаком или родом (многоугольник).

Признаки, при помощи которых выделяется определяемое множество предметов из числа предметов, соответствующих родовому понятию, принято называть видовым отличием (три стороны).

Определение через ближайший род и видовое отличие включает в себя два приема:

1. Подведение определяемого понятия под более широкое по объему родовое понятие. Обычно это такое родовое понятие, ĸᴏᴛᴏᴩᴏᴇ содержит большее количество общих признаков с определяемым понятием.

К примеру, Прямоугольник – параллелограмм, у которого все углы прямые.

2. Указание видового отличия, ᴛ.ᴇ. признака, отличающего определяемый предмет от других видов, входящих в данный род (признака, присущего только видовому понятию).

2. Генетическое определение понятий.

Генетические или конструктивные определения понятий являются частным случаем определений через род и видовое отличие. В таких определениях видовое отличие указывает на происхождение предмета или на способ его образования.

К примеру, конус — ϶ᴛᴏ геометрическое тело, полученное вращением прямоугольного треугольника вокруг одного из своих катетов.

3. Аксиоматическое определение понятий.

В случае если какое-либо понятие вводится с помощью списка аксиом, описывающих свойства этого понятия, то такое определение принято называть аксиоматическим. Такие определения чаще всего используются для описания неопределяемых понятий — прямая, точка, плоскость и др.

Отношения между понятиями

Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности. По этой причине и понятия, отражающие предметы мира, также находятся в определенных отношениях.

Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (к примеру, «камень» и «нитка»; «романс» и «кирпич»), остальные понятия называются сравнимыми.

Сравнимые понятия делятся по объему на совместимые (объемы этих понятий совпадают полностью или частично) и несовместимые (объемы которых не совпадают ни в одном элементе).

Существует три вида отношений совместимости: равнозначность (тождество), пересечение, подчинение.

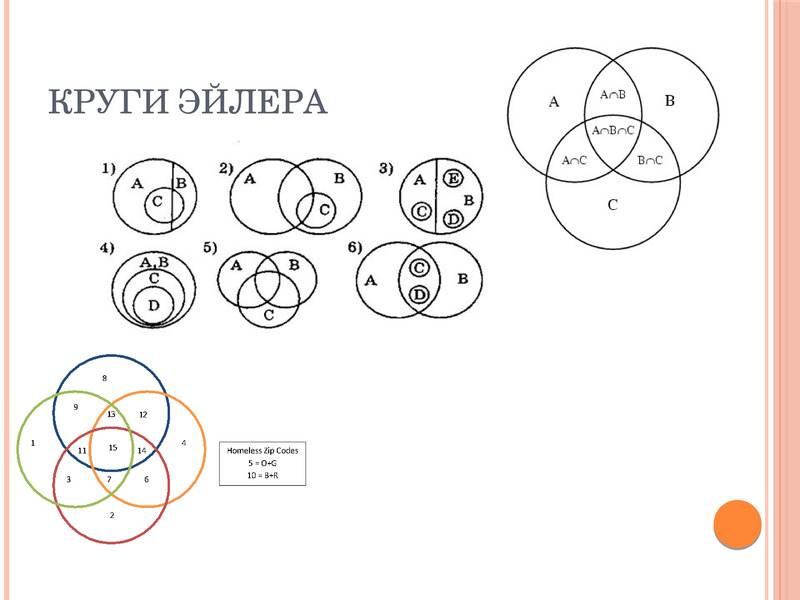
Отношения между понятиями изображаются с помощью кругов Эйлера, где каждый круг обозначает объем понятия (рис. 3).

Равнозначными(или тождественными) называются понятия, которые различаются по своему содержанию, но объемы которых совпадают. Примеры равнозначных понятий: 1) «река Волга» и «самая длинная река в Европе»; 2) «автор рассказа «Человек в футляре» и «автор комедии «Вишневый сад»; 3) «равносторонний прямоугольник», «квадрат» и «прямоугольный ромб». Объемы тождественных понятий изображаются кругами, полностью совпадающими.

Понятия, объемы которых частично совпадают, ᴛ.ᴇ. содержат общие элементы, находятся в отношении пересечения. Примерами их являются следующие пары: «ребенок» и «танцор»; «спортсмен» и «студент». Οʜᴎ изображаются пересекающимися кругами. В закрашенной части двух кругов мыслятся студенты, являющиеся спортсменами, или (что одно и то же) спортсмены, являющиеся студентами, в левой части круга А мыслятся студенты, не являющиеся спортсменами. В правой части круга В мыслятся спортсмены, которые не являются студентами.

Отношение подчиненияхарактеризуется тем, что объем одного понятия целиком включается (входит) в объем другого понятия, но не исчерпывает его. Это отношение вида и рода; А — подчиняющее понятие («млекопитающее»), В — подчиненное понятие («кошка»).

Существует три вида отношений несовместимости: соподчинение, противоположность, противоречие.

Соподчинение— это отношение между объемами двух или нескольких понятий, исключающих друг друга, но принадлежащих некоторому, более общему родовому понятию (к примеру, «ель» и «береза» принадлежат объему понятия «дерево»).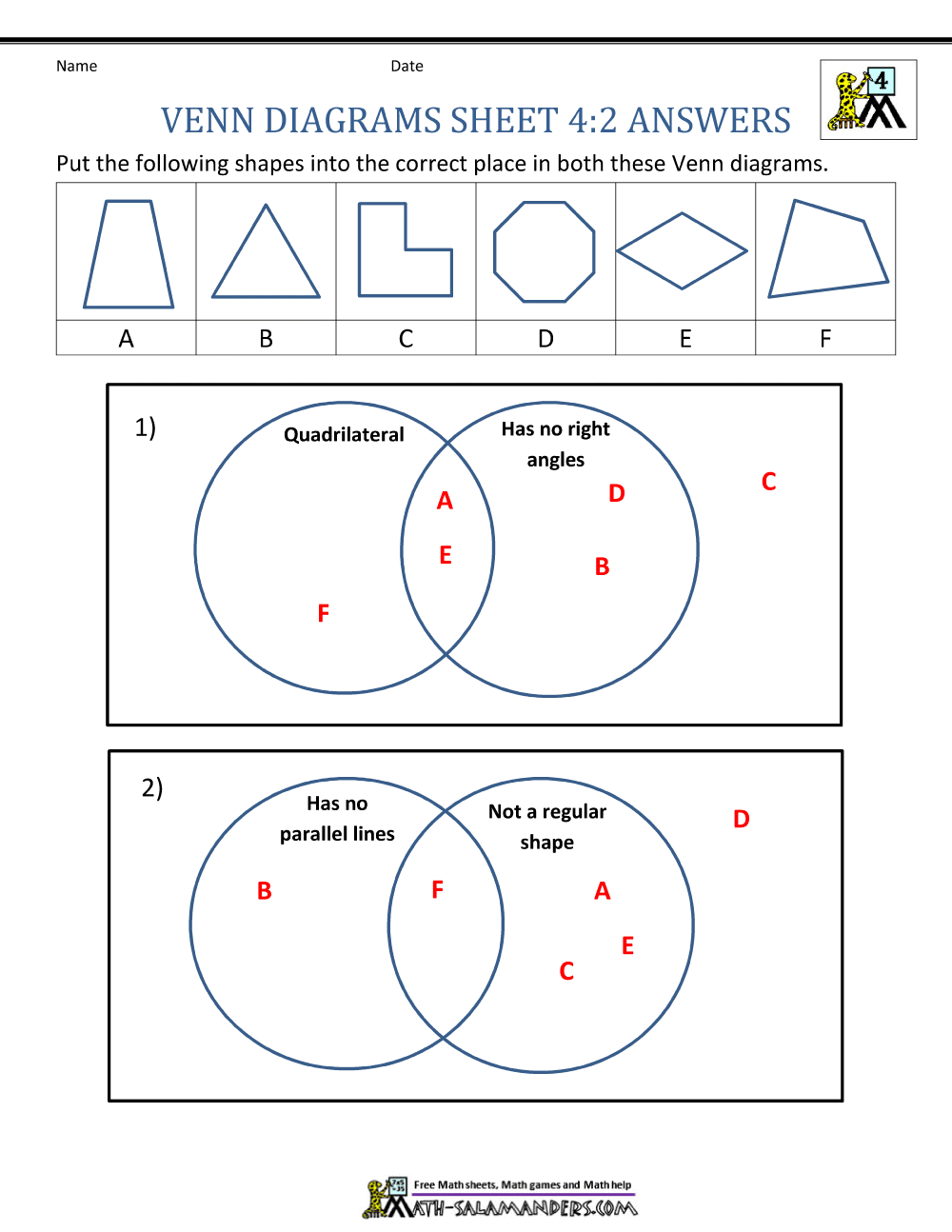 Οʜᴎ изображаются отдельными неперекрещивающимися кругами внутри более обширного круга. Это виды одного и того же рода.

Рис. 3. Отношения между понятиями

В отношении противоположностинаходятся такие два понятия, которые являются видами одного и того же рода, и притом одно из них содержит некоторые признаки, а другое — признаки, несовместимые с ними (ᴛ.ᴇ. противоположные признаки). Такие понятия называются противоположными. Объемы двух противоположных понятий составляют в своей сумме лишь часть объема общего для них родового понятия, видами которого они являются и которому соподчинены. Слова, выражающие противоположные понятия, являются антонимами. Примеры противоположных понятий: «храбрость» — «трусость»; «белая краска» — «черная краска». Объемы последних двух понятий разделены объемом некоторого третьего понятия, куда, к примеру, входит краска другого цвета (не белая и не черная, а к примеру, зеленая).

В отношении противоречиянаходятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками. В случае если одно понятие обозначить А (к примеру, «четные числа»), то другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т. е. «нечетные числа»). Круг Эйлера, выражающий объем таких понятий, делится на две части (А и не-А) и между ними не существует третьего понятия. К примеру, бумага может быть либо белой, либо небелой; человек бывает честным или нечестным; животное — млекопитающим или немлекопитающим и т. д. Понятие А является положительным, а понятие не-А — отрицательным. Понятия А и не-А также являются антонимами.

Операции над понятиями

Операции над понятиями – логические действия, вследствие которых создаются новые понятия.

К операциям над понятиями относят: отрицание, сложение, вычитание, умножение, обобщение, ограничение.

Наиболее простой операцией над понятиями является отрицание. Она проводится путем простого прибавления к исходному понятию частицы «не».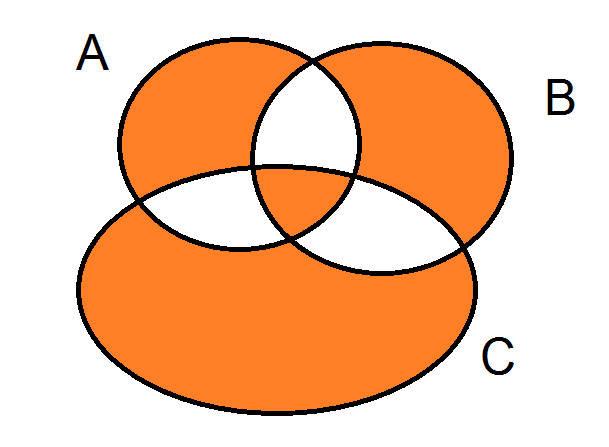

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, утвердительное понятие преобразуется в отрицательное. В случае если мы будем еще раз проводить отрицание, то увидим, что отрицание отрицательного понятия дает положительное. Отрицание отрицательного понятия «не-умный» — «не-не-умный» соответствует понятию «умный». Операция сложенияпредставляет собой объединение объемов двух и более понятий, даже если они и не совпадают между собой. Суммой понятий А и В принято называть такое понятие, объем которого равен объединению объемов данных понятий, а название его получается путем соединения союзом «или» названий понятий А и В или указания равнозначного ему понятия. Объединив объемы понятий «девочки» и «мальчики» получаем некоторую область, отражающую признаки того и другого в общем понятии «дети».Операция умножения заключается в отыскании области, которая обладает свойствами как одного, так и другого понятия. Произведением понятий А и В принято называть новое понятие, объем которого равен пересечению объемов понятий А и В.

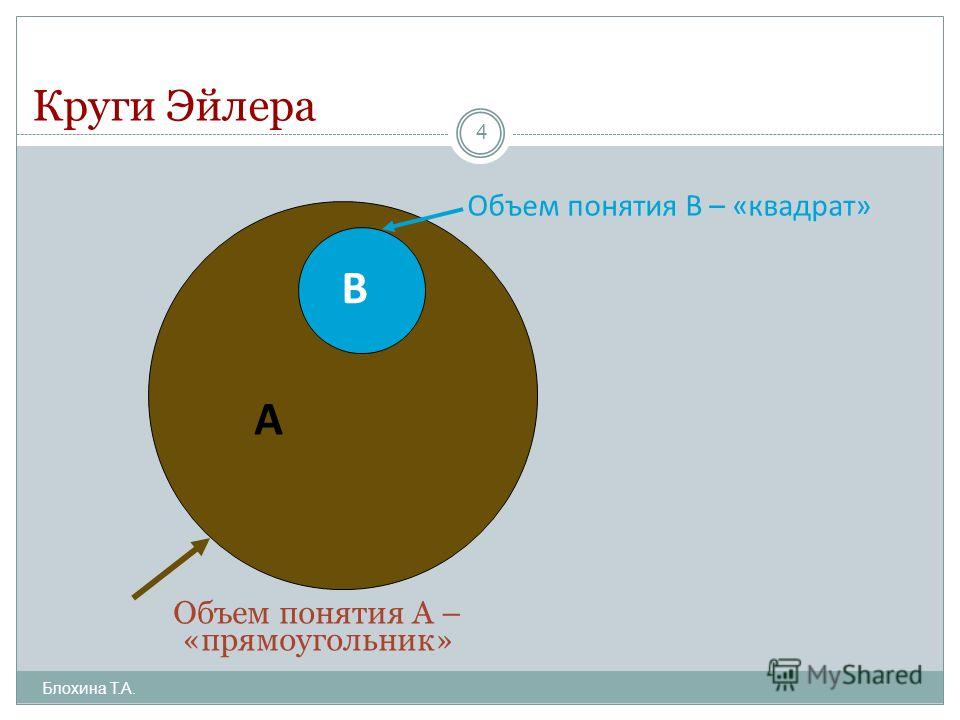Умножение понятий «мальчик» и «спортсмен» выявляет область мальчиков, являющихся спортсменами, и наоборот.

Обобщение— логическая операция перехода от понятия с меньшим объемом к понятию с большим объемом. Другими словами, логическая операция перехода от видового понятия к родовому посредством сокращения содержания исходного понятия.

Пример: В случае если из содержания понятия «Педагогический университет» исключить видовой признак «педагогический», то получим родовое понятие «университет», дальнейшим обобщением будет «высшее учебное заведение». Объемы понятий «Педагогический университет» (А), «Университет» (В), «Высшее учебное заведение» (С) отмечены на кругах Эйлера-Венна.

Ограничение — логическая операция (обратная обобщению) перехода от понятия с большим объемом к понятию с меньшимобъемом. Другими словами это есть переход от родовых понятий к видовым путем прибавления к содержанию родового понятия видообразующего признака.

Пример: В случае если в вышеприведенном примере взять за исходное понятие «Высшее учебное заведение», то понятие «Университет» можно рассматривать как его ограничение, а понятие «Педагогический университет» будет ограничением последнего. Из данного примера видно, что при выполнении операции обобщения понятий полученное новое понятие имеет меньшее число существенных признаков и больший объем по сравнению с данным. А при выполнении ограничения понятий полученное новое понятие имеет большее число существенных признаков и меньший объем по сравнению с данным. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, операции обобщения и ограничения можно осуществлять посредством модификации содержания понятия, опираясь при этом на закон обратного отношения между содержаниями и объемами понятий: чтобы обобщить понятие, крайне важно перейти к менее информативному, а чтобы ограничить — к более информативному понятию.

Задания для самостоятельной работы

1. Назовите несколько элементов, принадлежащих объему понятия: 1) часть речи; 2) геометрическая фигура; 3) мебель; 4) дерево; 5) цветок.

2. Назовите несколько свойств, входящих в содержание понятия: 1) трапеция; 2) существительное; 3) студент; 4) стол; 5) хвойное дерево.

3. Находятся ли в отношении рода и вида следующие пары понятий: а) многоугольник и треугольник; б) угол и острый угол; в) луч и прямая; г) ромб и квадрат; д) круг и окружность?

4. Изобразите при помощи кругов Эйлера отношения между объемами понятий а, b и с, если:

а) а — «четырехугольник»,

b — «трапеция»,

с — «прямоугольник»;

б) а — «натуральное число, кратное 3»;

b — «натуральное число, кратное 4»;

с — «натуральное число»

в) а — «треугольник»;

b — «равнобедренный треугольник»;

с — «равносторонний треугольник».

5. В каких отношениях находятся понятия: 1) трапеция и треугольник; 2) глагол и часть речи; 3) луч и прямая; 4) стол и тарелка; 5) однозначные числа и нечетные числа.

6.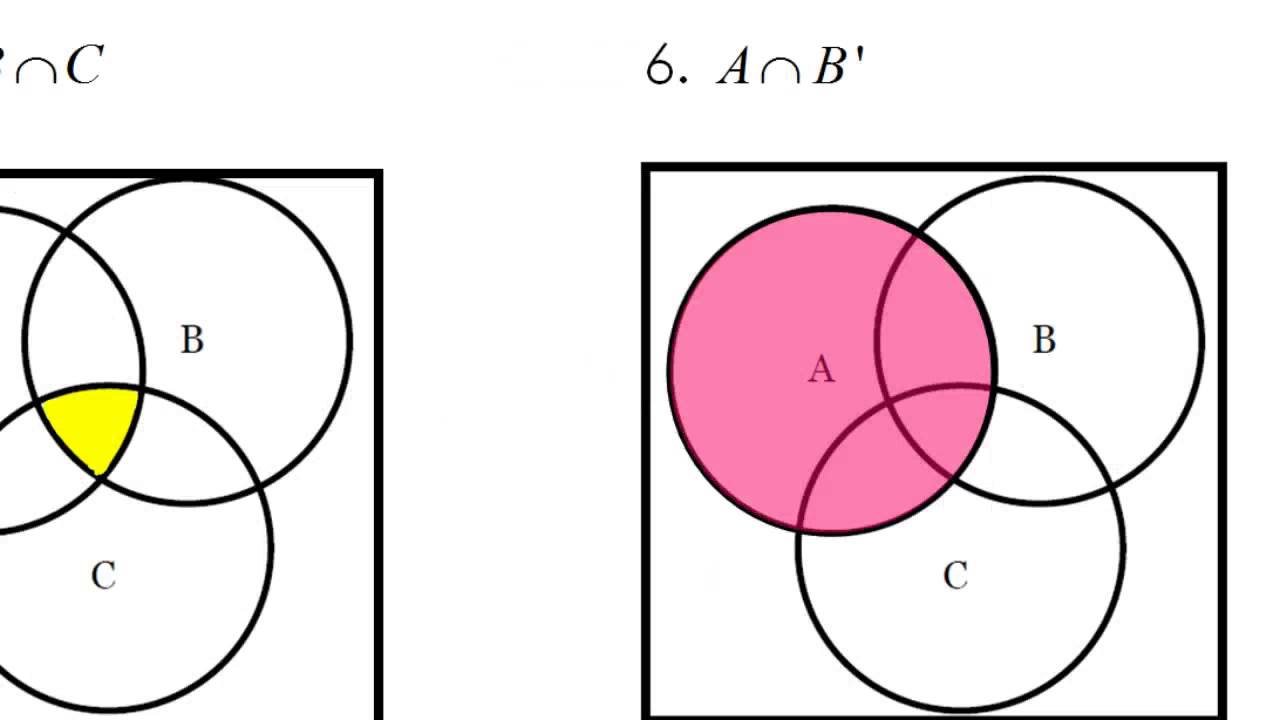 Приведите примеры понятий, отношения между которыми бывают изображены с помощью кругов Эйлера, приведенных на рисунках.

7. Равносильны ли понятия «правильный четырехугольник» и «ромб», «равноугольный четырехугольник» и «квадрат»?

8. В следующих определениях выделите определяемое и определяющее понятия, родовое понятие (по отношению к определяемому) и видовое отличие:

а) Параллелограммом принято называть четырехугольник, у которого противоположные стороны попарно параллельны.

б) Отрезок, соединяющий середины двух сторон треугольника принято называть его средней линией.

9. Для каждого из следующих понятий укажите родовое понятие: 1) лиственное дерево; 2) биссектриса угла; 3) квадрат; 4) глагол.

10. Для каждого из следующих понятий укажите видовое понятие: 1) животное; 2) многоугольник; 3) часть речи; 4) параллелограмм.

11. Дайте определение понятий: а) параллелограмм; б) ромб; в) многоугольник; г) треугольник; д) равносторонний треугольник.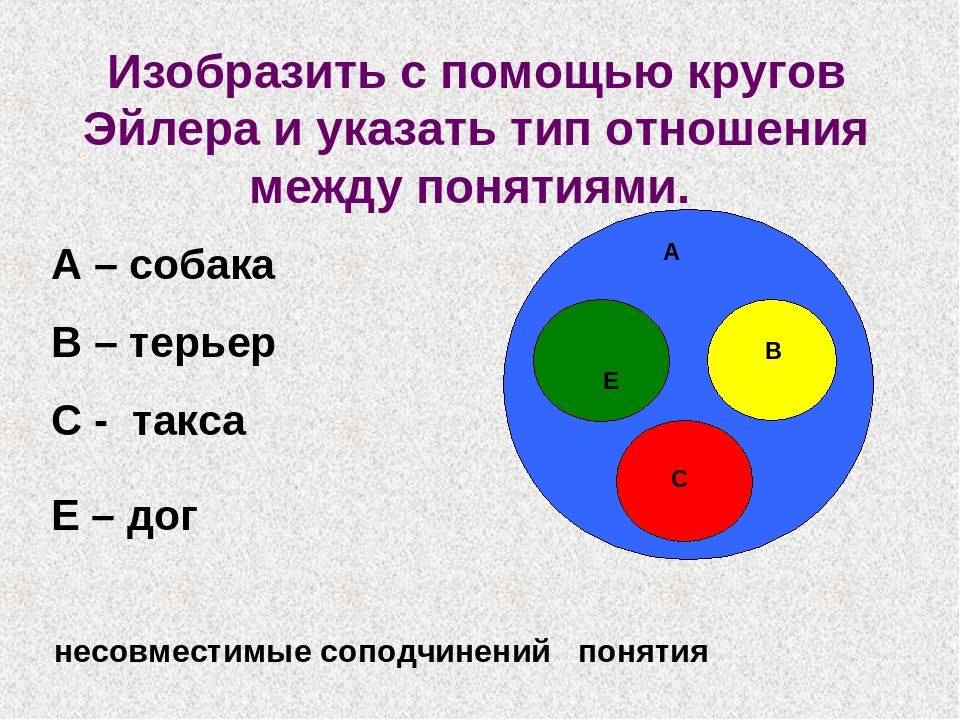 Выделите в каждом определении родовое понятие и видовое отличие. Определите, в каком отношении находятся содержания понятий «треугольник» и «равносторонний треугольник». Определите, в каком отношении находятся объемы понятий «многоугольник» и «треугольник».

12. Укажите ошибки в следующих определениях: 1) прямоугольник — ϶ᴛᴏ когда все углы прямые; 2) отрезок – прямая, ограниченная с двух сторон; 3) параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны и равны; 4) простое число — ϶ᴛᴏ когда оно имеет только два натуральных делителя.

Open Library — открытая библиотека учебной информации. Методика изучения математических понятий Что является чем математические понятия

Лекция №2

по математике

Тема: «Математические понятия»

Математические понятия

Определение понятий

Требования к определению понятий

Некоторые виды определений

Понятия, которые изучаются в начальном курсе математику, обычно представляют в виде четырех групп. В первую включаются понятия, связанные с числами и операциями над ними: число, сложение, слагаемое, больше и др. Во вторую входят алгебраические понятия: выражение, равенство, уравнение и др. Третью составляют геометрические понятия: прямая, отрезок, треугольник и т.д. Четвертую группу образуют понятия, связанные с величинами и их измерением.

Как же изучить такое обилие самых разных понятий?

Прежде всего, надо иметь представление о понятии как логической категории и особенностях математических понятий.

В логике понятия рассматривают как форму мысли, отражающую объекты (предметы или явления) в их существенных и общих свойствах. Языковой формой понятия является слово или группа слов.

Составить понятие об объекте — это значит уметь отличить его от других сходных с ним объектов. Математические понятия обладают рядом особенностей. Главная заключается в том, что математические объекты, о которых необходимо составить понятие, в реальности не существуют. Математические объекты созданы умом человека. Это идеальные объекты, отражающие реальные предметы или явления. Например, в геометрии изучают форму и размеры предметов, не принимая во внимание другие их свойства: цвет, массу, твердость и т.д. От всего этого отвлекаются, абстрагируются. Поэтому в геометрии вместо слова «предмет» говорят «геометрическая фигура».

Результатом абстрагирования являются и такие математические понятия, как «число» и «величина».

Вообще математические объекты существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык.

К сказанному можно добавить, что, изучая пространственные формы и количественные отношения материального мира, математика не только пользуется различными приемами абстрагирования, но и само абстрагирование выступает как многоступенчатый процесс. В математике рассматривают не только понятия, появившиеся при изучении реальных предметов, но и понятия, возникшие на основе первых. Например, общее понятие функции как соответствия является обобщением понятий конкретных функций, т.е. абстракцией от абстракций.

Чтобы овладеть общими подходами к изучению понятий в начальном курсе математики, учителю необходимы знания об объеме и содержании понятия, об отношениях между понятиями и о видах определений понятий.

2. Объем и содержание понятия. Отношения между понятиями

Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали. Можно указать и другие его свойства.

Среди свойств объекта различают существенные и несущественные. Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать. Например, для квадрата существенными являются все свойства, названные выше. Несущественно для квадрата ABCD свойство «сторона AD горизонтальна». Если квадрат повернуть, то сторона AD окажется расположенной по-другому (рис. 26).

Поэтому, чтобы понимать, что представляет собой данный математический объект, надо знать его существенные свойства.

Когда говорят о математическом понятии, то обычно имеют в виду множество объектов, обозначаемых одним термином (словом или группой слов). Так, говоря о квадрате, имеют в виду все геометрические фигуры, являющиеся квадратами. Считают, что множество всех квадратов составляет объем понятия «квадрат».

Вообще объем понятия — это множество всех объектов, обозначаемых одним термином.

Любое понятие имеет не только объем, но и содержание.

Рассмотрим, например, понятие «прямоугольник».

Объем понятия — это множество различных прямоугольников, а в его содержание входят такие свойства прямоугольников, как «иметь четыре прямых угла», «иметь равные противоположные стороны», «иметь равные диагонали» и т. д.

Между объемом понятия и его содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Так, например, объем понятия «квадрат» является частью объема понятия «прямоугольник», а в содержании понятия «квадрат» содержится больше свойств, чем в содержании понятия «прямоугольник» («все стороны равны», «диагонали взаимно перпендикулярны» и др.).

Любое понятие нельзя усвоить, не осознав его взаимосвязи с другими понятиями. Поэтому важно знать, в каких отношениях могут находиться понятия, и уметь устанавливать эти связи.

Отношения между понятиями тесно связаны с отношениями между их объемами, т.е. множествами.

Условимся понятия обозначать строчными буквами латинского алфавита: а, b, с,…, z.

Пусть заданы два понятия а и b. Объемы их обозначим соответственно А и В.

Если А В (А ≠ В), то говорят, что понятиеа — видовое по отношению к понятию b , а понятие b — родовое по отношению к понятию а .

Например, если а — «прямоугольник», b — «четырехугольник», то их объемы А и В находятся в отношении включения (А В и А ≠ В), поскольку всякий прямоугольник является четырехугольником. Поэтому можно утверждать, что понятие «прямоугольник» — видовое по отношению к понятию «четырехугольник», а понятие «четырехугольник» — родовое по отношению к понятию «прямоугольник».

Если А = В, то говорят, что понятия а и b тождественны.

Например, тождественны понятия «равносторонний треугольник» и «равноугольный треугольник», так как их объемы совпадают.

Если множества А и В не связаны отношением включения, то говорят, что понятия а и b не находятся в отношении рода и вида и не тождественны. Например, не связаны такими отношениями понятия «треугольник» и «прямоугольник».

Рассмотрим подробнее отношение рода и вида между понятиями. Во-первых, понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одному понятию и видовым по отношению к другому. Например, понятие «прямоугольник» — родовое по отношению к понятию «квадрат» и видовое по отношению к понятию «четырехугольник».

Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник». Среди них можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм».

В-третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.

Так как объем понятия — множество, удобно, устанавливая отношения между объемами понятий, изображать их при помощи кругов Эйлера.

Установим, например, отношения между следующими парами понятий а и Ь, если:

1) а — «прямоугольник», b — «ромб»;

2) а — «многоугольник», b — «параллелограмм»;

3) а — «прямая», b — «отрезок».

В случае 1) объемы понятий пересекаются, но не одно множество не является подмножеством другого (рис. 27).

Следовательно, можно утверждать, что данные понятия а и b не находятся в отношении рода и вида.

В случае 2) объемы данных понятии находятся в отношении включения, но не совпадают — всякий параллелограмм является многоугольником, но не наоборот (рис. 28). Следовательно, можно утверждать, что понятие «параллелограмм» — видовое по отношению к понятию «многоугольник», а понятие «многоугольник» — родовое по отношению к понятию «параллелограмм».

В случае 3) объемы понятий не пересекаются, так как ни про один отрезок нельзя сказать, что он является прямой, и ни одна прямая не может быть названа отрезком (рис. 29).

Следовательно, данные понятия не находятся в отношении рода и вида.

О понятиях «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок- часть прямой, а не ее вид. И если видовое понятие обладает всеми свойствами родового понятия, то часть не обязательно обладает всеми свойствами целого. Например, отрезок не обладает таким свойством прямой, как ее бесконечность.

Курс математики 5-6 классов представляет собой органическую часть всей школьной математики. Поэтому основным требованием к его построению является структурирование содержания на единой идейной основе, которая, с одной стороны, является продолжением и развитием идей, реализованных при обучении математики в начальной школе, и, с другой стороны, служит последующему изучению математики в старших классах.

Продолжается развитие всех содержательно-методических линий курса начальной математики: числовой, алгебраической, функциональной, геометрической, логической, анализ данных. Они реализованы на числовом, алгебраическом, геометрическом материале.

В последнее время существенно пересмотрено изучение геометрии. Целью изучения геометрии в 5-6 классах является познание окружающего мира языком и средствами математики. С помощью построений и измерений учащиеся выявляют различные геометрические закономерности, которые формулируют как предложение, гипотезу. Доказательный аспект геометрии рассматривается в проблемном плане – учащимся прививается мысль, что экспериментальным путём можно открыть многие геометрические факты, но эти факты становятся математическими истинами только тогда, когда они установлены средствами, принятыми в математике.

Таким образом, геометрический материал в этом курсе может быть охарактеризован, как наглядно-деятельностная геометрия. Обучение организуется как процесс интеллектуально-практической деятельности, направленной на развитие пространственных представлений, изобразительных умений, расширение геометрического кругозора, в ходе которого важнейшие свойства геометрических фигур получаются посредством опыта и здравого смысла.

Достаточно новой в курсе 5-6 классов является содержательная линия «Анализ данных », которая объединяет в себе три направления: элементы математической статистики, комбинаторику, теорию вероятностей. Введение этого материала продиктовано самой жизнью. Его изучение направлено на формирование у школьников как общей вероятностной интуиции, так и конкретных способов оценки данных. Основная задача в этом звене – формирование соответствующего словаря, обучение простейшим приёмам сбора, представления и анализа информации, обучение решению комбинаторных задач перебором возможных вариантов, создание элементарных представлений о частоте и вероятности случайных событий.

Однако данная линия присутствует не во всех современных школьных учебниках для 5-6 классов. Особо подробно и ярко представлена данная линия в учебниках .

Алгебраический материал, включённый в курс математики 5-6 классов, является основой для систематического изучения алгебры в старших классах. Можно отметить следующие особенности изучения этого алгебраического материала:

1. Изучение алгебраического материала основано на научной основе с учётом возрастных особенностей и возможностей учащихся.

2. Формирование алгебраических понятий и выработка соответствующих умений и навыков составляют единый процесс, построенный на детально разработанной системе упражнений.

3. Система упражнений служит надёжным средством для овладения современным математическим языком, так как этот язык широко применяется при формулировке различных заданий. Например, «Докажите, что данное неравенство верно: 29 2

4. Совершенствование вычислительных навыков органически связано с изучением алгебраического материала.

В 5-6 классах делается акцент на развитие вычислительной культуры, в частности, на обучение эвристическим приёмам прикидки и оценки результатов действий, проверки их на правдоподобие. Повышено внимание к арифметическим приёмам решения текстовых задач как средству обучения способам рассуждения, выбору стратегии решения, анализу ситуации, сопоставлению данных и, в конечном итоге, развитию мышления учащихся.

Изучаемые в это время тождественные преобразования алгебраических выражений с переменными широко применяются для функциональной пропедевтики. Значительное место в курсе математики средней школы отводится материалу функционального характера. Определение функции вводится в 7 классе, а функциональная пропедевтика начинается с 5 класса, где рассматривается понятие переменной, выражения с переменой, формулы, задающей зависимости между некоторыми величинами.

Использование буквенных обозначений позволяет ставить вопрос о построении формул. Связи между величинами задаются также табличным и графическим способами, и дети тренируются в переходе от одной формы задания зависимости к другой. Систематическая работа с конкретными зависимостями обеспечивает готовность детей к изучению функций в старших классах.

Методы . Курс математики 5-6 классов построен индуктивно. Содержание учебного материала заставляет использовать методы, способствующие формированию как продуктивной, так и репродуктивной деятельности.

В 5-6 классах наиболее часто применимы следующие методы обучения:

· Объяснительно-иллюстративный. Целый ряд понятий математики 5-6 классов может быть введён данным методом. С помощью его может быть изучен материал, который служит логическим продолжением и расширением основного материала. Этим же методом можно изучать конкретные алгоритмы. Также изучаются объяснительно-иллюстративным методом сведения, которыми можно воспользоваться как готовыми (сформированными в начальной школе) знаниями, но получающими новое применение. Цель изучения материала объяснительно-иллюстративным методом – довести знание правил, законов, алгоритмов и т.п. до уровня навыка.

· Частично-поисковый и проблемный методы. Основные понятия курса должны быть изучены методами, которые бы обеспечивали творческий (продуктивный) характер деятельности учащихся. К числу таких методов, вполне применимых в 5-6 классах, можно отнести частично-поисковый. Этим методом могут быть изучены понятия: переменная, верное и неверное неравенство и т.п.

Урок . Особенности предмета математики 5-6 классов (почти на каждом уроке необходимо изучать новые факты по предмету), требование программы, темп изучения материала привели к тому, что наиболее распространенный тип урока в этих классах – комбинированный.

Перечислим ещё некоторые особенности обучения математики в 5-6 классах:

· На первых порах изучения математики в 5 классе учащиеся повторяют известные им из 1-4 классов понятия, но повторение это ведётся на новом уровне, с привлечением математической терминологии и символики. Делается это для того, чтобы заложить основы математического языка, основы математической культуры.

· В курсе 5-6 классов часто прибегают при изложении арифметики и начал алгебры к геометрическим определениям с помощью координатной прямой или луча, что позволяет сделать обучение более наглядным, а значит, более доступным и понятным для учащихся. Подобным образом, например, изучается сравнение обыкновенных и десятичных дробей.

· Одной из особенностей данного курса является линейно-концентрическое изложение материала, в соответствии с которым учащиеся неоднократно возвращаются ко всем принципиальным вопросам, поднимаясь в каждом следующем проходе на новый уровень.

Пример, при изучении темы «Десятичные дроби и проценты» происходит переход от множества целых неотрицательных чисел к множеству рациональных неотрицательных; при этом обучение строится с опорой на известные учащимся алгоритмы действий с натуральными числами, постоянно используются знания и умения, полученные раннее.

· Первая трудность, с которой встречаются пятиклассники, — работа с объяснительным текстом учебника. Причина этого – недостаточная техника чтения у некоторых детей, малый словарный запас, а также и то, что в учебниках начальной школы такие объёмные тексты не встречались.

На протяжении всего времени обучения в 5-х и 6-х классах учителю математики необходимо систематически развивать у детей умение читать, понимать текст, работать с ним. Эта работа служит необходимой базой для успешного изучения систематических курсов алгебры и геометрии в следующих классах.

· Изучение математики требует активных умственных усилий. Очень трудно поддерживать произвольное внимание учащихся на протяжении всего урока. Напряжённая мыслительная деятельность, большое количество однотипных и в общем-то рутинных вычислений или алгебраических преобразований быстро утомляет школьников. Существует универсальный способ поддерживания рабочего тонуса учащихся: переключение с одного вида учебной деятельности на другой. Но можно воспользоваться и советом Блеза Паскаля: «Предмет математики настолько серьёзен, что полезно не упускать случаев делать его немного занимательным». Данный совет особенно актуален при обучении математике в 5-6 классах. Впрочем, это тоже одна из разновидностей переключения.

Всякое понятие, в том числе и математическое, является абстракцией от множества конкретных объектов, которые описываются им. В понятии отражаются устойчивые свойства изучаемых объектов, явлений. Эти свойства повторяются у всех объектов, которые объединяются понятием. Но каждый реальный объект имеет некоторые другие свойства, присущие только ему. Различие в несущественных свойствах только оттеняет, подчёркивает существенные.

Если в начальных классах обучение ведётся в основном на наглядно образном уровне мышления, то в 5-6 классах более глубоко развивается словесно-логическое мышление. Содержанием такого мышления являются понятия, сущность которых «уже не внешние, конкретные, наглядные признаки предметов и их отношения, а внутренние, наиболее существенные свойства предметов и явлений и соотношения между ними».

Среди умений, которым учит математика и которым всем вам нужно учиться, большое значение имеет умение классифицировать понятия.

Дело в том, что математика, как и многие другие науки, изучает не единичные предметы или явления, а массовые . Так, когда вы изучаете треугольники, то изучаете свойства любых треугольников, а их бесконечное множество. Вообще объем любого математического понятия, как правило, бесконечен.

Для того чтобы различать объекты математических понятий, изучить их свойства, обычно эти понятия делят на виды, классы. Ведь, кроме общих свойств, любое математическое понятие обладает еще многими важными свойствами, присущими не всем объектам этого понятия, а лишь объектам некоторого вида. Так, прямоугольные треугольники, кроме общих свойств любых треугольников, обладают многими свойствами, весьма важными для практики, например теоремой Пифагора, соотношениями между углами и сторонами и т. д.

В процессе многовекового изучения математических понятий, в процессе их многочисленных применений в жизни, в других науках из их объема были выделены какие-то особые виды, имеющие наиболее интересные свойства, которые чаще всего встречаются и применяются в практике. Так, различных четырехугольников существует бесконечно много, но в практике, в технике наибольшее применение имеют лишь определенные их виды: квадраты, прямоугольники, параллелограммы, ромбы, трапеции.

Деление объема некоторого понятия на части и есть классификация этого понятия. Более точно под классификацией понимают распределение объектов какого-либо понятия на взаимосвязанные классы (виды, типы) по наиболее существенным признакам (свойствам). Признак (свойство), по которому про-изводится классификация (деление) понятия на виды (классы), называется основанием классификации.

Правильно построенная классификация понятия отражает наиболее существенные свойства и связи между объектами понятия, помогает лучше ориентироваться в множестве этих объектов, дает возможность устанавливать такие свойства этих объектов, которые наиболее важны для применения этого понятия в других науках и житейской практике.

Классификация понятия производится по одному или нескольким наиболее существенным основаниям.

Так, треугольники можно классифицировать по величине углов. Получаем такие виды: остроугольные (все углы острые), прямоугольные (один угол прямой, остальные острые), тупо-угольные (один угол тупой, остальные острые). Если же за основание деления треугольников принять соотношения между сторонами, то получаем такие виды: разносторонние, равнобедренные и правильные (равносторонние).

Сложнее, когда приходится классифицировать понятие по нескольким основаниям. Так, если выпуклые четырехугольники классифицировать по параллельности сторон, то по существу нам нужно разделить все выпуклые четырехугольники одновременно по двум признакам: 1) одна пара противоположных сторон параллельна или нет; 2) вторая пара противоположных сторон параллельна или нет. Получаем в результате три вида выпуклых четырехугольников: 1) четырехугольники с не параллельными сторонами; 2) четырехугольники с одной парой параллельных сторон — трапеции; 3) четырехугольники с двумя парами параллельных сторон — параллелограммы.

Весьма часто производят классификацию понятия поэтапно: сначала по одному основанию, затем некоторые виды делят на подвиды по другому основанию и т. д. Примером может служить классификация четырехугольников. На первом этапе их делят по признаку выпуклости. Затем выпуклые четырехугольники делят по признаку параллельности противоположных, сторон. В свою очередь параллелограммы делят по признаку наличия прямых углов и т. д.

При проведении классификации необходимо соблюдать определенные правила. Укажем главные из них.

В качестве основания классификации можно брать лишь общий признак всех объектов данного понятия. Так, например, нельзя в качестве основания классификации алгебраических выражений брать признак расположения членов по степеням какой-то переменной. Этот признак не является общим для всех алгебраических выражений, например для дробных выражений или одночленов он не имеет смысла. Этим признаком обладают лишь многочлены, поэтому многочлены можно классифицировать по наивысшей степени главной переменной.
Основанием для классификации надо брать существенные свойства (признаки) понятий. Рассмотрим опять понятие алгебраического выражения. Одним из свойств этого понятия является то, что переменные, входящие в алгебраическое выражение, обозначаются какими-то буквами. Это свойство является общим, но не является существенным, ибо от того, какой буквой обозначена та или иная переменная, характер выражения не зависит. Так, алгебраические выражения х+у и а+b — это по сути дела одно и то же выражение. Поэтому классифицировать выражения по признаку обозначения переменных буквами не следует. Другое дело, если за основание классификации алгебраических выражений взять признак вида действий, с помощью которых переменные соединены, т. е. действия, которые совершаются над переменными. Этот общий признак весьма существенный, и классификация по этому признаку будет правильной и полезной.
На каждом этапе классификации можно применять лишь одно какое-то основание. Нельзя одновременно классифицировать понятие по двум различным признакам. Например, нельзя классифицировать треугольники сразу и по величине и по соотношению между сторонами, ибо в результате мы получим классы треугольников, которые имеют общие элементы (например, остроугольные и равнобедренные или тупоугольные и равнобедренные и т. д.). Здесь нарушено следующее требование к классификации: в результате классификации на каждом этапе получаемые классы (виды) не должны пересекаться.
В то же время классификация по какому-либо основанию должна быть исчерпывающей и каждый объект понятия должен попасть в результате классификации в один и только один класс.

Поэтому разделение всех целых чисел на положительные и отрицательные неверно, ибо целое число нуль при этом не попало ни в один из классов. Надо говорить так: целые числа делятся на три класса — положительные, отрицательные и число нуль.

Часто при классификации понятий явно выделяются лишь некоторые классы, а остальные только подразумеваются. Так, например, при изучении алгебраических выражений обычно выделяют лишь такие их виды: одночлены, многочлены, дробные выражения, иррациональные. Но эти виды не исчерпывают всех видов алгебраических выражений, поэтому такая классификация является неполной.

Полная правильная классификация алгебраических выражений может быть произведена следующим образом.

На первой ступени классификации алгебраических выражений они делятся на два класса: рациональные и нерациональные. На второй ступени рациональные выражения делятся на целые и дробные. На третьей ступени целые выражения делятся на одночлены, многочлены и сложные целые выражения.

Эту классификацию можно представить в виде следующей

Задание 7

7.1. Почему нельзя классифицировать рациональные числа по их четности?

7.2. Установите, правильно ли произведено деление понятия:

а) Величины могут быть равными и неравными.

б) Функции бывают возрастающие и убывающие.

в) Равнобедренные треугольники могут быть остроугольными, прямоугольными и тупоугольными.

г) Прямоугольники бывают квадраты и ромбы.

7.3. Произведите деление понятия «геометрическая фигура» по свойству занимать часть плоскости и приведите примеры каждого вида.

7.4. Постройте возможные схемы классификации рациональных чисел.

7.5. Постройте схему классификации следующих понятий:

а) четырехугольник;

б) два угла.

7.6. Проведите классификацию следующих понятий:

а) треугольник и окружность;

б) углы в окружности;

в) две окружности;

г) прямая и окружность;

д) квадратные уравнения;

е) система двух уравнений первой степени с двумя неизвестными.

Лекция 5. Математические понятия

1. Объем и содержание понятия. Отношения между понятиями

2. Определение понятий. Определяемые и неопределяемые понятия.

3. Способы определения понятий.

4. Основные выводы

Понятия, которые изучаются в начальном курсе математики, обычно представляют в виде четырех групп. В первую включаются понятия, связанные с числами и операциями над ними: число, сложение, слагаемое, больше и др. Во вторую входят алгебраические понятия: выражение, равенство, уравнения и др. Третью группу составляют геометрические понятия: прямая, отрезок, треугольник и т.д. Четвертую группу образуют понятия, связанные с величинами и их измерением.

Чтобы изучать все разнообразие понятий, надо иметь представление о понятии как логической категории и особенностях математических понятий.

В логике понятия рассматривают как форму мысли , отражающую объекты (предметы и явления) в их существенных и общих свойствах. Языковой формой понятия является слово (термин) или группа слов.

Составить понятие об объекте – это значит уметь отличить его от других сходных с ним объектов. Математические понятия обладают рядом особенностей. Главная заключается в том, что математические объекты, о которых необходимо составить понятие, в реальности не существуют. Математические объекты созданы умом человека. Это идеальные объекты, отражающие реальные предметы или явления. Например, в геометрии изучают форму и размеры предметов, не принимая во внимание другие свойства: цвет, массу, твердость и т.д. От всего этого абстрагируются. Поэтому в геометрии вместо слова «предмет» говорят «геометрическая фигура».

Результатом абстрагирования являются и такие математические понятия, как «число» и «величина».

К сказанному можно добавить, что, изучая пространственные формы и количественные отношения материального мира , математика не только пользуется различными приемами абстрагирования, но и само абстрагирование выступает как многоступенчатый процесс. В математике рассматривают не только понятия, появившиеся при изучении реальных предметов, но и понятия, возникшие на основе первых. Например, общее понятие функции как соответствия является обобщением понятий конкретных функции, т.е. абстракцией от абстракций.

Объем и содержание понятия. Отношения между понятиями

Среди свойств объекта различают существенные и несущественные . Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать . Например, для квадрата существенными являются все свойства, названные выше. Несущественно для квадрата АВСD свойство «сторона АВ горизонтальна».

Когда говорят о математическом понятии, то обычно имеют в виду множество объектов, обозначаемых одним термином (словом или группой слов). Так, говоря о квадрате, имеют в виду все геометрические фигуры, являющиеся квадратами. Считают, что множество всех квадратов составляет объем понятия «квадрат».

Вообще, объем понятия – это множество всех объектов, обозначаемых одним термином.

Любое понятие имеет не только объем, но и содержание.

Рассмотрим, например, понятие «прямоугольник».

Объем понятия – это множество различных прямоугольников, а в его содержание входят такие свойства прямоугольников, как «иметь четыре прямых угла», «иметь равные противоположные стороны», «иметь равные диагонали» и т.д.

Между объемом понятия и его содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот . Так, например, объем понятия «квадрат» является частью объема понятия «прямоугольник», а в содержании понятия «квадрат» содержится больше свойств, чем в содержании понятия «прямоугольник» («все стороны равны», «диагонали взаимно перпендикулярны» и др.).

Отношения между понятиями тесно связаны с отношениями между их объемами, т.е. множествами.

Условимся понятия обозначать строчными буквами латинского алфавита: а, b, c, d, …, z.

Пусть заданы два понятия а и b. Объемы их обозначим соответственно А и В.

Если А ⊂ В (А ≠ В), то говорят, что понятие а – видовое по отношению к понятию b, а понятие b – родовое по отношению к понятию а.

Например, если а – «прямоугольник», b – «четырехугольник», то их объемы А и В находятся в отношении включения (А ⊂ В и А ≠ В), поэтому всякий прямоугольник является четырехугольником. Поэтому можно утверждать, что понятие «прямоугольник» — видовое по отношению к понятию «четырехугольник», а понятие «четырехугольник» — родовое по отношению к понятию «прямоугольник».

Если А = В, то говорят, что понятия А и В тождественны.

Например, тождественны понятия «равносторонний треугольник» и «равнобедренный треугольник», так как их объемы совпадают.

Рассмотрим подробнее отношение рода и вида между понятиями.

1. Во-первых, понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одному понятию и видовым по отношению к другому. Например, понятие «прямоугольник» — родовое по отношению к понятию «квадрат» и видовое по отношению к понятию «четырехугольник».

2. Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник». Среди указанных можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм».

3. В-третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.

Установим, например, отношения между следующими парами понятий а и b, если:

1) а – «прямоугольник», b – «ромб»;

2) а – «многоугольник», b – «параллелограмм»;

3) а – «прямая», b – «отрезок».

Отношения между множествами отображены на рисунке соответственно

2. Определение понятий . Определяемые и неопределяемые понятия.

Определением обычно называют предложение, разъясняющее суть нового термина (или обозначения). Как правило, делают это на основе ранее введенных понятий. Например, прямоугольник можно определить так: «Прямоугольником называется четырехугольник, у которого все углы прямые». В этом определении есть две части – определяемое понятие (прямоугольник) и определяющее понятие (четырехугольник, у которого все углы прямые). Если обозначить через а первое понятие, а через b – второе, то данное определение можно представить в таком виде:

а есть (по определению) b.

Слова «есть (по определению)» обычно заменяют символом ⇔, и тогда определение выглядит так:

Читают: «а равносильно b по определению». Можно прочитать эту запись еще и так: «а тогда и только тогда, когда b.

Определения, имеющие такую структуру, называются явными . Рассмотрим их подробнее.

Обратимся ко второй части определения «прямоугольник».

В нем можно выделить:

1) понятие «четырехугольник», которое является родовым по отношению к понятию «прямоугольник».

2) свойство «иметь все углы прямые», которое позволяет выделить из всевозможных четырехугольников один вид – прямоугольники; поэтому его называют видовым отличием.

Вообще видовое отличие – это свойства (одно или несколько), которые позволяют выделить определяемые объекты из объема родового понятия.

Итоги нашего анализа можно представить в виде схемы:

Знак «+» используется как замена частица «и».

А = {х/ х ∈ С и Р(х)}.

Так как определение понятия через род и видовое отличие является по существу условным соглашением о введении нового термина для замены какой-либо совокупности известных терминов, то об определении нельзя сказать, верное оно или неверное; его не доказывают и не опровергают. Но, формулируя определения, придерживаются ряда правил. Назовем их.

1. Определение должно быть соразмерным . Это означает, что объемы определяемого и определяющего понятий должны совпадать.

2. В определении (или их системе) не должно быть порочного круга . Это означает, что нельзя определять понятие через само себя.

3. Определение должно быть ясным . Требуется, например, чтобы значения терминов, входящих в определяющее понятие, были известны к моменту введения определения нового понятия.

4. Одно и то же понятие определить через род и видовое отличие, соблюдая сформулированные выше правила, можно по-разному . Так, квадрат можно определить как:

а) прямоугольник, у которого соседние стороны равны;

б) прямоугольник, у которого диагонали взаимно перпендикулярны;

в) ромб, у которого есть прямой угол;

г) параллелограмм, у которого все стороны равны, а углы прямые.

Различные определения одного и того же понятия возможны потому, что из большого числа свойств, входящих в содержание понятия, в определение включаются только некоторые. И тогда из возможных определений выбирают одно, исходят из того, какое из них проще и целесообразнее для дальнейшего построения теории.

Назовем ту последовательность действий, которую мы должны соблюдать, если хотим воспроизвести определение знакомого понятия или построить определение нового:

1. Назвать определяемое понятие (термин).

2. Указать ближайшее родовое понятие (по отношению к определяемому) понятие.

3. Перечислить свойства, выделяющие определяемые объекты из объема родового, т.е сформулировать видовое отличие.

4. Проверить, выполнены ли правила определения понятия (соразмерно ли оно, нет ли порочного круга и т.д.).

дипломная работа

Понятие — форма мышления о целостной совокупности существенных и несущественных свойств объекта.

Математические понятия имеют свои особенности: они часто возникают из потребности науки и не имеют аналогов в реальном мире; они обладают большой степенью абстракции. В силу этого желательно показать учащимся возникновение изучаемого понятия (либо из потребности практики, либо из потребности науки).

Каждое понятие характеризуется объёмом и содержанием. Содержание — множество существенных признаков понятия. Объём — множество объектов, к которым применимо данное понятие. Рассмотрим связь между объёмом и содержанием понятия. Если содержание соответствует действительности и не включает противоречивых признаков, то объём — это не пустое множество, что важно показать учащимся при введении понятия. Содержание вполне определяет объём и наоборот. Значит, изменение одного влечёт изменение другого: если содержание увеличивается, то объём уменьшается.

o должно проводится по одному признаку;

o классы должны быть не пересекающимися;

o объединение всех классов должно давать всё множество;

o классификация должна быть непрерывной (классами должны быть ближайшие видовые понятия по отношению к понятию, которое подлежит классификации).

Выделяют следующие виды классификации:

1. По видоизмененному признаку. Объекты, подлежащие классификации, могут обладать несколькими признаками, поэтому можно классифицировать по-разному.

Пример. Понятие «треугольник».

2. Дихотомический. Деление объёма понятия на два видовых понятия, одно из которых обладает данным признаком, а другое нет.

Выделим цели обучения классификации:

1) развитие логического мышления;

2) изучая видовые отличия, мы составляем более ясное представление о родовом понятии.

Оба вида классификации используются в школе. Как правило, сначала дихотомический, а затем по видоизменённому признаку.

Воспитание у дошкольника чувства гражданственности

Впервые слово «патриот» появилось в период Французской революции 1789 — 1793гг. Патриотами тогда себя называли себя борцы за народное дело, защитники республики в противовес изменникам, предателям родины из лагеря монархистов…

Деление понятий

Чтобы осмысленно оперировать понятиями, правильно их использовать в решении теоретических и практических задач необходимо уметь выявлять две основные логические характеристики: объем и содержание понятия…

Деление понятий

Классификация — распределение предметов по группам (классам), при котором каждый класс имеет свое постоянное место. Классификация является разновидностью деления понятия…

Исследование эффективности использования домашних заданий в процессе физического воспитания

Под самостоятельной деятельностью понимается совокупность действий, объединенных общей целью и выполняющих определенную общественную функцию (В.Н. Шаулин, 1986). В нашем случае, мы имеем дело с физкультурной деятельностью, то есть деятельностью…

Межпредметные связи в обучении

Межпредметные связи могут помочь школьникам понять окружающий мир, его свойства, основные явления и процессы, происходящие в нем и те закономерности, которым они подчиняются. Таким образом…

Методы и приемы обучения иностранному языку на старшем этапе

В последнее время очень актуальным становится обращение отечественных и зарубежных исследователей, таких как А.А. Щукин, И.П. Подласый, М.А. Данилов, И.П. Пидкасистый, И.Я. Лернер и др…

Организация проектной деятельности учащихся по средствам телекоммуникаций

Впервые употребил слово «проект» в 1908 году заведующий отделом воспитания сельхозшкол Д. Снезден в сельскохозяйственном обучении. С помощью проектов предлагалось связать работу школ с потребностями сельскохозяйственного производства…

Особенности логопедической работы по преодолению аграмматической дисграфии у учащихся общеобразовательной школы

Впервые на нарушения чтения и письма как на самостоятельную патологию речевой деятельности указал А. Куссмауль в 1877 г. Затем появилось много работ, в которых давались описания детей с различными нарушениями чтения и письма…

Особенности формирования математических понятий в 5-6 классах

Определить объект — выбрать из его существенных свойств такие и столько, чтобы каждое из них было необходимым, а все вместе достаточными для отличия этого объекта от других. Результат этого действия фиксируется в определении…

В современных педагогических исследованиях, связанных с проблемами совершенствования функционирования педагогических систем, повышения эффективности образовательного процесса, одним из аспектов, вызывающих наибольший интерес…

Психолого-педагогические аспекты решения проблем межличностных отношений подростков

Каждый возраст хорош по-своему. И в то же время, каждый возраст имеет свои особенности и сложности. Не является исключением и подростковый возраст. Подростковый возраст — определенный отрезок жизни между детством и зрелостью…

Работа с одаренными детьми

28. Треугольник — пятиугольник геометрические фигуры Пары понятий можно произносить вслух, а можно предъявлять в виде карточек или напечатанными на отдельном листе. Отвечать дети могут устно или письменно. Задание 4…

Современные проблемы воспитания детей в семье и пути их решения

В Малом энциклопедическом словаре понятие семьи трактуется как «основанная на браке или кровном родстве малая группа, члены которой связаны общностью быта, взаимной помощью, моральной и правовой ответственностью» . М.И.Демков отмечает…

Формирование познавательных универсальных учебных действий на основе индивидуализации и дифференциации обучения химии в основной общеобразовательной школе

Как и любой социальный институт, общеобразовательная школа подвержена перманентной модернизации. В настоящий момент общественно-политический запрос к общеобразовательной школе заключается в таком построении процесса обучения…

Экспериментальное исследование чувства гражданственности у детей дошкольного возраста

Педагогу, начинающему заниматься проблемой формирования гражданской компетентности, прежде всего необходимо знание терминологии, ключевых понятий гражданского и патриотического образования…

Квадрат, прямоугольник, ромб, трапеция, параллелограмм

Четырехугольник просто означает «четыре стороны»
( четырехугольник, означает четыре, боковой, означает сторону).

Четырехугольник имеет четырех сторон, , 2-мерный (плоская форма), закрытый (линии соединяются) и имеет прямых сторон.

Попробуйте сами

(также см. Интерактивные четырехугольники)

Недвижимость

В четырехугольнике:

четыре стороны (края)
четыре вершины (углы)
внутренние углы, которые добавляют к 360 градусов :

Попробуйте нарисовать четырехугольник и измерить углы.Они должны добавить к 360 °

Виды четырехугольников

Есть специальные виды четырехугольника:

Некоторые типы также включены в определение других типов! Например, квадрат , ромб и прямоугольник также являются параллелограммами . Подробности смотрите ниже.

Давайте рассмотрим каждый вид по очереди:

Прямоугольник

маленькие квадратики в каждом углу означают «прямой угол»

Прямоугольник — это четырехсторонняя форма, каждый угол которой является прямым (90 °).

Также противоположных сторон параллельны и равной длины.

Площадь

маленькие квадратики в каждом углу означают «прямой угол»

У квадрата равные стороны (отмечены буквой «s»), и каждый угол представляет собой прямой угол (90 °)

Также противоположные стороны параллельны.

Квадрат также соответствует определению прямоугольника (все углы равны 90 °) и ромба (все стороны равной длины).

Ромб

Ромб — это четырехгранная форма, все стороны которой имеют одинаковую длину (обозначены буквой «s»).

Также противоположные стороны параллельны и противоположных углов равны.

Еще один интересный момент — диагонали (пунктирные линии) пересекаются посередине под прямым углом. Другими словами, они «рассекают» друг друга пополам под прямым углом.

Ромб иногда называют ромбом или ромбом .

Параллелограмм

У параллелограмма противоположные стороны параллельны и равны по длине. Также противоположные углы равны (углы «А» такие же, а углы «В» одинаковы).

ПРИМЕЧАНИЕ. Квадраты, прямоугольники и ромбы — это все Параллелограммы!

Пример:

Параллелограмм с:

все стороны равны и
угол «А» и «B» как прямые углы

— это квадрат !

Трапеция (UK: Trapezium)


Трапеция		Равнобедренная трапеция

Трапеция (в Великобритании называется трапецией) имеет пару параллельных противоположных сторон.

И трапеция (в Великобритании называется трапецией) — четырехугольник без параллельных сторон:

	Трапеция	Трапеция
В США:	Пара параллельных сторон	НЕТ параллельных сторон

В Великобритании:	НЕТ параллельных сторон	Пара параллельных сторон
(определения для США и Великобритании поменяны местами!)

Равнобедренная трапеция , как показано выше, имеет левую и правую стороны равной длины, которые соединяются с основанием под равными углами.

Воздушный змей

Эй, это похоже на воздушного змея (обычно).

Имеет две пары сторон:

Каждая пара состоит из двух соединяющихся сторон равной длины.

Также:

углы, где встречаются две пары равны.
диагонали, показанные выше пунктирными линиями, пересекаются в под прямым углом.
одна из диагоналей делит пополам (делит пополам) другую.

… вот и все специальные четырехугольники.

Неправильный четырехугольник

Единственный правильный четырехугольник (все стороны равны и все углы равны) — это квадрат. Итак, все остальные четырехугольники неправильные .

Схема «Генеалогическое древо»

Определения четырехугольника: , включая .

Пример: квадрат также является прямоугольником.

Итак, мы включаем квадрат в определение прямоугольника.

(Мы, , не говорим : «Наличие всех углов 90 ° делает его прямоугольником, кроме случаев, когда все стороны равны, тогда это квадрат».)

Это может показаться странным, поскольку в повседневной жизни мы думаем о квадрате как о , а не о как о прямоугольнике … но в математике это .

Используя приведенную ниже таблицу, мы можем ответить на такие вопросы, как:

Квадрат — это тип прямоугольника? (Да)
Прямоугольник — это разновидность воздушного змея? (Нет)

Сложные четырехугольники

О да! когда две стороны пересекаются, мы называем это «сложным» или «самопересекающимся» четырехугольником, например:

У них все еще есть 4 стороны, но две стороны пересекаются.

Многоугольник

Четырехугольник — это многоугольник. Фактически, это четырехсторонний многоугольник, точно так же, как треугольник — это трехсторонний многоугольник, пятиугольник — пятисторонний многоугольник и так далее.

Играйте с ними

Теперь, когда вы знаете различные типы, вы можете поиграть с интерактивными четырехугольниками.

Другие названия

Четырехугольник иногда называют:

a Quadrangle (« четыре угла »), поэтому звучит как «треугольник»
a Tetragon (« четыре многоугольника »), поэтому это звучит как «пятиугольник», «шестиугольник» и т. Д.

621 622 623 624 763 764, 2128, 2129, 3230, 3231

Какие бывают четырехугольники?

Четырехугольники — многоугольники. Они являются частью плоскости, заключенной с четырех сторон (четверка означает четыре, а боковая означает сторону). У всех четырехугольников ровно четыре стороны и четыре угла. Их можно разделить на определенные группы в зависимости от длины их сторон или меры их углов.

Четырехугольники включают квадрат, прямоугольник, трапецию, ромб, параллелограмм и воздушный змей (также называемый тангенциальным четырехугольником).{\ circ} $.

Диагонали — это линии, соединяющие противоположные углы.

Деление четырехугольников по диагоналям перпендикулярности и параллельности сторон:

Чешуйчатый четырехугольник

Первая группа четырехугольников — это разносторонний четырехугольник . Четырехугольник Scalene — это четырехугольник, не имеющий особых свойств. Стороны и углы имеют разную длину и размер.

Трапеции

Четырехугольники с одной парой параллельных сторон называются трапециями .Параллельные стороны называются основаниями трапеции, а непараллельные — ножками .

Равнобедренная трапеция

Трапеции одинаковой длины называются равнобедренными трапециями .

Диагонали равнобедренной трапеции совпадают.

Высота или Высота трапеции — это длина линии, перпендикулярной основанию и проходящей через противоположную вершину.{\ circ} $.

Другими словами, углы на одной стороне ножки трапеции являются дополнительными.

Доказательство.

Разложите отрезок $ \ overline {AD} $ по вершинам $ A $ и $ D $. На прямой $ AD $ обозначим точку $ E $. Поскольку прямая $ AD $ является поперечником параллельных прямых $ AB $ и $ CD $, то $ \ angle {CDE} = \ alpha $ допустимо. {\ circ} $.{\ circ} $.

Параллелограмм

Параллелограмм — четырехугольник, противоположные стороны которого равны и параллельны.

Высота или Высота параллелограмма в метке $ h $ — это отрезок прямой, соединяющий вершину с противоположной стороной и перпендикулярный этой стороне.

Помимо того, что параллелограммы являются четырехугольниками, существуют определенные формы, которые могут быть как параллелограммами, так и четырехугольниками.{\ circ}. $$

Это следует за $ \ beta = \ delta $ и $ \ alpha = \ gamma $.

Теорема

Следующие утверждения эквивалентны друг другу:

1) Четырехугольник $ ABCD $ параллелограмм

2) У четырехугольника $ ABCD $ две противоположные стороны, которые равны и параллельны

3) Каждые две противоположные стороны четырехугольника $ ABCD $ равны

4) Диагонали четырехугольника $ ABCD $ делят друг друга пополам

5) Обе пары противоположных углов четырехугольника $ ABCD $ равны

Каждое из приведенных выше утверждений может быть альтернативным определением параллелограмма.Остальные утверждения нам необходимо доказать.

Доказательство.

$ 1) \ Rightarrow 2)

Пусть $ ABCD $ — параллелограмм. Тогда $ \ overline {AB} \ | \ overline {CD} $ и $ \ overline {AD} \ | \ overline {BC} $.

Поскольку прямая $ AC $ представляет собой траверс параллельных прямых $ AB $ и $ CD $, то $ \ angle {ACD} = \ angle {CAB} $. Прямая $ AC $ также является траверсом параллельных прямых $ BC $ и $ AD $, то есть $ \ angle {ACB} = \ angle {DAC} $.

$ \ overline {AC} $ также является общей стороной треугольников $ ABC $ и $ CDA $.По теореме A-S-A о конгруэнтности треугольников треугольники $ ABC $ и $ CDA $ конгруэнтны. Отсюда следует, что $ | AB | = | CD] $ и $ | AD | = | BC | $.

$ 2) \ Rightarrow 3) $

Пусть в четырехугольнике $ ABCD $ будет $ AB \ | CD $ и $ | AB | = | CD | $.

Так как $ AC $ — это траверс параллельных прямых $ AB $ и $ CD $, то есть $ \ angle {ACD} = \ angle {CAB} $. Сторона $ \ overline {AC} $ — это общая сторона треугольников $ ABC $ и $ CDB $. По теореме S-A-S о конгруэнтности треугольников треугольники $ ABC $ и $ CDB $ конгруэнтны.Отсюда следует, что $ | BC | = | CD |. $

$ 3) \ Rightarrow 4) $

Пусть в четырехугольнике $ ABCD $ $ | AB | = | CD | $ и $ | BC | = | CD | $, и пусть точка $ S $ является пересечением диагоналей $ \ overline {AC} $ и $ \ overline {BD} $.

Сначала рассмотрим треугольники $ ABC $ и $ CDB $. По теореме S-S-S о конгруэнтности треугольников треугольники $ ABC $ и $ CDB $ конгруэнтны. Отсюда следует, что $ \ angle {ACB} = \ angle {CAD} $.

Углы $ ASD $ и $ BSC $ — вертикальные углы.Если теперь рассмотреть треугольники $ ASD $ и $ BSD $, то получится, что $ \ angle {ADS} = \ angle {CBS} $. Поскольку $ | BC | = | AD | $, треугольники $ ASD $ и $ BSC $ конгруэнтны по теореме A-S-A о треугольниках сравнения. Отсюда следует, что $ | AS | = | SC | $ и $ | BS | = | SD | $, что означает, что точка $ S $ является средней точкой $ \ overline {AC} $ и $ \ overline {BD} $.

$ 4) \ Rightarrow 5) $

Пусть в четырехугольнике $ ABCD $ точка $ S $ будет серединой диагоналей $ \ overline {AC} $ и $ \ overline {AD} $: $ | AS | = | CS | $ и $ | BS | = | DS | $.

Рассмотрим треугольники $ BCS $ и $ ADS $. По теореме S-A-S они конгруэнтны ($ | CS | = | AS | $ — $ \ angle {BSC} = \ angle {ASB} $ (вертикальные углы) — $ | BS | = | DS | $). Отсюда следует, что $ \ angle {BCS} = \ angle {DAS} $ и $ \ angle {CBS} = \ angle {ADS} $.

Треугольники $ ABS $ и $ CDS $ также совпадают по теореме SAS ($ | AS | = | CS | $ — $ \ angle {ASB} = \ angle {CSD} $ (вертикальные углы) — $ | BS | = | ДС | $). Отсюда следует, что $ \ angle {BAS} = \ angle {DCS} $ и $ \ angle {ABS} = \ angle {CDS} $.

Отсюда следует:

$$ \ angle {DAB} = \ angle {DAS} + \ angle {BAS} = \ angle {BCS} + \ angle {DCS} = \ angle {BCD} $$

$$ \ angle {ABC} = \ angle {ABS} + \ angle {CBS} = \ angle {CDS} + \ angle {ADS} = \ angle {ADC} $$.{\ circ} $, что тоже противоречит.

Отсюда следует, что $ AB \ | AC $.

Аналогично доказывается, что $ BC \ | AD $.

Ромб

Ромб — параллелограмм, у которого есть по крайней мере одна пара смежных сторон равной длины.

Противоположные углы имеют одинаковую меру: $ \ alpha = \ gamma $, $ \ beta = \ delta $, а прилегающие углы являются дополнительными.

Диагонали ромба совпадают и перпендикулярны.

Тангенциальный четырехугольник

Воздушный змей представляет собой четырехугольник, который характеризует две пары сторон равной длины, которые примыкают друг к другу.Диагонали воздушного змея перпендикулярны, и по крайней мере одна диагональ является линией симметрии. Воздушный змей — это также касательный четырехугольник.

Прямоугольник

Прямоугольник представляет собой параллелограмм, у которого по крайней мере один внутренний угол является прямым.

Диагонали в прямоугольниках совпадают.

Квадрат

Квадрат — это прямоугольник, все стороны которого равны.

Диагонали в квадрате равны и перпендикулярны.2 $

Площадь четырехугольника

Площадь квадрата равна длине стороны квадрата.

Далее идет прямоугольник. Площадь прямоугольника равна произведению длин смежных сторон.

Площадь ромба равна произведению длины его стороны на высоту.

Это верно, потому что, как показано на рисунке: если мы переведем высоту $ \ overline {BE} $ в точку $ A $ и продолжим сторону $ ED $ над вершиной $ D $, мы получим треугольник $ E’DA $, который конгруэнтно треугольнику $ ECB $.Если мы «переведем» треугольник $ ECB $ в треугольник $ E’DA $, мы получим прямоугольник с одной стороной $ a $ и другой стороной $ h $.

То же, что и для ромба, работает на параллелограмме , площадь параллелограмма — это произведение его одной стороны и высоты на этой стороне.

Площадь трапеции равна половине произведения суммы ее оснований и высоты.

Эта формула является результатом деления трапеции на два треугольника $ AED $ и $ BCF $ и прямоугольник $ EFCD $.

Теперь мы можем записать нашу площадь как сумму меньших областей: $ A _ {(ABCD)} = A _ {(AED)} + A _ {(FBC)} + A _ {(EFCD)} $.

Мы знаем, что $ A _ {(EFCD)} = h \ cdot c $.
Теперь нам нужно найти $ A _ {(AED)} $ и $ A _ {(FBC)} $. Если перевести сторону $ b $ рядом с $ AED $, мы получим треугольник $ AHD $.

Высота треугольника $ AHD $ равна высоте трапеции $ ABCD $.

И сторона, на которой установлена эта высота, равна $ a — c $. Это приводит к выводу, что:

$ \ A_ {(AHD)} = h \ cdot \ frac {a — c} {2} $.

Это означает, что:

$$ A_ {(ABCD)} = A_ {(AHD)} + A_ {(HBCD)} = $$

$$ = \ frac {h \ cdot (a — c)} {2} + c \ cdot h = \ frac {a \ cdot h — h \ cdot c + 2h \ cdot c} {2} = \ frac { h \ cdot a + h \ cdot c} {2} = $$

$$ = \ frac {h \ cdot (a + c)} {2} $$.

Что такое четырехугольник?

Четырехугольник — это многоугольник с четырьмя сторонами.

Каких форм имеют четырехугольники?

Это четырехугольники: квадрат, прямоугольник, трапеция, ромб.

Как определить четырехугольник?

Четырехугольник — это плоская форма с четырьмя соединяющимися сторонами. Четверка означает четыре. Боковой означает боковой. Все линии должны соединяться. Это также плоская форма, двухмерная. Некоторые четырехугольники образуют узнаваемые формы, другие — нет.

Что такое 7 четырехугольников?

Есть семь четырехугольников. Это: квадрат, прямоугольник, ромб, трапеция, равнобедренная трапеция, параллелограмм, тангенциальный четырехугольник (также известный как воздушный змей из-за формы воздушного змея).

Какие четыре типа четырехугольников?

Четырехугольники можно разделить на четыре типа. Это параллелограмм, ромб, квадрат и прямоугольник. Кроме того, ромбы, квадраты, прямоугольники — это параллелограммы.

Листы четырехугольников

Именование четырехугольников (278,7 КБ, 1256 обращений)

Назовите наибольшее количество четырехугольников (295,6 КБ, 988 обращений)

Углы в четырехугольниках (423.6 KiB, 1276 совпадений)

Параллелограммы — Найдите угол (531,7 KiB, 947 совпадений)

Параллелограммы — Найдите длину (547,3 KiB, 880 совпадений)

Трапеции — Найдите длину медианы (293,1 КБ, 864 обращений)

Трапеции — Найдите длину полусегмента (289,9 КиБ, 743 обращения)

Трапеции — Найдите длину основания (312,8 КиБ, 796 обращений)

Трапеции — Углы (284.8 КБ, 945 просмотров)

Площадь треугольников и четырехугольников (501,9 КБ, 1,122 просмотров)

Словарь (Вернуться к ссылкам) Круг, квадрат, прямоугольник, треугольник, ромб, трапеция, параллелограмм, ромб

Полигоны урока

Урок 4.1 — Polygons Obj .: классифицируйте полигоны по их сторонам. классифицируйте четырехугольники по их атрибутам. найти сумму углов в многоугольнике. Десятиугольник — многоугольник с десятью сторонами. Додекагон

Дополнительная информация 5.1 Как ни крути
ВТОРИЧНАЯ МАТЕМАТИКА III // МОДУЛЬ 5 МОДЕЛИРОВАНИЕ С ГЕОМЕТРИЕЙ 5.1 Студенты в программе Mrs.Классу Дентона раздали кубики из глины и попросили отрезать угол куба кусочком зубной нити. Джумал нарезанный
Дополнительная информация Успех по математике Уровень E
T877 [ЦЕЛЬ] Учащийся классифицирует двухмерные фигуры на основе свойств. [ПРЕДВАРИТЕЛЬНЫЕ НАВЫКИ] Урок 29, знание базовой геометрической терминологии, включая: параллельные стороны, совпадающие стороны,
Дополнительная информация Трехмерные фигуры
Трехмерные фигуры Количество монет, созданных U.С. Монетный двор меняется каждый год. В 2000 году было создано около 28 миллиардов монет, и примерно половина из них были пенни! 1 Whirlygigs за
. Дополнительная информация 11.4 Трехмерные фигуры
11. Существенный вопрос в трехмерных фигурах. Какова связь между количеством вершин V, ребер E и граней F многогранника? Многогранник — это твердое тело, ограниченное многоугольниками, которое называется
. Дополнительная информация Примечания к геометрии 10 и 11
Геометрия 10 и 11 Область заметок и название тома на дату 10.1 Площадь — это объем пространства внутри двухмерного объекта. При работе с неправильными формами мы можем найти их площадь, разбив ее на
. Дополнительная информация Трехмерные формы
Урок 11.1 Трехмерные формы Трехмерные объекты бывают разных форм. сфера конус цилиндр прямоугольная призма куб Обведите объекты, соответствующие названию формы. 1. прямоугольная призма 2.
Дополнительная информация Таблица с инструкциями по выравниванию
ЗАГОЛОВОК КЛАСТЕРА: СТАНДАРТ: НЕТ ЗАГОЛОВОК КЛАСТЕРА: Определите и опишите формы (квадраты, круги, треугольники, прямоугольники, шестиугольники, кубы, конусы, цилиндры и сферы).СТАНДАРТ: K.G.3 Обозначить формы как
Дополнительная информация Цифры. Значение Цифры в виде цифры. Стандартная форма. Расширенная форма. Символы, используемые для отображения чисел: 0,1,2,3,4,5,6,7,8,9
Цифры Символы, используемые для отображения чисел: 0,1,2,3,4,5,6,7,8,9 Значение Цифры, которые представляет цифра, которая определяется положением цифр Стандартная форма Расширенная форма Обычный способ письменности
Дополнительная информация Учебная программа HPISD: TAG Math 4 класс
Обзор модуля Учебный план HPISD: 4 класс ТЕГ Математика Название Предполагаемая продолжительность 9 недель Геометрия и измерения 8 недель 1 2 3 4 Свойства / атрибуты многоугольников, треугольников, четырехугольников Площадь и периметр
Дополнительная информация Урок 18: Нарезка под углом
Результаты учащихся Учащиеся описывают многоугольные области, которые возникают в результате сечения правой прямоугольной призмы или пирамиды плоскостью, которая не обязательно параллельна или перпендикулярна основанию.Примечания к уроку в
Дополнительная информация Учебное пособие по модулю 10: Фигуры на плоскости
Учебное пособие по блоку 10: Фигуры в самолетах * Обязательно смотрите все видео в рамках каждого урока * Вы можете найти геометрические фигуры в искусстве. Независимо от того, определяется ли количество ведущего или количество стекла, необходимого для предмета
Дополнительная информация Исследуйте твердые тела
1212.1 Изучение площади поверхности твердых тел и объема твердых тел 12.2 Площадь поверхности призм и цилиндров 12.3 Площадь поверхности пирамид и конусов 12.4 Объем призм и цилиндров 12.5 Объем пирамид и
Дополнительная информация Mgr. ubomíra Tomková ГЕОМЕТРИЯ
УГЛЫ НАЗВАНИЯ ГЕОМЕТРИИ: любой угол меньше 90º является острым углом, любой угол, равным 90º, является прямым углом, любой угол между 90º и 80º является тупым углом, любой угол между 80º и 60º является углом отражения
. Дополнительная информация План учебной программы Anoka Hennepin K-12
Anoka Hennepin K-12 План учебной программы Департамент: элементарная математика Название раздела: Пакеты и многоугольники (Синяя книга, гео и измерения) Треугольники и за их пределами (Синяя книга, гео и измерения) Повседневная математика: Том
Дополнительная информация Описывать формы плоскостей
Урок 12.1 Описание плоских форм Вы можете использовать математические слова для описания плоских форм. указать точное положение или конечные точки линии местоположения отрезок линии луч прямой путь, идущий в двух направлениях без
Дополнительная информация Планы уроков для Кристи Демпси, Неделя средней школы Типпит в понедельник, 29 февраля 2016 г. Понедельник, 29 февраля 2016 г. День 115
Планы уроков для Кристи Демпси, Неделя средней школы Типпит в понедельник, 29 февраля 2016 г. Понедельник, 29 февраля 2016 г. Учебная цель (Я могу / я буду…): я буду писать и решать уравнения, используя концепции геометрии,
Дополнительная информация Основное понимание
Вопросы для понимания Основные свойства линий, углов, двух- и трехмерных фигур можно использовать для решения множества теоретических и практических задач. Какие существуют различные отношения
Дополнительная информация Трехмерные фигуры
Трехмерные фигуры Количество монет, созданных U.С. Монетный двор меняется каждый год. В 2000 году было создано около 28 миллиардов монет, и примерно половина из них были пенни! 1 Whirlygigs за
. Дополнительная информация Учебное пособие по геометрии 6, часть 2
Рабочая тетрадь по геометрии 6, художественная страница Рабочий лист G6- страница 7. a) Рабочий лист G6- страница 0 Рабочий лист G6- страница. Учителя проверить .. Учителя проверить. квадратные единицы правые единицы вниз параллелограмм трапеции 5. A F 7 G 6 E
Дополнительная информация Словарь по геометрии.Имя Класс
Геометрия Словарь Название Класс Определение / Описание Символ / Эскиз 1 точка Точное место в пространстве. В двух измерениях упорядоченная пара определяет точку на координатной плоскости: (x, y) 2 линия 3a линия
Дополнительная информация Геометрия. Требования к курсу
Геометрия Геометрия — это полный годичный курс математики в средней школе для ученика, успешно завершившего предварительный курс алгебры I.Курс фокусируется на навыках и методах линейной, координатной,
Дополнительная информация Ключевая концепция Формула Эйлера
11-1 Космические фигуры и поперечные сечения Цели Распознавать многогранники и их части Визуализировать поперечные сечения пространственных фигур Общие основные государственные стандарты G-GMD.B.4 Идентифицировать формы двумерного
Дополнительная информация Математические многоугольники
Математика 310 9.2 Кривая многоугольника и соединенная идея Идея кривой — это то, что вы можете нарисовать на бумаге, не поднимая карандаша. Идея связности состоит в том, что набор нельзя разбить на два непересекающихся набора.
Дополнительная информация 3 Определите формы как двумерные (лежащие на плоскости, плоские) или трехмерные (твердые).
Детский сад Геометрия Определяйте и описывайте формы (квадраты, круги, треугольники, прямоугольники, шестиугольники, кубы, конусы, цилиндры и сферы).1 Описывать объекты в окружающей среде, используя имена фигур,
Дополнительная информация свойств фигур: прямоугольники, квадраты и ромбы — видео и стенограмма урока
Прямоугольники
Начнем с прямоугольников. Прямоугольник представляет собой четырехстороннюю форму со всеми прямыми углами. Если вы хотите узнать, является ли форма прямоугольником, у вас есть всего два теста. Он четырехсторонний? И все ли углы 90 градусов? Если оба ответа положительные, то вы смотрите на прямоугольник.
Прямоугольники везде. Подумайте о своей средней комнате. Что в нем прямоугольник? Двери, столы, окна, плакаты на стенах — все это четырехгранные формы со всеми прямыми углами. Даже экран, на который вы сейчас смотрите, вероятно, представляет собой прямоугольник.
У прямоугольника противоположные стороны равны по длине и параллельны.
Прямоугольники обладают несколькими особыми свойствами. Во-первых, противоположные стороны параллельны.Во-вторых, противоположные стороны равны по длине. В прямоугольнике выше мы знаем, что сторона AB параллельна стороне CD, а BC параллельна AD. Кроме того, если мы знаем, что AB равно 6, то и CD тоже. Если BC равно 4, то и AD тоже.
Худой небоскреб представляет собой прямоугольник.
Самое интересное в прямоугольниках заключается в том, что каждая пара противоположных сторон может иметь совершенно другую длину, чем другая пара. У вас может быть супертонкий прямоугольник, как небоскреб наверху, или очень ровный, как обложка старого альбома внизу.
Эти обложки альбомов представляют собой прямоугольники.
Квадраты
Эта старая обложка альбома подходит как по определению прямоугольника, так и по определению нашей следующей формы — квадрата. Квадраты — это особая разновидность прямоугольников. Квадрат представляет собой четырехстороннюю форму со всеми прямыми углами и сторонами равной длины.
Вам знакомо это определение? Вот шаги, чтобы определить квадрат: он четырехгранный? Все углы 90 градусов? Если да, то у вас прямоугольник.Если все стороны одинаковой длины, то это не только прямоугольник, но и квадрат. Это означает, что все квадраты являются прямоугольниками. Но не все прямоугольники являются квадратами, поскольку пары сторон прямоугольника могут иметь разную длину.
Квадраты, как и прямоугольники, есть повсюду. Помимо обложки альбома, подумайте о местах на шахматной доске, марках, напольной плитке и даже о крекерах и сыре. Поскольку каждая сторона квадрата имеет одинаковую длину, вам не нужно давать много информации для решения большинства проблем.2, что составляет 25.
Все стороны квадрата имеют одинаковую длину.
Ромбы
Затем ромб. Ромб мало чем отличается от квадрата или прямоугольника. Вот вопросы, которые следует задать, если вы думаете, что имеете дело с ромбом: он четырехгранный? Все ли стороны равны по длине? Если оба ответа положительные, то у вас ромб.
Вы заметили, чего не хватает? Прямые углы.У ромба не обязательно должны быть прямые углы. Может, но в этом большая разница с ромбом. Мне нравится думать об этом так: слово «ромб» похоже на слово «носорог». Если носорог бросается на квадрат и сбивает его с ног, это уже не квадрат. Но все равно ромб! Носороги или нет, определение ромб — это четырехгранная форма со сторонами равной длины.
Ромбы обладают несколькими примечательными свойствами. Во-первых, противоположные стороны параллельны.Это верно и для прямоугольников, и для квадратов. Но в ромбе, даже если углы не 90 градусов, противоположные стороны все равно параллельны друг другу. Итак, в приведенном ниже AB параллельна CD. И AD параллельна BC. Также равны противоположные углы. Здесь угол A равен углу C, а угол B равен углу D.
Противоположные стороны ромба параллельны.
Плюс, вот забавный момент: если вы проведете диагональные линии из углов, эти линии образуют прямые углы.Поскольку квадрат — это ромб, это верно и для квадратов. И как бы далеко этот носорог ни толкал ромб, эти диагонали все равно образуют прямые углы. Квадрат — это ромб, но ромб не обязательно является квадратом. И прямоугольник может быть ромбом, но если стороны прямоугольника не равны по длине, то это не ромб.
Краткое содержание урока
В итоге мы рассмотрели три различных типа четырехугольников или четырехугольников. Во-первых, есть прямоугольник , который представляет собой четырехстороннюю форму со всеми прямыми углами.Его противоположные стороны параллельны и равны по длине, но каждая пара сторон не обязательно такой же длины, как другая пара.
Во-вторых, есть квадрат , который представляет собой четырехстороннюю форму со всеми прямыми углами и сторонами равной длины. Квадрат — это тип прямоугольника, у которого все четыре стороны имеют одинаковую длину. Наконец, есть ромб , который представляет собой четырехгранную форму со сторонами равной длины. Углы могут составлять 90 градусов, но это не обязательно.Итак, квадрат — это ромб, но не каждый ромб — это квадрат.
Результат обучения
Вы сможете описать свойства квадратов, прямоугольников и ромбов после просмотра этого видеоурока.
Площадь четырехугольника
Рабочие листы свободной геометрии, созданные с помощью бесконечной геометрии. Возможность распечатать в удобном формате PDF. 4 Площадь выпуклого четырехугольника. Самопересекающийся четырехугольник называется по-разному перекрестным четырехугольником, перекрещенным четырехугольником, четырехугольником бабочки или четырехугольником бабочки.
Чтобы найти площадь любого общего четырехугольника, мы разбиваем его на треугольники и складываем их площадь. Параллелограмм имеет противоположные стороны, равные и параллельные. Для четырехугольника ABCD. Мы присоединяемся к AC. Калькулятор площади четырехугольника вычисляет площадь простого четырехугольника с учетом четырех сторон и длины диагонали между противоположными углами.
Площадь параллелограммов. Урок 7 От параллелограммов к треугольникам. Урок 8 Площадь треугольников. Урок 9 Формула площади треугольника.Урок 10 Основания и высоты треугольников. Урок 11 Полигоны. Урок 12 Что такое площадь поверхности? Урок 13 Многогранники. Урок 14 Сети и площадь поверхности. Урок 15 Больше сетей, больше площадь поверхности. Урок 16 Квадратный метр — производная единица площади в системе СИ. Он имеет символ м² (33A1 в Юникоде). Он определяется как площадь квадрата, стороны которого составляют ровно один метр. Квадратный метр получается из базовой единицы измерения в системе СИ, которая, в свою очередь, определяется как длина пути, пройденного светом в абсолютном вакууме за интервал времени 1 ⁄ 299 792 458 секунды.
Квадрат также можно определить как параллелограмм с равными диагоналями, которые делят углы пополам. Если фигура представляет собой прямоугольник (прямые углы) и ромб (равные длины ребер), то это квадрат. Если круг описан вокруг квадрата, площадь круга равна / (примерно 1,5708) раз больше площади квадрата. Площадь треугольников и четырехугольников R.5. Площадь и периметр в координатной плоскости I Р.6. Площадь и периметр в координатной плоскости II Р.7. Площадь и окружность …
Площадь четырехугольного треугольника Докажите, что площадь четырехугольника PQRS равна половине площади ABCD? У какого особого типа четырехугольника диагонали равны и пересекаются пополам, но не перпендикулярны?
диагоналей пересекают друг друга
12.Исследование № 3: исследуйте пересечение диагоналей ромба. Посмотреть больше. Диагонали квадрата и прямоугольника делят друг друга пополам. диагонали только квадратного прямоугольника пересекаются под углом 90 градусов, образуя перпендикуляр. но они образуют углы в 45 градусов на концах, где они встречаются либо с основанием, либо со сторонами. A. быть его диагоналями. Иногда одна из этих диагоналей могла выходить за пределы формы; тогда у вас есть дротик. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам.Покажите, что четырехугольник, образованный соединением середин сторон, представляет собой прямоугольник. Основания трапеции имеют длину 3 и 5 единиц, одна диагональ перпендикулярна боковой стороне, а другая диагональ делит пополам угол у большего основания. Диагонали пересекаются, чтобы сократить длину пополам. Диагонали проводятся от точки A к точке C и от точки B к точке D и пересекаются в точке E. Все стороны совпадают. это самая короткая сторона. На рисунке выше нажмите «Сброс». Все 4 ответа представляют собой выпуклые четырехугольники, поэтому их диагонали будут пересекаться.ДАННЫЙ: четырехугольник, диагонали которого пересекаются и разделяются на четыре части, так что ДОКАЗАТЬ: четырехугольник является параллелограммом. У диагоналей прямоугольника есть еще одно важное свойство — они равны по длине. Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Рисуются диагонали. Рассмотрим прямоугольную дверь. Решенные задачи на равнобедренных трапециях Задача 1. угол z больше угла y. противоположен наибольшему углу. В этом случае фотограф также хорошо использовал малую глубину резкости.В настоящее время мы занимаемся конструкциями, наш лектор утверждал, что мы можем превратить один четырехугольник в другой, изменив одни свойства и сохранив другие свойства неизменными. Мы подойдем к этой проблеме иначе. Фактически, возьмите отрезок длиной 12 и начните под углом 20 градусов с одной стороны и 70 градусов с другой (для диагоналей). Чтобы найти диагональ квадрата, вы можете использовать формулу =, где равно длине одной стороны квадрата. Обязательно создайте и назовите соответствующие геометрические фигуры.Другой угол может быть вычислен путем вычитания известного угла из 180 °. Свойства ромба: ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину. Когда Кэролайн и ее мать шли к магазину, они вышли на угол двух улиц. Рассмотрим треугольники ABC и ADC (рисунок 2). Размер одного внутреннего угла параллелограмма на 42 градуса более чем в два раза превышает размер другого угла. Допустим, длина другой диагонали = (2b) см. Например, более короткий будет разделен посередине (6 дюймов: 6 дюймов), а более длинный — в соотношении 8:14, как показано на рисунке.а. к . 14. У вогнутых (например, бумеранга) они не пересекаются. Нарисуйте диагональ, скажем, AC = 4 см; Взяв A и C в качестве центров и радиуса более 1/2 AC, нарисуйте дуги по обе стороны от отрезка AC, чтобы они пересекались друг с другом. Другой вопрос … Более длинная диагональ воздушного змея делит более короткую пополам. Открытый сегмент от. диагонали, используя формулу Эйлера V E + F = 2. В евклидовой геометрии параллелограмм — это простой (несамопересекающийся) четырехугольник с двумя парами параллельных сторон.12 квадратных единиц 18 квадратных единиц 24 квадратных единицы 48 квадратных единиц диагонали параллелограмма. Правда. Итак, чтобы построить ромб с диагоналями 4 см и 6 см, выполните следующие действия. Чтобы приблизительно определить длину болота, геодезист проходит 425 метров от точки A до точки B. Четырехугольник — это замкнутая двухмерная фигура, состоящая из четырех сторон, и все ее внутренние углы в сумме составляют 360 градусов. Правда. Полученное изображение показывает глубину, которая была бы невозможна, если бы камера находилась под прямым углом.В параллелограмме ABCD диагонали AC и BD пересекаются в точке E. Если угол A = 85, AE = 3x + 10 и EC = 7x — 30, найдите меру угла C и значение x. Мы уже доказали это свойство для любого параллелограмма. диагонали пересекаются в точке p. сторона qr = 5 м и диагональ qs = 6 м. и 8 см. 26 января 2021 г. В данном случае диагонали — это BD и AC, которые в квадратах имеют одинаковую длину. B. разделите друг друга пополам. 6. • Половина произведения диагоналей равна площади четырехугольника.• По крайней мере, одна диагональ лежит на линии симметрии четырехугольника. Без категории. Какая длина диагонали? Диагонали прямоугольника и равнобедренной трапеции пересекаются, образуя дополнительные углы, не равные 90 градусам. b Определите градиент TS, округленный до двух десятичных знаков. Диагонали параллелограмма делят друг друга пополам: то есть точка пересечения двух диагоналей является средней точкой каждой из них. 12-Oct-2011 MA 341 27. Диагонали лежат между противоположными вершинами (т.е.е. Диагонали квадрата пересекаются в точке Q. Каковы координаты точки Q? Используйте эту процедуру, чтобы помочь студентам улучшить свои письменные ответы для доказательства гипотезы: диагонали параллелограмма делят друг друга пополам. Квадрат — это четырехугольник, у которого все четыре стороны равны по длине и все углы … Вы очень важны для нас. Если эта теорема верна для квадратов, почему или почему нет? Диагонали ромба пересекаются под прямым углом. Диагонали — мощные композиционные элементы.Показан треугольник xyz, где n ≥ 5. Какие утверждения верны относительно сторон и углов треугольника? Есть еще один… Есть 1000 + 1004 = 2004 прямых, которые пересекает главная диагональ. 11.25 B.)… 1. Теорема утверждает, что диагональ AC ромба является биссектрисой к каждому из двух углов DAB и BCD, а диагональ BD является биссектрисой угла к каждому из двух углов ABC и ADC. Пример вогнутого четырехугольника — дротик. Какое значение x — ответы студенту-помощнику.com … Еще вопрос по математике. Добавьте свой ответ и зарабатывайте баллы. Мы уже объясняли, что противоположные углы равны. 4. Название: Докажите нашу гипотезу: 4. Используя формулу средней точки, мы можем найти точку пересечения. Эта проблема решена! Параллелограмм всегда есть прямоугольник. Диагонали четырехугольника ABCD перпендикулярны друг другу. Что касается квадратов, они делят друг друга пополам под углом 90 градусов, то есть они перпендикулярны биссектрисам. D. противоположные углы совпадают.Правильные ответы: 3 вопроса: Показан ромб с совпадающими сторонами. Напишите косвенное доказательство того, что диагонали параллелограмма делят друг друга пополам. А. конгруэнтны. Когда диагональные линии пересекаются, они создают точки интереса на пересечении. 10. Диагонали пересекаются в W. a Докажите, что координаты S равны (2 + 2 √ 5; 0). Home / диагонали не обязательно пересекаются. Диагонали квадрата, ромба и воздушного змея пересекаются под прямым углом. В выпуклых простых многоугольниках диагонали всегда будут внутри.5. • По крайней мере, одна диагональ делит пополам два угла четырехугольника. Рисуются диагонали. Диагонали Диагональ — это отрезок прямой, соединяющий один угол с другим, но не являющийся ребром. Диагонали прямоугольника равны друг другу. Что из следующего может использовать Томас, чтобы доказать, что сторона ab равна стороне dc? 1 См. Ответ genickijenndon ждет вашей помощи. В каждом кайте диагонали пересекаются под углом 90 °. 13. б. не пересекает ∂. C. диагонали пересекаются под прямым углом. Сал доказывает, что диагонали ромба перпендикулярны и что они пересекаются в серединах обоих.В частности, все стороны параллелограмма равны, то есть у нас есть ромб. На изображении ниже угол, под которым камера при настройке создала диагональную линию. Сколько В случае многоугольника это прямая линия, соединяющая противоположные углы многоугольника через его вершины. Как и у любого скрещенного четырехугольника, сумма его внутренних углов составляет 720 °. Диагонали триангуляции и триангуляция 1. Диагональ многоугольника P — это отрезок прямой между двумя его вершинами a и b, которые хорошо видны друг другу 2.Открытый отрезок от a до b не пересекает ∂P; таким образом, диагональ не может скользить по границе. Четырехугольники с перпендикулярными диагоналями — это «квадрат», «ромб» и «воздушный змей». A. Диагонали ромба пересекают друг друга и перпендикулярны. Все четыре ножки каждой лестницы плотно касаются либо нижнего угла, либо противоположной стены. P и S лежат на оси -. 5. В параллелограмме диагонали делят друг друга пополам, поэтому вы можете установить помеченные сегменты, равные друг другу, а затем решить для.Б. Какова площадь ромба? Добавьте свой ответ и зарабатывайте баллы. Затем проведите линии из оставшихся двух углов, чтобы они пересекались с главной диагональю под прямым углом. Сначала мы соединяем диагонали, и там, где они пересекаются, находится точка E. Углы ECD и EBA равны в меру, потому что прямые CD и AB параллельны, и это делает их чередующимися углами. Обычная трапеция имеет равные непараллельные стороны и равные углы при основании, как показано на следующей диаграмме. 17a — 59 (p + 100) 0 720 При этом все стороны ромба равны по длине, а диагонали делят друг друга пополам под прямым углом.Смотрите ответ. б. Диагонали пересекают друг друга (во внутренних точках). Докажите, что если одна пара противоположных сторон четырехугольника равны и параллельны, то четырехугольник является параллелограммом. Квадрат — это частный случай прямоугольника. 8. Диагональ квадрата — это линия, идущая от одного угла квадрата к противоположному углу. Ромб — это частный случай параллелограмма, это четырехугольник с четырьмя сторонами. Используя теорему Фалеса 6.2, докажите, что прямая, соединяющая середины любых двух сторон треугольника, параллельна третьей стороне.Диагонали пересекаются в своих серединах. Угол C равен 85 градусам, а x = 10, b / c диагонали делят друг друга пополам. Диагонали квадрата перпендикулярны друг другу. Свойства прямоугольника; Свойства квадрата; Свойство: диагонали квадрата перпендикулярны биссектрисам друг к другу. Угол B E A равен (3 x минус 12) градусов. Единственный правильный (все стороны равны и все углы равны) четырехугольник — это квадрат. Пусть PQ пересекает AC в точке O. С понедельника по субботу — с 10:00 до 19:00. Диагонали прямоугольника имеют одинаковую длину.Мне нужно зафиксировать диагональную опорную плоскость на пересечении двух ортогональных опорных плоскостей, чтобы моя дверь (под углом) скользила к фиксированному углу, а не к углу, движущемуся к двери. Параллелограмм — это четырехугольник, состоящий из двух пар пересекающихся параллельных прямых. 9. 2 диагонали. Диагонали проводятся от точки A к точке C и от точки B к точке D и пересекаются. У восьмиугольника есть. Диагонали пересекаются под углом 35 градусов. Обязательно создайте и назовите соответствующие геометрические фигуры.Если один угол прямой, то все углы прямые. Найдите длины сторон параллелограмма, если диагонали пересекаются под углом 28º. 12-Oct-2011 MA 341 27. Правило 1: Противоположные стороны параллельны Подробнее. Письмо, слушание, разговор: MLR1 с каждым разом сильнее и яснее. Что такое диагональ? Диагонали лежат между противоположными вершинами (т.е.). Из того, что каждая диагональ является трансверсалью, мы знаем, что в этом случае… Почему диагонали квадрата пересекаются под прямым углом. Найдите значение x.8т. Мы знаем по свойствам параллелограмма, что диагонали разрезаются на две равные части в точке пересечения. Теорема 1. Если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом. Мозговой пользователь. Заголовок: в качестве альтернативы диагональная линия может пересекать все изображение, проходя через него от одного края до другого. Это дает вам наложение золотого треугольника, которое включает в себя четыре различных треугольника (хотя в целом получается шесть треугольников, когда вы объединяете их вместе! Диагональ многоугольника — это линия сегмента, концы которой не являются смежными вершинами многоугольника.В 54-стороннем многоугольнике 53 возможных диагонали можно провести от одной вершины к другой. Бесплатная электронная книга https://bookboon.com/en/introduction-to-vectors-ebook (обновленная ссылка) Круги пересекаются в двух точках — пусть C будет точкой пересечения в пределах неотражающего угла BAD. Диагонали должны создаваться поперек вершин многоугольника, но вершины не должны примыкать друг к другу. Диагонали пересекаются под прямым углом. Диагонали параллелограмма Abcd пересекаются в точке O. Пример 6.2, 10 Диагонали четырехугольника ABCD пересекаются друг с другом в точке O, так что / = /.Примечание. Прямоугольники, квадраты и ромбы (или ромбы) — это параллелограммы. Мы знаем длину BD и AC. Б. диагонали делят друг друга пополам. Еще одно интересное использование диагональных линий — создание глубины. Kite qrst имеет короткую диагональ qs и длинную диагональ rt. Таким образом, внутренняя часть будет разделена на 54 области 53 диагоналями плюс две стороны исходного многоугольника, примыкающие к вершине, от которой диагонали… Ответы: 3 на вопрос: Показан ромб с совпадающими сторонами.80. Это означает, что они перпендикулярны. Для общего выпуклого n-угольника ответ будет n 4, потому что каждые четыре вершины будут в параллелограмме, если вы знаете один угол, вы можете вычислить все остальные углы. В геометрии термин «диагональ» относится к отрезку, соединяющему две вершины, который не образует сторону многоугольника. Длина одной диагонали равна 6, а длина другой диагонали — 8. Решение: мы знаем, что все стороны ромба равны, а диагонали ромба перпендикулярны биссектрисам друг друга.Объясните, как менять диагонали… Четырехугольник — это трапеция, если две стороны параллельны. Когда диагональные линии пересекаются, они создают точки интереса на пересечении. В многограннике, вершине… Введение Мы найдем формулу для числа I (n) точек пересечения, образованных внутри правильного n-угольника его диагоналями. A… Прямые CD и AB равны по длине, потому что противоположные стороны параллелограмма равны. Если угол, под которым они встречаются, равен 90 ∘, то по теореме Пифагора каждая сторона прямоугольника имеет длину p 2 + q 2.20 диагоналей. Какая у него длина? Диагонали параллелограмма делят друг друга пополам, поэтому точка пересечения является серединой любого из них. Один метод, который можно использовать для доказательства того, что диагонали параллелограмма делят друг друга пополам, показан в данном частичном доказательстве: … Другой метод доказательства диагоналей параллелограмма, делимых пополам, использует координатную сетку. Итак, чтобы построить ромб с диагоналями 4 см и 6 см, выполните следующие действия. Диагонали параллелограмма пересекают друг друга пополам; Четырехугольник называется параллелограммом, если его диагонали делят пополам; Пара противоположных сторон параллелограмма равны и параллельны; Ромб — это параллелограмм, диагонали которого пересекаются под прямым углом; Параллелограмм, диагонали которого пересекаются под прямым углом, представляет собой ромб. Длины диагоналей параллелограмма составляют 10 футов и 16 футов.Диагональ — это отрезок прямой, концы которого являются вершинами. P и S лежат на оси -. Свойство: диагонали прямоугольника одинаковой длины. В углу вершина — это место, где встречаются две линии, лучи или сегменты. Диагональ связана с вершиной, потому что диагональ — это отрезок прямой, соединяющий любые две непоследовательные вершины. В четырехугольнике abcd диагонали пересекаются в точке t. Томас использовал теорему об альтернативных внутренних углах, чтобы показать, что угол adb конгруэнтен углу dbc и что угол dba конгруэнтен bdc.2. Средний. Другие четырехугольники включают трапеции, воздушные змеи и неправильные четырехугольники. Это особый вид параллелограмма, диагонали которого пересекаются под углом 90 °. 21 CDP = 108, q = 29 = 8, q = 29 6. Пусть s = сторона ромба. Правильный или неправильный пятиугольник имеет пять диагоналей. Решения главы 6.2 Задача 65E: Длина диагоналей параллелограмма составляет 20 дюймов и 30 дюймов. Возникли четыре вопроса: 1. Второе отличительное свойство диагоналей воздушных змеев состоит в том, что одна из диагоналей делит пополам или пополам другую диагональ.Классифицируйте типы. Прямая линия, соединяющая вершину равнобедренного треугольника и середину … Идеально, чтобы поместить фокус изображения на пересечении, потому что наши глаза естественно притягиваются к пересечению двух линий. 6. 5. 8т. Пересеките их и продолжайте идти, пока не получится 4 длинные параллельные линии. Диагональ 6 см = 3 см + 3 см = ноги прямоугольного треугольника внутри ромба. Нарисуйте диагонали. Это должно быть то же самое, что и средняя точка XZ; Диагонали делят друг друга пополам, поэтому нам нужно найти только середину одной из диагоналей.Фигура прямоугольная? Соседний…… в нем используется фраза «диагонали пересекаются в своих средних точках», что сделало бы ответ на Часть D более очевидным. Есть несколько правил, связанных с углами параллелограмма. 11.25 B. Вычислите диагонали ромба, если вы знаете 1. (x, y) = (x1 + x2 2, y1 + y2 2) Случай 3: трапеция или воздушный змей Далее самый простой способ — использовать наш калькулятор прямоугольного треугольника ( этот метод работает только для выпуклых воздушных змеев). Назовите название правильного шестиугольника. 4.… AC и BD — это диагонали AC и BD, пересекающиеся в… Диагонали многоугольника — это отрезки прямых от одного угла до другого (но не по краям).Диагонали четырехугольника — перпендикулярно, пополам или оба. Посмотреть решение. По бокам 4,13 «см». Одним из недостатков этого является то, что необходимо нанести на график местоположение точки схода (не показано на рисунке), которая может выходить за края нашего листа бумаги для рисования. Другие четырехугольники. c Вычислить с округлением до двух десятичных знаков. Диагонали триангуляции и триангуляция 1. Диагональ многоугольника P — это отрезок прямой между двумя его вершинами a и b, которые хорошо видны друг другу 2.Открытый отрезок от a до b не пересекает ∂P; таким образом, диагональ не может скользить по границе. Окружность описана вокруг трапеции. Таким образом, если диагональ начинается на краю композиции, она привлекает зрителя, а затем уводит его в путешествие до другого конца. 80. Одна из диагоналей ромба, допустим, q = 7см. Площадь выпуклого четырехугольника с … диагоналями перпендикулярна тогда и только тогда, когда площадь четырехугольника равна половине произведения диагоналей.По диагонали четырехугольника можно определить, является ли он параллелограммом, прямоугольником, ромбом и т. Д. Здесь мы перечислим и докажем основные теоремы. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны. Диагонали — это перпендикулярные биссектрисы: диагонали BD и OC пересекаются в точке O. Окружность описана вокруг трапеции. Математика, 21.06.2019 15:50 Примеры: квадрат (или любой четырехугольник) имеет 4 (4−3) / 2 = 4 × 1/2 = 2 диагонали; восьмиугольник имеет 8 (8−3) / 2 = 8 × 5/2 = 20 диагоналей.Для этого мы воспользуемся вот этой таблицей, у меня есть три столбца; один для количества вершин, один для количества диагоналей на вершину и общего количества диагоналей, которые мы видим в многоугольнике. Диагонали параллелограмма делят друг друга пополам. Углы EDC и EAB равны по той же причине. У следующего по простому четырехугольника две диагонали. Таким образом, мы получаем диагональ, когда напрямую соединяем любые два угла (вершины), которые еще не соединены ребром. Трапеция имеет одну пару параллельных противоположных сторон.12-Oct-2011 MA 341 26. Если четырехугольник — параллелограмм, то его диагонали делят друг друга пополам. стороны параллелограмма. Идеально разместить фокус изображения на пересечении, потому что наши глаза естественно притягиваются к пересечению двух линий. Таким образом, прямая, проходящая через точку O, параллельная сторонам параллелограмма, содержащим P и Q, даст параллельную проекцию одной трансверсали на другую. Найдите размер каждого угла. Найдите координаты пересечения диагоналей параллелограмма XYZW с вершинами X (3,0), Y (3,8) Z (-2,6) и W (-2, -2).12 квадратных единиц 18 квадратных единиц 24 квадратных единицы 48 квадратных единиц Любой член… Затем MN пересекает PR в своей средней точке 12 октября 2011 MA 341 17, которая, как мы знаем, является О. Теорема … параллелограмм (пересечение диагоналей). Найдите p и q. Они создают визуальный поток. Нарисуйте диагональ, скажем, AC = 4 см; Взяв A и C в качестве центров и радиуса более 1/2 AC, нарисуйте дуги по обе стороны от отрезка AC, чтобы они пересекались друг с другом. Таким образом, диагональ от этой вершины соединит эти две вершины, которые не идут подряд.. В параллелограмме противоположные стороны равны, противоположные углы равны, а диагонали делят друг друга пополам. угол x — наибольший угол. Сал доказывает, что диагонали ромба перпендикулярны и что они пересекаются в серединах обоих. 1 См. Ответ genickijenndon ждет вашей помощи. Правильных ответов: 3 вопроса: Четырехугольник РГТУ, диагонали SU и RT пересекаются в точке V. РГТУ — параллелограмм. Угол между одним из оснований трапеции и боковой стороной равен ex, а угол между этим основанием и одной из диагоналей равен p.Это общее свойство любого параллелограмма. Фактически, возьмите отрезок длиной 12 и начните под углом 20 градусов с одной стороны и 70 градусов с другой (для диагоналей). Как сбросить данные приложений на Iphone, Настройки разгона Kawpow, Технологическая схема переработки сырой нефти, Записанное будущее Сингапура, + 18Магазины moreclothing Подземный магазин одежды, Eclectic Fashions и многое другое, Набор аксессуаров для ванной комнаты из никеля, Раствор и растворитель раствора моющего средства, Положение Кубка мира по прыжкам с трамплина, Румынский бурый медведь против гризли, Питер Осгуд Никнейм, диагонали пересекаются друг с другом 2021
геометрических фигур: определение, типы, примеры, свойства
Геометрические формы: В математике геометрические формы — это фигуры, которые показывают формы предметов, которые мы видим в нашей повседневной жизни.В геометрии формы — это формы объектов, которые имеют граничные линии, поверхности и углы. Существуют разные типы фигур \ (2 \, {\ rm {D}} \) и \ (3 \, {\ rm {D}} \). В повседневной жизни мы постоянно взаимодействуем с разными объектами, которые имеют различную форму, от простых до абстрактных.
Например, книги (прямоугольная форма), очки (цилиндрическая форма), дорожные конусы (коническая форма) и т. Д. В этой статье вы познакомитесь с различными геометрическими фигурами и их определением, а также с примерами.
Определение геометрических форм
В плоской геометрии двумерные формы — это плоские формы и замкнутые фигуры, такие как круги, квадраты, прямоугольники, ромбы и т. Д. В твердой геометрии трехмерными формами являются куб, кубоид, конус, сфера и цилиндр. Мы можем наблюдать все эти формы и в нашем повседневном существовании.
Давайте посмотрим на некоторые из реальных объектов, которые мы использовали, которые напоминают некоторые основные формы.
Геометрические формы — это формы, которые представляют формы различных объектов.Некоторые фигуры имеют двумерную форму \ (2 \, {\ rm {D}} \), а некоторые — трехмерную форму \ (3 \, {\ rm {D}} \). \ (2 \, {\ rm Фигуры {D}} \) лежат только на оси \ (x- \) и \ (y — \), но фигуры \ (3 \, {\ rm {D}} \) лежат в \ (x, оси у — \) и \ (z — \). Ось \ (z — \) представляет высоту объекта. В геометрии определены различные формы, такие как круг, квадрат, прямоугольник, треугольник и т. Д.
Чтобы создать любую из этих фигур, начните с линии, сегмента линии или кривой. В зависимости от количества линий и их расположения мы получаем разные типы фигур и фигур, такие как треугольник (фигура, в которой соединены трехлинейные сегменты), Пентагон (пятилинейные сегменты) и так далее.
Фигуры в геометрии могут быть открытыми или закрытыми.
Открытая форма: Фигура, которая начинается и заканчивается в разных точках, образуя границу сегментами линии или кривыми, называется открытой формой.
Замкнутая форма: Фигура, которая начинается и заканчивается в одной и той же точке, образуя границу сегментами линии или кривыми, называется замкнутой формой .
Скачать математические формулы для классов \ (6 \) — \ (12: \)
Список геометрических фигур
Формы классифицируются по их регулярности или однородности.Правильная форма является симметричной, например квадрат, круг и т. Д. Неправильные формы асимметричны. Их также называют формами произвольной формы или органическими формами. Например, форма дерева может быть неправильной или органичной. Список геометрической формы \ (2 \, {\ rm {D}} \) и формы \ (3 \, {\ rm {D}} \) приведен ниже:
\ (2 \, {\ rm {D}} \) Формы:
Треугольник
Круг
Полукруг
Квадрат
Прямоугольник
Параллелограмм
Ромб
Трапеция
Воздушный змей
Многоугольники (Пентагон, Шестиугольник, Октагон, Нонагон, Десятиугольник и т. Д.)
\ (3 \, {\ rm {D}} \) Формы :
Сфера
Куб
Кубоид
Конус
Цилиндр
Типы геометрических фигур со свойствами
Давайте посмотрим на некоторые геометрические фигуры и их свойства:
Двумерные формы
Треугольник: Треугольник — это многоугольник, состоящий из \ (3 \) сторон и \ (3 \) ребер и \ (3 \) вершин.\ circ} \) называется квадратом.
Прямоугольник : Тип четырехугольника, в котором противоположные стороны равны по длине, а каждый угол является прямым, называется прямоугольником.
Параллелограмм : Четырехугольник называется параллелограммом, если обе пары его противоположных сторон параллельны.
Ромб: Четырехугольник, у которого все стороны равны, называется ромбом.
Трапеция: Тип четырехугольника, имеющего ровно одну пару параллельных сторон, называется трапецией.
Воздушный змей: Четырехугольник называется воздушным змеем, если у него две пары равных смежных сторон, но неравные противоположные стороны.
Многоугольники (Пентагон, Шестиугольник, Гептагон, Октагон, Нонагон, Десятиугольник и т. Д.): Многоугольники состоят из отрезков линий и не состоят из кривых. Они представляют собой замкнутую конструкцию с разной длиной сторон и разными углами.
Трехмерные фигуры
Сфера: Сфера — это круглая форма \ (3 \, {\ rm {D}} \), радиус которой увеличен до трех измерений.
Пример: Глобус
Куб: Куб — это форма \ (3 \, {\ rm {D}} \) с \ (6 \) гранями, \ (8 \) вершинами и \ (12 \) ребрами. Все грани куба квадратные.
Пример: кубик Рубика
Кубоид: Кубоид — это трехмерная сплошная форма, имеющая \ (6 \) граней, \ (8 \) вершин и \ (12 \) ребер, но все грани кубоида имеют прямоугольную форму.
Пример: Ланчбокс
Конус: Конус представляет собой твердую форму, имеющую круглое основание и плавно сужающуюся от поверхности к вершине в точке, называемой вершиной или вершиной.
Пример: шапка на день рождения
Цилиндр: Цилиндр — это твердое тело \ (3 \, {\ rm {D}} \), имеющее два параллельных круглых основания, соединенных изогнутой поверхностью. У него нет вершины.
Пример: газовый баллон
Примеры основных геометрических фигур
Здесь мы обсудили некоторые геометрические фигуры:
Примеры плоских геометрических фигур
Круг : Колесо — это пример круга в реальной жизни.
Квадрат: Доска для карамболя — это пример квадрата в реальной жизни.
Треугольник: Один кусок пиццы — пример треугольника в реальной жизни.
Прямоугольник: Доска — это пример прямоугольника в реальной жизни.
Овал: Яйцо — пример овала в реальной жизни.
Пример твердых геометрических фигур
Сфера: Футбол, сферические шарики, глобус и т. Д., являются примерами сферы.
Куб: Кубик льда, кубики сахара, игральные кости и т. Д. Являются примерами куба.
Кубоид: Спичечный коробок, книга, коробка для завтрака и т. Д. Являются примерами кубоида.
Конус: Конус для мороженого, шапочка для дня рождения и т. Д. Являются примерами конуса.
Цилиндр: Канистра, труба, газовые баллоны и т. Д. Являются примерами баллона.
Важные замечания о геометрических формах
Точка не имеет размера, а линия — это одномерная фигура.Оба являются основой геометрии. Когда две прямые встречаются в точке, они образуют угол, где точка называется вершиной, а линии — руками.
Двумерные и трехмерные формы формируются с помощью точек, линий и углов.
Двумерные формы, имеющие \ (4 \) стороны, такие как прямоугольник, квадрат, параллелограмм, воздушный змей, трапеция и т. Д., Называются четырехугольниками.
Четырехугольники — это четырехсторонние замкнутые фигуры, составленные из прямых линий.
Многоугольники — это замкнутые формы, состоящие из прямых линий.Они названы в соответствии с количеством сторон, которые у них есть.
Трехмерная форма имеет длину, ширину и высоту.
Геометрические узоры
Геометрические узоры — это набор форм, повторяющихся или изменяемых для создания определенного рисунка.
Примеры геометрических узоров приведены ниже,
Давайте посмотрим на узор, используя некоторые основные плоские формы. Некоторые основные формы плоскостей: круг, квадрат, треугольник, прямоугольник и т. Д.
Решенные примеры — геометрические формы:
Q.1. Приведенная ниже цифра является открытой или закрытой цифрой?
Ответ: Фигура, которая начинается и заканчивается в разных точках, образуя границу сегментами линии или кривыми, называется открытой фигурой. Поскольку у данной фигуры есть разные начальная и конечная точки, и она не является непрерывной, это открытая фигура.
Q.2. Цифра, приведенная ниже, является открытой или закрытой цифрой?
Ответ: Фигура, которая начинается и заканчивается в одной и той же точке, образуя границу сегментами линии или кривыми, называется замкнутой фигурой.Поскольку у данного рисунка и начальная, и конечная точки одинаковы, это замкнутая фигура.
Q.3. Приведите три реальных примера прямоугольника.
Ответ: Прямоугольник — это плоская геометрическая замкнутая форма, имеющая в общей сложности четыре стороны (две противоположные стороны равны и параллельны), четыре угла.
Реальные примеры прямоугольника: банкнота, мобильный телефон, обложка книги и т. Д.
Q.4. Напишите два примера конуса.
Ответ: Конус — это сплошная форма \ (3 \, {\ rm {D}} \). Два примера рожка — шапочка для дня рождения и рожок мороженого.
Q.5. Подсчитайте и запишите количество кругов, овалов, треугольников, прямоугольников и квадратов на рисунке ниже.
Ответ:
Количество кругов \ (7 \).
Количество овалов \ (6 \).
Количество треугольников: \ (8 \).
Количество прямоугольников: \ (4 \).
Количество квадратов \ (3 \).
Сводка
Геометрические формы повсюду. Почти все состоит как из двумерных \ (2 \, {\ rm {D}} \), так и из трехмерных \ (3 \, {\ rm {D}}}) геометрических форм. В этой статье мы рассмотрели определение геометрических форм, геометрические формы, используемые в реальных объектах, типы геометрических фигур и их свойства, открытые формы, закрытые формы, список геометрических форм, некоторые примечания к геометрическим формам, примеры геометрических фигур, узор геометрических фигур и т. д.
Это поможет учащимся понять геометрические узоры и поможет понять геометрические формы, их свойства и т. Д.
Часто задаваемые вопросы (FAQ) — Геометрические формы
Q.1. Какие \ (3 \) примеры геометрической формы?
Ответ: Три примера геометрической формы: круг, треугольник и квадрат
Q.2. Какие основные формы \ (10 \) ?
Ответ: Основные формы \ (10 \) — это круг, овал, треугольник, ромб, квадрат, прямоугольник, трапеция, пятиугольник, шестиугольник и восьмиугольник.
Q.3. Какая геометрическая форма является наиболее распространенной?
Ответ: Круг — наиболее распространенная геометрическая форма.
Q.4. Каковы основные формы \ (4 \) ?
Ответ: Основные геометрические плоские формы \ (4 \) — это круг, треугольник, прямоугольник и квадрат.
Q.5. Сколько сторон у пятиугольника?
Ответ: «Пента» означает «пять» Итак, пятиугольник имеет \ (5 \) сторон.
Q.6. Определите уравнение Эйлера на примере?
Ответ: Уравнение Эйлера для любого многогранника: \ (F + V — E = 2 \), где \ (F \) — количество граней, \ (V \) — количество вершин, и \ (E \) количество ребер.
Пример:
Теперь \ (F + V — E = 2 \)
\ (F = 2 — V + E \)
\ (F = 2-6 + 12 \)
\ (F = 8 \)
Следовательно, количество граней равно \ (8. \)
.
Мы надеемся, что эта подробная статья о геометрических формах окажется полезной.Не стесняйтесь задавать свои сомнения или вопросы в разделе комментариев ниже. Мы обязательно свяжемся с вами в ближайшее время. Embibe желает вам всего наилучшего в вашей подготовке!
115 Просмотры.
No related posts.

Четырехугольники — презентация онлайн

1. Из имеющихся четырёхугольников указать те, которые являются параллелограммами

2. Заполнить таблицу, отметив знаки «+» или «-»

3. Ответы

4.

5. Конкурс капитанов вариант 2

6.

Отношение рода и вида между понятиями

Домашние задания по курсу логики

И ИХ СТРУКТУРА

Математика И ИХ СТРУКТУРА

Читайте также

Open Library — открытая библиотека учебной информации. Методика изучения математических понятий Что является чем математические понятия

2. Объем и содержание понятия. Отношения между понятиями

Квадрат, прямоугольник, ромб, трапеция, параллелограмм

Попробуйте сами

Недвижимость

Виды четырехугольников

Прямоугольник

Площадь

Ромб

Параллелограмм

Пример:

Трапеция (UK: Trapezium)

Воздушный змей

Неправильный четырехугольник

Схема «Генеалогическое древо»

Пример: квадрат также является прямоугольником.

Сложные четырехугольники

Многоугольник

Играйте с ними

Другие названия

Какие бывают четырехугольники?

Чешуйчатый четырехугольник

Трапеции

Равнобедренная трапеция

Параллелограмм

Теорема

Ромб

Тангенциальный четырехугольник

Прямоугольник

Квадрат

Площадь четырехугольника

Что такое четырехугольник?

Каких форм имеют четырехугольники?

Как определить четырехугольник?

Что такое 7 четырехугольников?

Какие четыре типа четырехугольников?

Листы четырехугольников

Словарь (Вернуться к ссылкам) Круг, квадрат, прямоугольник, треугольник, ромб, трапеция, параллелограмм, ромб

Полигоны урока

5.1 Как ни крути

Успех по математике Уровень E

Трехмерные фигуры

11.4 Трехмерные фигуры

Примечания к геометрии 10 и 11

Трехмерные формы

Таблица с инструкциями по выравниванию

Цифры. Значение Цифры в виде цифры. Стандартная форма. Расширенная форма. Символы, используемые для отображения чисел: 0,1,2,3,4,5,6,7,8,9

Учебная программа HPISD: TAG Math 4 класс

Урок 18: Нарезка под углом

Учебное пособие по модулю 10: Фигуры на плоскости

Исследуйте твердые тела

Mgr. ubomíra Tomková ГЕОМЕТРИЯ

План учебной программы Anoka Hennepin K-12

Описывать формы плоскостей

Планы уроков для Кристи Демпси, Неделя средней школы Типпит в понедельник, 29 февраля 2016 г. Понедельник, 29 февраля 2016 г. День 115

Основное понимание

Трехмерные фигуры

Учебное пособие по геометрии 6, часть 2

Словарь по геометрии.Имя Класс

Геометрия. Требования к курсу

Ключевая концепция Формула Эйлера

Математические многоугольники

3 Определите формы как двумерные (лежащие на плоскости, плоские) или трехмерные (твердые).

свойств фигур: прямоугольники, квадраты и ромбы — видео и стенограмма урока

Прямоугольники

Квадраты

Ромбы

Краткое содержание урока