Круги эйлера примеры решения задач по информатике: Решение задач по информатике на тему «Решение логических задач с помощью кругов Эйлера» (10 класс)

где применяется и как построить

Что это такое? Диаграмма Эйлера кажется чем-то очень сложным на первый взгляд. Однако на самом деле это круги, накладываемые друг на друга при решение определенных задач. Их применяют в алгебре, информатике и даже в жизни, столкнувшись с каким-то выбором.

Как строить? Для начала нужно представить универсальное множество в виде прямоугольника. Внутри него будут эллипсы или круги, которые могут пересекаться, а могут и нет. Их можно дополнять, объединять, пересекать. Давайте рассмотрим все это на примере ниже.

В статье рассказывается:

1. Что собой представляет диаграмма Эйлера
2. Разница между диаграммой Эйлера и диаграммой Эйлера-Венна
3. Задачи, решаемые диаграммой Эйлера
4. Принцип построения диаграммы
5. Применение диаграмм для доказательства логических равенств
6. Пример решения задачи с помощью кругов Эйлера

7. Пройди тест и узнай, какая сфера тебе подходит:
   

   айти, дизайн или маркетинг.

   Бесплатно от Geekbrains

Что собой представляет диаграмма Эйлера

Так называется геометрическое изображение, которое используют, чтобы смоделировать множества и схематично отразить отношения между ними. На диаграмме Эйлера наглядно показаны утверждения о данных множествах.

При этом универсальное множество обозначено прямоугольником, а подмножества изображены в виде кругов. Поэтому диаграмму называют также «круги Эйлера». Такое схематичное изображение применяют при решении математических и логических задач, а также в менеджменте и различных прикладных целях.

Автор этого способа – математик XVIII века Леонард Эйлер, который хотел таким образом помочь размышлениям. Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. Диаграмма Эйлера стала признанным методом с момента своего появления.

Что собой представляет диаграмма Эйлера

Биография Леонарда Эйлера связана со Швейцарией, Пруссией и Россией. {n}} комбинаций π{\displaystyle n} свойств, то есть конечную булеву алгебру. При π = 3 диаграмма Эйлера-Венна обычно выглядит как три круга, имеющих одинаковый радиус, их центры совпадают с вершинами равностороннего треугольника, стороне которого приблизительно равны радиусы.

Если определённая комбинация свойств соответствует пустому множеству, на схеме эту область закрашивают. Диаграммы Эйлера могут быть не типичны, а иногда эквивалентны диаграммам Венна. Закрашенный участок схемы указывает на то, что это множество не содержит элементов, то есть пустое.

Задачи, решаемые диаграммой Эйлера

Прикладное значение, которое имеет диаграмма Эйлера: задачи на соотношение множеств в математике, логике, информатике, статистике становятся понятнее при её использовании. Круги Эйлера можно применять и в жизни, находя с их помощью взаимосвязи и отвечая на возникающие насущные вопросы.

Задачи, решаемые диаграммой Эйлера

Круги Эйлера можно разделить на такие группы:

• равнозначные;
• пересекающиеся;
• подчиненные;
• соподчиненные;
• противоречащие;
• противоположные.

Выполняя упражнения на развитие мышления, чаще всего можно столкнуться с двумя их видами:

• Круги, изображающие объединяющиеся понятия и вложенные один в другой, чтобы это показать.
• Круги, иллюстрирующие пересечения различных множеств, которые имеют те или иные общие признаки.

Топ-30 самых востребованных и высокооплачиваемых профессий 2023

Поможет разобраться в актуальной ситуации на рынке труда

Подборка 50+ ресурсов об IT-сфере

Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT

ТОП 50+ сервисов и приложений от Geekbrains

Безопасные и надежные программы для работы в наши дни

pdf 3,7mb

doc 1,7mb

Уже скачали 18715

Приведём пример использования кругов при выборе профессии. Можно перебирать варианты, обдумывая наиболее подходящий, а можно начертить схему, изобразив в виде кругов то, что вам нравится делать, что вы умеете, и что хорошо оплачивается. Получится диаграмма Эйлера. Пересечение этих трёх кругов и показывает, что будет наиболее вам подходить.

Метод прост в применении и подходит для всех. Его используют и при работе с дошкольниками в детском саду с 4-5 лет, и при обучении студентов (например, можно увидеть подобные задачи в ЕГЭ по информатике), и в научной среде.

Принцип построения диаграммы

При построении диаграммы Эйлера сначала рисуют большой прямоугольник, обозначающий универсальное множество U. Внутри этого прямоугольника располагают фигуры, которые являются изображением множеств: круги (если их не больше трёх) или круги и эллипсы (когда множеств четыре и больше). Фигуры пересекаются различными способами, в зависимости от условий задачи.

Допустим, у нас имеется выражение А. Изображаем на диаграмме круг, обозначающий множество А. Пространство внутри круга показывает значения, при которых выражение А будет истинным, а область снаружи обозначает ложь. Чтобы отобразить на схеме логическую операцию, заштрихуем те части диаграммы, в которых значения истинны.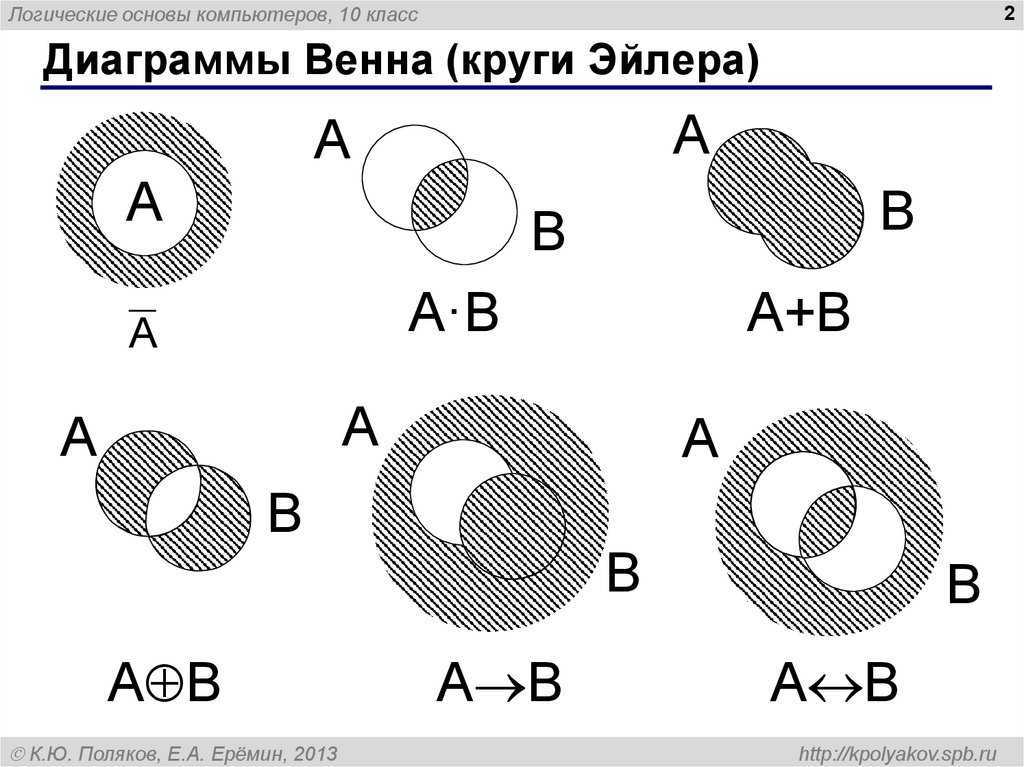

В результате мы отмечаем область, где множества пересекаются.

Принцип построения диаграммы

Можно доказать любой закон алгебры, представив его в виде графической схемы при помощи диаграммы Эйлера. Алгоритм действий таков:

1. Сначала чертим диаграмму и заштриховываем все множества, которые находятся с левой стороны от знака «равно».
2. Затем нужно начертить другую диаграмму и на ней заштриховать множества, находящиеся справа от знака равенства.
3. Если на диаграммах окажется заштрихованной одна и та же область, тождество будет истинным.

Сильнее углубимся в тему.

Дополнение множества

Дополнением к множеству A будет множество Его элементы не относятся к множеству А.

= {x | x ∉ A}

Но в включаются не все элементы, не относящиеся к А. По условиям применения диаграммы Эйлера, все множества, о которых идёт речь в задаче, будут включены в универсальное множество U, то есть являются его подмножествами. С учётом этого дополнение будет определяться так:

=U∖A

Объединение множеств

Объединением двух множеств (назовём их А и В) будет множество A ∪ B, состоящее из элементов, которые включаются хотя бы в одно из них.

Это можно записать так:

A ∪ B={x |x ∈ A или x ∈ B}

Пересечение множеств

Пересечение множеств A и B это множество A ∩ B. Оно состоит из элементов, которые входят и в множество А, и в то же время в множество В.

Точный инструмент «Колесо компетенций»

Для детального самоанализа по выбору IT-профессии

Список грубых ошибок в IT, из-за которых сразу увольняют

Об этом мало кто рассказывает, но это должен знать каждый

Мини-тест из 11 вопросов от нашего личного психолога

Вы сразу поймете, что в данный момент тормозит ваш успех

Регистрируйтесь на бесплатный интенсив, чтобы за 3 часа начать разбираться в IT лучше 90% новичков.

Только до 13 февраля

Осталось 17 мест

Записывается пересечение множеств так:

A ∩ B = {x | x ∈ A и x ∈ B}

Симметричная разность множеств

Симметричная разность – это множество A \ B, в которое включаются элементы, которые входят только в одно из множеств А и В, но не в оба сразу.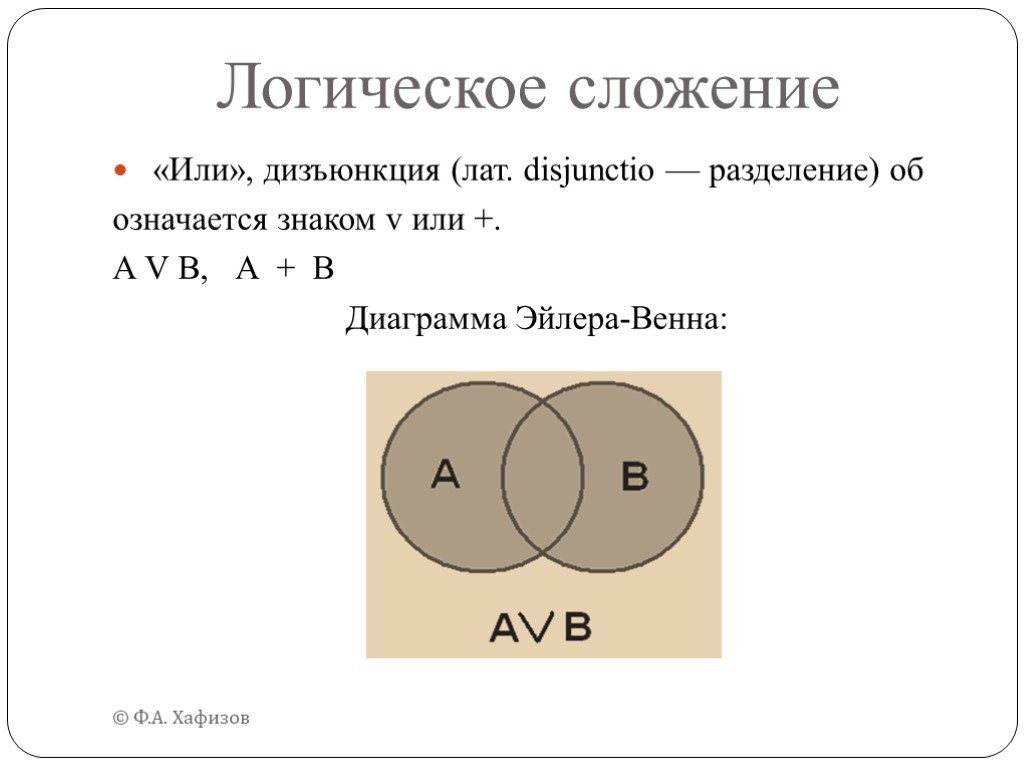

Запись симметричной разности выглядит таким образом:

A △ B = (A ∖ B) ∪ (B ∖ A)

Разность множеств

Разностью A \ B являются элементы множества A, не входящие в B.

Записанная разность множеств выглядит так:

A ∖ B = {x | x ∈ A и x ∉ B}

Применение диаграмм для доказательства логических равенств

Давайте рассмотрим, как применяется диаграмма Эйлера на примере доказательства логического равенства.

Применение диаграмм для доказательства логических равенств

Представим, что мы имеем конъюнкцию множеств A ∧ B.

Сначала работаем с левой частью равенства. Нужно с помощью диаграммы Эйлера построить множества А и В, заштриховать оба круга цветом и таким образом выделим дизъюнкцию.

Дальше нужно показать инверсию с помощью штриховки области за пределами этих множеств.

Теперь переключаемся на правую часть равенства. Сперва показываем цветной штриховкой за пределами круга А инверсию этого множества.

То же самое действие выполняем для множества В.

Штрихуем чёрным цветом все области пересечения и получаем графическое отображение конъюкции инверсий множеств А и В.

Сравнивая области, отображающие правую и левую части равенства, убеждаемся, что они равны. Таким образом, истинность логического равенства доказана при помощи диаграммы Эйлера.

Пример решения задачи с помощью кругов Эйлера

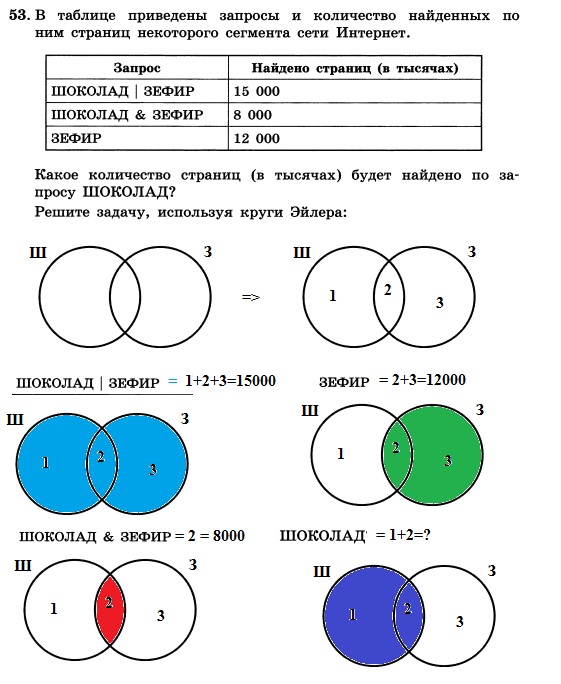
В демонстрационном тесте ЕГЭ по информатике и ИКТ была представлена задача, которую мы решим с применением этого метода.

Условия задачи:

В языке запросов поискового применяется символ «|» для логической операции «или» и символ «&», чтобы обозначить логическую операцию «и».

Таблица, приведённая ниже, отражает запросы в некотором сегменте сети Интернет и количество найденных страниц по этим запросам.

Запрос	Найдено страниц (в тысячах)
Крейсер | Линкор	7000
Крейсер	4800
Линкор	4500

Вопрос: какое количество страниц (в тысячах) найдётся, если запрос будет сформулирован в виде Крейсер & Линкор?

Принимаем версию, что все запросы выполняются в один отрезок времени, поэтому набор страниц, которые включают искомые слова, остался неизменным.

Решение:

Покажем условие задачи при помощи диаграммы Эйлера. Используем цифры 1, 2 и 3 для обозначения полученных областей.

Используя условия задачи, составляем уравнения:

1. Крейсер | Линкор: 1 + 2 + 3 = 7000
2. Крейсер: 1 + 2 = 4800
3. Линкор: 2 + 3 = 4500

Искомая область Крейсер & Линкор обозначенная на чертеже цифрой 2, находится путём подстановки уравнения (2) в уравнение (1). Получаем следующее:

4800 + 3 = 7000, откуда получаем область 3, равную 2200.

Полученный результат мы подставляем в уравнение (3). Получаем результат:

Область 2 + 2200 = 4500, значит, она равна 2300.

Ответ: будет найдено 2300 страниц по запросу Крейсер & Линкор.

Этот пример показывает, что можно решать с помощью диаграммы Эйлера задачи, являющиеся достаточно сложными или запутанными.

Пример решения задачи с помощью кругов Эйлера

Можно сделать вывод, что круги Эйлера не просто занимательный, но и полезный в плане решения учебных и бытовых задач метод.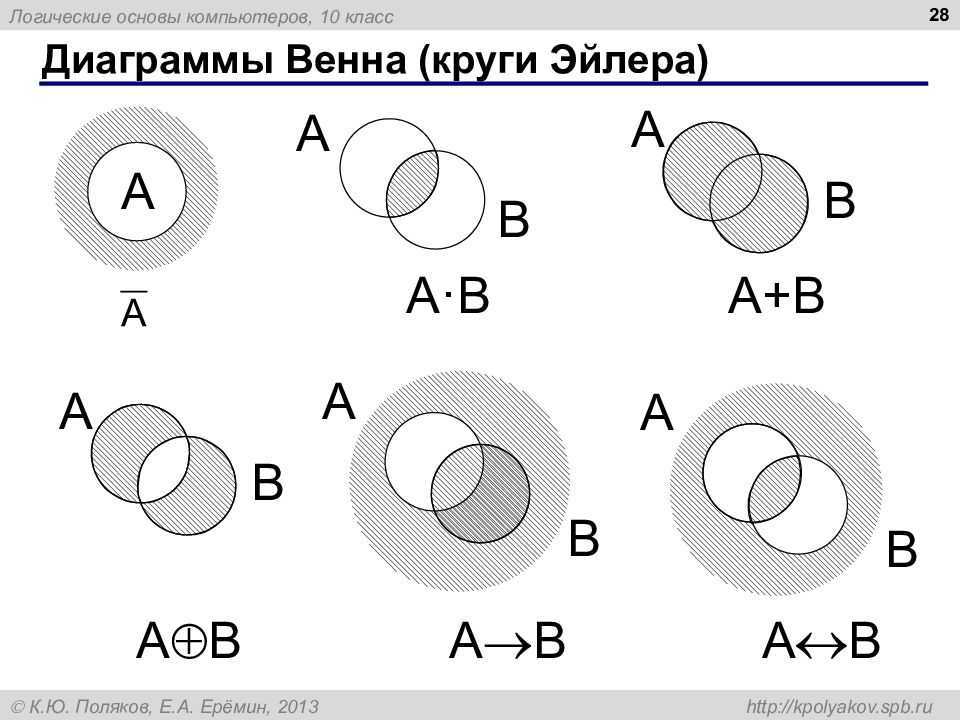 Многие вещи можно представить в виде множеств, а поможет наглядно представить их пересечение или объединение диаграмма Эйлера.

Любопытно, что современная массовая культура применяет круги Эйлера для создания мемов, а также их можно встретить в таких сериалах, как «Теория большого взрыва» и «4исла».

Советуем применять этот метод для решения задач и непременно поделитесь этим полезным и наглядным способом с друзьями.

Рейтинг: 5

( голосов 1 )

Поделиться статьей

Презентация — решение задач с помощью кругов эйлера. Презентация по информатике на тему Круги Эйлера (8 класс) Презентация

Вычислите значение выражения. Ничего не сказала рыбка, лишь хвостом по воде плеснула и ушла в глубокое море. Сказка о мертвой царевне и семи богатырях. Из какой сказки этот отрывок. Сказка о золотом петушке. Сказка о царе Салтане. К 213–летию со дня рождения А.С.Пушкина. Выполните действия, результаты найдите в таблице и отгадайте зашифрованные слова. Найдите значение выражения. Устная работа. Ответы уравнений в конкурсе «Рыбалка».

«Координаты точек на координатной плоскости» — Карл Гаусс. Тренажер. Выбери нужную ячейку таблицы. Абсцисса точки. Учебники. Координатная плоскость. Координаты точки. Николай Иванович Лобачевский. Объяснение нового материала. Цвет. Леонард Эйлер. Исаак Ньютон. Четверть. Готфрид Лейбниц. Координата. Курсор. Координатная четверть. Точка лежит на оси Х. Великие математики. Тест. Технические рекомендации. Отметьте точку. Рене Декарт. Блез Паскаль.

«Приемы устного умножения» — Умножение и деление на 25 и 75. Значимость устных приёмов умножения. Умножение чисел, оканчивающихся на 1. Устные приёмы умножения двузначных натуральных чисел. Умножение чисел, близких к 100. Умножение двузначных чисел, у которых цифры десятков одинаковые. Умножение на 11. Умножение двузначных чисел, у которых сумма цифр десятков равна. Умножение чисел, оканчивающихся на 5. Умножение на число, оканчивающиеся на 5.

«Дни недели» — Воскресенье — день Солнца (старое название – неделя).

Понедельник. Воскресенье -день Солнца. У славян неделя называлась седмица. Суббота – день Сатурна. Гипотеза. Среда. Названия дней недели в русском и английском языках. Загадка. Библия говорит, что семидневная неделя создана Богом. Как появились 7 дней недели. Среда день Меркурия (среда – середина). Неделя днями красна. Конёк – Горбунок. Четверг – день Юпитера (четвёртый).

«Путешествие в мир математики» — Остров « Умейка». Решить с помощью координатной прямой. Измерим температуру за бортом корабля. Прибавить к числу А число В — значит изменить число А на число В. Сумма двух противоположных чисел равна нулю. Остров « Повторика». Найдём сумму чисел. Результаты двух последовательных изменений находят с помощью сложения. Найдём сумму чисел. Показания приборов на корабле. Любое число от прибавления положительного числа увеличивается.

«Десятичная система и двоичная» — Перевод целых десятичных чисел в двоичную систему счисления. Перевод целых чисел из двоичной системы счисления в десятичную.

Ей было 1100 лет, она в 101 класс ходила. Калькулятор. Какую цель перед собой мы ставили в начале первого урока. Переведите числа из двоичной системы счисления в десятичную. «Рождение» цветка. Необычное стихотворение. Закрасьте клеточки. Разделить целое десятичное число на 2.

Слайд 3

Один из величайших математиков петербургский академик, за свою долгую жизнь он написал более 850 научных работ. В одной из них появились эти круги. Эйлер писал, что «они очень подходят для того, чтобы облегчит наши размышления». Леонардо Эйлер 1707-1783

Слайд 4

Задача №1

В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?

Слайд 5

Решение

(По рисунку) в левом кругу (М) помещены все математики, а в правом – все биологи, те ребята, которые не ходят на кружки и помещены они в самый большой круг. Теперь посчитаем: Внутри большого круга 35 ребят. 2. А В С 5-1-0,5-1=2,5 4-1-0,5-1=1,5 3-1-0,5-1=0,5 1 1 АВС 0,5

Слайд 10

Задача №4

В классе 38 человек. Из них 16 играют в баскетбол, 17 – в хоккей, 18 – в волейбол. Увлекаются двумя видами спорта — баскетболом и хоккеем – четверо, баскетболом и волейболом – трое, волейболом и хоккеем – пятеро. Трое не увлекаются ни баскетболом, ни волейболом, ни хоккеем. Сколько ребят увлекается одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?

Слайд 11

Решение

Большой круг изображает всех учащихся класса, а три меньших круга Б, Х и В изображают соответственно баскетболистов, хоккеистов и волейболистов. Фигура БХВ обозначает ребят, увлекающихся всеми тремя видами спорта – z. Одним баскетболом занимаются 16-(4+z+3)=9-z, хоккеем 8-z, волейболом 10-z. Составляем уравнение: 38=3+(9-z)+(8-z)+(10-z)+4+3+5+z, откуда z=2 3 Б Х В 9-Z 8-Z 4 Z 3 5 10-Z

Слайд 12

П.А.Вакульчик «Нестандартные и олимпиадные задачи по математике» В. А.Гусев. А.Н.Орлов. А П. Розенталь «Внеклассная работа по математике» И.Л. Бабинская «Задачи математических олимпиад» А.В.Фарков «Готовимся к олимпиадам по математике» И.С.Петраков «Математические кружки» Литература: http://poznayko.at.ua/photo/16-2-0-0-2 http://www.math-on-line.com.forum-tur http://images.yandex.ru/yandsearch?text

Посмотреть все слайды

1 из 36

7,064
просмотра

Текст этой презентации

Для тех, кому интересно
«Решение задач с помощью кругов Эйлера»
5-6 класс

Изображение множеств в виде кругов подходит для того, чтобы облегчить рассуждения при решении задач

Задача:
Все мои друзья занимаются каким-нибудь видом спорта. 17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?

1.Изобразим два множества, так как два вида спорта. В одном будем фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом
2. Поскольку некоторые из друзей увлекаются и тем и другим видом спорта, то круги нарисуем так, чтобы у них была общая часть (пересечение)

2
15
12
17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта.
Расставить числа, согласно условию задачи: 1)В общей части ставим цифру 2(двое увлекаются и тем и другим видом спорта)
2)В оставшейся части «футболистов» круга ставим цифру 15 (17 − 2 = 15). В свободной части «баскетболистов» круга ставим цифру12 (14 − 2 = 12).
футболом
баскетболом
3)Всего друзей 15+2+12=29 Ответ:29 друзей

Задача:

1.Изобразим три множества, так как три увлечения. В одном будем фиксировать ребят из драмкружка, во втором ребят, которые поют. В третьем будем фиксировать ребят, которые увлекаются спортом.
2.Поскольку некоторые из ребят увлекаются всем, то круги нарисуем так, чтобы у них было пересечение.

драмкружок
хор
спорт

драмкружок
хор
спорт
3 спортсмена посещают и драмкружок и хор, поэтому заполняем эту общую часть.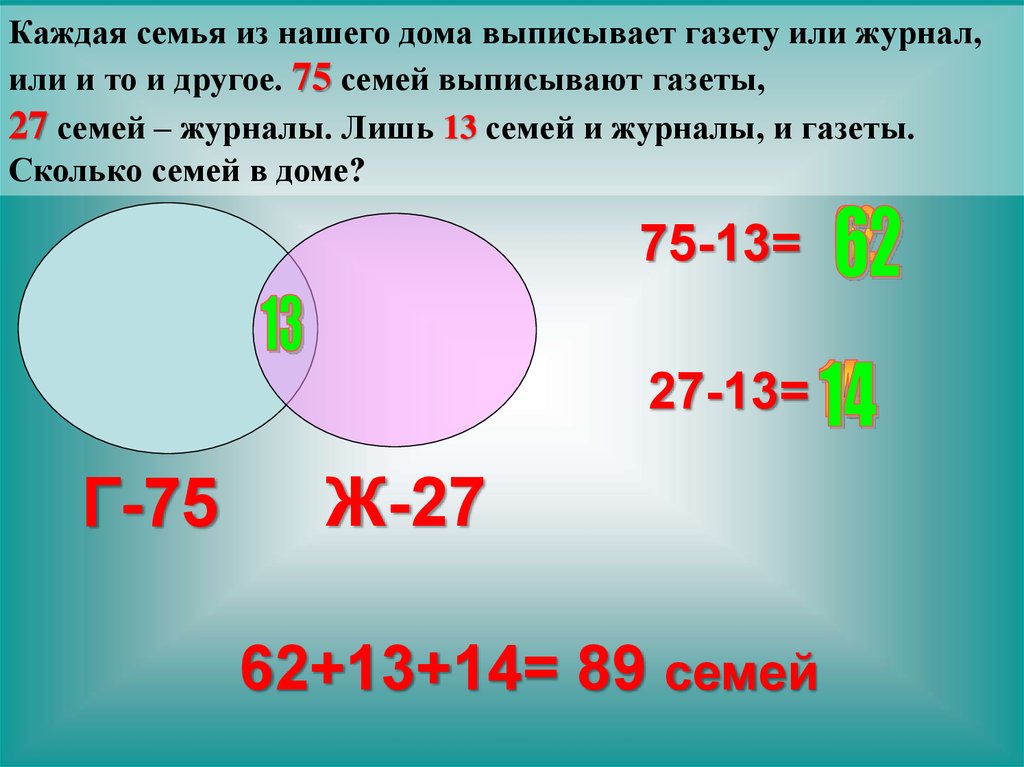
3
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает занятие ребят в драмкружке и хоре.

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в драмкружке 10 ребят из хора. А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 7 (10-3=7)

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
3
7

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает занятие спортсменов в драмкружке

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в драмкружке 8 спортсменов. А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 5 (8-3=5)

3
5
драмкружок
хор
спорт
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько спортсменов поют в хоре.

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в хоре 6 спортсменов. А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 3 (6-3=3)

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
3
3

драмкружок
хор
спорт
3
7
5
3

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько ребят в драмкружке

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию 27 занимаются в драмкружке. А так как в предыдущих рассуждениях поставлены числа 3,5,7 ,то в оставшейся части ставим число 12 (27-(3+5+7)=12)

драмкружок
хор
спорт
3
7
5
12
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько ребят поют в хоре

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию 32 поют в хоре. А так как в предыдущих рассуждениях поставлены числа 3,3,7 ,то в оставшейся части ставим число 19 (32-(3+3+7)=19)
3
7
3
19

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько ребят занимаются спортом.

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
По условию 22 человека увлекаются спортом. А так как в предыдущих рассуждениях поставлены числа 3,5,3 ,то в оставшейся части ставим число 11 (22-(3+5+3)=11)
драмкружок
хор
спорт

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

ЛЕОНАРД ЭЙЛЕР ИДЕАЛЬНЫЙ МАТЕМАТИК XVIII ВЕКА, который ввел понятие объединения и пересечения множеств

Эйлер писал, что «круги очень подходят для того, чтобы облегчить наши размышления». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».

Круги Эйлера Эйлеровы круги — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов.

Смысл логических связок становится более понятным, если проиллюстрировать их с помощью кругов Эйлера Круги Эйлера Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью. Школа 5-ые классы 9-ые классы 9 «А» класс Круги Эйлера – это тот метод, который наглядно демонстри-рует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ. Метод Эйлера является незаменимым при решении некоторых задач.

Задача 1. «Обитаемый остров» и «Стиляги» Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров » 11 человек смотрели фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение: Чертим два множества таким образом: 6 «Стиляги» «Обитаемый остров» 6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров». 11 – 6 = 5 – человек, которые смотрели только «Стиляги». Получаем: «Стиляги» «Обитаемый остров» 9 5 6 Ответ: 5 человек смотрели только «Стиляги».

Задача 2. «Гарри Поттер, Рон и Гермиона » На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 к ниг. Сколько книг прочитал только Рон?

Учитывая условия задачи, чертеж будет таков: Решение: 4 2 7 Гермиона Рон Гарри Поттер Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон. Ответ. 8 книг прочитал только Рон. 11 8

ВЫВОД: Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными

Источники информации: http:// f1.mylove.ru/0AkEJdLeQl.jpg http:// logika.vobrazovanie.ru/index.php?link=kr_e.html http:// inf. reshuege.ru/test?theme=256

Эйлеровы круги (круги Эйлера).

Цель урока: Познакомить обучающихся с решением простейших логических задач методом кругов Задачи урока Образовательная: дать обучающимся представление о методе кругов Эйлера; Развивающая: развитие логического и аналитического мышления; Воспитательная: воспитание умения выслушивать мнение других обучающихся и отстаивать свою точку зрения.

Эйлеровы круги (круги Эйлера) — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов, предложенный знаменитым математиком Л. Эйлером (1707–1783). Обозначение отношений между объемами понятий посредством кругов было применено еще представителем афинской неоплатоновской школы — Филопоном (VI в.), написавшим комментарии на «Первую Аналитику» Аристотеля.

1.Условно принято, что круг наглядно изображает объем одного какого-нибудь понятия. Объем же понятия отображает совокупность предметов того или иного класса предметов. Поэтому каждый предмет класса предметов можно изобразить посредством точки, помещенной внутри круга:

2. Группа предметов, составляющая вид данного класса предметов, изображается в виде меньшего круга, нарисованного внутри большего круга. Такое именно отношение существует между объемами понятий «небесное тело» (А) и «комета» (B). Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».

3 . Когда же ни один предмет, отображенный в объеме понятия A, не может одновременно отображаться в объеме понятия B, то в таком случае отношение между объемами понятий изображается посредством двух кругов, нарисованных один вне другого. Ни одна точка, лежащая на поверхности одного круга, не может оказаться на поверхности другого круга. Такое именно отношение существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник».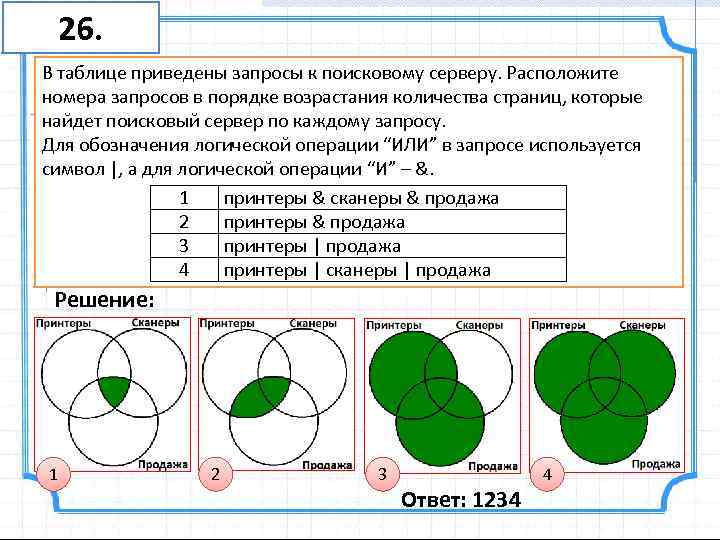 В объеме понятия «тупоугольный треугольник» не отображается ни один остроугольный треугольник, а в объеме понятия «остроугольный треугольник» не отображается ни один тупоугольный треугольник.

4 . Иначе выглядит схема отношения между объемами субъекта и предиката в общеутвердительном суждении, не являющемся определением понятия. В таком суждении объем предиката больше объема субъекта, объем субъекта целиком входит в объем предиката. Поэтому отношение между ними изображается посредством большого и малого кругов, как показано на рисунке:

5.Отношения между равнозначащими понятиями, объемы которых совпадают, отображаются наглядно посредством одного круга, на поверхности которого написаны две буквы, обозначающие два понятия, имеющие один и тот же объем: Такое отношение существует, например, между понятиями «родоначальник английского материализма» и «автор „Нового Органона“». Объемы этих понятий одинаковы, в них отобразилось одно и то же историческое лицо — английский философ Ф. Бэкон.

6 . Нередко бывает и так: одному понятию (родовому) подчиняется сразу несколько видовых понятий, которые в таком случае называются соподчиненными. Отношение между такими понятиями изображается наглядно посредством одного большого круга и нескольких кругов меньшего размера, которые нарисованы на поверхности большего круга: Такое именно отношение существует между понятиями «скрипка», «флейта», «пианино», «рояль», «барабан». Эти понятия в равной мере подчинены одному общему родовому понятию «музыкальные инструменты».

7. В тех случаях, когда между понятиями имеется отношение противоположности, отношение между объемами таких понятий отображается посредством одного круга, обозначающего общее для обоих противоположных понятий родовое понятие, а отношение между противоположными понятиями обозначается так: А — родовое понятие, B и C — противоположные понятия. Противоположные понятия исключают друг друга, но входят в один и тот же род, что можно выразить такой схемой: При этом видно, что между противоположными понятиями возможно третье, среднее, так как они не исчерпывают полностью объема родового понятия. Такое именно отношение существует между понятиями «легкий» и «тяжелый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и легкий, и тяжелый. Но между данными понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но также и среднего веса.

8.Когда же между понятиями существует противоречащее отношение, тогда отношение между объемами понятий изображается иначе: круг делится на две части так: А — родовое понятие, B и не-B (обозначается как B) — противоречащие понятия. Противоречащие понятия, исключают друг друга и входят в один и тот же род, что можно выразить такой схем ой: При этом видно, что между противоречащими понятиями третье, среднее, невозможно, так как они полностью исчерпывают объем родового понятия. Такое отношение существует, например, между понятиями «белый» и «небелый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и белый и небе лый.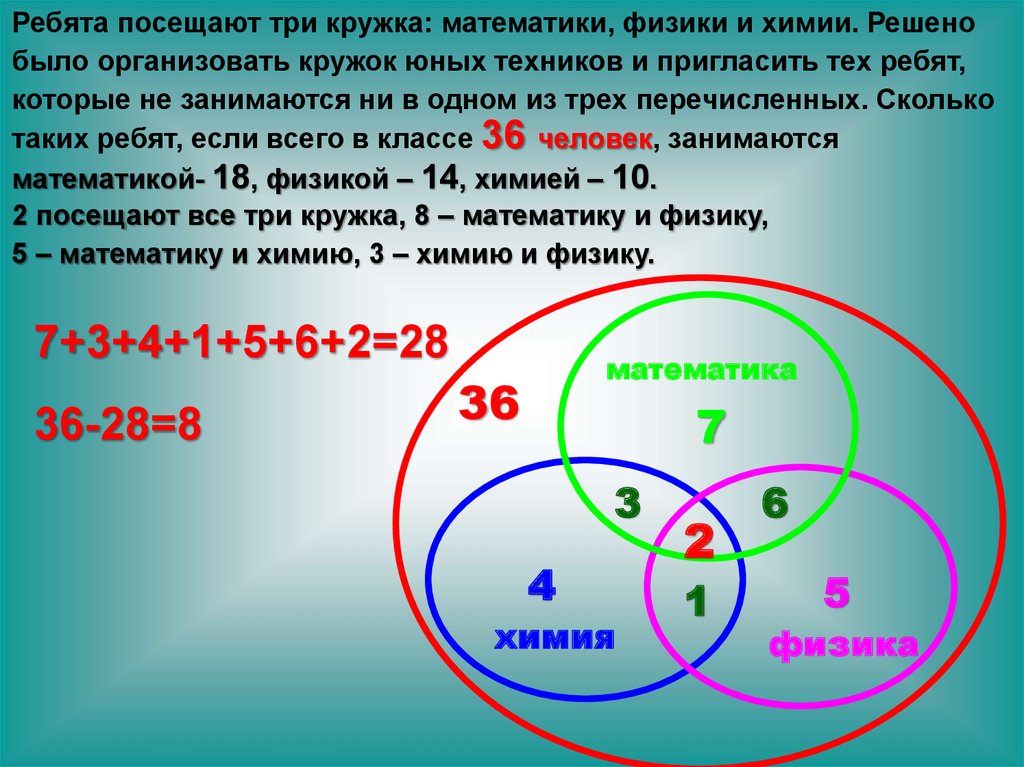

9.Посредством Эйлеровых кругов изображаются также отношения между объемами субъекта и предиката в суждениях. Так, в общеутвердительном суждении, выражающем определение какого-либо понятия, объемы субъекта и предиката, как известно, равны. Наглядно такое отношение между объемами субъекта и предиката изображается посредством одного круга, подобно изображению отношений между объемами равнозначащих понятий. Разница только в том, что в данном случае всегда на поверхности круга надписываются две определенные буквы: S (субъект) и P (предикат), как это показано на рисунке:

Задача 1. Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро — собак. И только у двоих есть и те и другте. Угадайте, сколько у меня подруг? Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом — собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части «кошачьего» круга ставим цифру 4 (6 — 2 = 4). В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

Ответ. 9 подруг.

Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки? Решение: Пусть круг Ш изображает читателей только школьной библиотеки, круг Р — только районной. Тогда ШР — изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно: (не Ш) = Р — ШР. Всего 30 учеников, Ш = 20 человек, Р = 15 человек. Тогда значение ШР может быть найдено так (см. рисунок): ШР = (Ш + Р) — 30 = (20 + 15) — 30 = = 5, т.е. 5 учеников являются читателями школьной и районной библиотек одновременно.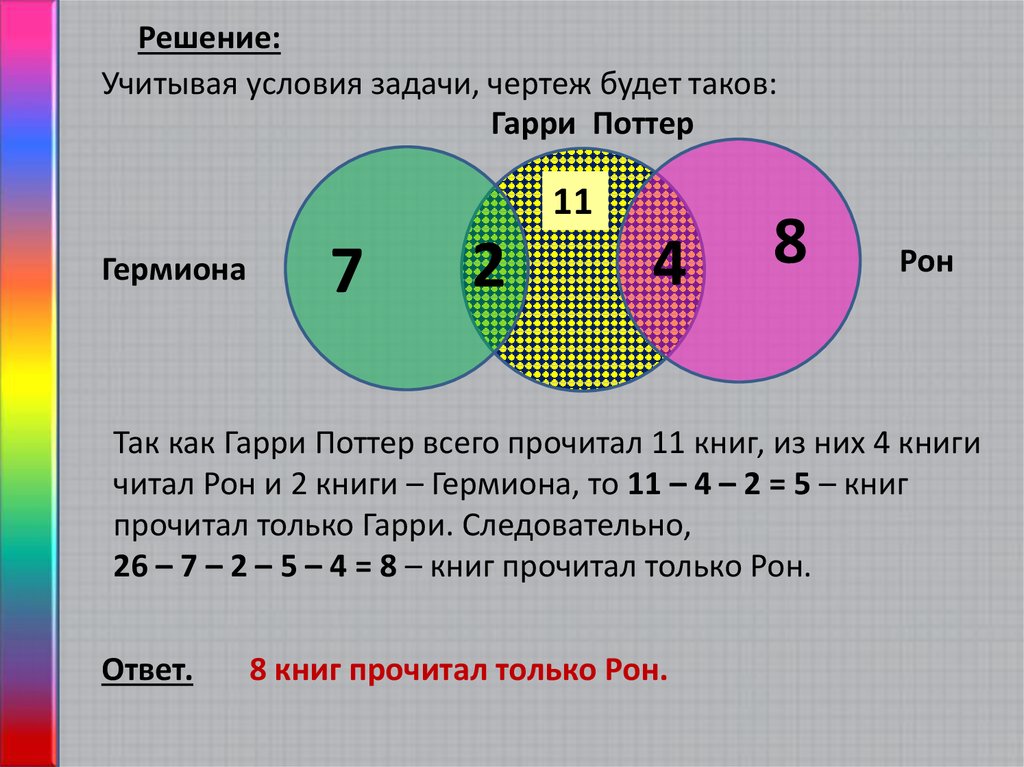 Тогда (не Ш) = = Р — ШР= 15 — 5= 10.

Ответ: 10 учеников не являются читателями школьной библиотеки.

Задача 3. Любимые мультфильмы. Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», » Винни Пух», «Микки Маус». Всего в классе 28 человек. «Белоснежку и семь гномов» выбрали 16 учеников, среди которых трое назвали еще «Микки Маус», шестеро — » Винни Пух», а один написал все три мультфильма. Мультфильм «Микки Маус» назвали 9 ребят, среди которых пятеро выбрали по два мультфильма. Сколько человек выбрали мультфильм » Винни Пух»? Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только «Белоснежку» выбрали 16-6-3-1=6 человек. Только «Микки-Маус» выбрали 9-3-2-1=3 человека. Только » Винни-Пух » выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что » Винни-Пух » выбрали 7+6+1+2=16 человек.

Задача 7. Спорт для всех. В классе 38 человек. Из них 16 играют в баскетбол, 17 — в хоккей, 18 — в футбол. Увлекаются двумя видами спорта — баскетболом и хоккеем — четверо, баскетболом и футболом — трое, футболом и хоккеем — пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом. Сколько ребят увлекаются одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта? Решение. Воспользуемся кругами Эйлера. Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта — баскетболом занимаются 16 — (4 + z + 3) = 9 — z ; одним лишь хоккеем 17 — (4 + z + 5) = 8 — z ; одним лишь футболом

18 — (3 + z + 5) = 10 — z . Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам: 3 + (9 — z) + (8 — z) + (10 — z) + 4 + 3 + 5 + z = 38,z = 2.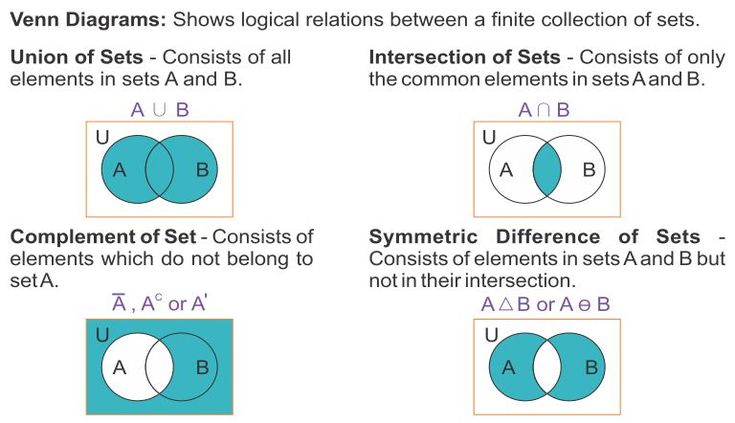 Таким образом, двое ребят увлекаются всеми тремя видами спорта. Складывая числа 9 — z , 8 — z и 10 — z , где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек. Ответ: Двое ребят увлекаются всеми тремя видами спорта человека. Увлекающихся лишь одним видом спорта: 21 человек.

Задача Спортивный класс. В классе 35 учеников. 24 из них играют в футбол, 18 — в волейбол, 12 — в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 — в футбол и баскетбол, а 5 — в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно? Домашнее задание

Что такое диаграмма Венна с примерами

1. Что такое диаграмма Венна?

Диаграмма Венна — это визуальное представление сходств и различий между двумя или более концепциями. Он изображает отношения между двумя или более наборами данных, используя круги в качестве иллюстрации. Каждый кружок представляет один конкретный набор данных. Перекрывающиеся круги представляют сходство, а отдельные круги представляют различия между наборами или понятиями.

С помощью диаграммы Венна можно легко описать любую связь между двумя или более понятиями. Использование кругов для представления данных упрощает отображение сходства между двумя или более фракциями. Вот почему эти диаграммы обычно используются для бизнес-презентаций, логических исследований и математики.

Обычно в диаграмме Венна можно использовать любое количество кругов, но чаще всего используется диаграмма с тремя кругами. Когда три круга частично перекрывают друг друга на диаграмме, они образуют треугольник в области пересечения. Этот треугольник представляет аналогичные данные в этих трех кругах. Это не только улучшает визуальное представление; макет также позволяет легко понять логику, стоящую за ним. Найдите другие примеры диаграмм Венна.

Источник изображения : pinterest.com

 

2. Символы диаграммы Венна

Если говорить о теории множеств, то вам придется выучить более 30 символов, но построить диаграмму Венна можно, только поняв несколько основных символов. Диаграмма представляет собой классификацию и сравнение наборов данных; поэтому вам нужно выучить только шесть символов, чтобы начать. Есть статья, в которой представлены символы диаграммы Венна.

Символ	Имя	Пример	Описание
А	Установить А		Буква А представляет собой круг со всеми элементами множества А на диаграмме.
ꓵ	Перекресток		А ꓵ В = {9, 10} Символ ꓵ между двумя наборами обозначает только похожие элементы. Он показывает элементы, которые есть только в обоих наборах.
∪	Союз		А ∪ В = {1, 2, 3, 4,…. ., 10} Символы ∪ между двумя наборами представляют все элементы обоих наборов.
−	Разница		А – В = {1, 2, 3, 4} По набору A из набора B вы получаете набор решений с элементами набора A, которых нет в наборе B.
А с	Комплектация набора		А с = U-А Вы можете найти дополнение множества A, вычитая все элементы множества A из универсального множества.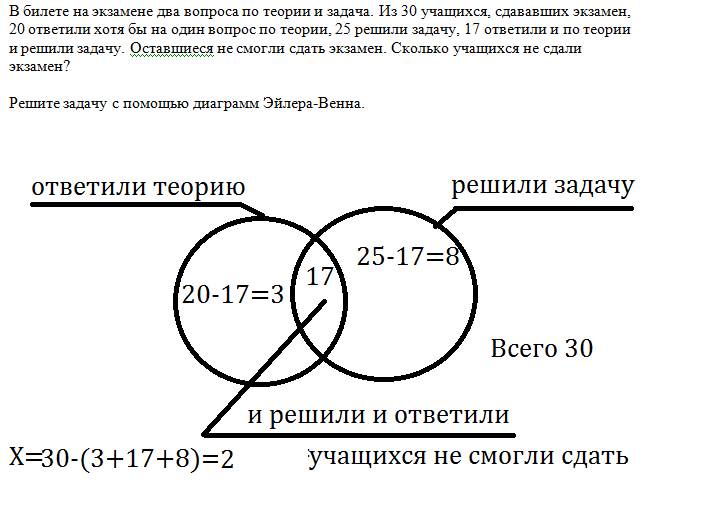
{}	Пустой набор		А={} Этот символ показывает, что множество не имеет элементов.
U	Универсальный набор		Этот символ представляет набор, который содержит все.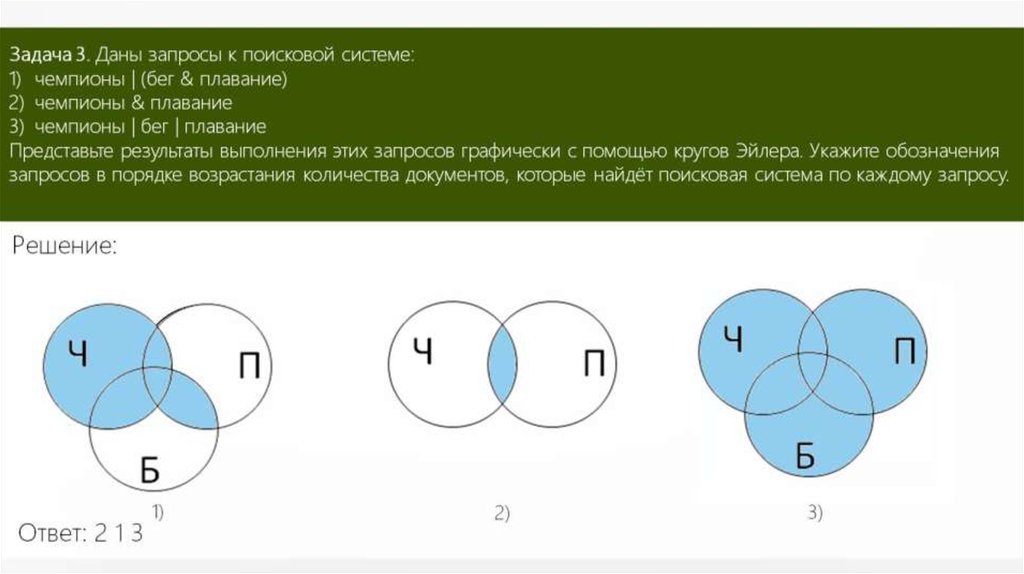 Универсальный набор является надмножеством каждого набора, включенного в диаграмму.

 

3. Примеры диаграммы Венна

Математическая диаграмма Венна

Первый пример диаграммы Венна находится в математике. Они доступны при освещении тем теории множеств и теории вероятностей.

На приведенной ниже диаграмме есть два набора: A = {1, 5, 6, 7, 8, 9, 10, 12} и B = {2, 3, 4, 6, 7, 9, 11, 12 , 13}. Раздел, в котором два набора перекрываются, имеет числа, содержащиеся как в наборе A, так и в наборе B, что называется пересечением двух наборов вместе, дает их объединение, которое включает все объекты в A, B, которые { 1 2 3 4 5 6 7 8 910 11 12 13}.

Источник изображения : bbc.co.uk

 

Бизнес-диаграмма Венна

В приведенном ниже примере диаграммы Венна анализируются общие черты и различия различных областей работы. Менеджеры по персоналу и эксперты по карьере используют его, чтобы консультировать людей по их карьерному пути.

Источник изображения : pinterest.com

 

Научные диаграммы Венна

Ученый использует диаграммы Венна для изучения здоровья человека и лекарств. На иллюстрации ниже вы можете увидеть аминокислоты, жизненно важные для жизни человека.

Источник изображения : researchgate.com

 

4. Почему важны диаграммы Венна?

Улучшенная классификация и сравнение данных благодаря визуальному представлению при сохранении простоты. Диаграммы Венна упрощают поиск сходств и различий между противоположными наборами данных. Вы можете группировать похожие данные в куски; это поможет вам легко идентифицировать пересекающуюся информацию, даже если ваша диаграмма сложна. Это означает, что вы можете создавать сложные диаграммы, не влияя на классификацию данных.

Решение сложных математических уравнений — причина, по которой большинство математиков предпочитают использовать диаграммы Венна для понимания различных концепций. Это обеспечивает лучшую классификацию действительных чисел в математике. Вы рисуете универсальный набор, решая математические уравнения. Внутри универсального набора вы используете круги или другие формы для представления наборов данных. Простое наблюдение поможет вам найти решение.

Творческий инструмент обучения для учащихся , представляющий простые понятия, начиная с начальной школы. Учащиеся понимают Диаграммы Венна на основе сравнения двух наборов и поиска сходства в математике. Это помогает им получить твердое представление о своих концепциях, начиная с уровня начальной школы.

Упрощение логики между двумя или более операторами очень помогает, когда речь идет о логических операциях и изучении вентилей. Диаграммы Венна позволяют легко понять логику любого процесса, подчеркивая сходство.

Использование бизнес-концепций с помощью диаграммы Венна позволяет легко занять нишу на рынке для любого бизнеса. Диаграммы помогают найти вероятности путем сравнения наборов данных. Вы также можете сравнить различные варианты, чтобы выбрать тот, который дает больше преимуществ и меньше рисков для вашего бизнеса.

 

5. Когда использовать диаграммы Венна?

Вы можете использовать Диаграммы Венна для демонстрации взаимосвязей в статистике, логике, вероятностях, лингвистике, информатике, организации бизнеса и во многих других областях.

В области математики, Диаграммы Венна являются учебным пособием, объясняющим математические понятия, такие как множества, объединения и пересечения. Они также решают серьезные задачи по высшей математике. Вы можете подробно прочитать о них в академических журналах в своей библиотеке и удивиться тому, насколько теория множеств является целостной ветвью математики.

Статистики используют идею диаграмм Венна , чтобы предсказать шансы конкретных событий. То же самое и в области предиктивной аналитики. Выборочные наборы данных сравниваются и тщательно изучаются, чтобы выявить их сходства и различия.

Источник изображения : pinterest.com

 

Они также эффективно определяют логические основания в аргументах и ​​выводах. Как и в дедуктивных рассуждениях, если посылки реальны и форма аргумента оказывается правильной, результат должен быть правильным. Диаграмма, аналогичная диаграмме Венна по логике, — это Таблица истинности. Он помещает переменные в столбцы, чтобы расшифровать то, что логически возможно. Еще одна диаграмма — это диаграмма Рэндольфа, также известная как R-диаграмма. В ней для объяснения множеств используются линии.

Источник изображения : youtube.com

 

В лингвистике диаграммы Венна помогают узнать, как языки различаются или соотносятся с точки зрения алфавита, гласных, произношения и т. д.

6 Источник изображения: slideshare.net

 

В компьютерных науках гики и программисты используют диаграммы Венна , чтобы получить четкое представление о языках и иерархиях в компьютерных системах.

Источник изображения : kdnuggets.com

 

Диаграммы также полезны в области продаж и маркетинга для сравнения и противопоставления продуктов, услуг, процессов и всего, что происходит в организации бизнеса. Они практичны и эффективны в улучшении продаж и прибыли, а также в широком управлении предприятиями.

Источник изображения : businessbullet.co.uk

 

6. Эволюция диаграммы Венна Схематическое и механическое представление утверждений и рассуждений.» Это было в «Философском журнале» и «Журнале науки». Джон Венн провел тщательное исследование этих диаграмм и предвидел их формализацию. Именно он первоначально обобщил их, недаром их именование, т. е.

Диаграммы Венна в 1918 году.

Существует небольшой разрыв между диаграммами Венна и диаграммами Эйлера, изобретенными в 18 веке Леонардом Эйлером, который также приложил руку к их развитию в 1700-х годах. Джон называл графики Эйлеровыми кругами.

Разработка диаграмм Венна продолжалась в 20 веке.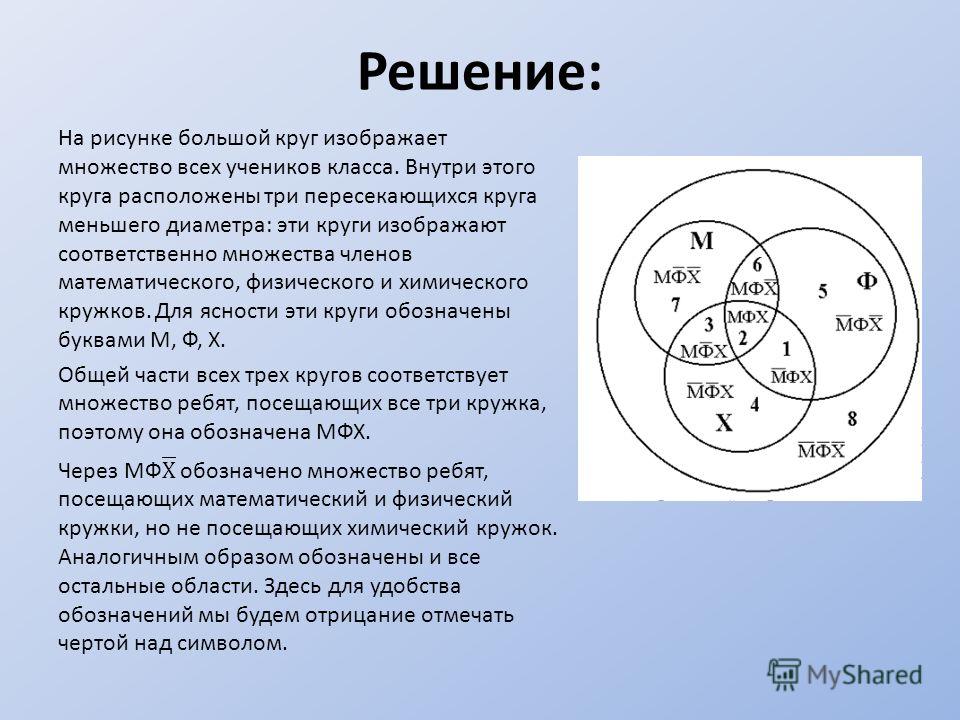 Например, примерно в 1963 году Д. В. Хендерсон обнаружил существование n-графа Венна, состоящего из n-кратной рациональной симметрии, что указывало на то, что n — простое число. Эта концепция была исследована четырьмя другими учеными в последующие годы, которые пришли к выводу, что вращательно-симметричные диаграммы Венна существуют только в том случае, если n — простое число.

С тех пор эти диаграммы стали частью современной учебной программы и иллюстрируют бизнес-информацию. Диаграммы Венна и Эйлера стали частью обучения теории множеств нового математического движения в 1960 году.

 

7. Как создать базовую диаграмму Венна за минуты?

Теперь мы будем использовать онлайн-программу EdrawMax. Он имеет все основные символы и формы, которые вам нужны, наряду с многочисленными бесплатными шаблонами Диаграмма Венна , а также модный и продвинутый интерфейс, который удобен для начинающих.

Прежде чем начать диаграмму Венна онлайн , вы должны убедиться, что вы:

• Определите цель, которую хотите достичь. Имейте четкое представление о том, что вы хотите сравнить и для чего это сравнение необходимо. Это облегчает определение множеств.
• Просмотрите и составьте список предметов, содержащихся в наборах.
• Просмотрите доступные шаблоны, чтобы получить представление о том, что вы собираетесь рисовать, а затем сделайте свой собственный Диаграмма Венна , используя следующие шаги.

 

Шаг 1: Войдите на веб-сайт программного обеспечения из EdrawMax Online. Если вы не создали учетную запись ранее, войдите в систему, используя действительные учетные данные, подтвердите свою учетную запись, а затем войдите в систему.

Шаг 2: Выберите параметры бизнес-диаграммы на вкладке «Доступные шаблоны» и дважды щелкните значок диаграммы Венна, чтобы отобразить пустую страницу, на которой вы будете рисовать.

Шаг 3: На левой панели экрана вы найдете все необходимые символы и формы диаграммы Венна. Перетащите соответствующие из них и поместите их на холст для рисования, чтобы создать диаграмму Венна.

Шаг 4: Сохраните готовую диаграмму Венна в доступных форматах или экспортируйте или поделитесь ею на других платформах непосредственно с веб-страницы Edraw.

Шаг 5: Кастомизация. Большинство встроенных фигур предназначены для изменения размера, редактирования и изменения цвета.

 

• Чтобы изменить цвет, коснитесь целевого круга несколько раз и выберите цвет на вкладке быстрого выбора цвета внизу.

• Чтобы включить личную тему и стиль, выберите один из доступных шрифтов, эффектов и цветовых схем. Создайте уникальную и профессиональную диаграмму Венна, нажав на то, что вы предпочитаете.

 

8. Часто задаваемые вопросы о диаграммах Венна

Ниже приведены ответы на некоторые из наиболее часто задаваемых вопросов о диаграммах Венна.

Для чего используется диаграмма Венна?

Вы можете использовать диаграмму Венна для многих вещей. Вы можете использовать его, чтобы найти нишу на рынке для вашего бизнеса. Это очень помогает вам с презентациями, касающимися классификации и сравнения данных. Вы также можете использовать его для решения сложных математических уравнений. Эти диаграммы также являются частью программ по психологии.

Что такое диаграмма Венна в математике

Математика является источником диаграммы Венна. Он исходит из теории множеств и помогает решать сложные уравнения и задачи. Учащиеся используют эти диаграммы для классификации отношений между элементами двух или более наборов. Они могут выделять похожие и разные элементы между множествами, используя различные операции над множествами, такие как объединение или пересечение.

Как читать диаграмму Венна?

Читать диаграмму Венна очень просто. Все, что вам нужно сделать, это посмотреть на круги на диаграмме. Если круги пересекаются друг с другом, то это означает, что в обоих наборах есть какие-то похожие элементы. Если круги не пересекаются, значит, подобных элементов нет.

EdrawMax Онлайн

Создайте более 280 типов диаграмм онлайн

Доступ к диаграммам в любом месте и в любое время

Все на рабочем столе + Сообщество шаблонов

Управление командой и сотрудничество

Интеграция личного облака и Dropbox

ПОПРОБУЙТЕ ОНЛАЙН

EdrawMax Desktop

Создайте более 280 типов диаграмм

Поддержка Windows, Mac, Linux

Полный доступ к ресурсам и шаблонам

Локальное программное обеспечение для бизнеса

Безопасность данных корпоративного уровня

СКАЧАТЬ СКАЧАТЬ СКАЧАТЬ

СКАЧАТЬ

 

Статьи по теме

Шаблон диаграммы Венна | Miro

О шаблоне диаграммы Венна

Не зря диаграммы Венна стали основным элементом деловых встреч и презентаций с 1800-х годов. Диаграммы Венна представляют собой четкий и эффективный способ визуальной демонстрации взаимосвязей между наборами данных. Они служат полезным наглядным пособием во время мозгового штурма, совещаний и презентаций. Шаблон диаграммы Венна от Miro поможет вам в этом.

Что такое диаграмма Венна?

Диаграмма Венна — это графическое представление сходств и различий между группами или понятиями с помощью перекрывающихся кругов. Области, в которых эти круги перекрываются, представляют отдельных лиц или аспекты, которые в равной степени принадлежат к перекрывающимся группам. Там, где кружки не пересекаются, различия подсвечиваются.

Диаграммы Венна, также известные как логические диаграммы или диаграммы множеств, широко используются для оценки вероятности в статистике, математике и технике. Диаграммы Венна часто путают с диаграммами Эйлера, поскольку обе они основаны на теории множеств. Итак, в чем разница между диаграммой Венна и диаграммой Эйлера? Основное отличие состоит в том, что на диаграмме Венна показаны все возможные отношения между множествами, а на диаграмме Эйлера — только соответствующие отношения.

Несмотря на то, что это может показаться очень техническим, диаграмма Венна — один из самых простых и легких способов представления понятий. В результате он также был принят в качестве мощного визуального инструмента в образовании, бизнесе и других областях. Диаграммы Венна бесконечно настраиваются и часто используются для организации информации таким образом, чтобы она была удобочитаемой и визуально привлекательной. Диаграммы Венна могут помочь командам разбить сложные идеи во время мозгового штурма или решения проблем.

Происхождение диаграммы Венна

Диаграмма Венна получила свое название от британского логика Джона Венна, который официально представил ее в научных статьях в конце 1800-х годов. Впервые он был опубликован в статье под названием «О механическом и диаграммном представлении предложений и рассуждений», опубликованной в престижных философских журналах и Journal of Science .

Еще до того, как она получила официальное название, концепция диаграммы Венна восходит к 1200-м годам, когда ее использовали средневековые философы и ученые.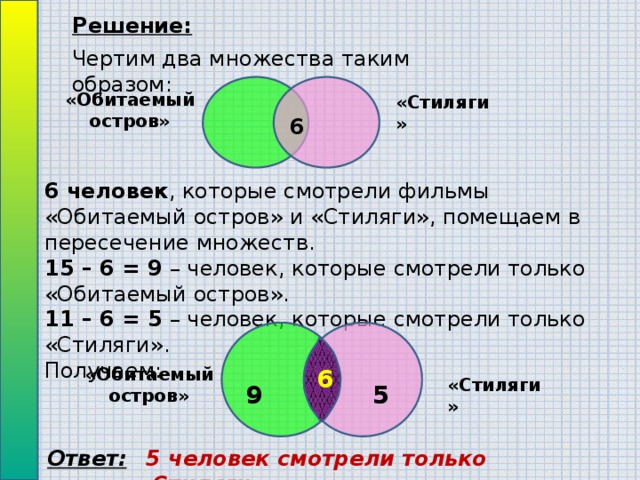 Есть записи испанского логика и философа Рамона Лулля, у которого были подобные теории. Диаграмма Эйлера, созданная швейцарским математиком Леонардом Эйлером в 1700-х годах, предшествовала диаграмме Венна и, вероятно, повлияла на нее, поскольку Джон Венн называл свои диаграммы эйлеровыми кругами. Сегодня диаграммы Венна различаются, однако их называют более ограничительной формой диаграмм Эйлера.

В развитие диаграммы Венна внесли свой вклад и другие, в том числе Карла Д. Сэвидж, Дэвид В. Хендерсон, Джеррольд Григгс и Питер Гамбургер. Все они добавили что-то новое, что привело к диаграмме Венна, какой мы ее знаем сегодня. При жизни сам Джон Венн никогда не называл диаграммы своим именем. Эта длинная история и постоянное использование диаграммы Венна во всех ее формах показывает, насколько полезны и необходимы эти диаграммы и что вы тоже можете ими воспользоваться.

Компоненты диаграммы Венна

Исследователи построили диаграммы Венна на основе математической теории множеств и разработали язык и системы, чтобы сделать их понятными и непротиворечивыми.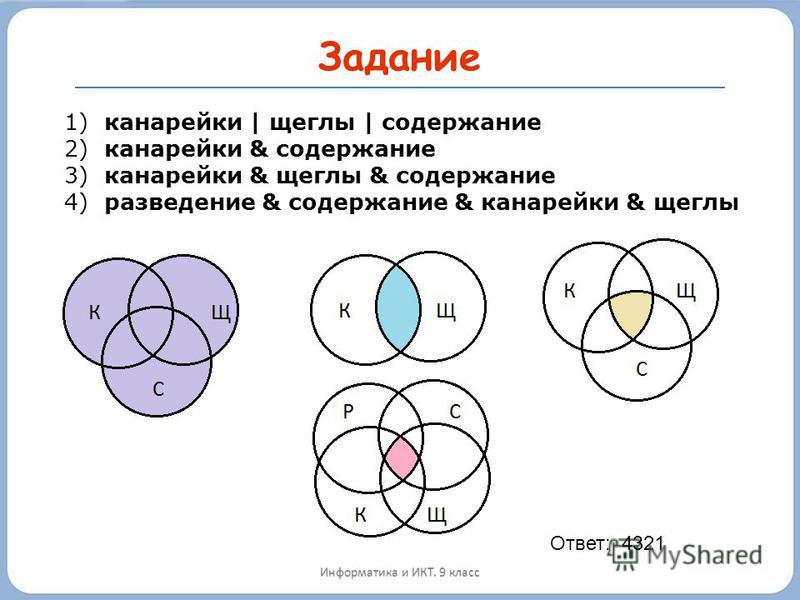 Чтобы правильно понимать диаграммы Венна, важно знать больше о множествах и компонентах диаграммы Венна.

Наборы: Также называемые элементами, наборы могут включать математические числа, идеи или даже объекты.

Объединение наборов: Мы используем символ ∪ для обозначения объединения двух или более наборов данных. Если у вас есть диаграмма Венна с двумя перекрывающимися кругами, ∪ представляет все, что попадает в одну категорию, другую категорию или обе категории.

Пересечение наборов: Символ ∩ представляет собой область пересечения наборов данных или общие черты между наборами.

Симметричная разность множеств : Включает все, кроме того, что находится на пересечении множеств.

Дополнение наборов: Представляет собой все, что не принадлежит определенному набору. Символ Ac представляет это. Это также называется абсолютным дополнением.

Относительное дополнение: Это относится ко всему в одном наборе, но не в другом.

Для чего можно использовать диаграмму Венна?

Диаграммы Венна полезны для любого количества предметов, и существует множество применений диаграмм Венна, которые различаются по сложности. Они чаще всего используются для математики и логики, но также хорошо подходят для лингвистики, информатики и бизнеса. Давайте рассмотрим это более подробно.

• Презентации: Наряду с круговыми и столбчатыми диаграммами диаграмма Венна является одним из наиболее часто используемых визуальных элементов в презентациях. Эти диаграммы позволяют с первого взгляда визуализировать большие объемы данных и сложные концепции и увидеть, как они взаимосвязаны или различаются.

• Образование: Учителя используют диаграммы Венна как наглядный инструмент. Это помогает учащимся лучше запоминать информацию, а учитель помогает объяснить намного лучше. Кроме того, учитель также может отправить его в качестве домашнего задания, чтобы учащиеся могли оптимально понять программу без необходимости запоминать.

• Бизнес : Диаграммы Венна полезны при сравнении услуг, продуктов или процессов. В деловом мире крайне важно уметь легко объяснять концепции заинтересованным сторонам и лицам, принимающим решения. Таким образом, создание графиков или использование диаграммы Венна может стать мощным инструментом для синтеза сложной информации и облегчения ее понимания.

• Статистика: Пожалуй, наиболее известным применением диаграмм Венна является определение вероятности. Диаграммы Венна используются во многих областях, включая математику, инженерию и другие области науки.

• Информатика : Диаграммы Венна могут использоваться для решения задач в области информатики. Программистам часто приходится кодировать сложные алгоритмы и вычисления. Визуальное понимание проблемы может помочь лучше понять, что необходимо учитывать.

• Лингвистика: Это еще одна область, в которой диаграммы Венна широко используются для изучения сходств и различий между различными языками и языковыми группами. Если несколько языков, например, произошли от латыни, в них может быть большое количество одинаковых терминов, несмотря на то, что языки разные.

• Принятие решений: Сравнив два или более вариантов и увидев, насколько они различаются и какие точки у них могут быть общими, можно облегчить процесс принятия решений с помощью диаграмм Венна. Это не обязательно должно быть ограничено профессиональным или образовательным использованием. Иногда использование диаграммы Венна может помочь вам решить и ваши личные проблемы!

Преимущества использования диаграмм Венна

Создание диаграмм Венна имеет ряд преимуществ в зависимости от ваших потребностей либо на более техническом уровне, либо для более простых целей.

Использование в теории вероятностей — Диаграммы Венна широко используются в статистике для изучения вероятностей и предсказания событий. Привнесение этого в любой бизнес или область исследования может помочь вам принимать более правильные решения.

Четкое представление информации — Простая структура и дизайн диаграмм Венна позволяют легко увидеть сходства и различия с первого взгляда, чтобы пользователи могли лучше понять информацию с первого взгляда.

Идеально подходит для стратегии . Диаграммы Венна помогут вам лучше понять различия и сходства между вашей компанией, продуктом или услугой и конкурентами. Вы также можете использовать это наглядное пособие при объяснении заинтересованным сторонам.

Улучшает коммуникацию — Являясь наглядным пособием, диаграммы Венна улучшают коммуникацию, позволяя легко объяснять сложные понятия вашей команде, членам организации или учащимся в классе.

Как создать диаграмму Венна 

Создать диаграмму Венна в Miro очень просто! Просто выберите наш шаблон диаграммы Венна, чтобы быстро создать диаграмму Венна онлайн. Используя виртуальную платформу для совместной работы Miro, вы можете редактировать и обсуждать свою диаграмму Венна в режиме реального времени со своей командой.

Следуйте нашим простым шагам для заполнения шаблона диаграммы Венна. Наш шаблон по умолчанию имеет диаграмму Венна с 3 кругами, но вы можете удалить или скопировать круги, чтобы получить диаграмму Венна из 2, 4 или даже 5 кругов, в зависимости от ваших потребностей!

Шаг 1: Определите группы, которые вы хотите представлять

После того, как вы определили количество групп, которые вы хотите представить, убедитесь, что у вас есть правильное количество кругов. Если вам нужна диаграмма Венна с двумя кругами, удалите круг. Если вам нужна диаграмма Венна с 4 или 5 кругами, просто скопируйте круги и наложите их так, как вам нужно. Не забудьте пометить группы.

Шаг 2: Обратите внимание на сходство

Там, где круги пересекаются друг с другом, круги имеют общие атрибуты. Обратите внимание на сходство между каждой из групп, которые вы определили здесь. В последнем наборе сходств все круги перекрываются (помечены как ABC).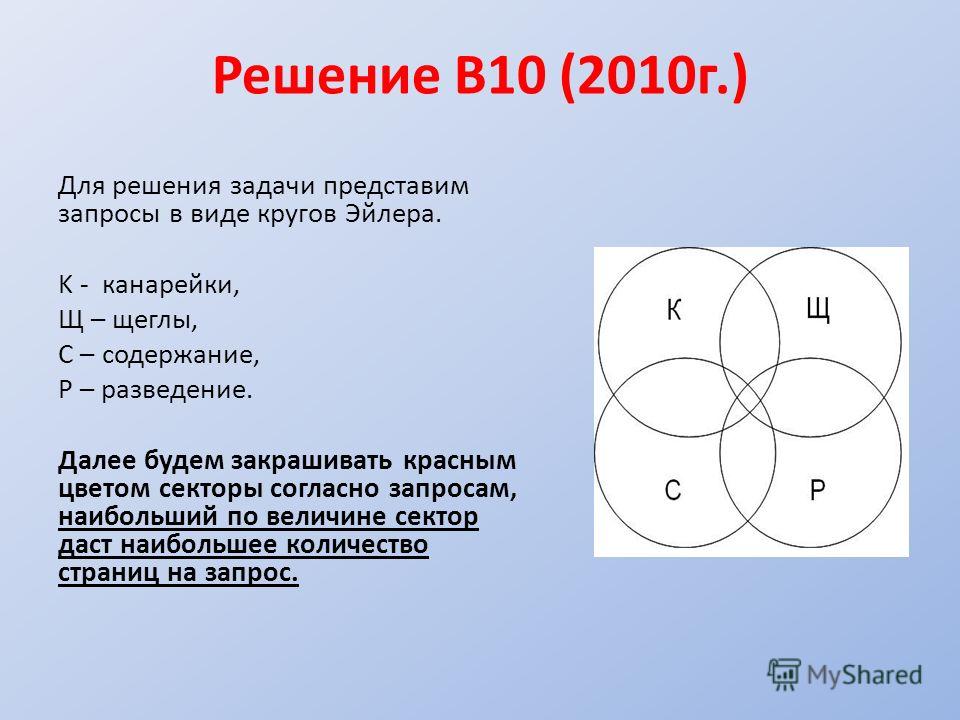 Сходства, которые вы идентифицируете между всеми группами, должны быть перечислены здесь.

Шаг 3: Определите различия

В пространстве, где ваши круги не пересекаются, вы можете отметить различия между группами, которые вы представляете на диаграмме Венна.

Шаг 4. Настройте цвета и шрифты шаблона диаграммы Венна

Шаблон диаграммы Венна Миро можно настроить по своему усмотрению. Вы можете не только изменить количество и размер используемых кругов, но также изменить цвет и шрифт.

Шаг 5. Добавьте изображения или значки (необязательно)

Если вы считаете, что вашей команде или аудитории будет полезно увидеть изображения или значки, вы также можете добавить их. Просто скопируйте и вставьте их в шаблон диаграммы Венна и измените их размер по мере необходимости.

Шаг 6. Поделитесь своей диаграммой Венна

Вы можете поделиться своей диаграммой Венна напрямую со своей командой или учениками на доске Miro. Существует также возможность сохранить настроенный вами шаблон диаграммы Венна в виде изображения JPEG или pdf. Просто нажмите на Экспортируйте этот значок платы в верхней части экрана и выберите «Сохранить как изображение», после чего вам будет предоставлена ​​возможность выделить только вашу диаграмму Венна.

Часто используемые диаграммы Венна

Диаграмма Венна с двумя кругами

Несмотря на то, что диаграмма Венна с двумя кругами невероятно проста, она может четко и наглядно показать различия и сходства между двумя отдельными наборами. На диаграмме Венна с двумя кругами есть две перекрывающиеся окружности (А и В), которые имеют пересечение (АВ).

Диаграмма Венна с тремя кругами

Диаграмма Венна с тремя кругами, также известная как трехсторонняя диаграмма Венна, возможно, наиболее часто используется и показывает, как элементы трех множеств связаны с помощью трех кругов (A, B, и С). Есть три пересечения между всеми комбинациями кругов, где они перекрываются (AB, BC и CA).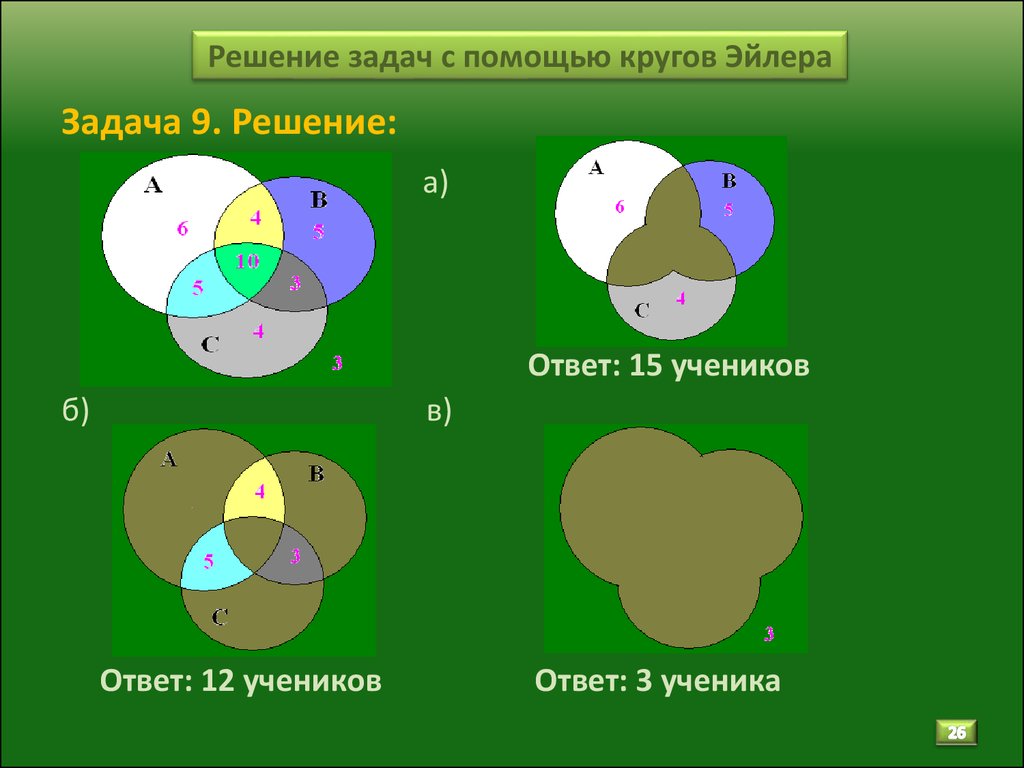 Там, где эти три окружности пересекаются (ABC), мы видим изогнутый треугольник, известный как треугольник Рело.

Диаграмма Венна с 4 кругами

Еще одна часто используемая диаграмма Венна, которую вы можете увидеть в презентациях и на иллюстрациях, — это диаграмма Венна с 4 кругами. Они более сложные, так как объединяют четыре круга или наборы данных (A, B, C и D). Все четыре круга будут пересекаться (ABCD), но будут и другие области пересечения, которые позволят вам увидеть сходства и различия между различными комбинациями двух или трех этих наборов или кругов.

Зачем использовать шаблон диаграммы Венна в Miro?

Miro позволяет создавать диаграммы Венна онлайн с вашей командой и обсуждать их в режиме реального времени или во время асинхронной работы. Добавление шаблона диаграммы Венна на доску Miro занимает всего несколько секунд, где вы можете легко настроить его, добавив текст, изображения и комментарии. Как визуальный инструмент, Miro очень интуитивно понятен, поэтому легко настроить размер кругов и изменить цвет.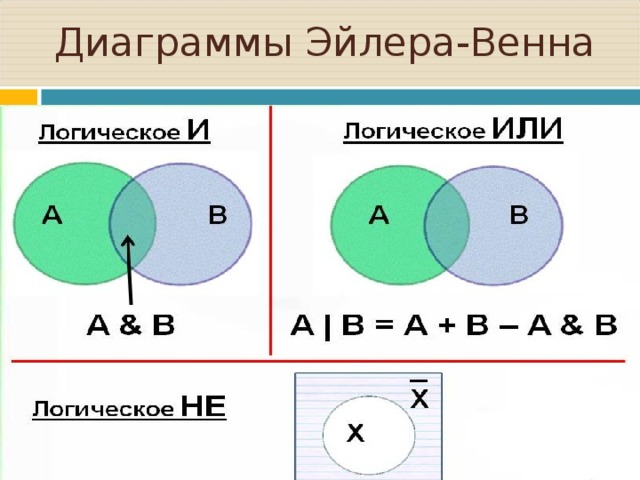 Добавлять или удалять круги так же просто.

Еще одно преимущество создания диаграммы Венна на доске Miro заключается в том, что это бесконечный холст, на котором вы можете добавлять другие заметки и идеи для своей работы. Miro имеет ряд интеграций с другими платформами, такими как G Suite, Microsoft Teams, Zoom и Slack, поэтому вы можете легко поделиться своей диаграммой Венна.

Примеры диаграмм Венна

Мы можем рассмотреть простой пример диаграммы Венна с использованием двух наборов (представленных кружками), которые могут иметь отношение к организации.

У нас есть один круг, представляющий команду по маркетингу (Круг A), а другой — команду продукта (Круг B). Мы хотим визуально показать отделы, с которыми сотрудничает каждая из этих команд, и они будут перечислены в каждом круге.

Circle A — команда маркетинга: работает с ИТ, веб-сайтами, разработчиками, дизайнерами, аналитиками и данными, а также с юридическими командами.

Circle B — это команда по продукту: работа с командами по дизайну, продажам, ремонту, обслуживанию клиентов, ИТ, исследованиям и разработкам.