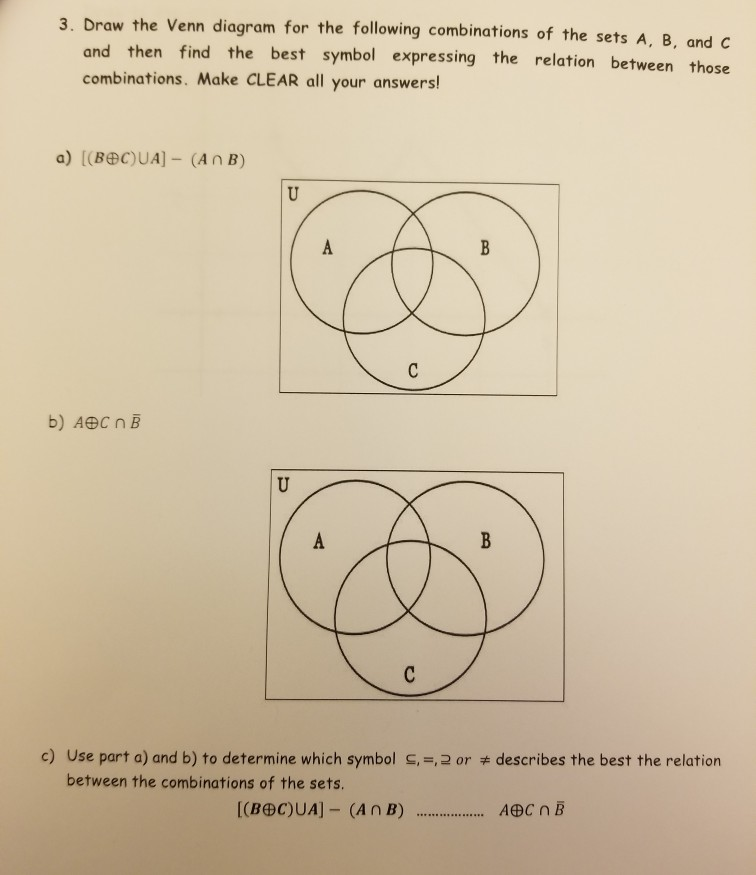
Применение Кругов Эйлера в Текстовых Задачах
Круги Эйлера — хороший, а главное удобный (графически иллюстрированный) способ решения текстовых задач.
В этом разделе будут рассмотрены 2 текстовых задачи, решенные этим методом.
Для полного понимания решения настоятельно рекомендуется учить все вовремя, а не как студент, выполнивший данный проект.
В классе 38 человек. Из них 16 играют в баскетбол, 17 — в хоккей, 18 — в футбол. Увлекаются двумя видами спорта — баскетболом и хоккеем — четверо, баскетболом и футболом — трое, футболом и хоккеем — пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом. Сколько ребят увлекаются одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?
Решение: Воспользуемся кругами Эйлера.
Пусть большой круг изображает всех учащихся класса,
а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов.
одним лишь хоккеем
одним лишь футболом
Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам:
Таким образом, двое ребят увлекаются всеми тремя видами спорта.
Складывая числа 9 — z, 8 — z и 10 — z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта:
Ответ:
Двое ребят увлекаются всеми тремя видами спорта человека.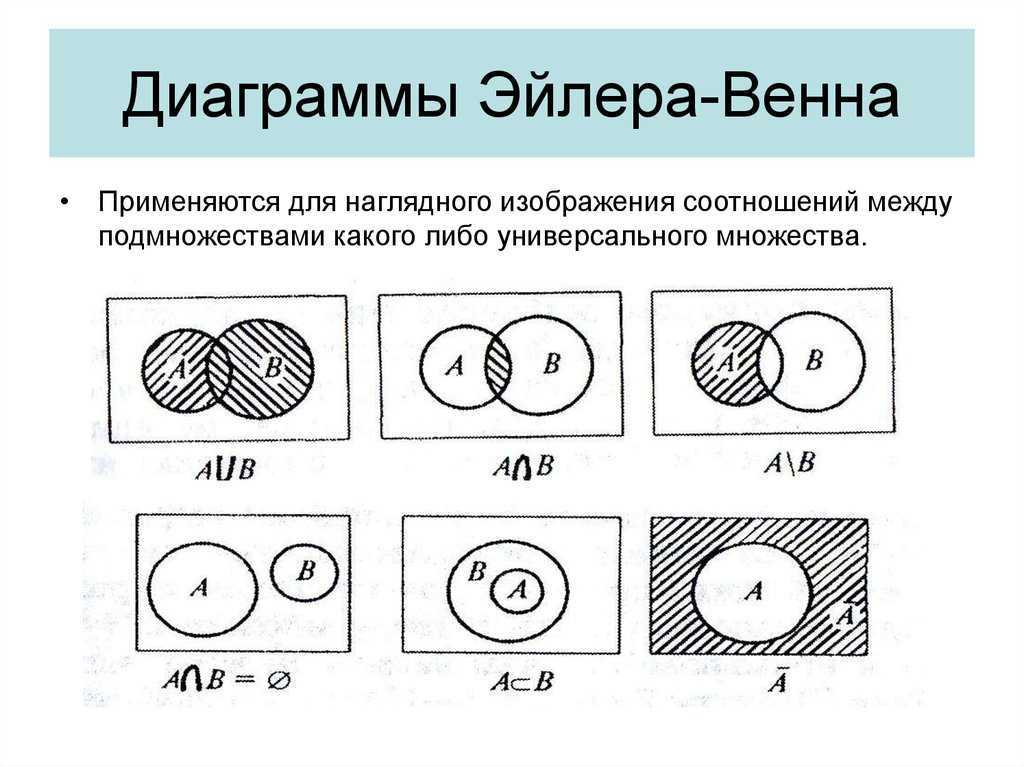
Увлекающихся лишь одним видом спорта: 21 человек.
13 Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3.
Сколько туристов не владеют ни одним языком?
Выразим условие этой задачи графически. Обозначим кругом тех кто знает английский, другим кругом — тех, кто знает французский, и третим кругом — тех, кто знают немецкий.
Тогда, например, те, кто владеет и английским и немецким, «попадут» в общую часть первого и третьего круга.
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языками владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.
Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста.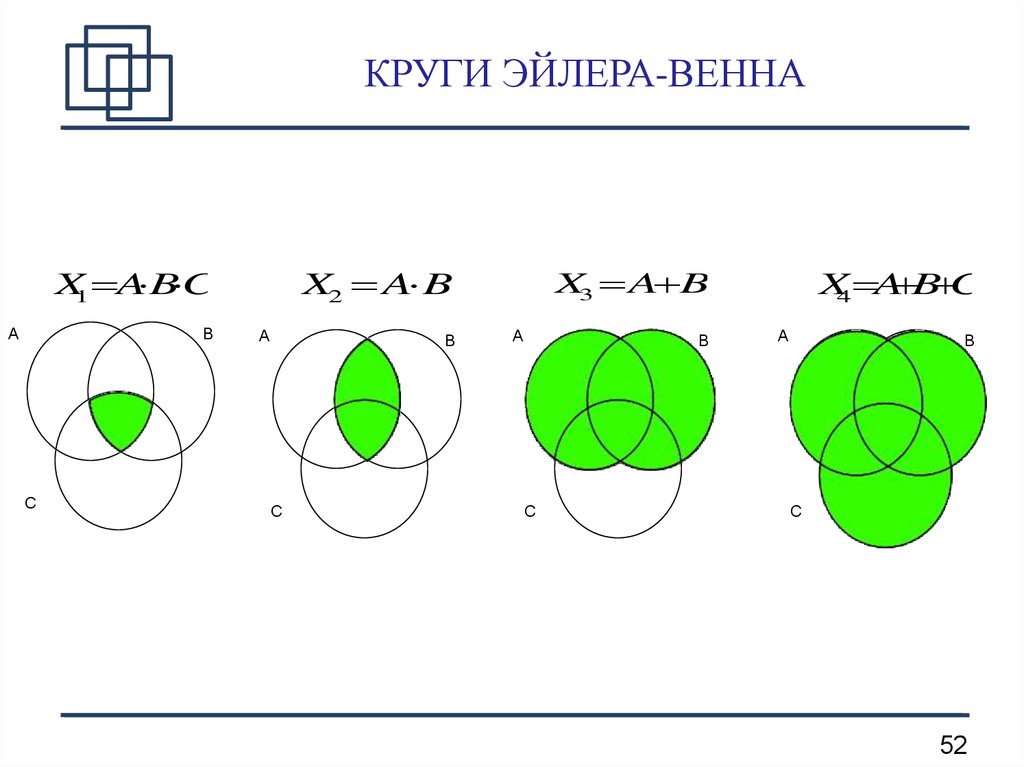 Вносим эти данные в соответствующие части.
Вносим эти данные в соответствующие части.
Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским — 30 человек.
По условию задачи всего 100 туристов.20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.
Ответ:
Только английским владеет 13 человек, только французским — 30, только немецким — 20 человек.
20 человек не знают ни одного из этих языков.
Круги Эйлера. Составление запросов для поисковых систем
Похожие презентации:
Пиксельная картинка
Информационная безопасность. Методы защиты информации
Электронная цифровая подпись (ЭЦП)
Этапы доказательной медицины в работе с Pico. Первый этап
Первый этап
История развития компьютерной техники
От печатной книги до интернет-книги
Краткая инструкция по CIS – 10 шагов
Информационные технологии в медицине
Информационные войны
Моя будущая профессия. Программист
1. Составление запросов для поисковых систем
Решение задач с помощьюдиаграмм Эйлера – Венна
Составление запросов
для поисковых систем
Диаграммы Эйлера — Венна
Диаграммы Эйлера — Венна —
общее название целого ряда
методов визуализации и способов
графической иллюстрации,
широко используемых в различных
областях науки:
• теории множеств,
• теории вероятностей,
• логике,
• статистике,
• менеджменте,
• компьютерных науках.
2
Леонард Эйлер
Швейцарский, немецкий и российский
математик и механик,
внёсший фундаментальный вклад
в развитие многих наук.
Леонард
Эйлер
(1707—1783)
Эйлер — автор более 850 работ
по математическому анализу,
дифференциальной геометрии,
теории чисел, приближённым
вычислениям, небесной механике,
математической физике, оптике,
баллистике, кораблестроению,
теории музыки и другим областям.
3
Круги Эйлера
При решении целого ряда
задач Леонард Эйлер
использовал идею
изображения множеств
с помощью кругов.
Леонард
Эйлер
(1707—1783)
Например:
А – люди
В – живые существа
С – неживые предметы
4
Готфрид Вильгельм Лейбниц
Однако, ещё до Эйлера
выдающийся немецкий
философ и математик
Готфрид Вильгельм Лейбниц
использовал этот метод
для геометрической
интерпретации логических
связей между понятиями,
но всё же предпочитал
использовать линейные схемы
Готфрид
Вильгельм
фон Лейбниц
(1646 — 1716)
5
Джон Венн
Особенного расцвета графические
методы достигли в сочинениях
британским философа, математика
и логика Джона Венна, изложившего
их в книге «Символическая логика»
в 1881 г.
Джон Венн
(1834—1923)
Поэтому такие схемы называют
Диаграммы Эйлера — Венна.
Венн расширил математическую
логику Буля и более всего известен
среди математиков и логиков за его
схематический способ
представления множеств и
их объединений и пересечений.
6
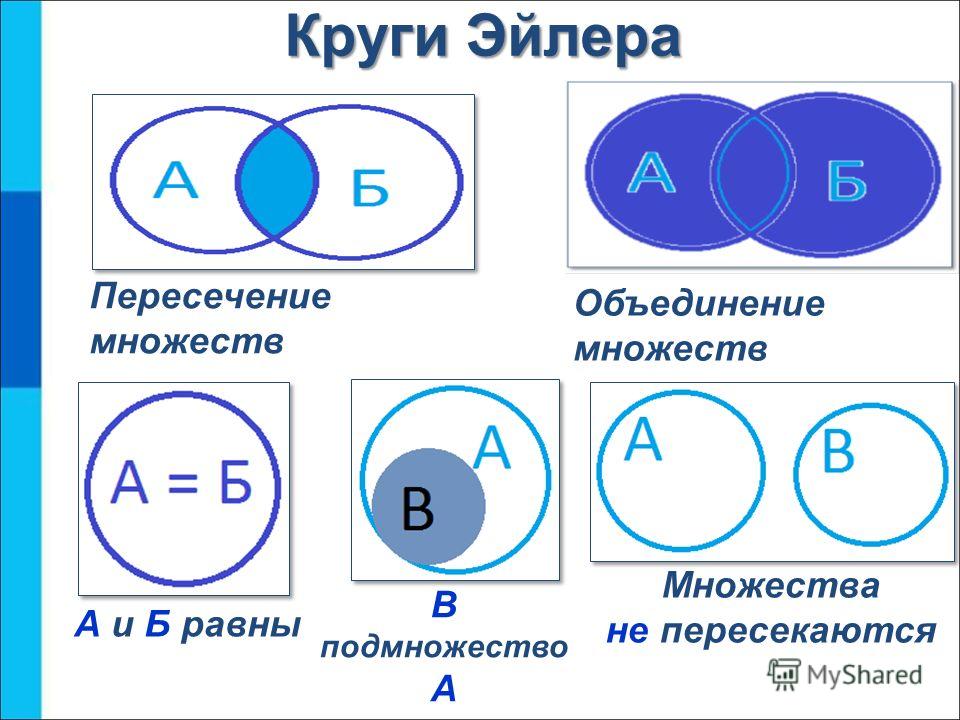
Диаграммы Эйлера — Венна
Пересечение множеств
А∩В
Объединение множеств
А
В
АUВ
7
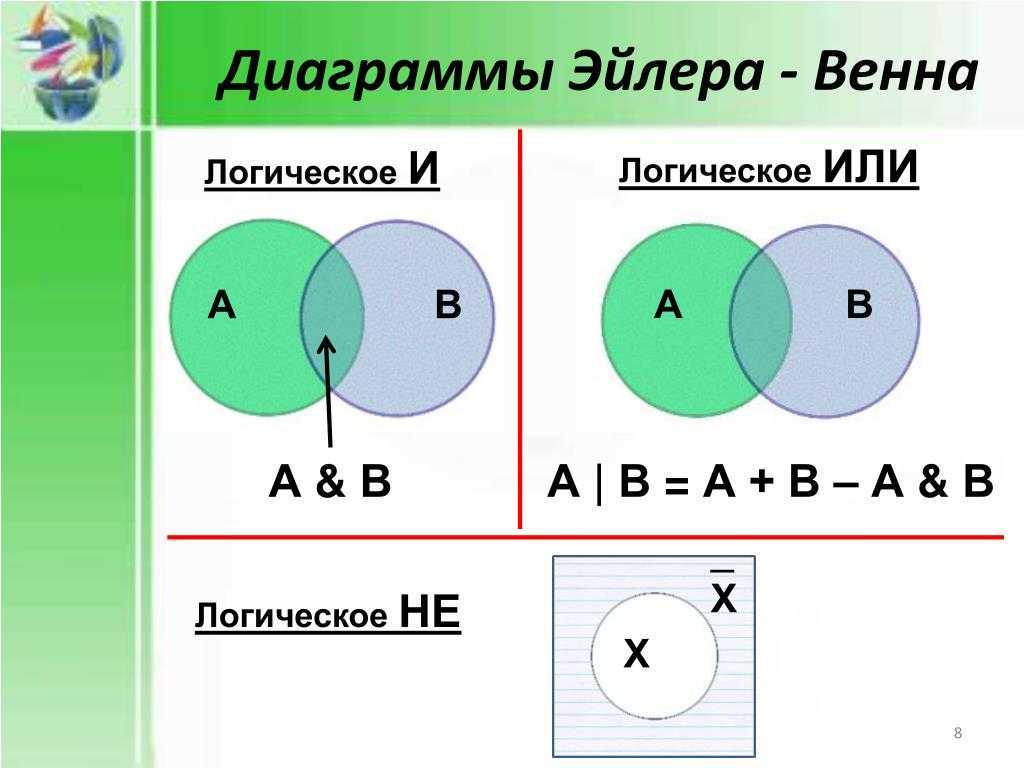
Диаграммы Эйлера — Венна
Логическое И
А
Логическое ИЛИ
А
В
А&В
Логическое НЕ
В
А|В=А+В–А&В
_
Х
Х
8
Диаграммы Эйлера — Венна
Пример
А
1+4=А&В
1
В
2+4=А&С
2
4
3+4=В&С
3
4=А&В&С
С
9
10. Задача 1
В таблице приведены запросы и количество найденныхпо ним страниц некоторого сегмента сети Интернет:
Запрос
Найдено страниц
(в тысячах)
Шахматы | Теннис
7770
Теннис
5500
Шахматы & Теннис
1000
Какое количество страниц (в тысячах)
будет найдено по запросу Шахматы?
Считается, что все запросы выполнялись
практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся
за время выполнения запросов.
10
11. Решение
Найдено страниц(в тысячах)
Запрос
Шахматы | Теннис
7770
Теннис
5500
Шахматы & Теннис
1000
Ш
Т
Ш|Т
Ш&Т
Ш = (Ш|Т) – Т + (Ш & Т) = 7770 – 5500 + 1000
Ответ: 3270
11
12.
 Задача 2В таблице приведены запросы и количество найденных
Задача 2В таблице приведены запросы и количество найденныхпо ним страниц некоторого сегмента сети Интернет:
Запрос
Найдено страниц
(в тысячах)
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) & Рубин
320
280
430
Какое количество страниц (в тысячах)
будет найдено по запросу
Рубин & Динамо & Спартак?
12
13. Решение
ЗапросОбласти
Найдено страниц
(в тысячах)
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) & Рубин
Рубин & Динамо & Спартак
1+2
2+3
1+2+3
2
320
280
430
?
Обозначим области,
которые соответствуют
каждому запросу:
Д
Р
1
2
3
С
Ответ: 170
13
14. Задача 3
Некоторый сегмент сети Интернет состоитиз 1000 сайтов. Поисковый сервер
в автоматическом режиме составил таблицу
ключевых слов для сайтов этого сегмента.
Вот ее фрагмент:
Ключевое
слово
сканер
принтер
монитор
Количество сайтов, для которых
данное слово является ключевым
200
250
450
14
15.
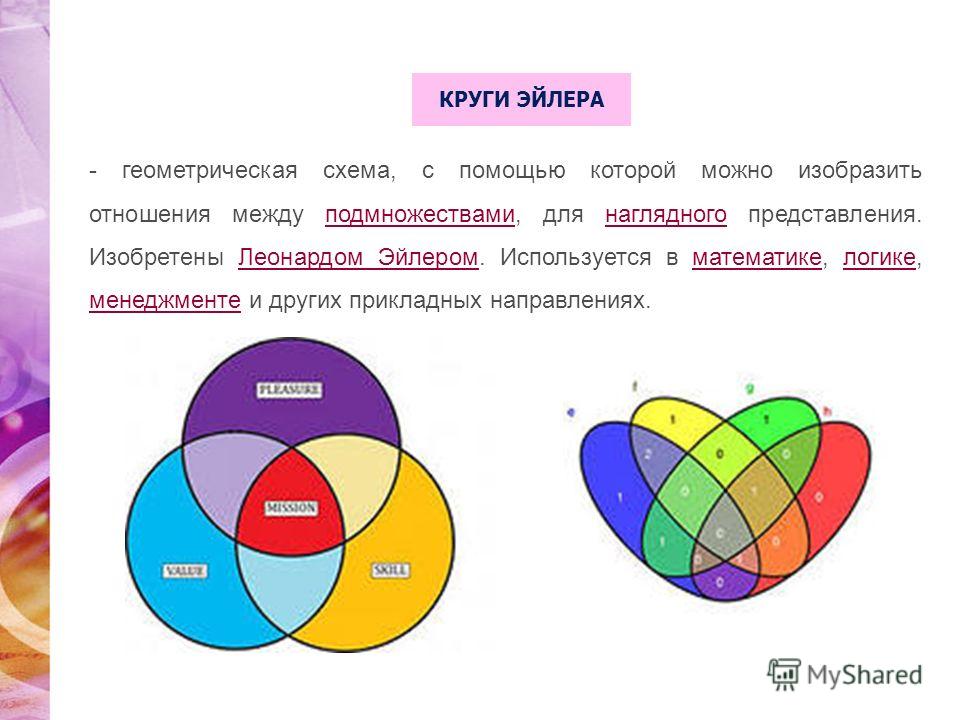 Задача 3Ключевое
Задача 3Ключевоеслово
сканер
принтер
монитор
Количество сайтов, для которых
данное слово является ключевым
200
250
450
Сколько сайтов будет найдено по запросу
(принтер | сканер) & монитор
если было найдено:
по запросу принтер | сканер 450 сайтов,
по запросу принтер & монитор – 40,
по запросу сканер & монитор – 50?
15
16. Решение
Ключевоеслово
сканер
принтер
монитор
Количество сайтов, для которых
данное слово является ключевым
200
250
450
Заметим, что в этом сегменте сети нет
сайтов, на которых ключевыми
словами являются одновременно
принтер и сканер: П & С= 0
(П|С) & М = (П & М) | (С & М) =
= 40 + 50 = 90
Ответ: 90
50
40
16
17. Задача 4
В таблице приведены запросы к поисковомусерверу. Расположите номера запросов в порядке
возрастания количества страниц, которые найдет
поисковый сервер по каждому запросу.

1) принтеры & сканеры & продажа
2) принтеры & сканеры
3) принтеры | сканеры
4) принтеры | сканеры | продажа
11
Ответ: 1234
22
33
44
17
18. Задачи для тренировки
1) В таблице приведены запросы к поисковому серверу, условнообозначенные буквами от А до Г. Расположите запросы в
порядке возрастания количества страниц, которые найдет
поисковый сервер по каждому запросу. Ответ запишите в виде
последовательности соответствующих букв.
А) Гренландия & Климат & Флора & Фауна
Б) Гренландия & Флора
В) (Гренландия & Флора) | Фауна
Г) Гренландия & Флора & Фауна
2) В таблице приведены запросы к поисковому серверу.
Расположите номера запросов в порядке убывания количества
страниц, которые найдет поисковый сервер по каждому
запросу.
1) барокко | (классицизм & ампир)
2) барокко | классицизм
3) (классицизм & ампир) | (барокко & модерн)
18
4) барокко | ампир | классицизм
19.
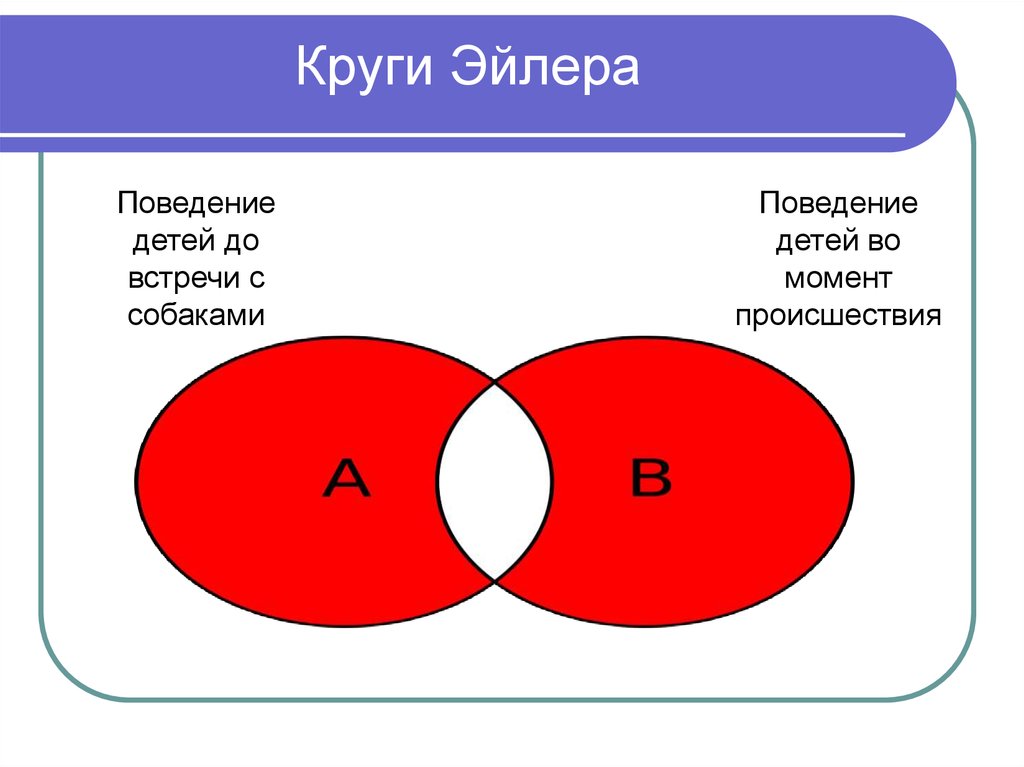 Задачи для тренировки3) Некоторый сегмент сети Интернет состоит
Задачи для тренировки3) Некоторый сегмент сети Интернет состоитиз 1000 сайтов. Поисковый сервер составил таблицу
ключевых слов для сайтов этого сегмента. Вот ее
фрагмент:
Количество сайтов, для которых
Ключевое слово
данное слово является ключевым
сомики
250
меченосцы
200
гуппи
500
Сколько сайтов будет найдено по запросу
сомики | меченосцы | гуппи,
если по запросу сомики & гуппи было найдено 0
сайтов, по запросу сомики & меченосцы – 20,
а по запросу меченосцы & гуппи – 10?
19
20. Задачи для тренировки
4) В таблице приведены запросы и количествостраниц, которые нашел поисковый сервер
по этим запросам в некотором сегменте
Интернета:
Запрос
Количество страниц (тыс.)
Атос & Портос
Атос & Арамис
Атос & Портос & Арамис
335
235
120
Сколько страниц (в тысячах) будет найдено
по запросу Атос & (Портос | Арамис)?
20
Задачи для тренировки
5) В таблице приведены запросы и количество
найденных по ним страниц некоторого
сегмента сети Интернет:
Запрос
Найдено страниц (в тысячах)
март & май
май & апрель
май & (март | апрель)
472
425
620
Сколько страниц (в тысячах) будет найдено
по запросу март & апрель & май?
21
Ответы
1)
2)
3)
4)
5)
АГБВ
4213
920
450
277
Посмотреть решения
Завершить показ
22
Решение
Ответы
1)
АГБВ
А
Б
1
2
В
Г
2)
4213
3
4
3)
920
С | М | Г = 250 + 200 + 500 – 20 – 10 = 920
23
Решение
Ответы
4)
1
3 2
450
Атос & (Портос | Арамис) = 1 + 2 + 3 = ?
1 + 2 = 335
2 + 3 = 235
2 = 120
5)
277
март & апрель & май = 2 = ?
3 + 2 = 472
2 + 4 = 425
3 + 2 + 4 = 620
24
25.
 Источники информации 1. Акимов О.Е., Дискретная математика. Операции
Источники информации 1. Акимов О.Е., Дискретная математика. Операциилогики Буля.
2. Официальный информационный портал ЕГЭ
www.ege.edu.ru
3. Преподавание, наука и жизнь. http://kpolyakov.spb.ru
5. http://ru.wikipedia.org/wiki
25
English Русский Правила
Описанная окружность | Math Wiki
В геометрии описанной окружности или описанной окружности многоугольника — это окружность, проходящая через все вершины многоугольника. Центр этой окружности называется центром описанной окружности .
Многоугольник, имеющий описанную окружность, называется циклическим многоугольником . Все правильные простые многоугольники, все треугольники и все прямоугольники цикличны.
Родственное понятие — это понятие минимального ограничивающего круга, который является наименьшим кругом, который полностью содержит внутри себя многоугольник. Не у каждого многоугольника есть описанная окружность, поскольку не обязательно, чтобы все вершины многоугольника лежали на окружности, но у каждого многоугольника есть уникальная минимальная ограничивающая окружность, которую можно построить с помощью алгоритма линейного времени.
Содержимое
- 1 Окружности треугольников
- 1.1 Диаметр
- 1.2 Радиус
- 1.3 Зона
- 1.4 Периметр
- 2 Описанные окружности четырехугольников
- 3 Окружности многоугольников
- 3.1 Площадь и периметр
- 4 Уравнения описанной окружности
- 5 Координаты центра окружности
- 5.1 Декартовы координаты
- 5.2 Барицентрические координаты как функция длин сторон
- 5.3 Барицентрические координаты из перекрестных и скалярных произведений
- 6 Параметрическое уравнение
- 7 Углы, под которыми окружность встречается со сторонами
- 8 Центры треугольника лежат на описанной окружности треугольника ABC
- 9 Вписанные четырехугольники
- 10 См.
 также
также - 11 Внешние ссылки
- 11.1 Интерактивный
Все треугольники циклические, т. е. каждый треугольник имеет описанную окружность.
Центр описанной окружности треугольника можно найти как пересечение трех серединных перпендикуляров. (А биссектриса — это линия, образующая прямой угол с одной из сторон треугольника и пересекающая эту сторону в ее середине.) Это связано с тем, что центр описанной окружности равноудален от любой пары точек треугольника, а все точки на биссектрисе перпендикуляра равны равноудалены от этих точек треугольника.
В прибрежной навигации описанная окружность треугольника иногда используется как способ определения линии положения с помощью секстанта, когда компас недоступен. Горизонтальный угол между двумя ориентирами определяет описанную окружность, на которой лежит наблюдатель.
Положение центра описанной окружности зависит от типа треугольника:
- Тогда и только тогда, когда треугольник остроугольный (все углы меньше прямого угла), центр описанной окружности лежит внутри треугольника
- Тогда и только тогда, когда он тупой (имеет один угол больше прямого), центр описанной окружности лежит вне
- Тогда и только тогда, когда это прямоугольный треугольник, центр описанной окружности лежит на одной из его сторон (а именно, на гипотенузе).
 Это одна из форм теоремы Фалеса.
Это одна из форм теоремы Фалеса.
Диаметр
Диаметр описанной окружности можно вычислить как длину любой стороны треугольника, деленную на синус противоположного угла. (По закону синусов не имеет значения, какую сторону взять: результат будет тот же.) Девятиконечная окружность треугольника имеет половину диаметра описанной окружности. Диаметр описанной окружности треугольника равен
где длины сторон треугольника и полупериметр. Радикал во втором знаменателе выше — это площадь треугольника по формуле Герона.
В любом треугольнике центр описанной окружности всегда лежит на одной прямой с центром тяжести и ортоцентром. Прямая, проходящая через их все, называется прямой Эйлера.
Изогональное сопряжение центра описанной окружности является ортоцентром.
Полезная минимальная ограничивающая окружность из трех точек определяется либо описанной окружностью (где три точки находятся на минимальной ограничивающей окружности), либо двумя точками самой длинной стороны треугольника (где две точки определяют диаметр окружности) .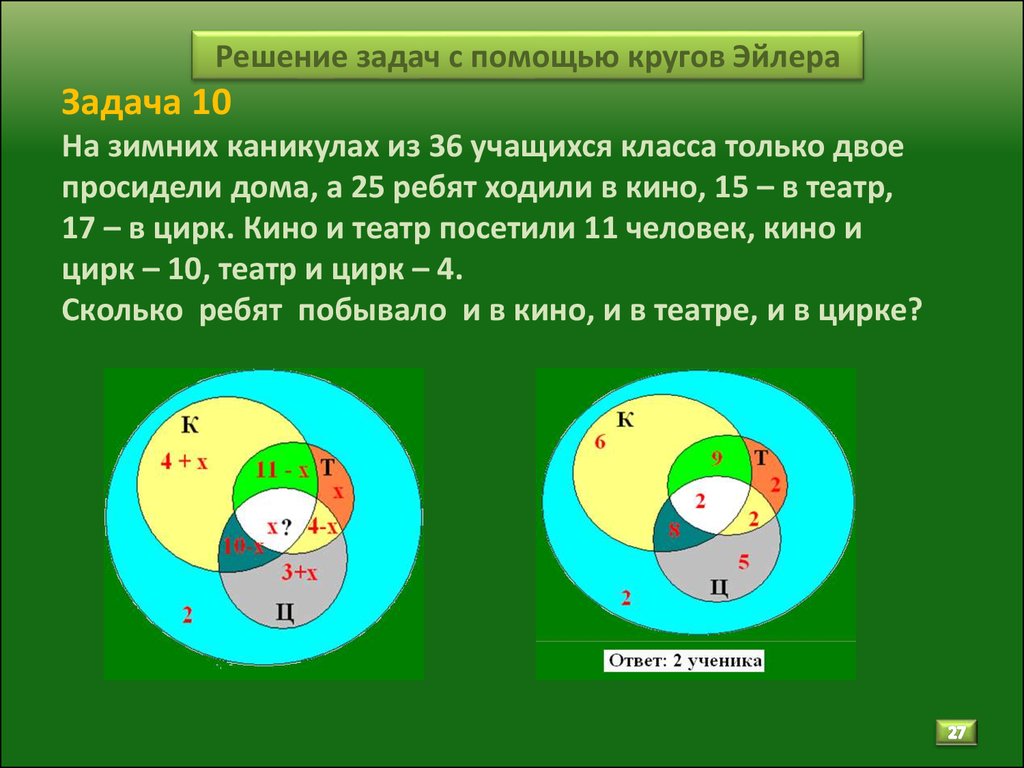
Радиус
Окружность, описанная тремя коллинеарными точками, — это линия, на которой лежат эти 3 точки, часто называемая окружностью бесконечного радиуса . Почти коллинеарные точки часто приводят к численной нестабильности при вычислении описанной окружности.
Окружности треугольников тесно связаны с триангуляцией Делоне множества точек.
Радиус:
Для прямоугольного треугольника:
Зона
Район:
Периметр
Периметр:
Радиус
Для прямоугольника
Для любого четырехугольника
Окружности многоугольников
Радиус описанной окружности правильного n-стороннего многоугольника равен:
Для диаметра:
Площадь и периметр
Периметр окружности:
Уравнения окружности
Следующее содержимое либо скопировано в Википедию, либо скопировано из нее. Тот или иной источник должен цитировать исходное содержание.
Тот или иной источник должен цитировать исходное содержание.
На евклидовой плоскости можно явно дать уравнение описанной окружности через декартовы координаты вершин вписанного треугольника. Итак, предположим, что
— координаты точек. Тогда описанная окружность является геометрическим местом точек на декартовой плоскости, удовлетворяющих уравнениям
, гарантируя, что все точки находятся на одинаковом расстоянии от общего центра окружности. Используя поляризационное тождество, эти уравнения сводятся к условию, что матрица
имеют ненулевое ядро. Таким образом, описанную окружность можно альтернативно описать как геометрическое место нулей определителя этой матрицы:
Расширение по кофактору, пусть
тогда мы имеем и, предполагая, что три точки не лежат на одной линии (иначе описанная окружность — это та линия, которую также можно рассматривать как обобщенную окружность с S в бесконечности), , что дает центр описанной окружности и радиус описанной окружности . Аналогичный подход позволяет вывести уравнение описанной сферы тетраэдра.
Аналогичный подход позволяет вывести уравнение описанной сферы тетраэдра.
Уравнение описанной окружности в трилинейных координатах:
Уравнение описанной окружности в барицентрических координатах:
Изогональное сопряжение описанной окружности — это линия на бесконечности, заданная в трилинейных координатах как и в барицентрических координатах как .
Координаты центра окружности
Декартовы координаты
Декартовы координаты центра окружности
с
Без ограничения общности это можно выразить в упрощенном виде после переноса вершины А в начало декартовой системы координат, т. е. при . В этом случае координаты вершин и представляют собой векторы из вершины А’ в эти вершины. Обратите внимание, что этот тривиальный перенос возможен для всех треугольников, а координаты центра описанной окружности треугольника следуют как
с
Barycentric coordinates as a function of the side lengths
The circumcenter has trilinear coordinates (cos( α ), cos( β ), cos( γ )) where α , β , γ — углы треугольника.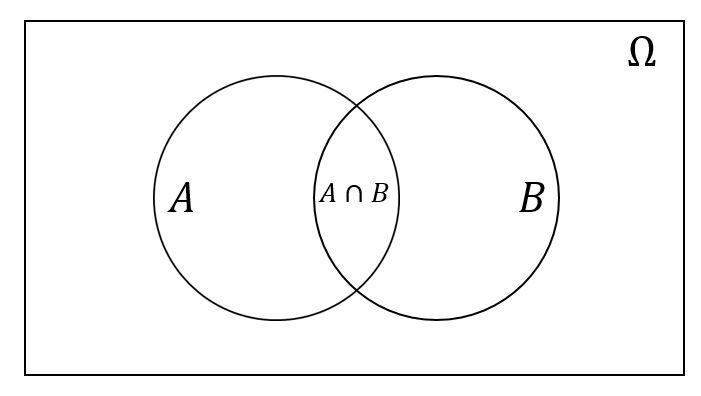 Центр окружности имеет барицентрические координаты
Центр окружности имеет барицентрические координаты
где a , b , c длины ребер ( BC , CA , AB соответственно) треугольника.
Барицентрические координаты из перекрестных и скалярных произведений
В евклидовом пространстве существует единственная окружность, проходящая через любые заданные три неколлинеарные точки P 1 , P 2 , и
3 3 . Используя декартовы координаты для представления этих точек в виде пространственных векторов, можно использовать скалярное произведение и векторное произведение для вычисления радиуса и центра круга. Позволять
Тогда радиус окружности равен
Центр окружности задается линейной комбинацией
где
Параметрическое уравнение
Отсюда, учитывая радиус, r , центр, P c , точка на окружности, P 0 и единичная нормаль плоскости, содержащей окружность, , одно параметрическое уравнение окружности, начинающееся с точки P 0 и действуя в положительно ориентированном (т.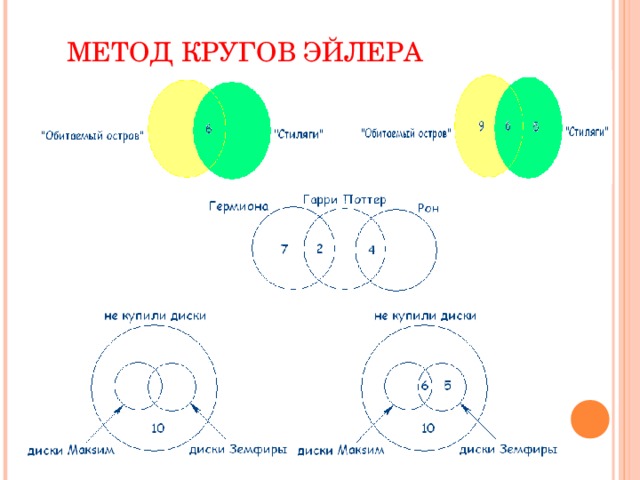 е. правостороннем) смысле примерно следующее:
е. правостороннем) смысле примерно следующее:
Углы, под которыми окружность встречается со сторонами
Углы, под которыми описанная окружность встречается со сторонами треугольника, совпадают с углами, под которыми стороны пересекаются. Сторона, противоположная углу α, встречается с окружностью дважды: по одному разу с каждого конца; в каждом случае под углом α (аналогично для двух других углов). Теорема альтернативного сегмента утверждает, что угол между касательной и хордой равен углу альтернативного сегмента.
Центры треугольника лежат на описанной окружности треугольника ABC
В этом разделе углы при вершинах обозначены A , B , C , а все координаты являются трехлинейными координатами:
- Точка Штейнера = = невершинная точка пересечения описанной окружности с эллипсом Штейнера. (Эллипс Штейнера с центром = центроид ( ABC ) является эллипсом наименьшей площади, который проходит через A , B и C .
 Уравнение для этого эллипса: 1/( x ) + 1/( x ) + 1/( cz ) = 0.)
Уравнение для этого эллипса: 1/( x ) + 1/( x ) + 1/( cz ) = 0.)
- Точка дегтя = sec( A + ω) : sec ( B + ω) : sec( C + ω) = антипод точки Штейнера
- Фокус параболы Киперта = csc( B — C ) — 9 : csc( 4 ) — 9 : csc( 4 ) A ) : csc( A − B )
Вписанные четырехугольники
Четырехугольники, которые можно описать, обладают особыми свойствами, включая тот факт, что противоположные углы являются дополнительными углами (в сумме они составляют или радианы).
См. также
- Вписанный круг
- Теорема Юнга, неравенство, связывающее диаметр точки множества с радиусом ее минимальной ограничивающей окружности
- Теорема Лестера
- Описанная сфера
Внешние ссылки
- Описанная окружность с известными координатами вершин треугольника в Атласе геометрии.
- Центры треугольников Антонио Гутьерреса из книги «Геометрия шаг за шагом из страны инков».

Интерактивный
- Треугольник с описанной окружностью и центром описанной окружности С интерактивной анимацией
- Интерактивный Java-апплет для центра окружности
Pi | Определение, символ, номер и факты
- Ключевые люди:
- Архимед аль-Каши Адриан-Мари Лежандр Иоганн Генрих Ламберт Чжао Юцинь
- Связанные темы:
- теорема Пи круг трансцендентное число
Просмотреть весь связанный контент →
Популярные вопросы
Что такое число пи?
Пи — отношение длины окружности к ее диаметру.
Чему равно число пи?
Значение числа пи приблизительно равно 3,14 или 22/7. До 39 знаков после запятой число пи равно 3,141592653589793238462643383279502884197. Пи — иррациональное число, то есть оно не равно отношению любых двух целых чисел. Его цифры не повторяются.
Как обозначается число Пи?
Символ числа пи — π. Он был разработан британским математиком Уильямом Джонсом в 1706 году для представления отношения и позже популяризирован швейцарским математиком Леонардом Эйлером.
Он был разработан британским математиком Уильямом Джонсом в 1706 году для представления отношения и позже популяризирован швейцарским математиком Леонардом Эйлером.
Для чего используется число Пи?
Пи используется для решения задач, связанных с длинами дуг или других кривых, площадями эллипсов, секторов и других искривленных поверхностей, а также объемами многих твердых тел. Он также используется в различных формулах физики и техники для описания движения маятников, вибрации струн и переменных электрических токов.
пи , в математике отношение длины окружности к её диаметру. Символ π был изобретен британским математиком Уильямом Джонсом в 1706 году для обозначения отношения, а позже популяризирован швейцарским математиком Леонардом Эйлером. Поскольку число пи иррационально (не равно отношению любых двух целых чисел), его цифры не повторяются, и для повседневных вычислений часто используется такое приближение, как 3,14 или 22/7. До 39 знаков после запятой число пи равно 3,141592653589793238462643383279.502884197.
До 39 знаков после запятой число пи равно 3,141592653589793238462643383279.502884197.
Вавилоняне (ок. 2000 г. до н.э.) использовали 3,125 для приближения числа пи, значение, которое они получили, вычислив периметр шестиугольника, вписанного в круг, и предположив, что отношение периметра шестиугольника к длине окружности равно 24/25. . Папирус Райнда (ок. 1650 г. до н. э.) указывает, что древние египтяне использовали значение 256/81 или около 3,16045. Архимед (ок. 250 г. до н. э.) сделал большой шаг вперед, разработав метод получения числа пи с любой желаемой точностью при наличии достаточного терпения. Вписывая и описывая правильные многоугольники вокруг окружности, чтобы получить верхнюю и нижнюю границы, он получил 223/71 < π < 22/7, или среднее значение около 3,1418. Архимед также доказал, что отношение площади круга к квадрату его радиуса является той же константой.
Викторина «Британника»
Числа и математика
В последующие столетия китайские, индийские и арабские математики увеличили число десятичных разрядов, известных в результате утомительных вычислений, а не усовершенствований метода Архимеда. Однако к концу 17 века новые методы математического анализа в Европе предоставили улучшенные способы вычисления числа пи с использованием бесконечных рядов. Например, Исаак Ньютон использовал свою биномиальную теорему для быстрого вычисления 16 знаков после запятой. В начале 20 века индийский математик Сриниваса Рамануджан разработал исключительно эффективные способы вычисления числа Пи, которые позже были включены в компьютерные алгоритмы. В начале 21 века компьютеры вычислили число пи до 62 831 853 071,79.6 знаков после запятой, а также его двухквадриллионная цифра при выражении в двоичном виде (0).
Однако к концу 17 века новые методы математического анализа в Европе предоставили улучшенные способы вычисления числа пи с использованием бесконечных рядов. Например, Исаак Ньютон использовал свою биномиальную теорему для быстрого вычисления 16 знаков после запятой. В начале 20 века индийский математик Сриниваса Рамануджан разработал исключительно эффективные способы вычисления числа Пи, которые позже были включены в компьютерные алгоритмы. В начале 21 века компьютеры вычислили число пи до 62 831 853 071,79.6 знаков после запятой, а также его двухквадриллионная цифра при выражении в двоичном виде (0).
Пи встречается в различных математических задачах, касающихся длины дуг или других кривых, площадей эллипсов, секторов и других изогнутых поверхностей, а также объемов многих твердых тел. Он также используется в различных формулах физики и техники для описания таких периодических явлений, как движение маятников, вибрация струн и переменные электрические токи.
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена Эриком Грегерсеном.

 также
также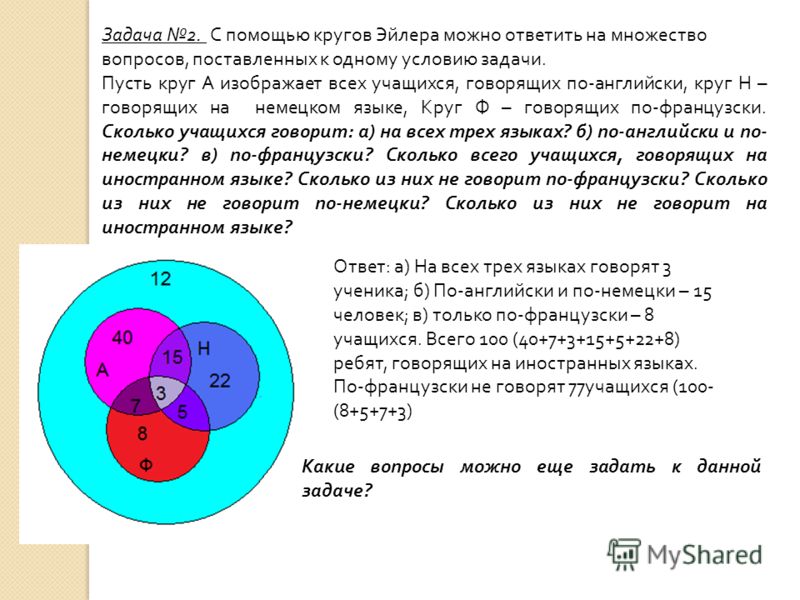 Это одна из форм теоремы Фалеса.
Это одна из форм теоремы Фалеса. Уравнение для этого эллипса: 1/( x ) + 1/( x ) + 1/( cz ) = 0.)
Уравнение для этого эллипса: 1/( x ) + 1/( x ) + 1/( cz ) = 0.)