Решение кубических уравнений: примеры, метод Виета-Кардано
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Решение двучленного кубического уравнения вида Ax3+B=0
Кубическое уравнение, содержащее двучлен, имеет вид Ax3+B=0 . Его необходимо приводить к x3+BA=0 с помощью деления на А, отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x3+BA=0x+BA3x2-BA3x+BA23=0
Результат первой скобки примет вид x=-BA3, а квадратный трехчлен — x2-BA3x+BA23, причем только с комплексными корнями.
Пример 1Найти корни кубического уравнения 2×3-3=0.
Решение
Необходимо найти х из уравнения. Запишем:
2×3-3=0x3-32=0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
Тогда получим, что
x3-32=0x-3326×2+3326x+923=0
Раскроем первую скобку и получим x=3326. Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x=3326.
Решение возвратного кубического уравнения вида Ax3+Bx2+Bx+A=0
Вид квадратного уравнения — Ax3+Bx2+Bx+A=0, где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
Ax3+Bx2+Bx+A=Ax3+1+Bx2+x==Ax+1×2-x+1+Bxx+1=x+1Ax2+xB-A+A
Корень уравнения равен х=-1, тогда для получения корней квадратного трехчлена Ax2+xB-A+A необходимо задействовать через нахождение дискриминанта.
Пример 2Решить уравнение вида 5×3-8×2-8x+5=0.
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5×3-8×2-8x+5=5×3+1-8×2+x==5x+1×2-x+1-8xx+1=x+15×2-5x+5-8x==x+15×2-13x+5=0
Если х=-1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5×2-13x+5:
5×2-13x+5=0D=(-13)2-4·5·5=69×1=13+692·5=1310+6910×2=13-692·5=1310-6910
Ответ:
x1=1310+6910×2=1310-6910×3=-1
Решение кубических уравнений с рациональными корнями
Если х=0, то он является корнем уравнения вида Ax3+Bx2+Cx+D=0.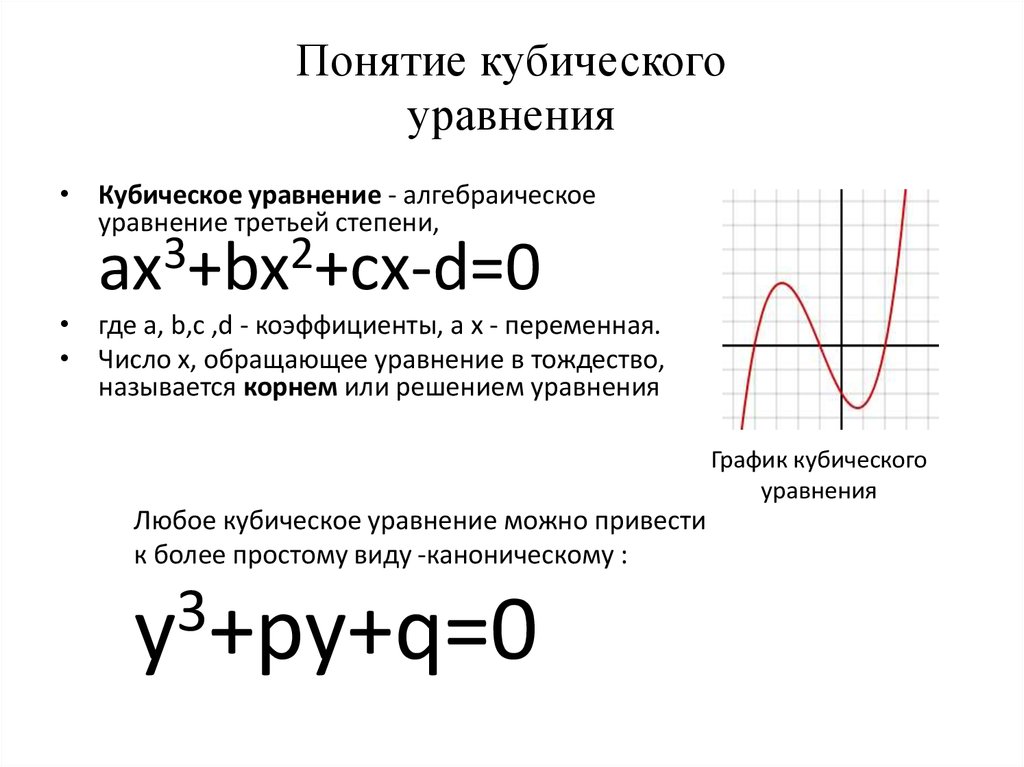 При свободном члене D=0 уравнение принимает вид Ax3+Bx2+Cx=0. При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид xAx2+Bx+C=0.
При свободном члене D=0 уравнение принимает вид Ax3+Bx2+Cx=0. При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид xAx2+Bx+C=0.
Найти корни заданного уравнения 3×3+4×2+2x=0.
Решение
Упростим выражение.
3×3+4×2+2x=0x3x2+4x+2=0
Х=0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3×2+4x+2. Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D=42-4·3·2=-8. Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х=0.
Когда коэффициенты уравнения Ax3+Bx2+Cx+D=0 целые, то в ответе можно получить иррациональные корни. Если A≠1, тогда при умножении на A2 обеих частей уравнения проводится замена переменных, то есть у=Ах:
Ax3+Bx2+Cx+D=0A3·x3+B·A2·x2+C·A·A·x+D·A2=0y=A·x⇒y3+B·y2+C·A·y+D·A2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными.
Найти корни заданного уравнения 2×3-11×2+12x+9=0.
Решение
Необходимо произвести преобразование с помощью умножения на 22 обеих частей, причем с заменой переменной типа у=2х. Получаем, что
2×3-11×2+12x+9=023×3-11·22×2+24·2x+36=0y=2x⇒y3-11y2+24y+36=0
Свободный член равняется 36, тогда необходимо зафиксировать все его делители:
±1,±2,±3,±4,±6,±9,±12,±36
Необходимо произвести подстановку y3-11y2+24y+36=0, чтобы получить тождество вида
13-11·12+24·1+36=50≠0(-1)3-11·(-1)2+24·(-1)+36=0
Отсюда видим, что у=-1 – это корень. Значит, x=y2=-12.
Далее следует деление 2×3-11×2+12x+9 на x+12 при помощи схемы Горнера:
| xi | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | -11 | 12 | 9 | |
-0. 5 5 | 2 | -11+2·(-0.5)=-12 | 12-12·(-0.5)=18 | 9+18·(-0.5)=0 |
Имеем, что
2×3-11×2+12x+9=x+122×2-12x+18==2x+12×2-6x+9
После чего необходимо найти корни квадратного уравнения вида x2-6x+9. Имеем, что уравнение следует привести к виду x2-6x+9=x-32, где х=3 будет его корнем.
Ответ: x1=-12, x2,3=3.
ЗамечаниеАлгоритм можно применять для возвратных уравнений. Видно, что -1 – это его корень, значит, левая часть может быть поделена на х+1. Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A0x3+A1x2+A2x+A3=0 необходимо найти B1=A1A0, B2=A2A0, B3=A3A0.
После чего p=-B123+B2 и q=2B1327-B1B23+B3.
Полученные p и q в формулу Кардано. Получим, что
y=-q2+q24+p3273+-q2-q24+p3273
Подбор кубических корней должен удовлетворять на выходе значению -p3. Тогда корни исходного уравнения x=y-B13. Рассмотрим решение предыдущего примера, используя формулу Кардано.
Тогда корни исходного уравнения x=y-B13. Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2×3-11×2+12x+9=0.
Решение
Видно, что A0=2, A1=-11, A2=12, A3=9.
Необходимо найти B1=A1A0=-112, B2=A2A0=122=6, B3=A3A0=92.
Отсюда следует, что
p=-B123+B2=—11223+6=-12112+6=-4912q=2B1327-B1B23+B3=2·-112327—112·63+92=343108
Производим подстановку в формулу Кордано и получим
y=-q2+q24+p3273+-q2—q24+p3273==-343216+34324·1082-49327·1233+-343216-34324·1082-49327·1233==-3432163+-3432163
-3432163 имеет три значения. Рассмотрим их ниже.
-3432163=76cosπ+2π·k3+i·sinπ+2π·k3, k=0, 1, 2
Если k=0, тогда -3432163=76cosπ3+i·sinπ3=7612+i·32
Если k=1, тогда -3432163=76cosπ+i·sinπ=-76
Если k=2, тогда -3432163=76cos5π3+i·sin5π3=7612-i·32
Необходимо произвести разбиение по парам, тогда получим -p3=4936.
Тогда получим пары: 7612+i·32 и 7612-i·32, -76 и -76, 7612-i·32 и 7612+i·32.
Преобразуем при помощи формулы Кордано:
y1=-3432163+-3432163==7612+i·32+7612-i·32=7614+34=76y2=-3432163+-3432163=-76+-76=-146y3=-3432163+-3432163==7612-i·32+7612+i·32=7614+34=76
Значит,
x1=y1-B13=76+116=3×2=y2-B13=-146+116=-12×3=y3-B13=76+116=3
Ответ: x1=-12, x2,3=3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения. Поделиться:
| ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | ||||||
Формула кубического уравнения — Узнайте формулу кубического уравнения
Формула кубического уравнения используется для представления кубического уравнения. Многочлен третьей степени известен как кубический многочлен, или мы можем назвать его кубическим уравнением. Кубические уравнения имеют по крайней мере один действительный корень, и они могут иметь до 3 действительных корней. Корни кубического уравнения также могут быть мнимыми, но по крайней мере 1 должен быть действительным. Формула кубического уравнения вместе с несколькими решенными примерами объясняется ниже. Давайте исследуем их.
Что такое формула кубического уравнения?
Формулу кубического уравнения также можно использовать для получения кривой кубического уравнения. Представление кубического уравнения с помощью формулы кубического уравнения очень полезно для нахождения корней кубического уравнения. Многочлен степени n будет иметь n нулей или корней. Кубическое уравнение имеет следующий вид:
Кубическое уравнение имеет следующий вид:
ax 3 +bx 2 +cx+d=0
Кубическое уравнение можно решить двумя способами
i) Пробная версия — Ошибка и синтетическое разделение
ii) Факторизация.
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Закажите бесплатный пробный урок
Давайте посмотрим на применение формулы кубического уравнения в следующих решенных примерах.
Примеры использования формулы кубического уравнения
Пример 1: Выберите кубические многочлены из следующих:
- p(x): 5x 2 + 6x + 1
- р(х): 2х + 3
- q(z): z 2 − 1
- г(г): г 2 + (√2) 9
- г(г): √5z 2
- с(х): 10х
- р(у): у 3 − 6 лет 2 + 11 лет − 6
- q(y): 81 год 3 − 1
- г(г): г + 3
Решение: Кубические многочлены среди приведенных выше многочленов:
| Кубические многочлены |
р(у): у 3 − 6 лет 2 + 11 лет − 6 q(y): 81 год 3 − 1 г(г): г 2 + (√2) 9 |
Пример 2. Найдите корни следующего кубического уравнения 2x 3 + 3x 2 – 11x – 6 = 0
Найдите корни следующего кубического уравнения 2x 3 + 3x 2 – 11x – 6 = 0
Решение:
Найти: Корни данного уравнения.
Это уравнение не может быть решено с помощью метода факторизации, мы будем использовать метод проб и ошибок, чтобы найти один корень.
Обычно мы начинаем со значения «1».
f (1) = 2 + 3 – 11 – 6 ≠ 0
f (–1) = –2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0
Значение «2» делает L.H.S равным «0». Следовательно, два — это один из трех корней.
Теперь мы воспользуемся методом синтетического деления, чтобы найти два других корня.
Мы разделим наше уравнение на (x-2) и частное даст нам два других корня. Мы разделим наше уравнение на (x-2), и частное даст нам два других корня.
Частное: (2x 2 + 7x + 3)
Факторизация этого частного,
(2x+1) (x+3)
Отсюда мы получаем значения x as,
x = -1/2 и x = -3
Ответ: Итак, три корня кубического уравнения: x = 2, x = -1/2 и x = -3
Пример 3: Используя формулу кубического уравнения, решите кубическое уравнение x 3 – 2x 2 – x + 2.
Решение:
Сначала мы проверим, можем ли мы разложить кубическое уравнение на множители или нет, если его нельзя разложить на множители, мы должны использовать метод синтетического деления. Но в этом случае, посмотрев, мы можем сказать, что это уравнение можно решить с помощью факторизации. Посмотрим, как.
х 3 – 2х 2 – х + 2.
= х 2 (х – 2) – (х – 2)
= (х 2 – 1) (х – 2)
= (х + 1) (х – 1) (х – 2)
Мы можем сделать вывод, что
x = -1, x = 1 и x = 2.
Ответ: Итак, три корня кубического уравнения: x = -1, x = 1 и x = 2.
Часто задаваемые вопросы по формуле кубического уравнения
Что такое формула кубического уравнения?
Формулу кубического уравнения также можно использовать для получения кривой кубического уравнения. Представление кубического уравнения с помощью формулы кубического уравнения очень полезно для нахождения корней кубического уравнения. Многочлен степени n будет иметь n нулей или корней. Кубическое уравнение имеет следующий вид: ax 3 +bx 2 +cx+d=0
Многочлен степени n будет иметь n нулей или корней. Кубическое уравнение имеет следующий вид: ax 3 +bx 2 +cx+d=0
Как решать кубические полиномы, используя формулу кубического полинома?
Наиболее часто используемая стратегия решения кубического уравнения:
- Шаг 1. Приведение кубического многочлена к квадратному уравнению.
- Шаг 2: Решите квадратное уравнение, используя квадратную формулу.
Что такое уравнение для формулы кубических многочленов?
Кубическое уравнение — это алгебраическое уравнение третьей степени, имеющее вид ось 3 + bx 2 + cx + d = 0, где a, b и c — коэффициенты, а d — константа.
Рабочие листы по математике и визуальный учебный план
Объяснение урока: Решение кубических уравнений: Извлечение кубических корней
В этом пояснении мы научимся решать кубические уравнения, используя свойство кубического корня.
Начнем с того, что вспомним, что кубический корень числа 𝑎, записанный √𝑎, — это число, куб которого равен 𝑎. Другими словами, √𝑎=𝑎. Мы можем использовать это для упрощения или вычисления выражений. Например, мы знаем, что
2=8; следовательно, мы можем оценить √8=2.
Другими словами, √𝑎=𝑎. Мы можем использовать это для упрощения или вычисления выражений. Например, мы знаем, что
2=8; следовательно, мы можем оценить √8=2.
Это не единственное использование кубического корня. Мы также можем использовать эту идею для решения уравнений. Например, представьте, что нам сказали, что объем куба 8 см 3 . Тогда мы можем сказать, что у куба длины сторон 𝑥 см, чтобы получилось следующее.
Объем этого куба равен 𝑥, поэтому мы можем составить следующее уравнение: 𝑥=8.
Мы знаем, что 2=8; однако мы также можем решить это уравнение, взяв кубические корни из обеих частей уравнения. Это дает √𝑥=√8.
Мы знаем, что √𝑥=𝑥 и √8=2; следовательно, 𝑥=2.
Стоит отметить, что мы знаем, что это единственное значение 𝑥, которое решает это уравнение, так как увеличение длины стороны увеличит объем
а уменьшение длины стороны уменьшит объем. В целом это верно: увеличение значения 𝑥 увеличит значение
𝑥, а уменьшение значения 𝑥 приведет к уменьшению значения 𝑥. Следовательно, 𝑥=𝑎
будет иметь только одно решение для любого действительного значения 𝑎.
Следовательно, 𝑥=𝑎
будет иметь только одно решение для любого действительного значения 𝑎.
Это не относится к квадратному корню, так как 2=4, но и (−2)=4. Это причина того, что мы находим положительный и отрицательный корень при извлечении квадратных корней из обеих частей уравнения, но есть единственное решение при извлечении кубических корней.
Давайте теперь рассмотрим пример решения некоторых кубических уравнений.
Пример 1. Решение кубического уравнения перестановкой
Решите кубическое уравнение 𝑥=8 в ℚ.
Ответ
Возьмем кубический корень из обеих частей уравнения, чтобы увидеть 𝑥=√8.
Затем мы вспоминаем, что 2=8, поэтому √8=2. Следовательно, 𝑥=√8=2.
В нашем следующем примере мы увидим, как решить кубическое уравнение, где переменная в кубе равна рациональному числу.
Пример 2. Решение кубического уравнения с дробью
Решите 𝑥=278.
Ответ
Начнем с извлечения кубических корней из обеих частей уравнения, где заметим, что √𝑥=𝑥.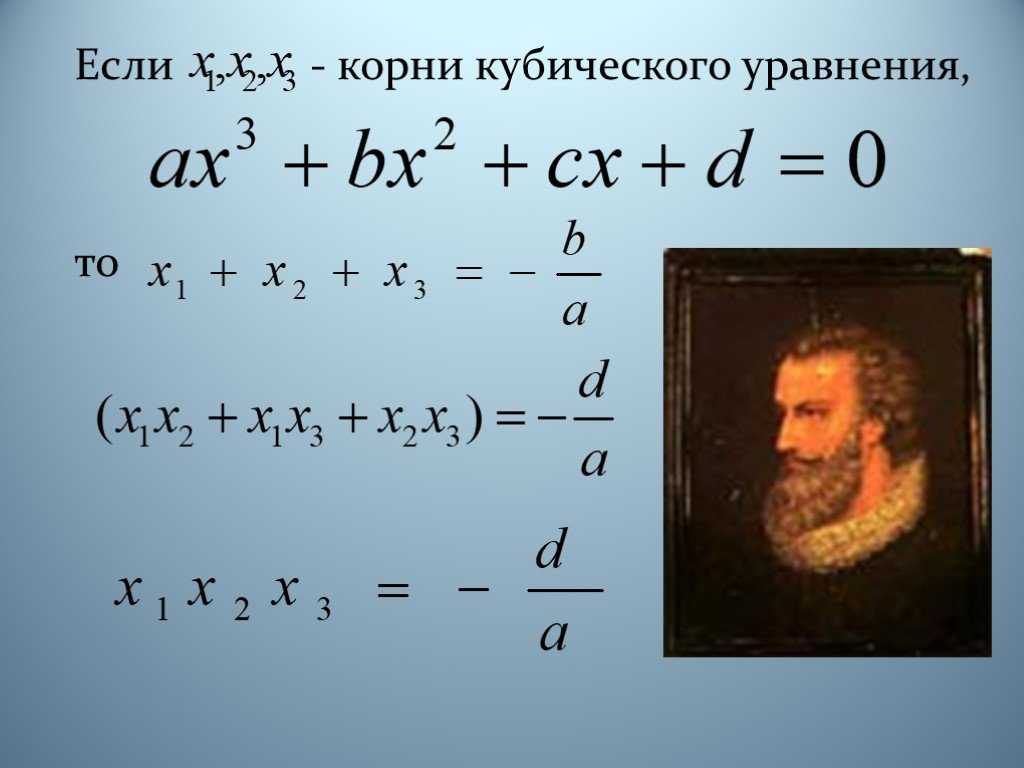 Это дает
𝑥=278.
Это дает
𝑥=278.
Затем мы вспоминаем, что если 𝑎 и 𝑏 — совершенные кубы и 𝑏≠0, то 𝑎𝑏=√𝑎√𝑏. Заметим, что √27=3 и √8=2, поэтому оба являются совершенными кубами и, следовательно, 𝑥=278=√27√8=32.
Следовательно, 𝑥=32.
В нашем следующем примере мы будем решать кубическое уравнение с помощью первой перестановки.
Пример 3. Решение кубического уравнения перестановкой
Найдите значение 𝑦 при условии, что −1000𝑦−27=0.
Ответ
Поскольку переменная в этом уравнении возведена в куб, нам нужно будет извлечь кубические корни из обеих частей уравнения. Однако для того, чтобы сделать это, сначала нам нужно изменить уравнение так, чтобы кубический фактор был изолирован на одной стороне уравнения.
Сначала мы добавляем 27 к обеим частям уравнения, чтобы получить −1000𝑦=27.
Затем разделим обе части уравнения на −1000; это дает 𝑦=−271000.
Теперь мы можем взять кубические корни из обеих частей уравнения, чтобы получить
𝑦=−271000.
Тогда вспомним, что если 𝑎=𝑛, 𝑏=𝑚 и 𝑏≠0, то 𝑛𝑚=√𝑛√𝑚=𝑎𝑏. Заметим, что √−27=−3 и √1000=10; следовательно, 𝑦=−271000=√−27√1000=−310.
В нашем следующем примере мы решим другое уравнение путем перестановки.
Пример 4. Преобразование уравнения в кубическое уравнение и его решение
Учитывая, что 𝑥∈ℝ и −𝑥10=100𝑥, определите значение 𝑥.
Ответ
Чтобы решить уравнение этой формы, мы должны отметить, что умножение уравнения на 𝑥 соберет все переменные в единый термин. Чтобы оправдать умножение уравнения на 𝑥, отметим, что мы делим на 𝑥 в исходном уравнении, поэтому 𝑥 не может быть нулем. Следовательно, −𝑥10×𝑥=100𝑥×𝑥.
Мы сократим общий множитель 𝑥 в правой части уравнения, поскольку 𝑥≠0, и упростим; это дает −𝑥10=100.
Затем мы умножаем уравнение на −10, чтобы получить 𝑥=−1000.
Наконец, мы берем кубические корни из обеих частей уравнения, где мы отмечаем, что (−10)=−1000, поэтому √−1000=−10. Это дает
𝑥=√−1000=−10.
Это дает
𝑥=√−1000=−10.
До сих пор мы имели дело только с простыми уравнениями, включающими кубы. Однако операции могут выполняться внутри кубической операции. Например, представьте, нам говорят, что отцу 65 лет и он на год старше, чем в два раза больше возраста его сына в кубе. Мы можем использовать кубический корень определить возраст сына.
Во-первых, нам нужно преобразовать эту информацию в уравнение. Для этого будем работать в обратном направлении. Назовем возраст сына 𝑥. Нам говорят, что отцу 65 лет и он на год старше, чем в два раза больше возраста его сына в кубе. Итак, нам нужно кубик дважды 𝑥 и затем прибавляем 1; тогда это равно 65. Мы имеем (2𝑥)+1=65.
Мы можем вычесть 1 из обеих частей, чтобы получить (2𝑥)=64.
Затем мы можем взять кубические корни из обеих частей уравнения; это дает 2𝑥=√64=4.
Затем мы делим уравнение на 2, чтобы получить 𝑥=2.
Итак, возраст сына 2 года.
В общем случае мы можем решать уравнения вида (𝑎𝑥+𝑏)+𝑐=𝑑, если 𝑎≠0, и мы можем найти кубический корень из 𝑑−𝑐. Для этого нам нужно изменить уравнение, чтобы найти 𝑥. Мы можем сделать это, используя следующий метод.
Как: Решение кубического уравнения
Чтобы решить кубическое уравнение вида (𝑎𝑥+𝑏)+𝑐=𝑑, где 𝑎, 𝑏, 𝑐 и 𝑑 константы и 𝑎≠0, нам нужно изменить уравнение для 𝑥. Мы можем сделать это, выполнив следующие шаги:
- Вычтите 𝑐 из обеих частей уравнения, чтобы получить (𝑎𝑥+𝑏)=𝑑−𝑐.
- Извлеките кубический корень из обеих частей уравнения, чтобы получить 𝑎𝑥+𝑏=√𝑑−𝑐.
- Вычтите 𝑏 с обеих сторон, чтобы получить 𝑎𝑥=√𝑑−𝑐−𝑏.
- Разделите уравнение на 𝑎, чтобы получить 𝑥=√𝑑−𝑐−𝑏𝑎.
Давайте теперь рассмотрим несколько примеров применения этого метода для решения кубических уравнений.
Пример 5. Решение кубического уравнения перестановкой после извлечения кубического корня
Найдите значение 𝑦 при условии, что (2𝑦−14)−36=28.
Ответ
Сначала заметим, что в этом уравнении есть кубический член, который включает переменную. Это означает, что мы будем брать кубические корни из обеих частей уравнения. решить для 𝑦. Однако мы не можем сделать это непосредственно с уравнением, поскольку член в кубе не изолирован с одной стороны уравнения. Поэтому мы начинаем с добавления 36 к обеим частям уравнения, чтобы получить (2𝑦−14)=28+36=64.
Теперь мы можем взять кубические корни из обеих частей уравнения, чтобы получить (2𝑦−14)=√64.
Мы знаем, что √𝑎=𝑎, поэтому (2𝑦−14)=2𝑦−14 и что 64=4, поэтому √64=4.
Следовательно, уравнение упрощается и дает 2𝑦−14=4.
Теперь мы можем найти 𝑦. Мы добавляем 14 к обеим частям уравнения, что дает 2𝑦=4+14=18.
Затем мы делим уравнение на 2, чтобы получить 𝑦=182=9.
В нашем последнем примере мы будем решать кубическое уравнение, включающее перестановку уравнения, в котором коэффициент переменной отрицательный.
Пример 6. Решение кубического уравнения перестановкой после извлечения кубического корня
Найдите значение 𝑥 при условии, что (15−3𝑥)+2=29, где 𝑥∈ℝ.
Ответ
Сначала нам нужно изменить уравнение так, чтобы кубический член был изолирован в левой части уравнения. Мы можем сделать это, вычитая 2 с обеих сторон уравнения; это дает (15−3𝑥)=29−2=27.
Затем мы можем взять кубические корни из обеих частей уравнения, где заметим (15−3𝑥)=15−3𝑥 и √27=3. Следовательно, 15−3𝑥=3.
Теперь мы можем найти 𝑥. Вычтем 15 из обеих частей уравнения, чтобы получить −3𝑥=−12.
Затем мы делим на −3, чтобы получить 𝑥=4.
Давайте закончим повторением некоторых важных моментов из этого объяснения.
Ключевые моменты
- Мы можем решать уравнения, извлекая кубические корни из обеих частей уравнения. В частности, если 𝑥=𝑎, то 𝑥=√𝑎.
- В отличие от квадратного корня, извлечение кубических корней из обеих частей уравнения дает единственное решение.


 Математический, Физический алфавит, Научный алфавит.
Математический, Физический алфавит, Научный алфавит. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
 (Для продвинутых — три различных вещественных корня)
(Для продвинутых — три различных вещественных корня)
 Корни уравнения (2) выражаются следующим образом:
Корни уравнения (2) выражаются следующим образом: При этом имеем
При этом имеем
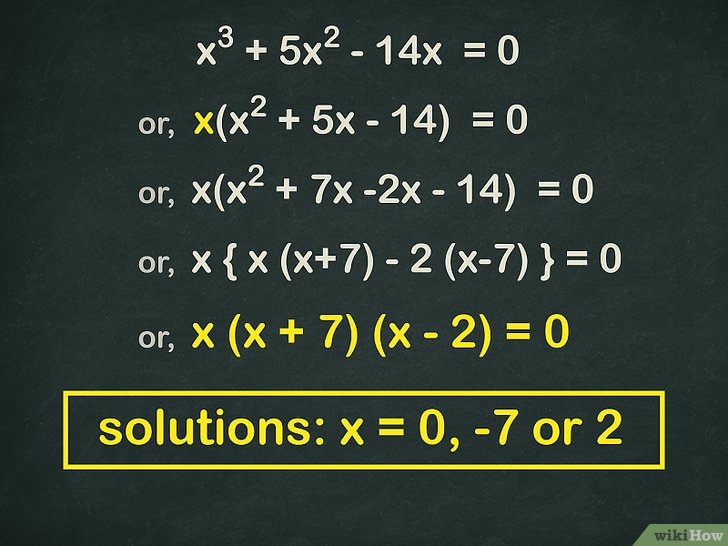 Введите свой запрос:
Введите свой запрос: