Квадратичные неравенства — подготовка к ЕГЭ по Математике
Покажем, как с помощью графика функции y = ax2 + bx + c решать квадратные неравенства.
Квадратичная функция, или парабола, — это функция вида
Вспомним свойства этой функции:
Координаты вершины параболы:
Если , ветви вверх
Если , ветви вниз
Точки пересечения с осью X: и
где и — корни квадратного уравнения
Точка пересечения с осью Y: М (0; с).
Вспомним также, как выражение раскладывается на множители.
где и — корни квадратного уравнения
1. Часто на тестировании мы предлагаем решить неравенство
x2 < 400
Справляются далеко не все. Очень часто, не задумываясь, выдают «ответ»: x < ± 20.
Однако сама эта запись — абсурдна! Представьте, что вы слышите прогноз погоды: «Температура будет меньше плюс-минус двадцати градусов». Что, спрашивается, надеть — рубашку или шубу? 🙂
Давайте решим это неравенство с помощью графика.
Изобразим схематично график функции y = x2 и отметим все значения x, для которых y < 400.
Теперь мы видим правильный ответ: x ∈ (−20; 20).
Запомним: извлекать корень из неравенства нельзя. Такого действия просто нет.
2. Следующее неравенство:
Переносим всё в левую часть неравенства. Раскладываем левую часть на множители.
Рисуем ось X. Рисуем параболу с ветвями вверх.
Эта парабола пересекает ось X в точках — 4 и 4. Отмечаем знаки выражения в левой части на каждом интервале.
Записываем ответ:
3. Решим неравенство: x2 − 3x − 10 ≥ 0.
Графиком функции y = x2 − 3x − 10 служит парабола, ветви которой направлены вверх. Решая квадратное уравнение x2 − 3x − 10 = 0, находим x1 = −2 и x2 = 5 — в этих точках парабола пересекает ось X. Нарисуем схематично нашу параболу:
Мы видим, что при x ∈ (−2; 5) значения функции отрицательны (график проходит ниже оси X).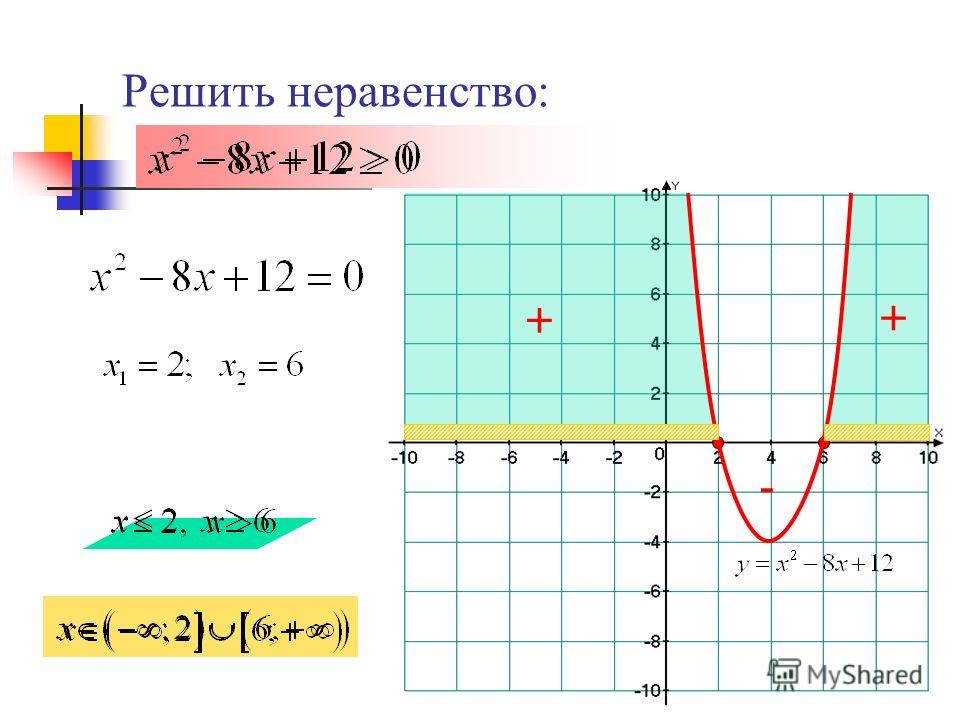
В точках −2 и 5 функция обращается в нуль, а при x < −2 и x > 5 значения функции положительны. Следовательно, наше неравенство выполняется при .
Обратите внимание, что для решения неравенства нам достаточно было схематично изобразить параболу. Ось Y вообще не понадобилась!
4. Ещё одно неравенство: x2 + 2x + 4 > 0.
Ветви параболы y = x2 + 2x + 4 направлены вверх. Дискриминант отрицателен, т. е. уравнение x2 + 2x + 4 = 0 не имеет корней. Стало быть, нет и точек пересечения параболы с осью X.
Раз ветви параболы направлены вверх и она не пересекает ось X — значит, парабола расположена над осью X.
Получается, что значения функции положительны при всех возможных x. Иными словами, решения нашего неравенства — это все действительные числа.
Ответ: .
Квадратные неравенства являются неотъемлемой частью ЕГЭ. Разберём типичные примеры из банка заданий ЕГЭ.
5. Следующее квадратичное неравенство:
Разложим его левую часть на множители.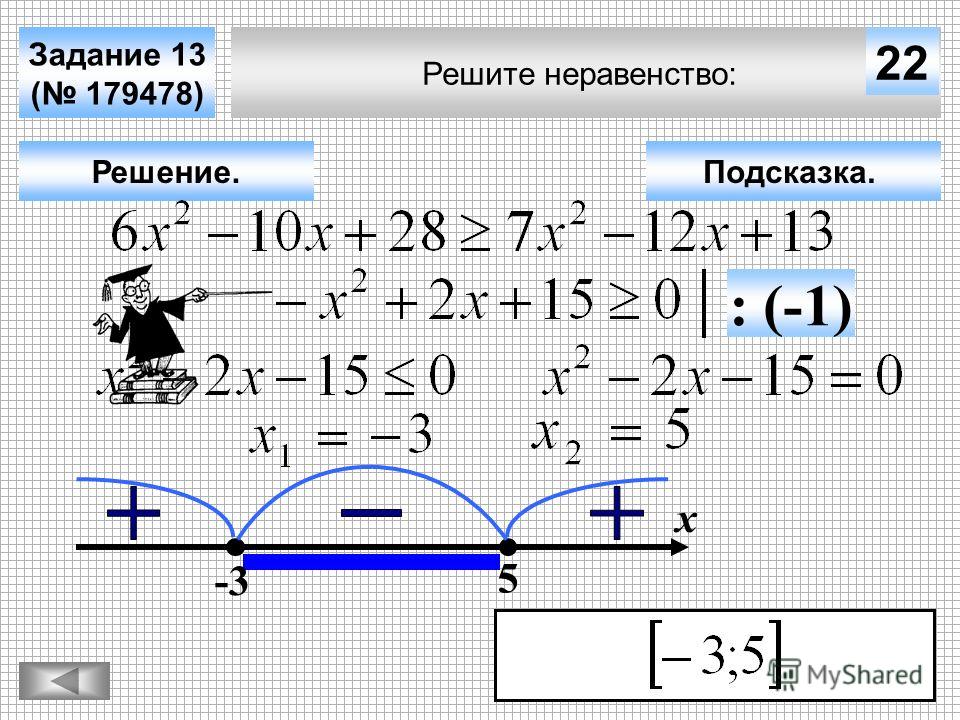
Получим:
И больше ничего не пишем. Рисуем ось X. Рисуем параболу с ветвями вверх.
Эта парабола пересекает ось X в точках 1 и 5. Отмечаем знаки выражения в левой части на каждом интервале.
Записываем ответ:
6. Еще неравенство:
Квадратное уравнение не имеет решений — его дискриминант отрицателен. Это значит, что парабола нигде не пересекает ось X. Ветви этой параболы направлены вверх. Все значения функции положительны. Неравенство выполняется для всех действительных X.
Соберем в одну таблицу примеры решения различных квадратичных неравенств.
Квадратные неравенства повышенной сложности 8 класс онлайн-подготовка на Ростелеком Лицей
Методы решения квадратных неравенств
Квадратными называются неравенства вида .
Методы решения квадратных неравенств, основанных на свойствах квадратичной функции.
1. Чтобы решить, например, неравенство , нужно рассмотреть функцию:
2.
Найти корни функции, с целью построить схематический график параболы. Корни в данном случае
3. Рассмотреть схематический график функции (Рис. 1).
Ветви параболы направлены вверх. Внутри интервала корней и вне интервала корней функция сохраняет знак. Если старший коэффициент больше нуля, то вне интервала корней функция положительная. Внутри интервала корней функция отрицательная.
Рис. 1. График квадратичной функции
4. Решением данного неравенства являются все значения в интервале: . Границы интервала входят в ответ, т. к. условие допускает равенство трехчлена нулю.
Рассмотрим аналогичное неравенство: . Мы можем построить график функции для данного квадратного трехчлена (Рис. 2):
Интересующие нас значения находятся все на том же интервале
Так, мы видим, что при умножении неравенства на минус единицу ответ не изменяется, и любое неравенство с отрицательным старшим коэффициентом можно преобразовать и получить положительное
Рис.
2. График квадратичной функции
Пример №1 (сложные коэффициенты)
Решить неравенство:
Один из корней явно угадывается , потому что получаем верное числовое решение
Поскольку один корень уравнения найден, дискриминант его больше либо равен нулю.
Второй корень находим по теореме Виета. Произведение и сумма корней легко выражаются через коэффициенты.
Находим второй корень:
Строим схематический график параболы (Рис. 3):
Ветви параболы направлены вверх, проходят через точки . Вне интервала корней функция положительна, внутри интервала корней функция отрицательна. Нам нужны те значения, при которых функция отрицательна. Это
Рис. 3. График квадратичной функции
Ответ: .
Какие могут быть сопутствующие задачи для такого вида неравенств?
Допустим: найти целочисленные решения для данного неравенства.
находится левее , затем , а не входит в ответ, значит, целочисленное решение:
Пример №2 (замена переменных)
Решить неравенство:
Обозначим за новую переменную ; Тогда неравенство превращается в следующее квадратное неравенство
Решение:
Рассматриваем функцию:
Находим корни, используя обратную теорему Виета.
Схематически рисуем график функции (Рис. 4).
Ветви параболы направлены вверх. Внутри интервала корней и вне интервала корней функция сохраняет знак. Если старший коэффициент больше нуля, то вне интервала корней функция положительная. Внутри интервала корней функция отрицательная.
Рис. 4. График квадратичной функции
Решение неравенства: , но Так, получаем
Переходим к старой переменной.
Переходим к системе:
Первое неравенство системы выполняется всегда.
Рассматриваем график функции: (Рис. 5).
Рис. 5. График квадратичной функции
Корни:
График очевиден. Ветви параболы направлены вверх. Внутри интервала корней все значения отрицательные.
Решение неравенства:
Пример №3
Решить неравенство:
Обозначим за новую переменную ; Тогда неравенство превращается в следующее квадратное неравенство
Решение:
1. Рассматриваем функцию:
2.
Находим корни, используя обратную теорему Виета.
3. Схематически рисуем график функции (Рис. 6).
Ветви параболы направлены вверх. Внутри интервала корней и вне интервала корней функция сохраняет знак. Если старший коэффициент больше нуля, то вне интервала корней функция положительная. Внутри интервала корней функция отрицательная.
Рис. 6. График квадратичной функции
4. Решение неравенства: или но
5. Переходим к старой переменной.
6. Переходим к системе: ; первое неравенство не имеет решений.
7. Рассматриваем график функции: (рисунок 53.5). Корни:
8. График очевиден. Ветви параболы направлены вверх. Внутри интервала корней все значения отрицательные, вне интервала – положительные.
9. Решение неравенства: или
Подведение итога урока
На данном уроке была рассмотрена тема: «Квадратные неравенства повышенной сложности». Вы вспомнили свойства квадратичных функций, на основании которых решаются квадратные неравенства любой сложности.
К квадратичной функции сводятся любые неравенства, несмотря на их сложность.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- ЕГЭ по математике (Источник).
- Frezzii.narod.ru (Источник).
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Видеоуроки для школьников (Источник).
Домашнее задание
- Решить неравенство:
- Какие квадратные неравенства относятся к неравенствам повышенной сложности?
- №555, 557.
Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010.
Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010.
9.8 Решение квадратных неравенств — средний уровень алгебры 2e
Цели обучения
К концу этого раздела вы сможете:
- Решать квадратные неравенства графически
- Алгебраическое решение квадратных неравенств
Приготовься 9.22
Прежде чем начать, пройдите этот тест на готовность.
Решите: 2x−3=0,2x−3=0.
Если вы пропустили эту проблему, просмотрите пример 2.2.
Приготовься 9.23
Решите: 2y2+y=152y2+y=15.
Если вы пропустили эту проблему, просмотрите пример 6.45.
Приготовься 9.24
Решите 1×2+2x−8>01×2+2x−8>0
Если вы пропустили эту задачу, просмотрите пример 7.56.
Ранее мы научились решать линейные неравенства и рациональные неравенства. Некоторые из методов, которые мы использовали для их решения, были одинаковыми, а некоторые отличались.
Теперь мы научимся решать неравенства, имеющие квадратное выражение. Мы будем использовать некоторые приемы решения линейных и рациональных неравенств, а также квадратных уравнений.
Квадратные неравенства будем решать двумя способами — и графически, и алгебраически.
Графическое решение квадратных неравенств
Квадратное уравнение имеет стандартный вид, если его записать в виде x 2 + bx + c = 0. Если мы заменим знак равенства знаком неравенства, мы получим квадратное неравенство в стандартной форме.
Квадратное неравенство
Квадратное неравенство — это неравенство, содержащее квадратное выражение.
Стандартная форма квадратного неравенства записывается:
ax2+bx+c<0ax2+bx+c≤0ax2+bx+c>0ax2+bx+c≥0ax2+bx+c<0ax2+bx+c≤ 0ax2+bx+c>0ax2+bx+c≥0
График квадратичной функции f ( x ) = ax 2 + bx + c = 0 является параболой.
Когда мы спрашиваем, когда ax 2 + bx + c > 0, мы спрашиваем, когда f ( x ) > 0. Мы хотим знать, когда парабола выше х -ось.
Пример 9,64
Как решить квадратное неравенство графически
Решить x2−6x+8<0x2−6x+8<0 графически. Запишите решение в интервальной записи.
Решение
Попытайся 90,127
ⓐ Решить x2+2x−8<0x2+2x−8<0 графически и ⓑ записать решение в интервальной записи.
Попытайся 9.128
ⓐ Решить x2−8x+12≥0x2−8x+12≥0 графически и ⓑ записать решение в интервальной записи.
Перечислим шаги, необходимые для графического решения квадратного неравенства.
Как
Решите квадратное неравенство графически.
- Шаг 1. Запишите квадратное неравенство в стандартной форме.
- Шаг 2. Постройте график функции f(x)=ax2+bx+c.f(x)=ax2+bx+c.
- Шаг 3. Найдите решение по графику.
В последнем примере парабола открылась вверх, а в следующем — вниз. В обоих случаях мы ищем часть параболы, лежащую ниже оси x , но отмечаем, как положение параболы влияет на решение.
Пример 9,65
Решите -x2-8x-12≤0-x2-8x-12≤0 графически. Запишите решение в интервальной записи.
Решение
Квадратное неравенство в стандартной форме. | −x2−8x−12≤0−x2−8x−12≤0 | |
| Постройте график функции f(x)=−x2−8x−12f(x)=−x2−8x−12. | Парабола открывается вниз. | |
| Найдите линию симметрии. | x=-b2ax=-b2a x=—82(-1)x=—82(-1) x=-4x=-4 | |
| Найдите вершину. | f(x)=-x2-8x-12f(x)=-x2-8x-12 f(-4)=-(-4)2-8(-4)-12f(-4)=- (−4)2−8(−4)−12 f(−4)=−16+32−12f(−4)=−16+32−12 f(−4)=4f(−4)= 4 Вершина (−4,4)(−4,4) | |
| Найдите пересечения x . Пусть f(x)=0f(x)=0. | f(x)=-x2-8x-12f(x)=-x2-8x-12 0=-x2-8x-120=-x2-8x-12 | |
Фактор. Использовать свойство нулевого продукта. | 0=-1(х+6)(х+2)0=-1(х+6)(х+2) х=-6х=-2х=-6х=-2 | |
| Постройте параболу. | x -пересечения (−6,0),(−2,0)(−6,0),(−2,0) | |
| Определите решение по графику. Мы включаем точки пересечения «меньше или равно». | (-∞,-6]∪[-2,∞)(-∞,-6]∪[-2,∞) |
Попытайся 9.129
ⓐ Решить −x2−6x−5>0−x2−6x−5>0 графически и ⓑ записать решение в интервальной записи.
Попытайся 9.130
ⓐ Решите −x2+10x−16≤0−x2+10x−16≤0 графически и ⓑ запишите решение в интервальной записи.
Алгебраическое решение квадратных неравенств
Алгебраический метод, который мы будем использовать, очень похож на метод, который мы использовали для решения рациональных неравенств.
Найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знак только тогда, когда оно равно нулю.
Мы будем использовать критические точки, чтобы разделить числовую прямую на интервалы, а затем определить, будет ли квадратное выражение положительным или отрицательным в интервале. Затем находим решение неравенства.
Пример 9,66
Алгебраическое решение квадратных неравенств
Алгебраическое решение x2−x−12≥0x2−x−12≥0. Запишите решение в интервальной записи.
Решение
Попытайся 9.131
Решить x2+2x−8≥0x2+2x−8≥0 алгебраически. Запишите решение в интервальной записи.
Попытайся 9.132
Решить x2−2x−15≤0x2−2x−15≤0 алгебраически. Запишите решение в интервальной записи.
В этом примере, поскольку выражение x2−x−12×2−x−12 прекрасно факторизуется, мы также можем найти знак в каждом интервале так же, как мы делали это при решении рациональных неравенств.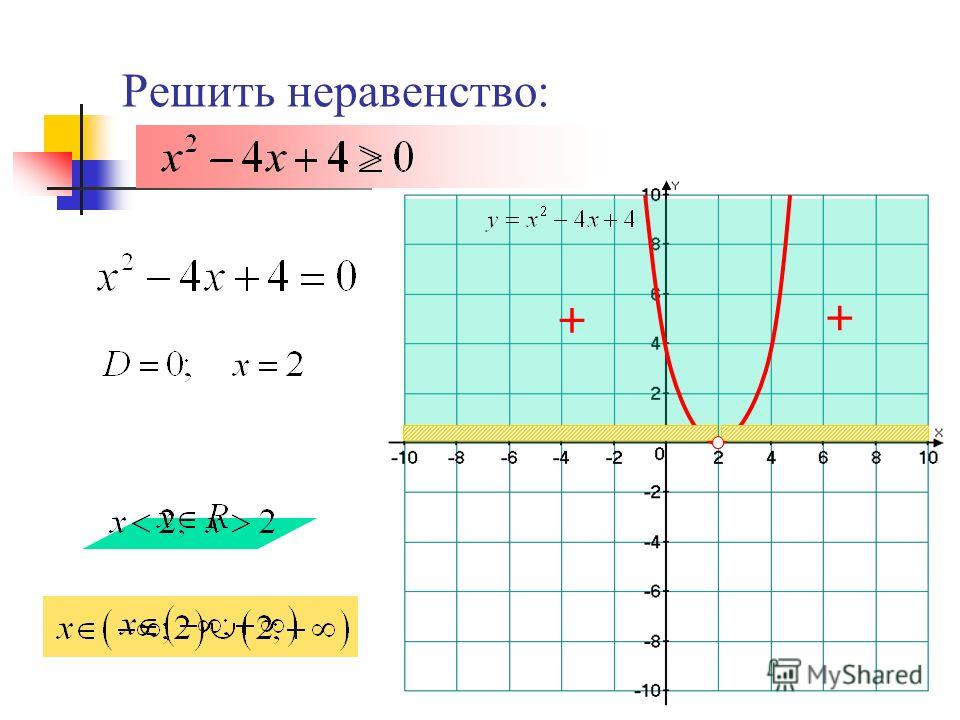
Результат такой же, как и при использовании другого метода.
Здесь мы суммируем шаги.
Как
Алгебраически решить квадратное неравенство.
- Шаг 1. Запишите квадратное неравенство в стандартной форме.
- Шаг 2. Определите критические точки — решения соответствующего квадратного уравнения.
- Шаг 3. Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Шаг 4. Над числовой линией покажите знак каждого квадратного выражения, используя контрольные точки из каждого интервала, подставленного в исходное неравенство.
- Шаг 5. Определите промежутки, на которых неравенство верно. Запишите решение в интервальной записи.
Пример 9,67
Решить -x2+6x−7≥0-x2+6x−7≥0 алгебраически. Запишите решение в интервальной записи.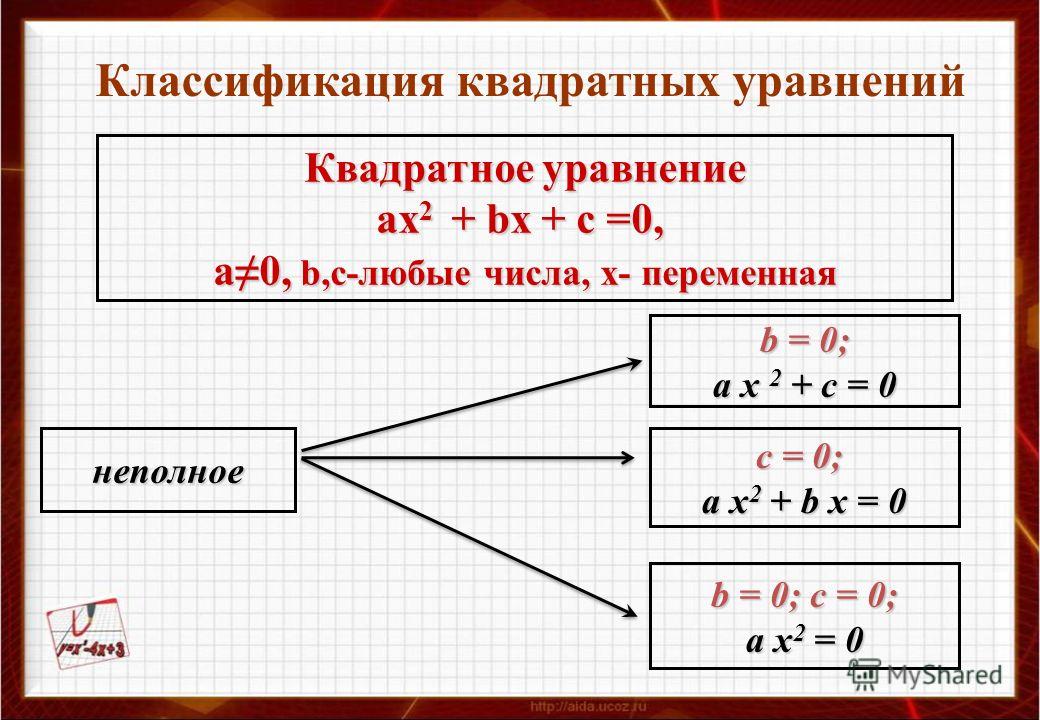
Решение
| Запишите квадратное неравенство в стандартной форме. | −x2+6x−7≥0−x2+6x−7≥0 |
| Умножьте обе части неравенства на −1−1. Не забудьте поменять знак неравенства. | x2−6x+7≤0x2−6x+7≤0 |
| Определите критические точки, решив соответствующее квадратное уравнение. | х2-6х+7=0х2-6х+7=0 |
| Напишите квадратную формулу. | х=-b±b2-4ac2ax=-b±b2-4ac2a |
| Затем подставьте значения a,b,ca,b,c. | х=-(-6)±(-6)2-4⋅1⋅(7)2⋅1x=-(-6)±(-6)2-4⋅1⋅(7)2⋅1 |
Упрощение. | х=6±82х=6±82 |
| Упростите радикальное. | х=6±222х=6±222 |
| Удалить общий делитель, 2. | х=2(3±2)2х=2(3±2)2 х=3±2х=3±2 х=3+2х=3-2х=3+2х=3-2 х≈1,6 х≈4,4х≈1,6х≈4,4 |
| Используйте критические точки, чтобы разделить числовую прямую на интервалы. Тестовые числа из каждого интервала в исходном неравенстве. | |
| Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи. | −x2+6x−7≥0−x2+6x−7≥0 в среднем интервале [3−2,3+2][3−2,3+2] |
Попытайся 9.
133Решить -x2+2x+1≥0-x2+2x+1≥0 алгебраически. Запишите решение в интервальной записи.
Попытайся 9.134
Решить -x2+8x-14<0-x2+8x-14<0 алгебраически. Запишите решение в интервальной записи.
Решениями квадратных неравенств в каждом из предыдущих примеров были либо интервал, либо объединение двух интервалов. Это произошло из-за того, что в каждом случае было найдено два решения соответствующего квадратного уравнения x 2 + bx + c = 0. Затем эти два решения дали нам либо два пересечения x- для графика, либо две критические точки для разделения числовой прямой на интервалы.
Это коррелирует с нашим предыдущим обсуждением количества и типа решений квадратного уравнения с использованием дискриминанта.
Для квадратного уравнения вида ах 2 + bx + с = 0, а≠0.
а≠0.
Последняя строка таблицы показывает нам, когда параболы никогда не пересекают ось x . Используя квадратную формулу для решения квадратного уравнения, подкоренное число является отрицательным. Получаем два комплексных решения.
В следующем примере решения квадратного неравенства будут результатом комплексного решения квадратного уравнения.
Пример 9,68
Решите, записав любое решение в интервальной записи:
ⓐ x2−3x+4>0x2−3x+4>0 ⓑ x2−3x+4≤0x2−3x+4≤0
Решение
ⓐ
| Запишите квадратное неравенство в стандартной форме. | −x2−3x+4>0−x2−3x+4>0 |
| Определите критические точки, решив соответствующее квадратное уравнение. | х2-3х+4=0х2-3х+4=0 |
Напишите квадратную формулу. | х=-b±b2-4ac2ax=-b±b2-4ac2a |
| Затем подставьте значения a,b,ca,b,c. | х=-(-3)±(-3)2-4⋅1⋅(4)2⋅1x=-(-3)±(-3)2-4⋅1⋅(4)2⋅1 |
| Упрощение. | х=3±-72х=3±-72 |
| Упростите подкоренное число. | х=3±7i2x=3±7i2 |
| Комплексные решения говорят нам, что парабола не пересекает ось x . Также парабола открывается вверх. Это говорит нам, что парабола полностью выше оси x . | Комплексные растворы |
Нужно найти решение x2−3x+4>0.x2−3x+4>0.
Так как для всех значений xx график выше x -ось, все значения x делают неравенство верным. В интервальных обозначениях мы пишем (−∞,∞).(−∞,∞).
ⓑ
| Запишите квадратное неравенство в стандартной форме. | x2−3x+4≤0x2−3x+4≤0 |
| Определите критические точки, решив соответствующее квадратное уравнение | х2-3х+4=0х2-3х+4=0 |
Поскольку соответствующее квадратное уравнение такое же, как в части (а), парабола будет такой же. Парабола открывается вверх и находится полностью над 9Ось 0038 x — никакая ее часть не находится ниже оси x .
Нужно найти решение x2−3x+4≤0.x2−3x+4≤0. Поскольку для всех значений x график никогда не находится ниже оси x , никакие значения x не делают неравенство верным.
Неравенство не имеет решения.
Попытайся 9.135
Решите и запишите любое решение в интервальной записи:
ⓐ −x2+2x−4≤0−x2+2x−4≤0 ⓑ −x2+2x−4≥0−x2+2x−4≥0
Попытайся 90,136
Решите и запишите любое решение в интервальной записи:
ⓐ x2+3x+3<0x2+3x+3<0 ⓑ x2+3x+3>0x2+3x+3>0
Раздел 9.8 Упражнения
Практика ведет к совершенству
Графическое решение квадратных неравенств
В следующих упражнениях ⓐ решите графически и ⓑ запишите решение в интервальной записи.
363.
х2+6х+5>0х2+6х+5>0
364.
х2+4х-12<0х2+4х-12<0
365.
x2+4x+3≤0x2+4x+3≤0
366.
x2−6x+8≥0x2−6x+8≥0
367.
−x2−3x+18≤0−x2−3x+18≤0
368.
−x2+2x+24<0−x2+2x+24<0
369.
−x2+x+12≥0−x2+x+12≥0
370.
−x2+2x+15>0−x2+2x+15>0
В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи.
371.
x2+3x−4≥0x2+3x−4≥0
372.
x2+x−6≤0x2+x−6≤0
373.
х2-7х+10<0х2-7х+10<0
374.
х2-4х+3>0х2-4х+3>0
375.
x2+8x>−15×2+8x>−15
376.
x2+8x<−12x2+8x<−12
377.
x2−4x+2≤0x2−4x+2≤0
378.
−x2+8x−11<0−x2+8x−11<0
379.
x2−10x>−19×2−10x>−19
380.
x2+6x<−3x2+6x<−3
381.
−6×2+19x−10≥0−6×2+19x−10≥0
382.
−3×2−4x+4≤0−3×2−4x+4≤0
383.
−2×2+7x+4≥0−2×2+7x+4≥0
384.
2×2+5x−12>02×2+5x−12>0
385.
х2+3х+5>0х2+3х+5>0
386.
x2−3x+6≤0x2−3x+6≤0
387.
−x2+x−7>0−x2+x−7>0
388.
−x2−4x−5<0−x2−4x−5<0
389.
−2×2+8x−10<0−2x2+8x−10<0
390.
−x2+2x−7≥0−x2+2x−7≥0
Письменные упражнения
391.
Объясните критические точки и то, как они используются для алгебраического решения квадратных неравенств.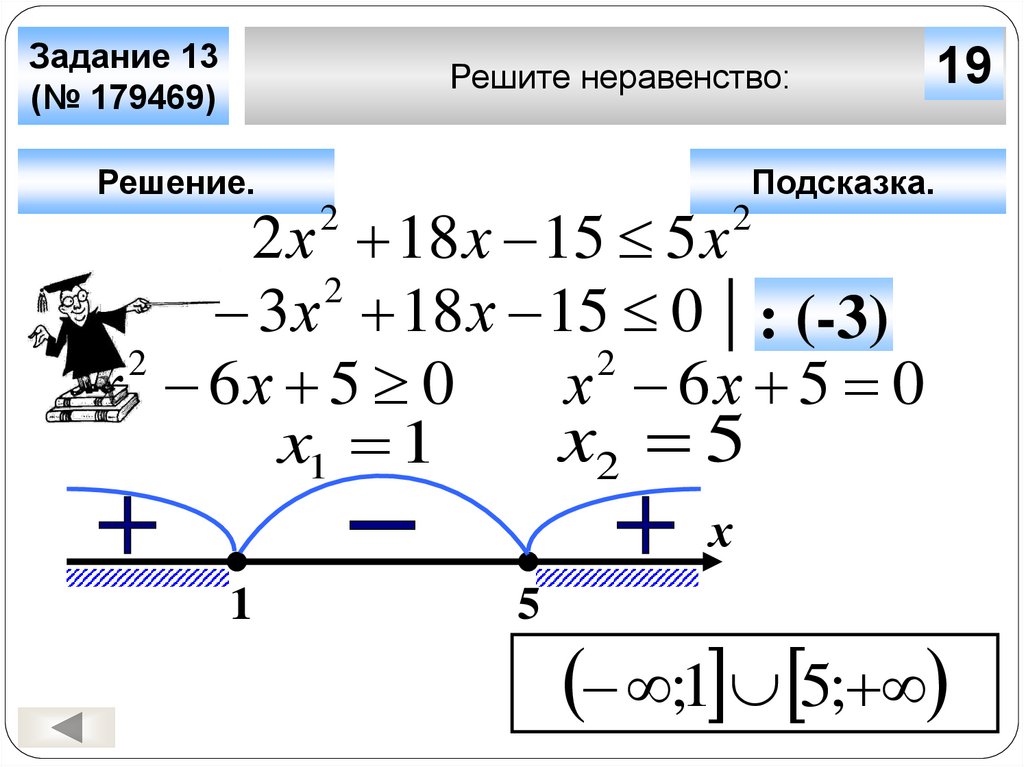
392.
Решить x2+2x≥8×2+2x≥8 как графически, так и алгебраически. Какой метод вы предпочитаете и почему?
393.
Опишите шаги, необходимые для графического решения квадратного неравенства.
394.
Опишите шаги, необходимые для алгебраического решения квадратного неравенства.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ По шкале от 1 до 10, как бы вы оценили свое знание этого раздела в свете ваших ответов на контрольный список? Как вы можете улучшить это?
Объяснение урока: Квадратные неравенства с одной переменной
В этом объяснении мы научимся решать квадратные неравенства с одной переменной алгебраически и графически.
Вспомните, что в уравнении у нас есть два выражения, которые равны друг другу, и мы
поставить знак равенства, =, между ними.
Когда у нас есть два выражения, которые
не равны друг другу, мы можем связать выражения с помощью знака неравенства.
У нас могут быть такие неравенства, как 𝑥≥4,6≤𝑥,2𝑥−7>5.
В каждом из этих неравенств 𝑥 имеет ряд возможных решений. Когда мы есть неравенство, такое как 𝑥≥4, мы можем сказать это словами как «𝑥 больше или равно четырем». Это означает, что значение 𝑥, равное четырем и более, удовлетворяет этому неравенству. Мы используем четыре символа неравенства: >, ≥, ≤. Больше чем больше, чем равно меньше, чем меньше, чем равно
. Мы можем решать неравенства в процессе, аналогичном решению уравнений, если мы
выполнить одну и ту же математическую операцию с обеими частями неравенства. Однако, как
неравенства имеют направление, мы должны тщательно рассмотреть, какая сторона неравенства
выражение включено. Когда мы умножаем или делим на отрицательное число, мы должны переключать
неравенство. Например, если у нас есть −𝑥≤−2,
то при делении на −1 мы должны изменить неравенство, чтобы получить
𝑥≥2.
Давайте теперь посмотрим, как решить неравенство и представить ответ в виде интервала. До для этого нам нужно повторить некоторые обозначения. Если рассматривать интервал чисел от 0 до 10, который включает 0, но не 10, мы могли бы представить это с помощью неравенства как 0≤𝑥10.
Строгое неравенство справа говорит нам, что 10 не входит в неравенство, и нестрогое неравенство слева говорит нам, что 0 включен. Другой способ запись этого интервала будет [0,10[.
Здесь закрытая квадратная скобка говорит нам о том, что 0 включен, а открытая квадратная скобка говорит нам, что 10 не включено. Здесь также стоит напомнить, что символ бесконечности ∞. Это часто используется для представления интервалов, которые больше или меньше одного числа. Например, 𝑥>3 в обозначение интервала будет ]3,∞[.
В этом объяснении мы сосредоточимся на квадратных неравенствах. Это отличается от линейных неравенств, которые выглядят примерно так:
−2𝑥+3≤5.
Напомним, что процедура решения неравенств этой формы достаточно проста. Первое, что мы хотим сделать, это изменить неравенство так, чтобы все 𝑥-термы находятся на одной стороне, а все постоянные члены — на другой. Мы делаем это, вычитая 3 с обеих сторон: −2𝑥≤2.
Затем, чтобы получить это с точки зрения только 𝑥, мы делим каждую сторону на −2, помня, что когда мы делим неравенство на отрицательное число, нам нужно поменять знак неравенства. Это дает нам 𝑥≥−1.
Итак, 𝑥 — это все числа, большие или равные −1. Это также может быть выражено в виде интервала, как [−1,∞[.
Точно так же, как у нас есть различные уравнения, такие как линейные и квадратные уравнения, мы могут иметь квадратные неравенства в следующих формах.
Определение: квадратное неравенство
Квадратное неравенство может быть представлено в одной из следующих форм: , где 𝑎, 𝑏 и 𝑐 — константы, а 𝑎≠0.
Когда мы решаем квадратное неравенство, нам нужно найти диапазон решений или интервалы,
для которого верно неравенство.
По сравнению с линейным случаем это сложнее и может включать более одного отдельного интервала. Мы можем решить квадратные неравенства, используя шаги процесса, описанные ниже.
Как решить квадратное неравенство алгебраически 𝑓(𝑥), с одной стороны, с неравенством, связывающим это с нулем. За например, 𝑓(𝑥)≤0 или 𝑓(𝑥)>0.
В следующем примере мы рассмотрим, как мы можем использовать диаграмму знаков для определения положительных и отрицательные значения интервалов неравенства.
Пример 1. Решение квадратного неравенства с помощью таблицы знаков
Опишите все решения неравенства 15−𝑥−2𝑥0.
Ответ
Чтобы начать решать неравенство 15−𝑥−2𝑥0, сначала преобразовать и переставить это, чтобы получить положительный коэффициент 𝑥. Мы можно умножить все члены коэффициента на −1, вспомнив, что когда мы умножив неравенство на отрицательное число, мы должны переставить неравенство. Это дает нам 15−𝑥−2𝑥0𝑥+2𝑥−15>0,
Теперь нам нужно решить 𝑓(𝑥)=0, где 𝑓(𝑥)=𝑥+2𝑥−15. Мы можем факторизовать наше уравнение, чтобы получить 𝑥+2𝑥−15=0(𝑥−3)(𝑥+5)=0.
Следовательно, 𝑥=3𝑥=−5.or
Чтобы решить неравенство (𝑥−3)(𝑥+5)>0, нам нужно определите регионы, где это действительно так. Так или иначе (𝑥−3)(𝑥+5)>0 зависит от знаков факторов (𝑥−3) и (𝑥+5).
Мы можем создать сетку, чтобы определить, будет ли каждый фактор положительным или отрицательным в
интервалы меньше, больше и между нашими решениями 𝑥=−5 и
𝑥=3. В сетке мы можем разместить интервалы между нашими решениями
по горизонтали и наши факторы 𝑓(𝑥) по вертикали, с произведением
приведенные ниже факторы.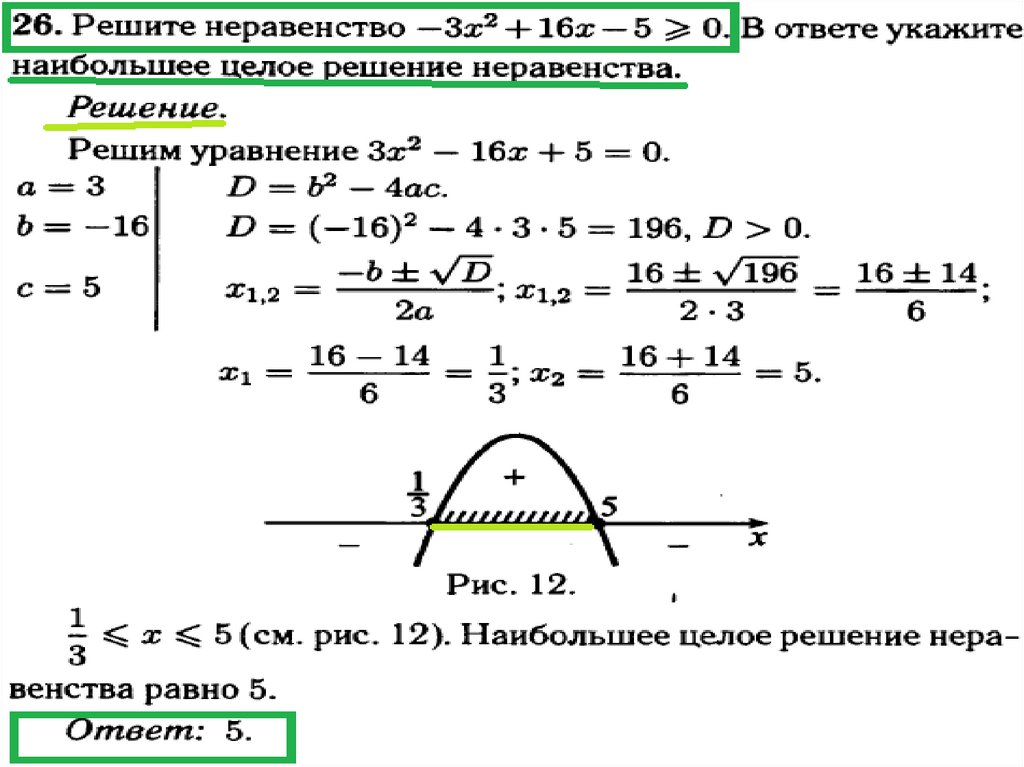
Затем мы можем вычислить, будет ли произведение факторов
положительный или отрицательный.
| 𝑥−5 | −5𝑥3 | 𝑥>3 | |
|---|---|---|---|
| (𝑥−3) | − | − | + |
| (𝑥+5) | − | + | + |
| (𝑥−3)(𝑥+5) | + | − | + |
, наши значения (𝑥−3) и (𝑥+5) будут равны отрицательное, поэтому произведение этих двух отрицательных значений, (𝑥−3)(𝑥+5) будет положительным.
Проверяя знак (𝑥−3)(𝑥+5) в сетке, мы видим что оно будет положительным, то есть (𝑥−3)(𝑥+5)>0, когда 𝑥−5 или 𝑥>3. Другими словами, неравенство 15−𝑥−2𝑥0 выполняется, когда 𝑥 не удовлетворяет −5≤𝑥≤3. В интервальных обозначениях мы можем выразить наш ответ как ℝ−[−5,3].
В первом примере мы смогли точно проследить процесс решения квадратного неравенства, сначала решив квадратное, а затем используя таблицу знаков,
но мы должны знать, что это не всегда то, что желательно или необходимо.
В следующем примере мы рассмотрим квадратное неравенство, которое нельзя разложить на множители.
Пример 2. Решение квадратного неравенства
Найдите все решения неравенства 𝑥+121≤0. Запишите ответ в виде интервала.
Ответ
Поскольку это неравенство было дано нам со всеми членами на одной стороне уравнения, никакой перестановки не потребуется. Обычно, чтобы начать поиск решений, мы попытаемся решить 𝑓(𝑥)=0, где 𝑓(𝑥)=𝑥+121. Однако на самом деле это не имеет решений, поскольку 𝑥 всегда будет больше нуля для любого действительного значения 𝑥. То есть у нас есть 𝑥≥0⟹𝑥+121≥121𝑥+121>0.
Итак, левая часть неравенства всегда будет строго больше нуля, то есть 𝑥+121≤0 никогда не будет истинным.
Графически это можно увидеть, если учесть, что график 𝑓(𝑥)=𝑥+121 никогда не пересекает 𝑥-ось, как показано ниже.
Записанное в виде интервала решение представляет собой пустое множество ∅.
В предыдущих двух примерах мы решали квадратные неравенства, где правая часть неравенства равна
равен нулю.
Когда обе части неравенства содержат ненулевые выражения, нам нужно сначала
упростить неравенство до точки, где одна его часть равна нулю. В следующем примере мы будем
рассмотрим пример, когда обе части неравенства содержат квадратные выражения. После
упрощая это неравенство, будем решать его как алгебраически, так и графически.
Пример 3. Решение квадратного неравенства
Определите множество решений неравенства (𝑥+3)≤(5𝑥−9).
Ответ
Чтобы начать решать это неравенство, сначала упростим его так, чтобы одна сторона была равна нулю. Хотя это заманчиво, мы не можем просто взять здесь квадратный корень из каждой стороны равенства. Поскольку квадратный корень может принимать как положительные, так и отрицательные значения, извлечение квадратного корня из
неравенство может привести к неверному ответу. Вместо этого мы можем умножать через круглые скобки в
обе части неравенства, чтобы получить
(𝑥+3)≤(5𝑥−9)𝑥+6𝑥+9≤25𝑥−90𝑥+81.
Теперь нам нужно собрать все члены на одной стороне неравенства. Для того, чтобы сохранить положительный коэффициент при 𝑥, мы можем вычесть все члены на левая часть от каждой части неравенства, что дает нам 0≤25𝑥−90𝑥+81−𝑥+6𝑥+9.
также можно написать это как 24𝑥−96𝑥+72≥0, отметив, что две стороны неравенства поменялись местами.
Поскольку 24 является общим множителем, мы можем разделить все члены на 24, что дает нам
| 𝑥−4𝑥+3≥0. | (1) |
Мы упростили данное неравенство до такой степени, что одна его сторона равна нулю. В настоящее время, мы закончим решать это неравенство, используя два различных метода: алгебраический метод и графический метод.
Метод 1
Сначала решим это неравенство алгебраически. Установка нашего 𝑓(𝑥)=0 и факторинг дают нам 𝑥−4𝑥+3=0(𝑥−1)(𝑥−3)=0,
Следовательно,
𝑥=1𝑥=3.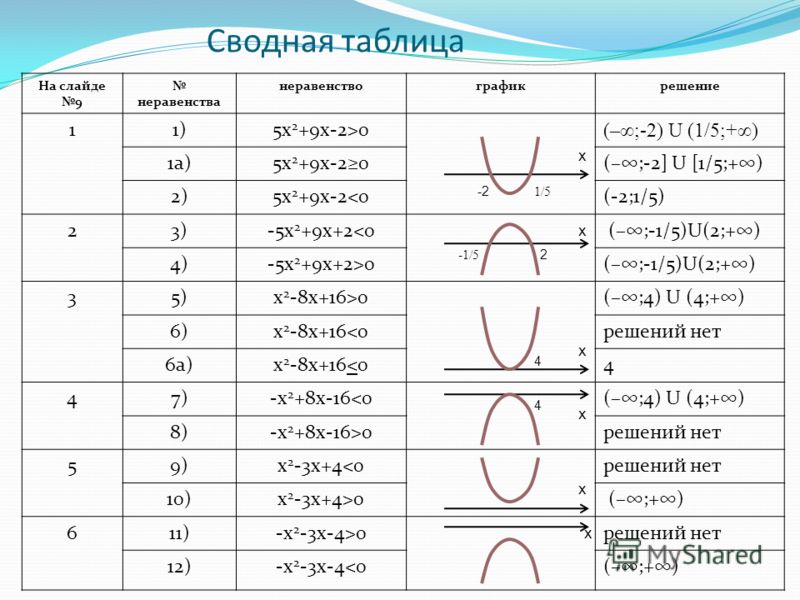
or
В факторизованной форме неравенство (1) записывается как (𝑥−1)(𝑥−3)≥0, и нам нужно определить регионы, в которых это неравенство верно. Независимо от того, (𝑥−1)(𝑥+3)≥0 зависит от факторов (𝑥−1) и (𝑥−3).
Мы можем создать сетку, чтобы определить, будет ли каждый фактор положительным или отрицательным в интервалы меньше, больше и между нашими решениями 𝑥=1 и 𝑥=3. Поскольку у нас есть нестрогое неравенство, мы также можем записать значения, когда 𝑥=1 и 𝑥=3. Затем мы можем вычислить, является ли произведение факторов будет положительным или отрицательным.
| 𝑥1 | 𝑥=1 | 1𝑥3 | 𝑥=3 | 𝑥>3 | |
|---|---|---|---|---|---|
| (𝑥−1) | − | 0 | + | + | + |
| (𝑥−3) | − | − | − | 0 | + |
| (𝑥−1)(𝑥−3) | + | 0 | − | 0 | + |
Из сетки видно, что интервалы, где (𝑥−1)(𝑥−3)≥0, соответствуют 𝑥≤1 и когда 𝑥≥3.
В других
словами, неравенство (𝑥+3)≤(5𝑥−9)
выполняется, когда 𝑥 не удовлетворяет 1𝑥3. В интервальных обозначениях мы можем выразить наш ответ как ℝ−]1,3[.
Метод 2
Рассмотрим, как решить неравенство (1) графически. Начнем с построения графика 𝑓(𝑥)=𝑥−4𝑥+3. Учитывая, что коэффициент при 𝑥 положительна, мы знаем, что кривая параболы откроется вверх. В методе 1 мы идентифицировали корни равенство 𝑥=1 и 𝑥=3, это означает, что кривая пройдет через координаты (1,0) и (3,0).
Для решения неравенства 𝑥−4𝑥+3≥0 рассмотрим точки на график 𝑓(𝑥)=𝑥−4𝑥+3, где 𝑓(𝑥)≥0. Это будет выше оси 𝑥, при значениях, где 𝑥≤1 и где 𝑥≥3. Как показано в методе 1, наш ответ в интервальной записи можно записать как ℝ−]1,3[.
В предыдущем примере мы решили квадратное неравенство как алгебраически, так и графически. Требуются оба метода
упрощая данное неравенство до точки, где одна его часть равна нулю.
Отсюда легко решить
квадратное неравенство графически, пока мы можем набросать график квадратичной функции. Мы будем использовать графический
метод решения квадратных неравенств в остальных примерах.
Рассмотрим еще один пример графического решения квадратного неравенства.
Пример 4. Решение квадратного неравенства с помощью графика
Решите неравенство 2𝑥≤15𝑥−27.
Ответ
Начнем с упрощения данного неравенства до точки, где одна его сторона равна нулю. Мы можем вычесть 15𝑥 с обеих сторон, что дает нам 2𝑥≤15𝑥−272𝑥−15𝑥≤−27.
Затем мы можем добавить 27 к обеим частям неравенства, что даст нам 2𝑥−15𝑥+27≤0.
Чтобы решить неравенство графически, нарисуем график 𝑓(𝑥)=2𝑥−15𝑥+27. Для этого сначала нужно найти точки пересечения уравнения 𝑥-ось, часто называемая корнями уравнения.
Установив 𝑓(𝑥)=0, мы можем разложить это на множители, что даст нам 2𝑥−15𝑥+27=0(2𝑥−9)(𝑥−3)=0,
Итак, 𝑥=4,5𝑥=3.
или
Теперь нам нужно установить форму кривой 𝑓(𝑥)= 2𝑥−15𝑥+27. Поскольку коэффициент при 𝑥, 2, положителен, это означает, что кривая параболы разомкнется вверх.
Итак, поскольку корни уравнения равны 𝑥=4,5 и 𝑥=3, мы можем построить координаты (4.5,0) и (3,0) и нарисуйте кривую параболы, как показано ниже.
Далее нам нужно определить области, для которых неравенство 2𝑥−15𝑥+27≤0 Справедливо. Из скетча видно, что 𝑓(𝑥)=2𝑥−15𝑥+27 находится в значениях меньше нуля между значениями 𝑥=3 и 𝑥=4,5. Следовательно, 𝑥 должно удовлетворять 3≤𝑥≤4,5. В интервальных обозначениях мы можем записать это как [3,4.5].
Рассмотрим еще один пример графического решения квадратного неравенства.
Пример 5. Решение квадратного неравенства с помощью графика
Решите неравенство (𝑥−5)(𝑥−7)≥−5𝑥+35.
Ответ
Начнем с упрощения данного неравенства до точки, где одна его сторона равна нулю. Умножая через скобки, получаем (𝑥−5)(𝑥−7)≥−5𝑥+35𝑥−12𝑥+35≥−5𝑥+35𝑥−7𝑥+35≥35𝑥−7𝑥≥0,
Чтобы решить неравенство графически, нарисуем график 𝑓(𝑥)=𝑥−7𝑥.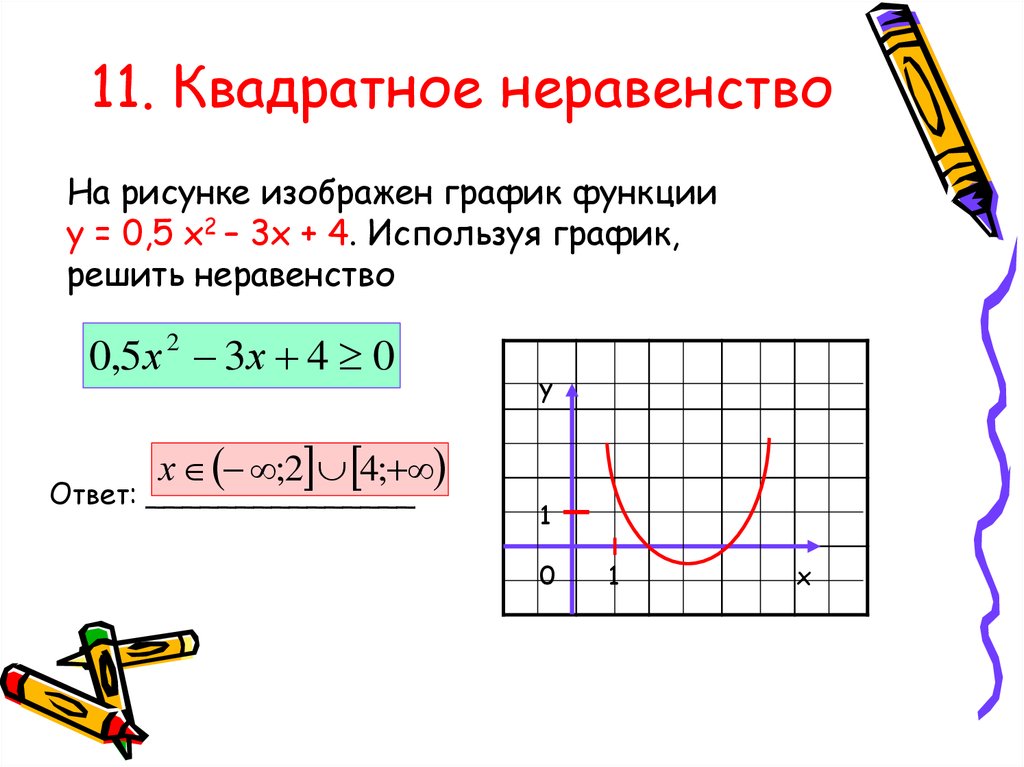
Для этого сначала нужно найти корни квадратичной функции 𝑓(𝑥). Эти корни можно найти, установив 𝑓(𝑥)=0 и решив, что даст нам
𝑥−7𝑥=0,
Факторинг, имеем 𝑥(𝑥−7)=0.
Следовательно, 𝑥=0𝑥=7.или
Как коэффициент при 𝑥 в уравнении 𝑓(𝑥)=𝑥−7𝑥 равно 1, это значение больше нуля; поэтому кривая параболы будет открываться вверх. Как корни уравнения равны 𝑥=0 и 𝑥=7, это означает, что кривая пройдет через координаты (0,0) и (7,0). Мы можем сделать набросок график, показанный ниже.
Для решения неравенства 𝑥−7𝑥≥0 рассмотрим точки на
график 𝑓(𝑥)=𝑥−7𝑥, где 𝑓(𝑥)≥0. Это будет выше оси 𝑥 при значениях, где
𝑥 меньше 0 и где 𝑥 больше 7. Поскольку у нас нет строгого неравенства, 𝑥 также может быть точно равно
до 0 или 7. Другой способ выразить это — сказать, что 𝑥 — это все
значения, исключая точки, где 0𝑥7. Мы можем
выразите этот окончательный ответ в интервальной записи как ℝ−(0,7).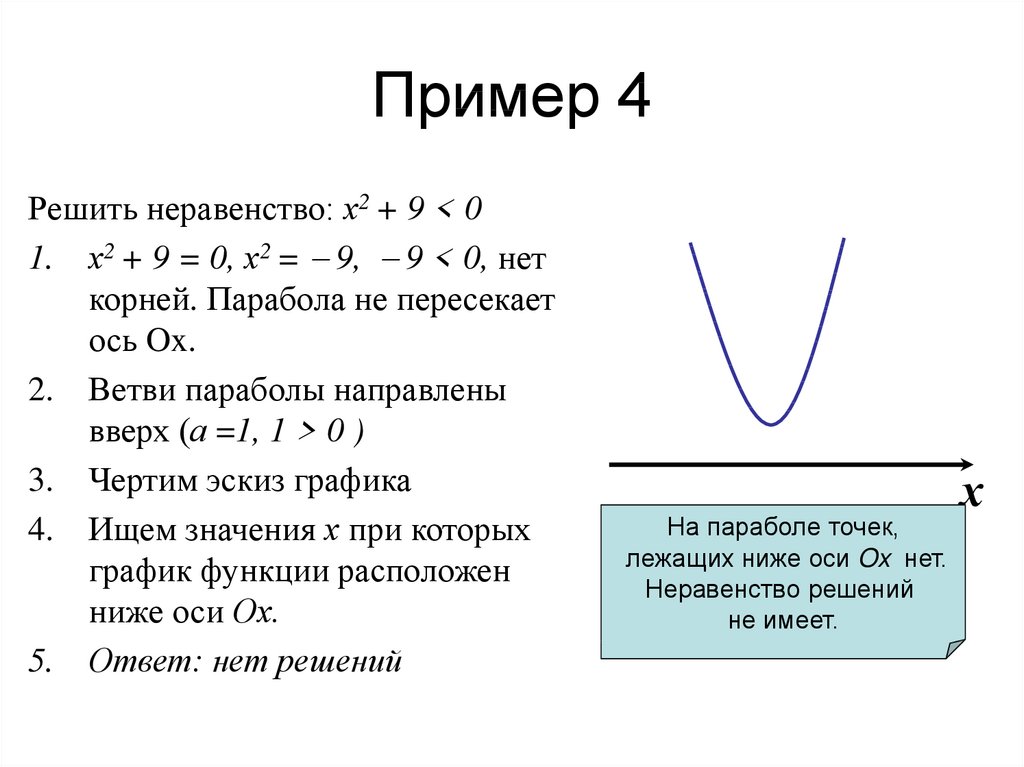
Давайте закончим повторением нескольких важных понятий из объяснения.
Ключевые моменты
- Решением квадратного неравенства является интервал или объединение интервалов. Когда это объединение двух интервалов, мы можем использовать обозначение множества разностей для запишите его как дополнение одного интервала.
- Чтобы решить квадратное неравенство алгебраически, выполните следующие шаги:
- Перестройте неравенство так, чтобы все члены выражения были стороны, с неравенством, связывающим это с нулем, например, 𝑓(𝑥)>0.
- Фактор неравенства, установив 𝑓(𝑥)=0, чтобы определить корни выражения 𝑓(𝑥).
- Определите интервалы, удовлетворяющие неравенству, используя контрольные точки в каждом интервальная или знаковая диаграмма. Мы также можем нарисовать график функции.
- Чтобы решить квадратное неравенство графически, выполните следующие действия.
