Квадратичные функции и их графики: Свойства квадратичной функции y = ax² — урок. Алгебра, 8 класс.

Квадратичная функция вида ​​y=ax²+bx+c (a ≠ 0), ее свойства и график – методическая разработка для учителей, Лизунова Мария Николаевна

Ожидаемый  результат:	учащиеся знают формулы для нахождения вершины параболы; умеют строить график функции у=ах2+вх+с (а≠0) и устанавливают ее свойства; владеют навыками работы в виртуальной лаборатории образовательной платформы «BilimLand» для построения графика квадратичной функции.
Цель  урока:	сформировать представление о квадратичной функции вида у=ах2+вх+с (а≠0), ее свойствах и графике.
Задачи:	— образовательные:   систематизировать у учащихся знания о квадратичной функции; отработать алгоритм построения графика квадратичной функции;  научить учащихся  выбирать рациональные способы построения графиков, сформировать навык самостоятельной работы с электронными образовательными ресурсами. — воспитательные:   воспитывать умение слушать и вступать в диалог, участвовать в обсуждении проблем, работать в коллективе, формировать коммуникативную компетенцию учащихся; воспитывать ответственность и аккуратность. — развивающие:  развивать умение искать и анализировать  информацию; представлять информацию в виде алгоритма, осуществлять исследовательскую деятельность;  способствовать развитию познавательного интереса к предмету посредством использования ИКТ.
Тип урока:	урок с использованием ИКТ.
Формы работы учащихся:	фронтальная работа, самостоятельная работа (тесты), работа у доски, работа с ЭОР.
Необходимое техническое оборудование:	компьютер, интерактивная доска,  листы контроля (Приложение 1), карточки рефлексии (Приложение 2).
Образовательные ресурсы:	виртуальная лаборатория образовательной платформы  «BilimLand», интерактивные тесты сайта iTest, учебник «Алгебра 8 класс» А. Е. Абылкасымова и др., «Мектеп» 2016.

 

 

Ход урока

	Деятельность учителя	Деятельность обучающихся	Ресурсы
1 мин.	1. Организационный момент. Ребята, послушайте, какая тишина! Это в школе начались уроки. Мы не будем тратить время зря, И приступим все к работе. — И сегодня на уроке вы будете оценивать свои знания самостоятельно. Ознакомьтесь, пожалуйста, с листом контроля.	Знакомятся с листом контроля	Листы контроля
8 мин.	2. Проверка домашнего задания  — Вопрос: как справились с домашним заданием? Учащимся, которые не смогли выполнить домашнее задание, выдаются карточки с алгоритмом выполнения домашнего задания (к следующему уроку они должны показать выполненные задания). На протяжении пяти уроков мы занимаемся по теме «Квадратичная функция». Вы хорошо усвоили эту тему? Какую задачу вы поставите перед собой на этом уроке? — Ребята, сегодня на уроке вы будете использовать полученные знания по сдвигу функций.   — А сейчас ребята мы проверим, кто готов к уроку, а кто нет! Рассаживайтесь за компьютеры. Перед вами открыт сайт iTest (itest. 2 — n)». По истечении отведенного времени заканчивают тест и выставляют процент выполнения теста в лист контроля.	Сигнальные карточки зеленого, желтого и красного цвета. Карточки с алгоритмом для учащихся, которые не справились с домашним заданием. iTest (индивидуально на компьютерах) Листы контроля.
6 мин.	3. Актуализация знаний.   — Закончите предложение (фронтальный опрос): Чтобы построить график функции (y=f(x+m)) ….что необходимо? Чтобы построить график функции (y=f(x-m))….что необходимо? Чтобы построить график функции  (y=f(x)+n) ….что необходимо? Чтобы построить график функции  (y=f(x)-n) ….что необходимо? А чтобы построить график функции (y=f(x+m)+n) ? — Молодцы! Я вижу: вы готовы к уроку!  Давайте откроем тетради и запишем в них сегодняшнее число, тему и поработаем письменно. 2+bx+c;(a eq0))». Давайте вместе изучим ее свойства и построим график.	Отвечают на вопросы учителя.   Открывают рабочие тетради, записывают число и тему   Один ученик у доски, остальные работают в тетрадях у=2х2-8х+6=2х2-8х+8-2=2(х2-4х+4)-2=2(х-2)2-2   Отвечают (парабола) (Сдвиг по оси Ох на 2 единицы вправо и по оси Оу на 2 единицы вниз) (Затрудняются.)   Соглашаются
7 мин.	4. Изучение нового  материала.  Вводим понятие квадратичной функции,  используя виртуальную лабораторию (Математика. График квадратичной функции) образовательной платформы «BilimLand» (https://bilimland. kz/ru/courses/math-ru/nachala-analiza/nachala-analiza/funkcziya-i-sposoby-ee-zadaniya/lesson/kvadratichnaya-funkcziya-i-ee-grafik)    — Ребята! Запишите формулы нахождения вершины параболы квадратичной функции, оси параболы и формулу преобразования функции. Давайте попробуем построить нашу функцию: у=2х2+12х+17.  — Посмотрите, как преобразовалась запись функции. О чем говорит коэффициент  a?  Если коэффициент а больше нуля, как выглядит парабола?  А если а меньше нуля, куда направлены ветви?  — Молодцы ребята! А какими свойствами обладает квадратичная функция?	Слушают учителя, знакомятся с виртуальной лабораторией «Математика. Квадратичная функция» образовательной платформы «BilimLand» (https://bilimland.kz/ru/courses/simulyaczii/matematika/lesson/grafik-kvadratichnoj-funkczii)                 Делают записи в тетрадях     Один учащийся выходит к интерактивной доске и вносит коэффициенты функции. 2)	Виртуальная лаборатория (Математика. График квадратичной функции) образовательной платформы «BilimLand» (https://bilimland.kz/). Учебник «Алгебра 8 класс» А.Е.Абылкасымова и др.-  «Мектеп» 2016.
10 мин.       2 мин.	5. Первичное закрепление изученного материала.   — А теперь, ребята, давайте запишем алгоритм построения графика квадратичной функции и попробуем сами построить несколько графиков. При помощи виртуальной лаборатории образовательной платформы «BilimLand» (Математика. Квадратичная функция) будем проверять ваши построения.                6. Физминутка  “Полиглот”. Ребята, в школе вы изучаете три языка: русский, казахский и английский. Сейчас я буду произносить слова на разных языках. Если вы услышите математический термин на английском языке, топайте ногами, если на казахском языке — хлопайте в ладоши, если на русском языке — прыгайте. Еven number, шаршы, функция, құбылмалы, multiplier, корень,  парабола, discriminant   — Молодцы. Спасибо большое!	Записывают в тетради алгоритм построения графика квадратичной функции (стр 109)   По очередности учащиеся выходят к доске, находят вершину и ось параболы, выполняют построения. № 267                     Выполняют физминутку.	Виртуальная лаборатория (Математика. График квадратичной функции) образовательной платформы «BilimLand» (https://bilimland.kz/ru/courses/simulyaczii/matematika/lesson/grafik-kvadratichnoj-funkczii) Урок   Учебник «Алгебра 8 класс» А.Е.Абылкасымова и др.-  «Мектеп» 2016.
5 мин.	7. Закрепление изученного материала. Выполнение упражнений из учебника № 270, 276	По желанию учащиеся выходят к доске, находят вершину и ось параболы, выполняют построения	Учебник «Алгебра 8 класс» А.Е.Абылкасымова и др.-  «Мектеп» 2016.
4 мин.	8. Контроль полученных знаний. Используем iTest (https://itest.kz/ru/exam_test?test_id=414203182 Математика. 8 класс. Квадратичная функция и ее свойства. ) Учащимся предлагают выполнить тесты. Ребята, возьмите листки контроля. Напротив каждого номера поставьте ответ, который вы считаете правильным. После выполнения теста учитель показывает  на доске правильные ответы. А теперь поставьте напротив каждого правильного ответа 1 балл.	Выполняют два тестовых задания проецируемые на интерактивной доске.   Выставляют баллы в лист контроля.
2 мин.	9. Итоги урока. Домашнее задание. Рефлексия.  — Вот и закончился, ребята, наш урок! Домашнее задание разноуровневое: — уровень госстандарта, т.е. знание программного материала и готовность его воспроизвести; этот уровень обязателен для всех учащихся; — задание на творческое применение (перенос) усвоенных способов, знаний, моделей; — задание на чистое творчество на базе полученных знаний и способов в соответствии с индивидуальными особенностями личности. 1) № 265 2) № 275 3) Составить (придумать) квадратичную функцию, построить ее график, исследовать функцию на монотонность, найти экстремумы функции на промежутке (-3,12). Учитель предлагает продолжить предложение. Принцип «Телеграмма». (Ученики продолжают одно из предложений). «Сегодня на уроке Я повторил … Я закрепил … Я научился … Я узнал …» Учитель предлагает отметить карточкой  то высказывание, которое больше всего подходит к качеству  усвоения материала на уроке А). Все понял, могу помочь другим – зеленый круг Б). Было интересно, запомню надолго – желтый круг В). Могу решать такие задания, но нужна помощь – красный круг — До свидания ребята, свою комплексную оценку за урок вы можете посмотреть у себя в электронных дневниках после уроков. А на следующий урок получите листы контроля с обратной связью.	Записывают в дневники домашнее задание         На карточках рефлексии продолжают одно из предложений.         Отмечают цвет круга, который соответствует качеству усвоения материала на уроке. Сдают листы контроля и карточки рефлексии учителю.	Листы самоконтроля. Карточки рефлексии.

 

 

Итог урока:______________________________________________________________________________________________

 

 

Положительные стороны урока: ____________________________________________________________________________

________________________________________________________________________________________________________

 

Отрицательные стороны урока:_____________________________________________________________________________

________________________________________________________________________________________________________

 

 

Список использованных источников.

1.  Учебник «Алгебра 8 класс» А.Е.Абылкасымова и др. — Алматы: «Мектеп», 2016 год.

 

2.     infourok.ru/avtorskaya_metodicheskaya_razrabotka_uroka_izuchenie_svoystv_kvadratichnoy_funkcii_i_postroenie-391201.htm

Презентация «Квадратичная функция и ее график» | Презентация к уроку по алгебре (9 класс):

Опубликовано 29.01.2019 — 22:17 — Игнатюк Светлана Васильевна

Данная презентация предназначена для использования при изучении темы «Квадратичная функция и ее график»

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Построение графика квадратичной функции.

Слайд 2

y= ax 2 +bx + c — квадратичная функция, где a, b, c — числа ( а ≠ 0).

Слайд 3

1 2 0 3 -3 -2 -1 -1 1 2 3 x y 4 Свойства квадратичной функции при а>0; а

Слайд 4

1 2 0 3 -3 -2 -1 -1 1 2 3 x y 4 а

Слайд 5

Задание 1: На координатной плоскости постройте графики функций: х у 1 2 -1 -1 2 1 -2 -3

Слайд 6

x y 1 2 3 1 2 -3 -2 -1 -1 -2 -3 0 Определение наибольшего и наименьшего значения функции.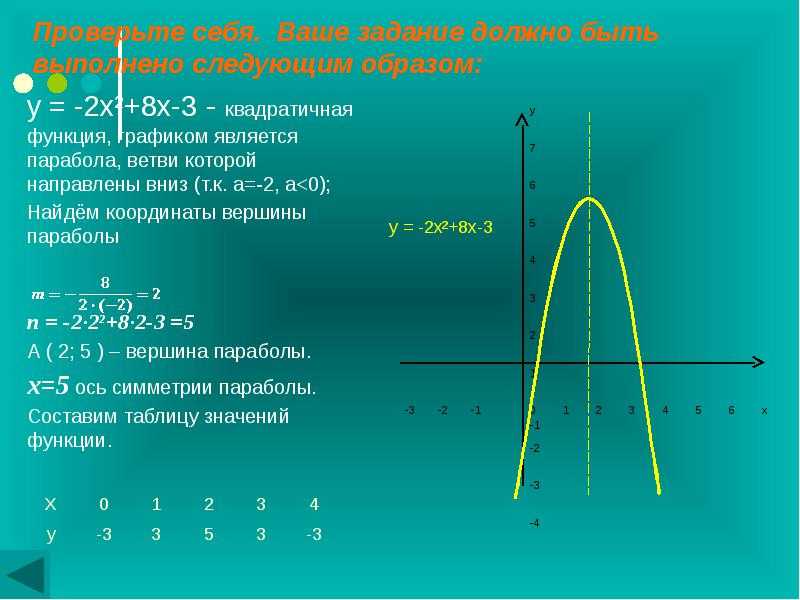

Слайд 7

2 0 3 -3 -2 -1 -1 1 2 3 x y 1 ? Задание 2: Какой график соответствует функции:

Слайд 8

Правила построения параболы: Найти координаты вершины параболы: (2;-1). Провести ось симметрии: х=2. Найти нули функции при у=0: (1;0) и (3;0) Найти дополнительные точки: при х=0, у=3; при х=4, у=3. Соединить полученные точки. х у 1 2 -1 -1 1 2 3 0 3

Слайд 9

Задание 2: На координатной плоскости постройте график функции: Координаты вершины параболы: (1;-4). Провести ось симметрии: х=1. Найти нули функции при у=0: (3;0) и (-1;0) Найти дополнительные точки: при х=0, у=-3; при х=4, у=5. Соединить полученные точки . х у 1 -1 0 2 -4 -3 -2 -1 1 4 4

По теме: методические разработки, презентации и конспекты

Методика построения графика квадратичной функции и использование графика для решения неравенств. (развивающее обучение)

Каждому  учителю необходимо помнить о следующих структурных элементах урока:·       Постановка цели и мотивация учебной деятельности учащихся. ·…

Разработка учебного занятия по теме» Применение производной к исследованию функций и построеннию графиков. Схема исследования функции»

Разработка учебного занятия по теме :» Применение производной к исследованию функций и построеннию графиков. Схема исследования функции».  Урок является логическим продолжением изучаемого материала. Р…

Административный контроль Алгебра 9 класс Тема: «Исследование функции и построение графика функции»

Пояснительная записка    Данная проверочная работа  предназначена для подготовки выпускников 9-ых классов МБОУ СОШ № 35 г.о. Самара к экзаменационной работе по математике в новой ф…

Открытый урок по теме:»Линейная функция и её график.График функции у=IхI.

Открытый урок по теме:»Линейная функция и её график.График функции у=IхI.»содержит следующие материалы:1)Описание открытого урока.2)Презентацию №1 для 1 этапа урока,созданную учителем,3)Презентацию №2…

Открытый урок по теме:»Линейная функция и её график.

График функции у=IхI.

Открытый урок по теме:»Линейная функция и её график.График функции у=IхI.»содержит следующие материалы:1)Описание открытого урока.2)Презентацию №1 для 1 этапа урока,созданную учителем,3)Презентацию №2…

Функция. Свойства и графики функций

Одним из самых важных вопросов при изучении алгебры является функция. Изучение начинается еще в 7 классе. Однако учащиеся часто воспринимают материал с большим трудом. И даже в 11 классе тема вызывает…

Учебное занятие внеаудиторной деятельности в 9 классе «Функции и их графики. Квадратичная функция»

Использование технологии уровневой дифференциации для  подготовки учащихся к ГИА по математике.Дидактическая цель: Систематизация, обобщение и закрепление знаний учащихся по теме “Функции и их гр…

Поделиться:

 

5.1 Квадратичные функции и их графики – Колледж алгебры для управленческих наук

Перейти к содержимому

Квадратичные уравнения обычно возникают из задач, связанных с областями, а также доходом и прибылью, обеспечивая некоторые интересные приложения.

Фермер на заднем дворе хочет выделить прямоугольное пространство для нового сада. Она купила 80 футов проволочного ограждения, чтобы огородить 3 стороны, и поставит 4-ю сторону у забора заднего двора. Найдите формулу площади ограждения, если стороны ограждения, перпендикулярные существующему ограждению, имеют длину л .

В подобных сценариях, связанных с геометрией, часто бывает полезно нарисовать картинку. Также может быть полезно ввести временную переменную W для представления стороны забора, параллельной 4-й стороне или забору заднего двора.

 

Поскольку мы знаем, что у нас есть только 80 футов забора, мы знаем, что , или проще говоря, . Это позволяет нам представить ширину, W , через L : .

Теперь мы готовы написать уравнение для площади, которую окружает забор. Мы знаем, что площадь прямоугольника равна длине, умноженной на ширину, поэтому

Эта формула представляет площадь забора с точки зрения переменной длины L .

 

Поведение при коротком прогоне : Вершина

Теперь мы исследуем интересные особенности графиков квадратичных уравнений. В дополнение к точкам пересечения у квадратичных уравнений есть интересная особенность, заключающаяся в изменении направления, называемая вершиной .

Стандартная форма для квадратного числа есть , но вы также увидите их написанными в форме . Чтобы понять почему, рассмотрим этот пример.

Нарисуйте график

Мы можем создать таблицу значений, которую мы можем использовать для построения нескольких точек и соединения их плавной кривой.

х	г(х)
-5	1,5
-4	-1
-3	-2,5
-2	-3
-1	-2,5
0	-1
1	1,5

Обратите внимание, что точка поворота графика, где он меняется с убывающей на возрастающую, находится в точке (-2,-3). Мы называем эту точку вершиной квадратичного уравнения. Обратите внимание, что также можно написать . Сравнивая это с формой , вы можете видеть, что вершина графа (-2,3) соответствует точке .

 

Стандартная форма квадратичной функции равна

Вершина формы квадратичной функции равна

• Вершина квадратичной функции находится в точке , где h и k — числа в вершинной форме функции.
• Форма графика квадратичной функции называется параболой.
• Графики квадратичных функций также симметричны относительно вертикали, проходящей через вершину . Эта линия называется осью симметрии .

Когда a > 0, график квадратичного уравнения открывается вверх. Это называется вогнутым вверх.

a > 0

Когда a < 0, график квадратичного уравнения открывается вниз. Это называется вогнутым вниз.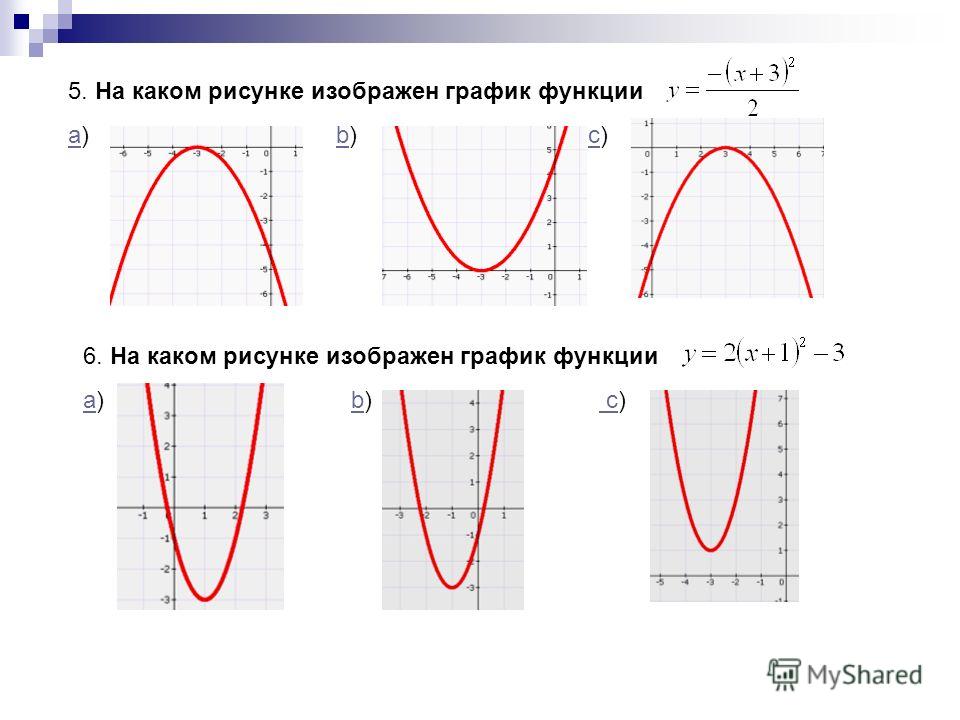

а < 0

Вершинная форма квадратичного уравнения является простейшей формой графа. Посмотрите на график в предыдущем примере, .

Обратите внимание на это, и парабола раскрывается. Также обратите внимание, что если мы двигаемся от вершины и идем влево или вправо на 1 единицу от вершины, точка на графике поднимается на 1/2 единицы вверх, а если вы проходите еще одну единицу, вы поднимаетесь на 1 1\2 или 3 1/. 2 единицы вверх, то есть единицы. Этот же шаблон можно использовать с любым квадратным числом для быстрого наброска графика.

Учитывая квадратичную функцию в форме вершины, мы можем выполнить следующие шаги, чтобы построить ее график.

1. Начните с графического изображения вершины в точке .
2. Переместиться вправо на 1 единицу от вершины, а затем
   1. Если двигаться вверх единиц.
   2. Если двигаться вниз единиц.
3. Шагните еще на 1 единицу вправо и переместитесь на единицу вверх или вниз на единицу .
4. При необходимости сдвиньте еще одну единицу вправо и переместите единицы вверх или вниз за .
5. Используйте свою ось симметрии, чтобы нарисовать другую сторону, или выполните те же шаги, двигаясь вместо этого влево.
6. Проведите через точки гладкую параболу.

Нарисуйте график следующих квадратичных функций:
а.
б.

Обратите внимание на отсутствие числа перед круглыми скобками, это понятная 1. Итак, наш . Поскольку это положительно, наша парабола вогнута.

Вершина Итак, наш первый шаг — изобразить эту точку на графике.

Затем идем вправо, вверх на один до . справа другой и до 3 до и справа еще и до 5 до .

Используя симметрию, мы делаем все это снова влево, используя ось симметрии в x = 3, чтобы найти точки , и . Затем нарисуйте нашу параболу, см. анимацию ниже:

Давайте посмотрим на часть b, мы замечаем, что a отрицательно, . Поскольку это отрицательно, наша парабола вогнута вниз.

Вершина такова, что это будет первая точка на графике.

Затем мы пойдем направо один, вниз 2 с a отрицательно, и у нас есть точка .

Затем мы снова идем вправо и вниз на 6 (), что дает нам точку на

Теперь, забегая вперед, если мы снова пойдем вправо, нам придется спуститься на 5(2)=10 единиц и, вероятно, оказаться вне сетки. , поэтому остановимся на тех точках, которые у нас есть.

Используя ось симметрии , мы замечаем, что у нас также есть точки в точках (-2,3), (-3,-3).

Затем мы просто рисуем нашу параболу, см. анимацию ниже:

Обратите внимание, что во втором примере мы использовали только 5 точек для построения параболы. Как правило, для построения линии необходимо минимум 2 точки, а для построения параболы — минимум 5 точек. Хорошо иметь 7 или более, чтобы иметь более точную картину, но по мере того, как становится больше, графики квадратичных функций увеличиваются или уменьшаются очень быстро, и мы часто не можем поместиться в последние точки на графике.

График

Мы также можем использовать форму вершины и те же самые идеи, чтобы посмотреть на графически изображенную параболу и вычислить ее уравнение.

Найдите уравнение для параболы, изображенной здесь:

Во-первых, мы замечаем, что вершина, поэтому мы начинаем с

Теперь нам просто нужно вычислить а, мы можем сделать это одним из двух способов. Мы знаем, что она отрицательна, чтобы мы могли узнать, как далеко мы спустимся на 1 единицу влево или вправо от вершины. Если это трудно увидеть, то мы можем использовать другую точку в нашем уравнении и найти .

Таким образом, уравнение для функции будет или

Найдите уравнение для графика:

Пишите в стандартной форме.

Чтобы записать это в стандартной полиномиальной форме, мы могли бы расширить формулу и упростить термины:

В предыдущем примере мы видели, что можно переписать квадратичную функцию, заданную в вершинной форме, и переписать ее в стандартной форме, расширив формулу. Было бы полезно обратить этот процесс вспять, так как форма преобразования раскрывает вершину.

Расширение общей формы преобразования квадратного числа дает:

Это должно быть равно стандартной квадратичной форме:

Члены второй степени уже равны. Чтобы линейные члены были равны, коэффициенты должны быть равны:
, поэтому

Это дает нам метод определения горизонтального сдвига квадратичного уравнения от стандартной формы. Точно так же мы могли бы установить константы равными find:
, поэтому

Однако на практике обычно легче запомнить, что это выходное значение функции, когда входное значение равно , поэтому .

Для квадратичной функции в стандартной форме вершина расположена по адресу:

   

Найдите вершину квадратичной функции. Перепишите квадратное уравнение в вершинную форму и график.

Горизонтальная координата вершины будет равна

Вертикальная координата вершины будет равна

Переписав в вершинную форму, значение останется таким же, как и в исходном квадрате.

и теперь мы можем изобразить это на графике. Мы знаем, что вершина равна 9.0003

, что положительно, и, таким образом, парабола раскрывается, поэтому мы идем вправо 1, вверх 2 и получаем точку , еще вправо вверх 6, поэтому , затем мы используем симметрию для другой стороны и получаем и

 

Данному уравнению запишите уравнение в стандартной форме, найдите вершину, запишите в вершинной форме и начертите.

В дополнение к упрощению графического изображения квадратного числа, записанного в стандартной форме, нахождение вершины служит еще одной важной цели — позволяет определить максимальное или минимальное значение функции в зависимости от того, в какую сторону открывается график.

а. Возвращаясь к нашему фермеру на заднем дворе из начала раздела, какие размеры она должна сделать в своем саду, чтобы максимально увеличить огороженную площадь?

Ранее мы определили площадь, которую она может оградить 80-футовым забором с трех сторон, задаваясь уравнением . Обратите внимание, что квадратичное значение было отражено по вертикали, так как коэффициент при квадрате члена отрицательный, поэтому график будет открыт вниз, а вершина будет максимальным значением для площади.

При нахождении вершины мы проявляем осторожность, так как уравнение не записано в стандартной полиномиальной форме с убывающими степенями. Но мы знаем, что a — это коэффициент при квадрате члена, поэтому a = -2, b = 80 и c = 0,

Нахождение вершины:

Максимальное значение Функция представляет собой площадь 800 квадратных футов, которая возникает, когда L = 20 футов. Когда более короткие стороны составляют 20 футов, остается 40 футов ограждения для более длинной стороны. Чтобы максимизировать площадь, она должна окружить сад так, чтобы две более короткие стороны имели длину 20 футов, а длинная сторона, параллельная существующему забору, имела длину 40 футов.

b. В настоящее время у местной газеты 84 000 подписчиков, ежеквартальная плата составляет 30 долларов. Исследование рынка показало, что если они повысят цену до 32 долларов, то потеряют 5000 подписчиков. Предполагая, что подписка линейно связана с ценой, какую цену должна взимать газета за ежеквартальную подписку, чтобы максимизировать свой доход?

Доход — это сумма денег, которую приносит компания. В этом случае доход можно определить, умножив плату за подписку на количество подписчиков. Мы можем ввести переменные, C для оплаты за подписку и S для количества подписчиков, что дает нам уравнение:
Доход = CS

Поскольку количество подписчиков меняется вместе с ценой, нам нужно найти взаимосвязь между переменными. Мы знаем, что в настоящее время S = 84 000 и C = 30, и что если они поднимут цену до 32 долларов, они потеряют 5 000 подписчиков, что даст вторую пару значений, C = 32 и S = ​​79 000. Отсюда мы можем найти линейное уравнение, связывающее две величины. Рассматривая C как вход и S как выход, уравнение будет иметь форму. Уклон будет

Это говорит нам о том, что газета потеряет 2500 подписчиков на каждый доллар, на который они повысят цену. Затем мы можем решить для вертикального пересечения

Это дает нам линейное уравнение, связывающее стоимость и количество подписчиков. Теперь вернемся к нашему уравнению доходов.

Теперь у нас есть квадратное уравнение для дохода как функции платы за подписку. Чтобы найти цену, которая максимизирует доход газеты, мы можем найти вершину:

Модель говорит нам, что максимальный доход будет получен, если газета взимает 31,80 доллара за подписку. Чтобы определить максимальный доход, мы можем оценить уравнение дохода:
Max R =
Максимальный доход составляет 2 528 100 долларов США

.

Обратите внимание, что уравнение, которое мы нашли в последнем примере, по существу является функцией спроса — соотношением между ценой (C) и спросом (S) . Это распространенный тип экономического приложения.

Для решения задачи, связанной с максимизацией выручки или прибыли при наличии данных о спросе при различных уровнях цен,

1. Используйте предоставленные данные для создания уравнения спроса, связывающего цену и объем спроса. Обычно это линейная функция.
2. Создайте уравнение дохода. Начните с Доход = цена, умноженная на количество , затем подставьте уравнение спроса, чтобы создать уравнение дохода только с точки зрения количества.
3. Если задача заключается в максимизации прибыли, создайте уравнение прибыли. Прибыль = (Доход) – (Стоимость)
4. Найдите вершину функции Доход или Прибыль, чтобы найти количество, которое максимизирует доход или прибыль.
5. При необходимости используйте это количество с функцией спроса, чтобы найти цену, которая максимизирует доход или прибыль.

Компания планирует продать новое смарт-устройство для фитнеса. Разработка продукта будет стоить 700 000 долларов, а производство каждого продукта будет стоить 30 долларов. Исследования рынка показывают, что если они продадут устройство за 100 долларов, они смогут продать 30 000 единиц. По их оценкам, на каждые 10 долларов, которые они снижают, они продадут еще 5000 товаров. Предполагая, что величина спроса линейно связана с ценой, определите цену, которая максимизирует прибыль 9.0034

Пусть p будет ценой за единицу, а q будет количеством, которое компания может продать. Начнем с создания линейной функции спроса в форме .

Если они продадут устройство за 100 долларов, они смогут продать 30 000 единиц, получив балл (30 000, 100).

Нам говорят, что на каждые 10 долларов они снижают цену, по их расчетам, они продадут еще 5000 товаров. Мы можем либо напрямую интерпретировать это как наклон, либо использовать его для создания второй точки. Снижение цены до $90 увеличит количество проданных товаров до 35 000, что даст второй балл (35 000, 90).

Нахождение наклона:

Уравнение спроса будет выглядеть как . Подставив для решения b :

Теперь у нас есть функция спроса: .

Теперь мы построим нашу функцию дохода, используя нашу кривую спроса:

Заменив в функции спроса p

Теперь, глядя на затраты, мы знаем, что постоянные затраты составляют 700 000 долларов, а затраты на единицу товара составляют 30 долларов. , что приводит к уравнению стоимости

Наконец, мы можем построить уравнение прибыли:
Прибыль = Доход – Затраты

Теперь, чтобы найти максимум, мы найдем вершину квадратного уравнения:

используйте функцию спроса:

Чтобы максимизировать прибыль, компания должна установить цену на устройство в 95 долларов. По этой цене они должны продать 32 500 единиц продукции с общей прибылью:

Новый автор с Аляски написал детскую книгу. Стоимость настройки печати составляет 5000 долларов США, при этом стоимость одной книги составляет 0,70 доллара США. Исследования рынка показывают, что если они будут продавать книги по 10 долларов каждая, они смогут продать 2000 книг, но если они будут продавать их по 20 долларов, они продадут только 1000 книг. Предположим, что спрос линейно связан с ценой, найдите цену, которая максимизирует прибыль, количество, которое следует напечатать, и максимальную прибыль.

3. в стандартной форме, в форме вершины, точка пересечения по вертикали в точке (0,13).
4. Функция спроса: , Доход: , Стоимость: Прибыль:   Максимальная прибыль Количество спроса: 1465, Цена для максимальной прибыли: 15,35 долл. США, Максимальная прибыль 16 462,25 долл. США

Media Attributions

• gardenbackyard
• example51graph
• happygraph
• sadgraph
• takenote находится под лицензией Public Domain
• examplewritingeqofquad
• tin512
• examplegraph51
• bookgraph511
• tinanswer513

License

College Algebra for the Management Sciences by Terri Manthey находится под лицензией Creative Commons Attribution-ShareAlike 4. 0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

Quadratic Functions Video Tutorial & Practice

Изучите самые сложные понятия алгебры с помощью пошаговых видеоуроков и попрактикуйтесь в решении задач с помощью преподавателей мирового уровня

Квадратичные функции

Распознавание характеристик парабол

ВИДЕО

Предыдущие видео для

4

ПРАКТИКА

• Вопрос из учебника

  Среди всех пар чисел, разность которых равна 14, найдите пару, произведение которой минимально возможно. Какой минимальный продукт? 92 + 14x — 106

Квадратичные функции

Определите минимальную или максимальную квадратичную функцию

Предыдущие видео для

. Следующие видео для

.

ВИДЕО

Предыдущие видео для

Следующие видео для

Полиномиальные функции и их графики

Определение полиномиальных функций

VIDEOS

Previous videos for

Next videos for

Polynomial Functions and Their Graphs

Recognize Characteristics of Graphs of Polynomial Functions

VIDEOS

Previous videos for

Next videos for

Полиномиальные функции и их графики

Определение конечного поведения

ВИДЕО

Предыдущие видео для

Следующие видеоролики для

полиномиальные функции и их графики

Используйте факторинг для поиска нулей полиномиальных функций

видео

Предыдущие видео для

. Их кратности

ВИДЕО

Предыдущие видео для

Следующие видео для

Полиномиальные функции и их графики

Используйте теорему промежуточного значения

Видео

Предыдущие видео для

Следующие видео для

Полиномиальные функции и их графики

Понимание между степенями и поворотными моментами

видео

Предыдущие видео для

Предыдущие видео

видео для

Полиномиальные функции и их графики

График полиномиальных функций

ВИДЕО

Предыдущие видео для 92 — 2x + 1) ÷ (x + 1)

Разделение полиномов

Используйте теорему фактора для решения полиномиального уравнения

видео

Предыдущие видео для

Следующие видео для

9047

. Функции

Использование теоремы о рациональном нуле для поиска возможных рациональных нулей

ВИДЕО

Предыдущие видео по

Следующие видео по

ПРАКТИКА

• Вопрос из учебника 92 -14x + 5

нули полиномиальных функций

Решение полиномиальных уравнений

Видео

Предыдущие видео для

Следующие видео для

. 40003

• . найти полиномиальную функцию n-й степени с вещественными коэффициентами, удовлетворяющую заданным условиям. Проверьте реальные нули и заданное значение функции. п = 3; 2 и 2 — 3i — нули; f(1) = -10

  93 — 2x — 1 имеет действительный нуль между 1 и 2.

Нули полиномиальных функций

Используйте теорему о линейной факторизации для поиска полиномов с заданными нулями

ПРАКТИКА

• Вопрос из учебника

  Для упражнений 40–46, (a) Перечислите все возможные рациональные корни или рациональные нули. (b) Используйте правило знаков Декарта, чтобы определить возможное количество положительных и отрицательных действительных корней или действительных нулей. (c) Используйте синтетическое деление, чтобы проверить возможные рациональные корни или нули и найти фактический корень или ноль. (d) Используйте частное из пункта (c), чтобы найти все оставшиеся корни или нули. 2 — 4 92 + 8 = 0 не имеет действительных корней.

Рациональные функции и их графики

Найдите домены рациональных функций

видео

Предыдущие видео для

.

Предыдущие видео для

Следующие видео для

Рациональные функции и их графики

Определение вертикальных асимптот

VIDEOS

Previous videos for

Next videos for

Rational Functions and Their Graphs

Identify Horizontal Asymptotes

VIDEOS

Previous videos for

Next videos for

Rational Functions and Their Graphs

Использование преобразований для построения графиков рациональных функций

ВИДЕО

Предыдущие видео для

Следующие видео для

Рациональные функции и их графики

Graph Rational Functions

VIDEOS

Previous videos for

Next videos for

Rational Functions and Their Graphs

Identify Slant Asymptotes

VIDEOS

Previous videos for

Next videos for

Rational Функции и их графики

Решение прикладных задач, связанных с рациональными функциями

ВИДЕО

Предыдущие видео для

Следующие видео для

Polynomial and Rational Inequalities

Solve Polynomial Inequalities

VIDEOS

Previous videos for

Next videos for

Polynomial and Rational Inequalities

Solve Rational Inequalities

VIDEOS

Previous videos for

Next видео для

Полиномиальные и рациональные неравенства

Задачи, моделируемые полиномиальными или рациональными неравенствами

Видео

Предыдущие видео для

Следующие видео для

Моделирование с использованием вариации

Решить проблемы с прямыми вариациями

видео

Предыдущие видео для

.

No related posts.