Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5.  СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1.  ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ§ 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3.  КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4.  СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4.  СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2.  ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. 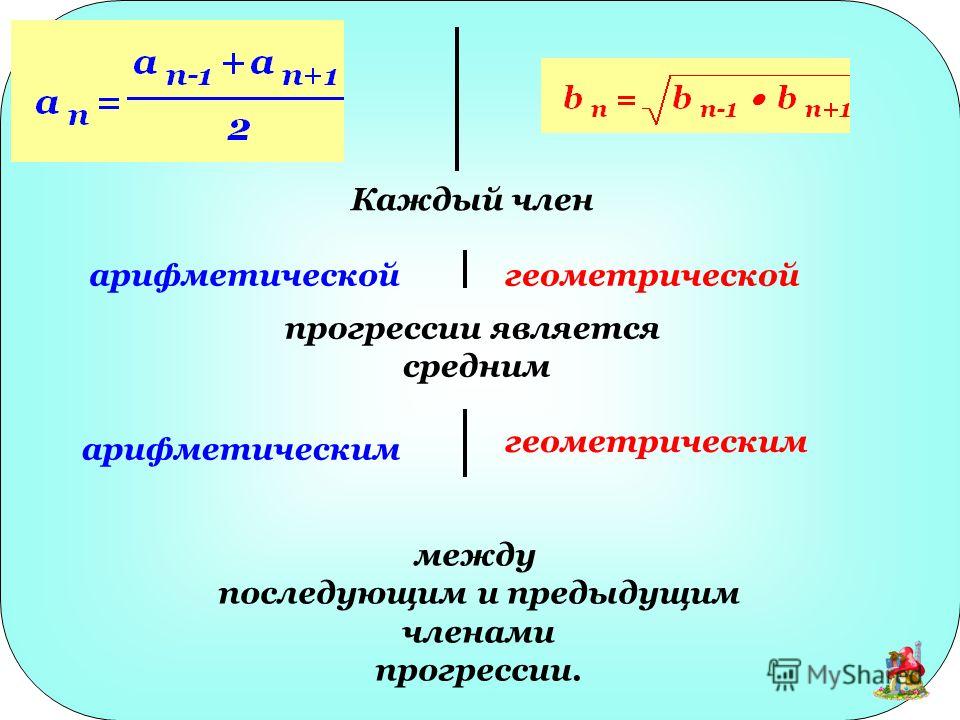 ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Прогрессии — Формулы, теоремы, определения
Типы материалов
- формулы
- теоремы
- определения
- статьи
Показывать разделы
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Формула N-й член арифметической прогрессии
\[a_n = a_1 + (n-1)d = a_{n-1} + d = \frac{a_{n-1} + a_{n+1}}{2}\]
изменить / сообщить об ошибке
Формула Сумма n первых членов арифметической прогрессии
Входящие величины
\(a_1\) — первый член прогрессии
\(a_n\) — n-ый член прогрессии
\(n\) — количество членов прогрессии
\(S_n\) — сумма n членов арифметической прогрессии
\(d\) — разность прогрессии
\[S_n = \sum_{i=1}^n a_i = \frac{a_1 + a_n}{2} n = \frac{2 a_1 + (n-1)d}{2} n\]
изменить / сообщить об ошибке
Определение Арифметическая прогрессия
Арифметическая прогрессия это такая последовательность чисел, в которой разность между последующим и предыдущим членами прогрессии остается неизменной.
n-1)}{q-1}\]
изменить / сообщить об ошибке
Формула Сумма бесконечно убывающей прогрессии
Сумма бесконечно убывающей прогрессии это число, к которому неограниченно приближается сумма первых n членов убывающей прогрессии при неограниченном возрастании числа n. Сумма бесконечно убывающей прогрессии выражается формулой:
\[S = \frac{b_1}{1 — q}\]
изменить / сообщить об ошибке
Определение Геометрическая прогрессия
Геометрическая прогрессия это такая последовательность чисел, в которой отношение между последующим и предыдущим членами прогрессии остается неизменным. Это неизменное отношение называется знаменателем прогрессии.
Возрастающая геометрическая прогрессия
Геометрическая прогрессия называется возрастающей, когда абсолютная величина ее знаменателя больше единицы.
Убывающая геометрическая прогрессия
Геометрическая прогрессия называется убывающей, когда абсолютная величина ее знаменателя меньше единицы.
Замечание Знаменатель прогрессии может быть и отрицательным числом, но прогрессии с отрицательным знаменателем практического значения не имеют.
изменить / сообщить об ошибке
Что такое геометрическая прогрессия?
В математике так много различных элементов, что становится трудно справиться с каждым из них. Пока вы сосредотачиваетесь на теореме Пифагора, геометрическая прогрессия остается на втором плане. Не волнуйтесь, мы здесь, чтобы помочь вам понять, что такое геометрические прогрессии и как их вычислять. В этом руководстве мы объясним все, что вам нужно знать, от того, как вычислить следующее число в геометрической последовательности, до подробностей того, что на самом деле означает обыкновенное отношение.
Что такое геометрическая прогрессия?
Геометрическая прогрессия — это особый вид прогрессии/последовательности. Чтобы последовательность чисел считалась геометрической прогрессией, все они должны быть умножены на обыкновенный коэффициент.
Предыдущее число в последовательности, умноженное на обыкновенный коэффициент, даст вам следующее число в геометрическом ряду.
Например, если ваш общий номер равен 2, последовательность будет следующей:
2, 4, 8, 16, 32…
Мы можем наблюдать геометрическую прогрессию, поскольку каждый последующий член равен предыдущему члену, умноженному на два. Итак, 2 x 2 = 4, затем 4 x 2 = 8, затем 8 x 2 = 16, затем 16 x 2 = 32.
Нанять репетитора по математике
Почему это называется геометрической прогрессией?
Если бы вы думали, что геометрическая прогрессия как-то связана с формами и геометрией, вы бы не были первым. Так почему именно геометрическая прогрессия называется геометрической прогрессией? Что ж, ответ частично связан с геометрией, даже если поначалу так может показаться.
Термин геометрическая прогрессия происходит от идеи среднего геометрического. Среднее геометрическое помогает создавать идеальные прямоугольные треугольники, поскольку каждая предыдущая длина стороны умножается на обыкновенный коэффициент, чтобы увеличить длину стороны треугольника через равные промежутки времени.
Следовательно, хотя при решении последовательности мы в основном имеем дело с числами, их можно использовать и в геометрических целях, отсюда и название.
В чем разница между геометрической прогрессией и арифметической прогрессией?
Между геометрической последовательностью и арифметической последовательностью существует много различий, хотя люди часто путаются между ними. Ниже приводится разбивка основных отличий:
- GP имеет общий коэффициент, AP не имеет
- AP имеет общее отличие, а GP — нет
- Следующее в последовательности является произведением предыдущего числа и знаменателя
- Следующее в последовательности является суммой предыдущего числа и общей разности
- Вариант GP нелинейный
- Изменение точки доступа является линейным
Сколько геометрических прогрессий возможно?
В любой заданной последовательности возможно бесконечное количество геометрических прогрессий.
Хотя начальный член может быть всего лишь 2, постоянное умножение на обыкновенное отношение позволит вам увеличивать число до бесконечности. Следовательно, для последовательностей прогрессии возможны бесконечные сроки. Однако есть некоторые типы GP, которые специально определяются как конечные прогрессии.
Каковы свойства геометрической прогрессии (ГП)?
У всех геометрических прогрессий есть некоторые общие свойства, которые помогают нам сгруппировать последовательности вместе и лучше понять их. Ниже приведены основные свойства, которые вам необходимо знать:
- Если умножить ненулевое количество на каждый член GP, то результирующая последовательность будет иметь общее различие и также будет GP .
- Если вы разделите ненулевое количество на каждый член ОП, то результирующая последовательность разделит общую разность и также будет ОП
- Обратные значения всех членов ГП также образуют ГП
- Если все термины в ОП возвести в одну степень, то новый ряд будет и в ОП .
- Если y² = xz, то три ненулевых члена x, y и z находятся в GP .
Формулы геометрической прогрессии
N-й срок
Формула N-Th выглядит следующим образом:
A N = AR N -1 (OR) A N = R A N -1 (OR) A N = R A N -1 (OR) A N = R A N -1 (OR) A N = R A N
Все, что вам нужно, чтобы найти n-й член последовательности, это начальный член и знаменатель. В формуле каждая буква означает следующее:
a = начальный срок
r = общий рацион
n = последовательные условия, которые необходимо рассчитать
Это одна из наиболее полезных формул при расчете сроков в GP. Это связано с тем, что его не нужно использовать для вычисления соседних членов, но вместо этого его можно использовать для вычисления любого члена в последовательности. Вы можете использовать его, чтобы найти 3-й член, 8-й термин, 15-й термин или даже 100-й термин, так что вы можете выйти далеко за рамки просто соседних терминов.
Почему важно соблюдать порядок действий?
Формула суммы геометрической прогрессии
Если вам нужно вычислить сумму всех чисел в вашей последовательности, вы можете использовать формулу суммы геометрической прогрессии. Формула суммы отличается в зависимости от того, вычисляете ли вы сумму конечного или бесконечного ряда.
Формула конечной суммы выглядит следующим образом:
S n = a(1 − r n )/(1 − r) для r ≠ 1 и
S n = an для r = 1
Формула бесконечной суммы выглядит следующим образом:
S ∞ = a/(1 – r), когда |r| < 1
Сумма не может быть найдена, когда |r| ≥ 1
Услуги репетитора по математике
Если вы изо всех сил пытаетесь разобраться с геометрическими прогрессиями, наши преданные наставники в Tutorax всегда готовы помочь. Мы понимаем, что некоторые понятия в математике просто трудно уложить в голове, поэтому мы полностью стремимся максимально упростить процесс обучения.
Мы предлагаем как личное, так и онлайн-обучение, поэтому ваши занятия могут идеально вписаться в ваш график.
Найти репетитора
Геометрическая прогрессия (ГП): Знать определение, формулу, типы здесь
ГП — это прогрессия, в которой каждый член данной последовательности сохраняет постоянное отношение к предыдущему члену. Геометрическая прогрессия, арифметическая прогрессия и гармоническая прогрессия являются одними из важных тем, связанных с последовательностями и рядами, а также со статистикой . В этой статье вы узнаете все о формуле геометрической прогрессии для нахождения суммы n-го члена, общей форме, свойствах и решенных примерах. Эта тема важна даже для экзаменационных баллов IIT JEE Main и JEE Advanced наряду с техническими экзаменами, такими как GATE EC и UPSC IES.
Геометрическая прогрессия
Тип прогрессии, в котором следующий член получается путем умножения фиксированного члена (который также известен как обыкновенное отношение) каждый раз на предыдущий член, является определением геометрической прогрессии.
Следовательно, согласно определению, вы можете указать, что в GP:
- Последовательность состоит из ненулевых чисел.
- Соотношение термина и предшествующего ему члена остается постоянным.
- Постоянное отношение также известно как обыкновенное отношение (r).
Математически мы можем утверждать, что; последовательность \(a_1, a_2, a_3, a_4, a_5, a_6, \dots\dots a_n\) называется ВП, если \(\frac{a_{n+1}}{a_n} \)= константа.
Также прочтите Свойства арифметических прогрессий.
Geometric Progression Formulas
Check the important geometric progression formulas below:
Term | Formula |
| General form of Geometric Progression 9n}{1-r}\right)\), когда |r|<1 | |
| Сумма бесконечных членов геометрической прогрессии | \(S_∞=\frac{a}{1-r}\) |
Общая форма геометрической прогрессии
Геометрическая прогрессия в математике может быть конечной или бесконечной в зависимости от заданного количества элементов.
{n-1}\). 9п}{1-г}\справа)\).
Также сумма сроков Г.П. ряд, когда количество членов в нем бесконечно, определяется как:
\(S_n=\frac{a}{1-r}\)
Ознакомьтесь с этой статьей о сумме гармонической прогрессии.
Свойства геометрической прогрессии (ГП)
Теперь, когда вы знаете общую форму, конечное и бесконечное представление ГП, а также формулу для суммы n членов. Давайте теперь изучим некоторые важные свойства, связанные с этой темой.
- Когда каждый термин G.P. умножается и делится на фиксированное ненулевое число, то полученная последовательность также является Г.П.
- Если есть две геометрические прогрессии A 1 , A 2 , A 3 , A 4 , 5 , A 6 , ……………. и б 1 , б 2 , б 3 , б 4 , б 5 , б 6 , ……… Затем 9{2}=ac\).
- Обратные значения всех компонентов в G.P находятся также в G.P.
Аналогично, если каждый член О.П. возвести в одинаковую степень, то новые последовательности и ряды также будут в О.П.
Для термов конечной ОП произведение термов, равноудаленных от начала и окончания, одинаково.
Также изучите различные свойства арифметической прогрессии здесь.
Решенные примеры на GP
Теперь, когда вы знаете подробности, касающиеся определения, суммы GP до бесконечности, суммы n терминов с подробными свойствами и связанными с ними вещами. Давайте перейдем к некоторым решенным задачам GP, чтобы понять эти вещи более ясно.
Решено Пример 1: Проверить, находится ли данная последовательность 8, 4, 2, 1, 1/2, 1/4…… в GP или нет.
Решение: Чтобы найти GP, давайте проверим общую разницу между терминами. Здесь \(a_1\)= 8, \(a_2\) = 4, \(a_3\)= 2, \(a_4\) = 1, \(a_5\) = 1/2 и \(a_6\) = 1/4.
Соотношение последовательных терминов равно;
\(\frac{a_2}{a_1}=\frac{4}{8}=\frac{1}{2},\frac{a_3}{a_2}=\frac{2}{4}=\ frac{1}{2},\ \frac{a_4}{a_3}=\frac{1}{2}=\frac{1}{2}\)
Поскольку отношение последовательных членов заданной последовательности равно 1/2, что является фиксированным числом, следовательно, данная последовательность находится в GP.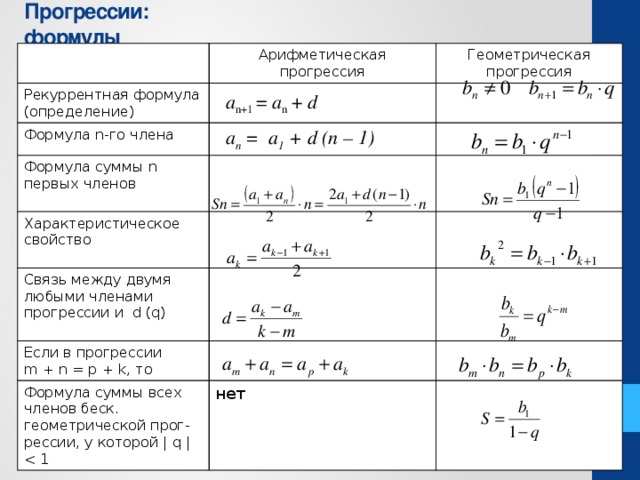
Решено Пример 2: Найдите следующие члены заданной геометрической прогрессии: 1,3,9,27,81,…
Решение: Дана GP равна 1,3,9,27,81,…
Согласно определению, GP представляет собой ряд чисел, в котором каждый член рассчитывается путем умножения предыдущего члена на обыкновенное отношение (фиксированное число).
Обычное отношение:
\(\frac{3}{1}=\frac{9}{3}=\frac{27}{9}\ =3\)
Следовательно, мы можем сказать, что 3 равно обыкновенное отношение данного ряда.
Чтобы проверить соотношение, 1,3,9,27,81,…
Если мы умножим 1 на 3 и получим 3. Это второй член данного ряда.
Далее, умножая 3 на 3, мы получаем 9 в качестве третьего члена и так далее. Следовательно, знаменатель равен 3. Значит, следующий член ряда равен 81, умноженному на 3, т. е. равен 243.
93\) =48 Таким образом, первые 4 члена ГП, начиная с 6 в качестве первого члена и 2 в качестве знаменателя, равны 6, 12, 24, 48.
n-1}{r-1}\right)\), когда |r|>1. 95-1}{2-1}\справа)\)
\(=5\слева(\frac{32-1}{2-1}\справа)\)
\(S_5=5\слева( \frac{31}{1}\right)=155\)
Перепроверьте полученные данные: 5+10+20+ 40+ 80 = 155.
Мы надеемся, что приведенная выше статья поможет вам понять и сдать экзамен. приготовления. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
9n}{1-r}\right)\), когда |r|
<1.Q.3 В чем разница между конечной и бесконечной геометрической прогрессией?
Ответ 3 Основное различие между конечной и бесконечной ПТ состоит в том, что в ПТ конечного типа определен последний член, тогда как в ПФ бесконечного типа последний член не определен.
В.4 В чем разница между арифметической прогрессией и геометрической прогрессией?
Отв.