Решение квадратных уравнений онлайн
С помощю этого онлайн калькулятора можно найти решение (корни) квадратного уравнения. Дается подробное решение с пояснениями. Для нахождения решений квадратного уравнения введите коэффициенты уравнения и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Квадратным уравнением называется уравнение следующего вида:
| ax2+bx+c=0, | (1) |
где x−переменная, а a, b, c некоторые числа (a≠0). Числа a, b, c называются коэффициентами квадратного уравнения. Коэффицинт c называется свободным членом.
Если a=1, то квадратное уравнение называется приведенным. Заметим, что любое квадратное уравнение можно привести к приведенному виду, разделив обе части уравнения на a. Действительно:
Если в квадратном уравнении (1) один из коэффициентов b, c равен нулю или оба коэффициента b, c равны нулю, то квадратное уравнение называется неполным.
Рассмотрим разные виды неполных квадратных уравнений.
1. При b=0 имеем:
| ax2+c=0. | (3) |
Для решения этого уравнения свободный член перенесем в правую часть уравнения:
Решая последнее уравнение относительно x получим корни квадратного уравнения (3):
Если , то квадратное уравнение не имеет действительных корней.
2. При c=0 имеем:
| ax2+bx=0, |
Разложим левую часть последнего уравнения на множители:
| x(ax+b)=0, | (4) |
Из (4) следует x=0 или ax+b=0.
Следовательно имеем следующие решения:
3. При b=0, c=0 имеем:
| ax2=0, |
и, следовательно
Рассмотрим, далее, алгоритм решения квадратных уравнений общего вида (1). Разделим обе части уравнения на a:
Сделаем эквивалентные преобразования уравнения (5):
Легко догадаться, что первые три слагаемые уравнения (6) образуют квадрат следующей суммы:
Тогда
Обозначим
| D=b2−4ac. | (8) |
D− называется дискриминантом квадратного уравнения (1). Так как a≠0, то 4a2>0. Знак правой части уравнения (7) определяется знаком дискриминанта D.
Учитывая (8) запишем (7) в следующем виде:
При решении последнего уравнения возможны следующие варианты:
1.
При D>0, имеем
Таким образом, при D>0, квадратное уравнение (1) имеет две корни:
2.При D=0, имеем
То есть, при D=0 квадратное уравнение (1) имеет единственный корень:
3. При D<0, правая часть уравнения (9) отрицательна, а так как квадрат числа не может быть отрицательным числом, то квадратное уравнение (1) не имеет корней.
Пример 1. Решить квадратное уравнение
| . | (10) |
Решение. Запишем коэффициенты квадратного уравнения (10):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант положительное число. Следовательно квадратное уравнение (10) имеет два решения.
Найдем решение квадратного уравнения используя следующую формулу:
. | (11) |
Подставляя значения коэффициентов a, b, c, D в (11), получим:
| , |
| . |
Ответ:
| x1=3, |
Пример 2. Решить следующее квадратное уравнение:
| . | (12) |
Решение. Запишем коэффициенты квадратного уравнения (12):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант равен нулю. Следовательно квадратное уравнение (12) имеет единственное решение. Найдем решение квадратного уравнения используя следующую формулу:
| . | (13) |
Подставляя значения коэффициентов a, b, c, D в (13), получим:
| , |
Ответ:
. |
Пример 3. Решить следующее квадратное уравнение:
| . | (14) |
Решение. Запишем коэффициенты квадратного уравнения (14):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант отрицательное число. Следовательно квадратное уравнение (14) не имеет действительных корней.
Ответ: Квадратное уравнение не имеет действительных корней.
Калькулятор квадратного уравнения — Калькулятор квадратного уравнения онлайн
Калькулятор квадратного уравнения используется для определения корней заданного квадратного уравнения. Квадратное уравнение — это алгебраическое уравнение с одной переменной и степенью уравнения, равной 2.
Что такое калькулятор квадратных уравнений?
Калькулятор квадратных уравнений — это онлайн-инструмент, который помогает решить заданное квадратное уравнение и найти его корни.
Стандартная форма квадратного уравнения задается осью 2 + bx + c = 0. Здесь x — переменная, a и b — коэффициенты, а c — константа. Чтобы использовать калькулятор квадратного уравнения , введите значения в поля ввода.
Калькулятор квадратных уравнений
ПРИМЕЧАНИЕ. Вводите значения только до двух цифр, а коэффициент x 2 не должен быть равен нулю.
Как пользоваться калькулятором квадратных уравнений?
Чтобы решить квадратное уравнение с помощью калькулятора квадратных уравнений, выполните следующие действия.
- Шаг 1: Воспользуйтесь онлайн-калькулятором квадратных уравнений Cuemath.
- Шаг 2: Введите значения в соответствующие поля ввода калькулятора квадратных уравнений.
- Шаг 3: Нажмите кнопку «Рассчитать» , чтобы решить данное квадратное уравнение.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор квадратных уравнений?
Когда мы решаем квадратное уравнение, мы получаем два значения x. Эти значения известны как корни. Существует 4 метода нахождения корней квадратного уравнения. Это завершение метода квадратов, факторизация квадратного уравнения, использование квадратной формулы и техника построения графиков. Из них самый быстрый способ найти корни данного квадратного уравнения — использовать квадратную формулу. Далее, применяя эту формулу, можно также сделать различные важные выводы относительно природы корней. Если квадратное уравнение задано как ось 2 + bx + c = 0, тогда квадратичная формула имеет вид:
x = (-b ± √(b 2 — 4ac))/2a.Мы можем найти природу корней, анализируя дискриминант (D). Это часть квадратичной формулы и задается следующим образом:
D = b 2 — 4ac.
- D > 0 корни квадратного уравнения действительны и различны.
- D = 0, корни вещественные и равные.
- D < 0, корней не существует, т. е. корни мнимые.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запишитесь на бесплатный пробный урок
Решенные примеры на калькуляторе квадратных уравнений
Пример 1:
Решите квадратное уравнение x 2 + 5x + 6 = 0 и проверьте его с помощью калькулятора квадратных уравнений.
Дано: a = 1, b = 5, c = 6
x = (-b ± √(b 2 — 4ac))/2a.
x = (-5 ± √(5 2 — 4 × 1 × 6))/2 × 1.
x = -2, -3
Следовательно, корни данного квадратного уравнения равны -2 , -3. Далее, при D > 0 корни вещественны и различны.
Пример 2:
Решить квадратное уравнение 2x 2 — 4x + 2 = 0 Проверить его с помощью калькулятора квадратных уравнений.
Решение:
Дано: a = 2, b = -4, c = 2
x = (-b ± √(b 2 — 4ac))/2a.
x = (-(-4) ± √((-4) 2 — 4 × 2 × 2))/2 × 2.
x = 1, 1
Следовательно, x = 1 Далее, как D = 0, корни вещественные и равные.
Точно так же вы можете попробовать калькулятор квадратных уравнений, чтобы решить следующие квадратные уравнения:
- 2x 2 + x — 3 = 0
- х 2 + 10х — 11 = 0
- Квадратные уравнения
- Квадратичные функции
Калькулятор квадратичного графика
Онлайн-калькулятор квадратичного графика — это калькулятор, который поможет вам построить график квадратного уравнения.
Калькулятор квадратичных графиков — это мощный инструмент, который помогает студентам и профессионалам быстро строить и решать сложные квадратные уравнения.
Что такое калькулятор квадратичных графиков?
A Quadratic Graph Calculator – это онлайн-калькулятор, который позволяет быстро строить графики сложных квадратичных функций независимо от их сложности.
Калькулятор квадратичных графиков требует только одного входа; квадратное уравнение графика. После ввода квадратного уравнения Калькулятор квадратичных графиков мгновенно строит график, когда вы нажимаете кнопку «Отправить» 9.кнопка 0165.
Как пользоваться калькулятором квадратичных диаграмм?
Чтобы использовать Калькулятор квадратичных графиков , вам нужно всего лишь ввести данные в соответствующее поле и нажать кнопку «Отправить».
Пошаговые инструкции по использованию Калькулятора квадратичных графиков приведены ниже:
Шаг 1
Сначала необходимо ввести квадратное уравнение или функцию в калькулятор.
Шаг 2
После ввода квадратного уравнения в калькулятор нажмите кнопку Кнопка «Отправить» .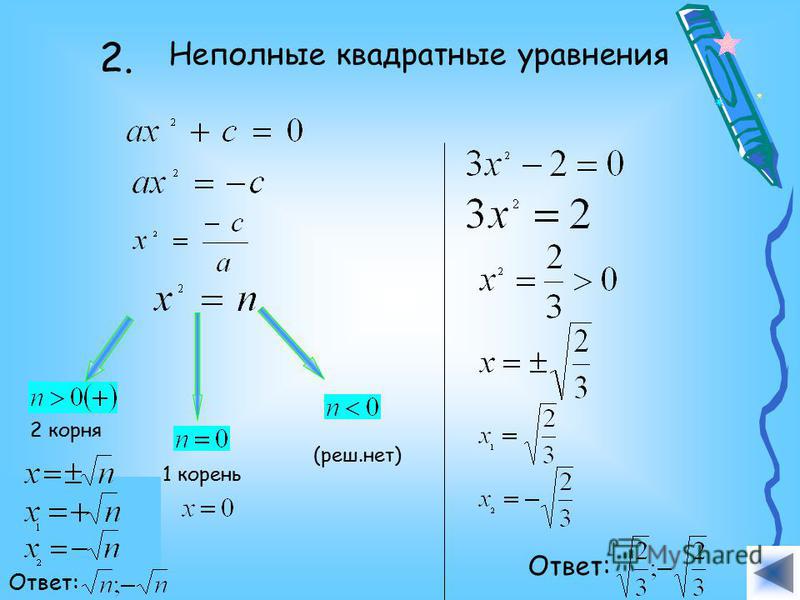
Калькулятор квадратичных графиков построит график уравнения и отобразит его в отдельном окне.
Как работает калькулятор квадратичных диаграмм?
Калькулятор квадратичных графиков работает, используя квадратное уравнение в качестве входных данных и вычисляя его график. Калькулятор также может легко строить графики для сложных многочленов и многочленов более высокой степени.
Квадратные уравнения, используемые в калькуляторе, должны быть аналогичны следующему уравнению: 9{2}+bx+c=0 \tag*{(1)}\]
Что такое квадратные уравнения?
Квадратное уравнение s являются алгебраическими операторами второй степени вида, заданного в уравнении (1). От термина «Квадрат», , что означает квадрат, происходит слово «Квадрат». Другими словами, квадратное уравнение — это уравнение второй степени.
Алгебраическое уравнение второй степени относительно x является квадратным уравнением. В уравнении (1) a и b — коэффициенты, x — переменная, а c — постоянный член.
это 9Сначала записывается член \mathsf{2}$, затем член x и, наконец, постоянный член записывается при построении квадратного уравнения в стандартной форме. Числовые значения a, b и c обычно выражаются как 90 164 целочисленные значения 90 165, а не дроби или десятичные дроби.
Квадратная формула
Квадратная формула — это самый простой метод определения решений квадратного уравнения. Некоторые квадратные уравнения трудно учитывать; в этих случаях мы можем быстро найти корни, используя 9{2}-4ac}}{2a} \]
Что такое корни квадратного уравнения?
Корни квадратного уравнения — это два значения x, полученные путем решения квадратного уравнения. Символы альфа ($\alpha$) и бета ($\beta$) используются для обозначения корней квадратного уравнения. 90 164 нуля 90 165 в уравнении — другое название этих корней квадратного уравнения.
Без фактического определения корней ($\alpha$, $\beta$) уравнения можно определить природу корней квадратного уравнения.