Разложение чисел на простые множители: способы и примеры разложения
Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.
Что значит разложить число на простые множители?
Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2·7·7·23 имеем, что у нас 4 простых множителя в виде 2,7,7,23.
Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30, тогда получим 2,3,5. Запись примет вид 30=2·3·5. Не исключено, что множители могут повторяться. Такое число как 144 имеет 144=2·2·2·2·3·3.
Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.
Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.
При z, относящемуся к целым числам, представляется в виде произведения а и b, где z делится на а и на b. Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1, то его разложение на множители p1, p2, …, pnпринимает вид a=p1, p2, …, pn. Разложение предполагается в единственном варианте.
Каноническое разложение числа на простые множители
При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p1, который встречается s1 раз и так далее pn – sn раз. Таким образом разложение примет вид a=p1s1·a=p1s1·p2s2·…·pnsn. Эта запись имеет название канонического разложения числа на простые множители.
При разложении числа 609840 получим, что 609 840=2·2·2·2·3·3·5·7·11·11,его канонический вид будет 609 840=24·32·5·7·112. При помощи канонического разложения можно найти все делители числа и их количество.
При помощи канонического разложения можно найти все делители числа и их количество.
Алгоритм разложения числа на простые множители
Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p1, p2, …,pnчисел a, a1, a2, …, an-1, это дает возможность получить a=p1·a1, где a1=a:p1, a=p1·a1=p1·p2·a2, где a2=a1:p2, …, a=p1·p2·…·pn·an, где an=an-1:pn. При получении an=1, то равенство a=p1·p2·…·pn получим искомое разложение числа а на простые множители. Заметим, что p1≤p2≤p3≤…≤pn.
Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z. При взятии простых чисел 2,3,5,11 и так далее, причем на них делим число z. Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z. Видно, что не существуют делителей z, тогда понятно, что z является простым числом.
Видно, что не существуют делителей z, тогда понятно, что z является простым числом.
Рассмотрим на примере числа 87. При его делении на 2 имеем, что 87:2=43 с остатком равным 1. Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87:3=29. Отсюда вывод – 3 является наименьшим простым делителем числа 87.
При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a. При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000.
Рассмотрим алгоритм разложения на простые множители:
- нахождение наименьшего множителя при делителе p1 числа a по формуле a1=a:p1, когда a1=1, тогда а является простым числом и включено в разложение на множители, когда не равняется 1, тогда a=p1·a1и следуем к пункту, находящемуся ниже;
- нахождение простого делителя p2 числа a1при помощи последовательного перебора простых чисел, используя a2=a1:p2 , когда a2=1, тогда разложение примет вид a=p1·p2, когда a2=1, тогда a=p1·p2·a2, причем производим переход к следующему шагу;
- перебор простых чисел и нахождение простого делителя p3 числа a2по формуле a3=a2:p3, когда a3=1, тогда получим, что a=p1·p2·p3, когда не равняется 1, тогда a=p1·p2·p3·a3и производим переход к следующему шагу;
- производится нахождение простого делителя pn числа an-1при помощи перебора простых чисел с pn-1, а также an=an-1:pn, где an=1, шаг является завершающим, в итоге получаем, что a=p1·p2·…·pn.

Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.
Полученный алгоритм можно применять при помощи разложения чисел на простые множители.
Примеры разложения на простые множители
Во время разложения на простые множители следует придерживаться основного алгоритма.
Пример 2Произвести разложение числа 78 на простые множители.
Решение
Для того, чтобы найти наименьший простой делитель, необходимо перебрать все простые числа, имеющиеся в 78. То есть 78:2=39. Деление без остатка, значит это первый простой делитель, который обозначим как p1. Получаем, что a1=a:p1=78:2=39. Пришли к равенству вида a=p1·a1, где 78=2·39. Тогда a1=39, то есть следует перейти к следующему шагу.
Остановимся на нахождении простого делителя p2 числа a1=39. Следует перебрать простые числа, то есть 39:2=19 (ост. 1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.
1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.
Наименьший простой делитель числа a2=13 ищется при помощи перебора чисел, начиная с 3. Получим, что 13:3=4 (ост. 1). Отсюда видно, что 13 не делится на 5,7,11, потому как 13:5=2 (ост. 3), 13:7=1 (ост. 6) и 13:11=1 (ост. 2). Видно, что 13 является простым числом. По формуле выглядит так: a3=a2:p3=13:13=1. Получили, что a3=1, что означает завершение алгоритма. Теперь множители записываются в виде 78=2·3·13(a=p1·p2·p3).
Ответ: 78=2·3·13.
Пример 3Разложить число 83 006 на простые множители.
Решение
Первый шаг предусматривает разложение на простые множители p1=2 и a1=a:p1=83 006:2=41 503, где 83 006=2·41 503.
Второй шаг предполагает, что 2, 3 и 5 не простые делители для числа a1=41 503, а 7 простой делитель, потому как 41 503:7=5 929. Получаем, что p2=7, a2=a1:p2=41 503:7=5 929. Очевидно, что 83 006=2·7·5 929.
Нахождение наименьшего простого делителя p4 к числу a3=847 равняется 7. Видно, что a4=a3:p4=847:7=121, поэтому 83 006=2·7·7·7·121.
Для нахождения простого делителя числа a4=121 используем число 11, то есть p5=11. Тогда получим выражение вида a5=a4:p5=121:11=11, и 83 006=2·7·7·7·11·11.
Для числа a5=11 число p6=11является наименьшим простым делителем. Отсюда a6=a5:p6=11:11=1. Тогда a6=1. Это указывает на завершение алгоритма. Множители запишутся в виде 83 006=2·7·7·7·11·11.
Каноническая запись ответа примет вид 83 006=2·73·112.
Ответ: 83 006=2·7·7·7·11·11=2·73·112.
Пример 4Произвести разложение числа 897 924 289 на множители.
Решение
Для нахождения первого простого множителя произвести перебор простых чисел, начиная с 2.
Второй шаг алгоритма заключается в переборе меньших простых чисел. То есть начинаем с числа 937. Число 967 можно считать простым, потому как оно является простым делителем числа a1=958 297. Отсюда получаем, что p2=967, то a2=a1:p1=958 297:967=991 и 897 924 289=937·967·991.
Третий шаг говорит о том, что 991 является простым числом, так как не имеет ни одного простого делителя, который не превосходит 991. Примерное значение подкоренного выражения имеет вид 991<402. Иначе запишем как 991<402. Отсюда видно, что p3=991 и a3=a2:p3=991:991=1. Получим, что разложение числа 897 924 289 на простые множители получается как 897 924 289=937·967·991.
Использование признаков делимости для разложения на простые множители
Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.
Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.
Если необходимо произвести разложение на множители 10, то по таблице видно: 2·5=10. Получившиеся числа 2 и 5 являются простыми, поэтому они являются простыми множителями для числа 10.
Пример 6Если необходимо произвести разложение числа 48, то по таблице видно: 48=6·8. Но 6 и 8 – это не простые множители, так как их можно еще разложить как 6=2·3 и 8=2·4. Тогда полное разложение отсюда получается как 48=6·8=2·3·2·4. Каноническая запись примет вид 48=24·3.
Пример 7При разложении числа 3400 можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на 10 и на 100. Отсюда получаем, что 3 400=34·100, где 100 можно разделить на 10, то есть записать в виде 100=10·10, а значит, что 3 400=34·10·10. Основываясь на признаке делимости получаем, что 3 400=34·10·10=2·17·2·5·2·5. Все множители простые. Каноническое разложение принимает вид 3 400=23·52·17.
Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число 75 в виде произведения множителей, то необходимо учитывать правило делимости на 5. Получим, что 75=5·15, причем 15=3·5. То есть искомое разложение пример вид произведения 75=5·3·5.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Разложение чисел на простые множители: способы и примеры разложения
Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.
Что значит разложить число на простые множители?
Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2·7·7·23 имеем, что у нас 4 простых множителя в виде 2,7,7,23.
В произведении вида 2·7·7·23 имеем, что у нас 4 простых множителя в виде 2,7,7,23.
Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30, тогда получим 2,3,5. Запись примет вид 30=2·3·5. Не исключено, что множители могут повторяться. Такое число как 144 имеет 144=2·2·2·2·3·3.
Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.
При z, относящемуся к целым числам, представляется в виде произведения а и b, где z делится на а и на b. Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1, то его разложение на множители p1, p2, …, pnпринимает вид a=p1, p2, …, pn. Разложение предполагается в единственном варианте.
Каноническое разложение числа на простые множители
При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p1, который встречается s1 раз и так далее pn – sn раз. Таким образом разложение примет вид a=p1s1·a=p1s1·p2s2·…·pnsn. Эта запись имеет название канонического разложения числа на простые множители.
Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p1, который встречается s1 раз и так далее pn – sn раз. Таким образом разложение примет вид a=p1s1·a=p1s1·p2s2·…·pnsn. Эта запись имеет название канонического разложения числа на простые множители.
При разложении числа 609840 получим, что 609 840=2·2·2·2·3·3·5·7·11·11,его канонический вид будет 609 840=24·32·5·7·112. При помощи канонического разложения можно найти все делители числа и их количество.
Алгоритм разложения числа на простые множители
Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p1, p2, …,pnчисел a, a1, a2, …, an-1, это дает возможность получить a=p1·a1, где a1=a:p1, a=p1·a1=p1·p2·a2, где a2=a1:p2, …, a=p1·p2·…·pn·an, где an=an-1:pn. При получении an=1, то равенство a=p1·p2·…·pn получим искомое разложение числа а на простые множители. Заметим, что p1≤p2≤p3≤…≤pn.
Заметим, что p1≤p2≤p3≤…≤pn.
Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z. При взятии простых чисел 2,3,5,11 и так далее, причем на них делим число z. Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z. Видно, что не существуют делителей z, тогда понятно, что z является простым числом.
Рассмотрим на примере числа 87. При его делении на 2 имеем, что 87:2=43 с остатком равным 1. Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87:3=29. Отсюда вывод – 3 является наименьшим простым делителем числа 87.
При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a. При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000.
Рассмотрим алгоритм разложения на простые множители:
- нахождение наименьшего множителя при делителе p1 числа a по формуле a1=a:p1, когда a1=1, тогда а является простым числом и включено в разложение на множители, когда не равняется 1, тогда a=p1·a1и следуем к пункту, находящемуся ниже;
- нахождение простого делителя p2 числа a1при помощи последовательного перебора простых чисел, используя a2=a1:p2, когда a2=1, тогда разложение примет вид a=p1·p2, когда a2=1, тогда a=p1·p2·a2, причем производим переход к следующему шагу;
- перебор простых чисел и нахождение простого делителя p3 числа a2по формуле a3=a2:p3, когда a3=1, тогда получим, что a=p1·p2·p3, когда не равняется 1, тогда a=p1·p2·p3·a3и производим переход к следующему шагу;
- производится нахождение простого делителя pn числа an-1при помощи перебора простых чисел с pn-1, а также an=an-1:pn, где an=1, шаг является завершающим, в итоге получаем, что a=p1·p2·…·pn.

Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.
Полученный алгоритм можно применять при помощи разложения чисел на простые множители.
Примеры разложения на простые множители
Во время разложения на простые множители следует придерживаться основного алгоритма.
Пример 2Произвести разложение числа 78 на простые множители.
Решение
Для того, чтобы найти наименьший простой делитель, необходимо перебрать все простые числа, имеющиеся в 78. То есть 78:2=39. Деление без остатка, значит это первый простой делитель, который обозначим как p1. Получаем, что a1=a:p1=78:2=39. Пришли к равенству вида a=p1·a1, где 78=2·39. Тогда a1=39, то есть следует перейти к следующему шагу.
Остановимся на нахождении простого делителя p2 числа a1=39. Следует перебрать простые числа, то есть 39:2=19 (ост. 1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.
1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.
Наименьший простой делитель числа a2=13 ищется при помощи перебора чисел, начиная с 3. Получим, что 13:3=4 (ост. 1). Отсюда видно, что 13 не делится на 5,7,11, потому как 13:5=2 (ост. 3), 13:7=1 (ост. 6) и 13:11=1 (ост. 2). Видно, что 13 является простым числом. По формуле выглядит так: a3=a2:p3=13:13=1. Получили, что a3=1, что означает завершение алгоритма. Теперь множители записываются в виде 78=2·3·13(a=p1·p2·p3).
Ответ: 78=2·3·13.
Пример 3Разложить число 83 006 на простые множители.
Решение
Первый шаг предусматривает разложение на простые множители p1=2 и a1=a:p1=83 006:2=41 503, где 83 006=2·41 503.
Второй шаг предполагает, что 2, 3 и 5 не простые делители для числа a1=41 503, а 7 простой делитель, потому как 41 503:7=5 929. Получаем, что p2=7, a2=a1:p2=41 503:7=5 929. Очевидно, что 83 006=2·7·5 929.
Нахождение наименьшего простого делителя p4 к числу a3=847 равняется 7. Видно, что a4=a3:p4=847:7=121, поэтому 83 006=2·7·7·7·121.
Для нахождения простого делителя числа a4=121 используем число 11, то есть p5=11. Тогда получим выражение вида a5=a4:p5=121:11=11, и 83 006=2·7·7·7·11·11.
Для числа a5=11 число p6=11является наименьшим простым делителем. Отсюда a6=a5:p6=11:11=1. Тогда a6=1. Это указывает на завершение алгоритма. Множители запишутся в виде 83 006=2·7·7·7·11·11.
Каноническая запись ответа примет вид 83 006=2·73·112.
Ответ: 83 006=2·7·7·7·11·11=2·73·112.
Пример 4Произвести разложение числа 897 924 289 на множители.
Решение
Для нахождения первого простого множителя произвести перебор простых чисел, начиная с 2.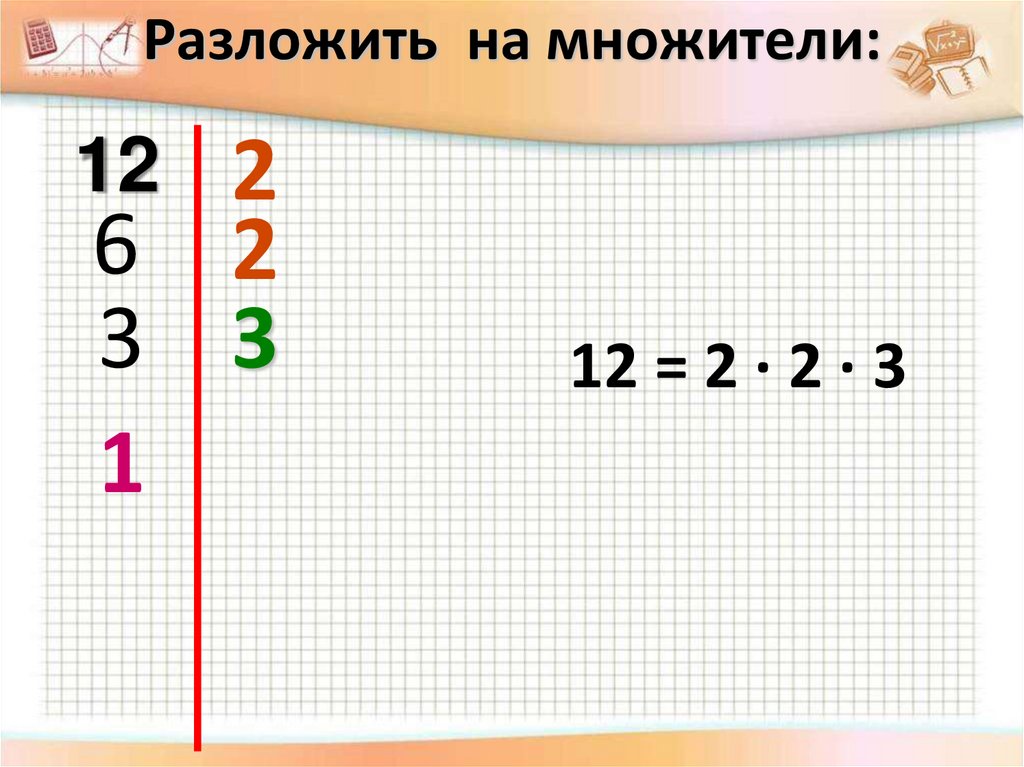 Конец перебора приходится на число 937. Тогда p1=937, a1=a:p1=897 924 289:937=958 297 и 897 924 289=937·958 297.
Конец перебора приходится на число 937. Тогда p1=937, a1=a:p1=897 924 289:937=958 297 и 897 924 289=937·958 297.
Второй шаг алгоритма заключается в переборе меньших простых чисел. То есть начинаем с числа 937. Число 967 можно считать простым, потому как оно является простым делителем числа a1=958 297. Отсюда получаем, что p2=967, то a2=a1:p1=958 297:967=991 и 897 924 289=937·967·991.
Третий шаг говорит о том, что 991 является простым числом, так как не имеет ни одного простого делителя, который не превосходит 991. Примерное значение подкоренного выражения имеет вид 991<402. Иначе запишем как 991<402. Отсюда видно, что p3=991 и a3=a2:p3=991:991=1. Получим, что разложение числа 897 924 289 на простые множители получается как 897 924 289=937·967·991.
Ответ: 897 924 289=937·967·991.
Использование признаков делимости для разложения на простые множители
Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.
Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.
Если необходимо произвести разложение на множители 10, то по таблице видно: 2·5=10. Получившиеся числа 2 и 5 являются простыми, поэтому они являются простыми множителями для числа 10.
Пример 6Если необходимо произвести разложение числа 48, то по таблице видно: 48=6·8. Но 6 и 8 – это не простые множители, так как их можно еще разложить как 6=2·3 и 8=2·4. Тогда полное разложение отсюда получается как 48=6·8=2·3·2·4. Каноническая запись примет вид 48=24·3.
Пример 7При разложении числа 3400 можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на 10 и на 100. Отсюда получаем, что 3 400=34·100, где 100 можно разделить на 10, то есть записать в виде 100=10·10, а значит, что 3 400=34·10·10. Основываясь на признаке делимости получаем, что 3 400=34·10·10=2·17·2·5·2·5. Все множители простые. Каноническое разложение принимает вид 3 400=23·52·17.
Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число 75 в виде произведения множителей, то необходимо учитывать правило делимости на 5. Получим, что 75=5·15, причем 15=3·5. То есть искомое разложение пример вид произведения 75=5·3·5.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Разложение числа на простые множители и наименьшее общее кратное
Результаты обучения
- Найти разложение числа на простые множители
- Найти наименьшее общее кратное списка чисел
Слово фактор может быть как существительным, так и глаголом. Разложить число на множители — значит переписать его, разложив на произведение меньших чисел. Например, мы можем разложить 24, написав это как [латекс]6\аст4[/латекс]. Мы говорим, что 6 и 4 являются делителями 24.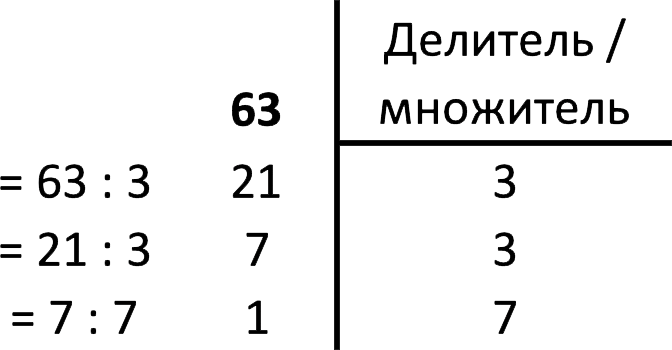 Но то же самое можно сказать и о 2 и 12. Есть много способов записать это число.
Но то же самое можно сказать и о 2 и 12. Есть много способов записать это число.
Полезным навыком при занятиях алгеброй является умение переписывать числа и выражения в удобной форме. Например, рассмотрим несколько различных форм числа 24.
[латекс]24 \qquad \dfrac{72}{3} \qquad \sqrt{576} \qquad 6\ast4 \qquad 2\cdot2\cdot2\cdot3 [ /латекс].
Составные числа , такие как 24, являются натуральными числами, которые могут быть записаны как произведения других натуральных чисел. Простые числа – это натуральные числа, которые имеют только два возможных делителя: самих себя и число 1. Окончательная форма числа 24 в приведенном выше списке, [latex]2\cdot2\cdot2\cdot3 [/latex], называется его простая факторизация . Когда мы записываем простую факторизацию числа, мы записываем его как произведение только его простых множителей. Умение находить простую факторизацию составного числа — особенно полезный навык при занятиях алгеброй.
Простая факторизация
Простая факторизация числа — это произведение простых чисел, равное числу.
При работе с этим разделом вы можете обратиться к следующему списку простых чисел, меньших [latex]50[/latex].
[латекс]2,3,5,7,11,13,17,19,23,29,31,37,41,43,47[/латекс]
Совет : Знание первых пяти простых чисел пригодится при сокращении дробей.
Факторизация простых чисел с использованием метода факторного дерева
Один из способов найти простую факторизацию числа состоит в том, чтобы построить дерево факторов. Начнем с того, что запишем число, а затем запишем его как произведение двух множителей. Мы записываем факторы под числом и соединяем их с числом небольшим отрезком линии — «ветвью» дерева факторов.
Если множитель простой, мы обводим его кружком (как почку на дереве) и больше не факторизуем эту «ветвь». Если множитель не является простым, мы повторяем этот процесс, записывая его как произведение двух множителей и добавляя новые ветви к дереву.
Продолжаем, пока все ветки не закончатся штрихом. Когда факторное дерево завершено, обведенные простые числа дают нам простую факторизацию.
Например, давайте найдем простую факторизацию [latex]36[/latex]. Мы можем начать с любой пары факторов, такой как [латекс]3[/латекс] и [латекс]12[/латекс]. Мы пишем [латекс]3[/латекс] и [латекс]12[/латекс] ниже [латекс]36[/латекс] с ответвлениями, соединяющими их.
Множитель [латекс]3[/латекс] является простым, поэтому мы его обводим. Множитель [latex]12[/latex] составной, поэтому нам нужно найти его множители. Давайте используем [латекс]3[/латекс] и [латекс]4[/латекс]. Запишем эти множители на дереве под [latex]12[/latex].
Множитель [латекс]3[/латекс] является простым, поэтому мы его обводим. Множитель [латекс]4[/латекс] является составным и делится на [латекс]2\cdot 2[/латекс]. Мы записываем эти факторы под [латекс]4[/латекс]. Поскольку [latex]2[/latex] — простое число, мы обводим оба [latex]2\text{s}[/latex]. 9{2}\end{array}[/latex]
9{2}\end{array}[/latex]
Обратите внимание, что мы могли бы начать наше дерево факторов с любой пары факторов [latex]36[/latex]. Мы выбрали [латекс]12[/латекс] и [латекс]3[/латекс], но результат был бы таким же, если бы мы начали с [латекс]2[/латекс] и [латекс]18, 4[/ латекс] и [латекс]9,\текст{ или }6\текст{ и }6[/латекс].
Найдите простую факторизацию составного числа, используя метод дерева
- Найдите любую пару множителей данного числа и используйте эти числа для создания двух ветвей.
- Если множитель простой, эта ветвь завершена. Обведите штрих.
- Если множитель не является простым, запишите его как произведение пары множителей и продолжите процесс.
- Запишите составное число как произведение всех обведенных простых чисел.
пример
Найдите простую факторизацию [latex]48[/latex], используя метод факторного дерева.
Решение:
 The prime factorization can be written as 2 times 2 times 2 times 2 times 3 or using exponents for repeated multiplication of 2 it can be written as 2 to the fourth power times 3.»>
The prime factorization can be written as 2 times 2 times 2 times 2 times 3 or using exponents for repeated multiplication of 2 it can be written as 2 to the fourth power times 3.»>Мы обводим [латекс]2[/латекс], потому что это простое число, и эта ветвь завершена.
Мы обводим [latex]2\text{s и }3[/latex], поскольку они простые. Теперь все ветви заканчиваются штрихом. 9{4}\cdot 3[/латекс]
Проверьте это самостоятельно, перемножив все коэффициенты. Результат должен быть [латекс]48[/латекс].
попробуйте
В следующем видео показано, как найти простую факторизацию [latex]60[/latex] с помощью метода факторного дерева.
пример
Найдите простую факторизацию [latex]84[/latex], используя метод факторного дерева.
Показать решение
попробуй
Есть и другие методы, которые хорошо работают для нахождения простой факторизации числа. Приемлем любой метод, который многократно выносит на множители небольшие простые числа, пока не останутся только простые множители. Посмотрите видео ниже для демонстрации использования деления с накоплением для нахождения простой факторизации.
Нахождение наименьших общих кратных
Рассмотрим кратные двух чисел, 3 и 4. Каково наименьшее общее кратное между ними?
Каково наименьшее общее кратное между ними?
Конечно, числа 3 и 4 имеют много общих кратных: 12, 24, 36 и т. д. Но 12 — наименьшее из них.
Наименьшее число, кратное двум числам, называется наименьшим общим кратным (НОК). Таким образом, LCM для [латекса]3[/латекса] и [латекса]4[/латекса] составляет [латекс]12[/латекс].
Одна из причин, по которой мы находим факторизации простых чисел, заключается в том, что они используются для нахождения наименьшего общего кратного двух или более чисел. Это будет полезно, когда мы будем складывать и вычитать дроби с разными знаменателями.
Метод простых множителей
Мы можем найти наименьшее общее кратное двух чисел, проверяя их простые множители. Мы будем использовать этот метод, чтобы найти LCM [latex]12[/latex] и [latex]18[/latex].
Начнем с нахождения разложения каждого числа на простые множители.
[latex]12=2\cdot 2\cdot 3 \qquad[/latex] и [latex] \qquad 18=2\cdot 3\cdot 3[/latex]
Затем мы находим наибольший экземпляр каждого простого числа появляется в любой факторизации. Здесь мы видим, что число 2 появляется дважды в факторизации 12, но только один раз в 18. А число 3 появляется дважды в 18, но только один раз в 12. Итак, мы выбираем [latex]2\cdot2[/latex ] и [latex]3\cdot3[/latex] и перемножьте их вместе, чтобы найти LCM.
Здесь мы видим, что число 2 появляется дважды в факторизации 12, но только один раз в 18. А число 3 появляется дважды в 18, но только один раз в 12. Итак, мы выбираем [latex]2\cdot2[/latex ] и [latex]3\cdot3[/latex] и перемножьте их вместе, чтобы найти LCM.
[латекс]12=2\cdot 2\cdot 3 \qquad \text{ и } \qquad 18=2\cdot 3\cdot 3[/латекс]
[латекс]\qquad 2\cdot2 \qquad \qquad \ast \qquad \qquad 3\cdot3 [/latex].
[латекс]\qquad\quad \qquad 2\cdot2\cdot3\cdot3=36[/латекс].
НОК 12 и 18 равен 36.
Если простое число встречается одинаковое количество раз в любой факторизации, просто выберите один экземпляр. Давайте найдем LCM списка чисел в качестве примера.
Найдите НОК чисел 12, 18, 20 и 60. Сначала запишем числа как произведения простых чисел.
[латекс]12 = 2\cdot2\cdot3 \qquad 18=2\cdot3\cdot3 \qquad 20=2\cdot2\cdot5 \qquad 60=2\cdot2\cdot3\cdot5[/latex]
Мы видим, что самый большой экземпляр числа 2 появляется в числах 12, 20 и 60. Но мы просто выбираем один самый большой экземпляр. Наибольшее число 3 встречается в 18, где есть два делителя 3. А число 5 встречается один раз в 20 и один раз в 60, поэтому мы выберем один 5.
Но мы просто выбираем один самый большой экземпляр. Наибольшее число 3 встречается в 18, где есть два делителя 3. А число 5 встречается один раз в 20 и один раз в 60, поэтому мы выберем один 5.
НОК 12, 18, 20 , а 60 — это
[латекс]2\cdot2\cdot3\cdot3\cdot5 = 180[/латекс].
Итак, 180 — это наименьшее число, на которое без остатка делятся 12, 18, 20 и 60.
Найдите НОК с помощью метода простых множителей
- Найдите разложение каждого числа на простые множители.
- Проверить каждую факторизацию на наличие наибольшего числа экземпляров каждого простого числа, появляющегося в каждой факторизации
- Выберите по одному набору каждого наибольшего экземпляра каждого появляющегося простого множителя.
- Перемножьте выбранные коэффициенты, чтобы получить LCM.
Может быть полезно написать простые множители рядом с каждым числом, сопоставив их по вертикали в столбцах, а затем сведя простые числа в каждом столбце, чтобы собрать множители, произведением которых является НОК. Следующие примеры иллюстрируют эту технику.
Следующие примеры иллюстрируют эту технику.
пример
Найдите LCM [латекс]15[/латекс] и [латекс]18[/латекс], используя метод простых множителей.
Показать решение
попробуйте
пример
Найдите НОК для [латекс]50[/латекс] и [латекс]100[/латекс], используя метод простых множителей.
Показать решение
попробуйте
В следующем видео мы увидим, как найти наименьшее общее кратное с помощью простой факторизации.
Факторизация простых чисел – объяснение и примеры
Факторизация простых чисел – это метод нахождения всех простых чисел, которые умножаются, образуя число. Факторы умножаются, чтобы получить число, а простые множители — это числа, которые можно разделить только на 1 или на себя.
Существует два метода нахождения простых множителей числа. Это повторное деление и факторное дерево.
Повторное деление
Число уменьшается путем его деления на несколько простых чисел. Простые делители числа 36 находятся повторным делением, как показано:
Таким образом, простые делители числа 36 равны 2 и 3. Это можно записать как 2 × 2 × 3 × 3. Целесообразно начать делить число на наименьшее простое число и переходим к большим множителям.
Пример 1
Каковы простые делители числа 16?
Решение
Лучший способ решить эту задачу — определить наименьший простой делитель числа, равный 2.
Разделить число на 16;
16 ÷ 2 = 8
Поскольку 8 не является простым числом, снова разделите его на наименьший множитель;
8 ÷ 2 = 4
4 ÷ 2 = 2
У нас есть простые делители числа 16, выделенные желтым цветом, и они включают: 2 x 2 x 2 x 2.
, которые можно записать в виде степени:
16 = 2 2
Пример 2
Найдите основной коэффициент
111111111111119 гг.
12 ÷ 2 = 6
6 не простое число, продолжайте;
6 ÷ 2 = 3.
Следовательно, 12 = 2 x 2 x 3
12 = 2 2 × 3
Известно, что все простые делители числа являются простыми.
Пример 3
Факторизация 147.
Решение
Начните с деления 147 на наименьшее простое число.
147 ÷ 2 = 73,5
Наш ответ не является целым числом, попробуйте следующее простое число 3.
147 ÷ 3 = 49
Да, 3 сработало, теперь переходите к следующему простому числу, которое может разделить 49.
49 ÷ 7 = 7
Следовательно, 147 = 3 x 7 x 7,
= 3 x 7 2 . Пример 4
Какова простая факторизация числа 19?
19 = 19
Решение
Другой метод факторизации состоит в том, чтобы разбить число на два целых числа.


