Проект по теме»10 способов решения квадратных уравнений»
МБОУ Новотроицкая СОШ
10 способов
решения квадратных уравнений
Выпонил: ученица 9 класса
Солодовникова Раиса
Руководитель проекта:
Чемоданогва Ирина Сергеевна
Работа допущена к защите «_____» _______________ 201____г.
Подпись руководителя проекта ____________________(__________________)
с. Новотроицк
2018 г.
ОГЛАВЛЕНИЕ
Введение
I. История развития квадратных уравнений
1.1. Из история квадратных уравнений
1.1.1. Квадратные уравнения в Древнем Вавилоне
1.1.2.Квадратные уравнения в Индии.
1.1.3. Квадратные уравнения у ал — Хорезми.
1.1.4. Квадратные уравнения в Европе XIII — XVII вв.
- Квадратные уравнения и их виды
II. Способы решения квадратных уравнений
2.1.Разложение левой части уравнения на множители
2.2.Метод выделения полного квадрата
Решение квадратных уравнений по формулам
Решение уравнений с использованием теоремы Виета
5.
Решение уравнений способом переброски».
- Свойства коэффициентов квадратного уравнения
7.Графическое решение квадратного уравнения
8.Решение квадратных уравнений с помощью циркуля и линейки
9.Решение квадратных уравнений с помощью номограммы
10. Геометрический способ решения квадратных уравнений
Заключение
Список информационных источников
Приложения
Введение
Теория уравнений в школьном курсе алгебры занимает ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Это связано с тем, что большинство жизненных задач сводится к решению различных видов уравнений.
В учебнике алгебры для 8 класса мы знакомимся с несколькими видами квадратных уравнений, и отрабатывали их решение по формулам. У меня возник вопрос «Существуют ли другие методы решения квадратных уравнений? Насколько сложны данные методы и можно ли ими пользоваться на практике?» Поэтому в этом учебном году я выбрала тему исследования связанную с квадратными уравнениями, в ходе работы она получил название «10 способов решения квадратных уравнений».
Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, это также может мне пригодится при решении более сложных задач, в том числе и при сдаче экзаменов.
Цели работы: изучить различные способы решения квадратных уравнений.
Исходя из данной цели, мною были поставлены следующие задачи:
— изучить историю развития квадратных уравнений;
— рассмотреть стандартные и нестандартные способы решения квадратных уравнений;
— выявить наиболее удобные способы решения квадратных уравнений;
— научиться решать квадратные уравнения различными способами.
Объект исследования: квадратные уравнения.
Предмет исследования: способырешения квадратных уравнений.
Методы исследования:
Теоретические: изучение литературы по теме исследования;
Internet –информации.
Анализ: информации полученной при изучении литературы;
результатов полученных при решении квадратных уравнений различными способами.
Сравнение способов на рациональность их использования при решении квадратных уравнений.
1. История развития квадратных уравнений.
1.1.1.Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
X2 + X = ¾; X2 — X = 14,5
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила.
Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
1.1.2.Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ах2 + bх = с, а > 0. (1)
В уравнении (1) коэфиценты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».
Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис).
Соответствующее задаче уравнение:
(x/8)2 + 12 = x
Бхаскара пишет под видом:х2 — 64х = -768
и, чтобы дополнить левую часть этого
уравнения до квадрата, прибавляет к обеим частям 322, получая затем:х2 — 64х + 322 = -768 + 1024,
(х — 32)2 = 256,
х — 32 = ± 16,
х1 = 16, х2 = 48.
1.1.3.Квадратные уравнения у ал — Хорезми.
В алгебраическом трактате ал — Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корнями», т.е. ах2 + с = bх.
2) «Квадраты равны числу», т.е. ах2 = с.
3) «Корни равны числу», т.е. ах = с.
4) «Квадраты и числа равны корням», т.е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т.е. ах2 + bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = ах2.
Для ал — Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал — джабр и ал — мукабала. Его решения, конечно, не совпадает полностью с современным решением. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал — Хорезми, как и все математики до XVII в.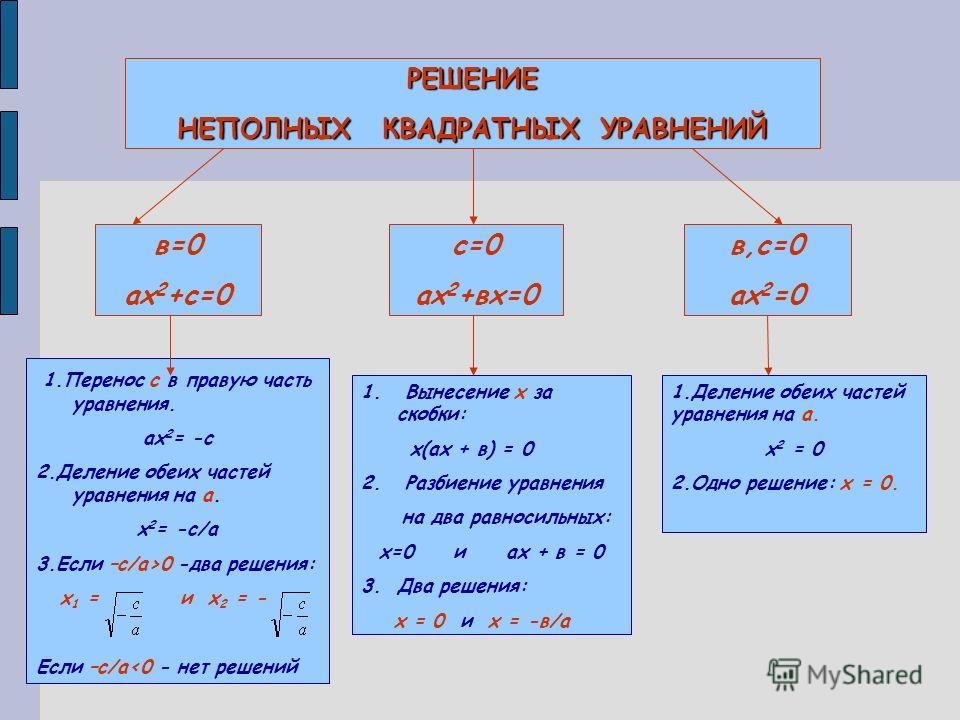
, не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал — Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.
Задача . «Квадрат и число 21 равны 10 корням. Найти корень»
(подразумевается корень уравнения х2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал — Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
1.1.4. Квадратные уравнения в Европе XIII — XVII вв.
Формулы решения квадратных уравнений по образцу ал — Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г.
итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду: х2 + bx = с,
при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в.
Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
1.2.Квадратные уравнения и их виды.
Уравнение вида ax2 + bx + c = 0, где a, b, c — действительные числа, причем a ≠ 0, называют квадратным уравнением.
Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным.
Числа a, b, c носят следующие названия: a — первый коэффициент, b — второй коэффициент, c — свободный член.
Если в квадратном уравнении ax2 + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.
Неполные квадратные уравнения бывают трёх видов:
1) ах2 + с = 0, где с ≠ 0;
2) ах2 + bх = 0, где b ≠ 0;
3) ах2 = 0.
II. Способы решения квадратных уравнений
2.1.Разложение левой части уравнения на множители.
Решим уравнение х2 + 10х — 24 = 0. Разложим левую часть на множители:
х2 + 10х — 24 = х2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:(х + 12)(х — 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х2 + 10х — 24 = 0.
2.2.Метод выделения полного квадрата.
Решим уравнение х2 + 6х — 7 = 0. Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:х2 + 6х = х2 + 2• х • 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так какх2 + 2• х • 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнениях2 + 6х — 7 = 0,прибавляя к ней и вычитая 32. Имеем:
х2 + 6х — 7 = х2 + 2• х • 3 + 32 — 32 — 7 = (х + 3)2 — 9 — 7 = (х + 3)2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 — 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
2.3. Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) — b2 + 4ac = 0,
(2ax + b)2 = b2 — 4ac,
2ax + b = ± √ b2 — 4ac,
2ax = — b ± √ b2 — 4ac,
• Примеры.
а) Решим уравнение: 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 — 4ac = 72 — 4 • 4 • 3 = 49 — 48 = 1,
D> 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b2 — 4ac>0 , уравнение ах2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b2 — 4ac = (-4)2 — 4 • 4 • 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение
ах2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b2 — 4ac = 32 — 4 • 2 • 4 = 9 — 32 = — 13 , D
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b2 — 4ac
ах2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
2.4.Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 + x2 = — p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q> 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p.
Если р
Например,
x2 – 3x + 2 = 0; x1 = 2 иx2 = 1, так какq = 2 > 0 иp = — 3
x2 + 8x + 7 = 0; x1 = — 7 иx2 = — 1, так какq = 7 > 0 иp= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q 0 .
Например,
x2 + 4x – 5 = 0; x1 = — 5 иx2 = 1, так какq= — 5 0;
x2 – 8x – 9 = 0; x1 = 9 иx2 = — 1, так какq = — 9
2.5.Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0,равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.Окончательно получаем х1 = у1/а и х1 = у2/а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
• Пример.
Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета
у1 = 5 х1 = 5/2 x1 = 2,5
у2 = 6 x2 = 6/2 x2 = 3.
Ответ: 2,5; 3.
2.6. Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1, х2 = с/а.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + b/a• x + c/a = 0.
Согласно теореме Виета
x1 + x2 = — b/a,
x1x2 = 1• c/a.
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x1 + x2 = — а + b/a= -1 – c/a,
x1x2 = — 1• ( — c/a),
т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.
• Примеры.
Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х1 = 1, х2 = c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х2 – 247х + 115 = 0.
Решение. Так кака + b + с = 0 (132 – 247 + 115 = 0), то
х1 = 1, х2 = c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k– четное число, то формулу корней
• Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D> 0, два различных корня;
Ответ: 2; 8/3
2.7.Графическое решение квадратного уравнения.
Если в уравнении х2 + px + q = 0перенести второй и третий члены в правую часть, то получим
х2 = — px — q.
Построим графики зависимости у = х2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости — прямая (рис.1). Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках,абсциссы точек пересечения являются корнями квадратного уравнения;- прямая и парабола могут касаться ( только одна общая точка), т.
е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Примеры.
1) Решим графически уравнение х2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4. Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13). Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1 = — 1 и х2 = 4. Ответ: х1 = — 1;
х2 = 4.
2) Решим графически уравнение (рис. 3) х2 — 2х + 1 = 0.
Решение. Запишем уравнение в виде х2 = 2х — 1.
Построим параболу у = х2 и прямую у = 2х — 1.
Прямую у = 2х — 1 построим по двум точкам М (0; — 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с
абсциссой х = 1. Ответ: х = 1.
3) Решим графически уравнение х2 — 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х2 = 5х — 5. Построим параболу у = х2 и прямую у = 2х — 5.
Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х2 — 2х + 5 = 0 корней не имеет.
2.8.Решение квадратных уравнений с помощью циркуля и линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах2 + bх + с = 0, и проходит через точкиА(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD.
2.9.Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построенапо формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), изподобия треугольников САН и CDF получим пропорцию, откуда после подстановок и упрощений вытекает уравнение
z2 + pz + q = 0,причем буква z означает метку любой точки криволинейной шкалы.
• Примеры.
1) Для уравнения z2 — 9z + 8 = 0 номограмма дает корни z1 = 8,0 и z2 = 1,0 (рис.12).
2) Решим с помощью номограммы уравнение
2z2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z2 — 4,5z + 1 = 0.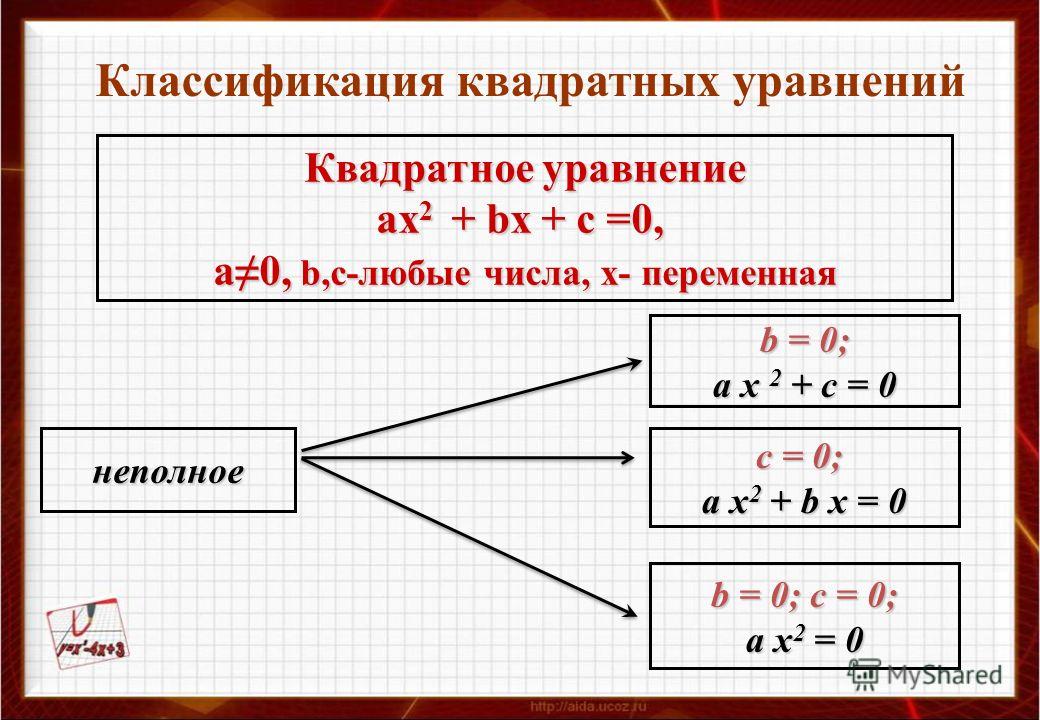
Номограмма дает корни z1 = 4 иz2 = 0,5.
3) Для уравнения
z2 — 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t,
получим уравнение
t2 — 5t + 2,64 = 0,
которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откудаz1 = 5t1 = 3,0 иz2 = 5t2 = 22,0.
2.10. Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S =х2 + 10х + 25. Заменяя
х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
2) А вот, например, как древние греки решали уравнение у2 + 6у — 16 = 0.
Решение представлено на рис. 16, где
у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой
один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = — 8 (рис.16).
Заключение
В ходе выполнения своей исследовательской работы я считаю, что с поставленной целью и задачами я справилась, мне удалось обобщить и систематизировать изученный материал по выше указанной теме.
Способов решения квадратных уравнений очень много. Я нашла 10 способов решения квадратных уравнений. Нужно отметить, что не все они удобны для решения, но каждый из них по-своему уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на контрольных работах и экзаменах. При работе над темой я ставил задачу выяснить какие методы являются стандартными, а какие нестандартными.
Итак, стандартные методы (используются чаще при решении квадратных уравнений):
- Решение квадратных уравнений по формулам
- Теорема Виета
- Графическое решение уравнений
- Разложение левой части на множители
- Выделение полного квадрата
Нестандартные методы:
- Решение способом переброски коэффициентов
- Свойства коэффициентов квадратного уравнения
- Решение квадратных уравнений, с помощью циркуля и линейки.
- Решение с помощью номограммы
- Геометрический способ
При решении квадратных уравнений для себя я сделала следующие выводы: Для того, чтобы хорошо решать любое квадратные уравнения необходимо знать:
- формулу нахождения дискриминанта;
- формулу нахождения корней квадратного уравнения;
- алгоритмы решения уравнений данного вида.
уметь:
- решать неполные квадратные уравнения;
- решать полные квадратные уравнения;
- решать приведенные квадратные уравнения;
- находить ошибки в решенных уравнениях и исправлять их;
- делать проверку.
Думаю, что моя работа будет интересна учащимся 8 классов, а также тем, которые хотят научиться решать рационально квадратные уравнения и хорошо подготовиться к выпускным экзаменам. Также она будет интересна и учителям математики, так как в своей работе я не только рассмотрела методы решения квадратных уравнений, но и историю их развития.
Список информационных источников
- Мордкович, А. Г. Алгебра.8 класс. Учебник для общеобразовательных учреждений/ А.Г. Мордкович.-М. : Мнемозина 2011.-260с.
- Мордкович, А.Г. Алгебра.8 класс. Задачник для общеобразовательных учреждений/ А.Г. Мордкович.-М. : Мнемозина 2011.-270с.
- Глейзер, Г.И. История математики в школе/ Г.И. Глейзер.-М.: Просвещение, 1982- 340с.
- Гусев, В.А. Математика. Справочные материалы/ В.А. Гусев, А.Г. Мордкович — М.: Просвещение, 1988, 372с.
- Брадис, В.М. Четырехзначные математические таблицы для средней школы/ В.М, Брадис-М.: Просвещение, 1990-
- Теорема Виета– Режим доступа:.http://phizmat.org.ua/2009-10-27-13-31-30/817-stihi-o-fransua-vieta/ Теорема Виета(ресурсы удаленного доступа (Internet)). 10.12.2013.
- Квадратные уравнения– Режим доступа: http://revolution.allbest.ru/pedagogics/00249255_0.html(ресурсы удаленного доступа (Internet)). 10.01.2014.
Квадратные уравнения – примеры, определение, виды, (математика, 6 класс)
4.4
Средняя оценка: 4.4
Всего получено оценок: 418.
4.4
Средняя оценка: 4.4
Всего получено оценок: 418.
Квадратные уравнения – это следующий шаг после линейных. Они открывают путь к изучению квадратичных зависимостей и графикам квадратичных функций. Решение квадратных уравнений очень часто встречается в физике, особенно в радиостроении. 2+2х-78=0$$ – уравнение такого вида уже можно решать.
Сколько корней у квадратного уравнения
Есть простое и действенное правило любого степенного уравнения: количество корней равняется старшей степени уравнения.
Почему только в степенных уравнениях число корней равняется степени старшего члена?
Объясним на примере рациональных уравнений. В рациональных уравнениях неизвестное находится под знаком корня, то есть старшая степень вполне может оказаться равной $1\over2$. А полкорня в уравнении быть не может. В дифференциальных уравнениях решение это всегда множество чисел, вне зависимости от старшей степени и т.д. У каждой группы уравнений свои особенности, которые нужно учитыватьКорней у квадратного уравнения всегда два. Просто они могут совпасть, тогда создается видимость одного корня. В ситуации, когда корней нет, они на самом деле есть, просто находятся среди чисел, которые в 6 классе не изучают – комплексных.
Виды квадратных уравнений
У квадратных уравнений всего 2 вида: полные и неполные. Неполные квадратные уравнения, у которых числа в или с равняются нулю. Обратите внимание, что если а равно нулю, то уравнение не квадратное, а линейное. Различать виды квадратных уравнений нужно, чтобы выбирать наиболее оптимальный путь решения. Например, в учебниках по математике составляют таблицы с быстрым решением неполных уравнений.
Специально, чтобы не путаться, коэффициентам дали название по порядку в уравнении:
- а-первый коэффициент
- в-второй коэффициент
- с-свободный член уравнения.
К слову, возможна ситуация, когда и в, и с равны нулю. Такое уравнение также будет считаться квадратным.
Что мы узнали?
Мы дали определение квадратному уравнению, назвали его коэффициент и определили общий вид квадратного уравнения и привели частные примеры квадратных уравнений. Поговорили о том, сколько корней бывает у таких уравнений, и обсудили всеобщее заблуждение по поводу количества корней в уравнении. Решили, что уравнение коэффициент а которого, равен 0, не может считаться квадратным.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Галина Садыкова
10/10
Вадим Змазнев
Илья Бондар
7/10
Валёк Шеловилов
10/10
Лена Баркарь
10/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 418.
А какая ваша оценка?
Квадратные уравнения Класс 10 Глава 4
Вы учитесь…
Получите решения NCERT для всех вопросов упражнений и примеры квадратичных уравнений главы 4 класса 10 бесплатно на Teachoo. Ответы на каждый вопрос обеспечены видео решениями.
В этой главе мы узнаем
- Что такое квадратное уравнение
- Что такое Стандартная форма квадратного уравнения
- Решение квадратного уравнения методом факторизации ( Метод разделения среднего члена )
- Решение квадратного уравнения с помощью Завершение квадрата
- Решение квадратного уравнения по формуле D (x = -b ± √b 2 — 4ac / 2a)
- Проверка того, являются ли корни действительными, равными или нет действительных корней (путем проверки значения D = b 2 — 4ac)
Эта глава разделена на две части: Последовательный порядок и Концепция
В разделе Последовательный порядок глава разделена на вопросы-упражнения и примеры.
В Concept Wise глава разделена на концепции. Сначала объясняются понятия, а затем решаются вопросы темы – от простого к сложному.
Мы предлагаем вам пройти главу из Concept Wise — это способ обучения Teachoo (टीचू).
Примечание: При переходе по ссылке открывается первый вопрос упражнения. Чтобы открыть другой вопрос упражнения, перейдите в конец страницы. Есть список со стрелками. В нем есть все вопросы с Важные вопросы также помечены.
Порядковый номер
Пример 4.1
Пример 4.2
Пример 4.3
Пример 4.4
Примеры
Вопросы, основанные на конкретных случаях (MCQ)
Концептуальные вопросы
Проверка квадратного уравнения
Составление квадратного уравнения
Решение путем разделения среднего члена — данное уравнение
Решение путем разделения среднего члена — Заявление дано
Решение путем заполнения квадрата
Природа корней
Решение по квадратичной формуле — Уравнение
Решение по квадратичной формуле — Составляемое уравнение
Teachoo дает вам лучший опыт, когда вы вошли в систему. Пожалуйста, войдите 🙂
Войти
Teachoo ответит на все ваши вопросы, если вы черный пользователь!
Присоединиться к Teachoo Черный
Квадратные уравнения 10 класса — основы, задачи и примеры решения
Красота математики может быть легко доказана на примере реальных объектов. Все, чему мы учимся, имеет какое-то практическое применение, или мы можем сказать, что каждая практическая ситуация имеет математическое решение. Интересно узнать, как, давайте обсудим, как квадратные уравнения используются в нашей жизни.
Уравнение второй степени, которое хотя бы на члене будет иметь степень двойки, называется квадратным уравнением.
Общая или стандартная форма квадратного уравнения с переменной x имеет вид «ax 2 + bx + c», где a, b и c — действительные числа, а a≠0.
Пример 1 : 2x 2 +3x+5=0, 3x 2 +7x+3=0 и т. д., все являются квадратными уравнениями
- Графическое представление квадратного уравнения решает многие реальные жизненные задачи, такие как движение маятника, траектория мяч, если бросить его вертикально и т. д.
Решение квадратного уравнения
Предположим, квадратное уравнение x 2 -2x +1=0. Поставив x=1 в приведенном выше уравнении, мы получим 1 2 -2+1 = 0, и, следовательно, левая сторона также становится 0 и равна правой, и поэтому мы говорим, что 1 является корнем, решением или нулем приведенного выше квадратного уравнения. .
Обычно мы говорим, что любое действительное число α называется корнем или решением квадратного уравнения ax 2 +bx+c=0 is α удовлетворяет квадратному уравнению aα 2 +bα+c=0. И, следовательно, α также называется нулем приведенного выше квадратного уравнения.
- Метод факторизации.
- Квадратичная формула
Рассмотрим квадратное уравнение ax 2 +bx+c=0, где a≠0.
Тогда формула становится
В приведенном выше уравнении сущность называется Дискриминантом квадратного уравнения.
Существование корней квадратного уравнения полностью зависит от дискриминанта квадратного уравнения.
Итак, квадратное уравнение ax 2 +bx+c=0 имеет
- Два действительных и различных корня, если > 0 .
- Два равных корня, если = 0
- Нет настоящих корней, если
Здесь следует помнить важные моменты:
- x поддерживает два значения, равные
-
Решенные примеры
Пример 5 : Если прямоугольный парк имеет периметр 40 м и площадь 200 м 2 затем найдите длину и ширину парка.
Решение : Пусть длина парка будет = x
Следовательно, периметр = 2(х+ширина) = 40
Следовательно, ширина = 20 – x.
Следовательно, площадь = 200 = х(20 – х)
200 = -х 2 +20х
Следовательно, уравнение становится
х 2 -20х+200=0
Здесь а=1, b=-20, с=200;
Теперь = 400 -800 = -400
Отсюда доказывается, что не может быть такого парка таких размеров.
Пример 6 : Натуральное число, увеличенное на 12, в 160 раз больше его обратного. Найдите число.
Решение : Пусть натуральное число = x
Следовательно, согласно вопросу
х+12 =
Отсюда уравнение принимает вид x(x+12)=60
x 2 +12x-160=0
Здесь а=1, b=12, с=160
Дискриминант b 2 -4ac = 144 +640 =784 > 0
Следовательно, корни будут реальными и различными:
. Подставив значения в квадратную формулу, мы получим
.х = 8 и х = -20.
Поскольку мы знаем, что натуральное число не может быть отрицательным, следовательно, ответ x = 8.
Практические вопросы
Q1) Какое из следующих уравнений является квадратным?
- x 2 +3x+4
- 3x+4
- 3-12x 2 =5x
- 4x 2 -3x 3 =45
Q2) Запишите значения a, b и c для следующих квадратных уравнений и, следовательно, найдите дискриминант значений.