Этапы урока | На доске (проекторе) | Деятельность учителя | Деятельность обучающихся | УУД | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Организационный момент. Задания на известный материал. | 1)Внесите множитель под знак корня: 2)Вынесите множитель из-под знака корня: 3)Решите уравнения: х2=4, х2= — 3, х2=7, х2=
— 5 | — Здравствуйте! Выполните
задания устно. — Вспомним правила. | Легко выполняют задания. Проговаривают правила. | Личностные (самоопределение) Регулятивные (соотнесение того, что уже усвоено и известно) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задания на новый материал. «Яркое пятно» | 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) | —
Перед вами несколько уравнений
(написаны на карточках, с обратной
стороны которых указаны буквы, стоящие
рядом с уравнениями с скобках). — Чем различаются уравнения в этих группах? — Давайте перевернем карточки с уравнениями первой группы и из открывшихся букв составим слово. — Что получили? | Выбирают по порядку 10 уравнений – в одну группу, остальные – в другую. — В 1-ой группе есть член, содержащий переменную х в квадрате, а во второй– нет. Учащиеся переворачивают карточки. — Получили слово КВАДРАТНЫЕ. | Познавательные (анализ с целью выделения признаков объектов, подведение под понятие) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формулирование темы урока. | Определение квадратного уравнения. | — Так как называются уравнения, содержащие переменную х в квадрате? —
Давайте запишем тему нашего урока в
тетрадях. | — Квадратные. Записывают тему урока в тетрадях. | Познавательные (формулирование познавательной цели) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Подводящий диалог (актуализация). |
| —
Посмотрите внимательно на выбранные
нами 10 уравнений. — В чем они схожи? — Чем отличаются? — Верно. Каждое из этих уравнений имеет вид ax2+bx+c=0, где х – переменная, a, b, c – числа, которые называются коэффициентами квадратного уравнения, и a≠0. — Что мы с вами получили? — Сформулируем еще раз. -Давайте проверим ваше умение определять коэффициенты в квадратных уравнениях. Впишите в таблицу коэффициенты квадратных уравнений. — Проверим правильность заполнения самостоятельно, за каждое верное уравнение – 1 балл.
 По предложенным коэффициентам восстановите квадратные уравнения: Проверим правильность заполнения самостоятельно, за каждое верное уравнение – 1 балл.
— Назовите коэффициенты уравнения — В уравнении — В уравнении -Какие выводы мы можем сделать? | — Во всех уравнениях есть х2 —
В каких-то есть переменная х и число,
где-то только х, где-то только число. — Определение квадратного уравнения. Формулируют. Учащиеся выполняют в тетрадях. Учащиеся проверяют и записывают свои баллы в листы оценивания. Выполняют алгоритм самооценки. Учащиеся проверяют и записывают свои баллы в листы оценивания. Выполняют алгоритм самооценки. a=1, b=0, c= — 4 a=1, b=2, c= — 8 a=2, b= — 3, c= 0 — Во всех уравнениях a≠0,но коэффициенты b и cмогут быть равны 0. | Познавательные (анализ с целью выделения признаков объектов, классификация, формулирование проблемы) Регулятивные (целеполагание, контроль, самоконтроль), Коммуникатив-ные (инициативное сотрудничество) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формулирование
проблемы. | — Как можно назвать такие уравнения? — Сформулируйте определение неполных квадратных уравнений. — Как же решать такие уравнения? — Все неполные уравнения можно разбить на три группы. По какому принципу? — Верно. Наша задача найти способы решения этих уравнений. | Предлагают свои варианты, среди которых есть НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ. — Если в квадратном уравнении хотя бы один из коэффициентов b или c равны 0, или оба вместе равны 0, то такие уравнения называются неполными квадратными. — Такие уравнения мы решать не умеем. — Группа, где b =0 — Группа, где c=0 — Группа, где b=0 и c=0 | Познавательные (формулирование проблемы, самостоятельное создание способов решения проблем творческого и поискового характера) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Материал
для выдвижения гипотез. | I. II. III. | — Все неполные квадратные уравнения разобьем на три группы. — Сейчас, разбившись на группы, будем решать уравнения. Разбивает класс на три группы. — Как можно решить уравнения? Ваши гипотезы? (контролирует работу групп) | Учащиеся разделили и записали на доске. . Учащиеся работают в группах, решают в тетрадях. | Познавательные Регулятивные (определение последовательности промежуточных целей, составление плана, прогнозирование) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Представление гипотез группами. | I группа (x-2)(x+2)=0, x1=2 и x2= — 2 x2=, x1= и x2= — x2= — 5, корней нет II группа x(2x-3)=0 x=0 или 2x-3=0 x=1,5 x( — x+30)=0 x=0 или — x+30=0 x=30 x( 3 x — 1)=0 x=0 или 3x— 1=0 x=1/3 III группа x=0 | —
Группы решите уравнения с помощью
своей гипотезы и прокомментируйте. — Ребята, обобщите все вышесказанное. — 2-я группа — Ребята обобщите все вышесказанное. — 3-я группа | — Переносим число в правую часть. Такие уравнения решать уже умеем. Оно имеет два корня. — Решаем аналогично. — Это уравнение корней не имеет, т. к. – 5 < 0. — Уравнение вида ax2+ c=0, где х – переменная, a, c – числа, с≠0 называется неполным квадратным и решается Если >0, то имеем два корня и . Если <0, то уравнение решений не имеет. —
Вынесем х за скобки. — Уравнение вида ax2+ bx=0, где х – переменная, a, b– числа, b≠0 называется неполным квадратным и решается x(ax+b)=0, x=0 или -Уравнение вида ax2=0, где х – переменная, a≠0 называется неполным квадратным и имеет единственное решение x=0. | Познавательные (выдвижение гипотез и их обоснование, построение логической цепи рассуждений) Коммуникатив-ные, Регулятивные (контроль и коррекция) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формулирование нового знания. (Выражение решения проблемы) | —
Ребята, давайте еще раз сформулируем
определение и способы решения неполных
квадратных уравнений. | Формулируют своими словами. | Познавательные | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Работа с учебником. | — Откроем учебник и сравним свои выводы. | Самостоятельно читают учебник, сверяют свои формулировки с формулировкой учебника, выводят окончательную. | Познавательные | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Применение нового знания. | Самостоятельная работа Вариант 1. 1)Решите уравнения: (за каждое верно решенное уравнение — 1 балл) А)10x2 +7x=0 Б)1 – 4 y2 =0 В)9х2 =0 2) Составьте уравнения, у которых корни равны: (за каждое верно составленное уравнение по 2 балла) А)-4 и 4; Б) 0 и -3 3)Решите уравнение: (3 балла) х2 -5=(х+5)(2х-1) Вариант
2. 1)Решите уравнения: (за каждое верно решенное уравнение — 1 балл) А)- 5x2 +6x=0 Б)1 – 9 y2 =0 В)-8х2 =0 2) Составьте уравнения, у которых корни равны: (за каждое верно составленное уравнение по 2 балла) А)-5 и 5; Б) 0 и 7 3)Решите уравнение: (3 балла) х(7 – 6х)=(1- 3х)(2х+1) | — А сейчас закрепим полученные знания на практике, выполним самостоятельную работу по вариантам. Решение. Вариант 1. №1 А)10x2 +7x=0; х(10х +7)=0; х=0 или 10х+7=0 х= — 0,7 Ответ: х=0, х= — 0,7. Б) 1 – 4 y2 =0; (1-2у)(1+2у)=0; 1-2у=0 или 1+2у=0 у=0,5 у= — 0,5 Ответ: у=0,5 ; у= — 0,5 В) 9х2 =0; х=0 Ответ:
х=0. №2 А) (х-4)(х+4)=0, х2-16=0 Б) х(х+3)=0, х2+3х=0 №3 х2 -5=(х+5)(2х-1) х2 -5=2х2— х+10х -5 х2+9х=0 х(х+9)=0 х=0 или х= — 9 Ответ: х=0, х= — 9. Вариант 2. №1 А) — 5x2 +6x=0; х(- 5 х+6)=0; х=0 или – 5х+6=0 х= 1,2 Ответ: х=0, х=1,2. Б) 1 – 9 y2 =0; (1-3у)(1+3у)=0; 1 – 3у=0 или 1+3у=0 у= у= Ответ: у= , у= В) -8х2 =0; х=0 Ответ: х=0. №2 А) (х+5)(х-5)=0, х2 – 25=0 Б) х(х-7)=0, х2 -7х=0 №3 х(7 – 6х)=(1- 3х)(2х+1) 7х – 6х2 =2х +1 – 6х2 -3х 7х-2х+3х=1 8х=1 х= Ответ:
х=. — Проверим ваши работы с помощью соседа (взаимопроверка) | Решают в тетрадях. Обмениваются тетрадями и проверяют. Решение написано на доске. Полученные баллы выставляют в лист оценивания. | Регулятивные (контроль и коррекция) Познавательные (выбор эффективного способа решения) Коммуникатив-ные | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашнее задание | Д.З. №24.3, №24.8, №24.11, п.24 | Выполнить №24.3, №24.8, №24.11, п.24 Возможность
усложнения некоторых заданий. | Обсуждение трудных этапов выполнения задания. | Регулятивные (целеполагание, контроль, оценка, коррекция) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Итог урока. Рефлексия деятельности. | Лист оценивания
Критерии оценивания: 22 балла – «5» 17-21 балл — «4» 11-16 баллов — «3» 0-10 баллов – «2» | — Какую проблему мы сегодня с вами решали? — Что нового узнали? —
Еще раз сформулируем эти правила. — Что вам особенно понравилось на уроке? Есть ли вопросы? На возникшие вопросы учитель отвечает. — Итак, мы сегодня очень плодотворно поработали, настала пора подводить итоги. Подсчитайте ваши баллы, заработанные на уроке, переведите их в оценку, согласно критериям. — Какую оценку каждый из вас поставил бы себе за урок? Учитель выставляет оценки и объясняет за что. -Урок закончен. | — Изучили определение квадратного уравнения, познакомились с неполными квадратными уравнениями и способами их решения. Формулируют. Отвечают. Ребята записывают оценки в своих листах. | Коммуникатив-ные (умение полно выражать свои мысли) Регулятивные (контроль, оценка, коррекция) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Презентация — Квадратные уравнени — Их решение по формуле
Слайд 1
Материал к урокам алгебры в 8 классе по теме:
Квадратные уравнения. Их решение по формуле.
Их решение по формуле.
Слайд 2
Вступление.
Данная работа может быть использована на обобщающем уроке по теме «Решение квадратных уравнений»с целью повторения и обобщения изученного материала
Отдельные части работы могут быть использованы и на обучающих уроках или во внеклассной работе с целью ознакомления с дополнительными сведениями.
Слайд 3
Содержание:
Теоретический материал
Примеры решения квадратных уравнений по формуле
Проверим знания (тест)
Кроссворд
Это интересно (дополнительные сведения о решении квадратных уравнений)
Из истории решения квадратных уравнений
Проверь себя (решение квадратного уравнения при помощи языка программирования)
Использованная литература
Слайд 4
Теоретические сведения
Определение квадратного уравнения
Примеры квадратных уравнений.
Алгоритм решения квадратного уравнения по формуле
Слайд 5
Определение квадратного уравнения.
Квадратным уравнением называется уравнение вида ах²+вх+с=0, где х – переменная, а,в,с – некоторые числа, причем а≠0. Числа а, в, с – коэффициенты квадратного уравнения. Число а – первый коэффициент, в – второй коэффициент, с – свободный член.
Если в квадратном уравнении ах²+вх+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется неполным квадратным уравнением.
Квадратное уравнение, в котором коэффициент а=1 называется приведенным квадратным уравнением.
Числа а, в, с – коэффициенты квадратного уравнения. Число а – первый коэффициент, в – второй коэффициент, с – свободный член.
Если в квадратном уравнении ах²+вх+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется неполным квадратным уравнением.
Квадратное уравнение, в котором коэффициент а=1 называется приведенным квадратным уравнением.
Слайд 6
Примеры квадратных уравнений:
Например: а) –х²+6х+1,2=0, где а=-1, в=6, с=1,2;
б) 5х²-2=0 – неполное квадратное уравнение, где а=5, в=0, с=-2;
в) -3х²+7х=0 — неполное квадратное уравнение, где а=-3, в=7, с=0;
г) 7х²=0 — неполное квадратное уравнение, где а=7, в=0, с=0;
д) х²+4х-12=0 – приведенное квадратное уравнение, где а=1, в=4, с=-12.
Слайд 7
Алгоритм решения квадратного уравнения:
ах²+вх+с=0
Определить
коэффициенты а,в,с
Если DВычислить дискриминант
D=в²-4ас
Если D=0, то
2 корня
Если D>0, то
1 корень
Уравнение не
имеет корней
Слайд 8
Примеры решения квадратных уравнений по формуле
Пример1: 3х²+11х+6=0 а=3; в=11;с=6. D=11²-4*3*6=121-72=49>0 – уравнение имеет 2 корня
D=11²-4*3*6=121-72=49>0 – уравнение имеет 2 корня
Слайд 9
Примеры решения квадратных уравнений по формуле:
Пример2. 9х²-6х+1=0
а=9; в=-11;с=1.
D=(-6)²-4*9*1=36-36=0=0 – уравнение имеет 1 корень.
Х=
Слайд 10
Примеры решения квадратных уравнений по формуле:
Пример 3: -2х²+3х-5=0
а=-2; в=3;с=-5.
D=3²-4*(-2)*5=9-40=-31
Слайд 11
Тест
Тест 1. Установить, истинны или ложны утверждения.
Тест 2. Установить верный ответ из числа предложенных.
Слайд 12
Тест 1. Установите, истинны или ложны следующие утверждения :
Ответы давать : да или нет. Время для выполнения – 10 минут.
Указание: не выполнять задания 8 и 9.
Текст теста:
Слайд 13
Тест 2. Выбрать правильный ответ из предложенных вариантов:
Время для выполнения – 15 минут.
Указание: не выполнять задания 6 и 7.
Текст теста:
Слайд 14
Кроссворд
1. Уравнение вида ах²+вх+с=о
2. Квадратные уравнения, у которых первый коэффициент равен 1.
3. Уравнения с одной переменной, имеющие одни и те же корни.
4. Числа а,в и с в квадратном уравнении.
5. Значение переменной, при котором уравнение обращается в верное равенство.
6. Равенство, содержащее неизвестное.
7. Неотрицательное значение квадратного корня.
8. Древнегреческий математик, который нашел приемы решения квадратных уравнений без обращения к геометрии.
9. Квадратное уравнение, в котором хотя бы один из коэффициентов в или с равен 0.
10. «Дискриминант» — по-латыни.
11. Коэффициент с квадратного уравнения.
12. Французский математик, который вывел формулы, выражающие зависимость корней уравнения от его коэффициентов.
Если вы разгадаете этот кроссворд верно, то сможете в выделенном вертикальном столбце прочитать термин, относящийся к теме.
Квадратные уравнения, у которых первый коэффициент равен 1.
3. Уравнения с одной переменной, имеющие одни и те же корни.
4. Числа а,в и с в квадратном уравнении.
5. Значение переменной, при котором уравнение обращается в верное равенство.
6. Равенство, содержащее неизвестное.
7. Неотрицательное значение квадратного корня.
8. Древнегреческий математик, который нашел приемы решения квадратных уравнений без обращения к геометрии.
9. Квадратное уравнение, в котором хотя бы один из коэффициентов в или с равен 0.
10. «Дискриминант» — по-латыни.
11. Коэффициент с квадратного уравнения.
12. Французский математик, который вывел формулы, выражающие зависимость корней уравнения от его коэффициентов.
Если вы разгадаете этот кроссворд верно, то сможете в выделенном вертикальном столбце прочитать термин, относящийся к теме.
1
2
3
4
5
6
7
8
9
10
11
12
Слайд 15
Это интересно (дополнительные сведения о нахождении корней квадратного уравнения в особых случаях):
1 случай. Если a+b+c=0, то х1=1; х2= с/а
2 случай. Если a-b+c=0, то х1=-1; х2= -с/а
Нахождение корней приведенного квадратного уравнения: х²+px+q=0. здесь полезно воспользоваться формулой:
Формула запоминается надолго, если выучить ее в стихотворной форме:
Если a+b+c=0, то х1=1; х2= с/а
2 случай. Если a-b+c=0, то х1=-1; х2= -с/а
Нахождение корней приведенного квадратного уравнения: х²+px+q=0. здесь полезно воспользоваться формулой:
Формула запоминается надолго, если выучить ее в стихотворной форме:
Слайд 16
Стихотворение для запоминания формулы
«Пэ», со знаком взяв обратным,
На два мы его разделим.
И от корня аккуратно
Знаком минут-плюс отделим.
А под корнем, очень кстати,
Половина «пэ» в квадрате,
Минус «ку». И вот решенье
Небольшого уравненья.
Слайд 17
Из истории решения квадратных уравнений.
Уравнения 2-ой степени умели решать еще в Древнем Вавилоне во II тысячелетии до н.э. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид – при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактатах. Например.
Например.
Слайд 18
Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте (около 598 г.).
Среднеазиатский ученый ал-Хорезми (IX в.) в трактате «Китаб аль-джебр валь -мукабала» получил эту формулу методом выделения полного квадрата с помощью геометрической интерпретации. См.подробнее.
Из истории решения квадратных уравнений.
Слайд 19
Вывод формулы корней квадратного уравнения ал-Хорезми:
Суть его рассуждений видна из рисунка (рассматривается решение уравнения х²+10х=39. Площадь большого квадрата равна (х+5)². Она складывается из площади х²+10х фигуры, закрашенной голубым цветом, равной левой части рассматриваемого уравнения, и площади четырех квадратов со стороной 5/2, равной 25. Таким образом, (х+5)²=39+25; х1=3; х2=-13.
х²
5х/2
5х/2
Слайд 20
Задача из китайского трактата «Математика в девяти книгах»(примерно II в. до н.э.)
до н.э.)
«Имеется город с границей в виде квадрата со стороной неизвестного размера, в центре каждой стороны находятся ворота. На расстоянии 20 бу(1 бу=1,6 м) от северных ворот (вне города) стоит столб. Если пройти от южных ворот прямо 14 бу, затем повернуть на запад и пройти еще 1775 бу, то можно увидеть столб. Спрашивается: какова сторона границы города?»
Решение смотри здесь:
Слайд 21
Решение задачи о границах города:
Обозначим сторону квадрата через х. Из подобия треугольников BED и ABC (см.рис.) получим: k/0.5x=(k+x+l)/d.
Поэтому, чтобы определить неизвестную сторону квадрата, получаем квадратное уравнение х2+(k+l)-2kd=0.
В данном случае уравнение имеет вид х2+34х-71000=0, откуда х=25000 бу.
Отрицательных корней (в данном случае х=-284) китайские математики не рассматривали, хотя в этом же трактате содержатся операции с отрицательными числами.
l
Слайд 22
Проверь себя ( решение задачи при помощи языка программирования):
Программа, позволяющая решать квадратные уравнения (язык Turbo Pascal)
Слайд 23
Использованная литература:
Алтынов П. А. Тесты. Алгебра.7-9 – Москва, «Дрофа», 2002 год
Макарычев Ю.Н. Алгебра, 8 класс – Москва, «Просвещение», 2000 год
Ткачева М.В. Домашняя математика, 8 класс- Москва, «Просвещение», 1996 год
Худадатова С.С. Математика в ребусах, кроссвордах – Москва, «Школьная Пресса», 2003 год
Энциклопедический словарь юного математика –Москва, «Педагогика», 1985 год
Энциклопедия «Я познаю мир. Математика» — Москва, АСТ, 1996 год.
А. Тесты. Алгебра.7-9 – Москва, «Дрофа», 2002 год
Макарычев Ю.Н. Алгебра, 8 класс – Москва, «Просвещение», 2000 год
Ткачева М.В. Домашняя математика, 8 класс- Москва, «Просвещение», 1996 год
Худадатова С.С. Математика в ребусах, кроссвордах – Москва, «Школьная Пресса», 2003 год
Энциклопедический словарь юного математика –Москва, «Педагогика», 1985 год
Энциклопедия «Я познаю мир. Математика» — Москва, АСТ, 1996 год.
Слайд 24
Брахмагупт(около 598-660 г.г.)
Индийский математик и астроном. Основное сочинение «Усовершенствованное учение Брахмы» («Брахмаспхутасиддханта», 628 г.), значительная часть которого посвящена арифметике и алгебре. Брахмагупта , изложил общее правило решения квадратных уравнений, приведенных к единой канонической
форме:
ax2 + bх = с, а> 0. (1)
В уравнении (1) коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
Слайд 25
Диофант Александрийский (около 3 в. ).
).
Древнегреческий математик. В основном труде «Арифметика» (сохранились 6 книг из 13), дал решение задач, приводящихся к т.н. диофантовым уравнениям, и впервые ввел буквенную символику в алгебру.
Слайд 26
Евклид (3 в. До н.э.)
Древнегреческий математик, работал в Александрии. Лавный труд «Начала»(15 книг), содержит основы античной математики, элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов, оказал огромное влияние на развитие математики.
Слайд 27
Аль-Хорезми.
Наибольших успехов в математике достиг согдиец Мухаммед ибн Муса аль-Хорезми (то есть, родом из Хорезма — с берегов Сыр-Дарьи). Он работал в первой половине 9 века и был любимцем ученейшего из халифов — Маамуна (сына знаменитого Гаруна ар-Рашида). Главная книга Хорезми названа скромно: «Учение о переносах и сокращениях», то есть техника решения алгебраических уравнений. По-арабски это звучит «Ильм аль-джебр ва»ль-мукабала»; отсюда произошло наше слово «алгебра». Другое известное слово — «алгоритм», то есть четкое правило решения задач определенного типа — произошло от прозвания «аль-Хорезми». Третий известный термин, введенный в математику знаменитым согдийцем — это «синус», хотя в этом деле не обошлось без курьеза.
В алгебраическом трактате ал-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
«Квадраты равны корням», т. е. ах2 = bх.
«Квадраты равны числу», т. е. ах2 = с.
«Корни равны числу», т. е. ах = с.
«Квадраты и числа равны корням», т. е. ах2 + с = bх.
«Квадраты и корни равны числу», т. е. ах2 + bх =с.
«Корни и числа равны квадратам», т. е. bх + с == ах2.
Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала.
Другое известное слово — «алгоритм», то есть четкое правило решения задач определенного типа — произошло от прозвания «аль-Хорезми». Третий известный термин, введенный в математику знаменитым согдийцем — это «синус», хотя в этом деле не обошлось без курьеза.
В алгебраическом трактате ал-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
«Квадраты равны корням», т. е. ах2 = bх.
«Квадраты равны числу», т. е. ах2 = с.
«Корни равны числу», т. е. ах = с.
«Квадраты и числа равны корням», т. е. ах2 + с = bх.
«Квадраты и корни равны числу», т. е. ах2 + bх =с.
«Корни и числа равны квадратам», т. е. bх + с == ах2.
Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно,не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Его решение, конечно,не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Слайд 28
Ответы к кроссворду:
1. Квадратное.
2. Приведенное.
3. Равносильное.
4. Коэффициент.
5. Корень.
6. Уравнение.
7. Арифметический.
8. Диофант.
9. Неполное.
10. Различитель.
11. Свободный.
12. Виет.
В выделенном столбце : ДИСКРИМИНАНТ
Слайд 29
Ответы к тесту 1.
Вариант 1. 1,2,3,4,10-да; 5,6,7 – нет.
Вариант 2. 1,3,4,10 – да; 2,5,6,7 — нет
Слайд 30
Ответ к тесту 2.
Вариант 1. 1 -г , 2-г , 3 — г, 4 -б , 5 -г .
Вариант 2. 1 — в, 2- б , 3 — в, 4 — б, 5 — б .
1 -г , 2-г , 3 — г, 4 -б , 5 -г .
Вариант 2. 1 — в, 2- б , 3 — в, 4 — б, 5 — б .
Задачи на квадратные уравнения с ответами для 8 класса
Вопросы 8 класса по квадратным уравнениям с решениями и пояснениями включены.
|
Математика средней школы (6, 7, 8, 9 классы) — Бесплатные вопросы и задачи с ответами
Математика средней школы (10, 11 и 12 классы) — Бесплатные вопросы и задачи с ответами
Математика средней школы ( 10, 11 и 12 классы) — Бесплатные вопросы и задачи с ответами
Начальная математика (4 и 5 классы) с бесплатными вопросами и задачами с ответами
Домашняя страница
Задачи на квадратные уравнения с решениями и пояснениями для 8 класса
Решения с полными пояснениями к вопросам 8 класса по квадратичным
уравнения. Некоторые из этих проблем могут быть сложными, и поэтому их стоит решить, даже если на это потребуется время. Мы учимся, решая проблемы, которые сначала не знаем, как решить.
Мы учимся, решая проблемы, которые сначала не знаем, как решить.
|

 Неполные
квадратные уравнения» с использованием проблемно-диалогической
технологии. Урок составлен на основе
учебника для учащихся общеобразовательных
учреждений «Алгебра. 8 класс» А. Г.
Мордковича и др.
Неполные
квадратные уравнения» с использованием проблемно-диалогической
технологии. Урок составлен на основе
учебника для учащихся общеобразовательных
учреждений «Алгебра. 8 класс» А. Г.
Мордковича и др.
 Попробуйте разделить эти уравнения
по внешнему виду на группы.
Попробуйте разделить эти уравнения
по внешнему виду на группы. (пишет на доске)
(пишет на доске)




 Произведение двух
множителей равно 0, если один или второй
множитель равен 0.
Произведение двух
множителей равно 0, если один или второй
множитель равен 0.





 Найдите два числа.
Найдите два числа.  Найдите длину и ширину прямоугольника, если его периметр равен 40 м.
Найдите длину и ширину прямоугольника, если его периметр равен 40 м.  Каковы эти три целых числа?
Каковы эти три целых числа?  Следовательно
Следовательно 




 Площадь треугольника равна 54 квадратных метра. Найдите основание и высоту треугольника.
Площадь треугольника равна 54 квадратных метра. Найдите основание и высоту треугольника. 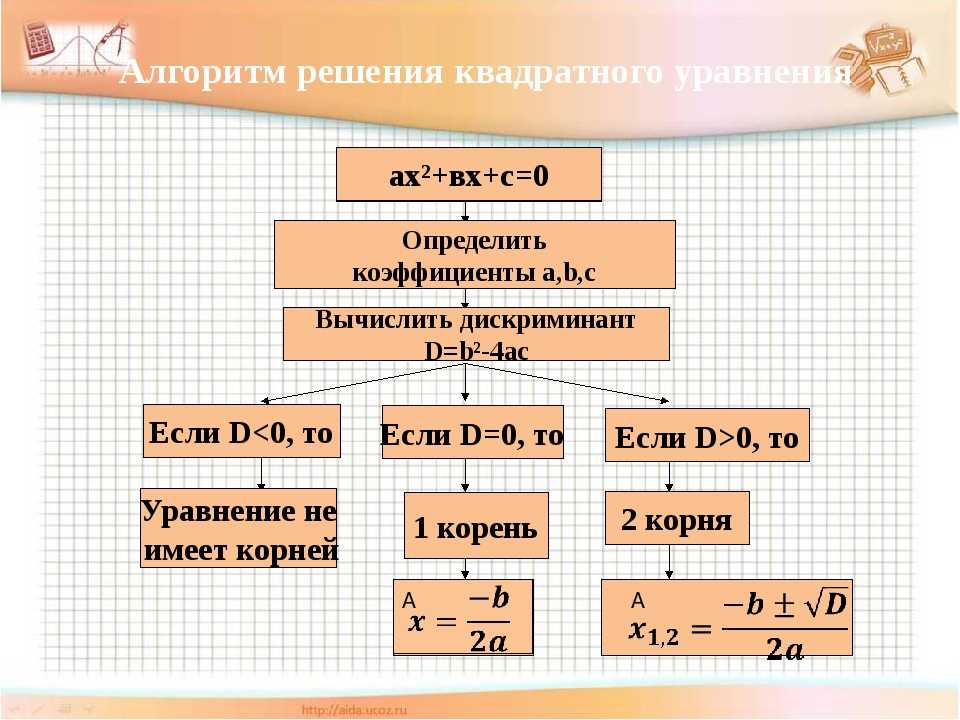 Найдите три целых числа.
Найдите три целых числа.  Следовательно, эта задача имеет бесконечное число решений, и любой набор из 3 последовательных чисел является решением данной задачи.
Следовательно, эта задача имеет бесконечное число решений, и любой набор из 3 последовательных чисел является решением данной задачи. 