Как решать дробные уравнения? | О математике понятно
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.
Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)
Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1. Дроби и действия с дробями и дробными выражениями.
2. Тождественные преобразования уравнений.
3. Решение линейных и квадратных уравнений.
Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т. д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)
д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)
Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Итак, вперёд!
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
Или такое:
Или вот такое:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.
Например:
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.
В общем, вы поняли.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).
Умножаем:
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
2∙3 = х+3
А его (надеюсь) уже решит каждый:
х = 3
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».
Вперёд!
А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!
Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.
(9 — х)∙х = 20
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
9х — х2 = 20
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
х1 = 4
х2 = 5
И все дела.)
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.
А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)
Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)
Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
x(x2+2x)(x+2)
и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)
Привет седьмому классу!)
А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х2+2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
х2+2х = х(х+2)
Отлично. Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).
Вот на х(х+2) и умножаем:
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
(x-3)(x+2) + 3 = x
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
x2 + 2x — 3x — 6 + 3 — х = 0
x2 — 2x — 3 = 0
И снова получили квадратное уравнение. ) Решаем и получаем два корня:
) Решаем и получаем два корня:
x1 = -1
x2 = 3
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Ну что, порешаем?)
Решить уравнения:
Ответы (как обычно, вразброс):
x = 3
x1 = 0,5; x2 = 3
x = 2
х = 6
x = 2,6
x1 = 2; x2 = 5
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!
Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…
Но об этом — дальше.)
Решать уравнения где. Решение простых линейных уравнений. Примеры решения уравнений
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления.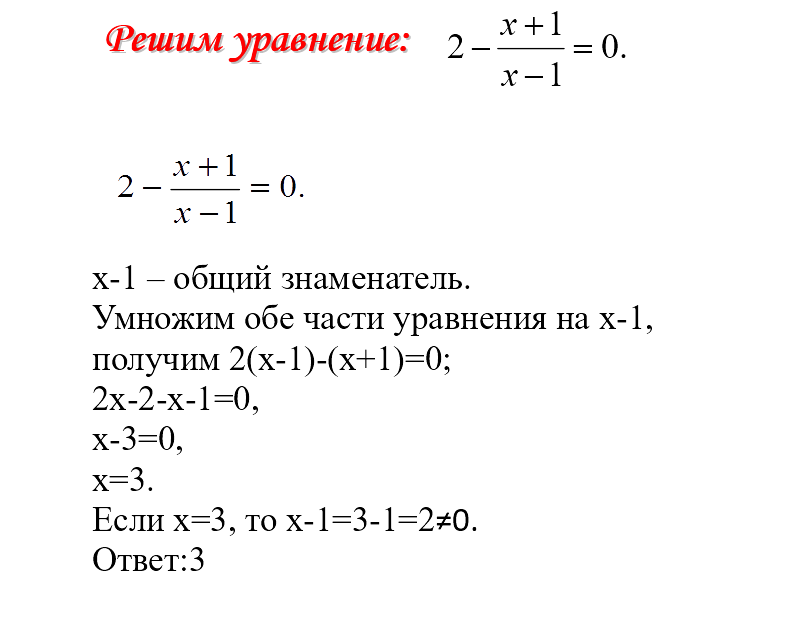 Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными.
- Правильной называется дробь, у которой числитель меньше знаменателя.
- Неправильная дробь – если у дроби числитель больше знаменателя.
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя:
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Выполнить сложение дробей путем сложения их числителей.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.

- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.

- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Онлайн калькуляторы и конвертеры:
На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или . База упражнений на нашем сайте постоянно дополняется и обновляется.
База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые
Сайт способен решать любые  Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в
Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax
2 + c
= 0 выполнено неравенство (−c
/a
) ≥ 0, корней будет два.
 Формула дана выше;
Формула дана выше; - Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Варенье из бузины: польза и вред
Узнать встретимся ли мы. Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания
Целые рациональные, дробно-рациональные и иррациональные уравнения
На этой странице вы узнаете:- Как не перепутать целое рациональное с дробно-рациональным уравнением?
- Чудо метод: как легко решить любое иррациональное уравнение?
- Без каких трёх букв не справиться с ЕГЭ?
Сравнить зарплату и расходы, рассчитать количество продуктов в блюде или решить, сколько плитки взять для ремонта в ванной — мы встречаем уравнения гораздо чаще, чем кажется.
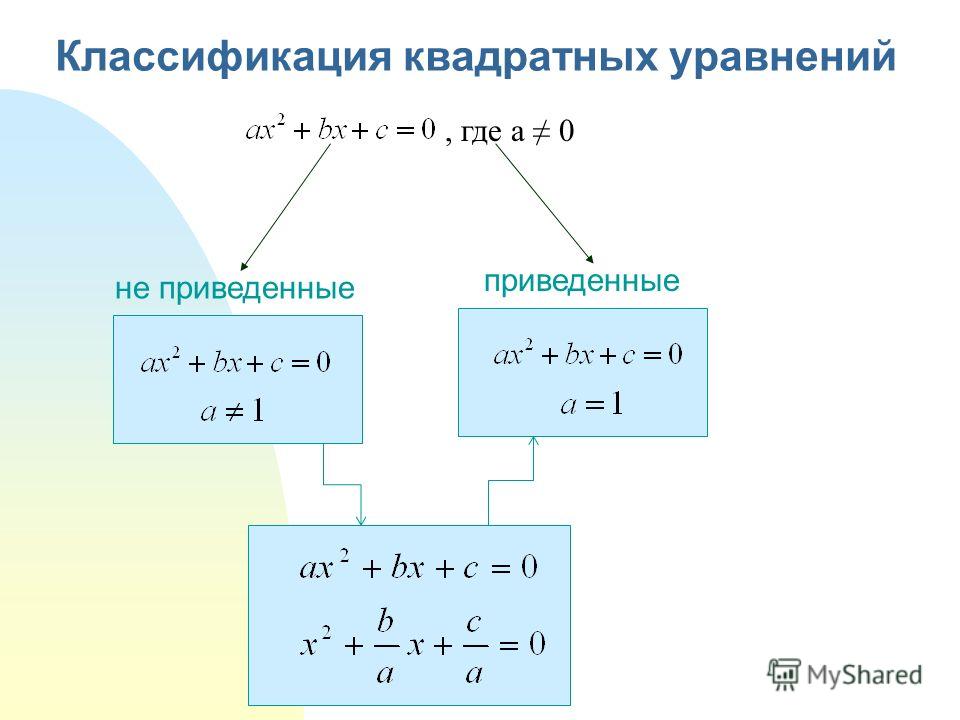
Виды уравненийУравнения могут быть рациональными и иррациональными.
Рациональные в свою очередь делятся на:
- целые рациональные и
- дробно-рациональные.
 {\frac{2}{3}} = 4\) – это иррациональные уравнения.
{\frac{2}{3}} = 4\) – это иррациональные уравнения.Иррациональные уравнения могут быть нескольких видов:
- \(\sqrt{f(x)} = g(x)\)
- \(\sqrt{f(x)} = \sqrt{g(x)}\)
- Разные комбинации корней.
Чудо метод: как легко решить любое иррациональное уравнение? Такие уравнения решаются методом возведения в квадрат. Он заключается в изоляции корня с одной стороны от знака равенства и переноса остальных слагаемых в другую сторону, далее нужно возвести обе части уравнения (и правую, и левую) в квадрат, чтобы избавиться от знака корня. Такой метод можно использовать столько раз, сколько потребуется, чтобы избавиться от всех корней в уравнении.
Что нужно учитывать при решении иррационального уравнения методом возведения в квадрат?
Корень не может быть отрицательным, поэтому обязательно нужно добавлять условие на выражение, к которому приравнивается корень. Такое выражение всегда больше или равно нулю.
 {2} + 2} = \sqrt{2x + 2}\)
{2} + 2} = \sqrt{2x + 2}\)- Перейдем к системе
- Заметим, что второе условие выполняется при любом х, а значит все корни первого уравнения будут являться решениями. Решим неполное квадратное уравнение, и получим корни 0 и 2.
Решение уравнения с тремя корнями:
Пример:
\(\large\sqrt{1 + x} — \sqrt{1 — x} = \sqrt{x}\)
- Найдем область допустимых значений (ОДЗ), то есть все значения, которые x может принимать в уравнении или неравенстве.
Для этого составим систему условий на подкоренные выражения, а после найдем решения этой системы:
\(\Large 0 \leq x \leq 1\)
Без каких трёх букв не справиться с ЕГЭ? Таким тремя буквами является аббревиатура ОДЗ.
В базовом ЕГЭ и первой части профильной математики можно обойтись и без ОДЗ. Но решить некоторые задания второй части профиля без ОДЗ не получится.Чтобы получить верный ответ последним действием нужно пересечь ОДЗ уравнения с его решениями.
 Промежутки, которые будут принадлежать и ОДЗ, и решению, пойдут в ответ.
Промежутки, которые будут принадлежать и ОДЗ, и решению, пойдут в ответ.- Перенесем одно слагаемое в правую часть
\(\large\sqrt{1 + x} = \sqrt{x} + \sqrt{1 — x}\)
- Возведем обе части уравнения в квадрат
\(\large 1 + x = x + 2 ⋅ \sqrt{x — 1} ⋅ \sqrt{x} + 1 — x\)
- Сложим подобные слагаемые и получим систему вида fx=gx
\(\large x = 2\sqrt{1 — x}\sqrt{x}\)
- Перейдем к системе уравнений
- Решим первое уравнение
x2 = 4x * (1 — x)
5x2 — 4x = 0
x * (5x — 4) = 0Оба корня подходят и под условие x ≥ 0, и под найденное ранее ОДЗ, значит корни данного уравнения 0 и \(\large\frac{4}{5}\) .
Фактчек- Рациональное уравнение – это уравнение, в котором есть только сложение, вычитание, умножение, деление и возведение в целую степень. Решается такое уравнения путем сведения к алгебраическому уравнению.
 {2} + 3x} = \sqrt{5x — 1}\)
{2} + 3x} = \sqrt{5x — 1}\)- 1 и 2
- 1
- 0 и 2
- 2
Ответы: 1. — 3; 2. — 2; 3. — 1; 4. — 1; 5. — 2
Алгебра. Квадратные уравнения. Часть II
Онлайн-заметки Пола
Главная / Алгебра / Решение уравнений и неравенств / Квадратные уравнения. Часть IIПоказать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон).
 Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Раздел 2-6: Квадратные уравнения — Часть II
Тема решения квадратных уравнений разбита на две части для удобства тех, кто просматривает это в Интернете. В качестве одного раздела время загрузки страницы было бы довольно долгим. Это второй раздел по решению квадратных уравнений.
В предыдущем разделе мы рассмотрели использование факторинга и свойства квадратного корня для решения квадратных уравнений. Проблема в том, что оба этих метода решения не всегда будут работать. Не каждое квадратное число факторизуемо, и не каждое квадратное число имеет форму, необходимую для свойства квадратного корня. 92}\]
Это не так просто вычислить.
 Однако, если вы снова вспомните, что это ВСЕГДА будет учитываться как \(y\) плюс синее число выше, нам не нужно беспокоиться о процессе факторинга.
Однако, если вы снова вспомните, что это ВСЕГДА будет учитываться как \(y\) плюс синее число выше, нам не нужно беспокоиться о процессе факторинга.Пришло время посмотреть, как мы используем завершение квадрата для решения квадратного уравнения. Процесс лучше всего виден, когда мы работаем на примере, поэтому давайте сделаем это.
Пример 2 Используйте заполнение квадрата для решения каждого из следующих квадратных уравнений.
92} — 6x + 1 = 0\) Показать решениеИтак, приступим.
Шаг 1 : Разделите уравнение на коэффициент члена x 2 . Напомним, что для заполнения квадрата при этом члене требовался коэффициент, равный единице, и это гарантирует, что мы его получим. Однако нам не нужно делать это для этого уравнения.
Шаг 2 : Составьте уравнение так, чтобы \(x\) были слева, а константы справа. 92} — 6х = — 1\]
Шаг 3 : Заполните квадрат с левой стороны.
 2} = \ гидроразрыва {92} & = \ frac {4} {9} \\ x — \ frac {1} {3} & = \ pm \ sqrt {\ frac {4} {9}} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма}x = \frac{1}{3} \pm \frac{2}{3}\end{align*}\]
2} = \ гидроразрыва {92} & = \ frac {4} {9} \\ x — \ frac {1} {3} & = \ pm \ sqrt {\ frac {4} {9}} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма}x = \frac{1}{3} \pm \frac{2}{3}\end{align*}\]В этом случае обратите внимание, что здесь мы можем выполнить арифметические действия, чтобы получить два целых и/или дробных решения. Мы всегда должны делать это, когда в нашем решении есть только целые числа и/или дроби. Вот два решения.
\[x = \frac{1}{3} + \frac{2}{3} = \frac{3}{3} = 1\hspace{0,25 дюйма}{\mbox{and}}\hspace{0,25 дюйма }x = \frac{1}{3} — \frac{2}{3} = — \frac{1}{3}\]
Небольшой комментарий к последнему уравнению, которое мы решили в предыдущем примере. Поскольку в качестве решений мы получили целые числа и дроби, мы могли бы просто разложить это уравнение на множители с самого начала, а не использовать завершение квадрата. В таких случаях мы могли бы использовать любой метод, и мы получили бы тот же результат.

Реальность такова, что заполнение квадрата — довольно долгий процесс, и в нем легко ошибиться. Таким образом, мы редко используем его для решения уравнений. Однако это не означает, что не важно знать процесс. Мы будем использовать его в нескольких разделах последующих глав, и он часто используется в других классах.
Квадратная формула
Это последний метод решения квадратных уравнений, который всегда будет работать. Не только это, но если вы помните формулу, это также довольно простой процесс.
Мы можем вывести квадратную формулу, заполнив квадрат общей квадратичной формулы в стандартной форме. Давайте сделаем это, и мы будем делать это медленно, чтобы убедиться, что все шаги понятны.
Во-первых, мы ДОЛЖНЫ иметь квадратное уравнение в стандартной форме, как уже отмечалось. Затем нам нужно разделить обе части на \(a\), чтобы получить коэффициент единицы на 92} + 2x — 7 = 0\]
Теперь мы можем определить значения для использования в квадратичной формуле.
 Для этого уравнения имеем.
Для этого уравнения имеем.\[a = 1\hspace{0,25 дюйма}b = 2\hspace{0,25 дюйма}c = — 7\]
Обратите внимание на «-» с \(c\). Важно убедиться, что мы несем любые знаки минус вместе с константами.
На данный момент больше нечего делать, кроме как вставить формулу. 92} — 4\left( 1 \right)\left( { — 7} \right)} }}{{2\left( 1 \right)}}\\ & = \frac{{ — 2 \pm \sqrt {32} }}{2}\end{align*}\]
У этого уравнения есть два решения. Есть также некоторое упрощение, которое мы можем сделать. Однако нам нужно быть осторожными. Одна из самых больших ошибок на этом этапе — «отменить» две двойки в числителе и знаменателе. Помните, что для того, чтобы исключить что-либо из числителя или знаменателя, это нужно умножить на весь числитель или знаменатель. Поскольку 2 в числителе не умножается на весь знаменатель, его нельзя отменить.
Чтобы сделать здесь какое-либо упрощение, нам сначала нужно уменьшить квадратный корень.
 В этот момент мы можем сделать некоторые отмены.
В этот момент мы можем сделать некоторые отмены.\[x = \frac{{ — 2 \pm \sqrt {\left( {16} \right)2} }}{2} = \frac{{ — 2 \pm 4\sqrt 2 }}{2} = \frac{{2\left( { — 1 \pm 2\sqrt 2 } \right)}}}{2} = — 1 \pm 2\sqrt 2 \]
Это гораздо более приятный ответ, и поэтому мы почти всегда будем делать такое упрощение, когда это возможно. 92} + 11 — 5q = 0\]
Это не совсем типичная стандартная форма. Тем не менее, мы должны отметить здесь, чтобы мы не сделали очень распространенную ошибку, которую допускают многие студенты, впервые изучая квадратную формулу.
Многие учащиеся просто получают все на одной стороне, как мы сделали здесь, а затем получают значения \(a\), \(b\) и \(c\) в зависимости от позиции. Другими словами, часто учащиеся просто позволяют \(a\) быть первым числом в списке, \(b\) быть вторым числом в списке, а затем \(c\) быть последним числом в списке. Однако это неправильно.
 2} — 4\ влево( 3 \вправо)\влево( {11} \вправо)} }}{{2\влево( 3 \вправо)}}\\ & = \frac{{5 \pm \sqrt {25 — 132} }} {6}\\ & = \frac{{5 \pm \sqrt { — 107} }}{6}\\ & = \frac{{5 \pm \sqrt {107} \,\,i}}{6 }\конец{выравнивание*}\]
2} — 4\ влево( 3 \вправо)\влево( {11} \вправо)} }}{{2\влево( 3 \вправо)}}\\ & = \frac{{5 \pm \sqrt {25 — 132} }} {6}\\ & = \frac{{5 \pm \sqrt { — 107} }}{6}\\ & = \frac{{5 \pm \sqrt {107} \,\,i}}{6 }\конец{выравнивание*}\]Как и во всех других рассмотренных нами методах решения квадратных уравнений, не забудьте преобразовать квадратные корни из отрицательных чисел в комплексные числа. Кроме того, когда \(b\) отрицательно, будьте очень осторожны с заменой. Это особенно верно для квадратной части под радикалом. Помните, что если вы возведете в квадрат отрицательное число, оно станет положительным. Одна из наиболее распространенных ошибок здесь — торопиться и забыть поставить знак минус после возведения в квадрат \(b\), так что будьте осторожны. 92} — 4\left( 7 \right)\left( { — 6} \right)} }}{{2\left( 7 \right)}}\\ & = \frac{{ — 19 \pm \sqrt {361 + 168} }}{{14}}\\ & = \frac{{ — 19 \pm \sqrt {529} }}{{14}}\\ & = \frac{{ — 19 \pm 23} }{{14}}\end{выравнивание*}\]
Теперь вспомните, что когда мы получаем решения, подобные этому, нам нужно сделать дополнительный шаг и фактически определить целые и/или дробные решения.
 В данном случае это
В данном случае это. \[т = \фрак{{ — 19+ 23}}{{14}} = \frac{2}{7}\hspace{0,25in}t = \frac{{ — 19 — 23}}{{14}} = — 3\]
Теперь, как и в случае с завершением квадрата, тот факт, что мы получили целые и/или дробные решения, означает, что мы могли бы также разложить это квадратное уравнение на множители.
d \(\frac{3}{{y — 2}} = \frac{1}{y} + 1\) Показать решение
Итак, уравнение с дробями. Первым шагом является идентификация ЖК-дисплея.
\[{\mbox{LCD:}}y\left({y — 2} \right)\]
Итак, похоже, нам нужно убедиться, что в наших ответах нет ни \(y = 0\), ни \(y = 2\), чтобы мы не получили деление на ноль.
Умножьте обе стороны на ЖК-дисплей, а затем приведите результат к стандартной форме.
\[\ begin{align*}\left( y \right)\left( {y — 2} \ right)\left( {\ frac {3}{{y — 2}}} \ right) & = \ left ( {\ frac {1} {y} + 1} \ right) \ left ( y \ right) \ left ( {y — 2} \ right) \\ 3y & = y — 2 + y \ left ( {y — 2} \right)\\ 3y & = y — 2 + {y^2} — 2y\\ 0 & = {y^2} — 4y — 2\end{align*}\] 92} + 16х = 0\]
Вот константы для использования в квадратичной формуле.

\[a = — 1\hspace{0,25 дюйма}b = 16\hspace{0,25 дюйма}c = 0\]
Об этих значениях следует помнить две вещи. Во-первых, у нас впервые есть отрицательный \(a\). Ничего страшного, но такое мы видим впервые. Во-вторых, что более важно, одно из значений равно нулю. Это хорошо. Это будет происходить время от времени, и на самом деле, если одно из значений равно нулю, это значительно упростит работу. 92} — 4\влево( { — 1} \вправо)\влево( 0 \вправо)} }}{{2\влево( { — 1} \вправо)}}\\ & = \frac{{ — 16 \ pm \sqrt {256} }}{{ — 2}}\\ & = \frac{{ — 16 \pm 16}}{{ — 2}}\end{align*}\]
Преобразование их в целые/дробные числа дает
\[x = \frac{{ — 16 + 16}}{{ — 2}} = \frac{0}{-2} = 0\hspace{0,25 дюйма}x = \frac{{ — 16 — 16}} {{ — 2}} = \frac{{ — 32}}{{ — 2}} = 16\]
Таким образом, мы получаем два решения: \(x = 0\) и \(x = 16\).
 Это именно те решения, которые мы получили бы, разложив уравнение на множители. 92} + x — \frac{1}{{10}} = 0\) Показать решение
Это именно те решения, которые мы получили бы, разложив уравнение на множители. 92} + x — \frac{1}{{10}} = 0\) Показать решениеЕсть два способа работы с этим. Мы можем либо оставить дроби, либо умножить на LCD (в данном случае 10) и решить это уравнение. В любом случае ответ будет один. Здесь мы будем рассматривать только дробный случай, так как в этом суть этой задачи. Вы должны попробовать другой способ, чтобы убедиться, что вы получаете то же решение.
В этом случае здесь приведены значения квадратной формулы, а также квадратичная формула работы для этого уравнения. 92} — 4 \ влево ( {\ гидроразрыва {1} {2}} \ вправо) \ влево ( { — \ гидроразрыва {1} {{10}}} \ вправо)}}} {{2 \ влево ( {\ frac{1}{2}} \right)}} = \frac{{ — 1 \pm \sqrt {1 + \frac{1}{5}} }}{1} = — 1 \pm \sqrt {\ дробь{6}{5}} \]
В таких случаях мы обычно делаем дополнительный шаг, удаляя квадратный корень из знаменателя, так что давайте также сделаем это,
\[x = — 1 \pm \frac{{\sqrt 6}}{{\sqrt 5}}\,\frac{{\sqrt 5}}{{\sqrt 5}} = — 1 \pm \frac{ {\ sqrt {\ влево ( 6 \ вправо) \ влево ( 5 \ вправо)}}} {5} = — 1 \ pm \ frac {{\ sqrt {30}}} {5} \] 92} — 0,23x + 0,09 = 0\) Показать решение
В этом случае не волнуйтесь о десятичных дробях.
 2} — 4\ влево({0,04}\вправо)\влево({0,09} \right)} }}{{2\left( {0,04} \right)}}\\ & = \frac{{0,23 \pm \sqrt {0,0529 — 0,0144} }}{{0,08}}\\ & = \frac{{0,23 \pm \sqrt {0,0385} }}{{0,08}}\end{align*}\]
2} — 4\ влево({0,04}\вправо)\влево({0,09} \right)} }}{{2\left( {0,04} \right)}}\\ & = \frac{{0,23 \pm \sqrt {0,0529 — 0,0144} }}{{0,08}}\\ & = \frac{{0,23 \pm \sqrt {0,0385} }}{{0,08}}\end{align*}\]Теперь об этом будет одно отличие этих задач от задач с целыми или дробными коэффициентами. Когда у нас есть десятичные коэффициенты, мы обычно идем дальше и вычисляем два отдельных числа. Итак, давайте так,
\[x = \frac{{0,23 \pm \sqrt {0,0385} }}{{0,08}} = \frac{{0,23 \pm 0,19621}}{{0,08}}\] \[\begin{align*}x = \frac{{0,23 + 0,19621}}{{0,08}}\hspace{0,25 дюйма}{\mbox{and}}\hspace{0,25 дюйма}x = \frac{{0,23 — 0,19621}}{{0,08}}\\ & \,\,\,\, = 5,327625\hspace{0,25 дюйма}{\mbox{и}}\hspace{0,25 дюйма}\,\,\,\, = 0,422375\конец{выравнивание*}\]
Обратите внимание, что мы использовали округление квадратного корня.
В течение последних двух разделов мы довольно много решили.
 {2}}-4ac}}{2a}[/latex]. Это уравнение известно как квадратичная формула. 9{2}+bx+c=0[/latex] называется стандартной формой квадратного уравнения. Прежде чем решать квадратное уравнение с помощью квадратной формулы, жизненно важно убедиться, что уравнение имеет именно такую форму. Если вы этого не сделаете, вы можете использовать неправильные значения для a , b или c , и тогда формула даст неверные решения.
{2}}-4ac}}{2a}[/latex]. Это уравнение известно как квадратичная формула. 9{2}+bx+c=0[/latex] называется стандартной формой квадратного уравнения. Прежде чем решать квадратное уравнение с помощью квадратной формулы, жизненно важно убедиться, что уравнение имеет именно такую форму. Если вы этого не сделаете, вы можете использовать неправильные значения для a , b или c , и тогда формула даст неверные решения.В следующих примерах показано, как убедиться, что ваше квадратное уравнение имеет стандартную форму, а затем правильно определить значения, которые вы будете использовать для a, b и c в квадратной формуле. 9{2}+bx+c=0[/латекс]. Чтобы использовать его, выполните следующие действия.
- Сначала приведите уравнение в стандартной форме.
- Определите коэффициенты a , b , и c . Не забудьте включить отрицательные знаки, если вычитаются члены bx или c .
- Аккуратно подставьте в уравнение значения, отмеченные на шаге [latex]2[/latex].
 Чтобы избежать ненужных ошибок, используйте круглые скобки вокруг каждого числа, введенного в формулу.
Чтобы избежать ненужных ошибок, используйте круглые скобки вокруг каждого числа, введенного в формулу. - Максимально упростить.
- Используйте [latex]\pm[/latex] перед радикалом, чтобы разделить решение на два значения: одно, в котором добавляется квадратный корень, и другое, в котором он вычитается .
- Упростите оба значения, чтобы получить возможные решения.
Много шагов. Давайте попробуем использовать квадратную формулу, чтобы сначала решить относительно простое уравнение; затем вы вернетесь и решите ее снова, используя другой метод факторинга.
Вы можете проверить эти решения, подставив [латекс]1[/латекс] и [латекс]−5[/латекс] в исходное уравнение. 9{2}+4\влево(-5\вправо)=5\,\,\,\,\,\\25-20=5\,\,\,\,\,\\5=5\,\ ,\,\,\,\end{массив}[/латекс]
Вы получаете два верных утверждения, поэтому вы знаете, что оба решения работают: [латекс]x=1[/латекс] или [латекс]-5[/латекс]. Вы успешно решили уравнение, используя квадратную формулу!
Попробуй
Иногда проще решить уравнение, используя обычные методы разложения на множители, такие как нахождение пар чисел, сумма которых равна одному числу (в данном примере [латекс]4[/латекс]) и которые дают определенный произведение (в данном примере [латекс]−5[/латекс]) при умножении.
 Сила квадратичной формулы в том, что с ее помощью можно решить любые квадратные уравнения , даже те, где нахождение числовых комбинаций не получится.
Сила квадратичной формулы в том, что с ее помощью можно решить любые квадратные уравнения , даже те, где нахождение числовых комбинаций не получится.В наших следующих двух видео-примерах мы увидим, во-первых, квадратное уравнение с двумя вещественными рациональными решениями, а во-вторых, квадратное уравнение, которое имеет иррациональные решения и которое не может быть решено с помощью факторинга.
В следующем видео-примере мы показываем, что квадратная формула полезна, когда квадратное уравнение имеет два иррациональных решения, которые нельзя было получить с помощью факторизации. 9{2}-2\влево(4\вправо)=6\влево(4\вправо)-16\\16-8=24-16\,\,\,\,\,\,\\8=8\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{массив}[/ латекс]
В следующем видео мы показываем пример использования квадратной формулы для решения квадратного уравнения, которое имеет одно повторяющееся решение.

В следующем примере мы покажем, что некоторые квадратные уравнения не имеют действительных решений. Поскольку мы упрощаем квадратичную формулу, мы можем получить отрицательное число под квадратным корнем, которое, как мы знаем, не определено для действительных чисел. 9{2}}-4ac}}{2a}[/latex] находится путем заполнения квадрата квадратного уравнения [latex] [/latex]. Когда вы упрощаете использование квадратной формулы и получаете отрицательное число, меньшее квадратного корня, у уравнения нет действительных чисел.
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
18.4: Решение квадратных уравнений с помощью квадратичной формулы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 46446
- OpenStax
- OpenStax
- Решать квадратные уравнения с помощью Квадратной формулы 9{2}-4 a b\), когда \(a=3\) и \(b=−2\).

- Упростить \(\sqrt{108}\).
- Упростить \(\sqrt{50}\).
- Ответить
\(b=-6, b=-4\)
- Ответить
\(x=-1+\sqrt{6}, x=-1-\sqrt{6}\)
- Ответить
- 9{2}+\dfrac{2}{3} u=\dfrac{1}{3}\).
Решение :
Наш первый шаг — очистить дроби.
Умножьте обе части на ЖК-дисплей, \(6\), чтобы очистить дроби. Умножить. Вычтите \(2\), чтобы получить уравнение в стандартной форме. 
Определите значения \(a, b\) и \(c\). Напишите квадратную формулу. Затем подставьте значения \(a, b,\) и \(c\). Упрощение. Упростите радикальное. Умножьте общий множитель в числителе. Удалите общие множители. Перепишите, чтобы показать два решения. Чек:
Мы оставляем вам чек!
 {2}-20 x=-25\).
{2}-20 x=-25\).Решение :
Добавьте \(25\), чтобы получить уравнение в стандартной форме. Определите значения \(a, b\) и \(c\). Напишите формулу квадрата. Затем подставьте значения \(a, b\) и \(c\). Упрощение. Упростите радикальное. Упростите дробь. Чек:
Мы оставляем вам чек!
9{2}-40 т=-16\). - Ответить
\(t=\dfrac{4}{5}\)
Использование дискриминанта для предсказания количества и типа решений квадратного уравнения
Когда мы решали квадратные уравнения в предыдущих примерах, иногда мы получали два действительных решения, одно действительное решение, а иногда два комплексных решения.
 Есть ли способ предсказать количество и тип решений квадратного уравнения без фактического решения уравнения?
Есть ли способ предсказать количество и тип решений квадратного уравнения без фактического решения уравнения?Да, выражение под радикалом квадратной формулы позволяет нам легко определить количество и тип решений. Это выражение называется дискриминантом .
Определение \(\PageIndex{2}\)
Дискриминант
Рисунок 9.3.85Давайте посмотрим на дискриминант уравнений в некоторых примерах, а также на количество и тип решений этих квадратных уравнений.
Квадратное уравнение (в стандартной форме) 9{2}-20 р+25=0\) - Ответить
- \(2\) действительные решения
- \(2\) комплексные растворы
- \(1\) действительное решение
Определите наиболее подходящий метод для решения квадратного уравнения
Ниже мы суммируем четыре метода, которые мы использовали для решения квадратных уравнений.

Методы решения квадратных уравнений
- Факторинг 9{2}=k\) мы используем свойство Square Root. Для любого другого уравнения, вероятно, лучше всего использовать квадратную формулу. Помните, что вы можете решить любое квадратное уравнение, используя квадратную формулу, но это не всегда самый простой метод.
Как насчет метода завершения квадрата? Большинство людей считают этот метод громоздким и предпочитают его не использовать. Нам нужно было включить его в список методов, потому что мы завершили квадрат в целом, чтобы вывести квадратную формулу. Вы также будете использовать процесс заполнения квадрата в других областях алгебры. 9{2}=125\)
- Ответить
- Квадратичная формула
- Факторинг или свойство квадратного корня
- Свойство квадратного корня
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики использования квадратичной формулы.

Цели обучения
К концу этого раздела вы сможете:
Решение квадратных уравнений с помощью квадратной формулы
Когда мы решали квадратные уравнения в последнем разделе, завершая квадрат, мы каждый раз выполняли одни и те же шаги. К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ «да». Математики ищут закономерности, когда делают что-то снова и снова, чтобы облегчить себе работу. В этом разделе мы выведем и используем формулу для нахождения решения квадратного уравнения.
Мы уже видели, как решить формулу для конкретной переменной «в общем», так что мы проделаем алгебраические шаги только один раз, а затем используем новую формулу, чтобы найти значение конкретной переменной. Теперь мы пройдем этапы заполнения квадрата, используя общую форму квадратного уравнения, чтобы решить квадратное уравнение относительно \(x\) .
Начнем со стандартной формы квадратного уравнения и решим его относительно \(х\), заполнив квадрат.
9{2}-4 a c}}{2 a} \label{quad}\]
Чтобы использовать квадратную формулу , мы подставляем значения \(a,b\) и \(c\) из стандартную форму в выражение в правой части формулы. Тогда упростим выражение. Результатом является пара решений квадратного уравнения.
Обратите внимание, что квадратичная формула (уравнение \ref{quad}) является уравнением. Убедитесь, что вы используете обе части уравнения.
Пример \(\PageIndex{1}\) Как решить квадратное уравнение с помощью квадратичной формулы 9{2}-4 \cdot 2 \cdot(-5)}}{2 \cdot 2}\)
Шаг 3 : Упростите дробь и найдите \(x\). \(\begin{array}{l}{x=\dfrac{-9 \pm \sqrt{81-(-40)}}{4}} \\ {x=\dfrac{-9 \pm \sqrt {121}}{4}} \\ {x=\dfrac{-9 \pm 11}{4}} \\ {x=\dfrac{-9+11}{4}}\quad x=\dfrac{ -9-11}{4} \\ {x=\dfrac{2}{4} \quad \quad\:\:\: x=\dfrac{-20}{4}}\\ {x=\dfrac {1}{2} \quad\quad\:\:\: x=-5}\end{массив}\) 9{2}+b х+с=0\).  {2}-6 x=-5\). 9{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \)
{2}-6 x=-5\). 9{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \)Упрощение. \(x=\dfrac{6 \pm \sqrt{36-20}}{2}\)
\(x=\dfrac{6 \pm \sqrt{16}}{2}\)
\(x=\dfrac{6 \pm 4}{2}\)
Перепишите, чтобы показать два решения. \(x=\frac{6+4}{2}, \quad x=\frac{6-4}{2}\) 9{2}+24=-10 б\).
Когда мы решали квадратные уравнения, используя свойство квадратного корня, мы иногда получали ответы, содержащие радикалы. Это также может произойти при использовании квадратичной формулы . Если мы получим радикал в качестве решения, окончательный ответ должен иметь радикал в его упрощенной форме.
 {2}+10 x+11=0\). 9{2}-4 а в}}{2 а}\)
{2}+10 x+11=0\). 9{2}-4 а в}}{2 а}\)Затем подставьте значения \(a, b\) и \(c\). Упрощение. \(x=\dfrac{-10 \pm \sqrt{100-88}}{4}\)
\(x=\dfrac{-10 \pm \sqrt{12}}{4}\)
Упростите радикальное. \(x=\dfrac{-10 \pm 2 \sqrt{3}}{4}\)
Вынесите общий множитель из числителя. \(x=\dfrac{\color{red}{2}(-5 \pm \sqrt{3})}{4}\)
Удалите общие множители. \(x=\dfrac{-5 \pm \sqrt{3}}{2}\)
Решение :
Это уравнение имеет стандартную форму. 
Определите значения \(a,b,c\). Напишите квадратную формулу. Затем подставьте значения \(a,b,c\). Упрощение. Упростите радикал, используя комплексные числа. Упростите радикальное. Умножьте общий множитель в числителе. Удалите общие множители. 9{2}+b х+с=0\). Иногда нам нужно будет выполнить некоторую алгебру, чтобы привести уравнение к стандартной форме, прежде чем мы сможем использовать квадратную формулу. Пример \(\PageIndex{5}\)
Решите с помощью квадратичной формулы: \(x(x+6)+4=0\).

Решение :
Наш первый шаг — привести уравнение к стандартной форме.
Распределите, чтобы получить уравнение в стандартной форме. Теперь это уравнение имеет стандартную форму. Определите значения \(a,b,c\). Напишите квадратную формулу. Затем подставьте значения \(a,b,c\). Упрощение. Упростите радикальное. Умножьте общий множитель в числителе. Удалите общие множители. Запишите двумя решениями. 
Чек:
Мы оставляем вам чек!
Таблица 9.3.6 Упражнение \(\PageIndex{9}\)
Решите с помощью квадратичной формулы: \(x(x+2)−5=0\).
Упражнение \(\PageIndex{10}\)
Решите с помощью квадратичной формулы: \(3y(y−2)−3=0\).


 {\frac{2}{3}} = 4\) – это иррациональные уравнения.
{\frac{2}{3}} = 4\) – это иррациональные уравнения. {2} + 2} = \sqrt{2x + 2}\)
{2} + 2} = \sqrt{2x + 2}\) Промежутки, которые будут принадлежать и ОДЗ, и решению, пойдут в ответ.
Промежутки, которые будут принадлежать и ОДЗ, и решению, пойдут в ответ. {2} + 3x} = \sqrt{5x — 1}\)
{2} + 3x} = \sqrt{5x — 1}\) Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Однако, если вы снова вспомните, что это ВСЕГДА будет учитываться как \(y\) плюс синее число выше, нам не нужно беспокоиться о процессе факторинга.
Однако, если вы снова вспомните, что это ВСЕГДА будет учитываться как \(y\) плюс синее число выше, нам не нужно беспокоиться о процессе факторинга. 2} = \ гидроразрыва {92} & = \ frac {4} {9} \\ x — \ frac {1} {3} & = \ pm \ sqrt {\ frac {4} {9}} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма}x = \frac{1}{3} \pm \frac{2}{3}\end{align*}\]
2} = \ гидроразрыва {92} & = \ frac {4} {9} \\ x — \ frac {1} {3} & = \ pm \ sqrt {\ frac {4} {9}} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма}x = \frac{1}{3} \pm \frac{2}{3}\end{align*}\]
 Для этого уравнения имеем.
Для этого уравнения имеем. В этот момент мы можем сделать некоторые отмены.
В этот момент мы можем сделать некоторые отмены. 2} — 4\ влево( 3 \вправо)\влево( {11} \вправо)} }}{{2\влево( 3 \вправо)}}\\ & = \frac{{5 \pm \sqrt {25 — 132} }} {6}\\ & = \frac{{5 \pm \sqrt { — 107} }}{6}\\ & = \frac{{5 \pm \sqrt {107} \,\,i}}{6 }\конец{выравнивание*}\]
2} — 4\ влево( 3 \вправо)\влево( {11} \вправо)} }}{{2\влево( 3 \вправо)}}\\ & = \frac{{5 \pm \sqrt {25 — 132} }} {6}\\ & = \frac{{5 \pm \sqrt { — 107} }}{6}\\ & = \frac{{5 \pm \sqrt {107} \,\,i}}{6 }\конец{выравнивание*}\] В данном случае это
В данном случае это
 Это именно те решения, которые мы получили бы, разложив уравнение на множители. 92} + x — \frac{1}{{10}} = 0\) Показать решение
Это именно те решения, которые мы получили бы, разложив уравнение на множители. 92} + x — \frac{1}{{10}} = 0\) Показать решение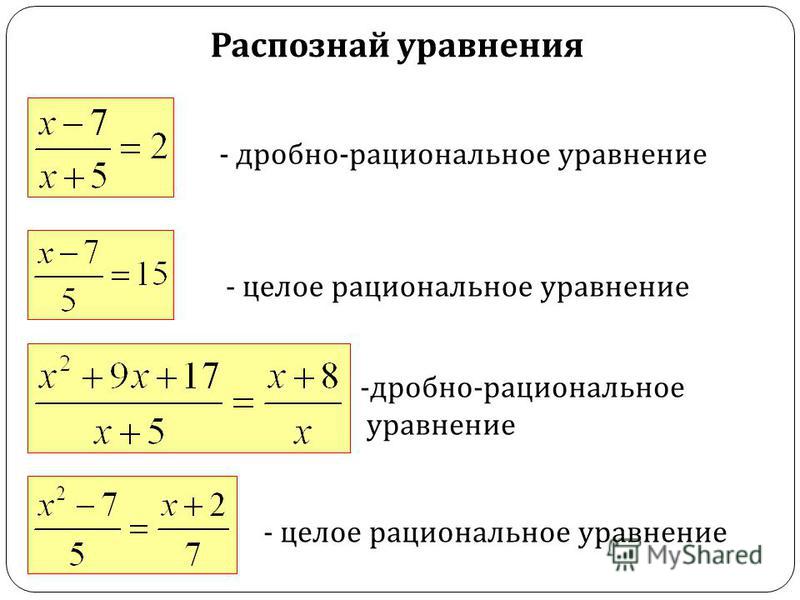 2} — 4\ влево({0,04}\вправо)\влево({0,09} \right)} }}{{2\left( {0,04} \right)}}\\ & = \frac{{0,23 \pm \sqrt {0,0529 — 0,0144} }}{{0,08}}\\ & = \frac{{0,23 \pm \sqrt {0,0385} }}{{0,08}}\end{align*}\]
2} — 4\ влево({0,04}\вправо)\влево({0,09} \right)} }}{{2\left( {0,04} \right)}}\\ & = \frac{{0,23 \pm \sqrt {0,0529 — 0,0144} }}{{0,08}}\\ & = \frac{{0,23 \pm \sqrt {0,0385} }}{{0,08}}\end{align*}\] {2}}-4ac}}{2a}[/latex]. Это уравнение известно как квадратичная формула. 9{2}+bx+c=0[/latex] называется стандартной формой квадратного уравнения. Прежде чем решать квадратное уравнение с помощью квадратной формулы, жизненно важно убедиться, что уравнение имеет именно такую форму. Если вы этого не сделаете, вы можете использовать неправильные значения для a , b или c , и тогда формула даст неверные решения.
{2}}-4ac}}{2a}[/latex]. Это уравнение известно как квадратичная формула. 9{2}+bx+c=0[/latex] называется стандартной формой квадратного уравнения. Прежде чем решать квадратное уравнение с помощью квадратной формулы, жизненно важно убедиться, что уравнение имеет именно такую форму. Если вы этого не сделаете, вы можете использовать неправильные значения для a , b или c , и тогда формула даст неверные решения. Чтобы избежать ненужных ошибок, используйте круглые скобки вокруг каждого числа, введенного в формулу.
Чтобы избежать ненужных ошибок, используйте круглые скобки вокруг каждого числа, введенного в формулу. Сила квадратичной формулы в том, что с ее помощью можно решить любые квадратные уравнения , даже те, где нахождение числовых комбинаций не получится.
Сила квадратичной формулы в том, что с ее помощью можно решить любые квадратные уравнения , даже те, где нахождение числовых комбинаций не получится.


 {2}-6 x=-5\). 9{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \)
{2}-6 x=-5\). 9{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \) {2}+10 x+11=0\). 9{2}-4 а в}}{2 а}\)
{2}+10 x+11=0\). 9{2}-4 а в}}{2 а}\)


 {2}-20 x=-25\).
{2}-20 x=-25\). Есть ли способ предсказать количество и тип решений квадратного уравнения без фактического решения уравнения?
Есть ли способ предсказать количество и тип решений квадратного уравнения без фактического решения уравнения?
