Найти объем параллелепипеда онлайн
Пример решили: 33908 раз Сегодня решили: 0 раз
Введите длины сторон параллелепипеда
Сторона a Сторона b Сторона c
Вычисление объема прямоугольного параллелепипеда
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Параллелепипед – это призма, основанием которой служит параллелограмм.
В параллелепипеде противоположные грани равны и параллельны.
Диагонали его пересекаются в одной точке, которая лежит на оси симметрий, и делятся ею пополам.
Объём параллелепипеда равен произведению его измерений.
Формула для вычисления объема параллелепипеда:
$$V = a \cdot b \cdot c$$
Примеры решений
- Найдите объем прямоугольного параллелепипеда, если его стороны равны 2,3,4 см.

Попробуйте другие сервисы
Найти объем куба
Найти объем шара
Найти объем цилиндра
Найти объем усеченного конуса
Найти объем усеченной пирамиды
Объем призмы
Для нахождения объема призмы применяется общая универсальная формула:V = Sh
где:
V — объем призмы
Vn — объем призмы, в основании которой лежит правильный многоугольник с n сторонами
Sb — площадь основания призмы
h — высота призмы
n — количество сторон правильного многоугольника, который лежит в основании призмы
a — длина стороны правильного многоугольника
Как найти объем треугольной призмы (с треугольником в основании)
Если в основании призмы лежит треугольник, то для нахождения ее объема можно применить формулы нахождения площади треугольника и умножить полученное значение на высоту призмы.
Объем треугольной призмы можно найти через высоту основания ha и сторону a, на которую эта высота опущена (Формула 2). Не путайте ha и h.
Объем треугольной призмы можно найти через радиус вписанной окружности r и сумму длин сторон основания (a,b,c).(Формула 3)
Объем треугольной призмы можно вычислить как произведение длин сторон основания на четыре радиуса описанной окружности R, умноженное на высоту призмы. (Формула 4)
Также, зная радиус описанной окружности, объем треугольной призмы можно найти как произведение синусов всех углов основания на квадрат радиуса описанной окружности, умноженное на удвоенную высоту призмы (Формула 5).
Если известен угол между двумя сторонами основания и сами эти стороны, то половина произведения сторон основания на синус угла между ними и на высоту призмы, также позволит вычислить ее объем (Формула 6).
Есть также формулы нахождения объема призмы для специальных случаев, когда в основании лежит геометрическая фигура с «особенностями». Например, если в основании прямой призмы лежит равносторонний, прямоугольный или равнобедренный треугольник, тогда количество формул, которыми можно воспользоваться для расчета объем призмы, существенно расширяется:
Например, если в основании прямой призмы лежит равносторонний, прямоугольный или равнобедренный треугольник, тогда количество формул, которыми можно воспользоваться для расчета объем призмы, существенно расширяется:
Объем правильной треугольной призмы (с правильным треугольником в основании)
На рисунке выше правильная треугольная призма изображена синим цветом.
Где:
V — объем правильной треугольной призмы
ha — высота основания, опущенная на сторону основания a
h — высота призмы
r — радиус вписанной в основание окружности
R
Объем призмы с прямоугольным треугольником в основании
Где:
V — объем призмы с прямоугольным треугольником в основании
h — высота призмы
α — угол основания, противолежащий стороне a (катету a) прямоугольного треугольника
β — угол основания, противолежащий стороне b (катету b) прямоугольного треугольника
a,b — катеты прямоугольного треугольника, который является основанием призмы
c — гипотенуза прямоугольного треугольника, который является основанием призмы
r — радиус вписанной в основание призмы окружности
R — радиус описанной вокруг основания призмы, которое является прямоугольным треугольником, окружности
Учтите, что если, вокруг прямоугольного треугольника описана окружность, то гипотенуза треугольника лежит на ее диаметре, то есть c = 2R.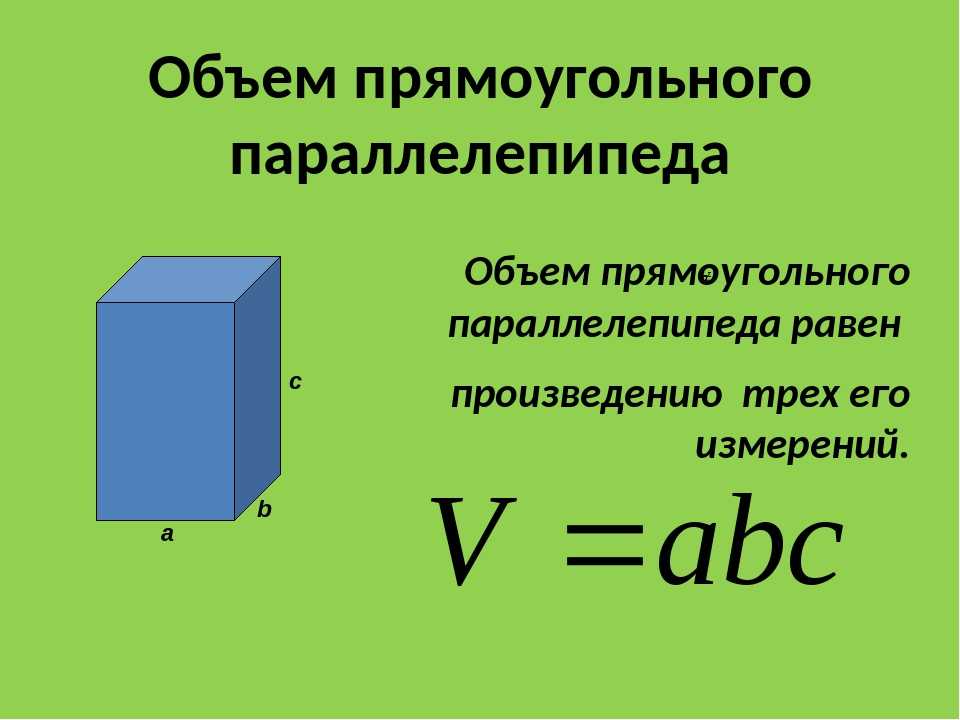
Объем призмы с равнобедренным треугольником в основании
Если в основании призмы лежит равнобедренный треугольник, для нахождения ее объема можно воспользоваться следующими формулами:
где:
V— объем призмы с равнобедренным треугольником в основании
h — высота призмы
hb — высота равнобедренного треугольника, опущенная на его основание
a — длина одной из равных сторон равнобедренного треугольника, лежащего в основании призмы
b — основание равнобедренного треугольника
α — угол между сторонами и основанием равнобедренного треугольника
β — угол между равными сторонами равнобедренного треугольника, который лежит в основании призмы
Объем параллелепипеда и куба
Если в основании прямой призмы лежит прямоугольник, то количество формул для нахождения объема такой призмы также будет больше:где:
V — объем призмы, в основании которой лежит прямоугольник
Vc — объем куба
h — высота призмы
a — длина стороны основания
b — длина второй стороны основания
R — радиус окружности, описанной вокруг основания куба
r — радиус окружности, вписанной в основание куба
0
Призма.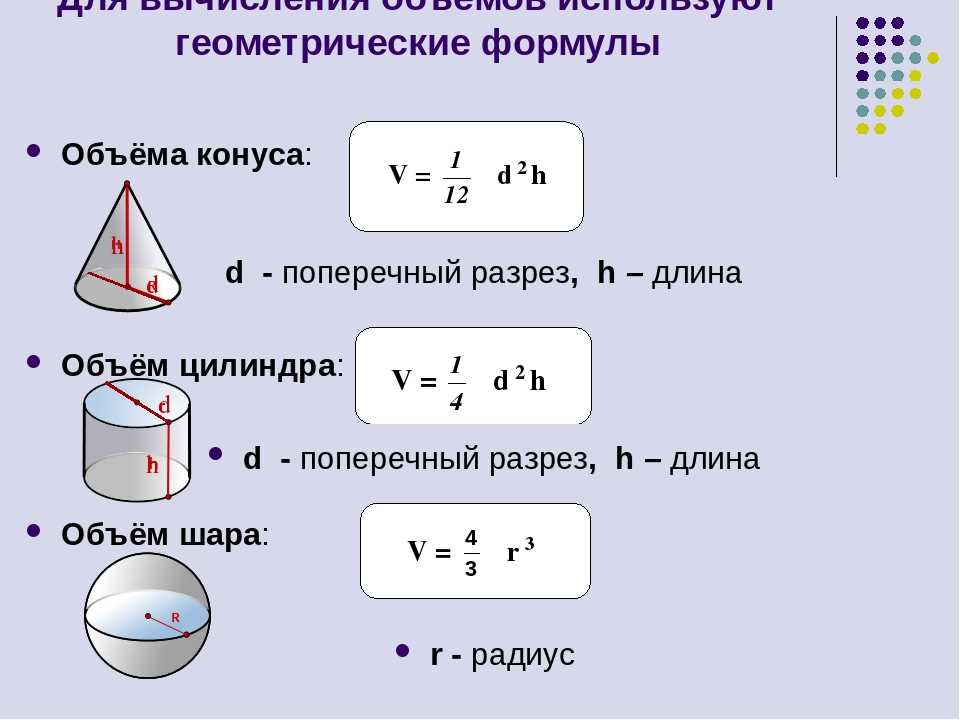 Параллелепипед. Куб. Решение задач |
Описание курса
| Площадь боковой поверхности призмы
Параллелепипед. Куб. Решение задач |
Описание курса
| Площадь боковой поверхности призмы
варианты задач и их решение :: SYL.ru
Современные технологии создают удивительные компьютерные программы. Они позволяют увидеть тела в объеме и покрутить их в разных направлениях, чтобы получше рассмотреть. Воображение человека не всегда на это способно. Немногие могут отчетливо представить предмет и увидеть его как бы насквозь. Но такое умение можно попытаться сформировать при решении задач по геометрии. Например, тех из них, в которых говорится о том, как найти объем куба. Это отличная практика для развития пространственного воображения.
Куб или параллелепипед?
Это непустой вопрос. Потому что классификация важна. Ведь куб — это особая форма прямоугольного параллелепипеда.
Последний представляет собой фигуру, в которой 6 граней, и все они прямоугольники. Углы, под которыми пересекаются все ребра, 90º. Соответственно, если эти грани станут квадратами, то и вся фигура преобразится в куб.
У прямоугольного параллелепипеда все линейные размеры, то есть высота, длина и ширина, могут существенно отличаться. В кубе же они всегда равны друг другу. Это его отличительный признак. Поэтому в задачах, которые требуют найти объем куба, рассмотренный момент непременно учитывается. Кстати, он существенно упрощает все математические записи и вычисления.
Условные обозначения в формулах и задачах
Без этого пункта будет сложно понять, как записаны формулы. Что подразумевается под каждой буквой и символом, подскажет следующая таблица.
| Символ | Название элемента |
| а | ребро фигуры |
| д | диагональ грани |
| Д | диагональ куба |
| общепринятые в геометрии символы | площадь |
| объем |
Как найти элементы куба по его стороне?
Поскольку грань фигуры — это квадрат, то ее площадь определится по формуле №1, в которой известную величину нужно возвести в квадрат:
А диагональ любой грани вычисляется по формуле №2, в которой сторона умножается на корень из 2:
Предыдущая формула получается из теоремы Пифагора.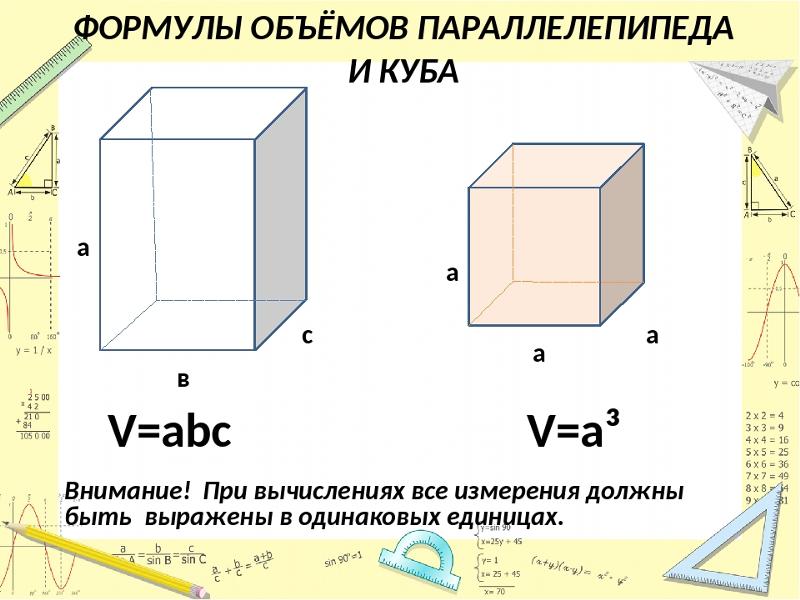 Это легко понять, если увидеть, что диагональ грани — это гипотенуза прямоугольного треугольника. А катетами его становятся стороны квадрата.
Это легко понять, если увидеть, что диагональ грани — это гипотенуза прямоугольного треугольника. А катетами его становятся стороны квадрата.
Чтобы определить диагональ куба, нужна будет следующая формула №3, содержащая известную сторону и квадратный корень из 3:
Она тоже получается из теоремы Пифагора. Только в качестве гипотенузы выступает искомая диагональ. Катетами же становятся сторона квадрата и его диагональ.
Иногда требуется знать формулу для вычисления площади боковой поверхности этой фигуры. В ней квадрат стороны умножается на 4. Вот она (№4):
Понять, как получается эта формула, несложно. Боковых граней — 4. А это значит, что их общая площадь — учетверенное значение площади одного квадрата.
Если нужно определить площадь всей поверхности, то используют эту запись, в которой ушестеряется квадрат ребра (формула №5):
Она получается аналогично предыдущей формуле, только число квадратов увеличилось до 6.
Что такое объем?
Если говорить просто, то это место, которое занимает любое тело в пространстве. Любой предмет ограничен в пространстве поверхностями. Их может быть несколько, но возможны случаи, когда только одна. Например, если тело — это шар. Но эти поверхности обязательно замкнуты. Пространство, которое занимает геометрическое тело, и будет его вместимостью, или объемом.
Любой предмет ограничен в пространстве поверхностями. Их может быть несколько, но возможны случаи, когда только одна. Например, если тело — это шар. Но эти поверхности обязательно замкнуты. Пространство, которое занимает геометрическое тело, и будет его вместимостью, или объемом.
Единицы измерения объема
Когда речь идет о твердых телах, то единицами объема всегда будут кубические величины. К примеру, метр, сантиметр или километр в кубе. Для жидкостей приняты литры, которые выражаются через кубические дециметры. Но если они занимают очень большие объемы, то их измеряют также в кубических метрах. Например, при учете расхода воды в квартире ее считают в м3. Так получается удобнее и проще в числовом выражении.
Способ 1: узнать объем куба, если известна сторона
Это самый простой из методов, который подскажет, как найти объем куба. Он заключается в том, чтобы просто возвести значение стороны в третью степень. Другими словами, нужно умножить сторону на себя три раза. По аналогии с произвольным прямоугольным параллелепипедом, когда нужно было умножать все его линейные размеры. Формула будет записана так (№6):
По аналогии с произвольным прямоугольным параллелепипедом, когда нужно было умножать все его линейные размеры. Формула будет записана так (№6):
Способ 2: известна площадь всей поверхности
В этом случае нужно будет разделить известную величину на 6. Из промежуточного ответа извлечь квадратный корень и возвести число в куб. Если записать это формулой, то получится следующее (№7):
Способ 3: дана диагональ грани куба
Для того чтобы узнать, как вычислить объем куба, в этом случае нужно выполнить следующие действия. Сначала возвести известное значение в куб, а потом умножить его на квадратный корень из 2 и разделить на 4. Формула для этой задачи (№8):
Это уравнение получается таким образом: известную диагональ нужно разделить на корень из двух. Потом число возвести в третью степень. После выполнения преобразований получается в числителе куб диагонали, а в знаменателе 2√2. Математика требует, чтобы под чертой не было иррационального числа. Поэтому от него избавляются путем умножения на √2.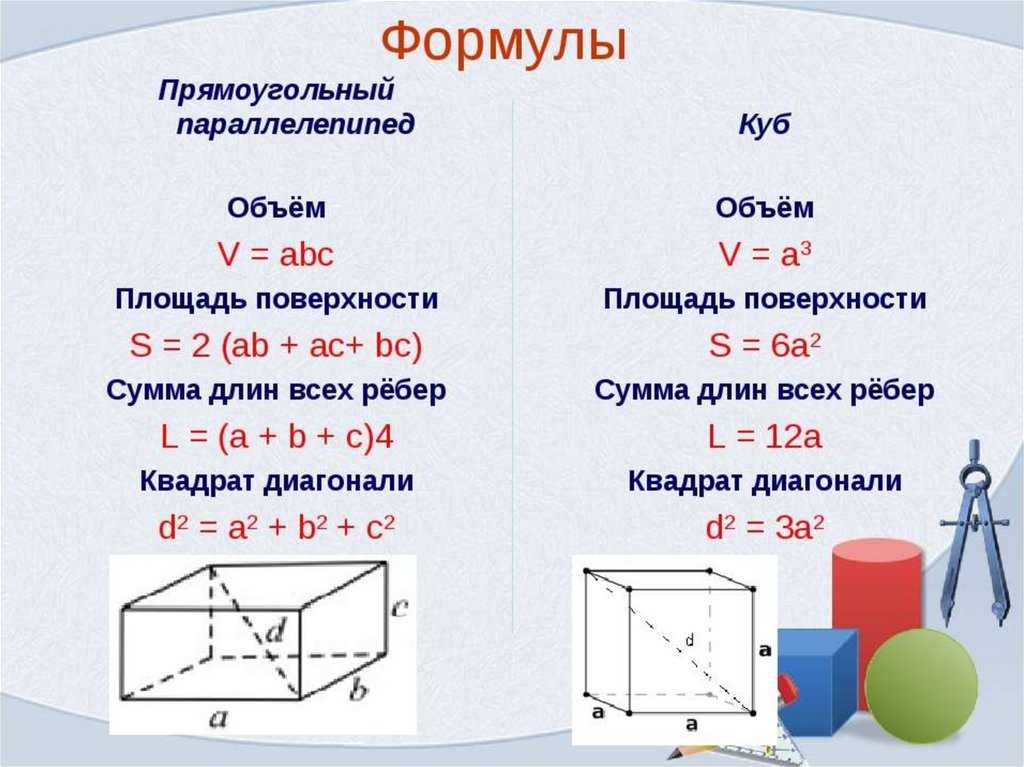 Тогда в числителе появляется √2, а в знаменателе получается 4.
Тогда в числителе появляется √2, а в знаменателе получается 4.
Способ 4: по диагонали куба
Формула, которая подскажет, как найти объем куба, будет содержать действия: возведение в квадрат диагонали, умножение ее на корень из 3 и деление всего на 9. Она будет записана так (№9):
Аналогично предыдущей формуле, в этой записи сначала диагональ делится на корень из трех и возводится в куб. После преобразований в знаменателе также появляется иррациональность, от которой нужно уходить. Так, в числителе возникает величина √3, а под чертой — 9.
Примеры заданий
Задача первая. Дан куб с ребром 12 см. Вычислить его объем и выразить ответ в квадратных метрах.
В этом задании будет сложнее перевести ответ в другие единицы, чем решить, как найти объем куба. Для выполнения первой части задания потребуется формула, записанная под номером 6. После возведения в куб числа 12 получится ответ 1728 см3. Теперь нужно вспомнить, как перевести их в кубические метры. Для этой цели ответ нужно разделить на 100 три раза. Сотня появилась из того факта, что в одном метре именно сто сантиметров. А деление выполняется трижды, потому что единицы в задании кубические. Итак, 1728 разделенное на 100 даст 17,28. После второго деления получится 0,1728. Третье действие даст ответ 0,001728 м3. Это и есть ответ задачи: объем куба равен 0,001728 м3 .
Для этой цели ответ нужно разделить на 100 три раза. Сотня появилась из того факта, что в одном метре именно сто сантиметров. А деление выполняется трижды, потому что единицы в задании кубические. Итак, 1728 разделенное на 100 даст 17,28. После второго деления получится 0,1728. Третье действие даст ответ 0,001728 м3. Это и есть ответ задачи: объем куба равен 0,001728 м3 .
Задача вторая. Имеется куб с площадью всей его поверхности, равной 600 дм2. Найти объем фигуры и выразить его в кубических метрах.
Для ответа на вопрос этого задания будет нужна формула номер 7. Первым действием известное число делится на 6. В ответе получается 100. Из него легко извлечь квадратный корень, он будет равен 10. Теперь десятку нужно возвести в куб. Так получается, что искомая величина равна 1000 дм3. Осталось перевести его в м3. Как и в предыдущей задаче, деление будет выполняться три раза, только делителем будет 10. Потому что в одном метре десять дециметров. После деления получается ответ равный 1 м3. Ответ: объем равен 1 м3.
После деления получается ответ равный 1 м3. Ответ: объем равен 1 м3.
Задача третья. Дан куб с длиной диагонали его грани, равной √2 мм. Нужно вычислить объем.
Восьмая формула поможет в том, как найти ответ в этой задаче. Первым делом нужно возвести в куб известную величину. Квадратный корень из 2 в третьей степени даст значение 2√2. После умножения на √2 получится число 4. Последним действием нужно его разделить на 4. Ответ: объем куба 1 мм3.
Задача четвертая. Известно, что диагональ куба равна 3 м. Требуется вычислить его объем.
Будет просто найти ответ на эту задачу по формуле под номером 9. Величину, которая дана в условии, нужно возвести в куб. Получится 27. После его деления на 9 ответ станет равен 3. И последним действием его нужно умножить на квадратный корень из 3. Ответом задачи будет 3√3 м3.
Объем – формула, определение, расчет, примеры
Объем – это мера емкости, которую держит объект. Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:
Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:
- Возьмите прямоугольный лист бумаги длиной ‘ l ‘ см и шириной ‘ h ‘ см.
- Соедините противоположные стороны листа бумаги, не сгибая лист.
- Вы создали трехмерный объект, который заключает в себе пространство, из двухмерного листа.
| 1. | Определение тома |
| 2. | Объем трехмерных фигур |
3. | Список формул объема |
| 4. | Как рассчитать объем? |
| 5. | Единицы объема |
| 6. | Калькулятор объема |
| 7. | Часто задаваемые вопросы о томе |
Определение тома
Объем определяется как объем, занимаемый трехмерной твердой формой. В любой форме это трудно визуализировать, но можно сравнить между формами. Например, объем ящика компаса больше объема помещенного в него ластика. Для вычисления площади любой двумерной фигуры мы делим часть на равные квадратные единицы. Точно так же при вычислении объема объемных фигур мы будем делить его на равные кубические единицы. Давайте узнаем, как рассчитать объем различных твердых фигур в нашем следующем разделе.
Объем 3D-фигур
Каждый объект в нашем окружении имеет свойство занимать пространство. Эти реальные объекты можно легко сравнить с основными трехмерными формами.
Объем кубоида
Предположим, у нас есть несколько прямоугольных листов длиной ‘l’ и шириной ‘ b’ . Если мы сложим их один поверх другого до высоты ‘h’ , мы получим прямоугольный параллелепипед размерности л, б, з . Это можно увидеть на следующем рисунке, на котором показаны длина, ширина (ширина) и высота образованного таким образом прямоугольного параллелепипеда.
Чтобы вычислить количество пространства, заключенного в этот прямоугольный параллелепипед, мы используем формулу: Объем кубоида = l × b × h
Объем куба
Куб является частным случаем параллелепипеда, где все три стороны равны по мере. Если мы представим это равное значение как «а», то объем этого куба можно будет рассчитать по формуле: Объем куба = а × а × а = а³. Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.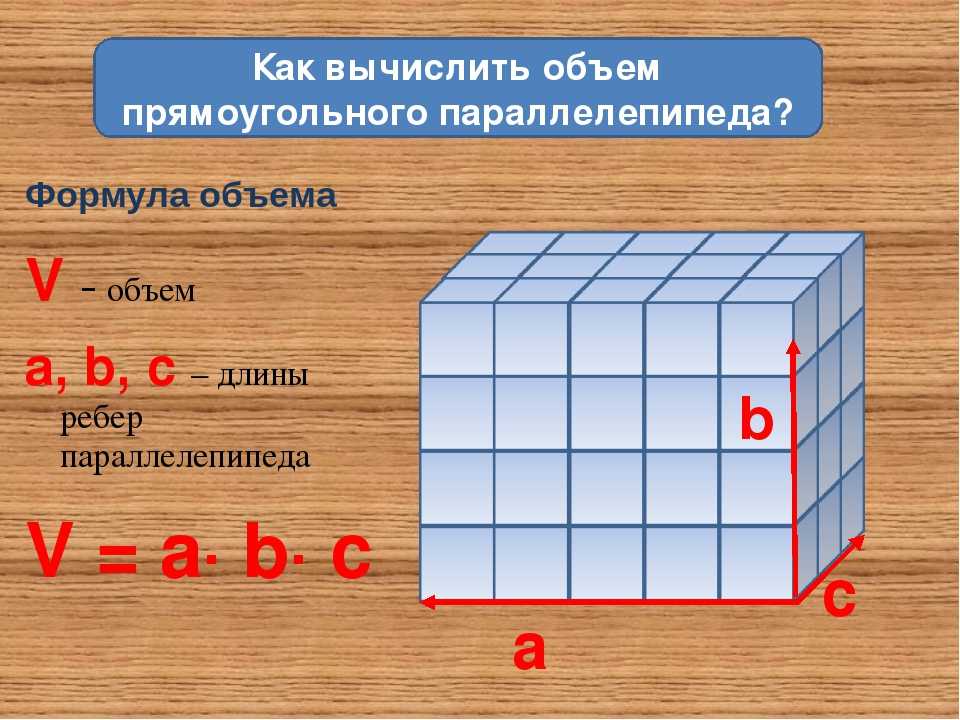
Объем цилиндра
Точно так же, как мы построили прямоугольный параллелепипед из прямоугольников, мы можем построить цилиндр из кругов того же размера.
Цилиндр представляет собой трубчатую структуру с двумя параллельными круглыми основаниями, которые соединены изогнутой поверхностью на фиксированном расстоянии от центра. Расстояние между этими двумя основаниями и есть высота цилиндра. Если мы рассмотрим «r» как радиус круглого основания (и вершины), а «h» как высоту цилиндра, то объем цилиндра можно выразить как объем цилиндра = π r² h
Объем пирамиды
Пирамиды имеют многоугольник в качестве основания и треугольные грани, которые сходятся на вершине. Объем пирамиды рассчитывается по формуле: Объем пирамиды = 1/3 × длина основания × ширина основания × высота пирамиды. Эту формулу также можно записать в виде 1/3 × площадь основания многоугольника × высота пирамиды.
Объем конуса
Разница между конусом и пирамидой в том, что основание конуса круглое, а основание пирамиды многоугольник. Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.
Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.
Объем шара
Объем шара – это занимаемое им пространство.
Объем сферы, радиус которой r равен 4/3 πr³.
Теперь, когда мы знакомы с формулами различных геометрических фигур, давайте взглянем на различные единицы объема.
Список формул объема
Ниже приведен подробный табличный список формул объема в двух словах, описывающий формулы объема для всех возможных трехмерных (твердых) форм.
Как рассчитать объем?
Вот шаги для расчета объема любой твердой формы:
- Определите все заданные параметры, которые являются полезными и которые необходимо заменить в соответствующей формуле объема. Например, радиус должен быть «r», а высота — «h», наклонная высота, диаметр и т. д.
- Убедитесь, что все параметры имеют одинаковые единицы измерения.
- Подставьте значения в формулу объема соответствующих форм.

- Запишите единицы измерения в кубических единицах.
Давайте разберемся с шагами на примере.
Пример: Найдите объем прямоугольного цилиндра радиусом 25 м и высотой 1 метр. Используйте π = 3,142.
Решение:
Радиус цилиндра равен r = 25 м.
Его высота h = 1 метр.
Объем цилиндра V = πr 2 h = (3,142)(25) 2 (1) = 1963,75 м 3 .
Объем баллона 1963,75 куб.м.
Единицы объема
Единицей объема в системе СИ является кубический метр (м 3 ), поскольку объем представляет собой количество трехмерного пространства, занимаемого формой или поверхностью. Однако наиболее часто используемой единицей измерения объема является литр. Кроме того, большие и малые объемы измеряются в других единицах, таких как миллилитры (мл), пинты, галлоны и другие. В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.
| Боковой блок | Единица объема | Метрический эквивалент |
|---|---|---|
| Дюйм | кубических дюймов (в 3 ) | 1 куб. дюйм = 16,387064 мл |
| Ножка | кубических футов ( 3 футов) | 1 куб.фут = 28,316846592 л |
| см | Кубический сантиметр (см 3 ) | 1 кубический сантиметр = 1 мл |
| Двор | Кубический ярд (ярд 3 ) | 1 куб. ярд = 764,554857984 л 1 куб.ярд = 0,764554857984 м 3 |
В то время как стандартной единицей измерения в США является кубический ярд или кубический дюйм, более широко используемыми единицами измерения являются галлоны, пинты или жидкие унции. В следующей таблице показаны некоторые из этих единиц и их эквивалентные метрические преобразования.
| Блок | Эквивалентное преобразование |
|---|---|
| 1 пинта (pt) | 2 чашки |
| 1 кварта (кварта) | 2 точки |
| 1 галлон (гал) | 3,78 литра |
| 1 литр | 1000 кубических сантиметров |
Калькулятор объема
Калькулятор объема помогает быстро и легко рассчитать объем любой заданной формы. Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.
Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.
☛Также проверьте:
- Калькулятор объема цилиндра
- Калькулятор объема сферы
- Калькулятор объема куба
- Калькулятор объема прямоугольного параллелепипеда
☛Статьи по теме
Ознакомьтесь со статьями, посвященными объему различных объемных форм.
- Объем конуса
- Объем цилиндра
- Объем кубоида
- Том Пирамиды
Примеры томов
Пример 1: У Эдвина есть конический сосуд радиусом 6 дюймов и высотой 7 дюймов. Каков объем сосуда? Используйте π = 22/7.
Раствор.
Сосуд имеет форму конуса.
Объем конуса = 1/3 π r² h = 1/3 × 22/7 × 6 × 6 × 7 = 264 дюйма³
∴ Объем судна 264 куб. дюйм
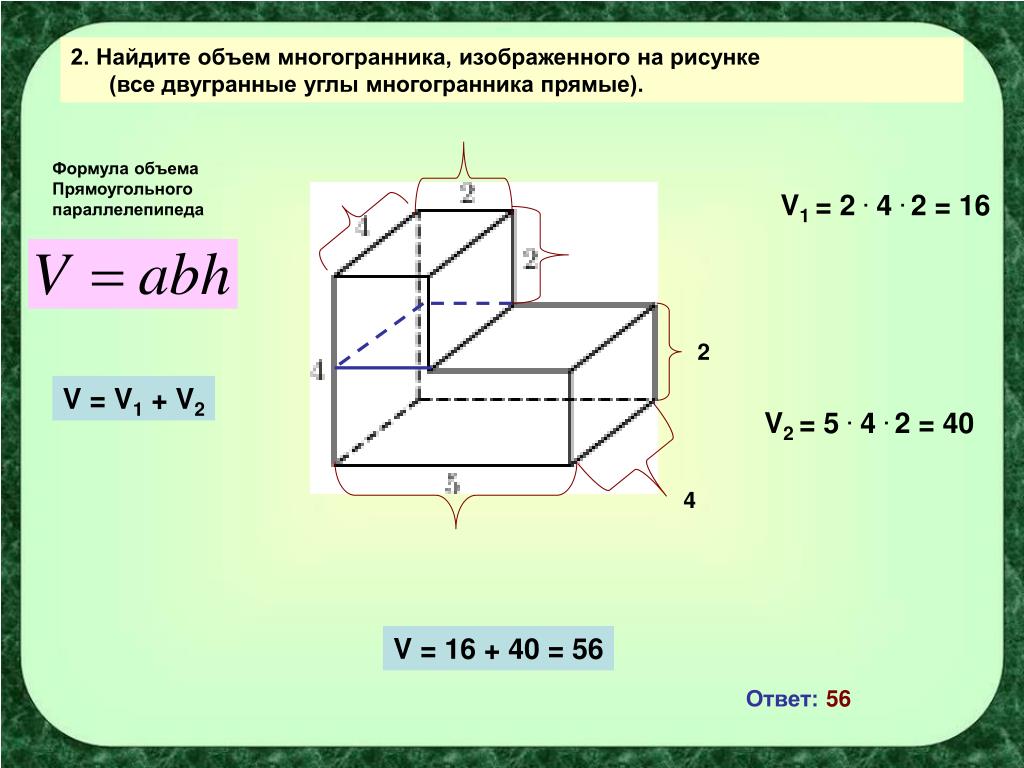
дюймПример 2: Джо любит играть со строительными блоками. Он построил конструкцию из 15 кубов. Если длина (ребро) каждого куба равна 3 дюймам, каков будет объем его конструкции?
Раствор.
Рассчитаем объем одного куба. Объем куба = ребро × ребро × ребро = 3 × 3 × 3 = 27 дюймов³
В его структуре 15 кубиков. Итак, объем всей конструкции:
Объем конструкции = 15 × объем одного куба = 15 × 27 = 405 дюймов³
∴ Объем конструкции 405 дюймов³.Пример 3: Если диаметр мяча составляет 14 дюймов, сколько воздуха может вместить мяч? Используйте π = 3,14
Решение.
Количество воздуха внутри шара займет все пространство в шаре. Итак, нам нужно найти объем шара.
Радиус шара 14/2 дюйма = 7 дюймов
Объем шара = 4/3 πr³
= [4/3 × 3,14 × (7)³]
= 1436,02 дюйма³
∴ Мяч содержит 1436,02 дюйма³ воздуха.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.0003
Часто задаваемые вопросы по тому
Что означает объем?
Объем — это мера емкости, которую содержит объект. Скажем, если чашка может вместить 1000 мл сока, говорят, что ее объем равен 1000 мл. В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.
☛Загрузите прямо сейчас, чтобы попрактиковаться.
- Объем Рабочие листы
- Объем кубов Рабочие листы
- Объем конуса Рабочие листы
- Объем цилиндра Рабочие листы
Какова формула объема частичного конуса?
Объем частичного конуса можно рассчитать по формуле: V = 1/3 × πh(R² + Rr + r²), где «R» — радиус основания конуса, а «r» — радиус верхней поверхности.
☛ Прочтите основы здесь:
- Объем правого кругового конуса
- Объем частичного конуса
- Объем конуса в единицах числа Пи
Как найти объем пирамид?
Объем пирамиды рассчитывается по формуле: V = 1/3 × Площадь основания × Высота.
☛ Также проверьте:
- Объем прямоугольной пирамиды
- Объем треугольной пирамиды
- Объем прямоугольной пирамиды
Как найти объем конуса?
Объем конуса составляет 1/3 объема цилиндра той же высоты и такого же основания. Формула, используемая для нахождения объема конуса: 1/3 × π r² h; где «r» — радиус, а «h» — высота конуса.
Как найти объем цилиндра?
Объем цилиндра рассчитывается по формуле: V = площадь основания цилиндра × высота, а также представляется как объем цилиндра = π r² h; где «r» — радиус цилиндра, а «h» — высота.
В чем разница между объемом и площадью?
Объем фигуры или твердого тела — это пространство, занимаемое им, которое также включает его высоту или глубину. Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.
Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.
☛ Проверьте список важных математических формул:
- Формулы площади
- Формулы площади поверхности
- Геометрические формулы
- Формулы измерения
Каков объем мяча?
Поскольку шар является сферой, его объем будет рассчитан по формуле объема сферы. Формула объема сферы: 4/3 πr³, где «r» — радиус сферы.
Какая формула объема цилиндра?
Формула объема цилиндра = πr²h; где «r» — радиус основания цилиндра, а «h» — высота.
Как найти объем призмы?
Мы можем найти объем призмы, записав заданные размеры призмы. Затем подставьте значения в формулу объема V = B × H, где «V», «B» и «H» — это объем, площадь основания и высота призмы. Получив значение объема призмы, в конце запишите единицу объема призмы (в кубических единицах).
☛Чек:
- Объем призмы
- Объем призм.
 Рабочие листы
Рабочие листы
Как найти объем бака?
Объем резервуара зависит от его формы. В зависимости от размера мы можем использовать приведенные ниже формулы:
- Объем параллелепипеда = l × b × h; где «l» — длина прямоугольного параллелепипеда, «b» — ширина (ширина) прямоугольного параллелепипеда, а «h» — высота прямоугольного параллелепипеда.
- Объем куба = a 3 , где «a» — ребро куба.
- Объем цилиндра = π r 2 ч; где «r» — радиус основания цилиндра, а «h» — высота цилиндра.
- Объем конуса = 1/3 π r² h, здесь «r» — радиус круглого основания конуса, а «h» — высота конуса.
- Объем сферы = 4/3 πr³, где «r» — радиус сферы.
Определение, формула и способы ее увеличения
Когда вы думаете об измерении успеха вашей компании, какие маркеры приходят вам на ум? Возможно, вы рассматриваете ключевые показатели эффективности дохода или регистрацию клиентов. Может быть, вы мечтаете о том, чтобы ваш пробег увеличивался по мере снижения себестоимости продаж. Каким бы успех ни казался вам, маловероятно, что вы измеряете его объемом продаж. Но, пожалуй, пора начинать.
Каким бы успех ни казался вам, маловероятно, что вы измеряете его объемом продаж. Но, пожалуй, пора начинать.
Объем продаж — это измерительный инструмент, которым часто пренебрегают, но его преимущества для вашей компании нельзя игнорировать. В этой части мы обсудим определение объема продаж, почему объем продаж имеет значение, способы расчета объема продаж и стратегии для улучшения показателей объема продаж.
Что такое объем продаж?
Объем продаж означает количество единиц, проданных вашей компанией за определенный отчетный период. Этот период может составлять месяц, квартал или год в зависимости от того, какой уровень объема продаж вы хотите проанализировать. Инвесторы часто смотрят на объем продаж, чтобы оценить состояние растущей или подрядной компании.
Объем продаж сам по себе мало что скажет о доходах или чистых продажах. Для этого вам нужно использовать формулу общего дохода. Но объем продаж по-прежнему может влиять на большое количество решений о продажах для вашей команды. Это отличный инструмент, который поможет вам понять ваши показатели продаж в отношении предпочтений клиентов, сообщить данные о продажах и помочь в прогнозировании продаж.
Это отличный инструмент, который поможет вам понять ваши показатели продаж в отношении предпочтений клиентов, сообщить данные о продажах и помочь в прогнозировании продаж.
Почему важен объем продаж?
Вы можете подумать, что объем продаж не имеет значения, если вы отслеживаете финансовый рост своей компании. Но правда в том, что они тесно связаны, и оба должны быть проанализированы на пути к успеху.
Предположим, ваша компания продает два продукта: продукт А стоит 5 долларов, а продукт Б стоит 20 долларов. За один месяц вы продаете 700 единиц продукта А и 300 единиц продукта Б. Финансовый анализ показывает, что продукт А принес 3500 долларов дохода, а продукт Б — 6000 долларов. Продукт B кажется более ценным для компании, поэтому вы можете подумать, что было бы разумно сократить производство продукта A.
Но анализ объема продаж тех же продуктов рисует другую картину. Убрав деньги из уравнения, было продано 700 единиц продукта А и 300 единиц продукта Б. С точки зрения объема продаж продукт А имел более высокий уровень успеха среди клиентов и больше пользы в маркетинге, чем продукт Б, а это означает, что его следует продвигать дальше.
С точки зрения объема продаж продукт А имел более высокий уровень успеха среди клиентов и больше пользы в маркетинге, чем продукт Б, а это означает, что его следует продвигать дальше.
Уравновешивание перспектив финансов и объема продаж является ключом к принятию разумных решений о продуктах.
Как рассчитать объем продаж
Существует несколько способов определения объема продаж. Выбор метода будет зависеть от того, для чего вы хотите его использовать. В следующем разделе мы рассмотрим основные способы расчета объема продаж, рассмотрим отклонение объема продаж и обсудим метод безубыточного объема продаж, когда дела идут на спад.
Формула объема продаж
Существуют две основные формулы для расчета объема продаж: формула единиц и формула процентов .
Формула единиц умножает количество единиц на период времени. Например, если пекарня продает 1000 кексов в месяц, то объем продаж кексов равен 1000.
Если бы той же пекарне требовалось ежеквартальное измерение, она взяла бы месячные объемы за этот квартал и сложила их вместе.
Эта формула может показаться здравой, но она полезна для отслеживания изменений в количестве проданных единиц, особенно если вы проводите сравнения всей линейки продуктов и рассматриваете снятие с производства.
Между тем, процентная формула вычисляет процент проданных единиц отдельного товара. Формула: (Продано единиц отдельного продукта x 100) ÷ Общее количество проданных единиц всех продуктов = Процент от общего объема продаж.
В этом примере остановимся на кексах. Скажем, пекарня продала 1000 кексов в прошлом месяце, как и раньше. Но также было продано 2000 печенья и 750 свадебных тортов. В этом случае формула будет выглядеть так:
Это означает, что из всех хлебобулочных изделий, проданных в течение месяца, кексы составили 26,7 процента единиц.
Важно отметить, что , а не учитывает цену. Тот факт, что на кексы приходилось 26,7% проданных единиц, не означает, что на них приходилось 26,7% полученного дохода. Тем не менее, этот процент чрезвычайно полезен при оценке клиентских тенденций и планировании на будущее.
Тот факт, что на кексы приходилось 26,7% проданных единиц, не означает, что на них приходилось 26,7% полученного дохода. Тем не менее, этот процент чрезвычайно полезен при оценке клиентских тенденций и планировании на будущее.
Если бы пекарня планировала, например, создать праздничную тему в этом месяце, ей нужно было бы точно заказывать продукты. Предполагая, что объем продаж кексов составляет около 26,7% каждый месяц, пекарня может заказать достаточное количество товаров, чтобы предположить, что продажи праздничных кексов составляют 26,7%. Тем не менее, большинство компаний в этой ситуации также хотят учитывать буфер, и именно здесь появляется разница в объеме продаж.
Формула отклонения объема продаж
Формула отклонения объема продаж помогает прогнозировать и вычислять отрицательное или положительное влияние продажи меньшего или большего количества единиц, чем вы ожидали.
Обычно используется следующая формула: (Продано единиц – Планируется продано единиц) x Цена за единицу = Отклонение объема продаж.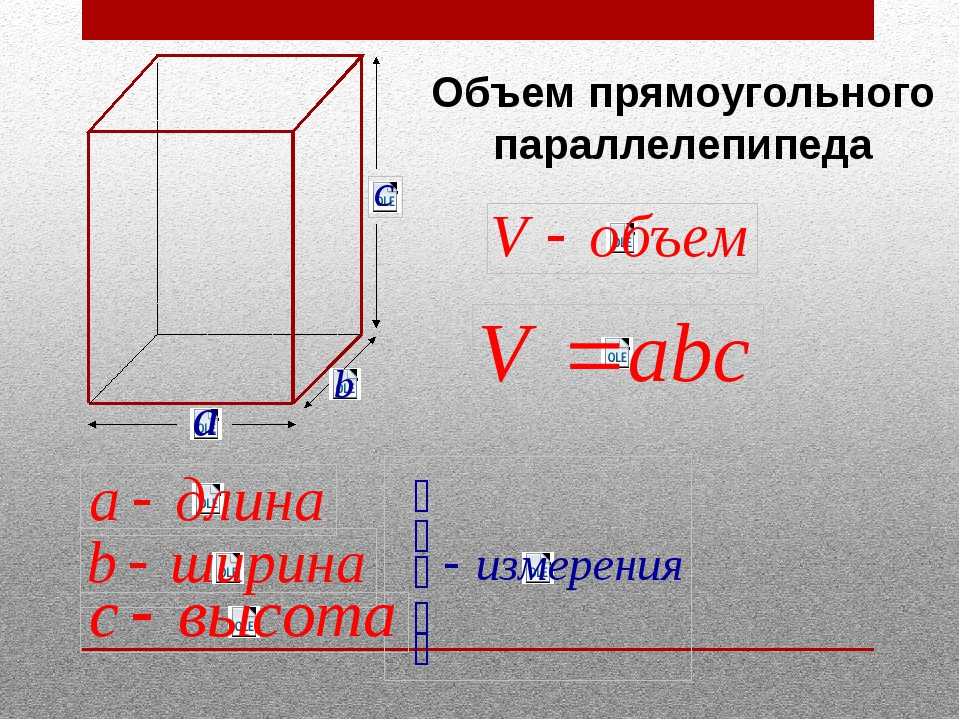
Давайте продолжим нашу пекарню, пока они работают в праздничный месяц. Основываясь на объеме продаж за предыдущие месяцы, пекарня предполагает, что около 26,7% их продаж придется на кексы. Учитывая, что они обычно продают 1000 кексов в месяц, а праздники, как правило, вызывают всплеск продаж, на их долю приходится продажа примерно 2000 кексов. В конце праздничного месяца в пекарне закончились запасы кексов, потому что они продали 2500 кексов. Их отклонение по объему продаж будет выглядеть следующим образом:
Конечно, это положительный пример дисперсии. Через дорогу могла открыться новая пекарня, в результате чего наша пекарня продала всего 1500 кексов, что привело к отрицательному отклонению:
Ситуационное отклонение, подобное приведенным выше примерам, обязательно произойдет. Тем не менее, если вы постоянно видите отрицательную дисперсию в анализе объема продаж, возможно, пришло время взглянуть на изменение продуктов или ценообразования, чтобы превратить это отрицательное в положительное.
3 ключа к созданию измеримой воронки продаж
Узнайте, как создать измеримую воронку продаж, которая обеспечит воспроизводимый и предсказуемый рост продаж.
Да, пожалуйста
Формула безубыточности объема продаж
Один из способов попытаться изменить отрицательное отклонение — это посмотреть на безубыточный объем продаж. Это количество единиц определенного продукта, которое вам нужно продать, чтобы получить прибыль в размере 0 долларов США. Это полезная формула, если вы решаете, стоит ли отказываться от определенного продукта, или оцениваете, когда сократить расходы.
Формула для безубыточного объема продаж: Прогнозируемые расходы за период времени ÷ Цена единицы продукта = Количество единиц безубыточности.
Что касается кексов, допустим, наша пекарня тратила примерно 20 000 долларов в месяц. Предполагая, что они продали только кексы по 6 долларов, их формула объема продаж для безубыточности будет выглядеть так: им нужно либо усилить свои маркетинговые усилия, либо повысить цены на свои кексы. К счастью, есть много способов увеличить объем продаж.
К счастью, есть много способов увеличить объем продаж.
Как увеличить объем продаж
Даже самые успешные компании постоянно стремятся увеличить объем продаж. Но как лучше всего добиться этого увеличения? И где эти стратегии должны быть реализованы в вашей воронке продаж?
Стратегии
Давайте рассмотрим шесть ключевых стратегий увеличения объема продаж.
1. Знайте, что делает ваш продукт особенным
Очень немногие компании производят совершенно уникальные продукты. В результате вам необходимо точно знать, что отличает ваш продукт от конкурентов, чтобы ваши маркетинговые материалы могли сосредоточиться на этих качествах. Потратьте время, чтобы посмотреть на каждый из ваших продуктов и отметить по крайней мере две вещи, которые делают его действительно особенным. Если вы ничего не можете придумать, то и ваши клиенты, вероятно, тоже не смогут. Может быть, пришло время убрать этот продукт из ротации.
2. Используйте потребности клиентов
Ваш продукт продается не потому, что он первоклассный — он продается, потому что решает проблемы клиентов или удовлетворяет потребности. Чем больше вы знаете о своих клиентах и почему они покупают ваши продукты, тем больше вы сможете увеличить продажи. Если наша любимая пекарня продает продукты без глютена каждый день, но не увеличивает количество производимых продуктов без глютена, это огромная упущенная возможность.
3. Поддерживайте и вознаграждайте квалифицированных лидов
Не каждый потенциальный покупатель становится клиентом, и это нормально. Важно убедиться, что вы не теряете потенциальных клиентов, которые заинтересованы в вашем продукте, позволяя им забыть о вас. Если потенциальные клиенты проявляют интерес, свяжитесь с ними. Это может быть кампания по электронной почте, персонализированное предложение или таргетированная реклама. Обязательно отметьте своих квалифицированных потенциальных клиентов в своем программном обеспечении CRM.
4. Пересмотрите свою маркетинговую стратегию
Это может показаться нелогичным, но если у вас есть продукт, который хорошо продается, иногда лучше инвестировать маркетинговые деньги в этот продукт, а не в тот, который терпит неудачу. Помните формулу безубыточности: неудачный продукт не обязательно будет стоить вложений в маркетинг, но успешный продукт будет стоить.
5. Ускорьте цикл продаж
Жесткие продажи не всегда являются решением, но есть способы ускорить путь клиента по циклу продаж. Сократите свои демонстрации или пробные версии, настройте одношаговую систему оформления заказа, устраните возражения клиентов, усилив продажи в социальных сетях и инвестируйте свои усилия в методы с наилучшими результатами. Чем быстрее вы сможете подтолкнуть потенциальных клиентов к покупке, тем быстрее будет расти объем ваших продаж.
6. Мотивируйте свой отдел продаж
Мы уделяем большое внимание клиентам, но важно также активизировать ваших торговых представителей. Помните, что именно они взаимодействуют лицом к лицу с большинством ваших клиентов. Подумайте о том, как наилучшим образом создать позитивную атмосферу, в которой члены команды поощряются к совместной работе. Успешная компания — это, как правило, компания, в которой первоклассные продавцы хотят, чтобы работал.
Помните, что именно они взаимодействуют лицом к лицу с большинством ваших клиентов. Подумайте о том, как наилучшим образом создать позитивную атмосферу, в которой члены команды поощряются к совместной работе. Успешная компания — это, как правило, компания, в которой первоклассные продавцы хотят, чтобы работал.
Как CRM может помочь увеличить объем продаж
Существует седьмая стратегия увеличения объема продаж, о которой мы еще не упоминали, и это партнерство с надежной CRM. Когда у вас есть легкодоступные и хорошо организованные записи ваших взаимодействий с клиентами, перечисленные выше стратегии намного проще реализовать и извлечь из них пользу.
Благодаря Zendesk Sell видимость вашей воронки продаж становится главным приоритетом, что упрощает взаимодействие и согласование между отделами продаж, маркетинга и администрирования. Zendesk также сотрудничает с сотнями приложений и программ, поэтому, если вы занимаетесь продажами B2B, ваша новая CRM естественным образом будет согласовываться с программами ваших деловых партнеров.
Запросите демонстрацию сегодня и узнайте, как наше программное обеспечение CRM может увеличить объем ваших продаж.
3 ключа к созданию измеримой воронки продаж
Узнайте, как создать измеримую воронку продаж, которая обеспечит воспроизводимый и предсказуемый рост продаж.
Да, пожалуйста
Том
Можно вычислить
масса
любого объекта путем умножения
плотность
материала по объему объекта.
Объем объекта – это трехмерное пространство,
заняты объектом, и нас учат
формулы для вычисления объема некоторых простых трехмерных
предметы в средней школе. На этом слайде мы перечисляем некоторые уравнения для
вычисление объема объектов, которые часто встречаются в
аэрокосмический. Есть аналогичные уравнения
для вычисления
область
объектов.
Величина
аэродинамические силы
зависит от площади поверхности объекта, а
сила гравитации
и определенные
термодинамические эффекты
зависит от объема предмета. 3
3
Вот некоторые специальные уравнения объема, которые используются для носовых обтекателей ракет:
Для конуса расстояние от вершины до основания называется высота . Основание представляет собой круг диаметром d . Объем V конуса равен pi (3,14159), умноженному на диаметр d квадрат умножить на высоту ч разделить на двенадцать; 92*ч/12
Параболический конус имеет гладкую криволинейную поверхность и острый заостренный носик. На стандартном конусе есть край между носом и цилиндром, который образует тело ракета. Но на параболическом конусе поверхность входит в основание с наклоном, равным нулю. Есть отсутствие ребра между параболическим носовым обтекателем и цилиндрическим корпусом ракеты. Уравнение для объем в два раза pi 92*ч/6
Усеченный конус образуется, если вершина срезана параллельно основанию.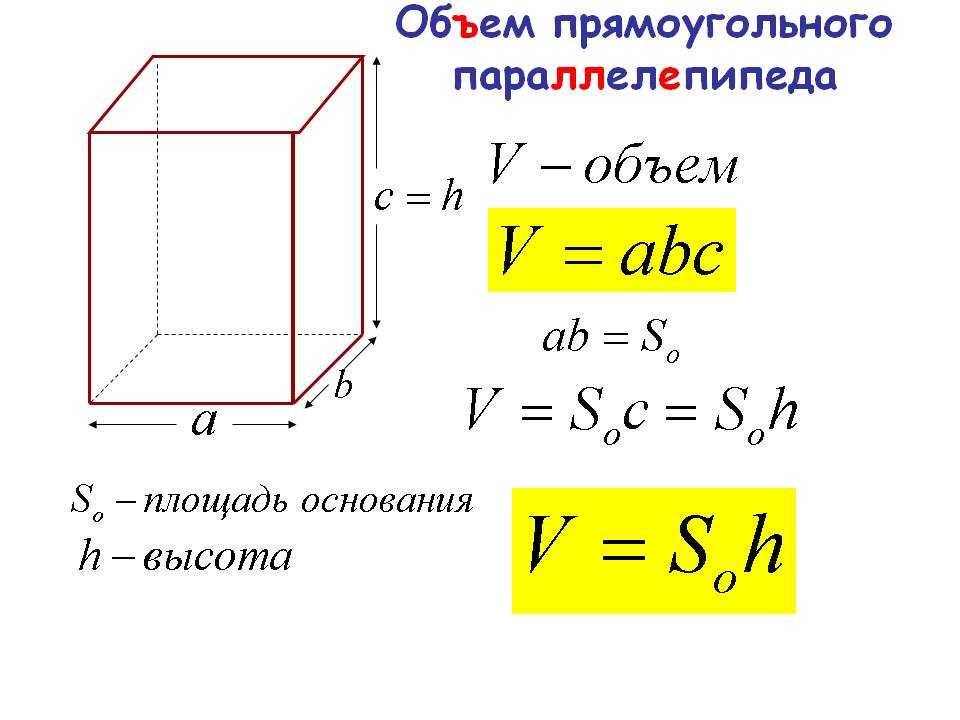 Формы усеченного конуса часто встречаются на моделях ракет в виде обтекателей между цилиндрическими
участки тела.
Уравнение для
объем равен pi умножить на высоту h разделить на двенадцать раз
количество: диаметр основания b в квадрате плюс диаметр основания, умноженный на диаметр разреза d плюс диаметр реза в квадрате:
92)
Формы усеченного конуса часто встречаются на моделях ракет в виде обтекателей между цилиндрическими
участки тела.
Уравнение для
объем равен pi умножить на высоту h разделить на двенадцать раз
количество: диаметр основания b в квадрате плюс диаметр основания, умноженный на диаметр разреза d плюс диаметр реза в квадрате:
92)
Примечание. Для всех фигур с изогнутыми (круглыми) поверхностями мы используем диаметр
круг при выводе объема. Мы не используем радиус, который часто используется в математике.
текстовые книги. Причина такого выбора в том, что
большинство стандартных инженерных измерений основаны на диаметре, а не на радиусе. Легче точно измерить
диаметр круглого объекта, чем для измерения радиуса. Чтобы использовать радиус, вам нужно определить, где
лежит центр окружности. Для трубы в центре круга нет материала. Для сферы,
до центра нельзя добраться, так как он находится внутри тела. Вы можете преобразовать диаметр в радиус
(радиус = диаметр / 2).


 дюйм
дюйм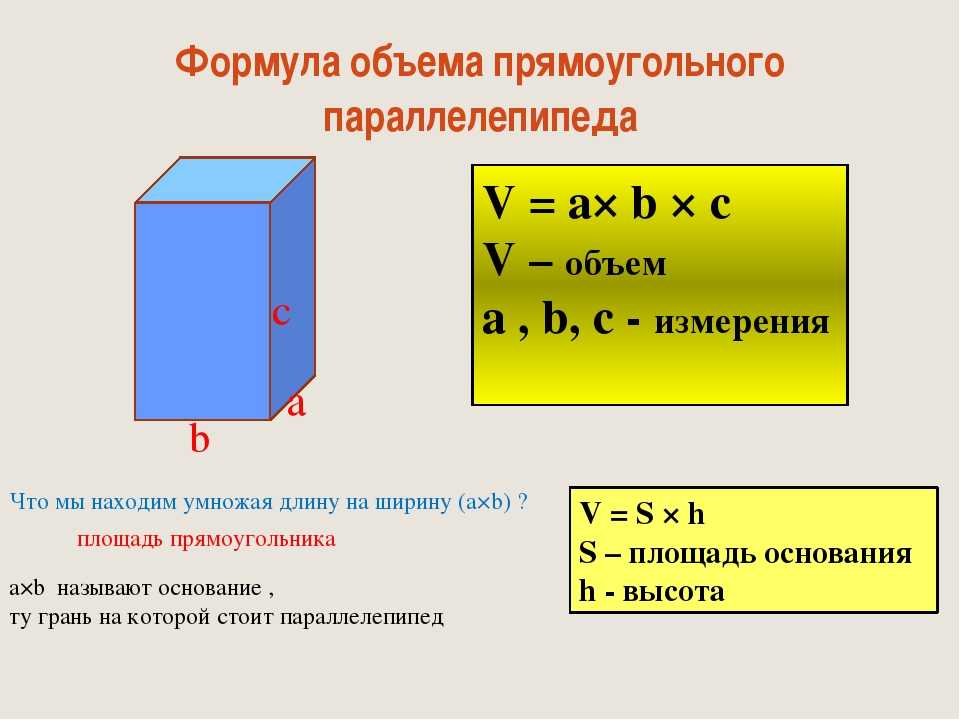
 Рабочие листы
Рабочие листы