Помогите вычислить арифметический квадратный корень. Алгебра. 8 класс. Пар.№20. Упр.№307. Учебник Алимов Ш.А. – Рамблер/класс
Помогите вычислить арифметический квадратный корень. Алгебра. 8 класс. Пар.№20. Упр.№307. Учебник Алимов Ш.А. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Здравствуйте! Помогите вычислить арифметический квадратный корень из числа: 81; 64; 100; 0,16; 0,09; 0,25; 1,44; 4900; 6400.
ответы
Привет Денис! Лови ответ:
√81 = 9 √64 = 8 √100 = 10 √0,16 = 0,4
√0,25 = 0,5 √1,44 = 1,2 √4900 = 70 √6400 = 80
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
ЕГЭ
10 класс
9 класс
похожие вопросы 5
Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.
..)
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
ГДЗЕГЭРусский языкЦыбулько И.П.
10. Выпишите слово, в котором на месте пропуска пишется буква И. Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
10.
Выпишите слово, в котором на месте пропуска пишется буква (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Урок-конкурс «Арифметический квадратный корень».
Алгебра 8-й классЦели:
- повторение теоретического материала (правил) по разделу, закрепление умений учащихся находить значение арифметического квадратного корня, решать уравнения вида а=х2 и более сложные уравнения, почерпнуть новое из истории математики;
- развитие логического мышления, фантазии, вычислительных навыков, интереса к предмету;
- воспитание чувства ответственности за коллектив в процессе творческой работы.
Оформление:
- Формулы ,
Тема урока: «Арифметический квадратный корень»
Рисунок обезьяны с бананами, на которые прикреплены карточки с заданиями (на магнитной доске)
Организационный момент.
Проверка домашнего задания (ассистенты
докладывают о проверке домашнего задания (работа
в группах)).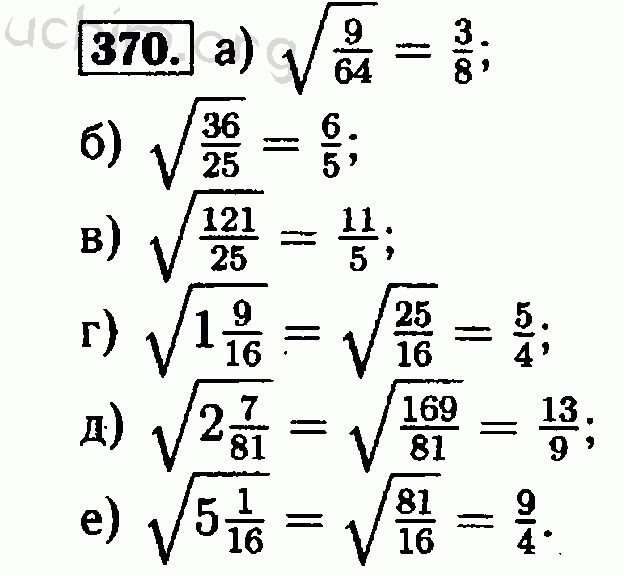
Слово учителя:
Сегодня — урок-конкурс. На этом уроке мы вспомним теоретический материал, правила по теме «Арифметический квадратный корень». Вы покажете, как умеете решать уравнения по данной теме и вычислять значение арифметического квадратного корня. Класс делится на две команды: «Корень» и «Уравнение». На доске — табло, где будем фиксировать баллы.
1 конкурс — Математический футбол
Учитель поочередно задает вопрос. Если команда отвечает, она задает свой вопрос сопернику. Если не отвечает, вопрос опять задает учитель.
Вопросы:
- Что называется арифметическим квадратным корнем из числа а?
- Сколько корней имеет уравнение х2=7?
- Сколько корней имеет уравнение х2=-7?
- Сколько корней имеет уравнение х2=0?
- При каком значении а выражение имеет смысл? и т.
д.
д.2 конкурс — Угадай график (на экране)
(слайды 1-4 Приложения 1)
3 конкурс — Математическое кафе, где можно немного отдохнуть (слайд 5Приложения 1)
Отгадай ребус (слайды 6-8 Приложения 1)
Анаграммы РИФГАК (график), ЕРОНЬК (корень), ЛИДАКАР (радикал), НЕСЬПЕТ (степень) (слайды 9-12 Приложения 1)
Угадай известного математика: для нас он прежде всего математик, живший в 6 веке до н.э. Его именем названы улицы некоторых городов мира, а его родина — остров Самос в Эгейском море. В настоящее время этот остров назван его именем. Математик создал школу, где кроме математики занимались музыкой, танцами, писали стихи. Число 5 для его учеников — символ здоровья и знак принадлежности к этой школе. Кто этот ученый? (Пифагор) (слайд 13 Приложения 1)
Угадай имя другого ученого
Он был задумчив и спокоен,
Загадкой круга увлечен.
Над ним невежественный воин
Взмахнул разбойничьим мечом.
Прошла столетий вереница,
Научный подвиг не забыт,
Никто не знает, кто убийца,Но знают все, кто был убит.
Эти стихи об известном математике древности, который погиб от меча римского солдата, гордо воскликнув: «Отойди, не трогай моих чертежей!» (Архимед)
(слайд 13 Приложения 1)
Расположите в порядке возрастания (слайд 14 Приложения 1):
- 7; ; 5; ; .
- 0,3; ; ; 1.
4 конкурс — Мини-самостоятельная работа по карточкам с последующей проверкой
(слайды 15, 16 Приложения 1)
5 конкурс — Конкурс знатоков
Участники команд выходят к доске по очереди и выбирают себе задание (задание записано на банане, которые щедро раздает нарисованная обезьяна).
Мартышка к старости слаба глазами стала,
Хотела съесть банан, но не увидела и не достала!
В банане том — задание из умной книжки,
Реши его и помоги мартышке.
(капитан назначает игроков)
Задание:
1) Упростить:
а) , если а0;
б) , если х0;
2) Упростить:
, если а0;
3) Решить уравнение:
= — х;
4) Решить уравнение:
5+=х
Дополнительный конкурс загадок
1. Двое убегают, двое догоняют, отдыхают вместе.
2. На одной яме сто ям с ямкой.
3. У двух матерей по пять сыновей, у всех одно имя.
4. Две головы, четыре уха, две спины, два брюха, шесть ног, один хвост.
Итоги конкурса.
Подводятся итоги (учитываются скорость и правильность решения), определяется команда-победитель. Выставляются оценки каждому учащемуся.
квадратов и квадратных корней | Предварительная алгебра | Вещественные числа и прямоугольные треугольники
Дополнительные темы
по квадратам и квадратным корнямПопулярные учебные пособия
по квадратам и квадратным корнямКак найти квадратный корень из числа, не являющегося полным квадратом?
Хотите упростить радикал, подкоренная часть которого не является полным квадратом? Нет пота! Ознакомьтесь с этим руководством и узнайте, как записать это подкоренное число в качестве его простой факторизации.
Затем перепишите любые повторяющиеся множители, используя показатели степени, разбейте радикал, используя свойство квадратных корней, и упростите. Чтобы увидеть этот процесс шаг за шагом, посмотрите это руководство!Как умножить два радикала?
Чтобы умножить радикалы, вы можете использовать свойство произведения квадратных корней, чтобы умножить содержимое каждого радикала вместе. Тогда это просто вопрос упрощения! В этом уроке вы увидите, как перемножить два радикала вместе, а затем упростить их произведение. Проверьте это!
Что такое свойство произведения квадратных корней?
Свойство произведения квадратных корней очень полезно, когда вы упрощаете радикалы. Это свойство позволяет вам извлечь квадратный корень из произведения чисел и разбить радикал на произведение отдельных квадратных корней. Посмотрите этот урок и узнайте о свойстве произведения квадратных корней!Что такое частное свойство квадратных корней?
Частное свойство квадратных корней очень полезно, когда вы пытаетесь извлечь квадратный корень из дроби.
Это свойство позволяет разделить квадратный корень между числителем и знаменателем дроби. Этот урок знакомит вас с частным свойством квадратных корней. Взглянем!Как найти квадратный корень из полного квадрата?
Извлечение квадратного корня из полного квадрата всегда дает целое число. В этом учебном пособии показано, как извлечь квадратный корень из 36. Когда вы закончите просмотр этого учебного пособия, попробуйте извлечь квадратный корень из других полных квадратов, таких как 4, 9, 25 и 144.
Как вычислить квадратный корень из несовершенного квадрата?
Пытаетесь извлечь квадратный корень из числа, которое не является полным квадратом? Думаете, вам нужен калькулятор? Подумайте еще раз! Этот урок покажет вам, как вычислить квадратный корень из числа, не являющегося полным квадратом, без использования калькулятора!
Что такое идеальный квадрат?
Каждый раз, когда вы возводите целое число в квадрат, получается идеальный квадрат! Числа 4, 9, 16 и 25 — это всего лишь несколько идеальных квадратов, но их бесконечно больше! Посмотрите этот урок, а затем посмотрите, сможете ли вы найти еще несколько идеальных квадратов!
Затем перепишите любые повторяющиеся множители, используя показатели степени, разбейте радикал, используя свойство квадратных корней, и упростите. Чтобы увидеть этот процесс шаг за шагом, посмотрите это руководство!
Это свойство позволяет разделить квадратный корень между числителем и знаменателем дроби. Этот урок знакомит вас с частным свойством квадратных корней. Взглянем!Квадратные корни — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 Следующая →
Алгебра II Помощь » Математические отношения и основные графики » Радикалы » Понимание радикалов » Квадратные корни
Упростите, рационализировав знаменатель:
Возможные ответы:
Правильный ответ:
Объяснение:
Умножьте числитель и знаменатель на сопряженное значение знаменателя, то есть .
Затем воспользуйтесь распределительными свойствами и разницей шаблонов квадратов:
Сообщить об ошибке
Оценить квадратный корень из с точностью до десятых.
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомним, что мы ищем число, которое при умножении само на себя дает . Мы ищем идеальные квадраты, окружающие и находим и . Таким образом, мы знаем, что наше число должно быть между и намного ближе к и, таким образом, оно будет очень близко к , но все же меньше, а именно .
Сообщить об ошибке
является действительным числом для каких значений ?
Возможные ответы:
Все отрицательные и некоторые положительные значения
Все положительные значения только
Все значения
Все отрицательные значения только
Все положительные значения и некоторые негативные значения
Правильный ответ:
202020202020202020202 только положительные значенияОбъяснение:
Извлечение квадратного корня из положительного числа даст положительное число, а возведение любого положительного числа в любую степень даст положительное число.
Извлечение квадратного корня из отрицательного числа приведет к квадратному корню из абсолютного значения числа, умноженному на i
ex. if
Когда выражение имеет , возведение выражения в четную степень избавит вас от мнимого числа «i» и сделает ответ отрицательным. Отрицательные числа — это действительные числа, которые принадлежат числовой прямой.
напр.
Однако, поскольку выражение возведено в 53-ю степень, оно сохраняет «i» в выражении для любого отрицательного значения x. Следовательно, только положительные числа (и 0, который не включен в варианты ответов) удовлетворяют требованиям, предъявляемым к действительным числам.
Report an Error
Estimate the square root of 110 to the nearest tenth without using a calculator`
Possible Answers:
9.9
13
10.8
10.4
11.
1
Правильный ответ:
10,4
Объяснение:
Ближайшими к 110 квадратами являются 100 и 121. Квадратный корень из 100 равен 10, а квадратный корень из 121 равен 11. 110 находится почти посередине, что дает ответ 10.4.
10,9 слишком много, потому что это сделало бы квадрат ближе к диапазону 119-120.
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы упростить, мы должны найти квадраты, которые находятся под каждым радикалом (это может быть легче увидеть после некоторого разложения):
Теперь квадраты легче идентифицировать! Мы можем вытащить их из корня после извлечения их квадратного корня, оставив позади все, что не является квадратом:
Сообщить об ошибке.
Объяснение:
Упростите радикалы в скобках.
Упростите условия по порядку операций. Сначала решите условия в скобках.
Ответ:
Сообщить об ошибке
Упростите радикалы:
Возможные ответы:
Правильный ответ:
Пояснение:
Перепишите числитель, взяв в качестве общего знаменателя квадратный корень из трех. Таким образом, нам не нужно умножать, чтобы рационализировать знаменатель.
Обратите внимание, что теперь мы можем удалить радикал из знаменателя. Полностью упростите и перепишите числитель.
Разделите это число на три, так как в знаменателе одинокая тройка.
Ответ:
Сообщить об ошибке Объяснение:
Мы можем переписать выражение, используя общие множители.
Подкоренной квадратный корень из девяти — это полный квадрат.
Два других радикала могут быть перемножены вместе, чтобы сформировать один радикал.
Ответ:
Сообщить об ошибке
Оценить радикал:
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы получить максимально упрощенный ответ, не перемножайте все числа вместе, а объединяйте в один радикал.
Перепишите каждый радикал в наиболее упрощенной форме.
Умножьте члены.
Обратите внимание, что при умножении квадратного корня из числа на самого себя останется только целое число и будут удалены радикалы.
Условия становятся:
Ответ:
Отчет о ошибке
Оценка квадратного корня:
Возможные ответы:
101101101101101101101110111011101110111011101110111011101110111011101110111011101110111011101110111АРЕ Объяснение:
Коэффициенты членов имеют один и тот же квадратный корень.