Чему равен квадрат минус 3? – Обзоры Вики
Функция квадратного корня доступна только в том случае, если подкоренное число, число или выражение под знаком корня (знак квадратного корня), является неотрицательным значением. Следовательно, «-3″ не имеет квадратного корня в действительных числах.
Итак, является ли квадратный корень из отрицательного числа иррациональным? Отрицательные числа не имеют настоящих квадратных корней поскольку квадрат либо положительный, либо 0. Квадратные корни чисел, не являющихся полным квадратом, являются членами иррациональных чисел. Это означает, что они не могут быть записаны как частное двух целых чисел.
Как решить корень 8? Квадратный корень из 8 в радикальной форме представлен как √8, что также равно 2√2, а в виде дроби он равен 2.828 примерно.
…
Таблица квадратного корня от 1 до 15.
| Число | Площади | Квадратный корень (до 3 десятичных знаков) |
|---|---|---|
| 6 | 6 2 = 36 | √6 = 2. 449 449 |
| 7 | 7 2 = 49 | √7 = 2.646 |
| 8 | 8 2 = 64 | √8 = 2.828 |
| 9 | 9 2 = 81 | √9 = 3.000 |
Дополнительно Каковы корни числа 4? Квадратный корень от 1 до 50
| Число | Квадратный корень |
|---|---|
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
Чему равен квадрат минус 4? -4 — отрицательное число. Поэтому его квадратный корень это невозможно, т.е. ✓-4 невозможно. Такие числа называются мнимыми числами.
Является ли квадратный корень из минус 121 рациональным или иррациональным?
Ответ и пояснение: Квадратный корень из 121 равен рациональное число. Вы можете легко сказать это, потому что 121 — идеальный квадрат.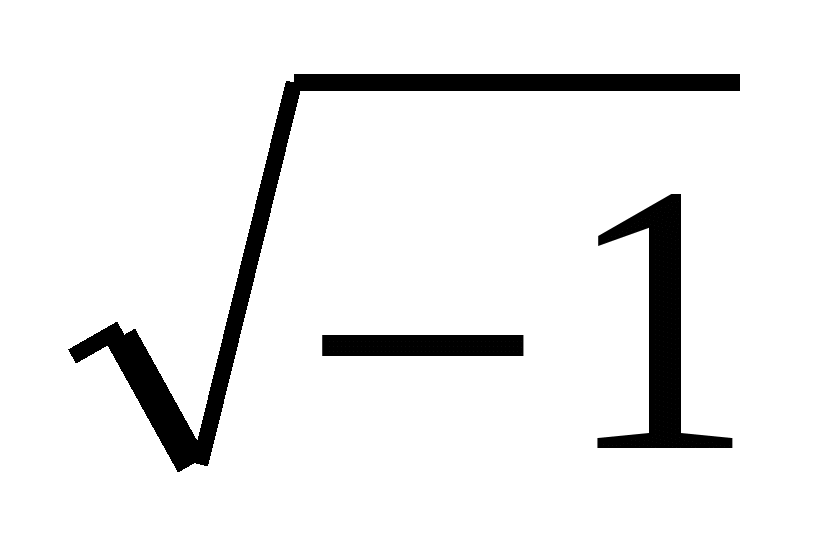
Минус 1 рациональный или иррациональный? Число 1 можно классифицировать как: натуральное число, целое число, совершенный квадрат, совершенный куб, целое число. Это возможно только потому, что 1 РАЦИОНАЛЬНОЕ число.
Отрицательное число 1 — действительное число? Реальные числа могут быть положительными или отрицательными.и включите число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел. Мнимые числа — это числа, которые невозможно определить количественно, например квадратный корень из -1.
Как найти квадратный корень из 52?
Также Что такое упрощенный квадратный корень из 45? Упрощенная радикальная форма квадратного корня из 45: 3√5.
Что такое упрощенный квадратный корень 24?
Что в квадрате 5? Список идеальных квадратов
| НОМЕР | ПЛОЩАДЬ | КВАДРАТНЫЙ КОРЕНЬ |
|---|---|---|
| 5 | 25 | 2. 236 236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
• 17 ноября 2021 г.
Как найти рут 5?
Как найти квадратный корень из 5?
- √5 = √5.
- √5 = 2.23.
Является ли квадратный корень из минус 4 действительным числом?
Квадратный корень -4 не настоящее число. Квадратный корень отрицательного действительного числа всегда является мнимым числом (мнимое число — это комплексное число, которое может быть записано как действительное число, умноженное на мнимую единицу, которая определяется ). Обратите внимание, что 0 также можно рассматривать как мнимое число ().
Чему равно 2i? я2 равно -1, реальное число!
Является ли √ 84 рациональным или иррациональным?
√84 — это иррациональное число.
Как найти квадратный корень из 625? Квадратный корень из 625 равен 25. Это положительное решение уравнения x 2 = 625 . Число 625 представляет собой полный квадрат.
…
Корень квадратный из 625 в радикальной форме: √625.
| 1. | Что такое квадратный корень из 625? |
|---|---|
| 2. | Является ли квадратный корень из 625 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 625? |
| 4. | Часто задаваемые вопросы о квадратном корне из 625 |
Является ли квадратный корень из 81 рациональным или иррациональным?
Является ли квадратный корень из 81 рациональным или иррациональным? Рациональное число определяется как число, которое может быть выражено в виде частного или деления двух целых чисел, т. е. p/q, где q не равно 0. Оба числа могут быть представлены в виде рационального числа. Следовательно, квадратный корень из 81 рациональное число.
Пи действительное число? Независимо от размера круга, это отношение всегда будет равно числу пи. В десятичной форме значение числа пи составляет примерно 3.14. Цель пи — иррациональное число, что означает, что его десятичная форма не заканчивается (например, 1/4 = 0.25) и не становится повторяющейся (например, 1/6 = 0.166666…). (Всего с 18 десятичными знаками число пи равно 3.141592653589793238.)
Является ли пи целым числом?
Так как пи иррационально (не равно отношению любых двух целых чисел), его цифры не повторяются, и для повседневных вычислений часто используется такое приближение, как 3.14 или 22/7.
Является ли пи рациональным числом? Пи это иррациональное число, что означает, что это действительное число, которое не может быть выражено простой дробью. … Хотя это иррациональное число, некоторые используют рациональные выражения для оценки числа пи, например, 22/7 из 333/106.
Онлайн тести з алгебри для 8 класу
очистити
Класи
Усі класи1 клас2 клас3 клас4 клас5 клас6 клас7 клас8 клас9 клас10 клас11 клас
ПредметОберіть предмет. ..АлгебраАнглійська моваАстрономіяБіологіяВсесвітня історіяГеографіяГеометріяГромадянська освітаЕкологіяЕкономікаЕтикаЗарубіжна літератураЗахист УкраїниІнформатикаІспанська моваІсторія УкраїниКресленняЛітературне читанняЛюдина і світМатематикаМистецтвоМови національних меншинМузичне мистецтвоНавчання грамотиНімецька моваОбразотворче мистецтвоОснови здоров’яПольська моваПравознавствоПриродничі наукиПриродознавствоТехнологіїТрудове навчанняУкраїнська літератураУкраїнська моваФізикаФізична культураФранцузька моваХіміяХудожня культураЯ досліджую світ
..АлгебраАнглійська моваАстрономіяБіологіяВсесвітня історіяГеографіяГеометріяГромадянська освітаЕкологіяЕкономікаЕтикаЗарубіжна літератураЗахист УкраїниІнформатикаІспанська моваІсторія УкраїниКресленняЛітературне читанняЛюдина і світМатематикаМистецтвоМови національних меншинМузичне мистецтвоНавчання грамотиНімецька моваОбразотворче мистецтвоОснови здоров’яПольська моваПравознавствоПриродничі наукиПриродознавствоТехнологіїТрудове навчанняУкраїнська літератураУкраїнська моваФізикаФізична культураФранцузька моваХіміяХудожня культураЯ досліджую світ
КласКлас…1 клас2 клас3 клас4 клас5 клас6 клас7 клас8 клас9 клас10 клас11 клас
Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома
Створити тест
Тести Алгебра 8 клас
12
Контрольна робота «Додавання і віднімання раціональних дробів»
Алгебра, 8 клас
Кривошей В. В.
В.
Копія з тесту: Контрольна робота «Додавання і віднімання раціональних дробів»
Приклад запитання: Додати дроби
12
Контрольна робота з теми: «Раціональні вирази. Додавання і віднімання раціональних дробів»
Алгебра, 8 клас
Кривошей В. В.
Копія з тесту: Контрольна робота з теми: «Раціональні вирази. Додавання і віднімання раціональних дробів»
Приклад запитання:
Виберіть вирази, областю визначення яких є будь-яке число.16
Підготовка до контрольної роботи за темою «Раціональні дроби»
Алгебра, 8 клас
Шевченко О. О.
Копія з тесту: Підготовка до контрольної роботи за темою «Алгебраїчні дроби. Додавання і віднімання раціональних дробів»
Приклад запитання: Знайдіть допустимі значення змінної у виразі.
7
8кл. Піднесення раціонального дробу до степеня.
Алгебра, 8 клас
Krupenia O.
Копія з тесту: Піднесення раціонального дробу до степеня.
10
додавання і віднімання раціональних дробів
Алгебра, 8 клас
Чихун А. О.
Копія з тесту: додавання і віднімання раціональних дробів 8-а
Приклад запитання: Знайдіть суму
6
Додавання і віднімання раціональних дробів з однаковими знаменниками. Самостійна робота.
Алгебра, 8 клас
Грицак О. М.
Копія з тесту: Додавання і віднімання раціональних дробів з однаковими знаменниками.
Приклад запитання: 1. Знайти різницю дробів.
6
Додавання і віднімання раціональних дробів з однаковими знаменниками.
Алгебра, 8 клас
Хлібороб Ю. С.
Створено 7 жовтня
Приклад запитання: Виконайте дію:
9
07.10 Додавання і віднімання раціональних дробів
Алгебра, 8 клас
Лейчук А.
Копія з тесту: Додавання раціональних дробів
Приклад запитання: Додайте дроби
12
Додавання і віднімання раціональних дробів з однаковими знаменниками.
Алгебра, 8 клас
Войтів М.
Копія з тесту: Додавання і віднімання раціональних дробів з однаковими знаменниками.
Приклад запитання: Виконайте дію
12
Контрольна робота «Додавання і віднімання раціональних дробів»
Алгебра, 8 клас
Кучинська Т. В.
Копія з тесту: Контрольна робота «Додавання і віднімання раціональних дробів»
Приклад запитання: Додати дроби
6
Додавання та віднімання раціональних дробів з різними знаменниками
Алгебра, 8 клас
Ivanina E.
Копія з тесту: Додавання та віднімання раціональних дробів з різними знаменниками
Приклад запитання: Додати дроби
9
Контрольна робота з теми: «Раціональні вирази. Додавання і віднімання раціональних дробів»
Алгебра, 8 клас
Руденко О. А.
Створено 6 жовтня
Приклад запитання: Виберіть вирази, областю визначення яких є будь-яке число.
12
Додавання і віднімання раціональних дробів з однаковими знаменниками.
Алгебра, 8 клас
Чечель Л. К.
Створено 6 жовтня
Приклад запитання: Виконайте дію
8
8 клас Раціональні дроби. Додавання і віднімання раціональних дробів
Алгебра, 8 клас
Карташова А. О.
Копія з тесту: 8 клас Раціональні дроби. Додавання і віднімання раціональних дробів
Приклад запитання: При якому значені змінної вираз не має змісту?
6
Контрольна робота «Додавання та віднімання раціональних дробів»
Алгебра, 8 клас
Карташова А. О.
Копія з тесту: Контрольна робота «Додавання та віднімання раціональних дробів»
Приклад запитання: При яких значеннях змінної х дріб не має змісту?
11
Додавання та віднімання раціональних дробів
Алгебра, 8 клас
Іванівна О.
Копія з тесту: Додавання та віднімання раціональних дробів
Приклад запитання: Вкажіть правильну область допустимих значень для раціонального дробу
7
Додавання та віднімання дробів з однаковими знаменниками
Алгебра, 8 клас
Ткаченко Ю.
Копія з тесту: Додавання та віднімання дробів з однаковими знаменниками
Приклад запитання: Знайти суму
4
А8. Розкладення на множники
Алгебра, 8 клас
Радова А.
Створено 6 жовтня
Приклад запитання: Розкладіть на множники:8а-10b
12
Контрольна робота «Додавання і віднімання раціональних дробів»
Алгебра, 8 клас
Сисуненко С.
Копія з тесту: Контрольна робота «Додавання і віднімання раціональних дробів»
Приклад запитання: Додати дроби
10
Самостійна робота «Додавання та віднімання раціональних дробів»
Алгебра, 8 клас
Карасьова Л. М.
Копія з тесту: Самостійна робота «Додавання та віднімання раціональних дробів»
Приклад запитання: Скоротіть дріб
12
КР «Основна властивість раціонального дробу. Додавання та віднімання дробів»
Алгебра, 8 клас
Паламарчук Г. О.
Копія з тесту: КР «Основна властивість раціонального дробу. Додавання та віднімання дробів»
Приклад запитання: Скоротіть дріб
12
Основна властивість дробу. Додавання і віднімання дробів
Алгебра, 8 клас
Полюшкина И.
Копія з тесту: Основна властивість дробу. Додавання і віднімання дробів
Приклад запитання: Скоротіть дріб
12
Основна властивість дробу. Додавання і віднімання дробів
Алгебра, 8 клас
Полюшкина И.Копія з тесту: Основна властивість дробу. Додавання і віднімання дробів
Приклад запитання: Скоротіть дріб
9
Додавання раціональних дробів
Алгебра, 8 клас
Полюшкина И.
Копія з тесту: Додавання раціональних дробів
Приклад запитання: Додайте дроби
11
Додавання та віднімання раціональних дробів
Алгебра, 8 клас
Полюшкина И.
Копія з тесту: Додавання та віднімання раціональних дробів
Приклад запитання: Вкажіть правильну область допустимих значень для раціонального дробу
12
Контрольна робота «Додавання і віднімання раціональних дробів»
Алгебра, 8 клас
Полюшкина И.
Копія з тесту: Контрольна робота «Додавання і віднімання раціональних дробів»
Приклад запитання:
10
Скорочення, додавання та віднімання раціональних дробів
Алгебра, 8 клас
Полюшкина И.
Копія з тесту: Скорочення, додавання та віднімання раціональних дробів
Приклад запитання: Знайти суму:
5
Додавання і віднімання раціональних дробів з різними знаменниками.
Алгебра, 8 клас
Полюшкина И.
Копія з тесту: Додавання і віднімання раціональних дробів з різними знаменниками.
Приклад запитання: Виконайте дії:
5
Домашня самостійна робота за темою: Додавання та віднімання раціональних дробів.
Алгебра, 8 клас
Полюшкина И.
Копія з тесту: Домашня самостійна робота за темою: Додавання та віднімання раціональних дробів.
Приклад запитання: Виконайте дії:
10
Додавання і віднімання дробів з різними знаменникамиАлгебра, 8 клас
Полюшкина И.
Копія з тесту: Додавання і віднімання дробів з різними знаменниками
Приклад запитання: 1. Виконайте додавання
Реєстрація на сайті «На Урок»
Зареєструватись за допомогою Facebook
Зареєструватись за допомогою Google
або
Прізвище
Пароль
Реєструючись, ви погоджуєтеся з угодою користувача та політикою конфіденційності.
Вже зареєстровані? Спробуйте увійти
Давай дружити!
Оновлення «На Урок» — в кожну стрічку Facebook
Дякую, Я вже давно з вами
Българче е новият световен шампион по умствена скоростна математика ᐉ Новини от Fakti.
 bg — България
bg — БългарияБългария »
Българче е новият световен шампион по умствена скоростна математика
6 Октомври, 2022 05:16 2 32011
- математика-
- победител-
- калоян гешев
Снимка: БНТ
Тихомир ШумовАвтор във Fakti.bgБългарче е новият световен шампион по умствена скоростна математика за деца до 12 години, предаде БНТ. На финала в Германия Калоян Гешев от София се изправи срещу 56 конкуренти от 13 страни и успя да спечели най-много точки в оспорвано състезание.
Пише с лявата ръка. Скоро ще стане на 12. Не смята, че е специален. Но умножава и дели редици от трицифрени числа по-бързо от калкулатор. Аритметиката е любимата му дисциплина. А математиката е:
«Вид забавление бих казал», казва малкият шампион.
На ден се упражнява поне по 2-3 часа. Казва, че не му омръзва. Точните корени, факторите и сумите на квадрат приема за детска игра. И има любимо число:
Точните корени, факторите и сумите на квадрат приема за детска игра. И има любимо число:
«6, защото е най-високата оценка, която можеш да изкараш»
Калоян е новият световен шампион по ментална скоростна математика за деца до 12 години. В Германия разгромява конкуренцията и за втори път в историята на конкурса наградата остава в Европа. Досега азиатците са хегемони. Според нашето момче тайната е в соробана.
«Едно сметало, на което са наредени едни топчета и по тях изчисляват и след определено време оставят сметалото и започват с пръсти да го смятат», казва Калоян.
Неговият метод е друг.
«Аз ползвам чисто умствено без да използвам такива пръсти и соробани. Най-важното на първо място е да имаш дарба».
При него тя е несъмнена. А обяснението ѝ — трудно, дори за математик.
«Това е уникално нещо. И наистина е много трудно да бъде разбрана за някой, който не е запознат с тази материя. Или който не го е видял. Но е толкова сериозно и огромно, че само можем да се преклоним», коментира Пламен Румпалов, преподавател по математика в 125 СОУ «Боян Пенев».
Калоян обича дългите разходки сред природата и мечтае да стане учител. За да може повече деца да не се страхуват от математиката. И да открият себе си в нея. Калоян Гешев — един наистина «красив ум».
«За това дете съм сигурен, че светът ще говори в следващите години!», категоричен е преподавателят Пламен Румпалов.
Поставете оценка:
☆ ☆ ☆ ☆ ☆
4.5
Оценка 4.5 от 33 гласа.
Свързани новини
Новини по градове:
Новини Айтос, Новини Балчик, Новини Банкя, Новини Банско, Новини Благоевград, Новини Бургас, Новини Бяла, Новини Варна, Новини Велико Търново, Новини Велинград, Новини Видин, Новини Враца, Новини Габрово, Новини Добрич, Новини Каварна, Новини Казанлък, Новини Калофер, Новини Карлово, Новини Карнобат, Новини Каспичан, Новини Китен, Новини Кнежа, Новини Козлодуй, Новини Копривщица, Новини Котел, Новини Кресна, Новини Кърджали, Новини Кюстендил, Новини Летница, Новини Ловеч, Новини Лом, Новини Луковит, Новини Мездра, Новини Монтана, Новини Несебър, Новини Нова Загора, Новини Нови Пазар, Новини Обзор, Новини Оборище, Новини Омуртаг, Новини Павликени, Новини Пазарджик, Новини Перник, Новини Петрич, Новини Плевен, Новини Пловдив, Новини Поморие, Новини Правец, Новини Радомир, Новини Разград, Новини Разлог, Новини Русе, Новини Самоков, Новини Сандански, Новини Сапарева Баня, Новини Свети Влас, Новини Свиленград, Новини Свищов, Новини Своге, Новини Севлиево, Новини Силистра, Новини Симитли, Новини Сливен, Новини Смолян, Новини Созопол, Новини Сопот, Новини София, Новини Средец, Новини Стара Загора, Новини Стрелча, Новини Суворово, Новини Тетевен, Новини Троян, Новини Трън, Новини Трявна, Новини Тутракан, Новини Търговище, Новини Харманли, Новини Хасково, Новини Хисаря, Новини Царево, Новини Чепеларе, Новини Червен бряг, Новини Черноморец, Новини Чипровци, Новини Чирпан, Новини Шабла, Новини Шумен, Новини Ябланица, Новини Ямбол, Новини Всички градове
комплексных чисел — Чему равен квадратный корень из минус $i$?
Спросил
Изменено 3 года, 8 месяцев назад
Просмотрено 11 тысяч раз
$\begingroup$
Можно ли войти в кроличью нору рекурсивно?
Если $ \sqrt{-1} = i $, то чему равно $ \sqrt{-i} $?
- комплексные числа
$\endgroup$
94 = 1/4$ и поэтому $a=\pm1/\sqrt{2}$ мы знаем $b=-1/2a$
Итак, когда $a = 1/\sqrt{2}$, тогда $b = — 1/\sqrt{2}$
аналогично, когда $a = -1/\sqrt{2}$, тогда $b = 1/\sqrt{2}$
Наконец, подставив значения $a$ и $b$, мы получить два корня для $\sqrt{-i}$
$$(-1/{\sqrt{2}}) + i. (1/\sqrt{2})$$ и $$(1/\ sqrt{2}) — i.(1/\sqrt{2})$$
(1/\sqrt{2})$$ и $$(1/\ sqrt{2}) — i.(1/\sqrt{2})$$
Вы увидите, что возводя в квадрат любое из приведенных выше решений, вы получите $-i$
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
| 1 | Фактор | 93-8|||
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
Уравнения с квадратными корнями — Magoosh GRE
Уравнения с квадратными корнями. Тест иногда дает нам решить уравнение, включающее квадратный корень. В таком уравнении переменная будет стоять под радикалом. Так, например, это будет уравнение с квадратными корнями. Квадратный корень из х плюс 3 равен х минус 3. Мы решим это позже в видео.
Тест иногда дает нам решить уравнение, включающее квадратный корень. В таком уравнении переменная будет стоять под радикалом. Так, например, это будет уравнение с квадратными корнями. Квадратный корень из х плюс 3 равен х минус 3. Мы решим это позже в видео.
В, так что это тип уравнения, о котором мы будем говорить в этом уроке. Конечно, мы извлекаем квадратный корень, возводя его в квадрат, и нам всегда разрешается возводить в квадрат обе стороны. Иногда для простейших радикальных уравнений все, что нам нужно сделать, это возвести в квадрат обе части. Так, например, если у нас есть что-то вроде квадратного корня из х плюс 2 равно 3.
Возводим в квадрат обе стороны, получаем x плюс 2 слева, получаем 9 справа, вычитаем и получаем x равно 7. Фантастика. Но это уравнение было слишком простым, чтобы его можно было увидеть в тесте. На самом деле тест не подарит нам что-то простое на блюдечке с голубой каемочкой, он будет немного сложнее.
Прежде чем мы продолжим, давайте подумаем об этом. Всегда ли верно для любого значения k, что если мы возьмем квадратный корень из k в квадрате, то вернемся к k? Другими словами, квадратный корень отменяет возведение в квадрат и всегда возвращает нас туда, откуда мы начали. Всегда ли это так?
Всегда ли верно для любого значения k, что если мы возьмем квадратный корень из k в квадрате, то вернемся к k? Другими словами, квадратный корень отменяет возведение в квадрат и всегда возвращает нас туда, откуда мы начали. Всегда ли это так?
Конечно, нет. Уравнение верно для положительных чисел и для 0. Но не для отрицательных значений k. Например, если k равно отрицательному числу 4, то, конечно, при возведении его в квадрат мы получим положительное число 16. Возведение отрицательного числа 4 в квадрат равно положительному числу 16.
А когда мы извлечем квадратный корень из 16, мы получим 4. Другими словами , мы не возвращаемся к исходному начальному номеру. Так что это важно. Это говорит о том, что мы можем столкнуться с некоторыми проблемами, когда возникают отрицательные значения. Так что это на нашем радаре. Что происходит, когда мы получаем отрицательные значения, в частности, когда вещь под радикалом является отрицательной?
Мы должны обратить на это внимание. Получается, что в радикальных уравнениях надо учитывать посторонние корни. Когда мы делаем всю нашу алгебру правильно, включая возведение в квадрат обеих частей уравнения, алгебра может привести к ответам, которые на самом деле не работают в исходном уравнении. Это посторонние корни.
Получается, что в радикальных уравнениях надо учитывать посторонние корни. Когда мы делаем всю нашу алгебру правильно, включая возведение в квадрат обеих частей уравнения, алгебра может привести к ответам, которые на самом деле не работают в исходном уравнении. Это посторонние корни.
Так вот хочу подчеркнуть, речь не идет об ошибке, иными словами, даже если мы делаем всю алгебру правильно, просто в силу того, что мы возводим в квадрат, мы получаем лишние корни, лишние корни, которые не являются единицами которые фактически решают исходное уравнение. Важно понимать, что в радикальном уравнении будут возникать посторонние корни, даже если вы сделаете всю алгебру правильно.
Теперь мы можем взглянуть на уравнение, которое у нас было в начале. Итак, вот уравнение с самого начала. Итак, конечно, что мы сделаем, так это возведем обе стороны в квадрат. Конечно, тот бином, возведенный в правую сторону, мы, мы, мы превращаем его в х в квадрате минус 6х плюс 9. Возможно, вы помните схему квадрата разности.
Затем мы соберем все на одну сторону, так что мы получим квадратное число, равное 0. Мы разложим это на множители, это очень легко, и мы получим два корня, 1 и 6. Теперь, как правило, с алгеброй, вы’ я думаю хорошо, мы должны закончить, мы нашли значение X. Но с радикальными уравнениями мы должны быть осторожны. Знаем ли мы, что оба эти корня работают?
Может быть, они оба, или, может быть, один из них является посторонним корнем. Итак, мы должны проверить наши ответы. Мы должны проверить каждый ответ, который мы нашли, чтобы убедиться, что он работает, потому что правильно, теперь, просто взглянув на них 1 и 6, мы не знаем. Являются ли они оба истинными корнями, они оба являются посторонними корнями? Работают ли они в исходном уравнении?
Единственный способ, который мы найдем, это подключить их. Итак, вот исходное уравнение. Вот корни, которые мы нашли из алгебры. Итак, прежде всего, мы проверим первое, x равно 1. Подставим его в левую часть, получим квадратный корень из 1 плюс 3 квадратный корень из 4, что равно 2. Подставим в правую сторону, получим 1 минус 3, что отрицательное 2,
Подставим в правую сторону, получим 1 минус 3, что отрицательное 2,
Итак, две части уравнения не равны. Одна сторона равна 2, одна сторона равна минус 2. Так что этот корень не работает. Теперь мы проверим другой. Подключим его к левой стороне, получим квадратный корень из 6 плюс 3, конечно, это 9. Квадратный корень из 9 равен 3.
С другой стороны, мы получим 6 минус 3, что также равно 3. Две стороны работать, так что человек действительно работает на законных основаниях. И это решило проблему. Итак, у этого уравнения есть одно решение, которое работает, x равно 6. Это единственное решение, которое работает. X equals — это посторонний корень, потому что, хотя мы правильно следовали алгебре, и хотя алгебра дала нам этот корень, этот корень на самом деле не работает в исходном уравнении.
Нам нужно выровнять обе стороны, чтобы отменить радикал, но само это действие может привести к появлению посторонних корней. Если мы получим квадратное число после возведения в квадрат, что часто встречается в тесте, алгебра приведет к двум корням. Иногда работают оба корня. Иногда работает один корень, а один посторонний.
Иногда работают оба корня. Иногда работает один корень, а один посторонний.
Иногда оба являются посторонними, и уравнение не имеет решения. Итак, вот проблема с практикой. Поставьте видео на паузу, а потом поговорим об этом. Хорошо. Итак, здесь у нас есть радикал с обеих сторон.
Радикальное равно радикальному. Так что, конечно, мы просто будем выравнивать обе стороны. Получаем 2x минус 2 равно x минус 4. Что ж, очень легко решить уравнение. И мы получаем, что x равно отрицательному значению 2. Хорошо, очень хорошо.
Но что произойдет, если мы подставим это обратно в исходное уравнение? Когда мы подключаем это, это приводит к квадратному корню из отрицательного значения с обеих сторон. Итак, мы получаем квадратный корень из отрицательной 6, а квадратный корень из отрицательной 6 — это нечто вне действительной системы счисления, оно не живет нигде на числовой прямой. Так что мы не можем сделать математику с этим. Вот только для наших целей это просто ошибка и это уравнение не имеет решения.
Наконец, имейте в виду, что мы должны возводить в квадрат обе стороны только тогда, когда радикал сам по себе находится на одной стороне уравнения. Если радикал появляется с другими терминами с одной стороны, нам придется изолировать радикал с одной стороны, прежде чем будет иметь смысл квадратировать обе стороны. Итак, вот видео с практической задачей, а потом мы поговорим об этом.
Итак, радикала как такового у нас нет. Итак, самое первое, что нам нужно сделать, это вычесть эти 2 с обеих сторон. Таким образом, мы получаем радикал, 4 минус 3x равно x минус 2. Теперь мы можем возвести в квадрат обе стороны. И, конечно же, мы получаем квадрат разницы.
Квадрат этого двучлена. И это расширяется до x в квадрате минус 4x плюс 4. Теперь мы собираемся вычесть 4 с обеих сторон и добавить 3X к обеим сторонам, и это приведет нас к x в квадрате минус x. Очень легко разложить это на множители на х, умноженное на х минус 1. И алгебра приводит нас к решениям: х равно 0 и х равно 1.
Теперь нам нужно проверить эти ответы. Хорошо. Итак, это те корни, которые нашла для нас алгебра. Прежде всего, проверьте, что x равен 0. Подставьте это в левую часть, и мы получим 2 плюс корень 4, что равно 2 плюс 2, что равно 4.
Вставьте его в правую сторону, это 0. И, конечно же, 4 не равно 0. Так что этот не работает. Так что это будет посторонний корень. Теперь проверьте, что x равно 1. Подставьте это в левую часть, мы получим 2 плюс 4 минус 3 умножить на 1, так что 4 минус 3.
И, конечно же, это будет 1. Итак, это будет 2 плюс 1, что равно 3. И, конечно же, это не равно 1. Не равно x, который равен 1 на другой стороне уравнения. Так что и этот не работает. Так вот, ни один из корней, которые нам дала алгебра, не работает.
Значит, это уравнение просто не имеет решения. Оба решения, которые давала алгебра, были посторонними корнями. Таким образом, чтобы отменить радикальное уравнение, нам нужно возвести в квадрат обе его части. Мы должны двигаться, иногда перемещать что-то еще на другую сторону, чтобы изолировать радикал, прежде чем возвести его в квадрат.
