Квадратный корень какая степень. Квадратный корень. Исчерпывающий гид (2019)
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень . Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней .
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат.
То из них, квадрат которого равен исходному числу, и будет корнем.
То из них, квадрат которого равен исходному числу, и будет корнем.Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
…
90 2 = 8100;
100 2 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
[Подпись к рисунку]
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа .
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 6 | 7 | 8 | 9 | 0 | |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня.
Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
2 2 = 4;
8 2 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]
Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:)
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
[Подпись к рисунку]
Для начала выясним, между какими числами лежит число 576:
400 20 2
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
Осталось возвести каждое число в квадрат и сравнить с исходным:
24 2 = (20 + 4) 2 = 576
Отлично! Первый же квадрат оказался равен исходному числу.
Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
900 30 2
Смотрим на последнюю цифру:
1369 → 9;
33; 37.
Возводим в квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
2500 50 2
Смотрим на последнюю цифру:
2704 → 4;
52; 58.
Возводим в квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
3600 60 2
Смотрим на последнюю цифру:
4225 → 5;
65.
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень.
Но давайте все-таки возведем его в квадрат и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.
Среди множества знаний, которые являются признаком грамотности, на первом месте стоит азбука. Следующим, таким же «знаковым» элементом, являются навыки сложения-умножения и, примыкающие к ним, но обратные по смыслу, арифметические операции вычитания-деления. Усвоенные в далеком школьном детстве навыки, служат верой и правдой денно и нощно: ТВ, газета, СМС, И везде читаем, пишем, считаем, складываем, вычитаем, умножаем.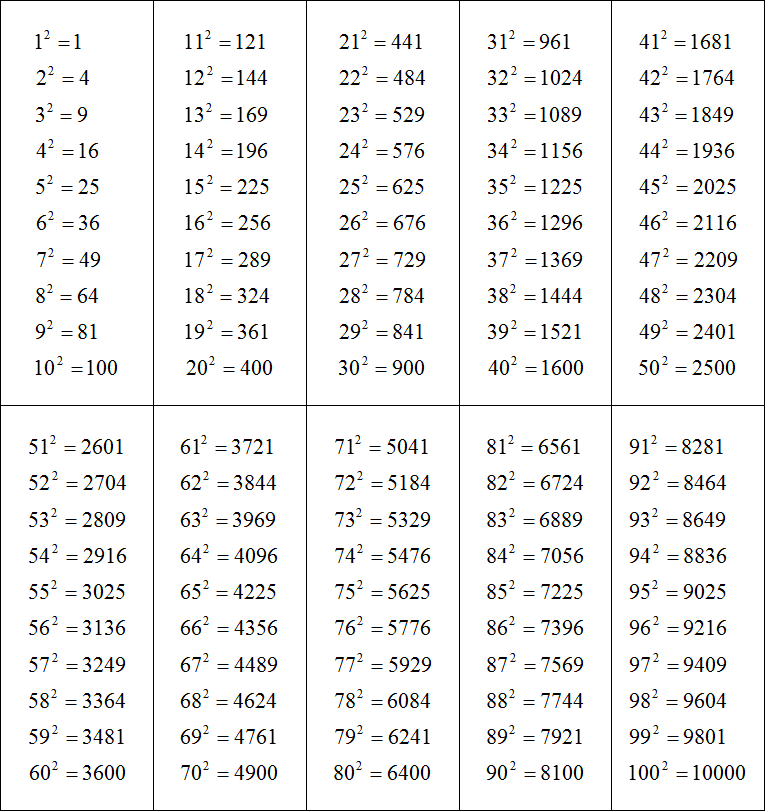
Сначала уточним, что же это такое — квадратный корень числа. Вообще говоря, «извлечь корень из числа» означает выполнить арифметическое действие противоположное возведению в степень — вот вам и единство противоположностей в жизненном приложении. допустим, квадрат, это умножение числа на самое себя, т.е., как учили в школе, Х * Х = А или в другой записи Х2 = А, а словами — «Х в квадрате равняется А». Тогда обратная задача звучит так: квадратный корень числа А, представляет собой число Х, которое будучи возведено в квадрат равно А.
Извлекаем квадратный корень
Из школьного курса арифметики известны способы вычислений «в столбик», которые помогают выполнить любые подсчеты с применением первых четырех арифметических действий.
А если серьезно, то вычисление квадратного корня часто выполняют, используя прием «артиллерийской вилки»: сначала берут число, квадрат которого, примерно, соответствует подкоренному выражению. Лучше, если «наш квадрат» чуть меньше этого выражения. Затем корректируют число по собственному умению-разумению, например, умножают на два, и… вновь возводят в квадрат.
Да, чуть не забыл, чтобы подтвердить свою возросшую грамотность, вычислим квадратный корень ранее указанного числа 12345. Делаем пошагово:
1. Возьмем, чисто интуитивно, Х=100. Подсчитаем: Х * Х = 10000. Интуиция на высоте — результат меньше 12345.
2. Попробуем, тоже чисто интуитивно, Х = 120. Тогда: Х * Х = 14400.И опять с интуицией порядок — результат больше 12345.
3. Выше получена «вилка» 100 и 120. Выберем новые числа — 110 и 115. Получаем, соответственно, 12100 и 13225 — вилка сужается.
4. Пробуем на «авось» Х=111. Получаем Х * Х = 12321. Это число уже достаточно близко к 12345.
В соответствии с требуемой точностью «подгонку» можно продолжить или остановиться на полученном результате. Вот и все. Как и было обещано — все очень просто и без калькулятора.
Совсем немного истории…
Додумались до использования квадратных корней еще пифагорейцы, ученики школы и последователи Пифагора, за 800 лет до н.э. и тут же, «нарвались» на новые открытия в области чисел. И откуда что взялось?
1. Решение задачи с извлечением корня, дает результат в виде чисел нового класса. Их назвали иррациональными, иначе говоря, «неразумными», т.к. они не записываются законченным числом. Самый классический пример такого рода — квадратный корень из 2. Этот случай соответствует вычислению диагонали квадрата со стороной равной 1 — вот оно, влияние школы Пифагора. Оказалось, что у треугольника с вполне конкретным единичным размером сторон, гипотенуза имеет размер, который выражается числом, у которого «нет конца». Так в математике появились
2. Известно, что Оказалось, что эта математическая операция содержит еще один подвох — извлекая корень, мы не знаем, квадратом какого числа, положительного или отрицательного, является подкоренное выражение.
Эта неопределенность, двойной результат от одной операции, так и записывается.
Изучение связанных с этим явлением проблем стало направлением в математике под названием теория комплексной переменной, имеющим большое практическое значение в математической физике.
Любопытно, что обозначение корня — радикал — применил в своей «Универсальной арифметике» все тот же вездесущий И. Ньютон, а в точности современный вид записи корня известен с 1690 года из книги француза Ролля «Руководство алгебры».
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же.
Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Возведение в степень предполагает, что данное число необходимо умножить само на себя определенное количество раз. Например, возведение числа 2 в пятую степень будет выглядеть следующим образом:
Число, которое нужно умножать само на себя, называется основанием степени, а количество умножений – ее показателем. Возведению в степень соответствуют два противоположных действия: нахождение показателя и нахождение основания.
Извлечение корня
Нахождение основание степени называется извлечением корня. Это означает, что необходимо найти число, которое нужно возвести в степень n, чтобы получить данное.
Например, необходимо извлечь корень 4-й степени из числа 16, т.е. определить, нужно умножить само на себя 4 раза, чтобы в итоге получить 16. Это число – 2.
Такое арифметическое действие записывается с помощью особого знака – радикала: √, над которым слева указывается показатель степени.
Арифметический корень
Если показатель степени является четный числом, то корнем могут оказаться два числа с одинаковым модулем, но с – положительное и отрицательное. Так, в приведенном примере это могут быть числа 2 и -2.
Выражение должно быть однозначным, т.е. иметь один результат. Для этого и было введено понятие арифметического корня, который может представлять собой только положительное число. Быть меньше нуля арифметический корень не может.
Таким образом, в рассмотренном выше примере арифметическим корнем будет только число 2, а второй вариант ответа – -2 – исключается по определению.
Квадратный корень
Для некоторых степеней, которые используются чаще других, в существуют специальные названия, которые изначально связаны с геометрией. Речь идет о возведении во вторую и третью степени.
Во вторую степень длину стороны квадрата, когда нужно вычислить его площадь. Если же нужно найти объем куба, длину его ребра возводят в третью степень. Поэтому называется квадратом числа, а третья – кубом.
Соответственно, корень второй степени называется квадратным, а корень третьей степени – кубическим. Квадратный корень – единственный из корней, при записи которого над радикалом не ставится показатель степени:
Итак, арифметический квадратный корень из данного числа – это положительное число, которое необходимо возвести во вторую степень, чтобы получить данное число.
Что такое квадратный корень?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже.
..»)
Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня ) в математике обозначается вот таким значком:
Сам значок называется красивым словом «радикал «.
Как извлечь корень? Это лучше рассмотреть на примерах .
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:
А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:
Уловили, что такое квадратный корень? Тогда считаем примеры :
Ответы (в беспорядке): 6; 1; 4; 9; 5.
Решили? Действительно, уж куда проще-то?!
Но… Что делает человек, когда видит какое-нибудь задание с корнями?
Тосковать начинает человек.
.. Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень …
Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах…
Пунктик первый. Корни надо узнавать в лицо!
Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…
В этом и есть сложность извлечения корней . Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.
Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните квадраты популярных чисел.
Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да…
Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.
И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…
Итак, что такое квадратный корень и как извлекать корни — думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.
Пунктик второй. Корень, я тебя не знаю!
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя их извлекать.
Попробуем вычислить вот такой корень:
Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.
Что, не подбирается? 2 2 даёт +4. (-2) 2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.
Такая же история будет с любым отрицательным числом. Отсюда вывод:
Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла ! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно! Или, другими словами:
Квадратные корни из отрицательных чисел извлечь нельзя!
Зато из всех остальных — можно. Например, вполне можно вычислить
На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов.
Жизнь станет проще!
Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:
Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:
Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называют иррациональными . Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:
Если при решении примера у вас получилось что-то неизвлекаемое, типа:
то так и оставляем. Это и будет ответ.
Нужно чётко понимать, что под значками
Конечно, если корень из числа извлекается ровно , вы обязаны это сделать. Ответ задания в виде, например
вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения:
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Пунктик третий. Самый хитрый.
Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!
Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!
Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…
Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ
правильный, а ответ
грубейшая ошибка. Вот так.
Так в чём же дело?
Действительно, (-2) 2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.
Но! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: из числа а — это неотрицательное число, квадрат которого равен а .
Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические . Хотя особо об этом не упоминается.
Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.
Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.
Уравнение простое, пишем ответ (как учили):
Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух ответов:
Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда неотрицательное! А здесь один из ответов — отрицательный ! Непорядок. Это первая (но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:
Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня . Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения .
Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
Вот так. Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:
Потому, что это — арифметический квадратный корень .
Но если вы решаете какое-нибудь квадратное уравнение, типа:
то всегда получается два ответа (с плюсом и минусом):
Потому, что это — решение уравнения.
Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)
Всё это — в следующих уроках.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.
)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Квадратный корень из 51 | Thinkster Math
Методы
Что такое квадратный корень из 51?
Квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. Например, квадратный корень из 25 равен 5, потому что 5 x 5 = 25. Выражаясь в радикальной форме: √25 = 5. Следовательно, находя квадратный корень из 51, мы находим, что квадратных корней из 51 7,141 . Всегда помните: ваш ответ может быть как целым, так и десятичным числом.
Является ли квадратный корень из 51 иррациональным?
Числа можно разделить на подмножества, называемые рациональными и иррациональными числами. Примером иррациональных чисел являются десятичные дроби, которые не имеют конца или не заканчиваются. Распространенная путаница заключается в том, что, поскольку у десятичной дроби нет конца, это большое число, стремящееся к бесконечности, хотя это неверно.
Взгляните на экспоненциальную константу e, e имеет значение 2,7182818… и является неограниченным, но не огромным значением, потому что в конце дня e никогда не будет больше 3. С другой стороны, рациональные числа — это десятичные дроби, которые можно записать в виде дробей, делящих два целых числа (если знаменатель не равен 0). Таким образом, для этой задачи, поскольку квадратный корень из 51, или 7,141, является неконечной десятичной дробью, квадратный корень из 51 иррационален.
Методы нахождения квадратного корня из 51
Для начала есть два способа вычисления квадратного корня из числа: разложение на простые множители и деление на множители. Обычно простая факторизация используется для идеальных квадратов, а длинное деление используется, когда значение квадратного корня является десятичным.
Поскольку мы знаем, что 51 — десятичное число, мы знаем, что подходящим методом будет деление в длинную сторону. Этот метод работает очень похоже на обычное длинное деление, за исключением того, что в этом методе есть еще несколько правил, которые помогают нам получить ответ.
Взгляните на этот пример, в котором подробно рассказывается о том, что представляет собой этот метод, как его использовать, а также приводится несколько решенных примеров. Таким образом, результат после использования метода деления в длину равен 7,141.
Нахождение квадратного корня из других чисел
Нахождение квадратного корня любого числа можно выполнить с помощью того же метода, который показан выше. Посмотрите, как найти квадратный корень из этих других конкретных примеров, нажав на любую из ссылок ниже:
Квадратный корень из 3708
Квадратный корень из 4967
Квадратный корень из 4393
Квадратный корень из 1477
Квадратный корень из 2106
Загрузите БЕСПЛАТНЫЕ математические ресурсы
Воспользуйтесь нашими бесплатными загружаемыми ресурсами и учебными материалами для обучения дома.
8 математических хитростей и хитростей, которые превратят вашего «хорошего» студента-математика в чемпиона по математике!
Мы учим наших студентов в Thinkster тому, что есть несколько способов решить математическую задачу.
Это помогает нашим ученикам научиться мыслить гибко и нелинейно.
Как сделать так, чтобы ваш ребенок добился больших успехов и стал миллионером
Как родитель, вы надеетесь, что ваш ребенок станет очень успешным и, вероятно, станет следующим Гейтсом, Цукербергом или Мег Уитман. Чтобы направить ребенка на правильный путь, существует множество навыков и качеств, которые вы можете начать формировать и развивать прямо сейчас. Это закладывает семена будущего успеха.
Получить PDFЧто такое диаграмма квадратного корня?
Арифметическое значение, которое используется для представления количества и используется в расчетах, определяется как Числа. Такие символы, как «4,5,6», обозначающие число, называются цифрами. Без чисел мы не можем вести подсчет вещей, даты, времени, денег и т. д. Эти числа также используются для измерения и используются для маркировки.
Свойства чисел делают их полезными при выполнении над ними арифметических операций.
Эти числа могут быть записаны в числовой форме, а также в словах.
Например, 3 записывается словами три, 35 записывается словами тридцать пять и т. д. Учащиеся могут написать числа от 1 до 100 словами, чтобы узнать больше.
Существуют разные типы чисел, которые мы можем выучить. Это целые и натуральные числа, нечетные и четные числа, рациональные и иррациональные числа и т. д.
Что такое система счисления?
Система счисления — это метод записи чисел, представляющий собой математический способ представления чисел данного набора с использованием чисел или символов математическим способом. Система записи для обозначения чисел с использованием цифр или символов логическим образом определяется как система счисления.
Мы можем использовать цифры от 0 до 9, чтобы составить все числа. С помощью этих цифр любой может составить бесконечное число.
Пример: 156, 3907, 3456, 1298, 784859 и т. д.
Что такое квадратный корень? Значение числа квадратных корней, которое при умножении само на себя дает исходное число.
Предположим, что a — это квадратный корень из b, тогда он представляется как a = √b, или мы можем выразить то же уравнение как 2 = b. Здесь «√» этот символ, который мы использовали для обозначения корня чисел, называется радикалом. Положительное число, когда его нужно умножить само на себя, представляет собой квадрат числа. Квадратный корень из квадрата любого положительного числа дает исходное число.
Например, квадрат 4 равен 16, 4 2 = 16, а квадратный корень из 16 √16 = 4. Так как 4 — полный квадрат, то легко найти квадратный корень таких чисел. , но для несовершенного квадрата это действительно сложно.
Квадратный корень представлен как «√». Его называют радикальным символом. Чтобы представить число «а» в виде квадратного корня, используя этот символ, можно записать как: «√a», , где а — это число.
Число здесь под подкоренным символом называется подкоренным. Например, квадратный корень из 4 также представлен как радикал из 4.
Оба представляют одно и то же значение, и формула для нахождения квадратного корня: b = √a
Свойства квадратных корней
Он определяется как функция «один к одному», которая принимает положительное число в качестве входных данных и возвращает квадратный корень из заданного входного числа.
f(x) = √x
Например, здесь, если x = 9, функция возвращает выходное значение как 3.
Это свойства квадратного корня: если число является совершенным квадратным числом, то точно существует совершенный квадратный корень. Легко найти квадратный корень из числа, являющегося полным квадратом. Совершенные квадраты — это положительные числа, которые можно записать как произведение числа на себя, или можно сказать, что совершенный квадрат — это число, равное степени 2 любого целого числа. Число, которое можно представить как произведение двух равных целых чисел. Например, 16 — это идеальный квадрат , потому что он является произведением двух равных целых чисел, 4 × 4 = 16. Однако 24 не является идеальным квадратом, потому что его нельзя выразить как произведение двух равных целых чисел. Число, полученное возведением целого числа в квадрат, называется полным квадратом. Если предположить, что N является полным квадратом целого числа y, это можно записать как N = произведение y и y = y 2. Итак, формула идеального квадрата может быть выражена как: N = Y 2 Используем формулу со значениями. Если y = 5 и N = y 2 . Это означает, что N = 5 2 = 25. Здесь 25 — полный квадрат, потому что это квадрат целого числа. С помощью квадратных корней мы можем определить, является ли число полным квадратом или нет, и вычислим ли мы квадратный корень из данного числа. Если квадратный корень представляет собой целое число, то данное число будет полным квадратом, а если значение квадратного корня не является целым числом, то данное число не является полным квадратом. Например, чтобы проверить, является ли 24 полным квадратом, мы вычислим его квадратный корень. √24 = 4,898979. Как мы видим, 4,898979 — не целое число, поэтому 24 — не полный квадрат. Возьмем другой пример Число 49. √49 = 7. Мы видим, что 7 — целое число, следовательно, 49является совершенным квадратом. Диаграмма квадратного корня представляет собой представление квадратных корней различных чисел в табличной форме. Здесь является табличным представлением квадратной корневой диаграммы для значений от 1 до 51: Квадратный номер корня (√n) Квадратный корень (√n) ЧИСЛО КВАДРАТНОГО КОРНЯ (√N) √1 √18 √35 √2 √19 √36 √3 √20 √37 √4 √21 √38 √5 √22 √39 √6 √23 √40210 a0003 √24 √41 √8 √25 √42 √9 √26 √43 √10 √27 √44 √11 √28 √45 √12 √29 √46 √47 √14 √31 √48 √15 √32 √49 √16 √33 √50 √17 √34 √51 Perfect Square Chart От 1 до 20: Номер Perfect Square Номер Perfect Square Perfect Square 0204 1 2 1 11 2 121 2 2 4 12 2 144 3 2 9 13 2 169 4 2 16 14 2 196 5 2 25 15 2 225 6 2 36 16 2 256 7 2 49 17 2 289 8 2 64 18 2 324 9 2 81 19 2 361 10 2 100 20 2 400 .
(8 × 3 = 24).
Что такое диаграмма квадратного корня?
Значение value value value value value value value value value value value . ЗНАЧЕНИЕ 1 4. 
242 5.916 1.4142 4.358 6 1.7321 4.472 6.082 2 4.582 6.164 2.236 4.690 6.245 2,449 4.795 4.795 2.645 4.899 6.403 2.828 5 6. 
480 3 5.099 6.557 3.162 5.196 6.633 3.316 5.291 6.708 3,464 5,385 6.782 0 6.782 10 6.782 0 6.782 .0002 √30 5.477 6.855 3.741 5.567 6.928 3.873 5. 
656 7 4 5.744 7.071 4.123 5.831 7.141 Вопросы
