| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0.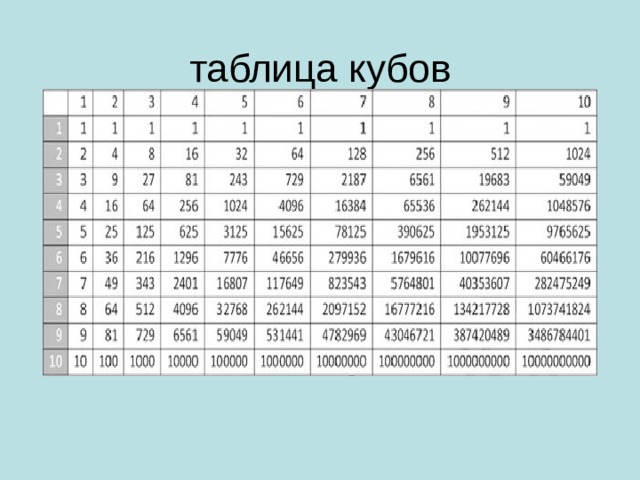 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Корень и его свойства — intmag24.
 ru
ruТема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.
Определение «Корень» Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √64 = 8 (√64 равно числу 8).
Формула: √a2 = a
Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.
Извлечь корень — значит найти значение корня (то есть найти число, при возведении которого в степень, получается подкоренное значение).
Например, извлечь корень из 64 – значит найти √64.
Найти корень из числа можно одним из следующих способов:
- Использование таблицы квадратов, таблицы кубов и т.д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует.
- Разложение подкоренного выражения (числа) на простые множители.
Порядок нахождения корня в этом случае будет следующим:
1. Разложение подкоренного значения на простые множители,
2. Объединение одинаковых множителей и их представление в виде степени с необходимым показателем.
Например, √144 = √2х2х2х2х3х3 = √(2х2)х(2х2)х(3х3) = √22х22х32 = √122 = 12
3. В случае, если невозможно найти корень из числа, то можно упростить подкоренное выражение (число). В этом случае применяется следующее правило: корень из произведения чисел равен произведению корней этих чисел.
Например, √72 = √2х2х2х3х3 = √(2х2)х2х(3х3) = √22х2х32 = √62х2 = 6√2 - Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.
Например, √130=√13х5х2 – упростить нельзя.
- Извлечение корня из дроби. В этом случае применяются следующие правила:
1. дробное число должно быть записано в виде обыкновенной дроби;
2. корень из дроби равен частному от деления корня числителя на корень знаменателя.
Например, √3,24 = √324/100 = √81/25 = √81 / √25 = 9/5 = 1,8.
- Извлечение нечетной степени из отрицательных чисел. Чтобы извлечь корень нечетной степени из отрицательного числа необходимо извлечь его из положительного числа и поставить перед ним знак минус.
Например, чтобы найти корень третьей степени из (-125), нужно найти корень третьей степени из 125 (будет 5) и подставить знак минуса (будет -5).
Скачать программу «Корни квадратные», которая формирует задания на вычисление квадратных корней, в том числе: приведение, сложение, вычитание, умножение и деление. |
Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.
Для этого воспользуемся следующим свойством дроби: a = n√an.
Например, есть квадратный корень (второй степени √2 ) и кубический корень (третьей степени 3√3).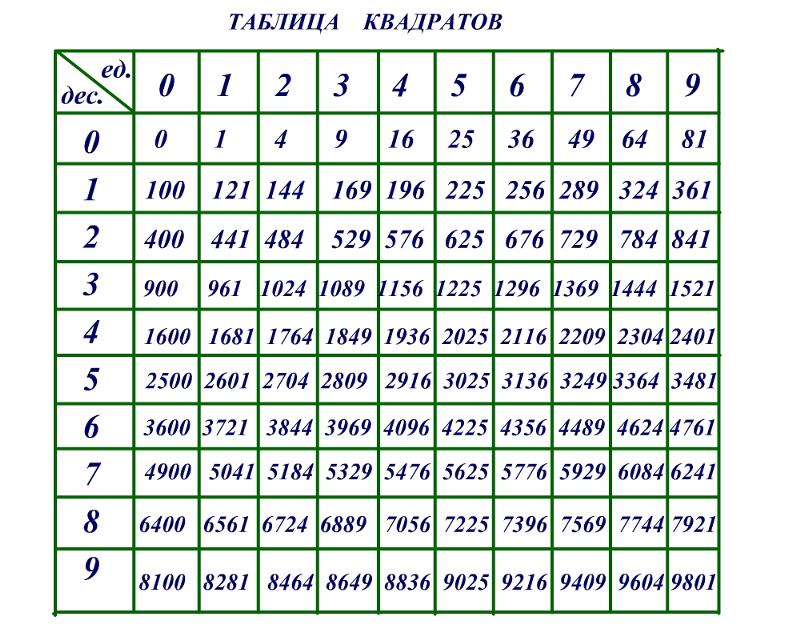
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n√an: √2 = 2√2 = 6√23 = 6√8; 3√3 = 6√32 = 6√9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.
Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.
Примеры:
2√3 + 3√3 = 5√3
2√3 + 2√4 – не выполняется.
При этом, нужно рассмотреть возможность упростить выражения.
Пример: 2√3 + 3√12 = 2√3 + 3√2х2х3 = 2√3 + 3√ 22х3 = 2√3 + 6√3 = 8√3.
Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Произведение корней из чисел равно корню из произведения этих чисел.
√a*b=√a*√b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√2 х √3 = √6
√6 х √3 = √18 = √3х3х2 = 3√2
При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√2 х √5 = (3х1) √(2*5) = 3√10
4√2 х 3√3 = (3х4) √(2х3) = 12√6
Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√a:b=√a:√b
В процессе деления квадратных корней дроби упрощаются.
Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √21:√3=√21:3=√7
При делении корней с множителями нужно отдельно разделить множители и подкорневые выражения (числа). Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
Пример. 12√32 : 6√16 = (12:6) √(32:16) = 2√2.
Скачать программу «Корни квадратные», которая формирует задания на вычисление квадратных корней, в том числе: приведение, сложение, вычитание, умножение и деление. |
Квадратные и кубические корни
Примечание: Квадратные и кубические корни, а также операции с ними часто включаются в книги по алгебре. Чтобы найти квадратный корень из числа, вам нужно найти число, которое при умножении само на себя дает исходное число. Другими словами, чтобы найти квадратный корень из 25, вам нужно найти число, которое при умножении само на себя дает 25. Таким образом, квадратный корень из 25 равен 5. Символом для квадратного корня является . Ниже приведен неполный список совершенных (целых) квадратных корней.
Ниже приведен неполный список совершенных (целых) квадратных корней.
Примечание: Если перед квадратным корнем не стоит знак (или знак плюс), требуется положительный ответ. Отсутствие знака означает, что позитив понят. Отрицательный ответ требуется только в том случае, если перед квадратным корнем стоит знак минус. Это обозначение используется во многих текстах, а также в этой книге. Следовательно,
Чтобы найти кубический корень числа, вам нужно найти некоторое число, которое при двукратном умножении само на себя дает исходное число. Другими словами, чтобы найти кубический корень из 8, нужно найти число, которое при двукратном умножении само на себя дает 8. Таким образом, кубический корень из 8 равен 2, поскольку 2 × 2 × 2 = 8. Обратите внимание, что символом кубического корня является подкоренной знак с маленькой тройкой (называемой индексом) сверху и слева, . Аналогично определяются и идентифицируются другие корни по заданному индексу.
Чтобы найти квадратный корень из числа, не являющегося полным квадратом, необходимо найти приблизительный ответ, используя процедуру, приведенную в примере .
Приблизительно.
находится между и
и
Следовательно,
Поскольку 42 находится почти посередине между 36 и 49, это почти посередине между и . То есть примерно 6,5. Для проверки умножьте следующее:
6,5 × 6,5 = 42,25 или около 42,
Приблизительно.
Поскольку немного ближе к , чем к ,
Проверьте ответ.
Приблизительно.
Сначала проведите операцию под радикалом.
Поскольку немного ближе к , чем к .
Квадратные корни несовершенных квадратов можно аппроксимировать, найти в таблицах или найти с помощью калькулятора. Вы можете иметь в виду эти два, потому что они обычно используются.
Вы можете иметь в виду эти два, потому что они обычно используются.
Иногда вам придется упростить квадратных корня или записать их в простейшей форме. В дробях можно упростить до . Квадратные корни можно упростить до .
Существует два основных метода упростить квадратный корень .
Метод 1:Разложите число под на два множителя, один из которых представляет собой максимально возможный правильный квадрат. (Совершенные квадраты — это 1, 4, 9, 16, 25, 36, 49 и т. д.)
Метод 2:
Полностью разложите число под на простые множители, а затем упростите, выделив все множители, которые шли парами.
Упростить .
Метод 1.
Извлеките квадратный корень из числа
в совершенном квадрате.Наконец, запишите это как одно выражение.
Метод 2.
Переписать парами под корнем
В Примере самый большой правильный квадрат легко увидеть, и метод 1, вероятно, является более быстрым методом.
Упростить .
Метод 1.
Метод 2.
В Примере не так очевидно, что самый большой полный квадрат равен 144, поэтому метод 2, вероятно, является более быстрым.
Упростить .
Метод 1.
Метод 2.
Запомните: Большинство квадратных корней не могут быть упрощены, поскольку они уже представлены в простейшей форме, например , , .
Квадратные и кубические корни | Показатели 9{2}\) (квадратный сантиметр), то стороны этого квадрата равны \(8 \text{ см}\).
Посмотрите на первые десять положительных квадратных чисел.
| Номер | $$\mathbf{1}$$ | $$\mathbf{2}$$ | $$\mathbf{3}$$ | $$\mathbf{4}$$ | $$\mathbf{5}$$ | $$\mathbf{6}$$ | $$\mathbf{7}$$ | $$\mathbf{8}$$ | $$\mathbf{9}$$ | $$\mathbf{10}$$ |
|---|---|---|---|---|---|---|---|---|---|---|
| Умножить на себя | $$1 \раз 1$$ | $$2 \ умножить на 2$$ | $$3\умножить на 3$$ | $$4 \ умножить на 4$$ | $$5 \умножить на 5$$ | 9{2}$$|||||
| Квадрат | $$1$$ | $$4$$ | $$9$$ | $$16$$ | $25$$ | $36$$ | $49$$ | $64$$ | $81$$ | $100$$ |
Видите закономерность в последней строке таблицы выше?
\[4 — 1 = 3\] \[9 — 4 = 5\] \[16 — 9 = 7\] \[25 — 16 = 9\] \[36 — 25 =\текст{ ?}\]Разница между последовательными квадратными числами всегда является нечетным числом.
Чтобы найти квадратный корень из числа, мы задаем вопрос: какое число было умножено само на себя, чтобы получить квадрат?
Квадратный корень из \(16\) равен \(4\), потому что \(4 \умножить на 4 = 16\).
Вопрос: «Какое число умножили само на себя, чтобы получить \(16\)?» записывается математически как \(\sqrt{16}\).
Ответ на этот вопрос записывается как \(\sqrt{16} = 4\).
Посмотрите на первые двенадцать квадратных чисел и их квадратные корни.
| Номер | $$\mathbf{1}$$ | $$\mathbf{4}$$ | $$\mathbf{9}$$ | $$\mathbf{16}$$ | $$\mathbf{25}$$ | $$\mathbf{36}$$ | $$\mathbf{49}$$ | $$\mathbf{64}$$ | $$\mathbf{81}$$ | $$\mathbf{100}$$ | $$\mathbf{121}$$ | $$\mathbf{144}$$ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Квадратный корень | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$7$$ | $$8$$ | $$9$$ | $$10$$ | $$11$$ | $12$$ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Чек | $$1 \раз 1$$ | $$2 \раз 2$$ | $$3\умножить на 3$$ | $$4 \ умножить на 4$$ | $$5 \умножить на 5$$ | $$6 \умножить на 6$$ | $$7 \умножить на 7$$ | $$8 \ умножить на 8$$ | $$9 \ умножить на 9$$ | $$10\умножить на 10$$ | $$11\умножить на 11$$ | $$12 \ умножить на 12$$ | {3}\) (кубических сантиметров), то стороны этого куба равны \(3 \text{ см}\).
| Номер | $$\mathbf{1}$$ | $$\mathbf{2}$$ | $$\mathbf{3}$$ | $$\mathbf{4}$$ | $$\mathbf{5}$$ | $$\mathbf{6}$$ | $$\mathbf{7}$$ | $$\mathbf{8}$$ | $$\mathbf{9}$$ | $$\mathbf{10}$$ |
|---|---|---|---|---|---|---|---|---|---|---|
| Умножить на себя дважды | $$1 \раз 1\раз 1$$ | $$2 \times 2 \times 2$$ | $$3 \раз 3\раз 3$$ | $$4 \раз 4\раз 4$$ | $$5 \раз 5 \раз 5$$ 9{3}$$ | |||||
| Куб | $$1$$ | $$8$$ | $27$$ | $64$$ | $125$$ | $216$$ | $343$$ | $$512$$ | $729$$ | $1000$$ |
Чтобы найти кубический корень числа, задаем вопрос: Какое число было умножено само на себя и еще раз на самому получить куб?
Кубический корень из \(64\) равен \(4\), потому что \(4 \умножить на 4 \умножить на 4 = 64\).
Вопрос: «Какое число умножили на себя и еще раз на себя (или возвели в куб), чтобы получить \(64\)?» математически записывается как \(\sqrt[3]{64}\).
Ответ на этот вопрос записывается как \(\sqrt[3]{64} = 4\).
Посмотрите на первые десять кубических чисел и их кубические корни.
| Номер | $$\mathbf{1}$$ | $$\mathbf{8}$$ | $$\mathbf{27}$$ | $$\mathbf{64}$$ | $$\mathbf{125}$$ | $$\mathbf{216}$$ | $$\mathbf{343}$$ | $$\mathbf{512}$$ | $$\mathbf{729}$$ | $$\mathbf{1 000}$$ |
|---|---|---|---|---|---|---|---|---|---|---|
| Кубический корень | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$7$$ | $$8$$ | $$9$$ | $$10$$ |
| Чек | $$1 \раз 1\раз 1$$ | $$2 \times 2 \times 2$$ | $$3 \раз 3\раз 3$$ | $$4 \раз 4\раз 4$$ | $$5 \умножить на 5 \умножить на 5$$ | $$6 \умножить на 6 \умножить на 6$$ | $$7\раз 7\раз 7$$ | $$8 \x 8 \times 8$$ | $$9\раз 9 \раз 9$$ | $$10\х10\х10$$ |
Иногда нужно произвести некоторые вычисления, чтобы найти корень.
Рабочий пример 3.6: Нахождение квадратных корней
Упростите и вычислите квадратный корень.
- \[\sqrt{4 \times 5 — 4}\]
- \[\sqrt{3 \times (10 + 2)}\]
- \[\sqrt{120 — 10 \умножить на 2}\]
- \[\sqrt{33\\раз\3 + 1}\]
Сначала вычислите квадратный корень.
- \[\sqrt{4 \times 5 — 4} = \sqrt{20 — 4} = \sqrt{16}\]
- \[\sqrt{3 \times (10 + 2)} = \sqrt{3 \times 12} = \sqrt{36}\]
- \[\sqrt{120 — 10 \times 2} = \sqrt{120 — 20} = \sqrt{100}\]
- \[\sqrt{33 \times 3 + 1} = \sqrt{99 + 1} = \sqrt{100}\]
Найдите квадратный корень из ответа.
- \[\sqrt{16} = 4\]
- \[\sqrt{36} = 6\]
- \[\sqrt{100} = 10\]
- \[\sqrt{100} = 10\]
Рабочий пример 3.
 7: Нахождение кубических корней
7: Нахождение кубических корнейУпрости и найди кубический корень.
- \[\sqrt[3]{200 + 16}\]
- \[\sqrt[3]{1000 — 271}\]
- \[\sqrt[3]{500 + 500}\]
- \[\sqrt[3]{13 + 26 + 25}\]
Сначала выполните вычисления с кубическим корнем.
- \[\sqrt[3]{200 + 16} = \sqrt[3]{216}\]
- \[\sqrt[3]{1000 — 271} = \sqrt[3]{729}\]
- \[\sqrt[3]{500 + 500} = \sqrt[3]{1000}\]
- \[\sqrt[3]{13 + 26 + 25} = \sqrt[3]{64}\]
Найдите кубический корень ответа.
- \[\sqrt[3]{216} = 6\]
- \[\sqrt[3]{729} = 9\]
- \[\sqrt[3]{1000} = 10\]
- \[\sqrt[3]{64} = 4\]
Упражнение 3. 8. Нахождение квадратных корней дробей и
десятичные дроби
8. Нахождение квадратных корней дробей и
десятичные дроби
Запишите дробь как произведение двух равных множителей для извлечения квадратного корня.
- \[\фракция{81}{121}\]
- \[\фракция{64}{81}\]
- \[\фракция{49}{169}\]
- \[\фракция{100}{225}\]
Мы знаем, что для нахождения квадратного корня нужно найти число, которое при умножении само на себя дает квадрат. В этом примере мы ищем произведение двух одинаковых дробей.
- \[\frac{81}{121} = \frac{9\times 9}{11 \times 11} = \frac{9}{11} \times \frac{9}{11}\]
- \[\frac{64}{81} = \frac{8 \times 8}{9 \times 9} = \frac{8}{9} \times \frac{8}{9}\]
- \[\frac{49}{169} = \frac{7 \times 7}{13 \times 13} = \frac{7}{13} \times \frac{7}{13}\]
- \[\frac{100}{225} = \frac{10 \times 10}{15 \times 15} = \frac{10}{15} \times \frac{10}{15}\]
Вы видите узор? Чтобы найти квадратный корень из дроби, найдите квадратный корень из
числитель и знаменатель. Итак, \(\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} =
\фракция{2}{3}\).
Итак, \(\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} =
\фракция{2}{3}\).
Определите следующее.
- \[\ sqrt{\ гидроразрыва {16} {25}}\]
- \[\ sqrt{\ гидроразрыва {9} {49}} \]
- \[\ sqrt{\ гидроразрыва {81} {144}} \]
- \[\ sqrt{\ гидроразрыва {400} {900}} \]
Используйте правило, которое вы открыли в вопросе 1, чтобы найти эти квадратные корни.
- \[\ sqrt {\ frac {16} {25}} = \ frac {\ sqrt {16}} {\ sqrt {25}} = \ frac {4} {5} \]
- \[\ sqrt {\ гидроразрыва {9{49}} = \ гидроразрыва {\ sqrt {9}} {\ sqrt {49}} = \ гидроразрыва {3} {7} \]
- \[\ sqrt {\ frac {81} {144}} = \ frac {\ sqrt {81}} {\ sqrt {144}} = \ frac {9} {12} \]
- \[\ sqrt {\ frac {400} {900}} = \ frac {\ sqrt {400}} {\ sqrt {900}} = \ frac {20} {30} = \ frac {2} {3} \ ]
- Используйте тот факт, что \(\text{0,01}\) можно записать как \(\frac{1}{100}\) для вычисления \(\sqrt{\text{0,01}}\ ).

Используйте тот факт, что \(\text{0,49}\) можно записать как \(\frac{49}{100}\) для вычисления \(\sqrt{\text{0,49}}\).
- Мы знаем, что \(\text{0,01}\) можно записать как \(\frac{1}{100}\).
Таким образом, 1}{10} = \text{0,1}\). - Мы знаем, что \(\text{0,49}\) можно записать как \(\frac{49}{100}\).
Таким образом, 7}{10} = \text{0,7}\).
Вы видите узор? Чтобы найти квадратный корень из десятичного числа:
Шаг 1: Найдите квадратный корень из числа без запятой.
Шаг 2: Проверьте количество цифр справа от запятой в заданном десятичном числе. Переместите запятую на половину числа мест в ответе.
Например, \(\sqrt{\text{0,36}}\).
Шаг 1: \(\sqrt{36} = 6\)
Шаг 2: \(\text{0,36}\) содержит две цифры после запятой. В ответе должна быть только одна цифра.
Итак, \(\sqrt{\text{0,36}} = \text{0,6}\).
Рабочий пример 3.8: Нахождение квадрата корни дробей и десятичных дробей
Рассчитайте следующее.
- \[\ SQRT {\ текст {0,09}}\]
- \[\sqrt{\текст{0,64}}\]
- \[\sqrt{\текст{1,44}}\]
- \[\sqrt{\текст{1,69}}\]
Найдите квадратный корень из числа без запятая.
- \[\sqrt{09} = 3\]
- \[\sqrt{64} = 8\]
- \[\sqrt{144} = 12\]
- \[\sqrt{169} = 13\]
Проверьте количество цифр справа от запятой в заданном десятичном числе.
 Переместите запятую наполовину
количество мест в ответе.
Переместите запятую наполовину
количество мест в ответе.\(\text{0,09}\) имеет две цифры после запятой, поэтому ответ содержит только одну цифру.
\(\sqrt{\text{0,09}} = \text{0,3}\) (\(\sqrt{9} = 3\) и только одно место после запятой: \(\text{0 ,3}\))
\(\text{0,64}\) имеет две цифры после запятой, поэтому ответ содержит только одну цифру.
\(\sqrt{\text{0,64}} = \text{0,8}\) (\(\sqrt{64} = 8\) и только один знак после запятой: \(\text{0 ,8}\))
\(\text{1,44}\) имеет две цифры после запятой, поэтому ответ содержит только одну цифру.
\(\sqrt{\text{1,44}} = \text{1,2}\) (\(\sqrt{144} = 12\) и только один знак после запятой: \(\text{1 ,2}\))
\(\text{1,69}\) имеет две цифры после запятой, поэтому ответ содержит только одну цифру.

\(\sqrt{\text{1,69}} = \text{1,3}\) (\(\sqrt{169} = 13\) и только один знак после запятой: \(\text{1 ,3}\))
Упражнение 3.9. Нахождение кубических корней дробей и десятичных дробей
Найдите кубические корни следующих дробей и десятичных дробей.
- \[\ sqrt [3] {\ гидроразрыва {8} {27}} \]
- \ [\ sqrt [3] {\ гидроразрыва {343} {1000}} \]
- \[\sqrt[3]{\text{0,343}}\]
- \[\sqrt[3]{\frac{8000}{27000}}\]
- \[\ sqrt [3] {\ frac {8} {27}} = \ frac {\ sqrt [3] {8}} {\ sqrt [3] {27}} = \ frac {2} {3} \ ]
- \[\ sqrt [3] {\ frac {343} {1000}} = \ frac {\ sqrt [3] {343}} {\ sqrt [3] {1000}} = \ frac {7} {10} = \текст{0,7}\]
- \[\sqrt[3]{\text{0,343}} = \text{0,7}\]
Убедитесь, что ответ работает: \(\text{0,7} \times \ \text{0,7} \times \text{0,7} = \text{0,49} \раз \текст{0,7} = \текст{0,343}\).