Как найти максимум функции через производную: Как найти экстремум (точки минимума и максимума) функции

обнаружение максимума и минимума OTUS

Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.

Максимум

Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело. Для этого нужно запомнить такое определение:

Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x₀). Оно будет при любом значении x€ X, x≠x₀ делает справедливым неравенство: f(x)≤f(x₀).

Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».

Минимум

Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.

Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:

Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x₀), которое при любом значении x€ X, x≠x₀ делает справедливым неравенство f(x)≥f(x₀).

Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x₀, а минимум – самое маленькое.

Стационарные точки

При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.

Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.

Здесь рекомендуется запомнить следующее:

1. Экстремум функции – это минимумы и максимумы.
2. Если определить производную в точках экстремумов, она будет равно 0.
3. Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.

 Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.

План действий

Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

1. Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
2. Если запись непрерывная – ищем производную.
3. После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
4. Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
5. Вычислить значения функции на концах отрезка [a, b].
6. Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

На отрезке

Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.

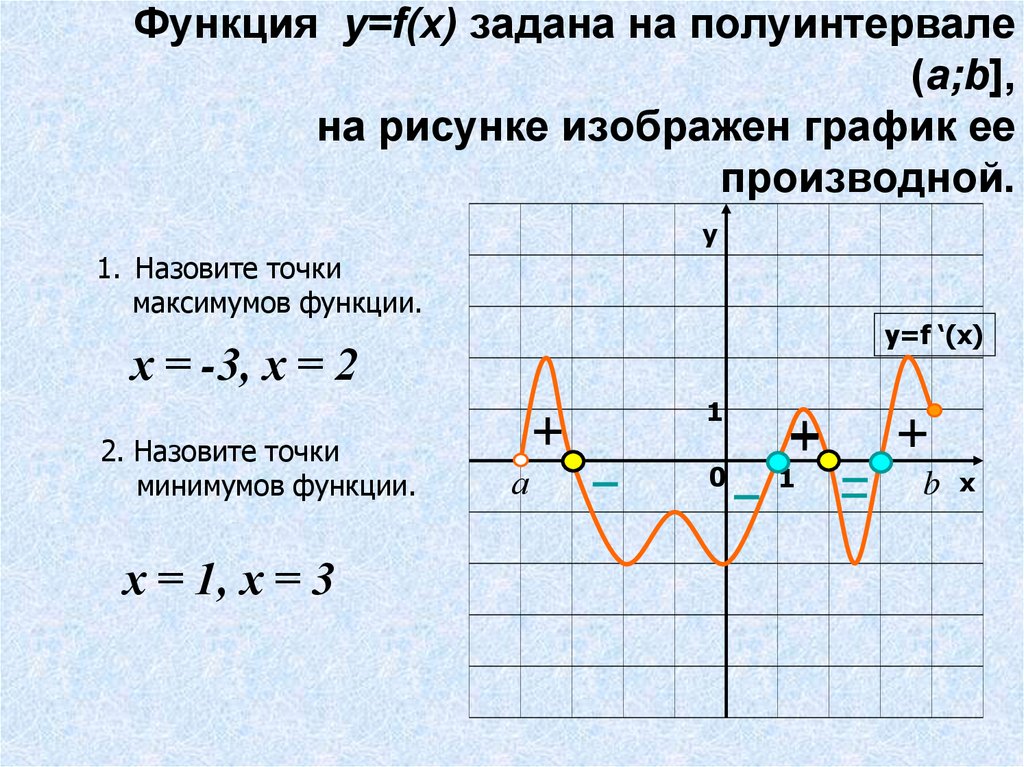
Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.

Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.

Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.

Открытый интервал

Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.

Здесь:

1. Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
2. Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
3. На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.

Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.

Бесконечность

Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:

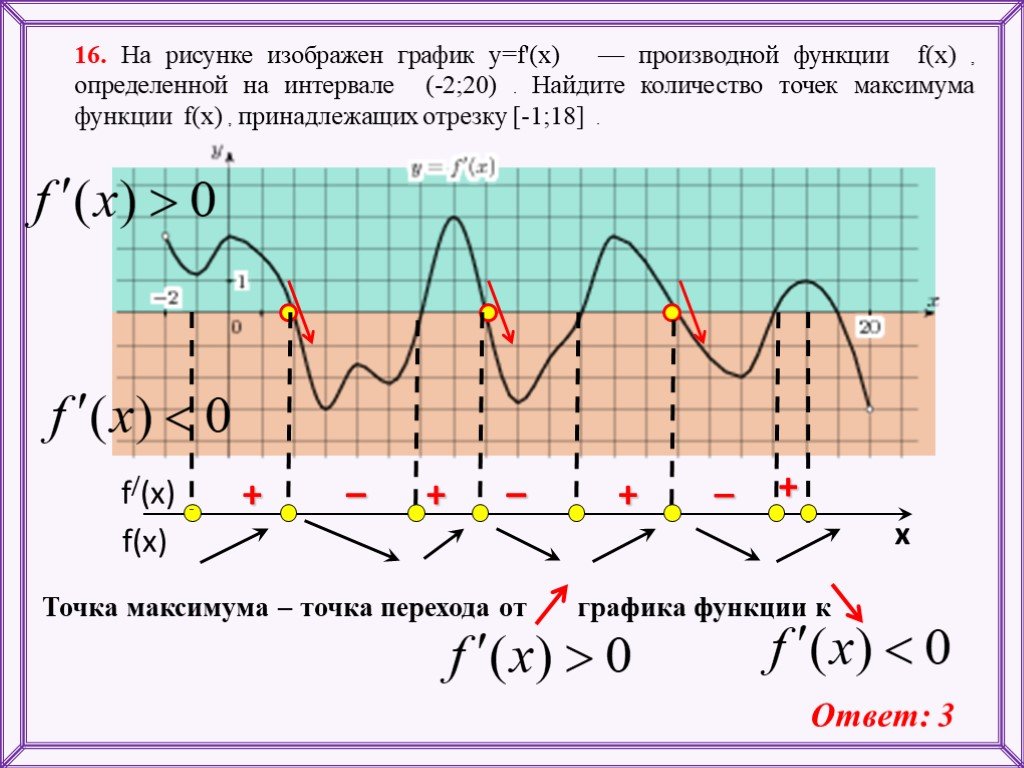
На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.

Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.

Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.

Как найти точки минимума и максимума функции, анализируя функцию, её производную и область определения

Поиск точки максимума и минимума функции — довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом «экстремум» подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом.

Содержание:

• Глобальный и локальный максимум
• Исследование
  • Область допустимых аргументов
  • Асимптоты
  • Производная и экстремумы
  • Концы интервала и сравнение результатов
• Видео

Глобальный и локальный максимум

Максимум бывает локальным или глобальным. Точка локального максимума — это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.

Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.

Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:

• экстремума, если она попадает в указанный отрезок,
• разрыва,
• ограничивающей заданный отрезок.

Исследование

Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):

1. Найти область допустимых аргументов и пересечения этой области с областью исследования. 2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.

   Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.

   Асимптоты

   Асимптота — это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.

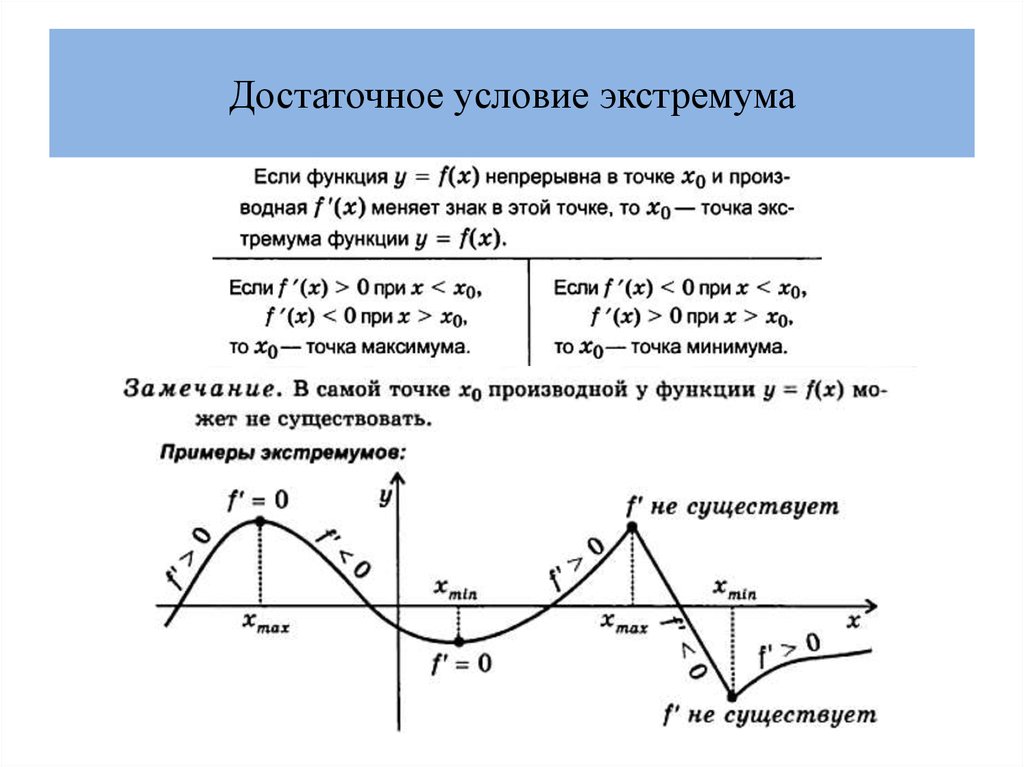
   Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. 3. У неё не может быть экстремумов, она убывает на всей оси аргументов.

   2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает — производная была положительной, а стала отрицательной.

   После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).

   Концы интервала и сравнение результатов

   При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.

   Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой. 3 — 3xy + 2$ 92 = 4$

   Но я не уверен, что делать дальше и как решить эти уравнения для $x$ и $y$ и $\lambda$. Честно говоря, я даже не уверен, что это лучший способ ответить на этот вопрос.

   Если бы кто-нибудь мог показать мне, как я могу найти максимум и минимум функции в этой области с помощью лучшего метода, или помочь мне продолжить с моим, это действительно помогло бы.

   • многомерное исчисление
   • частная производная
   • максимумы-минимумы 92 = 4$, $x = y$ дает точку $(\sqrt2, \sqrt2)$, которую вы должны проверить.

     Наконец, проверьте граничные точки $(0, 0), (2, 0)$ и $(0, 2)$.

     Максимум $10$ в точках $(2, 0)$ и $(0, 2)$, минимум $1$ в точке $(1, 1)$.

     $\endgroup$

     6

     $\begingroup$

     Напишите $\mu = \frac{2}{3} \lambda$, уравнения примут вид

     \begin{align} \мю х &= х^2 — у, \\ \mu у &= у ^ 2 — х, \\ х^2 + у^2 &=4. 2 &= 4. \end{выравнивание}

     $\endgroup$

     4

     исчисление — Максимальное значение функции

     $\begingroup$

     Является ли общим правилом/теоремой, что абсцисса максимального значения функции находится там, где производная этой функции равна нулю? Меня попросили найти абсциссу, когда интеграл максимален, поэтому я решил, что это будет та же абсцисса, где его производная равна нулю. Заранее спасибо.

     • исчисление
     • производные

     $\endgroup$

     4

     $\begingroup$

     Есть некоторые уточнения. Функция должна быть дифференцируемой и иметь максимум внутри рассматриваемого интервала (а не в конце). Если да, то производная функции в максимуме равна $0$.

     Может быть несколько точек, в которых производная равна $0$: это могут быть локальные максимумы, локальные минимумы или точки перегиба.

     $\endgroup$

     1

     $\begingroup$

     Функция не может иметь экстремум (максимум или минимум), если производная не равна нулю. Обратите внимание, что если производная не определена, то производная не равна ничему, кроме нуля. (Некоторая осторожность необходима при рассмотрении конечных точек.)

     Чтобы понять, почему это так, предположим, что вы ищете максимальное значение, а производная положительна. Затем вы можете увеличить значение функции, увеличив абсциссу (для тех, кто не знаком с «абсциссой», это в основном означает «x»). Если производная отрицательна, то можно найти большее значение, уменьшив абсциссу.

     Для интеграла интегрирование является обратным дифференцированию (с точностью до константы, поэтому вам нужен +C для неопределенных интегралов).

     No related posts.