Lim формулы: Формулы вычисления пределов

Свойства пределов

5.1Пределы и ограниченность

5.1.1Сходящаяся последовательность ограничена

Теорема 1. Пусть последовательность {an} сходится (то есть имеет предел). Тогда она ограничена.

Доказательство. Обозначим этот предел за A. Сформулируем все утверждения в кванторах.

У нас есть. limn→∞an=A, в кванторах записывается так:

∀ε>0 ∃N=N(ε) ∀n>N:|an−A|<ε.(5.1)

∀ε>0 ∃N=N(ε) ∀n>N:|an−A|<ε.(5.1)

Мы хотим получить. Последовательность {an} ограничена, то есть

∃C ∀n∈N:|an|≤C.(5.2)

Итак, мы хотим из (5.1) прийти к (5.2).

Начнём как обычно с картинки.

Рис. 5.1: Ограниченность последовательности, имеющей предел.

Хвост последовательности. На картинке видно, что кусок последовательности, начинающийся с номера n=N(ε)+1 («хвост»), явно ограниченный: все элементы живут в коридоре вокруг числа A и не могут от него далеко уходить. Из рисунка получается, что все эти элементы ограничены по модулю числом A+ε (верхняя граница коридора), но это потому, что мы его так нарисовали — если бы A было меньше нуля, картинка оказалась симметричной (относительно горизонтальной оси) и ограничение проходило бы по нижней границе коридора. Чтобы не возиться с разбором разных случаев, мы будем пользоваться свойствами модулей. Однако, прежде, чем мы перейдём к аккуратному построению, нужно решить важный вопрос. Дело в том, что у нас сейчас нет никакого ε. Нам сказано (в (5.1)), что N найдётся для любого ε>0, то есть ε мы можем задавать сами. Но как?

На самом деле, здесь можно выбрать любое значение ε>0. Например, положим ε=1. Пусть N=N(1) — теперь это какое-то зафиксированное число. Тогда для всех n>N,

|an−A|<1.

Итак, мы имеем оценку для |an−A| для хвоста последовательности. А хотим, как следует из (5.2), оценку для |an|. Как её получить? Воспользуемся неравенством треугольника!

Величина |an| — это расстояние от an до нуля.

Это расстояние не больше, чем сумма расстояний от an до A и от A до 0:

|an|=|an−0|≤|an−A|+|A−0|=|an−A|+|A|.

|an|=|an−0|≤|an−A|+|A−0|==|an−A|+|A|.

Но мы знаем, что для n>N, |an−A|<1. Следовательно, для тех же n,

|an|<|A|+1.(5.3)

Итак, для хвоста последовательности мы получили искомую оценку. Однако, это ещё не конец доказательства. Вдруг хвост ограниченный, а «голова» (элементы до N включительно) нет?

Начало последовательности. На самом деле, этого не может быть. Дело в том, что элементов от a1 до aN всего конечное число (их ровно N штук). А любое конечное множество обязательно ограниченно, потому что в нём есть максимальный элемент — такой элемент, который не меньше всех остальных. (Аккуратное доказательство этого утверждения — хорошее упражнение. Подсказка: можно сделать индукцию по числу элементов и воспользоваться тем фактом, что среди двух чисел всегда одно не меньше другого.

)

Сведём всё воедино. Итак, хвост последовательности можно ограничить числом |A|+1, а начало — максимальным из модулей чисел a1, a2, …, aN. Положим:

C:=max{|a1|,|a2|,…,|aN|,|A|+1}

По построению, C искомое. Действительно, для всех натуральных n, либо n≤N, и тогда |an|≤C по определению максимума, либо n>N, и тогда |an|<|A|+1≤C по (5.3).∎

5.1.2Бесконечные пределы

Итак, мы выяснили, что все сходящиеся последовательности ограничены. Однако, оказывается полезным выделить среди неограниченных последовательностей такие, чьё поведение похоже на поведение последовательностей, которые куда-то стремятся — только не к какому-то числу, а «к бесконечности». Аккуратный смысл этого выражения даётся следующими определениями.

Определение 1. Последовательность {an} стремится к бесконечности, если для всякого числа C∈R найдётся такое натуральное N=N(C), что для всех n>N выполняется неравенство |an|>C. В кванторах:

∀C∈R ∃N=N(C) ∀n>N:|an|>C.

Пишут:

limn→∞an=∞

или

an→∞ при n→∞.

Рис. 5.2: Последовательность стремится к бесконечности.

Определение 2. Последовательность {an} стремится к плюс бесконечности, если для всякого числа C∈R найдётся такое натуральное N=N(C), что для всех n>N выполняется неравенство an>C. В кванторах:

∀C∈R ∃N=N(C) ∀n>N:an>C.

Пишут:

limn→∞an=+∞

или

an→+∞ при n→∞.

Определение 3. Последовательность {an} стремится к минус бесконечности, если для всякого числа C∈R найдётся такое натуральное N=N(C), что для всех n>N выполняется неравенство an<C. В кванторах:

∀C∈R ∃N=N(C) ∀n>N:an<C.

Пишут:

limn→∞an=−∞

или

an→−∞ при n→∞.

Упражнение 1. Докажите следующие утверждения, используя приведенные выше определения.

1. Последовательность {an}, an=n, стремится к бесконечности, а также к плюс бесконечности.
2. Последовательность {(−1)nn} стремится к бесконечности, но ни к плюс бесконечности, ни к минус бесконечности не стремится.
3. Последовательность {n+(−1)nn} не стремится ни к какой бесконечности, хоть и является неограниченной.

5.2Арифметика пределов

Пусть есть две последовательности, {an} и {bn}. Над ними можно проводить арифметические операции: складывать, вычитать, умножать, делить. Операции над последовательностями проводятся поэлементно. Например, пусть последовательность {cn} является суммой последовательностей {an} и {bn}. Можно записать:

{cn}={an}+{bn},

что будет означать

∀n∈N:cn=an+bn.

Серия утверждений, которые мы докажем в этом разделе, говорит о том, как операция перехода к пределу взаимодействует с арифметическими операциями.

5.2.1Предел суммы

Теорема 2. Пусть даны две последовательности, {an} и {bn} и существуют пределы limn→∞an=A,limn→∞bn=B.(5.4)(5.5) Тогда предел последовательности {an+bn} тоже существует и равен A+B:

limn→∞(an+bn)=A+B.

Попросту говоря, «предел суммы равен сумме пределов».

Заметим, что A и B здесь — обязательно обычные вещественные числа, поскольку требуется, чтобы пределы существовали (см. замечание 2).

Доказательство. Перепишем формально, что нам дано, и что требуется доказать.

Нам дано.

∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A|<ε1.∀ε2>0 ∃N2=N2(ε2) ∀n>N2:|bn−B|<ε2.(5.6)(5.7)

∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A|<ε1.∀ε2>0 ∃N2=N2(ε2) ∀n>N2:|bn−B|<ε2.(5.6)(5.7)

Мы хотим доказать.

∀ε>0 ∃N=N(ε) ∀n>N:|(an+bn)−(A+B)|<ε.(5.8)

∀ε>0 ∃N=N(ε) ∀n>N:|(an+bn)−(A+B)|<ε.(5.8)

Утверждения (5. 6) и (5.7) можно понимать так: мы можем добиться того, чтобы an был близок к A, а bn был близок к B, накладывая подходящие условия на n. Утверждение (5.8), которое мы хотим доказать, звучит так: мы хотим научиться накладывать такие условия на n, чтобы сделать (an+bn) близким к (A+B). Выглядит логично: если an близко к A, а bn близко к B, то логично ожидать, что (an+bn) окажется близко к (A+B). Осталось доказать!

Начнём с преобразования левой части неравенства в конце (5.8):

|(an+bn)−(A+B)|=|(an−A)+(bn−B)|.

|(an+bn)−(A+B)|==|(an−A)+(bn−B)|.

Это тождественное преобразование (раскрыли скобки и перегруппировали слагаемые), но оно позволяет выделить в формуле те разности, которые мы умеем оценивать: (an−A) и (bn−B). Вернее, мы умеем оценивать их модули, поэтому нам понадобится одно из свойств модулей: модуль суммы не превосходит суммы модулей:

|(an−A)+(bn−B)|≤|an−A|+|bn−B|.(5.9)

|(an−A)+(bn−B)|≤≤|an−A|+|bn−B|.

(5.9)

Теперь заметим, что первое слагаемое мы можем сделать меньшим, чем ε1, а второе — меньшим, чем ε2. Но как выбрать ε1 и ε2? Мы хотим в конечном итоге прийти к неравенству, в правой части которого будет ε. Значит, можно выбрать ε1 и ε2 так, чтобы их сумма равнялась ε. Положим:

ε1=ε2,ε2=ε2.

Теперь мы можем подставить эти ε1 и ε2 в утверждения (5.6) и (5.7). Каждое из них выдаст нам в ответ своё N (вернее, N1 и N2) — номера членов, после которых выполняется соответствующая оценка для |an−A| и |bn−B|. Мы хотим, чтобы они выполнялись обе. Как обычно, это означает, что из получившихся значений нужно выбрать максимальное.

Итак, мы готовы сформулировать железобетонное доказательство. Для любого ε>0 положим ε1=ε/2 и ε2=ε/2. Из (5.6) и (5.7) получим такие N1=N1(ε1)=N1(ε/2) и N2=N2(ε2)=N2(ε/2), что для всех n>N1

|an−A|<ε1=ε2,(5.10)

и для всех n>N2

|bn−B|<ε2=ε2. (5.11)

Положим теперь:

N(ε):=max(N1(ε2),N2(ε2)).

Тогда для всех n>N(ε), будет выполнятья n>N1 и n>N2, и значит будут выполняться обе оценки (5.10) и (5.11).

Значит, согласно (5.9), для всех таких n, будет также выполняться оценка

|(an+bn)−(A+B)|≤|An−A|+|Bn−B|<ε2+ε2=ε.

|(an+bn)−(A+B)|≤≤|An−A|+|Bn−B|<<ε2+ε2=ε.

Таким образом, (5.8) доказано: мы научились по каждому положительному ε строить такое N, что для всех n>N выполнено неравенство |(an+bn)−(A+B)|<ε.

Ура!∎

5.2.2Упрощающая лемма

Давайте посмотрим ещё раз на доказательство теоремы 2. Нам пришлось довольно хитрым образом выбирать ε1 и ε2 по ε, чтобы в итоге получилось нужное неравенство. Этот момент выглядит немножко неестественным. Что было бы, если бы мы просто положили ε1=ε и ε2=ε? Тогда в конечном итоге было бы доказано такое утверждение:

∀ε>0 ∃N=N(ε) ∀n>N:|an−A|<2ε.

Это утверждение не является определением предела. Тем не менее, понятно, что оно эквивалентно определению предела: выбирать произвольное положительное значение ε и выбирать произвольное положительное значение 2ε — это одно и то же!

Следующая лемма, которой мы будем в дальнейшем пользоваться, формализует это соображение.

Лемма 1. Пусть нашлась такая константа C, что для всякого ε1>0 найдётся такое N1=N1(ε1) что для всякого n>N1 выполняется неравенство |an−A|<Cε1. Тогда limn→∞an=A.

Формально: пусть

∃C ∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A|<Cε1.

∃C ∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A|<Cε1.

тогда

limn→∞an=A.(5.12)

Иными словами, если при доказательстве утверждения (5.12) получилось доказать «испорченное» определение предела, где в правой части последнего неравенства вместо ε стоит 10ε или 15ε или какое-нибудь (M+1)2ε — ничего страшного, это всё равно победа. Главное, чтобы константа, стоящая перед ε, не зависела от n.

Доказательство. Во-первых, заметим, что C обязательно больше нуля. Действительно, модуль всегда неотрицателен, поэтому неравенство |an−A|<Cε1 может выполняться лишь при условии, что в правой части стоит положительное число, а ε1>0, значит C>0.

Перепишем условие (5.12) формально. Оно выглядит так:

∀ε>0 ∃N=N(ε) ∀n>N:|an−A|<ε.

Чтобы по ε найти N, возьмём ε1=εC (имеем право так написать, потому что C>0, и значит деление допустимо и не поменяет знак) и положим N=N1(ε1)=N1(ε/C). Тогда для всех n>N выполняется неравенство:

|an−A|<Cε1=CεC=ε.

Что и требовалось получить. Лемма доказана.∎

Теперь при доказательстве теорем, аналогичных теореме 2, мы не будем подбирать хитрым образом вспомогательные ε, а вместо этого просто будем считать ε1=ε2=ε и дальше воспользуемся только что доказанной леммой. Начнём с теоремы о пределе произведения.

5.2.3Предел произведения

Теорема 3. Пусть даны две последовательности, {an} и {bn} и существуют пределы limn→∞an=A,limn→∞bn=B.(5.13)(5.14) Тогда предел последовательности {anbn} тоже существует и равен AB:

limn→∞anbn=AB.

Попросту говоря, «предел произведения равен произведению пределов».

Доказательство. Как обычно, запишем, что нам известно, и что нужно доказать.

Нам дано. Равенства (5.13) и (5.14) записываются в виде:

∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A|<ε1.∀ε2>0 ∃N2=N2(ε2) ∀n>N2:|bn−B|<ε2.(5.15)(5.16)

∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A|<ε1.∀ε2>0 ∃N2=N2(ε2) ∀n>N2:|bn−B|<ε2.(5.15)(5.16)

Мы хотим доказать. Равенство (5.17):

∀ε>0 ∃N=N(ε) ∀n>N:|anbn−AB|<ε.(5.17)

∀ε>0 ∃N=N(ε) ∀n>N:|anbn−AB|<ε.(5.17)

Преобразуем левую часть последнего неравенства в (5.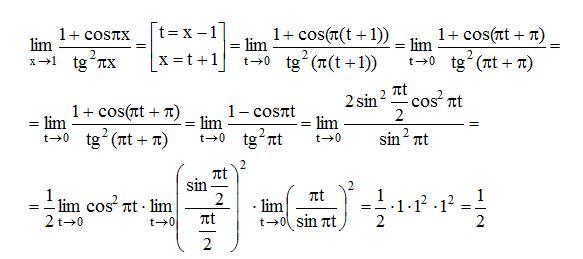 17). Для этого воспользуемся картинкой (см. рис. 5.5).

Геометрический смысл произведения — площадь прямоугольника с заданными сторонами. Построим прямоугольник со сторонами an и bn. Давайте для определенности считать, что A<an и B<bn (это предположение полезно для иллюстрации, но нас оно не будет ограничивать: простое алгебраическое доказательство нужной нам формулы его не требует). Тогда прямоугольник со сторонами A и B будет меньше первого прямоугольника и его можно разместить внутри, прижав к левому нижнему углу.

Рис. 5.5: Иллюстрация к формуле (5.18).

Выражение (anbn−AB) — разность площадей двух прямоугольников, которая выглядит как уголок. Можно разбить этот уголок на два прямоугольника, один со сторонами (an−A) и B, а другой со сторонами an и (bn−B). Имеем:

|anbn−AB|=|(an−A)B+an(bn−B)|.(5.18)

|anbn−AB|==|(an−A)B+an(bn−B)|.(5.18)

Раскрыв скобки и приведя подобные слагаемые, легко проверить, что это алгебраическое тождество. (Как правило переход слева направо в этом тождестве делается с помощью приёма «добавим и вычтем anB», что выглядит как фокус — нарисовав картинку мы раскрыли секрет этого фокуса.)

Воспользуемся теперь свойствами модулей: модуль суммы не превосходит суммы модулей, модуль произведения равен произведению модулей. Получаем такую оценку:

|(an−A)B+an(bn−B)|≤|an−A|⋅|B|+|an|⋅|bn−B|(5.19)

|(an−A)B+an(bn−B)|≤≤|an−A|⋅|B|++|an|⋅|bn−B|(5.19)

Заметим, что сомножители |an−A| и |bn−B| мы умеем делать маленькими благодаря известным нам пределам. А именно, положим ε1=ε2=ε и пусть N=max(N1(ε),N2(ε)). Тогда для всех n>N:

|an−A|<ε,|bn−B|<ε.

Разберемся теперь с остальными сомножителями (см. рис. 5.6).

Во-первых, |B|. С ним ничего делать не надо: это просто число, которое не зависит от n.

Далее, |an|. С этой штукой не так просто: она от n зависит. Однако, мы помним, что последовательность, имеющая предел, ограничена.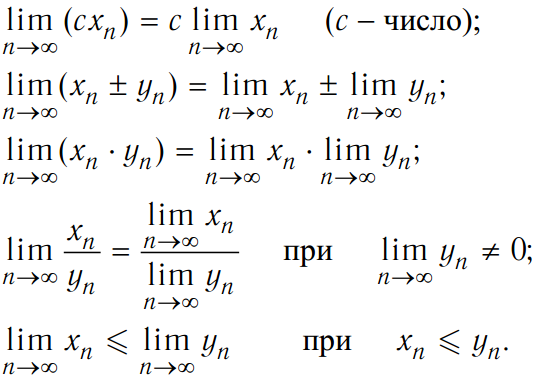 А последовательность {an} имеет предел по условию. Значит, найдётся такое C1, что для всех n, |an|<C1.

Рис. 5.6: Иллюстрация к формуле (5.20).

Все сомножители неотрицательны, и значит можно оценить каждый из сомножителей, оценить их произведение, а потом оценить сумму. Имеем:

|an−A|⋅|B|+|an|⋅|bn−B|<|B|ε+C1ε=(|B|+C1)ε.(5.20)

|an−A|⋅|B|++|an|⋅|bn−B|<<|B|ε+C1ε=(|B|+C1)ε.(5.20)

Соединяя (5.18), (5.19) и (5.20) в одну длинную цепочку неравенств, получаем неавенство, верное для всех n>N:

|anbn−AB|<(|B|+C1)ε.

Положим теперь C=|B|+C1 и по лемме 1 искомое утверждение доказано.∎

5.3Заключение

Мы продолжаем строить теорию пределов и в этой лекции определили новое понятие — бесконечные пределы, причём аж трёх видов (к счастью, очень похожих друг на друга). Мы также доказали ряд важных общих свойств конечных пределов. Во-первых, сходящаяся (к конечному числу) последовательность ограничена. Во-вторых, предел суммы равен сумме пределов, а предел произведения — произведению пределов (но только если все эти пределы существуют, то есть, опять же, конечны). Наконец, мы доказали очень полезную лемму, которой будем пользоваться в дальнейшем. В следующей лекции мы разберемся с пределом частного — с ним будет всё похитрее. Не переключайтесь!

---

← Предыдущая глава Следующая глава →

Свойства пределов функции, основные свойства пределов

Содержание:

• Предел функции
• Свойства пределов функции

Предел функции

Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x₀, если для всех значений x, достаточно близких к x₀, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Предел функции обозначается как

$$f(x) \rightarrow L \quad$ при $\quad x \rightarrow a$$

или через символ предела функции:

$$\lim _{x \rightarrow 0} f(x)=L$$

Если при прочтении данного материала у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме, также на форуме Вам помогут решить задачи по математике, геометрии, химии, теории вероятности и многим другим предметам.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

$$\lim _{x \rightarrow a} C=C$$

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

$$\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)$$

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

$$\lim _{x \rightarrow a}\left[f_{1}(x)+\ldots+f_{n}(x)\right]=\lim _{x \rightarrow a} f_{1}(x)+\ldots+\lim _{x \rightarrow 0} f_{n}(x)$$

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

$$\lim _{x \rightarrow a} k f(x)=k \lim _{x \rightarrow a} f(x)$$

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

$$\lim _{x \rightarrow 0}[f(x) g(x)]=\lim _{x \rightarrow 0} f(x) \cdot \lim _{x \rightarrow 2} g(x)$$

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

$$\lim _{x \rightarrow a}\left[f_{1}(x) f_{2}(x) \ldots f_{n}(x)\right]=\lim _{x \rightarrow a} f_{1}(x) \cdot \lim _{x \rightarrow 0} f_{2}(x) \cdot \ldots \cdot \lim _{x \rightarrow 2} f_{n}(x)$$

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

$$\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow \infty} f(x)}{\lim _{x \rightarrow 0} g(x)}, \quad$ ecл $\lim _{x \rightarrow a} g(x) \neq 0$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Формула предела — Что такое формула предела? Примеры

Формула предела используется для вычисления производной функции. Предел — это значение функции, приближающееся к указанному значению на входе. Пределы используются как способ приближения, используемого в расчетах, как можно ближе к фактическому значению величины. Давайте подробно разберем формулу предела в следующем разделе.

Что такое предельная формула?

Формула предела представляет поведение функции в определенной точке, и формула анализирует эту функцию. Предел описывает поведение некоторой величины, которая зависит от независимой переменной, когда эта независимая переменная приближается или приближается к определенному значению.

Предельная формула

Пусть y = f(x) как функция x. Если в точке х = а функция f(x) принимает неопределенный вид, то можно рассматривать значения функции, очень близкой к а. Если эти значения стремятся к некоторому определенному уникальному числу, когда x стремится к a, то полученное уникальное число называется пределом f(x) при x = a. Формулу можно записать так:

\(\mathop {\lim }\limits_{x \to a} f(x) = A \)

, где

• f(x) — функция
• x — переменная приближающаяся к значению a

Читается как предел функции от x, равного A, когда x приближается к a.

Формулы пределов

Формулы, упомянутые на изображении ниже, представляют собой несколько формул пределов.

Хотите найти сложные математические решения за считанные секунды? 92 + 10x+ 15. \) равно 99

Часто задаваемые вопросы о формуле лимита 

Что подразумевается под формулой лимита?

Формула предела используется для вычисления производной функции. Предел — это значение функции, приближающееся к указанному значению на входе. Пределы используются как способ приближения, используемого в расчетах, как можно ближе к фактическому значению величины. Формула \(\mathop {\lim }\limits_{x \to a} f(x) = A \)

Какова формула для нахождения предела?

Пусть y = f(x) как функция x. Если в точке х = а функция f(x) принимает неопределенный вид, то можно рассматривать значения функции, очень близкой к а. Если эти значения стремятся к некоторому определенному уникальному числу, когда x стремится к a, то полученное уникальное число называется пределом f(x) при x = a. Формулу можно записать так:

\(\mathop {\lim }\limits_{x \to a} f(x) = A \)

где

• f(x) — функция
• x — переменная приближающаяся к значению a

Читается как предел функции от x, равного A, когда x приближается к a.

Как называются свойства предельной формулы?

Свойства формулы предела: 

• Обозначение предела
• Правило суммы
• Правило расширенной суммы
• Правило постоянной функции
• Постоянное множественное правило
• Правило продукта
• Расширенное правило продукта
92 + 12. \) равно 22.

Формула предела — GeeksforGeeks

Если функция f(x) дает неопределенное значение в точке  , то для определения значений функции используется предел, не точный, а приближающийся к значению в точку. Если бы мы рассмотрели функцию f(x), которая не определена в точке. Итак, чтобы найти значение функции в этой точке. мы не можем найти его точное значение, но мы можем найти его ближайшее значение функции или приближающееся значение функции. Ближайшее и точное значение имеет очень маленькую разницу между ними, т. е. если точная точка равна 2, то приближающееся значение равно 1,9.999999… скоро.

Предельные формулы

Тригонометрические пределы: Чтобы вычислить тригонометрические пределы, мы должны привести члены функции к более простым терминам или к терминам sinθ и cosθ.

• lim _{x ⇢ 0}   sinx/x = lim _{x ⇢ 0} x/sinx = 1
• lim _{x ⇢ 0 lim ⇢} tanx9/x = lim 161 х/tanx =1

Как мы рассмотрели наш первый,

lim _{x ⇢ 0} sinx/x =1      

Используя L-Hospital

lim _{x ⇢ 0} cosx/1

lim _{x ⇢ 0} cos(0)/1 = 1/1 =1

используйте правило l-госпиталя.

Неопределенная форма

0/0, ∞/∞, ∞-∞, ∞/0, 0 ^∞ , ∞ ^{0 6} , 10 0 901 ^∞

Л- больница Правило

Если мы получаем неопределенный вид, то мы дифференцируем числитель и знаменатель отдельно, пока не получим конечное значение. Помните, что мы будем дифференцировать числитель и знаменатель одинаковое количество раз. Аналогично для всех тригонометрических функций

• lim _{х ⇢ 0} sin ^-1 х/х = lim _{х ⇢ 0} х/sin ^-1 х = 1

⇢

0

lim 1 грех ^-1 х /x =1

lim _{x ⇢ 0} 1/√1+x ²   [Использование L-Hospital]

= 1/√(1 + (0) ² ) 2 9018 То же самое здесь все тригонометрические функции0020

lim _{x ⇢ a} sin(x – a) / (x – a) 

=1

lim _{x ⇢ a} cos(x – a)/1 

⇢ a lim

5 = 8 cos(a – a) = cos(0) =1

• lim _x⇢∞ sinx/x = 0
• lim _x⇢∞ cosx/x = 0
⇢ lim 9015
• 161 sin(1/x) / (1/x) = 0

lim _{x ⇢ ∞} sin(1/x)/(1/x) = 0

Пусть 1/x = h

Итак, ограничивает изменения до 0

Поскольку 1\∞ = 0

lim _{ч ⇢ 0} sh/ч

Как мы видели ранее, если lim _{x ⇢ 0} sinx/x = 1

Итак, lim _{ч ⇢ 0} sh/h = 3 900 900 0013 Экспоненциальный пределы

• lim _{x ⇢ 0} e ^x – 1 /x = 1
• lim _{x ⇢ 0} а ^{x 9016 log e} – 91 /x8 = log e 020
• лим _{х ⇢ 0} e ^λx – 1 /x = λ

Здесь мы получаем желаемый результат, используя правило L-больницы.

Альтернативный метод: Использование расширения

e ^x = 1 + X + X ² /2! + Х ³ /3! + X ⁴ /4!+ … ∞

lim _{x ⇢ 0}  e ^x – 1 /x = 1

lim _{x ⇢ 0} (1 + X + X 229015! —) -1 /х

lim _{х ⇢ 0} (Х + Х ² /2! + —)/х

lim _{х ⇢ 0} 1 + Х + Х ² /2!+—

lim _{х ⇢ 0} 1 + 0 + 0 + 0 + 0— = 1

Логарифмические пределы

• lim _{x ⇢ 0} log(1 + x) /x = 1 19 лим _{х ⇢ 0} журнал _e (1 – x) /x  = -1
• lim _{x ⇢ 0} log _a (1 + x) /x = log _a e

Просто доказано с помощью L-hospital и расширения метод.

Некоторые важные дополнения

12. 0 (здесь гиперболическая функция sinx является 020

Примеры задач

Вопрос 1: Решить, lim _{x ⇢0}  (x – sinx ) /(1 – cosx).

Решение:

Использование L-больницы,

lim _{x ⇢ 0} (1 – cosx) / (sinx)

lim

x

sinx / cosx = sin(0) / cos(0) = 0/1 = 0 

 

 

 

Решение:

Использование больницы L 0  2(e ⁰ ) / cos4 (0) = 2/1= 2

Вопрос 3: Решить, lim _{x ⇢ 0} (1 – cosx) / x ²

Решение:

Использование больницы L ⇢ ∞

Решение:

lim _{х ⇢ ∞} (1 + )

1 + lim _{х ⇢ ∞}

900 03

Итак, 1/х = 0

1 + 0 = 0                                                                                                                      

Вопрос 5: Решить, lim _{x ⇢ π/2} (tanx) ^cosx 

Решение:

⇢ ⇢ lim x5 x5 x5  (tanx) ^cosx

Взятие log _e с обеих сторон,

 log _e Y = lim _{x ⇢ π/2}  log _e (tanx) ^{cosx 5 log e}

3 9 00003 9 161 Y = lim _{х ⇢ π/ 2}  cosx log _e (tanx)

log _e y = lim _{x ⇢ π/2} loge(tanx)/secx

Использование l-hospital,

log _e y = lim _{x ⇢ π/2} cosx /sin ^{2 0 2} x0 0 9 показатель степени с обеих сторон,

Y = lim _{x ⇢ π/2} e ⁰  

Y = lim _{x ⇢ π/2}  (tanx) ^cosx

= 0 3 9008 013 Вопрос 6: лим _{x ⇢ 0}  

Решение:

limx⇢0 \frac{1+\frac{x}{1!} + \frac{x ² }{2!} + \frac{x ³ }{3!} – ( 1+ x+ \frac{x ² }{2!} ) }{x ³ }

limx⇢ 0 \ frac {\ frac {x ³ } {3!}} {x ³ } = 1/3! =1/6

Вопрос 7: Решите, lim _{a ⇢ 0}   

Решение:

Используя l-больницу (дифференцирующий числитель) 0.

No related posts.