Упражнения
Написать в комплексной форме уравнение кривой :
.
Решение. 1-й способ. Согласно (2.1) имеем параметрическое уравнение кривой .
2-й способ. Легко видеть, что данная кривая – парабола . Перейдем в этом уравнении к комплексному переменному, воспользовавшись
формулами (2.2), , откуда получаем
.
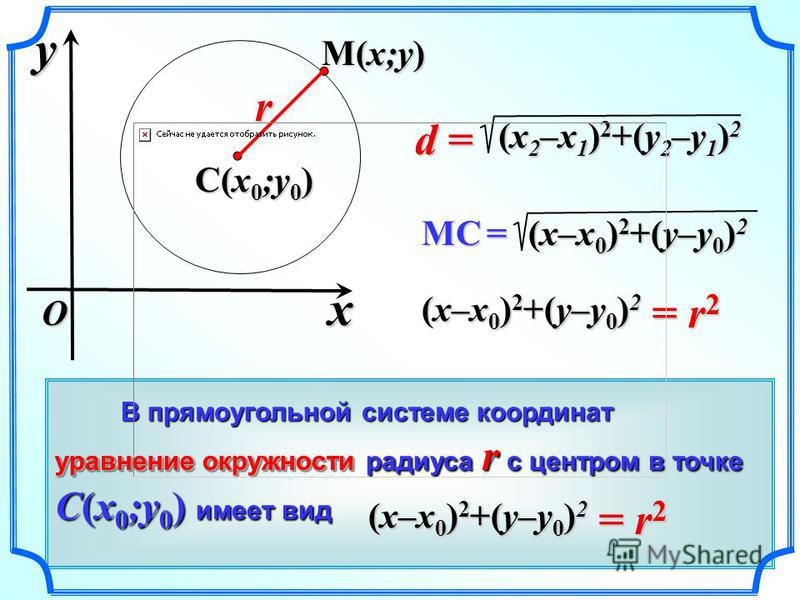
Написать уравнение окружности в комплексной форме.
Решение. 1-й способ. Рассмотрим окружность как множество точек , равноудаленных на расстояниеот центра. Тогда имеем.
2-й способ. Как известно, параметрические уравнения окружности радиуса с центром в точкеимеют вид
где .
Следовательно, . Если воспользоваться показательной формой комплексного числа, то полученное уравнение можно записать в виде.
Написать уравнение эллипса с фокусами в точках и, большая ось которого равна.
Рис.2.1 | Решение. По определению эллипса . Здесьирасстояния произ-вольной точкиэллипса до фокусовисоответственно (рис.2.1). Следовательно, уравнение эллипса в комплексной форме имеет вид. |
Расстояние между фокусами: , а малая полуось по известнымиопределяется из формулы.
Выяснить геометрический смысл уравнения .
Рис.2.2 | Решение. 1-й способ геометрический. В данном случае множество точек, равноудаленных от точеки. Очевидно, это есть прямая, перпендикулярная отрезкуи проходящая через его середину (рис.2.2). |
2-й способ аналитический. Пусть , тогда
.
Поскольку левые части последних соотношений равны, то равны и их правые части, т.е. . После упрощения получаем уравнение прямой линии.
Какая кривая определяется уравнением ?
Решение. Из области определения функции исключается точка , пусть. Тогда. Следовательно,. По условиюили, откуда следует, что данное условие определяет окружность,.
Определить, какое множество точек удовлетворяет условию .
Рис.2.3 | Решение. Так как по определению , то данное неравенство может быть записано в виде. Следовательно, искомое множество точек – полоса между прямымии, включая эти прямые (рис. 2.3). |
26. Построить на комплексной плоскости области, заданные условиями:
а) ; б),.
Решение. а) Искомое множество точек удовлетворяет
двум неравенствам:
и.
Первое условие определяет точку эллипса
с фокусамии,
для которого,,(уравнение эллипса в действительных
переменных:).
Второе уравнение – внутренность эллипса
с фокусами в тех же точках с полуосямии(уравнение эллипса в действительных
переменных).
Рис.2.4 | Искомое множество точек – часть плоскости, заключенная между двумя эллипсами (рис. 2.4), включая сами эллипсы. |
б) Легко видеть, что множество точек, удовлетворяющих условию , есть внутренность кольца, ограниченного окружностямиис центрами в начале координат и радиусами 1 и 2. Система неравенствопределяет множество точек, составляющих угол между лучамии, причем точки первого луча принадлежат области, а второго – нет.
Пересечение указанных множеств определяет искомую область , которая изображена на рис. 2.5.
27. Какое множество точек комплексной плоскости определяется условием ?
Решение.
Пусть
.
Тогдаи.
Следовательно,.
По условиюили.
Полученное неравенство определяет
множество точек, изображенных на рис.
2.6.
Рис.2.5 | Рис.2.6 |
Курс высшей математики, Т.1
Курс высшей математики, Т.1
ОглавлениеПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ 1. Величина и ее измерение. 2. Число. 3. Величины постоянные и переменные. 4. Промежуток. 5. Понятие о функции. 6. Аналитический способ задания функциональной зависимости. 7. Неявные функции. 8. Табличный способ. 9. Графический способ изображения чисел. 10. Координаты. 11. График и уравнение кривой. 12. Линейная функция. 13. Приращение. Основное свойство линейной функции. 14. График равномерного движения. 15. Эмпирические формулы. 16. Парабола второй степени. 17. Парабола третьей степени. 18. Закон обратной пропорциональности. 19. Степенная функция. 20. Обратные функции. 21. Многозначность функции. 22. Показательная и логарифмическая функции. 23. Тригонометрические функции.  24. Обратные тригонометрические, или круговые, функции. § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 25. Упорядоченное переменное. 26. Величины бесконечно малые. 27. Предел переменной величины. 28. Основные теоремы. 30. Монотонные переменные. 31. Признак Коши существования предела. 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью. 33. Примеры. 34. Непрерывность функции. 35. Свойства непрерывных функций. 36. Сравнение бесконечно малых и бесконечно больших величин. 37. Примеры. 38. Число е. 39. Недоказанные предложения. 40. Вещественные числа. 41. Действия над вещественными числами. 42. Точные границы числовых множеств. Признаки существования предела. 43. Свойства непрерывных функций. 44. Непрерывность элементарных функций. ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ 45. Понятие о производной. 46. Геометрическое значение производной.  47. Производные простейших функций. 48. Производные сложных и обратных функций. 49. Таблица производных и примеры. 50. Понятие о дифференциале. 51. Некоторые дифференциальные уравнения. 52. Оценка погрешностей. § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 53. Производные высших порядков. 54. Механическое значение второй производной. 55. Дифференциалы высших порядков. 56. Разности функций. § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ 57. Признаки возрастания и убывания функций. 58. Максимумы и минимумы функций. 59. Построение графиков. 60. Наибольшее и наименьшее значения функций. 61. Теорема Ферма. 62. Теорема Ролля. 63. Формула Лагранжа. 64. Формула Коши. 65. Раскрытие неопределенностей. 66. Различные виды неопределенностей. § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 68. Частные производные и полный дифференциал функции двух независимых переменных. 69. Производные сложных и неявных функций.  § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ 71. Выпуклость, вогнутость и кривизна. 72. Асимптоты. 73. Построение графиков. 74. Параметрическое задание кривой. 75. Уравнение Ван-дер-Ваальса. 76. Особые точки кривых. 77. Элементы кривой. 78. Цепная линия. 79. Циклоида. 80. Эпициклоиды и гипоциклоиды. 81. Развертка круга. 82. Кривые в полярных координатах. 83. Спирали. 85. Овалы Кассини и лемниската. ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ 86. Понятие о неопределенном интеграле. 87. Определенный интеграл как предел суммы. 88. Связь определенного и неопределенного интегралов. 89. Свойства неопределенного интеграла. 90. Таблица простейших интегралов. 91. Правило интегрирования по частям. 92. Правило замены переменных. Примеры. 93. Примеры дифференциальных уравнений первого порядка. § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 94. Основные свойства определенного интеграла.  95. Теорема о среднем. 96. Существование первообразной функции. 97. Разрыв подынтегральной функции. 98. Бесконечные пределы. 99. Замена переменной под знаком определенного интеграла. 100. Интегрирование по частям. § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 101. Вычисление площадей. 102. Площадь сектора. 103. Длина дуги. 104. Вычисление объемов тел по их поперечным сечениям. 105. Объем тела вращения. 106. Поверхность тела вращения. 107. Определение центров тяжести. Теоремы Гульдина. 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций. 109. Формула касательных и формула Понселе. 110. Формула Симпсона. 111. Вычисление определенного интеграла с переменным верхним пределом. 112. Графические способы. 113. Площади быстро колеблющихся кривых. 115. Разбиение промежутка на части и образование различных сумм. 116.  Интегрируемые функции.117. Свойства интегрируемых функций. ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 118. Понятие о бесконечном ряде. 119. Основные свойства бесконечных рядов. 120. Ряды с положительными членами. Признаки сходимости. 121. Признаки Коши и Даламбера. 122. Интегральный признак сходимости Коши. 123. Знакопеременные ряды. 124. Абсолютно сходящиеся ряды. 125. Общий признак сходимости. § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 126. Формула Тейлора. 127. Различные виды формулы Тейлора. 128. Ряды Тейлора и Маклорена. 129. Разложение exp(x). 130. Разложение sin x и cos x. 131. Бином Ньютона. 132. Разложение log(1+x). 133. Разложение arctg x. 134. Приближенные формулы. 135. Максимумы, минимумы и точки перегиба. 136. Раскрытие неопределенностей. § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 137. Свойства абсолютно сходящихся рядов. 138. Умножение абсолютно сходящихся рядов.  139. Признак Куммера. 140. Признак Гаусса. 141. Гипергеометрический ряд. 142. Двойные ряды. 143. Ряды с переменными членами. Равномерно сходящиеся ряды. 144. Равномерно сходящиеся последовательности функций. 145. Свойства равномерно сходящихся последовательностей. 146. Свойства равномерно сходящихся рядов. 147. Признаки равномерной сходимости. 148. Степенные ряды. Радиус сходимости. 149. Вторая теорема Абеля. 150. Дифференцирование и интегрирование степенного ряда. ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 152. О предельном переходе. 153. Частные производные и полный дифференциал первого порядка. 154. Однородные функции. 155. Частные производные высших порядков. 156. Дифференциалы высших порядков. 157. Неявные функции. 158. Пример. 159. Существование неявных функций. 160. Кривые в пространстве и поверхности. § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 161.  Распространение формулы Тейлора на случай функции от нескольких независимых переменных.162. Необходимые условия максимума и минимума функции. 163. Исследование максимума и минимума функции двух независимых переменных. 164. Примеры. 165. Дополнительные замечания о нахождении максимумов и минимумов функции. 166. Наибольшее и наименьшее значения функции. 167. Относительные максимумы и минимумы. 168. Дополнительные замечания. 169. Примеры. ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 170. Комплексные числа. 171. Сложение и вычитание комплексных чисел. 172. Умножение комплексных чисел. 173. Деление комплексных чисел. 174. Возвышение в степень. 175. Извлечение корня. 176. Показательная функция. 177. Тригонометрические и гиперболические функции. 178. Цепная линия. 179. Логарифмирование. 180. Синусоидальные величины и векторные диаграммы. 181. Примеры. 182. Кривые в комплексной форме.  183. Представление гармонического колебания в комплексной форме. § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ 185. Разложение многочлена на множители. 186. Кратные корни. 187. Правило Горнера. 188. Общий наибольший делитель. 189. Вещественные многочлены. 190. Зависимость между корнями уравнения и его коэффициентами. 191. Уравнение третьей степени. 192. Решение кубического уравнения в тригонометрической форме. 193. Способ итерации. 194. Способ Ньютона. 195. Способ простого интерполирования. § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ 196. Разложение рациональной дроби на простейшие. 197. Интегрирование рациональной дроби. 198. Интеграл от выражений, содержащих радикалы. 199. Интегралы вида… 200. Интегралы вида… 201. Интегралы вида… |
нахождение уравнения окружности в комплексной плоскости
Задавать вопрос
спросил
Изменено 6 лет назад
Просмотрено 8к раз
$\begingroup$
Итак, меня попросили найти уравнение окружности, проходящей через 1, i и 0
Теперь я знаю, что уравнение окружности в комплексной форме:
$|z — z_0| = r$, где $r$ — радиус.
Итак, на основе этих значений моя идея заключалась в том, чтобы получить радиус и попытаться найти начало моей окружности. Хорошая идея, но реализовать ее не получилось. Было предоставлено решение, и я пытаюсь установить связь между окончательным решением и тем, как получить начало моего круга и радиус. 9{1/2}}$
- комплексный анализ
- комплексные числа
$\endgroup$
2
$\begingroup$
Вы должны решить следующую систему уравнений:
$\left\{ \array{|c-0|=r\\|c-1|=r\\|c-i| =r}\right.$
, где $c$ — центр окружности, а $r$ — радиус.
Предполагая, что $c=x+iy$, после оценки получаем следующую систему: 92}\right.$
и затем:
$\left\{ \array{1-2x=0 \\ 1-2y =0}\right.$
Итак, $(x,y)= (\ frac{1}{2}, \frac{1}{2})$ и $c=\frac{i+1}{2}$
Вернемся к радиусу, возьмем любое из исходных уравнений, например первый:
$|c-0|=r$
И решить его для $r$
$|c|=r$
$r=\frac{\sqrt{2}}{2}$
Тогда уравнение окружности будет таким:
$|z-\frac{1+i}{2}| = \frac{\sqrt{2}}{2} $
$\endgroup$
$\begingroup$
Центр окружности должен иметь вид $z=x+ix$ для некоторого $x\in\mathbb{R}$, поскольку он должен лежать на прямой, проходящей через начало координат и перпендикулярной прямой, проходящей через $i$ и $1$.
2\,$, а также : 92 = (c-i)(\bar c + i) = \bcancel{c \bar c} + i(c — \bar c) +1
\end{случаи}
$$
Следовательно, $c+\bar c=1$ и $c-\bar c = -1 / i = i$, таким образом, $c=\frac{1}{2}\big((c+\bar c)+ (c-\bar c)\big) = \cfrac{1+i}{2}\,$.
Тогда $\,r=|c|=\cfrac{\sqrt{2}}{2}\,$, поэтому уравнение окружности равно $\left|z-\cfrac{1+i}{2} \right|=\cfrac{\sqrt{2}}{2}\,$.
$\endgroup$
Важные понятия и советы для JEE
Прямая линия может быть определена как неизогнутая прямая фигура с нулевой шириной. Его можно представить линейным уравнением, например, $ax+by+c=0$, где $a$ и $b$ — коэффициенты, а $c$ — константа. Существуют различные формы уравнений прямой линии, которые были введены в более ранних классах, такие как форма «точка-наклон», форма «две точки», форма «наклон-пересечение». 9{2}}$. На комплексной плоскости уравнение прямой имеет вид $\left| \левый. з-п \ справа | \право.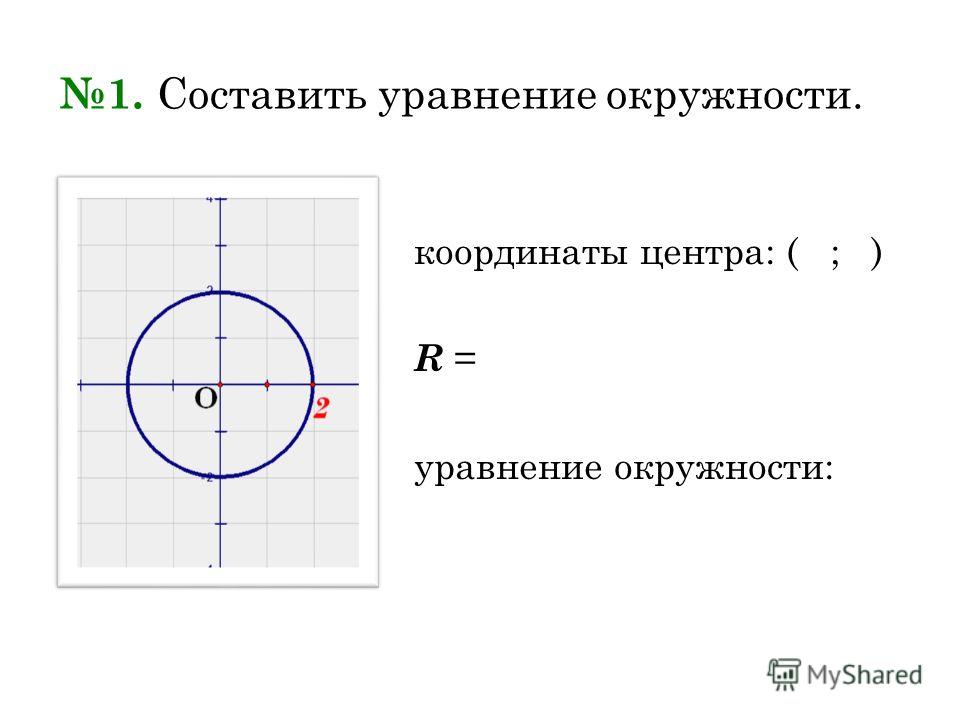
=\лево| \левый. г-д \ справа | \right.$, где p и q — два различных комплексных числа.
Приведенная выше прямая делит пополам отрезок, соединяющий точки p и q. Это геометрический способ уравнения прямой линии.
Формы уравнений прямой линии
Форма точки-наклона. Рассмотрим точку $A\left( {{x}_{1}},\text{ }{{y}_{1 }} \right)$, через которую проходит прямая, и ее наклон равен $m$. Тогда уравнение прямой задается как $y\text{ }-\text{ }{{y}_{1}}=\text{ }m\left( x\text{ }\text{-}{ {x}_{1}} \right)$.
Двухточечная форма. Рассмотрим две фиксированные точки как $A\left( {{x}_{1}},\text{ }{{y}_{1}} \right)$ & $ B\text{ }\left( {{x}_{2}},\text{ }{{y}_{2}} \right)$. Тогда линия, соединяющая эти точки, может быть представлена уравнением $y-{{y}_{1}}=\frac{{{y}_{2}}-{{y}_{1}}}{ {{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right).
$ Форма пересечения наклона- Пусть $ c$ — точка пересечения $y-$ прямой, т. е. прямая проходит через точку (0, c). Если наклон линии равен $m$, то уравнение линии задается как $y\text{ }=\text{ }mx\text{ }+\text{ }c.$
Форма пересечения. Рассмотрим линию L с пересечением по оси x a и пересечением по оси y b; линия будет пересекать ось X в точке $(a,0)$ и ось Y в точке $(0,b)$. Тогда уравнение линии имеет вид:
$ $\dfrac{x}{a}+\dfrac{y}{b}=1$
$xcos\beta+ysin\beta=l$
Уравнение прямой на комплексной плоскости
Комплексное число — это выражение вида $z=x+iy$, где $x$ — действительная часть $z$, а $y$ — мнимая часть. 92 = -1$
$\Rightarrow az+a\bar{z}-bi(z-\bar{z})+2c=0$
$\Rightarrow z(a-bi)+\bar{z }(a+bi)+C=0$
Пусть $a’=a+bi$ и $\bar{a’}=a-bi$
Тогда $\bar{a’}z+\bar{ z}a’+C=0$ , где $a’$ — комплексное число, а $C$ — действительное число …… (1)
Приведенное выше уравнение является общим уравнением прямой на комплексной плоскости.
Наклон прямой линии $\bar{a’}z+\bar{z}a’+C=0$ определяется как $-\dfrac{\text{коэффициент}\bar{z}}{\ text{коэффициент }z}$, т. е. $\dfrac{-a’}{\bar{a’}}$.
Параметрическое уравнение прямой
Пусть ${{z}_{1}}$ и ${{z}_{2}}$ — две точки комплексной плоскости. И z — любая произвольная точка на линии, соединяющей две точки, как показано ниже.
Линия на комплексной плоскости
Если рассматривать комплексные числа как векторы, то $z-{{z}_{1}}$ должно быть в том же направлении, что и $z-{{z}_{2 }}$. Тогда $z-{{z}_{1}}$ можно получить, умножив $z-{{z}_{2}}$ на некоторый скаляр, скажем, $\lambda $, т. е. $z-{{ z}_{1}}=\lambda \left( z-{{z}_{2}} \right),$где $\lambda \epsilon \mathbb{R}$
$\Rightarrow z-\lambda z={{z}_{1}}-\lambda {{z}_{2}}$
$\Rightarrow z=(\frac{1}{1-\ lambda }){{z}_{1}}-(\frac{\lambda}{1-\lambda}){{z}_{2}}$
$\Rightarrow z=t{{z}_ {1}}+(1-t){{z}_{2}}$, где $t=\frac{1}{1-\lambda} \epsilon\mathbb{R}$ …… (2)
Приведенное выше уравнение представляет собой параметрическую форму прямой на комплексной плоскости.
Условие параллельности двух линий
В координатной геометрии: если две прямые линии с наклоном $m_1$ и $m_2$ параллельны друг другу, то наклон обеих линий будет одинаковым.
Следовательно, $m_1 = m_2$
На комплексной плоскости: Рассмотрим две параллельные прямые, как показано ниже.
Две параллельные линии на комплексной плоскости
Наклон линии AB = $\dfrac{z_{1}-z_{2}}{\bar{z_{1}}-\bar{z_{2}}}$
Наклон линии CD = $\dfrac{z_{3}-z_{4}}{\bar{z_{3}}-\bar{z_{4}}}$
Теперь, если две приведенные выше линии параллельно, то
Arg$\left(\dfrac{z_{1}-z_{2}}{{z_{3}}-{z_{4}}}\right)$ = $0$ и $\pi$
Так как ее аргумент равен 0 и $\pi$, то эта точка будет лежать на вещественной оси. Поэтому мы можем написать, используя условие $z= \bar{z}$,
$\left(\dfrac{z_{1}-z_{2}}{{z_{3}}-{z_{4}}}\right)=\left(\dfrac{\bar{z_{1) }}-\bar{z_{2}}}{{\bar{z_{3}}}-{\bar{z_{4}}}}\right) $
$\dfrac{z_{1}- z_{2}}{\bar{z_{1}}-\bar{z_{2}}}$=$\dfrac{z_{3}-z_{4}}{\bar{z_{3}}- \bar{z_{4}}}$
Следовательно, если ${{w}_{1}}$ и ${{w}_{2}}$ — наклоны двух прямых $AB$ и $CD$ соответственно, то условие параллельности прямых ${{w}_{1}}={{w}_{2}}$.
Условие перпендикулярности двух прямых
В координатной геометрии: если две прямые линии с наклоном $m_1$ и $m_2$ перпендикулярны друг другу, то соотношение между наклоном обеих линий будет:
$m_1 \times m_2 = -1$
На комплексной плоскости: Рассмотрим две перпендикулярные прямые, как показано ниже.
Две перпендикулярные линии на комплексной плоскости
Наклон линии AB = $\dfrac{z_{1}-z_{2}}{\bar{z_{1}}-\bar{z_{2}}}$
Наклон линии CD = $\dfrac{z_{3}-z_{4}}{\bar{z_{3}}-\bar{z_{4}}}$
Теперь, если две приведенные выше линии перпендикулярно, то
Arg$\left(\dfrac{z_{1}-z_{2}}{{z_{3}}-{z_{4}}}\right)$ = $\pm \dfrac{\ пи{2}$
Так как ее аргумент $\pm \dfrac{\pi}{2}$, то эта точка будет лежать на воображаемой оси. Следовательно, мы можем написать:
$\left(\dfrac{z_{1}-z_{2}}{{z_{3}}-{z_{4}}}\right) + \left(\dfrac{\ bar{z_{1}}-\bar{z_{2}}}{{\bar{z_{3}}}-{\bar{z_{4}}}}\right) = 0$
$\ влево(\dfrac{z_{1}-z_{2}}{{z_{3}}-{z_{4}}}\right) = — \left(\dfrac{\bar{z_{1}}- \bar{z_{2}}}{{\bar{z_{3}}}-{\bar{z_{4}}}}\right)$
$\dfrac{z_{1}-z_{2 }}{\bar{z_{1}}-\bar{z_{2}}}$ = — $\dfrac{z_{3}-z_{4}}{\bar{z_{3}}-\bar {z_{4}}}$ 92$, то $x=r cos \theta$ и $y=r sin \theta$ являются параметрическими уравнениями.
Окружность – уравнение на комплексной плоскости
Окружность можно определить как геометрическое место точек, равноудаленных от фиксированной точки, т. е. центра; а расстояние точек от центра называется радиусом окружности.
Рассмотрим окружность с центром в точке ${{z}_{0}}$, где $z$ — геометрическое место точек на окружности. Пусть $r$ будет радиусом круга, как показано ниже на диаграмме. 92-к}$.
Резюме
Общее уравнение прямой на комплексной плоскости задается как $\bar{a’}z+\bar{z}a’+c=0$ , где $a’$ – комплексное число. и $c$ — действительное число.
Параметрическая форма прямой на комплексной плоскости задается как $z=t{{z}_{1}}+(1-t){{z}_{2}}$, где $t=\ frac{1}{1-\lambda} \epsilon\mathbb{R}$.
Условие параллельности двух прямых на комплексной плоскости задается как $w_{1}=w_{2}$, где ${{w}_{1}}$ и ${{w}_{ 2}}$ — наклоны прямых $AB$ и $CD$ соответственно.
