Lim ln 1 x 2 ln 1 x: Lim X-(бесконеч) П-2arctgX __________ ln(1 + (1/X) )

lim ln sqrt(1+x/1-x)/x — вопрос №2664698 — Учеба и наука

Ответы

научу пределам в чате. 20. 11.17

20. 11.17

20. 11.17

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

Проведены четыре плоскости.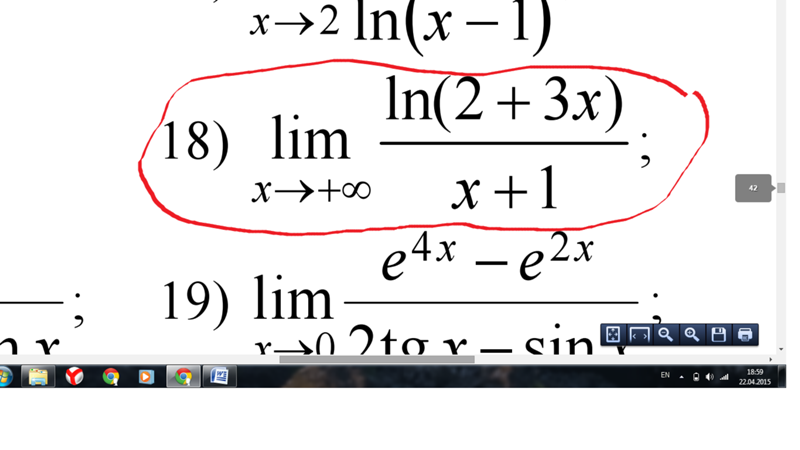 Каждые две из них пересекаются. Тогда наибольшее число прямых попарного пересечения плоскостей равно…

Коля, Дима и Саша собрали…

Через точку О,не лежащую между…

Клетки таблицы 4*7 раскрашены в черный и белый цвета. Пар соседних клеток разного цвета всего 26, пар соседних клеток черного цвета всего 9. Сколько соседних клеток белого цвета.

Решено

Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1

Пользуйтесь нашим приложением

30.Первый замечательный предел. Следствие. Ответ: Первый замечательный предел[править

limx→0sinx/x=1

Следствия

• limx→0tgxx=1

• limx→0arcsinxx=1

• limx→0arctgxx=1

• limx→01−cosxx22=1

Доказательство следствий  [скрыть]

limx→0tgxx=limx→0sinxxcosx=limx→0sinxx⋅limx→01cosx=1⋅1=1

limx→0arcsinxx=⎡⎣⎢⎢u=arcsinxx=sinuu→0x→0⎤⎦⎥⎥=limu→0usinu=1

limx→0arctgxx=⎡⎣⎢⎢u=arctgxx=tguu→0x→0⎤⎦⎥⎥=limu→0utgu=1

limx→01−cosxx22=limx→02⋅sin2x2x22=12=1

31.

Число e. Натуральные логарифмы. Второй замечательный предел. Следствие.

Ответ: e — основание натурального логарифма, математическая константа, иррациональное и трансцендентноечисло. Иногда число e называют числом Эйлера или числом Непера

. Обозначается строчной латинской буквой «e».

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log_e(x) или иногда просто log(x), если основание e подразумевается.^[1]

Натуральный логарифм числа x — это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389…) равен 2, потому что e²=7,389…. Натуральный логарифм самого числа e равен 1, потому что e¹= e, а натуральный логарифм единицы равен 0, поскольку e⁰ = 1.

Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой 

y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

eln(a)=a(a>0)

ln(ea)=a

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:

ln(xy)=ln(x)+ln(y)

Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в видефункции:

ln:R+→R.

x=e.

1. limu→0(1+u)1u=e

2. limx→∞(1+kx)x=ek

3. limx→0ln(1+x)x=1

4. limx→0ex−1x=1

5. limx→0ax−1xlna=1 для a>0, a≠1

6. limx→0(1+x)α−1αx=1

Доказательства следствий  [скрыть]

1. limu→0(1+u)1u=[u=1/xx→∞]=limx→∞(1+1x)x=e

2. limx→∞(1+kx)x=⎡⎣⎢⎢⎢u=x/kx=kuu→∞x→∞⎤⎦⎥⎥⎥=limu→∞(1+1u)ku=(limu→∞(1+1u)u)k=ek

3. limx→0ln(1+x)x=limx→01xln(1+x)=limx→0ln((1+x)1x)=lne=1

4. limx→0ex−1x=⎡⎣⎢⎢⎢u=ex−1x=ln(1+u)x→0u→0⎤⎦⎥⎥⎥=limu→0uln(1+u)=1

5. limx→0ax−1xlna=limx→0eln(ax)−1xlna=limx→0exlna−1xlna=⎡⎣u=xlnau→0x→0⎤⎦=limu→0eu−1u=1

6. limx→0(1+x)α−1αx=limx→0eαln(1+x)−1αx=limx→0eαln(1+x)−1αln(1+x)⋅limx→0ln(1+x)x=

=limx→0eαln(1+x)−1αln(1+x)⋅1=⎡⎣u=αln(1+x)x→0u→0⎤⎦=limu→0eu−1u=1

32.