Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
02.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
із двох населених пунктів,відстань між якими 42 км,виїхали одночасно на зустріч один одному двоє вершників.
Перший вершник рухався зі швидкістю 9…км/год,а другий 12 км/год.Через скільки годин вони зу
Решено
в первенстве школьных команд района по футболу участвовало 10 команд. каждая команда играет с каждой 1 матч. команда вымпел набрала 25 очков, а
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение
Площадь равнобедренного треугольника равна 81 корень 3 .Длина боковой стороны равна 18.Найти косинус угла ,лежащего напротив основания треугольника , если известно что этот угол тупой
Решено
С2-14. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и…
Пользуйтесь нашим приложением
Формулы двойного угла — Что такое формулы двойного угла? Примеры
Формулы двойных углов используются для выражения тригонометрических отношений двойных углов (2θ) через тригонометрические отношения одинарного угла (θ).
Формулы двойного угла являются частными случаями (и, следовательно, выводятся из) формул суммы тригонометрии, а некоторые альтернативные формулы выводятся с использованием тождеств Пифагора. Напомним формулы сумм тригонометрии.
- sin (A + B) = sin A cos B + cos A sin B
- cos (A + B) = cos A cos B — sin A sin B
- tan (A + B) = (tan A + tan B) / (1 — tan A tan B)
Что такое формулы двойного угла?
Мы получим формулы двойного угла для sin, cos и tan, подставив A = B в каждую из вышеприведенных формул суммы. Кроме того, мы выведем некоторые альтернативные формулы, полученные с использованием тождеств Пифагора. Вот формулы двойного угла, за которыми следует вывод каждой формулы.
Формулы двойного угла
Формулы двойного угла для sin, cos и tan:
- sin 2A = 2 sin A cos A (или) (2 tan A) / (1 + tan 2 A)
- cos 2A = cos 2 A — sin 2 A (или) 2cos 2 A — 1 (или) 1 — 2sin 2 A (или) (1 — tan 2 A) / (1 + загар 2 А)
- тангенс 2A = (2 тангенс A) / (1 — тангенс 2 A)
Вывод формул двойного угла
Давайте выведем формулу(ы) двойного угла для каждого из sin, cos и tan одну за другой.
Формула двойного угла Sin
Формула суммы функции синуса:
sin (A + B) = sin A cos B + cos A sin B
Когда A = B, приведенная выше формула принимает вид
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
Выведем альтернативную формулу для sin 2A в терминах tan , используя тождество Пифагора, сек. 92A} \end{align}\)
Таким образом, формула двойного угла функции синуса:
Формулы двойного угла для косинуса
Формула суммы функции косинуса:
cos (A + B) = cos A cos B — sin A sin B
Когда A = B, приведенная выше формула принимает вид
cos ( A + A) = cos A cos A — sin A sin A
cos 2A = cos 2 A — sin 2 A
Используем эту формулу в качестве базовой для вывода двух других формул для cos 2A с помощью Пифагорейское тождество sin 92A} \end{align} \)
Таким образом, формулы двойного угла функции косинуса: или) 1 — 2sin 2 A (или) (1 — tan 2 A) / (1 + tan 2 A)
Формулы двойного угла Tan
Формула суммы функции тангенса:
tan (A + B) = (tan A + tan B) / (1 — tan A tan B)
Когда A = B, приведенная выше формула принимает вид
tan (A + A) = (tan A + tan A ) / (1 — тангенс A тангенс A) = (2 тангенс A) / (1 — тангенс 2 A)
Таким образом, формула функции двойного угла для функции тангенса имеет вид ?
Станьте чемпионом по решению проблем, используя логику, а не правила.
Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Закажите бесплатный пробный урок
Давайте рассмотрим применение формул двойного угла в разделе ниже.
Примеры использования формул двойного угла 92x \end{align} \)
Ответ: Данное тождество доказано.
Пример 3: Используйте формулы двойного угла, чтобы вывести формулу для sin 3x.
Решение:
sin (3x) = sin (2x + x)
= sin 2x cos x + cos 2x sin x (используя sin (A + B) = sin A cos B + cos A sin B)
= (2 sin x cos x) cos x + (1 — 2 sin 2 x) sin x (используя формулы двойного угла)
= 2 sin x cos 2 x + sin x — 2 sin 3 x
= 2 sin x (1 — sin 2 x) + sin x — 2 sin 3 x
= 2 sin x — 2 sin 3 x + sin x — 2 sin 3 x
= 3 sin x — 4 sin 3 x
Ответ: sin 3x = 3 sin x — 4 sin 3 x.
Часто задаваемые вопросы о формулах двойного угла
Что такое формулы двойного угла?
Формулы двойного угла — это формулы в тригонометрии, которые имеют дело с двойными углами тригонометрических функций. Некоторые важные формулы двойного угла:
- sin 2A = 2 sin A cos A
- cos 2A = cos 2 A — sin 2 A
- тангенс 2A = (2 тангенс A) / (1 — тангенс 2 A)
Как получить формулы двойного угла?
Подставим A = B в формулы суммы функций sin, cos и tan, чтобы получить формулы двойного угла. Для более подробного и ясного объяснения, пожалуйста, обратитесь к разделу «Вывод формул двойного угла» на этой странице.
Каковы применения формул двойного угла?
Формулы двойного угла используются для нахождения значений двойных углов тригонометрических функций, используя значения их одиночных углов. Например, значение cos 30 o можно использовать для нахождения значения cos 60 o .
Кроме того, формулы двойного угла можно использовать для вывода формул тройного угла.
Как использовать формулы двойного угла в интегрировании?
При интегрировании используем формулы двойного интегрирования. Чтобы понять это, рассмотрим пример ниже.
∫ sin x cos x dx = (1/2) ∫ (2 sin x cos x) dx
= (1/2) ∫ sin 2x dx
= (1/2) (- cos 2x / 2) + C (используя замену 2x = u)
= -1/4 cos 2x + C
Если sinA=4/3, найти sin2A;cos2A | Wyzant Спросите эксперта
Тригонометрия Тригонометрия
Лакшми Б.
спросил 16.08.19Подписаться І 1
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Джейсон К.
ответил 16.08.
19
Репетитор
5 (6)
Помощь с домашним заданием по математике
Смотрите таких репетиторов
Смотрите таких репетиторов
Во-первых, если sinA = 4/3, поскольку 4/3 >
Тем не менее, я хочу показать вам, как бы вы решали эти задачи в любом случае: Итак, вот похожий пример:
Пример: Предположим, что sinA = 4/5, где A находится в Q2. Вычислите sin(2A) и cos(2A)
*Внимание: что бы вы ни делали, не думайте об этом как о sin(2A) = 2(4/5) = 8/5, так как 2A всего в два раза больше, чем A , Так никогда не бывает!!
Используя тождества двойного угла:
sin(2A) = 2sinAcosA…………(1)
cos(2A) = cos 2 A — sin 2 A ……(2)
= 2cos 2 A — 1………… (3)
= 1 — 2sin 2 A…………(4)
Таким образом, чтобы найти sin(2A), исходя из приведенной выше формулы (1), мы’ Нам нужно выяснить значение cosA.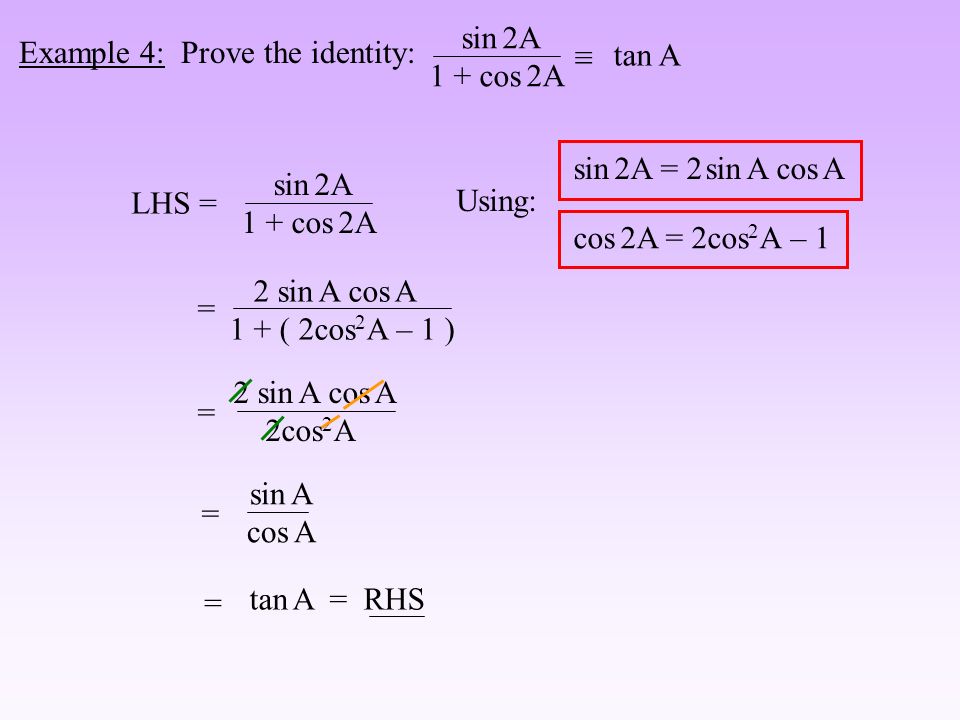
В этом случае, поскольку ∠A находится в Q2, значение cosA отрицательно. Чтобы выяснить, что такое cosA, используйте тождество Пифагора:
cosA = √(1 — sin 2 A)
= √(1 — (4/5) 2 )
= √(1 — 16/25)
= √(9/25)
= 3/5
, по (1) sin(2A) = 2sinAcosA
= 2(4/5)(-3/5)
= -24/25
Что касается cos(2A), вы можете использовать любую из формул из (2) — (4) и получите тот же ответ.
Если вы решите использовать (2) Если вы решите использовать (3) Если вы решите использовать (4)
cos(2A) = cos 2 A — sin 2 A cos(2A) = 2cos 2 A — 1 cos(2A) = 1 — 2sin 2 A
= (-3/5) 2 — (4/5) 2 = 2(-3/5) 2 — 1 = 1 — 2(4/5) 2
= 9/25 — 16/25 = 2(9/25) — 1 = 1 — 2(16/25)
= -7/25 = 18/25 — 1 = 1 — 32/25
= -7/25 = -7/25
Как видите, не имеет значения, какую из трех формул вы выберете, вы всегда будете в итоге получите тот же ответ для cos(2A).
————————
Последнее замечание: вот еще один способ понять, почему sinA = 4/3 не может дать фактический ответ:
Так как нужно найти cosA
cosA = √(1 — sin 2 А)
= √(1 — (4/3) 2 )
= √(1 — 16/9)
2 = √(-7/9) = мнимое ⇒ Нет решения!
В целом: значения cosA и sinA должны быть только МЕЖДУ -1 и 1 (они могут также включать в себя -1 и 1), но они никогда не должны превышать их. Итак, если кто-то дает вам cosA = 5/3, поскольку 5/3 > 1 ⇒ Нет решения
Надеюсь, это поможет
Мистер К.
Голосовать за 1 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.