1 0 предел
Вы искали 1 0 предел? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и lim в математике как решать, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 0 предел».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 0 предел,lim в математике как решать,mathprofi пределы,высшая математика как решать пределы,высшая математика пределы для чайников подробные объяснения,высшая математика пределы как решать,высшая математика пределы примеры решения,вычисление пределов примеры,вычисление пределов примеры с решением,вычисление пределов функции примеры решения,вычисления пределов примеры,вычислить предел функции lim примеры,как вычислить пределы функций примеры решений,как лимит решать,как решать lim в математике,как решать лимит,как решать лимиты,как решать лимиты в высшей математике,как решать предел,как решать пределы,как решать пределы высшая математика,как решать пределы для чайников,как решать пределы примеры,как решать пределы с бесконечностью,как решать пределы сложные,как решать примеры пределы,как решать сложные пределы,как решаются пределы,лимит в математике,лимиты алгебра,лимиты высшая математика,матан пределы,математика лимит,математика лимиты,найти предел функции примеры с решением,нахождение пределов примеры решения,нахождения пределов примеры,предел 1 0,предел как решить,предел примеры,предел функции примеры решений,предел число делить на ноль,пределов примеры решений,пределы mathprofi,пределы в математике примеры решения,пределы высшая математика как решать,пределы высшая математика примеры решения,пределы высшая математика с примерами,пределы для чайников примеры решений,пределы как решать для чайников,пределы как решать примеры,пределы как решить,пределы матанализ,пределы объяснение,пределы онлайн с подробным решением для чайников пошагово,пределы примеры,пределы примеры для самостоятельного решения,пределы примеры как решать,пределы примеры с решением,пределы примеры с решениями,пределы решение примеров,пределы с подробным решением,пределы с решением примеры,пределы сложные,пределы тема,пределы тема по математике,пределы функции примеры решения,пределы функции примеры решения задач,пределы функций для чайников,пределы функций примеры решений,пример решения пределов,примеры вычисление пределов,примеры вычисления пределов,примеры вычисления пределов с подробным решением,примеры как решать пределы,примеры на пределы с решениями,примеры нахождение пределов решения,примеры нахождения пределов,примеры предел,примеры пределов,примеры пределов с решением,примеры пределов с решениями,примеры пределы,примеры пределы с решением,примеры пределы с решениями,примеры пределы функций,примеры решение пределов,примеры решений пределы,примеры решения пределы функции,примеры с решением пределов,примеры с решением пределы,примеры с решениями на пределы,примеры с решениями пределов,примеры с решениями пределы,решение задач на пределы,решение пределов для чайников,решение пределов математика,решение пределов с подробным решением для чайников,решение пределов сложных,решение пределов стремящихся к бесконечности,решение пределы функции,решение примеров пределы,решение примеров с пределами,решение сложных пределов,решения пределов функции примеры решения,сложные пределы,сложные пределы как решать,среди перечисленных вариантов ответа выбрать значение предела lim,тема пределы,теория пределов математика примеры решений.
Решить задачу 1 0 предел вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Предел функции в точке, урок и презентация по алгебре 10 класс, примеры решение пределов
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Предел функции в точке (PDF)
Что будем изучать:
1. Что такое предел функции в точке.
2. Определение непрерывной функции.
3. Обобщение знаний о непрерывных функциях.
4. Свойства предела.
5. Примеры.
1) Что такое предел функции в точке?
Ребята, давайте посмотрим на три графика функции, приведенные ниже:
На первый взгляд, графики выглядят совершенно одинаково, но давайте внимательнее посмотрим на наши графики. Посмотрим внимательно на значения функции y=f(x) в точке а.
На Рис1. изображен график непрерывной функции. Значение нашей функции в точке a f(a)=b.
На Рис2. изображен график с так называемой выколотой точкой, значения нашей функции в точке а не существует, посмотрите внимательно на график, наше значение как будто взяли и выкололи.
На Рис3. изображен график значение, которого в точке а существует, но где то отдельно от всего графика, f(a) – расположена выше нашего графика.
На наших рисунках изображены графики трех разных функций. Если мы не будем рассматривать точку а, то графики функций совпадают. При xа графики совершенно одинаковые.
Все случаи описанные для наших рисунков, на математическом языке записывается как:
Читается как: предел функции y=f(x) при x стремящимся к а равен b.
Теперь давайте постараемся понять, что же написано выше. Если значения аргумента функции y=f(x) подбирать все ближе к числу а (если из а вычитать подобранные значения аргумента, то результатом будет число практически равное нулю), то соответствующие значения функции будут все ближе и ближе к b (если из b вычитать полученные значения функции, то результатом будет число практически равное нулю). При этом стоит заметить, что саму точку а не учитываем.
Посмотрим опять на первый график: Можно заметить что:
График функции на нашем рисунке непрерывен. Тогда, давайте напишем определение непрерывной функции:
Определение непрерывной функции.
Определение. Функцию y=f(x) называют непрерывной в точке x=a, если выполняется тождество:
Функцию y=f(x) называют непрерывной в точке x=a, если предел функции при x стремящимся к а, равен значению функции в точке x=a.
Функция непрерывна на отрезке [a,b], если она непрерывна в каждой точке нашего отрезка.
Обобщение знаний о непрерывных функциях.
Полезно: В курсе высшей математики или математическом анализе, существует ряд теорем и утверждений которые доказывают, что все функции, которые мы с вами рассматривали в ранних курсах алгебры являются непрерывными, мы с вами интуитивно и с помощью графиков понимали, что функция непрерывна. Давайте обобщим изученное, важным утверждением: Если выражение f(x) составлено из рациональных, иррациональных и тригонометрических выражений, то функция y=f(x) непрерывна в любой точке, в которой определенно выражение f(x).
Свойства функции
Если f(x)=b a g(x)=c то выполняются следующие свойства:
Примеры:
А) Найти предел функции:
Решение:
Наша функция непрерывна в точке x=2, тогда воспользуемся определением непрерывности функции в точке, которое говорит что если функция непрерывна в точке, то предел функции в этой точке равен значению функции в этой же точке.
Б) Найти предел функции:
Решение:
Давайте посмотрим не обращается ли знаменатель нашей функции при x=π/2 в нуль:
Знаменатель не равен нулю, тогда наша функция непрерывна в точке . Воспользуемся определением непрерывной функции и посчитаем предел нашей функции:
Ответ: -1/3
В) Найти предел функции:
Подставим x=2 в знаменатель нашей дроби, получили 0, но на ноль делить нельзя. Давайте внимательно посмотрим на числитель нашей дроби.
x2 — 4 = (x — 2)(x + 2)
Сократим нашу дробь
Тогда получаем:
y= x+2 непрерывна точке x=2, тогда воспользуемся определением непрерывности
Ответ: 4
Г)Найти предел функции:
Решение:
Область определения функции
Наша точка x=2 не попадает в область определения, тогда предел функции не существует.
Ответ: Не существует.
Д) Найти предел функции:
Решение:
Подставим x=1 в знаменатель нашей дроби, получили 0, но на ноль делить нельзя.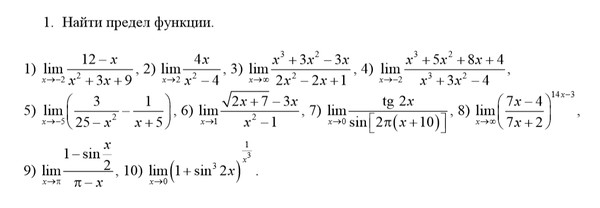
Ответ: -1
Е) Построить график функции y=f(x), которая обладает следующими свойствами:
1)Область определения – множество действительных чисел.
2)lim f(x)=3
3) f(2)=4
4) f(x)
Решение:
Покажем один из возможных графиков.
Примеры для самостоятельного решения:
1) Найти предел функции:
2) Найти предел функции:
3) Найти предел функции:
4) Найти предел функции:
5)Построить график функции y=f(x), которая обладает следующими свойствами:
а)Область определения – множество действительных чисел.
б)
в) f(-2)=3
г) f(x)
д) f(x)>0 при x>-1
Расчет пределов с помощью алгебры — AP Calculus AB
Все ресурсы AP Calculus AB
3 диагностических теста 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
AP Calculus AB Помощь » Функции, графики и ограничения » Ограничения функций (включая односторонние ограничения) » Вычисление пределов с использованием алгебры
Расчет
Возможные ответы:
10
0
Предела не существует 005
Объяснение:
Во-первых, мы замечаем, что замена x на 5 даст нам 0 в знаменателе.
Итак, мы упростим уравнение, заметив, что числитель — это разница двух квадратов.
Теперь мы можем заменить x на 5, и мы получим ответ 10.
Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
Объяснение:
Вынесите x-4 из числителя и упростите:
Оцените предел для x=4:
Несмотря на разрыв при x=4, предел при x=4 равен 10, потому что функция приближается к десяти слева и справа.
Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
Объяснение:
Умножьте числитель на множители и упростите выражение.
Оценить функцию при x=2.
Существует разрыв в точке x=2, но поскольку предел при приближении x к 2 справа равен пределу при приближении x к 2 слева, предел существует.
Сообщить об ошибке
Оценить следующий предел:
Возможные ответы:
5 9
не существует
005
Правильный ответ:
Объяснение:
Разложите числитель, чтобы оценить предел:
Оцените предел:
Имеется разрыв при x=0, но предел равен 8, потому что предел справа равен пределу слева.
Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
5
4 Объяснение:
Когда x приближается к бесконечности, значения x, возведенные в наивысшую степень, доминируют над функцией, а все остальные значения становятся незначительными.
В этом пределе x 3 имеет наивысший порядок в числителе, а 5x 2 имеет наивысшую степень всех значений в знаменателе. Мы можем упростить ограничение до следующего:
После вынесения x 2 легко увидеть, что предел расходится в бесконечность.
Сообщить об ошибке
Возможные ответы:
Не определено.
Правильный ответ:
Объяснение:
Первым шагом к оценке пределов всегда является попытка прямой подстановки значения в функцию. В этом случае это все, что вам нужно сделать.
Сообщить об ошибке. 015 Правильный ответ:
Объяснение:
Чтобы начать эту задачу, нам нужно разложить квадратное уравнение на множители.
Это приведет к дыре в , что позволит нам напрямую подставить предельное значение в результирующую функцию для определения предела.
Сообщить об ошибке
Возможные ответы:
Не определено.
Правильный ответ:
Объяснение:
Чтобы оценить этот предел, нам нужно прямо подставить рассматриваемое значение в нашу функцию. Обратите внимание, что это значение находится в домене функции, поэтому прямая подстановка — единственный метод, который нам здесь нужен.
Сообщить об ошибке. Объяснение:
Этот предел нельзя вычислить простой подстановкой; не определен в , поэтому сначала нужно немного упростить.
. (Старт)
. (Разложить на числитель)
. (Отменить условия)
.
(Замените в )
.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
← Предыдущая 1 2 3 4 Следующая →
Уведомление об авторских правах
Все ресурсы AP Calculus AB
3 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции
Краткое введение в алгебру пределов примеры
Теорема пределов алгебры используется для вычисления предела любого алгебраического выражения. Он широко используется в математике. Предел любого алгебраического выражения f(x) для определенного значения a приравнивается к тому, что x→a демонстрируется как
Lim x→a f(x) = l
.
которые лежат слева от выражения, являются левым пределом всего выражения. Левый предел демонстрируется как a, x→a− f(x). Правый предел демонстрируется как x→a+ f(x). В теореме об алгебре пределов вычислите эти два предела, чтобы получить значение алгебраического выражения.
Алгебра пределов
Алгебра пределов — это систематический процесс определения значений переменных в алгебраических выражениях с помощью пределов. Если правый предел равен левому пределу, то говорят, что функция определена, и значение, на котором определяется функция, является значением выражения. Это означает, что значение, которое мы получаем после вычисления предела, является нулем алгебраического выражения. Если мы подставим это значение в уравнение, либо мы получим ноль, либо та же самая величина будет записана в уравнение равным.
Примеры алгебры пределов
Некоторые примеры алгебры пределов;
Алгебра пределов Пример предела полиномиальной функции A
Решите: x→alim (x3 – x2 + 1)
Решение:
Подставьте значение x = 1 в данное уравнение.
x→alim (x3 – x2 + 1) = x→1lim (13 – 12 + 1)
x→alim (x3 – x2 + 1) = 1 – 1 + 1
x→alim (x3 – x2 + 1) = 1
Пример алгебры пределов рациональной функции путем прямой подстановки.
Решите: x→1lim = (x2 + 1)/(x + 100)
Решение:
Подставьте значение x = 1 в данное уравнение.
x→1lim = x2 + 1/ x + 100 = 12 + 1/ 1 + 100
= 1 + 1 / 1 + 100 + 100 = 2/101
Теорема пределов алгебры
Теорема пределов алгебры показывает, что если0334 Тогда
x→alim f(x).g(x) = l . m
Алгебра доказательства предельной теоремы
Давайте разберемся в алгебре доказательства предельной теоремы:
Дано,
x→alim f(x) = l
Или доказательство x→alim g(x) = m
5 : x→alim f(x).
g(x) = l .m
Доказательство:
Шаг 1: x→alim |f(x).g(x) – lm | = |f(x).g(x) – f(x).m + f(x).m – lm|
Шаг 2: x→alim |f(x).g(x) – lm | = |f(x).(g(x) – m) + m (f(x) – l)|
Шаг 3: x→alim |f(x).g(x) – lm | ≤ |f(x)||(g(x) – m)|+ |m| |(f(x) – l| …Уравнение (1)
Так как x→alim f(x) = l, где l→ 0, то f(x) → 0 в 0 < |x-a|< δ
Для некоторого δ > 0
Следовательно, f(x) ограничено в a.
Следовательно, существует k > 0 таким образом, что |f(x)| Всякий раз, когда 0 < |x – a|<δ Для некоторого δ2 < 0 Пусть задано E > 0, Поскольку, x→alim f(x) = l и, x→alim g(x) = m, Таким образом, что δ2 > 0. |f(x) – l| = E/ 2(1 + |m|) …. Уравнение (3). (Это для 0 < |x – a| < δ2) И, |g(x) – m| = E/ 2k …… Уравнение (4). (Это для 0 < |x – a| < §3) Если мы выберем § = min{δ1, δ2, δ3}, Тогда Алгебраические свойства пределов Итак, уравнение (1 ), уравнение (2) и уравнение (3) остаются в силе. Для 0 < |x – a| < δ Следовательно, из уравнения (1) |f(x).g(x) – lm | < к. Е/ 2к + |т|. E/ 2(1 + |m|) (Это для, 0 < |x – a| < §) Теперь , E/2 + E/2= E Следовательно, согласно определению, x→alim f(x).g(x) = l.m = x→alimf(x). x→alim g(x) Давайте узнаем об алгебраических свойствах пределов. Предел любой константы в алгебраических выражениях остается постоянным. limx→a cx + d = ca + d lim x→a x = a Lim x→a xn = an, в этом уравнении n — натуральное число 5 Lim
Алгебраические свойства пределов
