Простая физика — EASY-PHYSIC
Здравствуйте, читатели! Знакомимся мы с вами сегодня с обратными тригонометрическими функциями. Мы узнаем, что такое арксинусы, арккосинусы и арктангенсы – арккотангенсы, и научимся решать примеры с их участием.
Сначала вспомним определение:
Арксинусом числа , модуль которого не больше 1, называется такое число из промежутка , синус которого равен .
, если ,
Также мы можем записать это так: , если , а также справедливо: .
Еще нам пригодится такая формула: .
Арккосинусом числа , модуль которого не больше 1, называется такое число из промежутка , косинус которого равен .
, если ,
Также мы можем записать это так: , если , аналогично .
Еще нам пригодится такая формула: .
Арктангенсом числа называется такое число из промежутка , тангенс которого равен .
, если ,
Также мы можем записать это так: , , аналогично .
Будем пользоваться и такой формулой: .
Арккотангенсом числа называется такое число из промежутка , котангенс которого равен .
, если ,
Также мы можем записать это так: , , аналогично .
Будем пользоваться и такой формулой: .
Интересно, что .
Ну что ж, формул много, давайте попробуем их применять на практике.
Вычислить:
Задача 1. , так как
Задача 2.
Задача 3. , так как
Задача 4.
Так как , то выражение – это число, синус которого равен 0,6. Тогда косинус этого числа можно вычислить через основное тригонометрическое тождество:
Задача 5.
Задача 6.
Задача 7. . Так как , то . Но , а 6,28 – это . Тогда . Число меньше 1, и к нему применим формулу :
Задача 8.
По формуле приведения
Задача 9. . Рассуждаем так: – это такое число, синус которого равен .
Тогда по основному тригонометрическому тождеству косинус этолго числа: . Тогда тангенс этого числа – отношение синуса к косинусу:
Задача 10.
Применим формулу косинуса суммы:
Сначала отдельно рассчитаем значения выражений и :
– если синус угла равен , то косинус найдем через основное тригонометрическое тождество:
Аналогично : если синус числа равен 1/3, то косинус его равен .
Тогда получим:
Имеет ли смысл выражение:
Задача 11.
Так как , то выражение имеет смысл.
Задача 12. – выражение смысла не имеет.
Решить уравнение:
Задача 13.
Применим такой прием:
Тогда
Задача 14.
И снова тот же прием:
Доказать тождество:
Задача 15.
Сначала избавимся от отрицательного числа под знаком арккосинуса:
Теперь применим уже знакомый прием, определим косинус правой и левой частей:
Раскрываем по формуле «косинус суммы»:
Теперь определим :
Нам нужно определить косинус такого угла, синус которого равен , воспользуемся основным тригонометрическим тождеством:
Определим :
Нам нужно определить синус такого угла, косинус которого равен , воспользуемся основным тригонометрическим тождеством:
Вернемся к примеру:
Тождество доказано.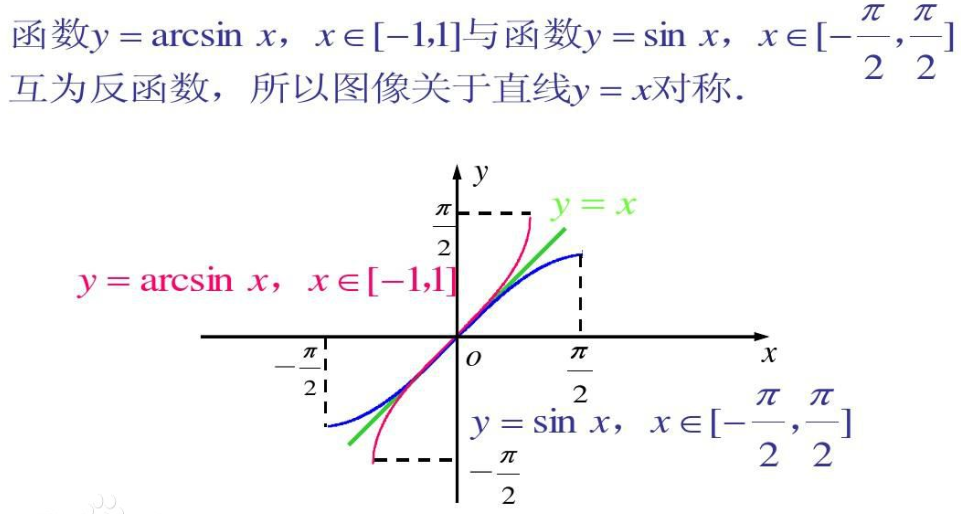
Задача 16.
Снова видим отрицательные числа под знаками арккосинусов, избавимся от них:
Поменяем знаки:
Применим операцию взятия косинуса от правой и левой частей:
Применяем формулу косинуса разности:
Определим :
Нам нужно определить синус такого угла, косинус которого равен , воспользуемся основным тригонометрическим тождеством:
Определим
Нам нужно определить синус такого угла, косинус которого равен , воспользуемся основным тригонометрическим тождеством:
Возвращаемся к примеру:
Тождество доказано.
Вычислить:
Задача 17.
По формулам приведения
Задача 18.
Применим формулу косинуса суммы:
Сначала отдельно рассчитаем значения выражений и :
– если синус угла равен 3/5, то косинус найдем через основное тригонометрическое тождество:
Аналогично : если синус числа равен 3/5, то косинус его 4/5 (определяем через основное тригонометрическое тождество).
Тогда получим:
Повторим тригонометрию: арксинус
Доброго времени суток! Сегодня я бы хотел повторить с вами тригонометрию. Нашей темой будет арксинус.
Укажем три свойства функции y = sin x на отрезке [-π/2; π/2]:
1) функция непрерывна,
2) на концах отрезка принимает значения -1 и 1,
3) возрастает.
Эти три условия позволяют нам утверждать, что для любого значения a из отрезка [-1; 1] , уравнение sinx = a на отрезке [-π/2; π/2] имеет решение и притом только одно.
Это решение (число) принято записывать в виде: arcsin a (рис. 1).
Можно сказать и так: arcsin a – это единственный корень системы
Итак, под записью arcsin a мы понимаем число, которое удовлетворяет двум условиям:
1) -π/2 ≤ arcsin a ≤ π/2 и 2) sin (arcsin a) = a .
Отметим, что запись «arcsin a» будет числом, если -1 ≤a ≤ 1. В противном случае эта запись теряет смысл.
Точку, соответствующую числу arcsin a, удобно отмечать и на числовой окружности (рис. 2).
Из точки a оси ординат проведем перпендикуляр к этой оси и точку его пересечения с правой полуокружностью обозначим буквой М. На точке М имеем бесконечно много чисел. Среди них находится и число arcsin a – число из отрезка [-π/2; π/2].
Число arcsin a, при девяти табличных значениях числа a, можно (и нужно) записывать в более простой форме (см. рис. 3).
Задача 1. Почему данные записи не имеют смысла (не являются числами):
Решение.
Запись arcsin a является числом лишь при условии -1 ≤ a ≤ 1. В приведенных записях это условие нарушено:
Задача 2. При каких значениях переменной x выражение arcsin(2 — |x- 3|) имеет смысл?
Решение.
Запись arcsin a имеет смысл тогда и только тогда, когда -1 ≤ a ≤ 1. Ответом нашей задачи будет решение двойного неравенства: -1 ≤ 2 — |x- 3| ≤1.
Задача 3. Найти значение числового выражения (вычислить):
Решение.
Задача 4. Вычислить: а) sin (arcsin 0,3) + sin (arcsin(-0,2));
Решение.
Воспользуемся равенством sin (arcsin a) = a .
а) sin (arcsin 0,3) + sin (arcsin (-0,2)) = 0,3 – 0,2 = 0,1.
Абитуриентам на заметку
Действительно, так как
Задача 5. Вычислить cos (arcsin(–0,8)) .
Решение.
Задача 6. Вычислить cos (arcsin 0,6 – arcsin 0,8) .
Решение.
Три свойства арксинуса
1) Арксинусы противоположных чисел противоположные числа:
arcsin(–a) = –arcsin a
Действительно, график функции y = sin x симметричен относительно начала координат и, значит, противоположным числам a и (—a) оси ординат соответствуют противоположные числа на отрезке [-π/2 ; π/2] оси абсцисс, т.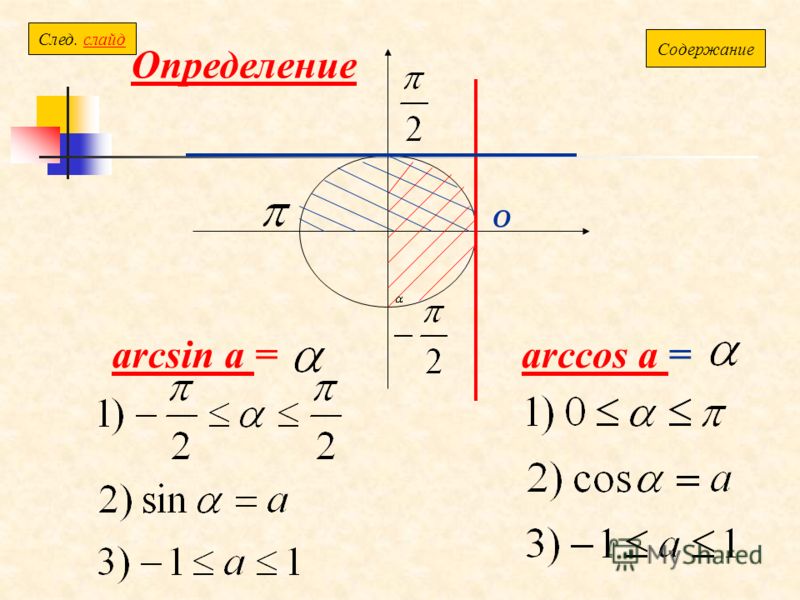
е. числа arcsina и arcsin(-a) противоположны:
arcsin a + arcsin(-a) = 0, откуда и получим arcsin(-a) = — arcsina (см. рис. 1).
Задача 7.
Вычислить:
Решение.
Так как числа (a – b) и (b – a) противоположные, то arcsin (a –b) = -arcsin (b –a).
2) Если a > b,то arcsin a > arcsin b и обратно, если arcsin a > arcsin b , то a > b.
Понятно, что числа a и b принадлежат отрезку [-1 ; 1].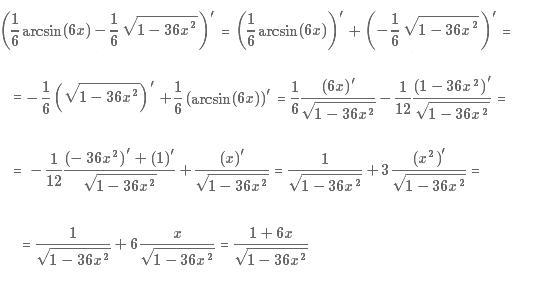
Убедиться в справедливости этого свойства можно из рисунков 1 или 2.
Задача 8. Расположить числа в порядке возрастания:
Решение. Так как
Задача 9. Принадлежит ли число arcsin (-0,75) интервалу (-1,06; -0,78)?
Решение. Из рисунка 3 замечаем, что
Ответ: да, принадлежит.
Задача 10. Решить неравенство arcsin(2x – 3) > arcsin(x – 2).
Решение.
3) Равенство arcsin a = arcsin b равносильно системе из двух условий: 1) a = b; 2) -1 ≤ a ≤ 1.
Разумеется, что в двойном неравенстве вместо числа a можно взять число b.
Задача 11. Решить уравнение: arcsin(|2x + 2| – 0,5 ) = arcsin (x + 2).
Решение.
Уравнение sin x = a
Областью значений функции y = sinx является отрезок [-1; 1], следовательно, уравнение sinx = a имеет решение тогда и только тогда, когда -1 ≤ a ≤ 1.
Пусть a некоторое внутреннее число из отрезка [-1; 1]. На числовой окружности имеем две точки, ордината которых равна числу a: точки M и N на рисунке 2.
Решить уравнение sinx = a – это значит найти все числа на этих точках.
Теперь найдем одно из чисел точки N, а затем и все числа этой точки.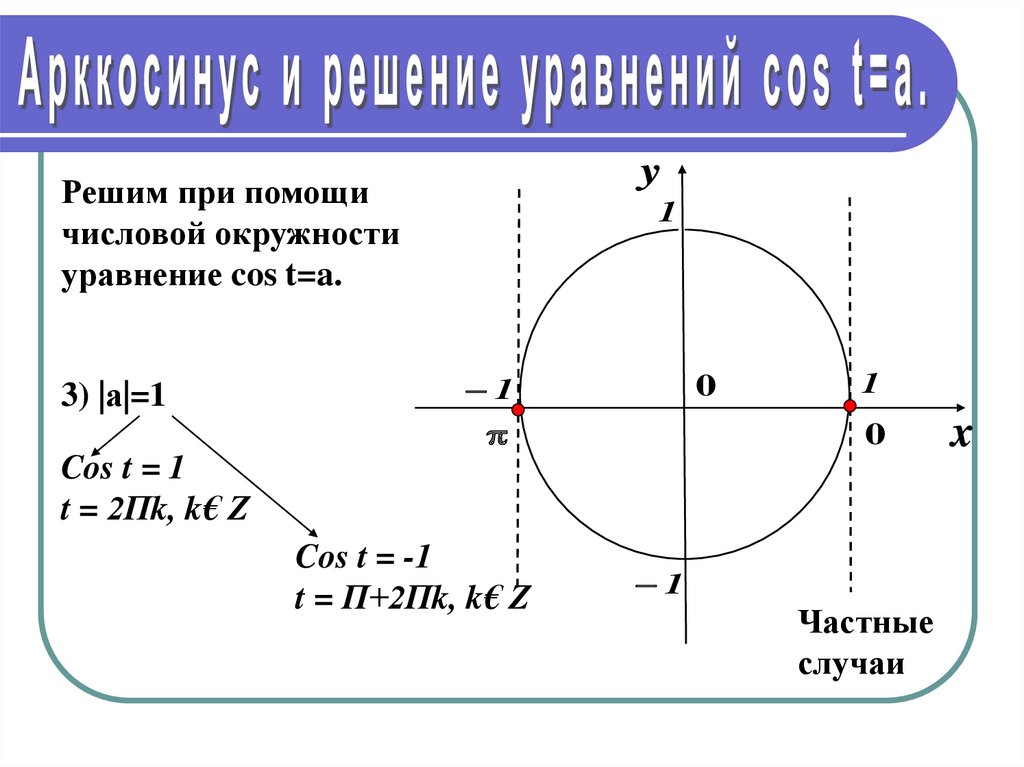
Так как точки M и K симметричны относительно оси абсцисс (MK– вертикальная хорда окружности), то число (-arcsin a) находится на точке K, а так как KN– диаметр, то число -arcsin a + π находится на точке N.
Теперь запишем все числа точки N: x = -arcsina + π + 2πn, где n = 0; ±1; ±2; … .
Формулы, задающие числа на точках M и N, можно объединить в одну:
При четных значениях k (k = 0; ±2; ±4; …) мы получим числа точки M, а при нечетных значениях k (k = ±1; ±3; ±5; …) – числа точки N.
Для девяти табличных значений числа a решение уравнения sin x = a, естественно, надо записывать в упрощенном виде http://www.tutoronline.ru/blog/prosteishie-trigonometricheskie-uravnenia.
Задача 12. Решить уравнения: а) sin x = -π/3; б) sin x = 0,3; в) sin x = -0,4.
Решение.
а) уравнение не имеет решений, т.к. –π/3 < -1;
Задача 13.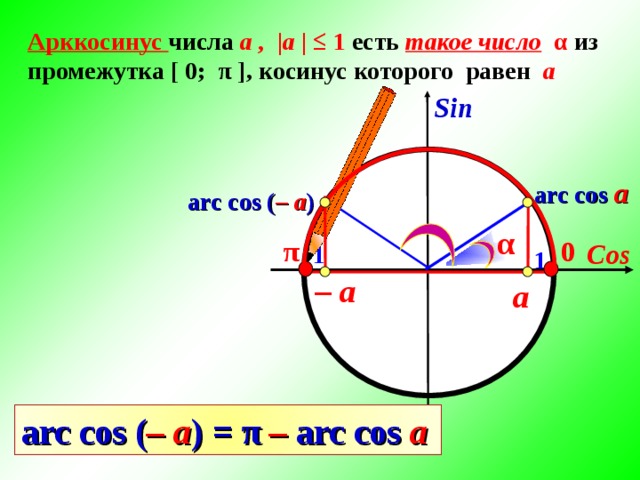
Решить уравнение
Решение. Данное уравнение равносильно системе
Спасибо за внимание! Жду Вас на своих занятиях! Репетитор Карен Мартиросян.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
{-1}{x}}{x}}$ $\,=\,$ $\displaystyle \large \lim_{y \,\to\, 0}{\normalsize \dfrac{y}{\sin{y }}}$Преобразование функции в известное предельное правило
В вычислениях используется тригонометрическое предельное правило.
$\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sin{x}}{x}} \,=\, 1$
Но наша функция обратна форма.
$\displaystyle \large \lim_{y \,\to\, 0}{\normalsize \dfrac{y}{\sin{y}}}$
Теперь запишите приведенную выше алгебраическую тригонометрическую функцию в ее обратной форме .
$\implies$ $\displaystyle \large \lim_{y \,\to\, 0}{\normalsize \dfrac{y}{\sin{y}}}$ $\,=\,$ $\displaystyle \large \lim_{y \,\to\, 0}{\normalsize \dfrac{1}{\dfrac{\sin{y}}{y}}}$
Согласно частному правилу пределов предел частное равно частному их пределов.
$\implies$ $\displaystyle \large \lim_{y \,\to\, 0}{\normalsize \dfrac{y}{\sin{y}}}$ $\,=\,$ $\dfrac {\ Displaystyle \ большой \ lim_ {у \, \ к \, 0} {\ normalsize (1)}} {\ Displaystyle \ большой \ lim_ {у \, \ к \, 0} {\ normalsize \ dfrac {\ грех {г}}{г}}}$
Оценка предела функции
В соответствии с правилом постоянного предела предел единицы всегда равен единице.
$\implies$ $\displaystyle \large \lim_{y \,\to\, 0}{\normalsize \dfrac{y}{\sin{y}}}$ $\,=\,$ $\dfrac {1}{\displaystyle \large \lim_{y \,\to\, 0}{\normalsize \dfrac{\sin{y}}{y}}}$
Предел sinx/x при приближении x к нулю равен единице. Следовательно, предел $\dfrac{\sin{y}}{y}$ при стремлении $y$ к $0$ также равен единице.
$\implies$ $\displaystyle \large \lim_{y \,\to\, 0}{\normalsize \dfrac{y}{\sin{y}}}$ $\,=\,$ $\dfrac {1}{1}$ 9{-1}{x}}{x}}$ $\,=\,$ $1$
Таким образом, доказано, что предел частного обратного синуса от переменной при стремлении переменной к нулю равен единице.
`arcsin(0)` Вычислить выражение без использования калькулятора
Цитата страницы Начать эссе значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«`arcsin(0)` Вычислите выражение без использования калькулятора» eNotes Editorial , 24 августа 2016 г., https://www.enotes.com/homework-help/arcsin-0-evaluate-expression-without-using -758938. По состоянию на 20 февраля 2023 г.
`arcsin(0)`
Пусть это выражение равно y.
`y = arcsin(0)`
Переписав это уравнение в терминах функции синуса, оно будет таким: синус равен нулю при углах 0 и `пи` .
`y = 0, pi`
Теперь, когда значения угла y известны, снова обратимся к исходному уравнению.
`y=arcsin (0)`
Обратите внимание, что диапазон функции арксинуса равен `-pi/2lt=y lt=pi/2` .
Между 0 и pi значение, принадлежащее этому интервалу, равно только 0. Итак, решение исходного уравнения:
`y=arcsin (0)`
`y=0`
Следовательно, `arcsin(0)=0` .
Изображений:
Это изображение было помечено как неприемлемое Нажмите, чтобы снять отметку
Изображение (1 из 1)
Утверждено редакцией eNotes
Математика
Что означают буквы R, Q, N и Z в математике?
14 Ответы педагога
Математика
Последний ответ опубликован 07 октября 2013 г.