Построение уравнения прямой регрессии Y на X
Продолжаем анализировать ответы к индивидуальным заданиям по теории вероятностей. Из этой статьи Вы научитесь составлять (строить) уравнение прямой регрессии Y на X (y=alpha*x+beta ). Такие примеры распространены в теории вероятностей для студентов экономических факультета и статистики. Приведенные решения взяты из программы для экономистов ЛНУ им. И.Франка. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения, поэтому много полезного для себя должен взять каждый студент.
Индивидуальное задание 1
Вариант 11
Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:
Записать выборочное уравнение прямой регрессии Y на X.
Решение: Вычисляем средние арифметические значения признаков Х та Y
Находим величины которые фигурируют в уравнении регрессии — alpha, beta
После вычислений выборочное уравнение регрессии Y на X записываем по формуле
y=2,02*x-0,99.
Чтобы подтвердить правильность предположения о линейности связи между признаками Х и Y находим выборочный коэффициент корреляции по формуле:
Так как выборочный коэффициент корреляции r(X,Y) является достаточно близким к единице, то предположение о линейной зависимости между X и Y — правильное. Кроме этого коэффициент корреляции положительный r>0, поэтому случайные величины X и Y увеличиваются одновременно.
Вариант 1
Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:
Записать выборочное уравнение прямой регрессии Y на X.
Решение: Находим величины которые необходимы для вычисления коэффициентов уравнения регрессии
Вычисляем alpha, beta
и составляем уравнение регрессии Y на X
y=19,7*x+0,935.
Xтобы убедиться что предположение о линейной свя связи между Х и Y является правильным, находим выборочный коэффициент корреляции по формуле:
Поскольку выборочный коэффициент корреляции =0,9962 достаточно близок к единице, то предположение о линейной связи между X и Y -правильное.
К тому же коэффициент корреляции положительный (r>0), поэтому и связь между X и Y является положительной, то есть эти случайные величины увеличиваются одновременно.
Вариант-12
Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:
Записать выборочное уравнение прямой регрессии Y на X.
Решение: Вычисляем средние арифметические значения каждой из выборок, а также остальные составляющие для построения уравнения регрессии Y на X:
Находим коэффициенты alpa, beta по формулам
Подставляем коэффициенты в уравнение прямой регрессии y=2,01*x+1,335.
Находим точечную оценку для коэффициента корреляции по формуле:
Поскольку выборочный коэффициент корреляции достаточно близок к единице то предположение о линейной зависимости между X и Y — правильное.
Также r>0, поэтому связь между X и Y положительная и эти случайные величины увеличиваются одновременно.
Теперь Вы знаете, как составить уравнение прямой регрессии Y на X .
Готовые решения по теории вероятностей
- Предыдущая статья — Формулы числовых характеристик статистического распределения
- Следующая статья — Как найти доверительный интервал?
- Назад
- Вперёд
Уравнение регрессии. Уравнение множественной регрессии :: SYL.ru
Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.
Определение понятия регрессии
В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).
Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).
Какие бывают типы связей между переменными
В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.
Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.
Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.
Виды регрессий
На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.
Гиперболическая, линейная и логарифмическая
Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.
Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.
Множественная и нелинейная
Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х1 , х2 …хс)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.
Обратные и парные виды регрессий
Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.
Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.
Понятие корреляции
Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.
Методы
Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.
Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции.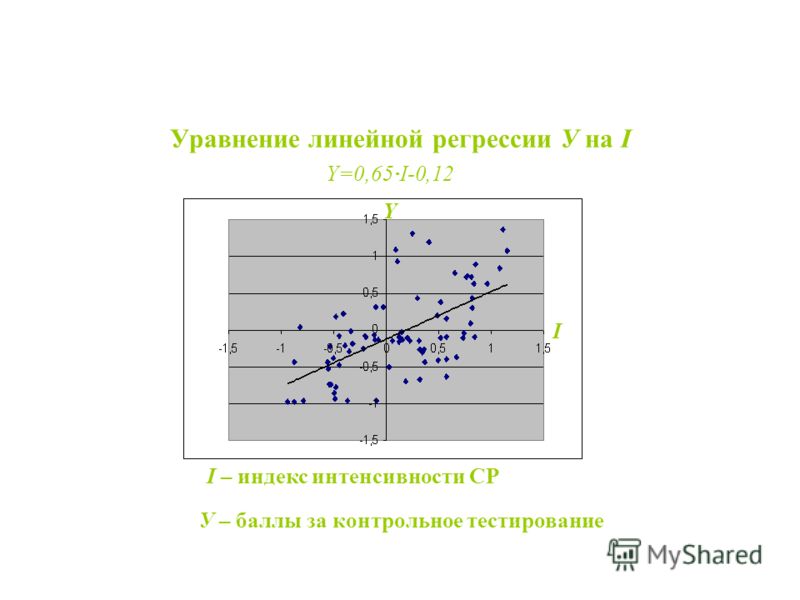 Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.
Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.
В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.
Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).
Корреляция для множественной регрессии
Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.
Уравнение множественной регрессии оценивают с помощью этого показателя.
Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.
Метод наименьших квадратов
Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.
Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.
Параметры уравнений
Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.
Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.
Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.
Сгруппированные данные
Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.
Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.
Множественное парное уравнение регрессии: оценка важности связи
Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x1,x2,…,xm)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.
Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.
Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.
Линейная функция изображается в форме такой взаимосвязи: у = а0 + a1х1 + а2х2,+ … + amxm. При этом а2, am, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.
Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах1b1 х2b2…xmbm. В данном случае показатели b1, b2….. bm – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.
Какие факторы необходимо учитывать при построении множественной регрессии
Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.
Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:
- Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.

- Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
- В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.
Методы построения
Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:
- Способ исключения.
- Способ включения.
- Пошаговый анализ регрессии.
Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.
Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.
Методы многомерного анализа
Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.
Формула регрессии | Пошаговый расчет (с примерами)
Формула регрессии оценивает взаимосвязь между зависимой и независимой переменными и выясняет, как она влияет на зависимую переменную при изменении независимой переменной.
Он представлен уравнением Y равно aX плюс b, где Y — зависимая переменная, a — наклон уравнения регрессии, x — независимая переменная, а b — константа.
В регрессионном анализе широко используются статистические методы для оценки отношений между одной или несколькими независимыми переменными и зависимыми переменными. РегрессияРегрессияРегрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее это мощный инструмент, поскольку он оценивает силу взаимосвязи между двумя или более переменными. Затем можно было бы использовать его для моделирования будущих отношений между этими переменными.
Y=a + bX + ∈
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Формула регрессии (wallstreetmojo.com)
Где:
- Y – зависимая переменная
- X – независимая (объясняющая) переменная
- a – точка пересечения
- b – наклон
- 1
- ∈ – и является невязкой (ошибкой)
Формула для точки пересечения «a» и наклона «b» может быть рассчитана, как показано ниже.
а= (Σy)(Σx 2 ) - (Σx)(Σxy)/ n(Σx 2 ) - (Σx) 2 b = n (σxy) - (σx) (σy) /n (σx 2 ) - (σx) 2
СОДЕРЖА
- Пример №1
- Пример №2
- Пример №3
Пояснение
Регрессионный анализ, как упоминалось ранее, в основном используется для поиска уравнений, которые соответствуют данным.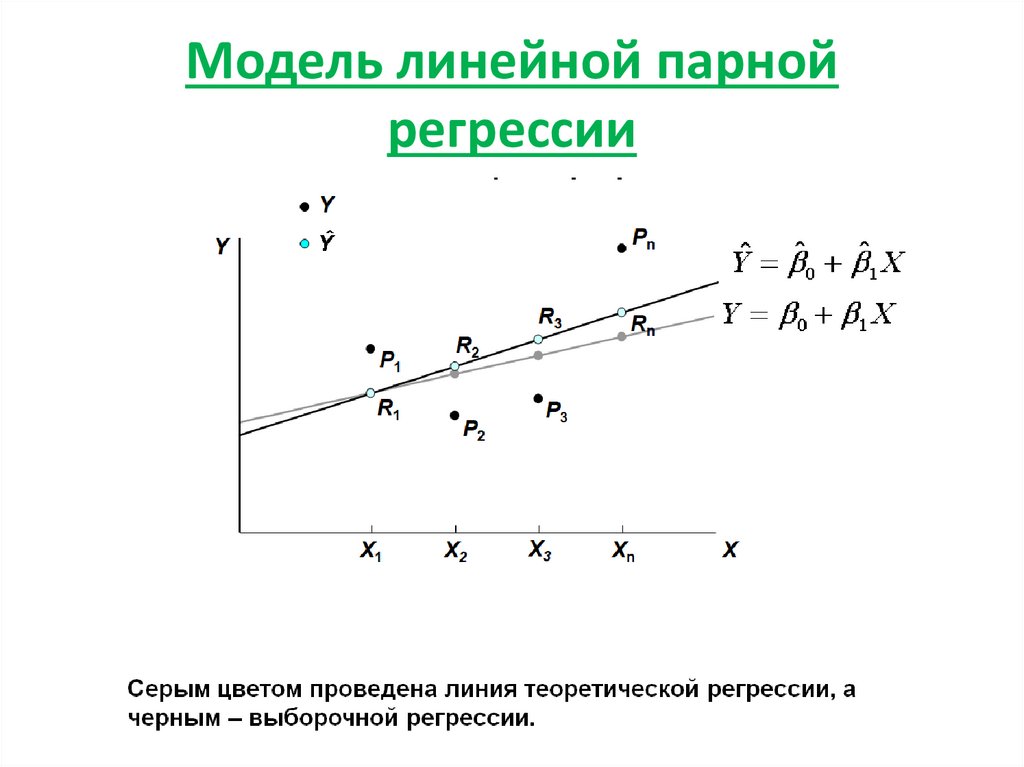 Линейный анализ — это один из видов регрессионного анализа. Например, уравнение для линии y = a + bX. Y является зависимой переменной в формуле, которая пытается предсказать, какой будет будущая стоимость. Будущая стоимость Формула будущей стоимости (FV) — это финансовая терминология, используемая для расчета стоимости денежного потока на футуристическую дату по сравнению с исходным чеком. Цель уравнения FV состоит в том, чтобы определить будущую стоимость предполагаемых инвестиций и определить, приносят ли доходы достаточную прибыль, чтобы учесть временную стоимость денег. Подробнее, если X, независимая переменная, изменяется на определенное значение. «а» в формуле — точка пересечения. Это означает, что значение остается постоянным независимо от изменений независимой переменной. Термин «b» в формуле представляет собой наклон, который означает, насколько зависимая переменная зависит от независимой переменной.
Линейный анализ — это один из видов регрессионного анализа. Например, уравнение для линии y = a + bX. Y является зависимой переменной в формуле, которая пытается предсказать, какой будет будущая стоимость. Будущая стоимость Формула будущей стоимости (FV) — это финансовая терминология, используемая для расчета стоимости денежного потока на футуристическую дату по сравнению с исходным чеком. Цель уравнения FV состоит в том, чтобы определить будущую стоимость предполагаемых инвестиций и определить, приносят ли доходы достаточную прибыль, чтобы учесть временную стоимость денег. Подробнее, если X, независимая переменная, изменяется на определенное значение. «а» в формуле — точка пересечения. Это означает, что значение остается постоянным независимо от изменений независимой переменной. Термин «b» в формуле представляет собой наклон, который означает, насколько зависимая переменная зависит от независимой переменной.
Вы можете скачать этот шаблон Excel с формулой регрессии здесь – Шаблон Excel с формулой регрессии
Пример № 1
Рассмотрим следующие две переменные x и y, вам необходимо выполнить расчет регрессии.
Решение:
Используя приведенную выше формулу, мы можем рассчитать линейную регрессию в excelЛинейная регрессия В ExcelЛинейная регрессия — это статистический инструмент Excel, который используется в качестве модели прогнозирующего анализа для изучения взаимосвязи между двумя наборами данных. Используя этот анализ, мы можем оценить взаимосвязь между зависимыми и независимыми переменными следующим образом.
У нас есть все значения в приведенной выше таблице с n = 5.
Теперь сначала вычислите точку пересечения и наклон для регрессии.
Расчет перехвата является следующим,
A = (628,33 * 88,017,46) — (519,89 * 106,206,14) / 5 * 88,017,46 — (519,89) 2
A = 0,52
.
b = (5 * 106 206,14) – (519,89 * 628,33) / (5 * 88 017,46) – (519,89) 2
b = 1,20
Давайте теперь введем значения в формулу регрессии, чтобы получить регрессию.
Отсюда линия регрессии Y = 0,52 + 1,20 * X
Пример #2
Государственный банк Индии недавно ввел новую политику, связывающую процентные ставки по сберегательным счетам со ставками репо. Поэтому аудитор Государственного банка Индии хочет провести независимый анализ решений, принятых банком в отношении изменения процентной ставки, и того, были ли они изменены всякий раз, когда происходили изменения в ставке репо. Таким образом, ниже приводится сводная информация о ставке репо и процентной ставке по сберегательному счету Банка, которая преобладала в эти месяцы.
Поэтому аудитор Государственного банка Индии хочет провести независимый анализ решений, принятых банком в отношении изменения процентной ставки, и того, были ли они изменены всякий раз, когда происходили изменения в ставке репо. Таким образом, ниже приводится сводная информация о ставке репо и процентной ставке по сберегательному счету Банка, которая преобладала в эти месяцы.
Аудитор Государственного банка Индии обратился к вам с просьбой провести анализ и представить его презентацию на следующей встрече. Используйте формулу регрессии и определите, изменилась ли ставка банка, как и когда она изменила ставку репо.
Решение:
Используя приведенную выше формулу, мы можем рассчитать линейную регрессию в Excel. Обращение с RepoRepoСоглашение об обратном выкупе или репо представляет собой краткосрочное заимствование для физических лиц, которые имеют дело с государственными ценными бумагами. Такое соглашение может заключаться между несколькими сторонами в трех типах: специализированная поставка, репо на хранении и репо с третьей стороной. Читать далее ставка как независимая переменная, то есть X, и учет ставки банка как зависимой переменной как Y.
Читать далее ставка как независимая переменная, то есть X, и учет ставки банка как зависимой переменной как Y.
У нас есть все значения в приведенной выше таблице с n = 6.
Теперь сначала вычислите точку пересечения и наклон для регрессии.
Расчет перехвата является следующим,
A = (24,17 * 237,69) — (37,75 * 152,06) /6 * 237,69 — (37,75) 2
A = 4,28
Расчет склона.
b = (6 * 152,06) — (37,75 * 24,17) / 6 * 237,69 — (37,75) 2
b = -0,04
Давайте теперь введем значения формул, чтобы получить цифру.
Следовательно, линия регрессии Y = 4,28 – 0,04 * X. Анализ: Государственный банк Индии действительно следует правилу связывания своей ставки сбережений со ставкой репо, поскольку некоторое значение наклона указывает на взаимосвязь между ставка репо и ставка сберегательного счета банка.
Пример #3
Лаборатория ABC исследует рост и вес и хотела узнать, есть ли какая-либо взаимосвязь, например, по мере увеличения роста будет увеличиваться и вес. Итак, они собрали выборку из 1000 человек для каждой категории и нашли средний рост в этой группе.
Итак, они собрали выборку из 1000 человек для каждой категории и нашли средний рост в этой группе.
Ниже приведены сведения, которые они собрали.
Вам необходимо выполнить расчет регрессии и прийти к выводу, что такие отношения существуют.
Решение:
Используя приведенную выше формулу, мы можем вычислить линейную регрессию в Excel. Рассматривая рост как независимую переменную, т.е. X, и вес как зависимую переменную как Y.
У нас есть все значения в приведенной выше таблице с n = 6
Теперь, во-первых, вычислите точку пересечения и наклон для регрессии.
Расчет перехвата является следующим образом,
A = (350 * 120,834) — (850 * 49 553) /6 * 120 834 — (850) 2
A = 68,63
Расчет склона — это следующее,
A = 68,63.
b = (6 * 49 553) – (850 * 350) / 6 * 120 834 – (850) 2
b = -0,07
Давайте теперь введем значения в формулу, чтобы получить цифру.
Отсюда линия регрессии Y = 68,63 – 0,07 * X
Анализ: Существует значительная, меньшая взаимосвязь между ростом и весом, поскольку наклон очень низкий.
Релевантность и использование формулы регрессии
Когда коэффициент корреляции Коэффициент корреляцииКоэффициент корреляции, иногда называемый коэффициентом взаимной корреляции, является статистической мерой, используемой для оценки силы взаимосвязи между двумя переменными. Его значения варьируются от -1,0 (отрицательная корреляция) до +1,0 (положительная корреляция). Читать дальше показывает, что данные могут предсказывать будущие результаты. Наряду с этим, точечная диаграмма одного и того же набора данных выглядит как линейная или прямая линия. Можно использовать простую линейную регрессию, используя наилучшее соответствие, чтобы найти прогностическое значение или прогностическую функцию. Регрессионный анализ имеет множество применений в финансах, поскольку он используется в CAPM, модели ценообразования капитальных активовМодель ценообразования капитальных активовМодель ценообразования капитальных активов (CAPM) определяет ожидаемый доход от портфеля различных ценных бумаг с различной степенью риска. Он также учитывает волатильность конкретной ценной бумаги по отношению к рынку. Читать далее метод в финансах. Его можно использовать для прогнозирования доходов и расходов фирмы.
Он также учитывает волатильность конкретной ценной бумаги по отношению к рынку. Читать далее метод в финансах. Его можно использовать для прогнозирования доходов и расходов фирмы.
Рекомендуемые статьи
Эта статья представляет собой руководство по формуле регрессии. Здесь мы узнаем, как рассчитать регрессию, используя ее формулу, практические примеры и загружаемый шаблон Excel. Вы можете узнать больше о моделировании в Excel из следующих статей: –
- Формула коэффициента Джини Формула коэффициента ДжиниКоэффициент Джини или индекс Джини – это статистическая дисперсия, отражающая дисперсию доходов среди населения страны, т.е. страна. читать дальше
- Формула корреляции
- Расчет коэффициента вариации Расчет коэффициента вариацииКоэффициент вариации — это систематизированная мера дисперсии вероятностного или частотного распределения. Он определяется как отношение стандартного отклонения к среднему. читать далее
- Регрессия против ANOVA
Что такое линейная регрессия? — Recast
Линейная регрессия — один из самых известных и понятных алгоритмов в статистике и машинном обучении. Любой, у кого есть доступ к Excel или Google Sheets, может использовать линейную регрессию, но не позволяйте ее простоте и доступности обмануть вас — она необоснованно эффективна для решения длинного списка общих проблем, что делает ее рабочей лошадкой в мире маркетинговой аналитики.
Любой, у кого есть доступ к Excel или Google Sheets, может использовать линейную регрессию, но не позволяйте ее простоте и доступности обмануть вас — она необоснованно эффективна для решения длинного списка общих проблем, что делает ее рабочей лошадкой в мире маркетинговой аналитики.
В этом посте вы увидите пример простой модели линейной регрессии и узнаете, как она работает, чтобы вы знали, как лучше всего использовать ее для получения информации из ваших маркетинговых данных. В этом посте вы узнаете:
- Как выглядит простая модель линейной регрессии в Excel / Google Таблицах
- Преимущества добавления дополнительных переменных с множественной линейной регрессией
- В чем разница между логистической и линейной регрессией
- Является ли линейной регрессия считается машинным обучением или просто статистика
- Что такое уравнение линейной регрессии и какие предположения мы делаем при его использовании
- Как использовать калькулятор линейной регрессии в Excel / Google Таблицах (+ бесплатный шаблон)
- Когда вместо этого имеет смысл использовать библиотеку Python SKLearn (+ бесплатный скрипт)
Вам не нужно много знать о статистике или математике, чтобы использовать линейную регрессию. Это введение в метод для начинающих, чтобы дать вам достаточно знаний, чтобы иметь возможность использовать его для решения бизнес-задач и понять, как лучше всего интерпретировать результаты проектов по науке о данных, которые вы делегируете своей команде.
Это введение в метод для начинающих, чтобы дать вам достаточно знаний, чтобы иметь возможность использовать его для решения бизнес-задач и понять, как лучше всего интерпретировать результаты проектов по науке о данных, которые вы делегируете своей команде.
Существует уже более 200 лет и изучается со всех сторон. К сожалению, это делает изучение линейной регрессии запутанным для новичка, потому что часто предполагается много предварительных знаний, а несколько имен используются взаимозаменяемо.
Простая модель линейной регрессии
В самом общем смысле линейная регрессия — это статистическая модель, которая предполагает наличие линейной зависимости между входными переменными (x) и одной выходной переменной (y). В частности, предполагается, что y можно вычислить из линейной комбинации входных переменных. Например, сумма, которую вы тратите на рекламу (x), влияет на количество продаж, которые вы получаете (y). Получив модель, мы можем оценить, сколько продаж вы получите на каждый доллар, потраченный на рекламу.
Формула линейной регрессии
Формула простой линейной регрессии с одной переменной x выглядит следующим образом:
y = B1*x + B0
Где
- y — количество продаж
- B1 — коэффициент рекламы , т. е. сколько продаж вы получите на каждый потраченный доллар
- x — сколько долларов вы потратите на рекламу
- B0 — сколько продаж вы получите, если потратите 0 долларов на рекламу
Когда коэффициент становится равным нулю, устраняет влияние этой переменной на модель. Если вы потратите ноль долларов на рекламу в течение одного месяца, модель предскажет базовый средний объем продаж или точку пересечения, представленную в формуле как B0.
Калькулятор линейной регрессии в Excel / Google Sheets
Если вы когда-либо строили линию тренда в Excel или Google Sheets, поздравляем, вы выполнили простую линейную регрессию! Отобразите уравнение на графике, и вы получите значения коэффициента (B1) и точки пересечения или константы (B0). Это, безусловно, самый простой способ запустить линейную регрессию, поэтому я предлагаю вам попробовать его сейчас, чтобы увидеть, насколько это просто, если вы еще этого не сделали.
Это, безусловно, самый простой способ запустить линейную регрессию, поэтому я предлагаю вам попробовать его сейчас, чтобы увидеть, насколько это просто, если вы еще этого не сделали.
Чтобы упростить понимание, мы создали калькулятор линейной регрессии в Google Sheets, который вы также можете загрузить в виде файла Excel. Он поставляется готовым с примерными данными, но вы можете вставить свои собственные, чтобы обновить диаграмму в шаблоне.
- Перейдите по этой ссылке, чтобы получить пример данных (если у вас нет собственных)
- Выберите все данные в двух столбцах, содержащих ваши переменные x и y.
- Нажмите «Вставка» > «Диаграмма» > «Точечная диаграмма». Ваша переменная y должна быть на вертикальной оси
- Добавьте линию тренда > Показать R2 > Показать уравнение для отображения формулы
Это то же уравнение регрессии, которое мы видели в предыдущем разделе, с моделью, оценивающей, что мы получаем 72,3 доллара в продажах на доллар, потраченный на рекламу (обе оси указаны в тысячах). Перехват или константа, то есть базовые продажи, которые мы получили бы без рекламы, оцениваются в 148 000 долларов.
Перехват или константа, то есть базовые продажи, которые мы получили бы без рекламы, оцениваются в 148 000 долларов.
Если мы хотим рассчитать, сколько продаж мы получим в неделю при еженедельном рекламном бюджете в 2000 долларов, мы можем подставить числа в уравнение, чтобы получить прогноз на основе модели.
72,3 * 2 + 148 = 292,6 тысячи долларов
Значение R2, равное 0,302, говорит нам, что эта модель может объяснить 30,2% данных о продажах, зная только сумму, потраченную на рекламу, что является относительно слабой корреляцией. Конечно, мы не можем полностью объяснить количество продаж, которое мы получим с помощью этой одной переменной — на продажи влияет множество различных факторов, таких как цена продукта или наличие праздника. Однако эта простая модель лучше, чем случайное угадывание, и на ее построение ушло очень мало времени и усилий.
Множественная линейная регрессия
При наличии одной входной переменной (x) метод называется простой линейной регрессией. Когда имеется несколько входных переменных, статистики называют этот метод множественной линейной регрессией.
Когда имеется несколько входных переменных, статистики называют этот метод множественной линейной регрессией.
В предыдущем разделе мы упоминали, что простая модель с одной переменной, представляющей сумму, потраченную на рекламу, не учитывает все факторы, влияющие на продажи. Если мы добавим дополнительные переменные x, мы сможем начать учитывать эти другие факторы и повысить точность нашей модели.
Для нескольких переменных мы больше не можем полагаться на линию тренда нашей диаграммы, поскольку каждая новая переменная представляет другое измерение. Мы можем работать с трехмерными диаграммами, но любые другие переменные не могут быть легко интерпретированы визуально. Теперь нам нужно перейти к использованию функции ЛИНЕЙН, предлагаемой как Excel, так и Google Sheets. Функция ЛИНЕЙН работает следующим образом:
ЛИНЕЙН(известные_y, [известные_x], [константа], [статистика])
Где
- известные_y — переменная y, которую мы пытаемся предсказать
- known_x — это несколько столбцов x, которые мы используем в качестве входных данных для нашей модели.

- const — хотим ли мы включить в нашу модель перехват или базовый уровень.
Совет для профессионалов: при использовании функции ЛИНЕЙН результаты выводятся в обратном порядке! Самая первая ячейка в первой строке — это коэффициент для последней введенной вами переменной, и оттуда они продолжаются в обратном порядке. Последнее число в верхней строке — это коэффициент для отрезка или константа.
- Перейдите по этой ссылке, чтобы получить доступ к шаблону и данным примера
- Используйте функцию ЛИНЕЙН, введя столбец y и несколько столбцов x
- Поставьте 1 для параметров const и stats
- Вывод первой строки ваши коэффициенты
- Первое число слева в третьей строке — это значение R2 вашей модели
В нашем примере мы видим, что наша модель намного лучше объясняет данные со значением R2 0,83. Также мы получаем кардинально обновленный коэффициент на рекламу. В нашей простой линейной регрессии он оценивался как 72,3 доллара продаж на один доллар, потраченный на рекламу, и теперь мы имеем более реалистичный коэффициент в 16 долларов.
 Коэффициент цены можно интерпретировать так: при увеличении цены продукта на 1 доллар мы теряем 17 000 долларов в продажах. Для праздника коэффициент означает, что мы зарабатываем 89 долларов.000 больше в праздники, чем не праздники. Наконец, в константе или перехвате говорится, что мы зарабатываем 415 000 долларов в среднем в неделю с учетом рекламы, цены и выходных.
Коэффициент цены можно интерпретировать так: при увеличении цены продукта на 1 доллар мы теряем 17 000 долларов в продажах. Для праздника коэффициент означает, что мы зарабатываем 89 долларов.000 больше в праздники, чем не праздники. Наконец, в константе или перехвате говорится, что мы зарабатываем 415 000 долларов в среднем в неделю с учетом рекламы, цены и выходных.Уравнение линейной регрессии
Рассчитать прогнозируемый объем продаж по нашей модели множественной регрессии немного сложнее, чем с помощью простой линейной регрессии, но это та же основная формула. У нас есть переменная y, которая является продажами, и B0, которая является константой или точкой пересечения, но на этот раз у нас есть несколько переменных x. Каждая переменная x умножается на соответствующую переменную B1, B2, B3, которая представляет собой коэффициент, затем эти значения складываются в конце.
y = B3*x3 + B2*x2 + B1*x1 + B0
Где
- y количество продаж
- B3 коэффициент для праздника, т.
 е. сколько продаж вы получаете, когда это праздник
е. сколько продаж вы получаете, когда это праздник - B2 — коэффициент для цены, т. е. сколько продаж вы теряете из-за увеличения цены
- B1 — коэффициент для рекламы, т. е. сколько продаж вы получаете на каждый потраченный доллар
- x3 — независимо от того, праздник сейчас или нет
- x2 — цена товара
- x1 — сколько долларов вы потратите на рекламу
- B0 — сколько продаж вы получите, если потратите 0 долларов на рекламу
Если мы хотим сделать прогноз с помощью этой модели множественной линейной регрессии, мы просто подставим коэффициенты как мы сделали раньше, и найдите значение y.
89 * 0 + -17 * 6,6 + 16 * 2 + 415 = 334,8 тысяч долларов
Из коэффициентов мы знаем, что праздничные дни приносят дополнительную прибыль в размере 89 000 долларов, и каждый доллар повышения цены приводит к потере 17 000 долларов в продажах, но нам нужно введите гипотетические будущие значения, чтобы сделать этот прогноз. Если мы введем ноль для праздника, этот термин умножится на ноль, так что эта переменная не окажет влияния.
 Для цены давайте использовать среднее значение, которое составляло 6,6 доллара. Наконец, давайте предположим, что мы тратим 2000 долларов на рекламу. Мы также должны не забыть добавить базовые продажи из константы, которая составляла 415 000 долларов.
Для цены давайте использовать среднее значение, которое составляло 6,6 доллара. Наконец, давайте предположим, что мы тратим 2000 долларов на рекламу. Мы также должны не забыть добавить базовые продажи из константы, которая составляла 415 000 долларов.Обыкновенный метод наименьших квадратов (OLS)
Как Excel или Google Таблицы на самом деле строят вашу модель линейной регрессии? Он использует обычные наименьшие квадраты (OLS), самый популярный метод построения модели линейной регрессии. По сути, он рисует линию наилучшего соответствия между точками данных, которые у вас есть, сводя к минимуму разницу между тем, где проходит линия, и точкой на диаграмме.
https://commons.wikimedia.org/wiki/File:Linear_least_squares_example2.pngТочнее, он минимизирует сумму квадратов разностей, то есть больше наказывает большие различия. Чем меньше различий, тем лучше модель соответствует данным. Результирующая модель может быть выражена простой формулой, особенно в случае простой линейной регрессии, в которой есть один регрессор в правой части уравнения регрессии.

МНК — не единственный метод оценки и не всегда лучший метод оценки, но он самый популярный и работает во многих ситуациях, поэтому он стал стандартом де-факто. Есть несколько предположений, которые необходимы для того, чтобы OLS был лучшим оценщиком для использования, и большая часть работы статистика или специалиста по данным при использовании линейной регрессии заключается в манипулировании данными или обновлении модели для удовлетворения этих условий.
Допущения линейной регрессии
Линейная регрессия — хороший алгоритм по умолчанию, но он не является лучшим во всех ситуациях. Он делает четыре важных предположения о данных. Если одно или несколько из этих предположений нарушаются, то результаты нашей линейной регрессии могут быть ненадежными или даже вводящими в заблуждение.
1. Линейная зависимость : Между каждой входной переменной x и выходной переменной y должна быть линейная зависимость.
2. Независимость : Ошибки – разница между прогнозируемыми и фактическими значениями – должны быть независимыми.
 Например, не должно быть корреляции между ошибками в последовательные дни в модели временных рядов.
Например, не должно быть корреляции между ошибками в последовательные дни в модели временных рядов.3. Гомоскедастичность : Ошибки имеют постоянную дисперсию на каждом уровне x. Когда это предположение не выполняется, вы, как правило, видите «разветвление» ошибок с течением времени.
4. Нормальность : Ошибки модели нормально распределены. т.е. они следуют распределению «колоколообразной кривой», когда вы наносите их на график.
Существует множество методов борьбы с нарушениями этих допущений. Например, если одна из ваших переменных x не имеет линейной связи с расходами, вы можете преобразовать данные, прежде чем включать их в свою модель. Это довольно распространенный прием при работе с убывающей отдачей от рекламы. Ответ также может состоять в том, чтобы удалить некоторые переменные, добавить другие переменные или собрать больше данных.
Байесовская линейная регрессия
Традиционная линейная регрессия представляет собой частотный подход, где модель представляет собой комбинацию значений x.
 Другая школа мысли — байесовская, где регрессия формулируется с использованием распределений вероятностей. Значение y не оценивается как единственное значение, вместо этого мы получаем вероятности его возможных значений.
Другая школа мысли — байесовская, где регрессия формулируется с использованием распределений вероятностей. Значение y не оценивается как единственное значение, вместо этого мы получаем вероятности его возможных значений.Целью байесовской линейной регрессии является не поиск единственного «наилучшего» значения параметров модели, а определение наиболее вероятного диапазона значений параметров модели. Это может обеспечить большую гибкость, поскольку позволяет нам «сообщить» модели то, что мы знаем о вероятном диапазоне значений, которые следует учитывать, используя априорные модели. Например, с помощью байесовского моделирования маркетингового комплекса мы можем указать, что маркетинговый канал вряд ли приведет к отрицательным продажам.
Байесовские методы позволяют провести экспертизу предметной области и дают нам оценку неопределенности в нашей модели. Если у нас нет хорошего представления о влиянии переменной, она будет иметь широкий «правдоподобный» диапазон. Используя моделирование методом Монте-Карло, мы можем учитывать это при составлении прогнозов и понимать вероятность потенциальных будущих результатов.
 Это может быть сложнее вычислить и использовать, чем OLS, но рекомендации лучше соответствуют нашей интуиции и тому, как мы на самом деле рассуждаем в реальном мире.
Это может быть сложнее вычислить и использовать, чем OLS, но рекомендации лучше соответствуют нашей интуиции и тому, как мы на самом деле рассуждаем в реальном мире.Логистическая и линейная регрессия
https://www.analyticsvidhya.com/blog/2020/12/beginners-take-how-logistic-regression-is-related-to-linear-regression/Линейная и логистическая регрессия похожи , поскольку они оба используют линейные уравнения для прогнозов. Однако функционал совершенно другой. Линейная регрессия используется для прогнозирования непрерывных переменных, таких как продажи или доход. Принимая во внимание, что логистическая регрессия используется для задач классификации, таких как прогнозирование того, нажмет ли пользователь на рекламный баннер или совершит покупку на веб-сайте. Для этого логистическая регрессия использует оценку максимального правдоподобия, а не обычный метод наименьших квадратов.
Является ли линейная регрессия машинным обучением?
Машинное обучение (МО) — это изучение компьютерных алгоритмов, которые могут автоматически улучшаться благодаря опыту и использованию данных, и считается подпадающим под категорию искусственного интеллекта.
 Машинное обучение в первую очередь связано с минимизацией ошибки модели или созданием максимально точных прогнозов, что часто достигается за счет объяснимости.
Машинное обучение в первую очередь связано с минимизацией ошибки модели или созданием максимально точных прогнозов, что часто достигается за счет объяснимости.Линейная регрессия была разработана в области статистики, но это не значит, что это не машинное обучение, поскольку относительно более новая область заимствует алгоритмы и методы из того, что было раньше. Линейная регрессия считается контролируемым алгоритмом машинного обучения, потому что модель учится на данных, как лучше всего соответствовать линии между независимыми (x) и зависимыми (y) переменными. В отличие от многих алгоритмов машинного обучения, линейная регрессия вполне объяснима и проста в использовании, поэтому она воспринимается как метод машинного обучения «начального уровня».
История линейной регрессии
- Лежандр публикует метод наименьших квадратов в 1805 г.
- Гаусс публикует дополнительную информацию по этой теме в 1809 г. «регрессия» введена Гальтоном в 1885 г.
- Фишер разъясняет некоторые допущения, необходимые в 1922 г.



 Он представлен уравнением Y равно aX плюс b, где Y — зависимая переменная, a — наклон уравнения регрессии, x — независимая переменная, а b — константа.
Он представлен уравнением Y равно aX плюс b, где Y — зависимая переменная, a — наклон уравнения регрессии, x — независимая переменная, а b — константа.
 Коэффициент цены можно интерпретировать так: при увеличении цены продукта на 1 доллар мы теряем 17 000 долларов в продажах. Для праздника коэффициент означает, что мы зарабатываем 89 долларов.000 больше в праздники, чем не праздники. Наконец, в константе или перехвате говорится, что мы зарабатываем 415 000 долларов в среднем в неделю с учетом рекламы, цены и выходных.
Коэффициент цены можно интерпретировать так: при увеличении цены продукта на 1 доллар мы теряем 17 000 долларов в продажах. Для праздника коэффициент означает, что мы зарабатываем 89 долларов.000 больше в праздники, чем не праздники. Наконец, в константе или перехвате говорится, что мы зарабатываем 415 000 долларов в среднем в неделю с учетом рекламы, цены и выходных. е. сколько продаж вы получаете, когда это праздник
е. сколько продаж вы получаете, когда это праздник Для цены давайте использовать среднее значение, которое составляло 6,6 доллара. Наконец, давайте предположим, что мы тратим 2000 долларов на рекламу. Мы также должны не забыть добавить базовые продажи из константы, которая составляла 415 000 долларов.
Для цены давайте использовать среднее значение, которое составляло 6,6 доллара. Наконец, давайте предположим, что мы тратим 2000 долларов на рекламу. Мы также должны не забыть добавить базовые продажи из константы, которая составляла 415 000 долларов.
 Например, не должно быть корреляции между ошибками в последовательные дни в модели временных рядов.
Например, не должно быть корреляции между ошибками в последовательные дни в модели временных рядов. Другая школа мысли — байесовская, где регрессия формулируется с использованием распределений вероятностей. Значение y не оценивается как единственное значение, вместо этого мы получаем вероятности его возможных значений.
Другая школа мысли — байесовская, где регрессия формулируется с использованием распределений вероятностей. Значение y не оценивается как единственное значение, вместо этого мы получаем вероятности его возможных значений. Это может быть сложнее вычислить и использовать, чем OLS, но рекомендации лучше соответствуют нашей интуиции и тому, как мы на самом деле рассуждаем в реальном мире.
Это может быть сложнее вычислить и использовать, чем OLS, но рекомендации лучше соответствуют нашей интуиции и тому, как мы на самом деле рассуждаем в реальном мире. Машинное обучение в первую очередь связано с минимизацией ошибки модели или созданием максимально точных прогнозов, что часто достигается за счет объяснимости.
Машинное обучение в первую очередь связано с минимизацией ошибки модели или созданием максимально точных прогнозов, что часто достигается за счет объяснимости.