Прэктная работа по теме «Системна линейных уравнений»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
МАЛАЯ АКАДЕМИЯ НАУК УЧАЩЕЙСЯ МОЛОДЕЖИ
| Отделение: математика |
Система линейных уравнений
| Работу выполнила: |
| Научный руководитель: |
Свердловск – 2018
СОДЕРЖАНИЕ
Введение…………………………………………………………………………3
1.
Система линейных уравнений с двумя переменными………………………7
1.1 Понятие о системах уравнений …………………………………………7
1.2 Способ подстановки………………………………………………………8
1.3 Способ алгебраического сложения………………………………………8
1.4 Способ сравнения………………………………………………………..10
1.5.Геометрическая
интерпретация решений системы
двух линейных уравнений с двумя неизвестными………………………11
2. Метод Гаусса…………………………………………………………………………………………………16
3.Метод Крамера ……………………………………………………………………………………………..19
4. Геометрическая интерпретация решения системы трех
линейных
уравнений с тремя неизвестными……………………………………………………………………24
5.Решение систем линейных уравнений с параметрами………………………………..27
6.Решение систем уравнений на EXCEL…………………………………………………………….30
Заключение……………………………………………………………………………32
Список используемых источников……………………………………………….33
ВВЕДЕНИЕ
«Перед
вами система линейных уравнений с двумя переменными Что
скрывается за этими скупыми значками? Математик даст общий ответ: «Это система
из двух линейных уравнений с двумя переменными.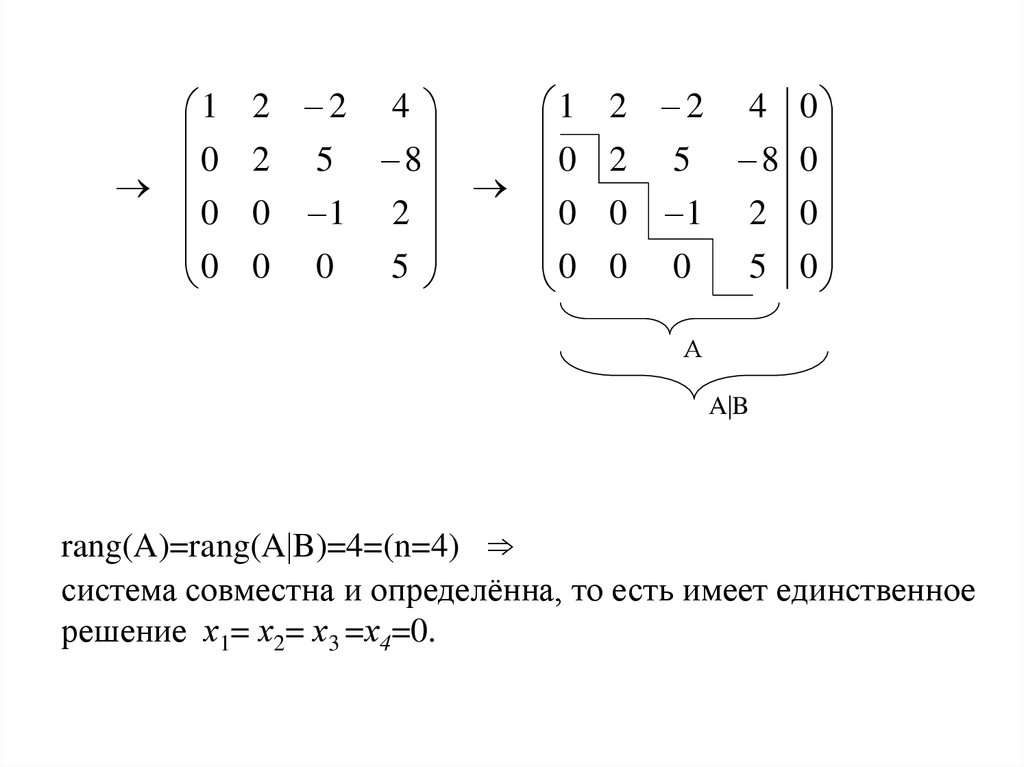
Но что она выражает, сказать не
могу» Если обратиться за ответом к инженерам разных специальностей, то услышим
разные ответы.
Инженер-электрик скажет, что передним уравнения напряжения или токов в электрической цепи с активными напряжениями.
Инженер-механик верен, что это уравнения равновесия сил для системы рычагов или пружин.
Инженер-строитель сообщит, что имеет дело с уравнениями, связывающими силы и деформации в какой-то строительной конструкции.
Инженер-плановик авторитетно заявит, что это уравнения для расчета загрузки станков. Так какой же из ответов правильный? Каждый из них верен. Да одна и та же система линейных уравнений может отображать равновесное состояние и электрической цепи, и рычагов, и строительной конструкции. Все зависит от того, что скрывается за постоянными коэффициентами и символами неизвестных — и.» (Пекелис1973,стр190-191)
Различные явления действительности имеют поразительное математическое сходство.
Так о системе уравнений и применении её в различных сферах производства говорится
в книге изданной почти полвека назад.
За это время мир очень изменился.
Только о системах линейных уравнений не забыли. Наоборот с развитием экономики возросла необходимость прогнозировать экономические риски, востребован их анализ , которые делаются на основе решения систем линейных уравнений со многими переменными. Внимание к методам решения систем линейных уравнений только возрастает.
В нашем примере фигурируют только уравнения с двумя переменными, а ведь количество переменных и уравнений в системе может быть неограниченным. При решении теоретических и практических задач в науке, технике, производстве приходится иметь дело с системами уравнений с несколькими неизвестными.
Системы линейных уравнений приходят на помощь, когда приходится иметь дело с заведомо малыми величинами, старшими степенями которых можно пренебречь, что сводит эти уравнения линейным.
Развитие
экономики, повлекшее за собой необходимость решать задачи математической
экономики, как правило, сводящихся к системе линейных уравнений с большим
числом переменных обусловило поиск различных способов решений систем уравнений.
Для решения систем линейных уравнений с переменными с давних времен использовали исключения.
В XVII—XVIII вв. над решением систем линейных уравнений работали такие ученые, как Ферма, Ньютон, Лейбниц, Эйлер, Лагранж и другие.
Решение системы уравнений выраженное формулами , впервые использовал в 1675г. немецкий математик Г.Лейбниц, что способствовало развитию теории определителей.
Интересно, что определители были открыты дважды .Сначала — без теоретического обоснования, но с правилами практического применения —в древнем Китае, еще в начале нашей эры, а может и раньше. А уже в XVIII В. Метод определителей открыл Лейбниц в процессе разработки универсального метода решения систем линейных уравнений, что и привело к введению понятия определителей.
Из изучения определителей, решения систем линейных уравнений с многими переменными начинается очень важный раздел современной математики — линейная алгебра.
Сталкиваясь
на уроках математики с системами линейных уравнений, мы их решали способом
подстановки, сложения и иллюстрировали их решение с помощью графиков.
При выполнении этой работы была поставлена цель, изучить различные способы решения систем линейных уравнений с последующим оптимальным применением того или иного способа при дальнейшем решении систем.
Актуальность работы вызвана тем, что с помощью линейных уравнений математически модулируют все большее число процессов в технике, экономике, производстве, науке.
В работе ставились следующие задачи:
1.Изучить литературу по методам решения систем линейных алгебраических
уравнений.
2.Рассмотреть способы решения систем линейных алгебраических уравнений
различными методами.
1.
СИСТЕМЫ
ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
1.1 Понятие о системах уравнений
Совокупность нескольких уравнений с несколькими переменными называют системой уравнений (неизвестное обозначенное одной и той же буквой в каждом из уравнений , должно обозначать одну и ту же неизвестную величину)
Система (1.1) где и — неизвестные, а —коэффициенты системы, а — свободные члены, называется системой двух линейных уравнений с двумя неизвестными.
Если , то система называется однородной, в остальных случаях — неоднородной.
Система
называется совместной, если она имеет хотя бы одно решение, и называется несовместной, если у нее нет ни одного решения.
Совместная система вида называется определенной, если она имеет
единственное решение; если у нее есть хотя бы два различных решения, то она
называется неопределенной.
Решением
системы уравнений с несколькими неизвестными называется совокупность значений
этих неизвестных, обращающая каждое уравнение системы в тождество.
Решить систему уравнений, значит найти множество все её решений или показать, что она решений не имеет.
Не существует общего аналитического способа решения систем, все методы основаны на численных решениях. Основная задача при решении — это правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. В школьном курсе математики подробно описаны такие методы как алгебраическое сложение, подстановка, а так же графический способ.
1.2 Способ подстановки
Чтобы решить систему (1.1), из первого уравнения системы найдем при . Подставив найденное значение во второе уравнение системы (1.1), получим , откуда . Если , то . Тогда . Итак, решением системы при (1.1) является пара чисел
Блок-схема решения системы (1.1) способом подстановки представлена на схеме 1.1.
Пример 1.Решим систему уравнений:
Решение
Ответ: (3,2)
Уравнения могут быть сложными, и выражение
переменной через вторую неизвестную окажется слишком громоздким для дальнейших
вычислений.
Когда неизвестных в системе больше 3-х решение подстановкой также
нецелесообразно.
1.3 Способ алгебраического сложения
Чтобы решить систему (1.1) способом алгебраического сложения, умножим обе части первого уравнения на второго на . Получаем Полагая что система имеет решение, складываем левые и правые части уравнений системы; получаем откуда находим при . Аналогично поступаем, чтобы найти умножим обе части первого уравнения системы (1.1) на а второго на Получаем складываем левые и
правые части уравнений: откуда при . Таким образом, если .
Поскольку система уравнений решена в предположении, что она имеет решения, то необходимо подстановкой убедиться, что найденная пара чисел — решения этой системы.
Для
применений данного метода необходима практика и наблюдательность. Решить
систему линейных уравнений методом сложения при количестве переменных 3 и более
непросто. Алгебраическое сложение удобно применять, когда в уравнениях
присутствуют дроби и десятичные числа.
Блок-схема решения системы (1.1) способом сложения представлена на схеме 1.2.
Пример 2. Решим систему уравнений:
Решение
Умножим обе части первого уравнения системы на 3, а второго на -2. имеем: Почленно сложим левые и правые части полученных уравнений: Подставим найденное значение в одно из уравнений системы и решим его:
Ответ: (-34, 5;-28)
1.4 Способ сравнения
Чтобы решить систему (1.1) способом сравнения, найдем или из каждого уравнения системы: и . Приравнивая полученные для выражения , найдем , . Таким образом, система если , имеет решение
Блок-схема решения системы (1.1) способом сравнения представлена на схеме 1.3.
Пример 3. Решим систему уравнений:
Решение
Выразим переменную из каждого уравнения системы: и . Приравняв полученные выражения имеем Подставим найденное значение в первое уравнение получим
Ответ: (2;5)
1.
5 Геометрическая
интерпретация решений системы двух линейных уравнений с двумя неизвестными
Если предположить, что в каждом уравнений системы, по крайней мере один из коэффициентов при переменных отличен от нуля, то каждое из уравнений является уравнением прямой линии.
Если определитель системы , то это означает, что если
1)все коэффициенты отличны от нуля, то и так как то обе прямые пересекаются в единственной точке, координаты которой и образуют решение системы. ( рис.1.1)
|
2) Если хотя бы
один из коэффициентов при переменных равен нулю, например , то, по нашему условию, и, следовательно, (иначе
). Поэтому данная система равносильна системе
уравнений перпендикулярных прямых (одна из
которых параллельна оси ординат, другая — оси абсцисс), пересекающихся в одной
точке.
(рис.1.2).
Если же
определитель системы равен нулю, то коэффициенты при переменных пропорциональны
и, следовательно, либо система эквивалентна одному уравнению и обе прямые
совпадают и система имеет бесконечное множество решений
(рис.1.3), либо система не имеет решений и обе прямые параллельны и не
совпадают (рис.1.4)
Блок-схема геометрической интерпретации решений представлена на схеме 1.4
Блок-схема
решения системы
двух линейных уравнений с двумя
переменными способом подстановки
Блок-схема
решения системы
двух линейных уравнений с двумя
переменными способом сложения
Блок-схема решения системы
двух линейных уравнений с двумя
переменными способом сравнения
| ||||
3
- МЕТОД ГАУССА
Рассмотрим решение систем линейных уравнений методом Гаусса. Пусть задана система трёх линейных уравнений с тремя неизвестными и: (3.1) .
Разделим обе части первого уравнения системы (3.1) на . Получим (3.2)
Умножим обе части уравнения (3.2) на и отнимим от второго уравнения системы (3.1). Получим:
Умножим обе части уравнения (3.2) на и отнимим от третьего уравнения системы (3.2). Получим: Имеем систему: Пусть Тогда (3.3)
Разделим обе части первого уравнения системы (3.3) на имеем Умножим обе части этого уравнения на отнимим его отвторого уравнения системы (3.3). Получим: Обозначим После проведенных преобразований получим систему треугольного
вида:
Теперь, начиная с последнего
уравнения, легко определить значения всех переменных.
Если то средикоэффициентов системы (3.1) при существует хотя бы один, отличный от
нуля. Это уравнение и считается первым.
Пример 1. Решите систему уравнений
Решение
Умножим обе части первого уравнения системы на 2 и отнимим его от второго уравнения, потом обе части первого уравнения умножим на 4 и отнимим его от третьего. Имеем систему Эта система имеет бесконечно много решений. Выразим через Подставив в первое уравнение исходной системы, имеем: Таким образом система имеет бесконечно много решений.
Ответ: ,
Пример2. Решите систему уравнений
Решение
Умножим обе части первого уравнения системы на 2 и отнимим его почленно от второго уравнения, потом отнимем первое уравнение от третьего. Получим систему уравнений Теперь прибавим второе и третье уравнения полученной системы. Имеем Поскольку третье уравнение системы не имеет решений , то система несовместна.
Ответ: система несовместна.
3.МЕТОД КРАМЕРА
Одним из наиболее распространенных методов решения линейных систем является метод Крамера.
Рассмотрим систему двух линейных уравнений с двумя неизвестными и : Числа называют коэффициентами системы, а — свободными членами. При решении системы линейных уравнений методом сложения были найдены следующие решения ; .
Проанализировав полученные результаты, можно установить правило, по которому составлены выражения для нахождения и. Коэффициенты системы образуют таблицу , которую называют квадратной матрицей второго порядка.
Число называют определителем этой матрицы. Его обозначают так: . Это определитель второго порядка, его называют определителем системы
Определитель второго порядка можно вычислить по схеме: =.
Обратим внимание на числители в формулах, полученных для
нахождения и .
Их тоже можно рассматривать как определители
второго порядка. Обозначаются они ; .
Теперь можно записать: ; .
Полученные формулы называют формулами Крамера. Анализируя их, видим, что при решении системы возможны такие случаи.
1.. Система имеет единственное решение; ; .
2.; ; . Система не имеет решений.
3. ;; . Система имеет бесконечно много решений.
Пример 1. Решите систему уравнений
Решение
;
; .
Следовательно, ; .
Ответ:.
Пример 2. Решите систему уравнений
Решение
;
; .
Следовательно, данная система имеет бесконечно много решений. Любое из них
можно получить, взяв произвольное значение , а
потом выразивши из уравнения. Например, если , то То
есть пара — одно из решений системы.
Ответ: система имеет множество решений.
Пример 3. . Решите систему уравнений
Решение
;
; .
Следовательно, данная система не имеет решений.
Ответ: система несовместна.
Формулы Крамера можно обобщить на случай системы трех линейных уравнений с тремя неизвестными.
Рассмотрим систему
— коэффициенты системы; — свободные члены системы
Запишем, как и в системе с двумя неизвестными, таблицу коэффициентов системы — квадратную матрицу третьего порядка: .
Число = называют определителем этой матрицы.
Вычисление определителя третьего порядка можно выполнить по такой схеме:
— .
Следовательно, ; ;.
То есть если , то решением системы будет тройка чисел , таких, что ; ; .
Эти формулы так же называют формулами Крамера.
Пример 4. . Решите систему уравнений
Решение
;
; =-4; .
Отсюда, ; ; .
Ответ: .
Пример 5. . Решите систему уравнений
Решение ; ; ; .
Ответ:
Пример 6. Решите систему уравнений
Решение
;
; ; .
Система не имеет решений.
Ответ: система несовместна.
Пример 7 Решите систему уравнений
Решение ; ;
;
Ответ: система имеет множество решений.
4.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ РЕШЕНИЙ СИСТЕМЫ ТРЕХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ТРЕМЯ НЕИЗВЕСТНЫМИ
Известно, что всякое линейное уравнение, (4.1) у которого хотя бы один из коэффициентов при переменных отличен от нуля, изображает в координатном пространстве плоскость. Более точно: в координатном пространстве существует такая плоскость , координаты каждой точки которой удовлетворяют уравнению (4.1), и, наоборот, всякая точка, координаты которой удовлетворяют уравнению (4.1), лежат в плоскости
Будем предполагать, что в каждом
уравнении системы трех линейных уравнений (4.2)
хотя бы один из коэффициентов при переменных отличен от нуля. Тогда каждое из
этих уравнений является уравнение плоскости в координатном пространстве, и,
следовательно, множество решений этой системы является множеством всех точек
координатного пространства, лежащих в каждой из этих плоскостей, и, значит,
совпадает, с их пересечением.
Пусть первое уравнение системы является
уравнением плоскости , второе — плоскости , третье —плоскости.
Решая систему (4.2) методом последовательного исключения переменных, мы получим треугольную систему, либо равносильную систему, в которой число уравнений меньше числа переменных и среди уравнений системы нет противоречивых уравнений, либо систему, в которой одно из уравнений противоречиво.
Рассмотрим геометрический смысл каждого из случаев.
1)Если данная система равносильна треугольной, то она имеет единственное решение. Геометрически это означает, что все три плоскости пересекаются в одной точке (рис.1).
2) а)Если данная система равносильна системе, состоящей из одного уравнения, то она имеет бесконечное множество решений, лежащих в одной плоскости. Геометрически это означает, что все три плоскости совпадают.
Пример1.
б)
Если данная система уравнений методом последовательного исключения переменных
сводится к равносильной совместной системе двух уравнений с тремя переменными,
то геометрически это означает, что она имеет бесконечное множество решений,
лежащих на линии пересечения всех трех плоскостей и (рис.
3)
Пример 2. Решить систему
Решение
Решим последнюю систему уравнений относительно переменных и
|
|
|
5
3)Если данная система уравнений методом последовательного исключения переменных сводится к системе противоречивых уравнений, то она решений не имеет. Геометрически это означает, что пересечение плоскостей и пусто. Так будет, например, если все три плоскости попарно параллельны и не совпадают(рис.4.3), или две плоскости параллельны ( но не совпадают), а третья их пересекает(рис.4.4), или плоскости попарно пересекаются, ограничивая бесконечную трехгранную призму.(рис.4.5)
5.РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ПАРАМЕТРАМИ
Решить систему уравнений с параметром
значит найти для любого допустимого значения параметра все решения заданной
системы.
Системаимеет единственное решение если ;
не имеет решений если ;
имеет множество решений если .
Пример 1. Найти все значения параметра, при которых система имеет единственное решение.
Решение
1) Система имеет единственное решение, если то есть при
2) отдельно нужно рассмотреть случаи и
При исходная система принимает вид: которая, решений не имеет.
При получим следовательно, система имеет единственное решение.
Ответ. Если
Пример 2. Найти все значения параметра, при которых
система не имеет решений.
Решение
Система не имеет решений, если
1)Отдельно рассмотрим каждый из случаев.
При получим систему, которая имеет бесконечно много решений.
При получим систему,
которая не имеет решений.
2)При получим систему которая
имеет единственное решение.
Ответ. Если
Пример 3 При каких значениях параметра cистема
имеет решение при любом значении параметра ?
Решение
Отнимем от первого уравнения второе. Получим равносильную систему: Первое
уравнение полученной системы, а также и вся система, имеет одно решение, если Если то
уравнение, а вместе с ним и исходная система, будет иметь множество решений в
случае, если
Ответ. Если
Пример 4. Определить при каких значениях система имеет единственное решение; бесчисленное множество решений; не имеет решений.
Решение
Найдем, при каких значениях определитель системы
равен нулю:
или откуда и
Если ито определитель системы т.е. система имеет единственное решение.
Проверим равенство при и При получаем или т.е. система имеет бесчисленное множество решений.
При получаем илит.е. система решений не имеет.
Ответ: при и система имеет одно решение;
при — бесчисленное множество решений;
при — не имеет решений.
6.
РЕШЕНИЕ
СИСТЕМ УРАВНЕНИЙ НА EXCEL
1) Метод обратной матрицы
Решим с помощью EXCEL систему
уравнений Откроем программу EXCEL. Запишем нашу
систему в виде двух таблиц: таблицы коэффициентов и свободных членов. Найдем
определитель системы, если он равен нулю, то система решений не имеет. Для
вычисления определителя в EXCEL есть функция «МОПРЕД». В одной из ячеек ниже
вычислим определитель нашей системы. Он равен 52, значит, система имеет
решение. Дальше вычислим обратную матрицу. Выделим такую же область ячеек, как
область таблицы с коэффициентами (в нашем случае это3х3), вводим функцию
«МОБР» и диапазон матрицы коэффициентов. Нажимаем «Ctrl»+
«Shift»+ «Enter» на клавиатуре и
фукция вычисляет обратную функцию. Для того чтобы умножитьобратную матрицу на
столбец свободных членов используем функцию «МУМНОЖ» Выделяем столбец в котором
колличество строк равно колличеству неизвестных нашей системы. После этого
нажимаем «=» и вводим функцию «МУМНОЖ», задаем диапазоны ячеек – сначала
обратной матрицы , затем – столбца свободных членов .
Жмем ОК.
В нашем примере, при умножении матрицы на столбец, получится столбец с тремя
строчками. Поэтому выделив первоначально столбец с тремя строками нажимаем F2,
затем Ctrl+Shift+Enter и получаем ответ.
Ответ: (2;3;1)
2)Метод Крамера
Решим методом Крамера Для этого найдем определители, используя функцию «МОПРЕД»
В ячейку В17 введем формулу =МОПРЕД(А3:С5),
В ячейку В18 введем формулу =МОПРЕД(F3:H5),
В ячейку В19 введем формулу =МОПРЕД(А10:С12),
В ячейку В20 введем формулу =МОПРЕД(F10:F12).
Найдем корни системы уравнений, для этого в ячейку G17 введем:=В18/D17, в ячейку G18 введем = В19/D17, в ячейку G20 введем В20/D17. Получим корни системы уравнений (3;1;2)
ЗАКЛЮЧЕНИЕ
Результаты исследования по теме «Системы линейных уравнений»
способствовали более глубокому понимании
алгоритмов решения систем линейных уравнений методами, применяемыми в школьном
курсе.
Также в процессе данного исследования мне пришлось познакомится с
методами Гаусса и Крамера , которые в дальнейшем понадобятся при обучении в высшей школе .Наибольший
интерес вызвала возможность решать системы уравнений с помощь компьютерной
программы EXCEL.
В перспективе было интересно рассмотреть и научиться решать системы линейных
уравнений другими способами , в частности методом Гаусса, а также с
использование он-лайн калькуляторов для решения систем.
Результаты даного исследовани могут быть полезны ученикам, которые приступают к узучению методов решения систем линейных уравнений. Вероятно работа будет полезна и учителям математики при знакомстве с методпми решения систем с помощью ESCEL.
Результаты исследования заставили меня задуматься о возможности различных подходов к решению тех или иных проблем. При решении тех или иных задач можно и нужно искать оптимальные варианты их решения. И это касается не только решений систем линейных уравнений.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1.