7. Полярная система координат. Построениие линии в полярной системе координат
Полярная система координат на плоскости задаётся точкой О, называемой полюсом, и направленной прямой Ох, называемой полярной осью. С каждой точкой Р плоскости, на которой задана полярная система координат, можно связать определённую пару чисел r, φ (полярные координаты). Полярный радиус r есть длина отрезка ОР, а полярный угол φ – радианная мера угла хОР, отсчитанного в направлении, противоположном вращению часовой стрелки (рис. 7.1) (в противном случае угол считается отрицательным).
Рис. 7.1
Угол φ определён с точностью до слагаемого 2kπ, где k –любое целое число. Точка (r; φ) по определению совпадает с точкой (–r; ± π): это условие связывает определённую точку плоскости с каждой парой чисел (
Для полюса О величина φ не определена.Если полюс и полярная ось совпадают, соответственно, с началом О и осью Ох прямоугольной системы координат (рис 7.1), то при условии, что для измерения r, х, у использованы равные единицы масштаба, от прямоугольной системы координат можно перейти к полярным и наоборот. Переход от полярных координат к прямоугольной системы осуществляется по следующим формулам:
(7.1)
Если необходимо от прямоугольной системы перейти к полярным координатам, то следует использовать преобразования:
(7.2)
Пример 1. Построить точки, заданные полярными координатами: А (3; π/4), В (2; 3π/4), С (–3; π/4), D (1; –π/4), Е (–4; π/3).
Решение. Выполним
построения (рис 7.
2)
Рис. 7.2
Пример 2. Определить, какую линию представляет уравнение r = 2 sinφ.
Решение. Переходя к прямоугольной системе координат, по формулам (7.2) имеем
то есть или .
Таким образом, данное уравнение представляет окружность радиуса 1 с центром в точке С (0; 1) (рис. 7.3), проходящую через полюс О и касающуюся полярной оси Ох.
Рис.7.3.
Пример
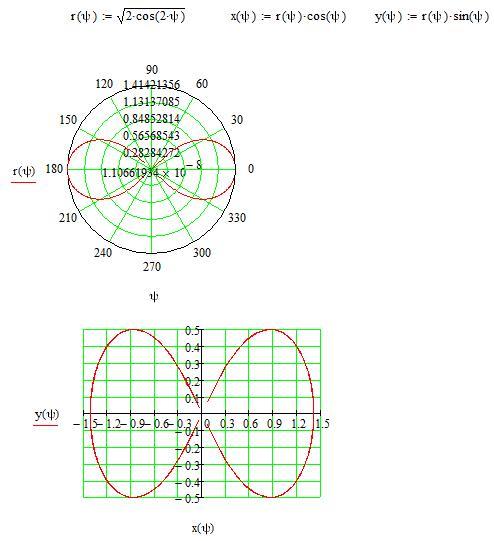
а) ; б) .
Решение. а) Используя калькулятор, составим таблицу значений функции r (вычисления выполняем с двумя знаками после запятой):
φ | r | φ | r | φ | r |
0 π/8 π/4 3π/8 π/2 5π/8 | ∞ 13,14 3,41 1,62 1 0,72 | 3π/4 7π/8 π 9π/8 5π/4 11π/8 | 0,59 0,52 0,5 0,52 0,59 | 3π/2 13π/8 7π/4 15π/8 2π | 1 1,62 3,41 13,14 ∞ |
По данным точкам
построим линию (рис.
7.4).
Рис. 7.4
По формулам (7.2) найдём уравнение линии в системе хОу:
.
Упростив последнее выражение, придём к уравнению
– х –1 = 0
Решив полученное иррациональное уравнение, имеем у2 = 2( х + 1/2).
Уравнение у2 = 2( х +1/2) в декартовой системе координат определяет параболу, симметричную относительно оси Ох с вершиной в точке у = 0, x = –1/2.б) Составим таблицу значений функции r (вычисления выполняем с двумя знаками после запятой):
φ
cos φ
r
φ
cos φ
r
0
1
–5
9π/8
–0,92
0,75
π/8
0,92
–7,19
5π/4
–0,71
0,86
π/4
0,71
29,14
11π/8
–0,38
1,10
3π/8
0,38
3,40
3π/2
0
1,67
π/2
0
1,67
13π/8
0,38
3,40
5π/8
–0,38
1,10
7π/4
0,71
29,14
3π/4
–0,71
0,86
15π/8
0,92
–7,19
7π/8
–0,92
0,75
2π
1
–5
π
–1
0,71
По данным точкам
построим линию (рис.
7.5):
Рис 7.5
Уравнение линии задано формулой
,
Решаем иррациональное уравнение:
9∙(x2 + y2 )= 25 +40x +16x2,
9x2 + 9y2 –40x
–16x2 = 25.Приведем уравнение линии к каноническому виду
9y2 –7x2 –40x = 25,
,
Разделим обе части уравнения на , получим
.
Последнее уравнение в декартовой системе координат определяет гиперболу с полуосями;
Данный пример
может быть использован при решении
номеров 41 – 50
контрольной работы № 1.
2.5. Полярная система координат
Говорят, что на плоскости введена Полярная система координат, если заданы:
1) некоторая точка 0, называемая Полюсом;
2) некоторый луч, исходящий из точки 0 И называемый Полярной осью.
Полярными координатами точки
Пусть на плоскости введены декартова и полярная системы координат, причем начало декартовой системы совпадает с полюсом, а полярная ось — с положительной полуосью абсцисс. Тогда прямоугольные координаты X, Y точки М и ее полярные координаты ρ, φ связаны следующими формулами:
,
,
Задание 4. Линия задана уравнением в полярной системе координат. Требуется:
1. Построить линию по точкам, придавая φ значения от до через промежуток .
2. Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.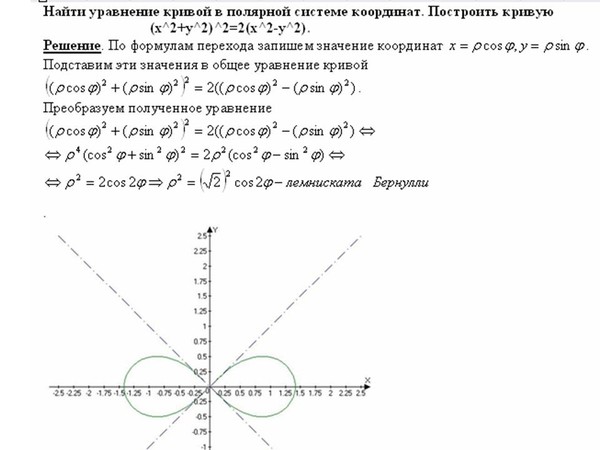
3. По уравнению в декартовой прямоугольной системе координат определить тип линии.
Решение.
1) Совместим декартову и полярную системы координат и рассмотрим окружность произвольного, достаточно большого радиуса С центром в полюсе. Построим радиусы, образующие углы с полярной осью, где принимает значения от до с шагом . Вычислим косинусы этих углов и по этим значениям найдем . Результаты вычислений занесем в таблицу:
0 | |||||||||||||||||
1 | 0,92 | 0,7 | 0,38 | 0 | -0,38 | -0,7 | -0,92 | -1 | -0,92 | -0,7 | -0,38 | 0 | 0,38 | 0,7 | 0,92 | 1 | |
0,16 | 0,17 | 0,19 | 0,24 | 0,33 | 0,53 | 1,11 | 4,16 | ∞ | 4,16 | 1,11 | 0,53 | 0,33 | 0,24 | 0,19 | 0,17 | 0,16 |
Построим точки () и по полученным точкам построим искомую линию:
2) Найдем уравнение данной линии в декартовой системе координат.
Для этого воспользуемся формулами:
.
Отсюда , .
Тогда имеем:
Или после упрощения
.
3) Чтобы определить тип линии, определяемой полученным уравнением,
Преобразуем его к каноническому виду:
Или
.
Окончательно получим:
,
Где ,. Таким образом, данное уравнение определяет параболу.
| < Предыдущая | Следующая > |
|---|
геометрия — функция полярных координат прямой линии
спросил
Изменено 1 год, 11 месяцев назад
Просмотрено 33 тысячи раз
$\begingroup$
У меня возникла проблема при попытке вывести функцию полярных координат с уравнением прямой линии.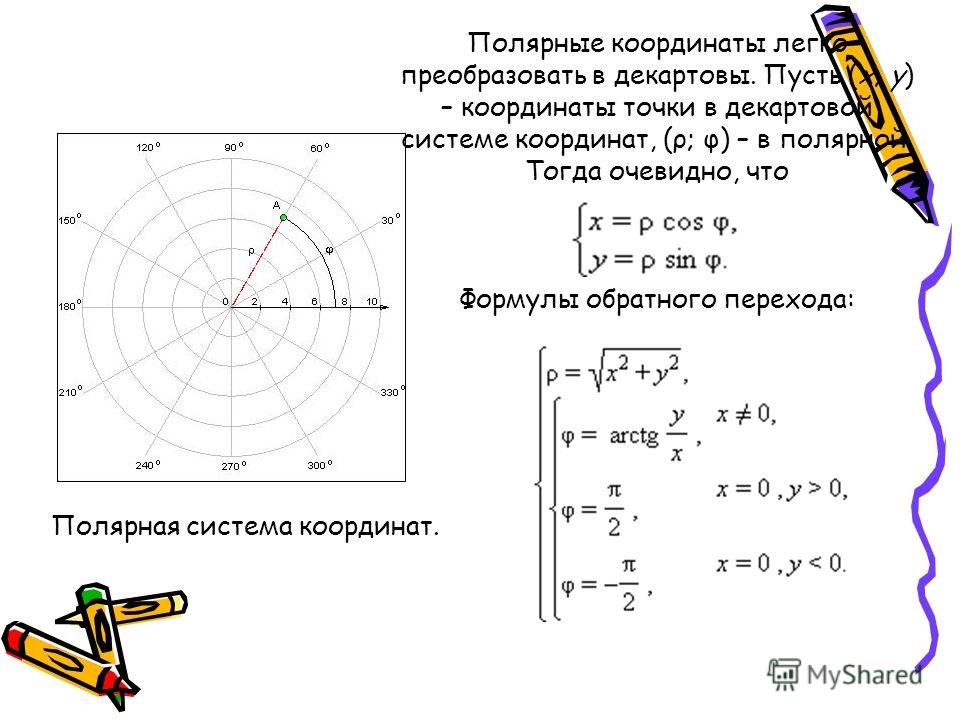
Я знаю, что размещать изображения здесь нехорошо, но, пожалуйста, потерпите меня, так как вопрос требует, чтобы мы решили уравнение по прямой линии на изображении.
Я попытался вывести неявную функцию для прямой линии L.
2x + 3y - 6 = 0
Но тогда я не уверен, как мне продолжить оттуда, чтобы выйти с функцией полярных координат. Есть идеи?
Спасибо!
- геометрия
- функции
- тригонометрия
$\endgroup$
4
$\begingroup$
$x = r\cos\тета\\ у = г \ грех \ тета \\ 2х + 3у — 6 = 0\\ 2r\cos\тета + 3r\sin\тета = 6\\ r(2\cos\theta + 3\sin\theta) = 6$
Теперь я мог бы сказать:
$r = \frac {6}{3\cos\theta + 2\sin\theta}$
и быть сделано.
Но я думаю, что это немного информативнее: 92}(\sin (\arctan \frac{3}{2})\sin\theta + \cos(\arctan\frac 32)\cos\theta) = 6\\ r\sqrt {13}(\cos(\theta — \arctan\frac 32)) = 6\\ r\sqrt {13}(\cos(\theta — \arctan\frac 32)) = 6\\ r = \frac {6}{\sqrt {13}} \sec (\theta — \arctan \frac 32)$
Поскольку это дает угол поворота и расстояние до линии.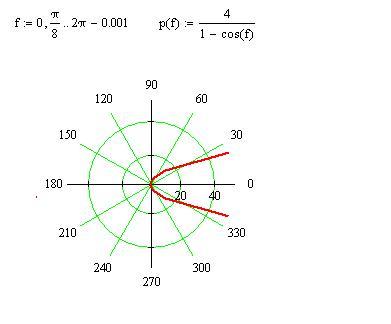
$\endgroup$
2
$\begingroup$
В декартовых координатах уравнение прямой имеет вид $y=mx+b$, где $m$ – числовой наклон, а $b$ – числовое значение точки пересечения $y$. Следуя правилам преобразования в полярные координаты, пусть $x=r\cdot cos\theta$ и $y=r\cdot sin\theta$. Найдите $r$ $$\left\{ r=-\frac{b}{m\;\operatorname{cos}\left(\theta\right)-\operatorname{sin}\left(\theta\right) }\право\}$$
Обычно я использую $0\le\theta\le 2\pi$ Идея построения графика в полярных координатах для меня больше любопытна, чем практическая. В Geogebra (например) на самом деле нет полярной системы построения графиков, но мы можем построить полярное уравнение путем преобразования в декартово. то есть $x=r(\theta)\cos\theta$ и $y=r(\theta)\sin\theta$. Затем Geogebra накладывает полярную сетку, и кажется, что мы построили график полярного уравнения.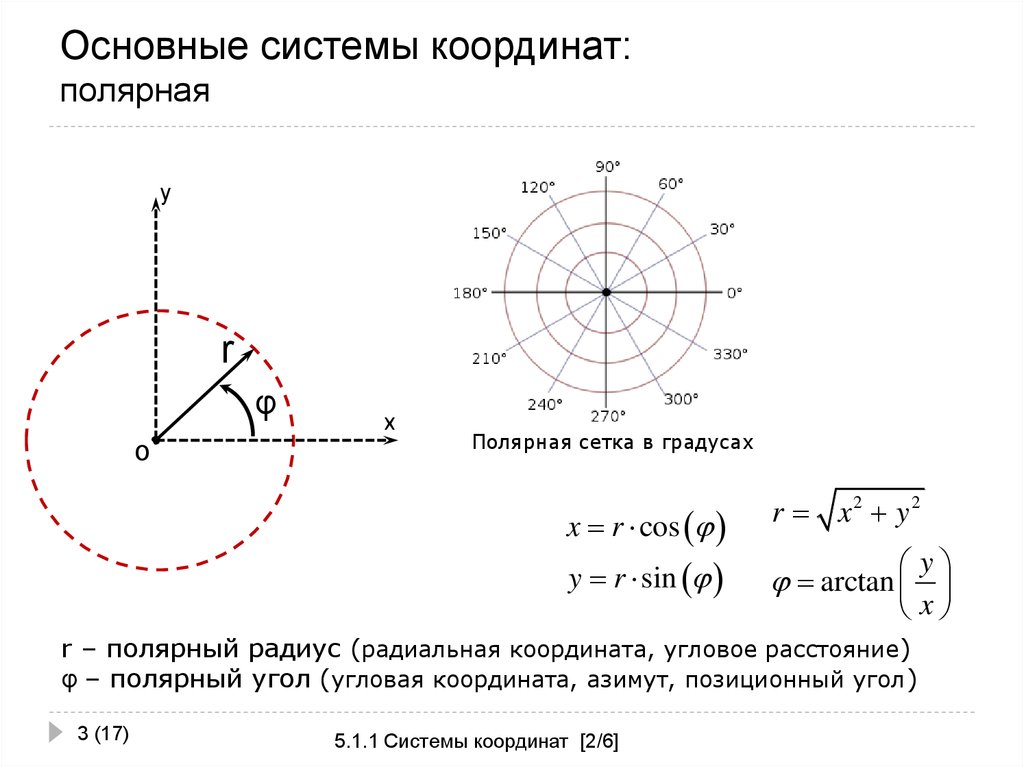
Итак… Никаких реальных ограничений на $r$, за исключением того, что $\theta$ должна иметь чрезвычайно высокую точность в определенных точках своего диапазона, иначе вы перепрыгнете через большие значения $r(\theta)$. Мне пришлось бы поиграть с этим некоторое время, чтобы дать вам лучший ответ.
$\endgroup$
3
$\begingroup$
Прямая, проходящая через $(0,2)\text{ и } (3,0)$, имеет уравнение $$y=-\frac{2}{3}x+2$$ Поскольку полярные координаты $(r,\alpha)$ соответствуют $(r\sin\alpha,r\cos\alpha)$, это переводится в $$ -\frac{2}{3}r\cos\alpha = r\sin\alpha+2$$
Осталось найти $r$.
$\endgroup$
9{-1} \frac{a}{b} \right ) $$$\endgroup$
$\begingroup$
Учитывая линейное уравнение в форме двух отрезков, x/a+y/b=1 Эквивалентная полярная форма: r=(a b сек(тета))/(b+tan(тета))
$\endgroup$
геометрия — Как преобразовать прямую в полярные координаты?
$\begingroup$
Прямая линия $y=mx+b$ может быть выражена в полярных координатах как:
$$\rho=x\cos(\theta) + y\sin(\theta)$$
Где $(\rho,\theta)$ определяет вектор от начала координат до ближайшей точки на прямой.