Натуральный логарифм минус 1. Функции LN и LOG для расчета натурального логарифма В EXCEL
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Совсем неплохо, правда? Пока математики подбирают слова, чтобы дать вам длинное путанное определение, давайте поближе посмотрим на это простое и ясное.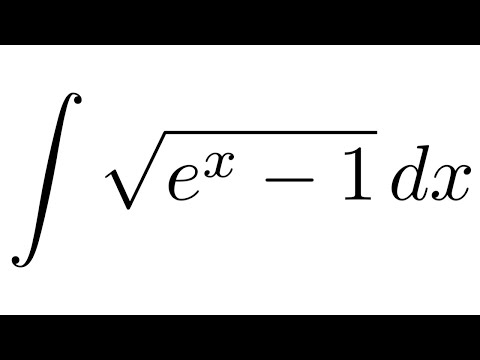
Число e означает рост
Число e означает непрерывный рост. Как мы видели в прошлом примере, e x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».
Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:
e x = e процент * время = e 1.0 * время = e время
Очевидно, что e x означает:
- насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
e x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.
Натуральный логарифм означает время
Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali
, отсюда и появилась аббревиатура ln.
Кстати, о причудах; по латыни он называется logarithmus naturali
, отсюда и появилась аббревиатура ln.
И что эта инверсия или противоположность означает?
- e x позволяет нам подставить время и получить рост.
- ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.
Например:
- e 3 равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
- ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).
Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.
Этот нестандартный логарифмический счёт
Вы проходили логарифмы — это странные существа. Как им удалось превратить умножение в сложение? А деление в вычитание? Давайте посмотрим.
Чему равняется ln(1)? Интуитивно понятно, что вопрос стоит так: сколько нужно ждать, чтобы получить в 1 раз больше того, что у меня есть?
Ноль. Нуль. Нисколько. У вас уже
это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.
Нуль. Нисколько. У вас уже
это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.
- ln(1) = 0
Хорошо, что насчёт дробного значения? Через сколько у нас останется 1/2 от имеющегося количества? Мы знаем, что при стопроцентном непрерывном росте ln(2) означает время, необходимое для удвоения. Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.
- ln(1/2) = -ln(2) = -0.693
Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = -ln(3) = -1.09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.
Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до -3?
Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ. .. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
.. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
- ln(отрицательное число) = неопределено
«Неопределено» означает, что нет такого промежутка времени, который надо было бы прождать, чтобы получить отрицательное значение.
Логарифмическое умножение — просто умора
Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.
Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):
- Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)
Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?
- ln(a*b) = ln(a) + ln(b)
Логарифм от A, умноженного на B, есть log(A) + log(B).
Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения. Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).
Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?
Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,
- ln(5/3) = ln(5) – ln(3)
Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается
- ln(a/b) = ln(a) – ln(b)
Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени.
Использование натурального логарифма при произвольном росте
Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»
Нет проблем. «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения e x . Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.
Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:
- e x = рост
- e 3.4 = 30
Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:
- e x = e ставка*время
- e 100% * 3.4 года = 30
Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?
- ln(30) = 3.
 4
4 - ставка * время = 3.4
- 0.05 * время = 3.4
- время = 3.4 / 0.05 = 68 лет
Я рассуждаю так: «ln(30) = 3.4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».
- 100% за 3.4 года = 1.0 * 3.4 = 3.4
- 200% за 1.7 года = 2.0 * 1.7 = 3.4
- 50% за 6.8 года = 0.5 * 6.8 = 3.4
- 5% за 68 года = .05 * 68 = 3.4 .
Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.
Отпадный пример: Правило семидесяти двух
Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.
Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?
Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.
Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?
Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:
- ставка * время = 0.693
- время = 0.693 / ставка
Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.
Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0. 10″:
10″:
- время на удвоение = 69.3 / ставка, где ставка выражена в процентах.
Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.
- время на удвоение = 72 / ставка
что и является правилом семидесяти двух. Всё шито-крыто.
Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить
- время на утроение = 110 / ставка
Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.
Что дальше?
Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.
Каждый раз, когда вы видите ln(x), вспоминайте «время, нужное, чтобы вырасти в Х раз». В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.
Дополнение: Натуральный логарифм от e
Быстрая викторина: сколько будет ln(e)?
- математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
- понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.
Мыслите ясно.
9 сентября 2013
Это может быть, например, калькулятор из базового набора программ операционной системы Windows. Ссылка на его запуск упрятана довольно в главное меню ОС — раскройте его щелчком по кнопке «Пуск», затем откройте его раздел «Программы», перейдите в подраздел «Стандартные», а затем в секцию «Служебные» и, наконец, щелкните пункт «Калькулятор». Можно вместо мыши и перемещений по меню использовать клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.
Можно вместо мыши и перемещений по меню использовать клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.
Переключите интерфейс калькулятора в расширенный режим, позволяющий осуществлять . По умолчанию он открывается в «обычном» виде, а вам нужен «инженерный» или « » (в зависимости от версии используемой ОС). Раскройте в меню раздел «Вид» и выберите соответствующую строку.
Введите аргумент, натуральный которого нужно вычислить. Это можно сделать как с клавиатуры, так и щелкая мышкой соответствующие кнопки в интерфейсе калькулятора на экране.
Кликните кнопку с надписью ln — программа рассчитает логарифма по основанию e и покажет результат.
Воспользуйтесь каким-либо из -калькуляторов в качестве альтернативного вычисления значения натурального логарифма. Например, тем, который размещен по адресу http://calc.org.ua . Его интерфейс предельно прост — есть единственное поле ввода, куда вам надо впечатать значение числа, логарифм от которого надо вычислить. Среди кнопок найдите и щелкните ту, на которой написано ln. Скрипт этого калькулятора не требует отправки данных на сервер и ответа, поэтому результат вычисления вы получите практически мгновенно. Единственная особенность, которую следует учитывать — разделителем между дробной и целой частью вводимого числа здесь обязательно должна быть точка, а не .
Среди кнопок найдите и щелкните ту, на которой написано ln. Скрипт этого калькулятора не требует отправки данных на сервер и ответа, поэтому результат вычисления вы получите практически мгновенно. Единственная особенность, которую следует учитывать — разделителем между дробной и целой частью вводимого числа здесь обязательно должна быть точка, а не .
Термин «логарифм » произошел от двух греческих слов, одно из которых обозначает «число», а другое — «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую надо возвести постоянное значение (основание), чтобы получить число, указанное под знаком логарифм а. Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».
Вам понадобится
- Доступ в интернет, Microsoft Office Excel или калькулятор.
Инструкция
Воспользуйтесь во множестве представленными в интернете -калькуляторами — это, пожалуй, и простой способ вычисления натурального а. Поиском соответствующего сервиса вам заниматься не придется, так как многие поисковые системы и сами имеют встроенные калькуляторы, вполне пригодные для работы с логарифм ами. Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.
Поиском соответствующего сервиса вам заниматься не придется, так как многие поисковые системы и сами имеют встроенные калькуляторы, вполне пригодные для работы с логарифм ами. Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.
Используйте соответствующую встроенную функцию, если необходимость вычисления значения натурального логарифм а возникает при работе с данными в популярном табличном редакторе Microsoft Office Excel. Эта функция здесь вызывается с использованием общепринятого обозначения такого логарифм а в верхнем регистре — LN. Выделите ячейку, в которой должен быть отображен результат вычисления, и введите знак равенства — так в этом табличном редакторе должны начинаться записи в ячейках, содержащих в подразделе «Стандартные» раздела «Все программы» главного меню. Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.
Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.
Видео по теме
Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.
Если , то .
Логарифм — крайне важная математическая величина , поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету.
Вконтакте
Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что означает, что:
Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.
Приведем некоторые тождества:
Приведем основные алгебраические выражения:
;
.
Внимание! может существовать только при x>0, x≠1, y>0.
Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.
Обозначения:
- lg x — десятичный;
- ln x — натуральный.
Используя тождество можно увидеть, что ln e = 1, как и то, что lg 10=1.
График натурального логарифмаПостроим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.
Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:
Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:
Для удобства мы можем взять пять опорных точек:
;
;
.
;
.
Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.
Построив по точкам график, получаем приблизительный график:
Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.
Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма .
Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .
Изучая график, возникает вопрос — как ведет себя функция при y
Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х
Предел натурального log можно записать таким образом:
Формула замены основания логарифмаИметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.
Начнем с логарифмического тождества:
Тогда любое число, либо переменную у можно представить в виде:
где х — любое число (положительное согласно свойствам логарифма).
Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:
Воспользуемся свойством (только вместо «с» у нас выражение):
Отсюда получаем универсальную формулу:
.
В частности, если z=e, то тогда:
.
Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.
Решаем задачиДля того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.
Задача 1 . Необходимо решить уравнение ln x = 3.
Решение: Используя определение логарифма: если , то , получаем:
Задача 2 . Решите уравнение (5 + 3 * ln (x — 3)) = 3.
Решение: Используя определение логарифма: если , то , получаем:
.
Еще раз применим определение логарифма:
.
Таким образом:
.
Можно приближенно вычислить ответ, а можно оставить его и в таком виде.
Задача 3. Решите уравнение .
Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:
.
Перед нами квадратное уравнение. Найдем его дискриминант:
Первый корень уравнения:
.
Второй корень уравнения:
.
Вспоминая о том, что мы производили подстановку t = ln x, получаем:
В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.
В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.
В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.
В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.
В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.
Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.
Натуральный логарифм Функция y=ln x ее свойства
Доказательство основного свойства натурального логарифма
Что такое логарифм?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:
1. Поймете, что такое логарифм .
2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.
3. Научитесь вычислять простые логарифмы.
Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…
Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!
Для начала решите в уме вот такое уравнение:
Если Вам нравится этот сайт. ..
.. Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Журналы и производные
Журналы и производные
Определение натурального логарифма
Напомним, что
Что
Определение: Для x > 0 мы определяем
Примечание: Вторая фундаментальная теорема исчисления говорит нам, что
d / dx (ln x ) = 1/ x
Свойства ln x
1 = 0
пер( аб ) = пер а + пер б
ln( a n ) = n п а
ln( a / b ) = ln a — пер б
Доказательство (3)
Так что
ln( x п )
и
n ln x
имеют одну и ту же производную. Следовательно,
Следовательно,
ln( x n ) = н л х + С
Подставив x = 1, мы получим C =
0.
Определение e
Пусть e таково, что
ln e = 1
т.е.
Примеры и упражнения
Пример
Найдите производную от0014 y = ln u , х = х 2 + 1
2 x
y ‘ = (2 x )(1/ u )
«=»
x 2 + 1
Найдите производные следующих функций:
длина (длина х )
( х )/ х
(длина x ) 2
лн (сек x )
лн (csc x )
Покажите, что
3 ln x — 4
является решением дифференциального уравненияху » + у ‘ = 0
Найдите относительные экстремумы
x ln x
Найдите уравнение касательной к
y = 3 x 2 — ln x
в (1,3)
Найти d y /d x для
ln( xy ) + 2 x 2 = 30
Вернуться к Домашняя страница Math 105
Вернуться на математический факультет Дом
вопросы по электронной почте и Предложения
Решения экспоненциальных и логарифмических задач
Это подробные решения экспоненциальной и логарифмической задач.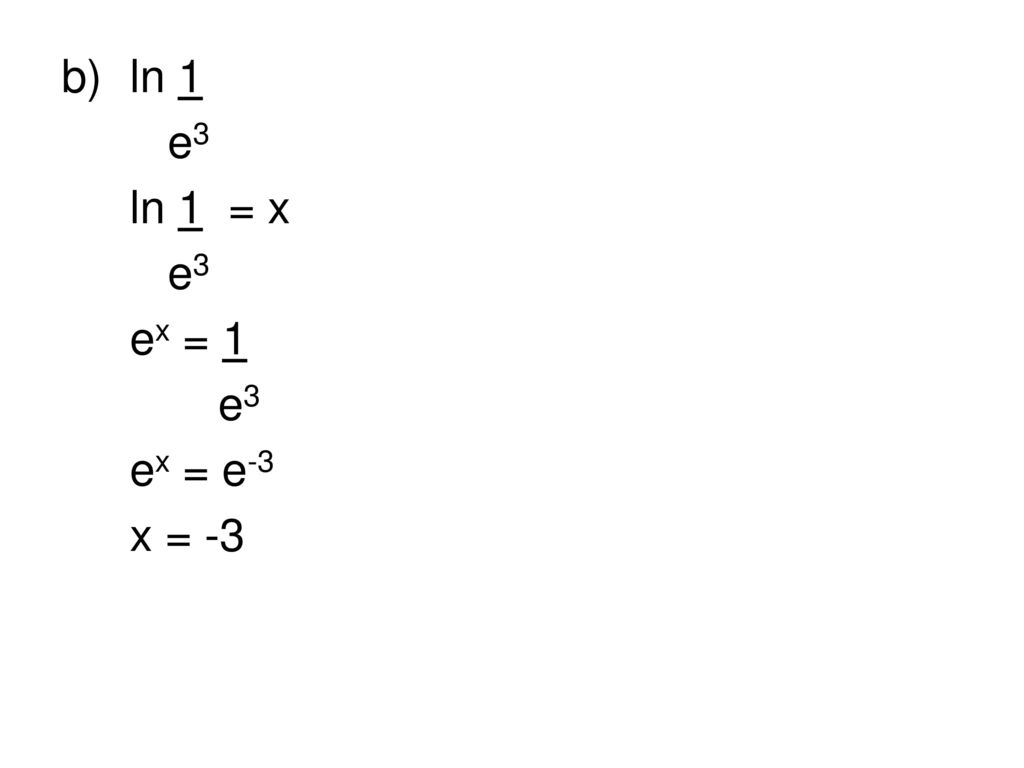
Решение проблемы 1: Решение проблемы 2: Решение задачи 3: Решение проблемы 4: Решение проблемы 5: Решение проблемы 6: Решение проблемы 7: Решение проблемы 8: Решение проблемы 9: |

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. 4
4




 Что дает начальную сумму, равную A или . Используя приведенное выше определение, мы можем написать
Что дает начальную сумму, равную A или . Используя приведенное выше определение, мы можем написать 


