Натуральный логарифм 1 2 равен. Значения ln x
Совсем неплохо, правда? Пока математики подбирают слова, чтобы дать вам длинное путанное определение, давайте поближе посмотрим на это простое и ясное.
Число e означает рост
Число e означает непрерывный рост. Как мы видели в прошлом примере, e x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».
Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:
e x = e процент * время = e 1.0 * время = e время
Очевидно, что e x означает:
- насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
- например, через 3 промежутка времени я получу в e 3 = 20.08 раз больше «штуковин».

e x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.
Натуральный логарифм означает время
Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali , отсюда и появилась аббревиатура ln.
И что эта инверсия или противоположность означает?
- e x позволяет нам подставить время и получить рост.
- ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.
Например:
- e 3 равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
- ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).
Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.
Этот нестандартный логарифмический счёт
Вы проходили логарифмы — это странные существа. Как им удалось превратить умножение в сложение? А деление в вычитание? Давайте посмотрим.
Чему равняется ln(1)? Интуитивно понятно, что вопрос стоит так: сколько нужно ждать, чтобы получить в 1 раз больше того, что у меня есть?
Ноль. Нуль. Нисколько. У вас уже это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.
- ln(1) = 0
Хорошо, что насчёт дробного значения? Через сколько у нас останется 1/2 от имеющегося количества? Мы знаем, что при стопроцентном непрерывном росте ln(2) означает время, необходимое для удвоения. Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.
- ln(1/2) = -ln(2) = -0.693
Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = -ln(3) = -1.
Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до -3?
Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ… минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
- ln(отрицательное число) = неопределено
«Неопределено» означает, что нет такого промежутка времени, который надо было бы прождать, чтобы получить отрицательное значение.
Логарифмическое умножение — просто умора
Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.
Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):
- Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)
Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?
Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?
- ln(a*b) = ln(a) + ln(b)
Логарифм от A, умноженного на B, есть log(A) + log(B). Это отношение сразу обретает смысл, если оперировать в терминах роста.
Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения. Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).
Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?
Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,
- ln(5/3) = ln(5) – ln(3)
Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается
В общем получается
- ln(a/b) = ln(a) – ln(b)
Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени. Не надо запоминать правила, попробуйте осознать их.
Использование натурального логарифма при произвольном росте
Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»
Нет проблем. «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения e x . Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.
Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:
- e x = рост
- e 3.4 = 30
Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:
Мы можем записать это уравнение в таком виде:
- e x = e ставка*время
- e 100% * 3.4 года = 30
Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?
- ln(30) = 3.4
- ставка * время = 3.4
- 0.05 * время = 3.4
- время = 3.4 / 0.05 = 68 лет
Я рассуждаю так: «ln(30) = 3.4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».
- 100% за 3.4 года = 1.0 * 3.4 = 3.4
- 200% за 1.7 года = 2.0 * 1.7 = 3.4
- 50% за 6.8 года = 0.5 * 6.8 = 3.4
- 5% за 68 года = .05 * 68 = 3.4 .
Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.
Отпадный пример: Правило семидесяти двух
Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.
Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.
Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?
Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.
Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?
Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:
- ставка * время = 0.693
- время = 0.
 693 / ставка
693 / ставка
Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.
Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0.10»:
- время на удвоение = 69.3 / ставка, где ставка выражена в процентах.
Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.
- время на удвоение = 72 / ставка
что и является правилом семидесяти двух. Всё шито-крыто.
Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить
- время на утроение = 110 / ставка
Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.
Что дальше?
Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.
Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.
Каждый раз, когда вы видите ln(x), вспоминайте «время, нужное, чтобы вырасти в Х раз». В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.
Дополнение: Натуральный логарифм от e
Быстрая викторина: сколько будет ln(e)?
- математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
- понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.
Мыслите ясно.
9 сентября 2013
нередко берут цифру е = 2,718281828 . Логарифмы по данному основанию именуют натуральным . При проведении вычислений с натуральными логарифмами общепринято оперировать знаком l n , а не log ; при этом число 2,718281828 , определяющие основание, не указывают.
Другими словами формулировка будет иметь вид: натуральный логарифм числа х — это показатель степени , в которую нужно возвести число e , чтобы получить x .
Так, ln(7,389…) = 2, так как e 2 =7,389…
Само число е определяет предел монотонной ограниченной последовательности
вычислено, что е = 2,7182818284… .
Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!
На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.
График натурального логарифма (функции y = ln x ) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:
Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a .
Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».
Если анализировать натуральный логарифм , как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:
e ln(a) =a (a>0)
ln(e a) =a
По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:
ln (xy ) = ln (x ) + ln (y )
ln (х/у)= lnx — lny
Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.
Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x . Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма выступает минус бесконечность ( -∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.
Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул.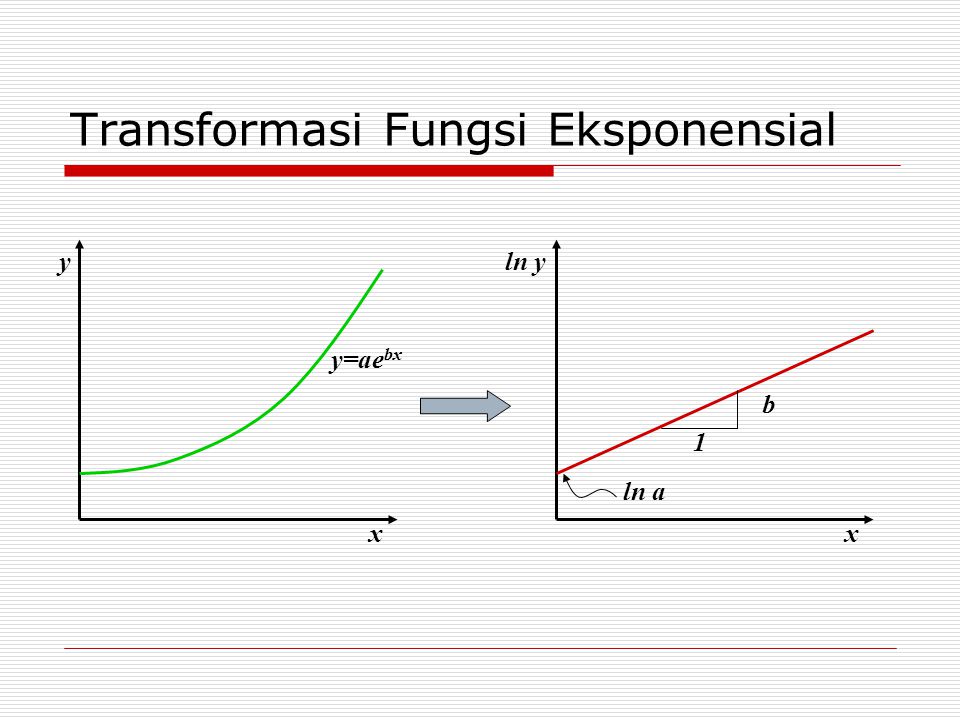 Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.
Определение
Натуральный логарифм — это функция y = ln x , обратная к экспоненте , x = e y , и являющаяся логарифмом по основанию числа е : ln x = log e x .
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln
x)′ = 1/
x
.
Исходя из определения , основанием натурального логарифма является число е :
е
≅ 2,718281828459045…
;
.
График функции y = ln x .
График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .
Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма является минус бесконечность ( — ∞ ).
При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a растет быстрее логарифма.
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
Значения ln x
ln 1 = 0
Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм» .
Обратная функция
Обратной для натурального логарифма является экспонента .
Если , то
Если , то .
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x
:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Интеграл вычисляется интегрированием по частям :
.
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексной переменной z
:
.
Выразим комплексную переменную z через модуль r и аргумент φ :
.![]()
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ
определен не однозначно. Если положить
,
где n — целое,
то будет одним и тем же числом при различных n
.
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Натуральный логарифм
График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x ).
Натуральный логарифм — это логарифм по основанию , где e — иррациональная константа, равная приблизительно 2,718281
828
. Натуральный логарифм обычно обозначают как ln(x ), log e (x ) или иногда просто log(x ), если основание e подразумевается.
Натуральный логарифм числа x (записывается как ln(x) ) — это показатель степени , в которую нужно возвести число e , чтобы получить x . Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a . Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа , о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции :
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
История
Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia , опубликованной в 1668 году , хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. Ранее его называли гиперболическим логарифмом, поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
Конвенции об обозначениях
Натуральный логарифм принято обозначать через «ln(x )», логарифм по основанию 10 — через «lg(x )», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x )» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln 2 ln 3 4x 5 = [ ln( 3 )] 2 .
Англо-американская система
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x )», либо «ln(x )» , а для обозначения логарифма по основанию 10 — «log 10 (x )».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x )» (или изредка «log e (x )»), когда они имеют в виду натуральный логарифм, а запись «log(x )» у них означает log 10 (x ).
log e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:
Если основание b равно e , то производная равна просто 1/x , а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора , чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.
Определение
Формально ln(a ) может быть определён как площадь под кривой графика 1/x от 1 до a , т. е. как интеграл :
е. как интеграл :
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская следующим образом:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
при условии, что y = (x −1)/(x +1) и x > 0.
Для ln(x ), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M (n ) ln n ). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M (n ) — вычислительная сложность умножения двух n -значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби , но можно использовать несколько обобщённых непрерывных дробей, в том числе:
Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e x для любого произвольного комплексного числа x , при этом используется бесконечный ряд с комплексным x . Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x , для которого e x = 0, и оказывается, что e 2πi = 1 = e 0 . Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e z = e z +2nπi для всех комплексных z и целых n .
Логарифм не может быть определён на всей комплексной плоскости , и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi . Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
См. также
- Джон Непер — изобретатель логарифмов
Примечания
- Mathematics for physical chemistry . — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5 , Extract of page 9
- J J O»Connor and E F Robertson The number e . The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано
- Cajori Florian A History of Mathematics, 5th ed . — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
- Flashman, Martin Estimating Integrals using Polynomials . Архивировано из первоисточника 12 февраля 2012.
Натуральный логарифм, функция ln x. Логарифм
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.
Определение
Натуральный логарифм — это функция y = ln x , обратная к экспоненте , x = e y , и являющаяся логарифмом по основанию числа е : ln x = log e x .
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/ x .
Исходя из определения , основанием натурального логарифма является число е :
е
≅ 2,718281828459045…
;
.
График функции y = ln x .
График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .
Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма является минус бесконечность ( — ∞ ).
При x → + ∞
пределом натурального логарифма является плюс бесконечность ( + ∞
). При больших x
логарифм возрастает довольно медленно.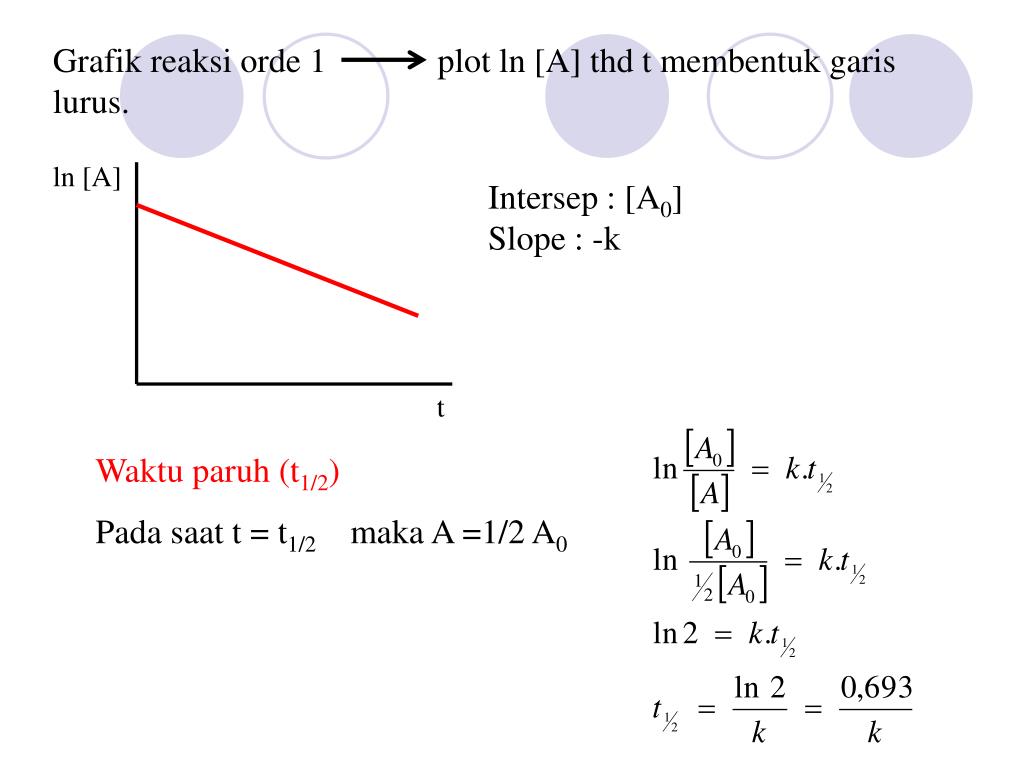 Любая степенная функция x a
с положительным показателем степени a
растет быстрее логарифма.
Любая степенная функция x a
с положительным показателем степени a
растет быстрее логарифма.
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
Значения ln x
ln 1 = 0
Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм» .
Обратная функция
Обратной для натурального логарифма является экспонента .
Если , то
Если , то .
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x
:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Интеграл вычисляется интегрированием по частям :
.
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексной переменной z
:
.
Выразим комплексную переменную z через модуль r и аргумент φ :
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ
определен не однозначно. Если положить
,
где n — целое,
то будет одним и тем же числом при различных n
.
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Натуральный логарифм
График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x ).
Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x ).
Натуральный логарифм — это логарифм по основанию , где e — иррациональная константа, равная приблизительно 2,718281 828 . Натуральный логарифм обычно обозначают как ln(x ), log e (x ) или иногда просто log(x ), если основание e подразумевается.
Натуральный логарифм числа x (записывается как ln(x) ) — это показатель степени , в которую нужно возвести число e , чтобы получить x . Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a . Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа , о чём будет сказано ниже.
Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа , о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции :
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма.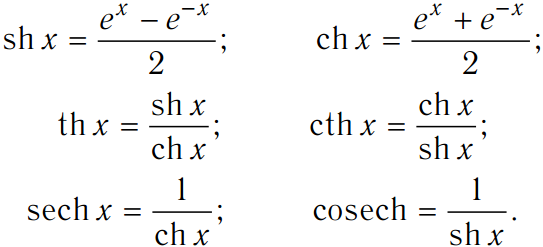 Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
История
Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia , опубликованной в 1668 году , хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. Ранее его называли гиперболическим логарифмом, поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
Конвенции об обозначениях
Натуральный логарифм принято обозначать через «ln(x )», логарифм по основанию 10 — через «lg(x )», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x )» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln 2 ln 3 4x 5 = [ ln( 3 )] 2 .
Англо-американская система
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x )», либо «ln(x )» , а для обозначения логарифма по основанию 10 — «log 10 (x )».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x )» (или изредка «log e (x )»), когда они имеют в виду натуральный логарифм, а запись «log(x )» у них означает log 10 (x ).
log e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:
Если основание b равно e , то производная равна просто 1/x , а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора , чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.
Определение
Формально ln(a ) может быть определён как площадь под кривой графика 1/x от 1 до a , т.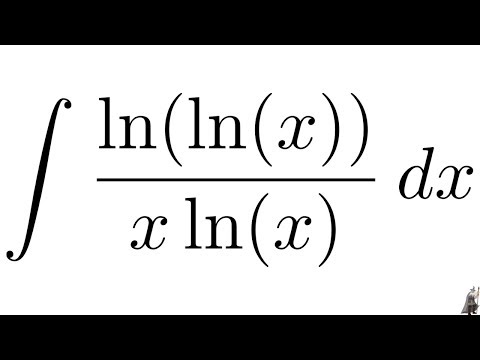 е. как интеграл :
е. как интеграл :
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская следующим образом:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
при условии, что y = (x −1)/(x +1) и x > 0.Для ln(x ), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M (n ) ln n ). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M (n ) — вычислительная сложность умножения двух n -значных чисел.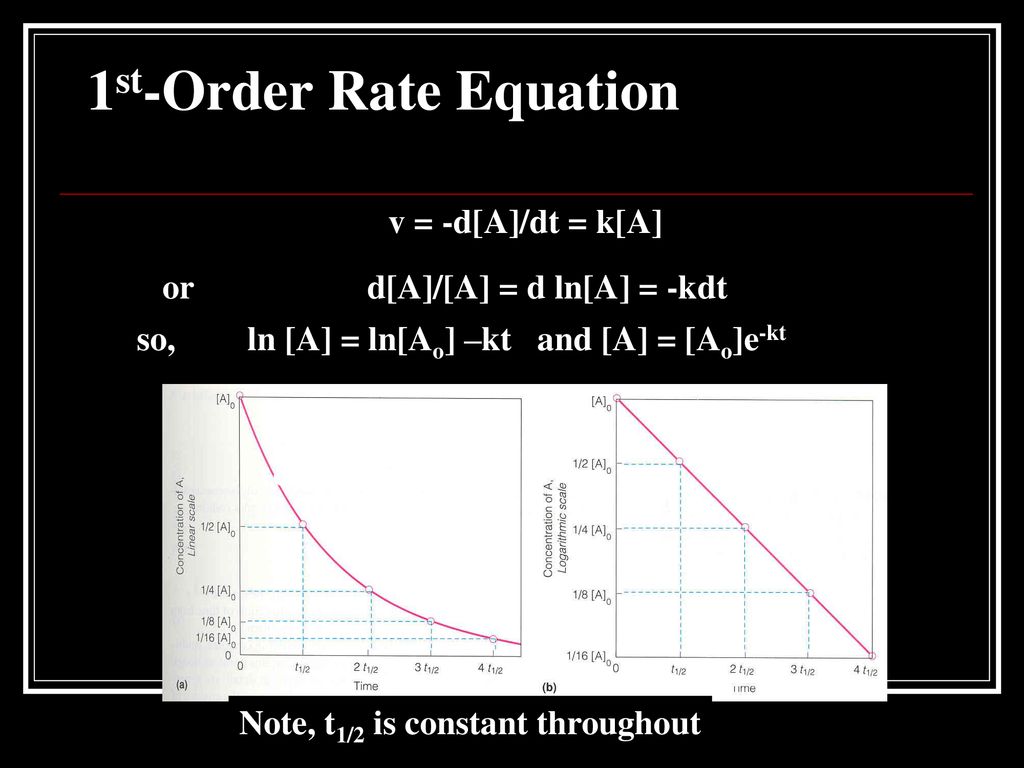
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби , но можно использовать несколько обобщённых непрерывных дробей, в том числе:
Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e x для любого произвольного комплексного числа x , при этом используется бесконечный ряд с комплексным x . Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x , для которого e x = 0, и оказывается, что e 2πi = 1 = e 0 . Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e z = e z +2nπi для всех комплексных z и целых n .
Логарифм не может быть определён на всей комплексной плоскости , и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi . Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
См. также
- Джон Непер — изобретатель логарифмов
Примечания
- Mathematics for physical chemistry . — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5 , Extract of page 9
- J J O»Connor and E F Robertson The number e . The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано
- Cajori Florian A History of Mathematics, 5th ed . — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
- Flashman, Martin Estimating Integrals using Polynomials . Архивировано из первоисточника 12 февраля 2012.
Это может быть, например, калькулятор из базового набора программ операционной системы Windows. Ссылка на его запуск упрятана довольно в главное меню ОС — раскройте его щелчком по кнопке «Пуск», затем откройте его раздел «Программы», перейдите в подраздел «Стандартные», а затем в секцию «Служебные» и, наконец, щелкните пункт «Калькулятор». Можно вместо мыши и перемещений по меню использовать клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.
Ссылка на его запуск упрятана довольно в главное меню ОС — раскройте его щелчком по кнопке «Пуск», затем откройте его раздел «Программы», перейдите в подраздел «Стандартные», а затем в секцию «Служебные» и, наконец, щелкните пункт «Калькулятор». Можно вместо мыши и перемещений по меню использовать клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.
Переключите интерфейс калькулятора в расширенный режим, позволяющий осуществлять . По умолчанию он открывается в «обычном» виде, а вам нужен «инженерный» или « » (в зависимости от версии используемой ОС). Раскройте в меню раздел «Вид» и выберите соответствующую строку.
Введите аргумент, натуральный которого нужно вычислить. Это можно сделать как с клавиатуры, так и щелкая мышкой соответствующие кнопки в интерфейсе калькулятора на экране.
Кликните кнопку с надписью ln — программа рассчитает логарифма по основанию e и покажет результат.
Воспользуйтесь каким-либо из -калькуляторов в качестве альтернативного вычисления значения натурального логарифма. Например, тем, который размещен по адресу http://calc.org.ua . Его интерфейс предельно прост — есть единственное поле ввода, куда вам надо впечатать значение числа, логарифм от которого надо вычислить. Среди кнопок найдите и щелкните ту, на которой написано ln. Скрипт этого калькулятора не требует отправки данных на сервер и ответа, поэтому результат вычисления вы получите практически мгновенно. Единственная особенность, которую следует учитывать — разделителем между дробной и целой частью вводимого числа здесь обязательно должна быть точка, а не .
Термин «логарифм » произошел от двух греческих слов, одно из которых обозначает «число», а другое — «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую надо возвести постоянное значение (основание), чтобы получить число, указанное под знаком логарифм а. Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».
Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».
Вам понадобится
- Доступ в интернет, Microsoft Office Excel или калькулятор.
Инструкция
Воспользуйтесь во множестве представленными в интернете -калькуляторами — это, пожалуй, и простой способ вычисления натурального а. Поиском соответствующего сервиса вам заниматься не придется, так как многие поисковые системы и сами имеют встроенные калькуляторы, вполне пригодные для работы с логарифм ами. Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.
Используйте соответствующую встроенную функцию, если необходимость вычисления значения натурального логарифм а возникает при работе с данными в популярном табличном редакторе Microsoft Office Excel. Эта функция здесь вызывается с использованием общепринятого обозначения такого логарифм а в верхнем регистре — LN. Выделите ячейку, в которой должен быть отображен результат вычисления, и введите знак равенства — так в этом табличном редакторе должны начинаться записи в ячейках, содержащих в подразделе «Стандартные» раздела «Все программы» главного меню. Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.
Видео по теме
Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0)       
Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
Два очевидных следствия определения логарифма log a a = 1 (a > 0, a ≠ 1) (3)log a 1 = 0 (a > 0, a ≠ 1) (4)
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.
Логарифм произведения и логарифм частного log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)Log
a
b
c
=
log
a
b −
log
a
c
(a > 0, a ≠ 1, b > 0, c > 0)
(6)
Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
Действительно, выражение log a (f (x) g (x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.
Преобразуя данное выражение в сумму log a f (x) + log a g (x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).
Степень можно выносить за знак логарифма log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
Log a (f (x) 2 = 2 log a f (x)
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)
Несколько простых примеров с логарифмамиПример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log 5 125 = 3. Мы использовали формулу перехода к новому основанию (8).
| a log a b = b (a > 0, a ≠ 1) |
| log a a = 1 (a > 0, a ≠ 1) |
| log a 1 = 0 (a > 0, a ≠ 1) |
| log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b p = p log a b (a > 0, a ≠ 1, b > 0) |
| log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) |
| log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) |
Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Определение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).

- Десятичный a, где основанием служит число 10.
- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
- Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение.
 Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Логарифм — frwiki.wiki
Статью с омофоном можно в Loga-Rythme .
Графики функций логарифма по основанию 2, e и 10.
В математике , то логарифм к основанию Ь в виде строго положительного действительного числа есть сила , к которой необходимо поднять базовую Ь , чтобы получить этот номер. В простейшем случае логарифм подсчитывает количество вхождений одного и того же множителя при повторном умножении: например, как 1000 = 10 × 10 × 10 = 10 3 , логарифм по основанию 10 из 1000 равен 3. Логарифм x в базе b обозначается log b ( x ). Итак, log 10 (1000) = 3.
John Napier логарифмы «s , разработанный в начале XVII — го века. В течение трех столетий, таблица логарифмов и логарифмическая линейка была использована для численных вычислений , вплоть до замены в конце XX — го века калькуляторов .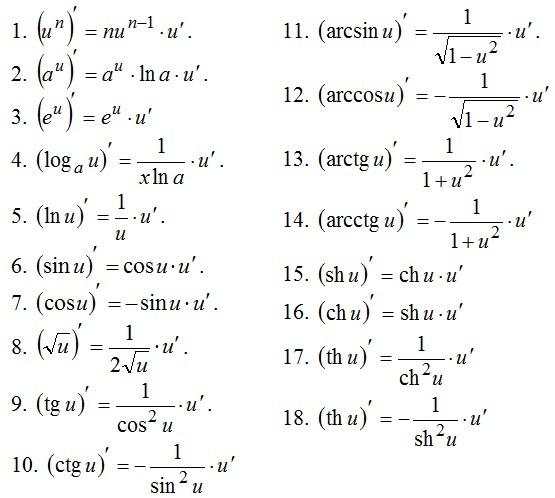
Замечательны три логарифма:
- Естественный (или натуральный ) логарифм , отметил пер , который использует число е в качестве основы, имеет фундаментальное значение в математическом анализе , потому что это первообразная функции отмены при 1 и обратной функции от экспоненциальной функции ;Икс↦1Икс{\ Displaystyle х \ mapsto {\ tfrac {1} {x}}}
- Для вычислений чаще всего использовался десятичный логарифм с основанием десять;
- Двоичный логарифм , который использует 2 в качестве основы, является полезным в теоретическом информатики и для некоторых прикладных расчетов.
Резюме
- 1 Мотивация
- 2 История
- 3 Свойства функций логарифмирования
- 3.1 Алгебраические свойства
- 3.2 Базовое изменение
- 3.3 Производная
- 3.4 Взаимная функция (антилогарифм)
- 4 Функции десятичного логарифма
- 4.1 Натуральный логарифм
- 4.2 Десятичный логарифм
- 4.
 3 Двоичный логарифм
3 Двоичный логарифм - 4.4 Кологарифм
- 5 Обобщения
- 6 Примечания и ссылки
- 7 См. Также
- 7.1 Статьи по теме
- 7.1.1 Практическое применение
- 7.2 Внешняя ссылка
- 7.1 Статьи по теме
Мотивация
Логарифмическая шкала позволяет изобразить на один и тот же номеров графа, порядки сильно отличается. Логарифмы являются общими в формулах , используемых в науке, измерить сложность из алгоритмов и фрактал, и появляются в формулах для подсчета простых чисел . Они описывают музыкальные интервалы или определенные модели психофизики .
Преобразует любой логарифм
- продукт в сумме :бревноб(Икс⋅у)знак равнобревнобИкс+бревнобу{\ displaystyle \ log _ {b} (x \ cdot y) = \ log _ {b} x + \ log _ {b} y \,}
- фактор в разнице :бревноб(Иксу)знак равнобревнобИкс-бревнобу{\ displaystyle \ log _ {b} \ left ({\ frac {x} {y}} \ right) = \ log _ {b} x- \ log _ {b} y \,}
- мощность продукта:бревноб(Иксп)знак равнопбревнобИкс.
 {p}) = p \ log _ {b} x. \,}
{p}) = p \ log _ {b} x. \,}
Исторический
К концу XVI — го века, развитие астрономии и навигации с одной стороны , и банковскими расчетами процентов по другим соединениям, нажимные математикам искать методы расчета упрощений и , в частности , заменяя умножения сумм.
Используя тригонометрические таблицы, математики Поль Виттих и Кристоф Клавиус (в своем трактате об Астролябии ) устанавливают соответствия между произведением или частным, с одной стороны, и суммой, разностью и делением на два, с другой стороны, для чисел от 0 до 1, используя тригонометрические соотношения , метод, известный как простаферез .
Спустя несколько лет логарифмические таблицы заменили тригонометрические таблицы. Саймон Стевин , генеральный управляющий голландской армии, составляет таблицы расчета сложных процентов . Йост Бюрги продолжил эту работу и опубликовал в 1620 году в своем Aritmetische und geometrische Progress-tabulen таблицу соответствия между n и 1. 0001 n . Таким образом, сумма в первом столбце соответствует продукту во втором столбце.
0001 n . Таким образом, сумма в первом столбце соответствует продукту во втором столбце.
В 1614 году Джон Напьер (или Непер) опубликовал свой трактат Mirifici Logarithmorum Canonis Descriptio . Он не думает, что создает новые функции, а только таблицы соответствия ( логотипы = отчет, отношение, арифметика = число) между двумя сериями значений, имеющими следующее свойство: продукту в столбце соответствует одна сумма в другой. Через несколько лет Кеплер будет использовать эти таблицы, изначально созданные для упрощения тригонометрических расчетов в астрономических расчетах . Обозначение Log как сокращение от логарифма появляется в 1616 году в английском переводе работы Непера. В 1619 году появилась его посмертная работа Mirifici Logarithmorum Canonis Constructio , в которой он объяснил, как построить таблицу логарифмов .
Английский математик Генри Бриггс продолжил эту работу и опубликовал в 1624 году свои таблицы десятичных логарифмов ( Arithmetica logarithmica ), указав методы использования таблиц для вычисления синусов или углов относительно их тангенса . .. Десятичный логарифм иногда называют логарифмом числа Бриггс в его честь. В том же году Иоганн Кеплер опубликовал Chilias logarithmorum, построенный с помощью геометрического процесса. Таблица Бриггса показывает 14-значные логарифмы чисел от 1 до 20 000 и от 90 000 до 100 000. Иезекиэль де Декер и Адриан Влак завершили таблицу логарифмов в 1627 году.
.. Десятичный логарифм иногда называют логарифмом числа Бриггс в его честь. В том же году Иоганн Кеплер опубликовал Chilias logarithmorum, построенный с помощью геометрического процесса. Таблица Бриггса показывает 14-значные логарифмы чисел от 1 до 20 000 и от 90 000 до 100 000. Иезекиэль де Декер и Адриан Влак завершили таблицу логарифмов в 1627 году.
В 1647 году Грегуар де Сент-Винсент , работая над квадратурой гиперболы , выделяет новую функцию, примитив функции, сокращающейся на 1. В 1661 году Гюйгенс заметит, что эта функция оказывается особой функцией логарифма. натуральный логарифм . Икс↦1Икс{\ Displaystyle х \ mapsto {\ tfrac {1} {x}}}
Соответствие между экспоненциальными и логарифмическими функциями появляется только после работы Лейбница по понятию функции (1697).
Свойства функций логарифмирования
В этом разделе мы даем свойства логарифмической функции независимо от ее основания b .
Алгебраические свойства
Функции логарифма по определению не- постоянно нуля непрерывных морфизмов из червей . {r}) = r}для любого рационального г .
{r}) = r}для любого рационального г .
Поскольку любое строго положительное вещественное число x является пределом последовательности, общий член которой имеет вид b r n , где ( r n ) — последовательность рациональных чисел, сходящаяся к действительному , мы определяем log b ( x ) как предел из г п . ℓ{\ displaystyle \ ell}
Базовое изменение
Две логарифмические функции отличаются только от мультипликативной константы: для всех строго положительных действительных чисел a и b, отличных от 1, и для всех действительных x > 0 ,
- бревноб(Икс)знак равнобревнов(Икс)бревнов(б){\ displaystyle \ log _ {b} (x) = {\ frac {\ log _ {a} (x)} {\ log _ {a} (b)}}}.
Следовательно, все функции логарифмирования могут быть выражены с использованием только одной функции, например функции натурального логарифма: для любого строго положительного вещественного числа b, отличного от 1, и для любого действительного числа x > 0 ,
- бревноб(Икс)знак равнопер(Икс)пер(б){\ displaystyle \ log _ {b} (x) = {\ frac {\ ln (x)} {\ ln (b)}}}.
 {\ log _ {b} (y)} = y.}
{\ log _ {b} (y)} = y.}Взаимные функции тесно связаны с исходными функциями. Их графики , которые соответствуют, когда координаты x и y меняются местами (или путем отражения относительно диагонали x = y ), показаны справа в случае, когда b — вещественное число, строго большее 1: точка ( u , t = b u ) на графике (красный) функции антилогарифма x ↦ b x обеспечивает точку ( t , u = log b ( t )) на графике (синий) логарифма и наоборот. Как Ь > 1 , функция журнала Ь является увеличение и когда х стремится к + ∞ , лог — б ( х ) стремится к + ∞ , в то время , когда х стремится к нулю, журнал Ь ( х ) стремится к -∞ . В случае, когда действительное значение b находится строго между 0 и 1, функция log b уменьшается, и эти пределы инвертируются.
 {*}}р{\ Displaystyle \ mathbb {R}}Икс↦1Икс{\ displaystyle x \ mapsto {\ frac {1} {x}}}
{*}}р{\ Displaystyle \ mathbb {R}}Икс↦1Икс{\ displaystyle x \ mapsto {\ frac {1} {x}}}- Функция Непера условно обозначается « ln » или « log », обозначение, обычно используемое в теории чисел и информатике.
- Основание функции натурального логарифма, обозначаемой е , называется числом Непера или числом Эйлера.
Приблизительное значение:
- е≈2 718{\ displaystyle \ mathrm {e} \ приблизительно 2 {,} 718}.
Десятичный логарифм
Это наиболее практичный логарифм в ручных числовых вычислениях, он обозначается как log или log 10 . Стандарт ISO 80000-2 гласит, что log 10 следует обозначать как lg , но это обозначение используется редко.
Его можно найти при создании логарифмических шкал , полулогарифмических или логарифмических эталонных показателей , в логарифмической линейке , при вычислении pH в децибелах .
Он указывает, в какую степень необходимо возвести 10, чтобы найти начальное число: изображение числа в бревне — это относительное целое число, до которого необходимо возвести 10, чтобы получить антецедент .
 {- 2} = 0,01}
{- 2} = 0,01}
Значение логарифма чисел, отличных от степени 10, требует приблизительного расчета. Например, расчет log (2) можно выполнить вручную, отметив, что 2 10 ≈ 1000, следовательно, 10 log 10 (2) ≈ 3, следовательно, log 10 (2) ≈ 0,3 .
Для любого строго положительного действительного b, отличного от 1, и для любого действительного x > 0 ,
- бревноб(Икс)знак равнобревно10(Икс)бревно10(б){\ displaystyle \ log _ {b} (x) = {\ frac {\ log _ {10} (x)} {\ log _ {10} (b)}}}.
Двоичный логарифм
Стандарт ISO 80 000 рекомендует, чтобы фунт был логарифмом по основанию 2.
Двоичный логарифм, особенно используемый при вычислении музыкальных интервалов из соотношения частот , для получения октав , полутонов или центов , нашел гораздо большее применение в информатике . В компьютерах, работающих в двоичной системе , вычисление логарифма по основанию 2 является наиболее точным и эффективным алгоритмом. {p} \ times m \ Longrightarrow {\ textrm {lb}} (x) = p + {\ textrm {lb}} (m).}
{p} \ times m \ Longrightarrow {\ textrm {lb}} (x) = p + {\ textrm {lb}} (m).}
Это возвращает вычисление к вычислению двоичного логарифма числа от 1 (включительно) до 2 (исключено). Если мы умножаем это число на себя, и результат превышает 2, это число больше √2: следующая цифра после десятичной точки равна 1, в противном случае — 0. Мы продолжаем итерацию до желаемой точности. достигается.
Два предыдущих логарифма выводятся из этого следующим образом:
- пер(Икс)знак равнолб(Икс)лб(е) а также бревно10(Икс)знак равнолб(Икс)лб(10){\ displaystyle \ ln (x) = {\ frac {\ mathrm {lb} (x)} {\ mathrm {lb} (\ mathrm {e})}} {\ text {and}} \ log _ {10} (x) = {\ frac {\ mathrm {lb} (x)} {\ mathrm {lb} (10)}}}.
Кологарифм
Отрицательный логарифм числа является отрицательным логарифмом этого числа и логарифм его обратным: . одеколонбИксзнак равно-бревнобИксзнак равнобревноб1Икс{\ displaystyle \ operatorname {colog} _ {b} x = — \ log _ {b} x = \ log _ {b} {\ frac {1} {x}}}
Обобщения
Комплексный логарифм является обратной функцией комплексной экспоненты , и , таким образом , обобщает понятие логарифма для комплексных чисел. Дискретный логарифм обобщающих логарифмов к циклическим группам и имеет приложение в криптографии с открытым ключом .
Дискретный логарифм обобщающих логарифмов к циклическим группам и имеет приложение в криптографии с открытым ключом .
Примечания и ссылки
(fr) Эта статья частично или полностью взята из английской статьи в Википедии под названием « Логарифм » ( см. список авторов ) .
- ↑ Жан-Пьер Фридельмейер, Изобретение логарифмов Непером и вычисление десятичных логарифмов Бриггсом .
- ↑ (in) Британская энциклопедия , « Джон Нэпьер », примечания 2.
- ↑ (in) Джулиан Хэвил ( преф. Фримен Дайсон ) Гамма: изучение константы Эйлера ( читать онлайн ) , гл.
 1 («Колыбель логарифма») , с. 1-2.
1 («Колыбель логарифма») , с. 1-2. - ↑ (in) Брайан Борчерс, » Prosthaphaeresis » , журнал Oughtred Society , vol. 14, п о 2, стр. 3-4 ( читать онлайн ).
- ↑ a и b Малая энциклопедия математики , Дидье , 1980, стр. 72 .
- ↑ Происхождение и история математических символов на сайте math93.com.
- ↑ Chilias Logarithmorum на сайте e-rara.ch.
- ↑ Эммануэль Ферран, Лоран Кёльблен, Матье Романьи, « Немного истории » ,
- ↑ (in) Джеймс Стюарт (in) , Исчисление с одной переменной: ранние трансценденталы , Томсон Брукс / Коул,, 7- е изд. ( читать онлайн ), раздел 1.6.
- ↑ Стандарт AFNOR NF X 02-1 01 от 1961 г. рекомендует использовать обозначение ln ( Числовые таблицы Дж. Лаборда, 1976 г., стр. VI).
- ↑ Языки C , Java , Javascript и др.
- ↑ Д. Гуинин и Б. Джоппин, Математика MPSI : Exercises , Bréal ,( читать онлайн ) , стр.
 О. Феррье, Математика для экономистов: Анализ в экономике , т. 1, Университет Де Бека ,( ISBN 978-2-8041-4354-1 ) , стр. 275.
О. Феррье, Математика для экономистов: Анализ в экономике , т. 1, Университет Де Бека ,( ISBN 978-2-8041-4354-1 ) , стр. 275. - ↑ Не путайте с различными другими «числами Эйлера» .
- ↑ ISO 80000-2: 2009 . Международная организация по стандартизации . По состоянию на 19 января 2012 г.
- ↑ Международная организация по стандартизации , « ISO 80000-2: 2019 » (по состоянию на 16 сентября 2012 г. ) .
- ↑ Ален Бувье , Мишель Джордж и Франсуа Ле Лионне , Математический словарь , Университетское издательство Франции ,( 1- е изд.
 , 1979), с. 159.
, 1979), с. 159.
Смотрите также
Статьи по Теме
- Комплексный логарифм
- Функция полилогарифма
- Голоморфная функция
- Закон Бенфорда
- Музыкальная акустика: звуковые интервалы и логарифмы
Практическое применение
- Логарифмическая линейка
- Логарифмическая шкала
- Таблица логарифмов
Внешняя ссылка
Симона Тромплер, История логарифмов , опубликованная в 2002 году в Интернете Брюссельским университетом.
Обычные математические функции | |
|---|---|
| Рациональная алгебраическая функция |
|
| Иррациональная алгебраическая функция |
|
| Трансцендентная функция |
|
<img src=»https://fr.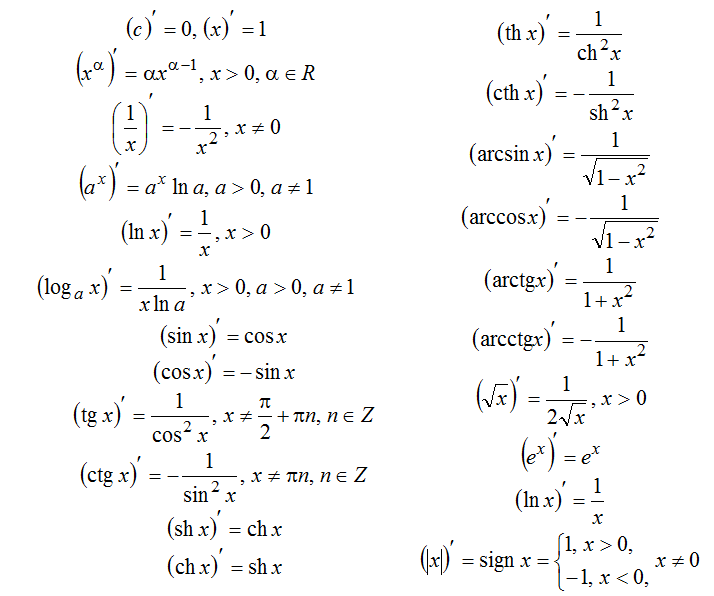 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
11 правил естественного бревна, которые вам нужно знать
Если вы изучаете математику в старшей школе или колледже, вы, скорее всего, будете изучать натуральные бревна. Но что такое натуральные бревна? Что такое лн? Почему буква е продолжает появляться?
Естественные журналы могут показаться сложными, но как только вы поймете несколько ключевых правил естественного журнала, вы сможете легко решать даже очень сложные задачи. В этом руководстве мы объясним четыре наиболее важных правила натурального логарифма, обсудим другие свойства натурального логарифма, которые вам следует знать, рассмотрим несколько примеров различной сложности и объясним, чем натуральный логарифм отличается от других логарифмов.
Что такое ln?
Натуральный логарифм, или ln, является обратным e . Буква « e» представляет собой математическую константу, также известную как натуральный показатель степени. Как и π, e является математической константой и имеет заданное значение. Значение e приблизительно равно 2,71828.
Как и π, e является математической константой и имеет заданное значение. Значение e приблизительно равно 2,71828.
e появляется во многих случаях в математике, включая сценарии сложных процентов, уравнения роста и уравнения распада. пер( x ) — это время , необходимое для роста до x , а e x — это величина роста , которая произошла после времени x .
Поскольку e так часто используется в математике и экономике, а людям, работающим в этих областях, часто приходится логарифмировать число по основанию e , чтобы решить уравнение или найти значение, был создан естественный логарифм. как быстрый способ записи и расчета базы журнала e . Естественный журнал просто позволяет людям, читающим задачу, знать, что вы берете логарифм с основанием 9.0016 e , номер. So ln( x ) = log e ( x ). Например, ln( 5 ) = log e ( 5 ) = 1,609.
4 ключевых правила естественного логарифма
Есть четыре основных правила, которые вам необходимо знать при работе с естественным логарифмом, и вы будете встречать каждое из них снова и снова в своих математических задачах. Знайте их хорошо, потому что они могут сбивать с толку в первый раз, когда вы их видите, и вы хотите убедиться, что у вас есть основные правила, подобные этим, до того, как перейти к более сложным темам логарифмов.
Правило продукта
- ln(x)(y) = ln(x) + ln(y)
- Натуральный логарифм произведения x и y равен сумме ln числа x и ln числа y.
- Пример: ln(8)(6) = ln(8) + ln(6)
Частное правило
- ln(x/y) = ln(x) — ln(y)
- Натуральный логарифм деления x и y равен разнице ln x и ln of y.
- Пример: ln(7/4) = ln(7) — ln(4)
Правило взаимности
- ln(1/x) = −ln(x)
- Натуральный логарифм обратной величины x противоположен ln x.

- Пример: ln(⅓)= -ln(3)
Степенное правило
- ln( x y ) = y * ln(x)
- Натуральный логарифм x, возведенный в степень y, равен y, умноженному на ln числа x.
- Пример: ln(5 2 ) = 2 * ln(5)
Ключевые свойства натурального бревна
В дополнение к четырем правилам натурального логарифма, рассмотренным выше, есть также несколько свойств ln, которые вам необходимо знать, если вы изучаете натуральный бревно. Запомните их, чтобы вы могли быстро перейти к следующему шагу задачи, не тратя время на запоминание общих свойств ln.
| Сценарий | Л-н Имущество |
| Номер отрицательного числа | Индикация отрицательного числа не определена |
| № 0 | ln(0) не определено |
| № 1 | лн(1)=0 |
| Инфинити | ln(∞)= ∞ |
| лн е | ln(e)=1 |
| Число e, возведенное в степень x | ln( e х ) = х |
| e в степени ln | е ln(x) =x |
Как видно из последних трех строк, ln( e )=1, и это верно, даже если одно возводится в степень другого. Это потому, что ln и e являются обратными функциями друг друга.
Это потому, что ln и e являются обратными функциями друг друга.
Примеры задач Natural Log
Теперь пришло время проверить свои навыки и убедиться, что вы понимаете правила ln, применяя их к примерам задач. Ниже приведены три примера задач. Попробуйте решить их самостоятельно, прежде чем читать объяснение.
Задача 1
Вычислить ln(7 2 /5)
Сначала воспользуемся правилом частных, чтобы получить: ln(7 2 ) — ln(5).
Затем мы используем правило степени, чтобы получить: 2ln(7) -ln(5).
Если у вас нет калькулятора, вы можете оставить уравнение в таком виде или рассчитать натуральные логарифмические значения: 2(1,946) — 1,609 = 3,891 — 1,609 = 2,282.
Задача 2
Вычислить ln( e ) /7
Для этой задачи нам нужно помнить, чем ln( e )=1
Это означает, что задача упрощается до 1/7, что и является нашим ответом. в круглых скобках вы хотите сделать e основанием, а все остальное — показателем степени e . Тогда вы получите ln и e рядом друг с другом и, как мы знаем из правил естественного логарифма, e ln(x) =x.
Тогда вы получите ln и e рядом друг с другом и, как мы знаем из правил естественного логарифма, e ln(x) =x.
SO, уравнение становится E LN (5x-6) = E 2
С E LN (x) = x , E LN ( x , E 5 LN-6x-6x-6x-5x-5x- x , E . ) = 5x-6
Следовательно, 5 x -6= e 2
Поскольку e является константой, вы можете вычислить значение , используя либо 3 , 6 e 9003 нажмите клавишу e на вашем калькуляторе или используйте оценочное значение e, равное 2,718.
5 x -6 = 7,389
Теперь мы добавили бы 6 к обеим сторонам
5 x = 13,389
Наконец, мы разделим обе стороны на 5.
x = 2,678
Чем натуральные логарифмы отличаются от других логарифмов?
Напоминаем, что логарифм противоположен степени. Если вы возьмете логарифм числа, вы отмените экспоненту. Основное различие между натуральным логарифмом и другими логарифмами заключается в используемом основании. Логарифмы обычно используют основание 10 (хотя это может быть другое значение, которое будет указано), в то время как натуральные журналы всегда будут использовать основание e .
Если вы возьмете логарифм числа, вы отмените экспоненту. Основное различие между натуральным логарифмом и другими логарифмами заключается в используемом основании. Логарифмы обычно используют основание 10 (хотя это может быть другое значение, которое будет указано), в то время как натуральные журналы всегда будут использовать основание e .
Это означает, что ln(x)=log e ( x )
Если вам нужно преобразовать логарифмы в натуральные логарифмы, используйте следующие два уравнения: х ) = пер(х) / пер(10)
За исключением разницы в основании (что является большой разницей), правила логарифмирования и правила натурального логарифма одинаковы:
| Правила логарифмирования | лн Правил |
| лог(ху)=лог(х)+лог(у) | 1n(x)(y)= 1n(x)+ln(y) |
| лог(х/у)=лог(х)-лог(у) | пер (х/у) = пер (х) — пер (у) |
| журнал (x a ) = a log( x ) | ln(x a )= a ln( x ) |
| log(10 х ) = х | ln( e х )= х |
| 10 log(x) = x | е ln(x) = х |
Резюме: Правила естественного логарифма
Натуральный логарифм, или ln, является обратным числом 9. 0016 е. Правила естественного бревна поначалу могут показаться нелогичными, но как только вы их выучите, их будет довольно просто запомнить и применять к практическим задачам.
0016 е. Правила естественного бревна поначалу могут показаться нелогичными, но как только вы их выучите, их будет довольно просто запомнить и применять к практическим задачам.
Четыре основных правила ln:
- ln(x)(y) = ln(x) + ln(y)
- ln(x/y) = ln(x) — ln(y)
- ln(1/x)=−ln(x)
- n( x y ) = y*ln(x)
Основное различие между натуральным логарифмом и другими логарифмами заключается в используемом основании.
Что дальше?
Пишете исследовательскую работу для школы, но не знаете, о чем написать? В нашем справочнике по темам для научных работ более 100 тем в десяти категориях, так что вы обязательно найдете идеальную тему для себя.
Хотите узнать самый быстрый и простой способ конвертации градусов Фаренгейта в Цельсий? Мы вас прикроем! Ознакомьтесь с нашим руководством по лучшим способам преобразования градусов Цельсия в градусы Фаренгейта (или наоборот).
Сдавать SAT или ACT? Учащимся часто труднее всего справиться с математическим разделом этих тестов, но ознакомьтесь с нашими подробными руководствами по математике SAT и ACT по математике, чтобы узнать все, что вам нужно знать, чтобы справиться с этими математическими вопросами.
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Кристин Сарикас
Об авторе
Кристин окончила Мичиганский государственный университет со степенью в области экологической биологии и географии и получила степень магистра в Университете Дьюка. В старшей школе она набрала 99-й процентиль по SAT и была названа финалистом национальных заслуг. Она преподавала английский язык и биологию в нескольких странах.
В старшей школе она набрала 99-й процентиль по SAT и была названа финалистом национальных заслуг. Она преподавала английский язык и биологию в нескольких странах.
Mathscene — Экспоненты и логарифмы
Mathscene — Экспоненты и логарифмы — Урок 3| 2007 Расмус Эхф и Джанн Сак Птурссон | Экспоненты и логарифмы | распечатать |
Урок 3
Естественный логарифмы
Поскольку калькуляторы и компьютеры стали инструменты для большинства числовых операций, логарифмы с основанием 10 стали менее полезно. С другой стороны, логарифм с другим основанием чем 10, становится все более полезным во многих науках.
Эта функция называется функцией натурального логарифма и имеет символ пер.
f(x)=ln x
Основанием натуральных логарифмов является число e
которые вы видите на своем калькуляторе.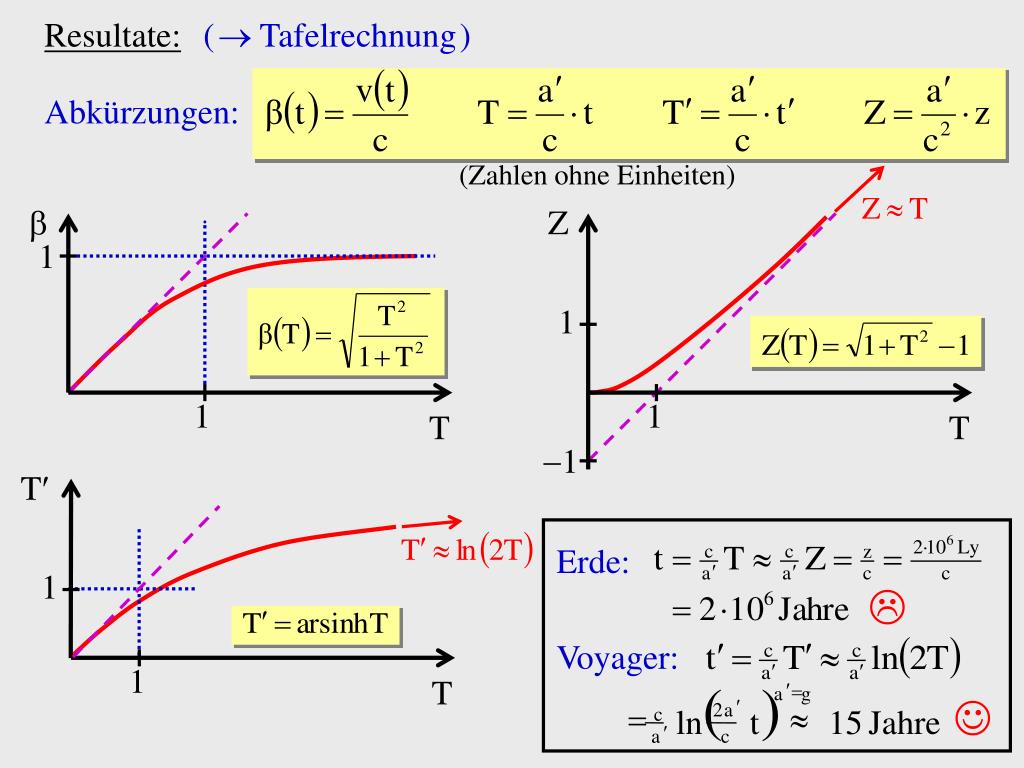
e — иррациональное число e2,718
| Пример 1 |
Вот как вы находите натуральный логарифм 2 на калькуляторе CASIO:
Ответ примерно 0,693 — это степень, в которую нам нужно возвести e, чтобы получить 2,
.e 0 . 693 ≈ 2
Проверь это на себе калькулятор:
Ответ: 1,9997 ≈ 2,
.Функции f(x) = ln x и g(x) = e x отменить каждое other out, когда одна функция используется на выходе другой. Это то же самое происходит с f(x) = log x и g(x) = 10 x или возведение числа в квадрат, а затем извлечение квадратного корня из результата. Другими словами, функция f(x) = ln x обратна функции g(x) = e х .
Верно следующее: x = x og e ln х = х
Число e иррационально
и поэтому мы не можем найти точное значение для него.
Мы можем вычислить его значение до любого числа знаков после запятой, выбрав большее
и большие значения x и подставляя их в следующую формулу.
Пример 2
Рассчитайте e, подставив x = 1000 в формулу и с помощью калькулятора.
С помощью EXCEL получаем значение 2,7182818284591 для эл. Таким образом, выбор x = 1000 дает нам только два правильных цифры. Теперь попробуйте вычислить e, используя x = 1000000.
Теперь у нас есть пять правильных цифр. Чем выше значение x тем больше точность в нашем вычислении e.
Пример 3
Нарисуйте графики функции f(x) = ln x и g(x) = e х .
Первый составить таблицу значений:
| х | ф(х) = е х | х | г(х) = ln х | |
| -3 | 0,05 | -1,39 | ||
| -2 | 0,14 | -0,69 | ||
| -1 | 0,37 | 1 | 0 | |
| 0 | 1 | 2 | 0,69 | |
| 1 | 2,72 | 4 | 1,39 | |
| 2 | 7,39 | 8 | 2,08 |
Обратите внимание, что нет отрицательных
значения в столбце для g(x) = e x и в столбце x нет отрицательных значений для обратной функции g(x) =
х .
Домен для f(x) = ln x множество {xR | х > 0}.
Обратите внимание, что когда мы рисуем оба графика в одном и том же
система координат они зеркальное отображение каждого
прочие (симметричные) в ряд через точки, где у = х.
Это верно для графиков любых двух функций, которые являются обратными друг другу.
Те же правила действуют для натуральная логарифмическая функция
Следующие примеры показывают как эти правила используются.
Пример 4
Решите следующее уравнения :
а)
| Шаг
2 и напишите как власть. Подставьте базовое число e в обе части уравнения. e и ln отменяют друг друга оставив нам квадратное уравнение. Переместить x над знаком равенства. Разложите на множители и решите x |
x = 0 невозможно, так как
нельзя записать 0 как степень.
б)
| Запись
левая часть как один логарифм.
Положить в основном числе e. ln и e компенсируют друг друга.
|
в)
|
| Упрощение слева, записав как один логарифм. |
| Вставить основание e с обеих сторон. |
Пример 5
Решите следующее уравнения:
а)
| Взять логарифм обеих сторон . |
б)
Использование правила: и х а у = а х + у , x / y = а х-у a n d(а п ) м = а нм по
запишите каждую сторону как степень e .
|
в)
Использование правила: и х a y = a x+y и a x /a y = a x−y , чтобы записать каждую сторону как мощность эл.
|
Пример 6
Решите уравнения:
а)
Взять журнал обеих частей уравнения, затем используйте правило а x = x ln a для перемещения неизвестное значение перед пер.
|
б)
Взять
члены в x в одну часть уравнения и другие члены в другую
сторона.
|
в)
Отдельный степени числа 5. Разделите обе части на 25, затем найдите x, как и раньше: .
|
Пройди тест 3 по экспоненциалам и логарифмы.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Демистификация натурального логарифма (ln) – BetterExplained 9x$, уже достаточно странный показатель.
Но есть свежее интуитивное объяснение: Естественный бревно дает вам время, необходимое для достижения определенного уровня роста .
Предположим, вы инвестируете в мармеладных мишек (у кого нет?) с процентной ставкой 100% в год, которая постоянно растет. Если вам нужен 10-кратный рост, при непрерывном начислении сложных процентов , вам придется подождать всего $\ln(10)$ или 2,302 года. Не понимаете, почему для десятикратного роста требуется всего несколько лет? Не видите, почему шаблон не 1, 2, 4, 8? Подробнее об эл. 93$ это 20.08. Через 3 единицы времени мы получаем в 20,08 раз больше, чем мы начали.
Со мной? Естественный журнал дает нам время, необходимое для достижения желаемого роста.
Логарифмическая арифметика ненормальна
Вы уже изучали бревна раньше, и это были странные звери. Как они превратили умножение в сложение? Деление на вычитание? Посмотрим.
Что такое $\ln(1)$? Интуитивно возникает вопрос: как долго мне ждать, чтобы получить 1x мою текущую сумму?
Ноль. Почтовый индекс Нада. Вы уже в 1x вашей текущей суммы! Чтобы вырасти с 1 до 1, не требуется времени.
Почтовый индекс Нада. Вы уже в 1x вашей текущей суммы! Чтобы вырасти с 1 до 1, не требуется времени.
- $\ln(1) = 0$
Хорошо, а как насчет дробного значения? Как долго я получу 1/2 моей текущей суммы? Предполагая, что вы непрерывно растете на 100 %, мы знаем, что $\ln(2)$ — это время, за которое удвоится. Если мы реверсируем это (т. е. возьмем отрицательное время), мы получим половину нашего текущего значения.
- $\ln(.5) = – \ln(2) = -.693$
Логично, правда? Если мы вернемся назад на 0,693 единицы (скажем, минус секунды), у нас будет половина текущего количества. В общем, вы можете перевернуть дробь и взять отрицательное значение: $\ln(1/3) = – \ln(3) = -1,09$. Это означает, что если мы вернемся на 1,09 единицы времени назад, у нас будет треть того, что у нас есть сейчас.
Хорошо, а как насчет натурального логарифма отрицательного числа? Сколько времени требуется, чтобы «вырастить» вашу колонию бактерий с 1 до -3?
Это невозможно! У вас не может быть «отрицательного» количества бактерий, не так ли? В лучшем случае (э. .. как минимум) у вас может быть ноль, но нет никакого способа получить отрицательное количество маленьких тварей. Отрицательные бактерии просто не имеют смысла.
.. как минимум) у вас может быть ноль, но нет никакого способа получить отрицательное количество маленьких тварей. Отрицательные бактерии просто не имеют смысла.
- $\ln(\text{отрицательное число}) = \text{undefined}$
Undefined просто означает, что «у вас нет времени ждать», чтобы получить отрицательную сумму. (Что ж, если использовать воображаемые экспоненты, решение есть. Но сегодня давайте оставим его реальным.)
Логарифмическое умножение — это очень весело
Сколько времени потребуется, чтобы увеличить текущее количество в 9 раз? Конечно, мы могли бы просто использовать ln(9). Но это слишком просто, давайте будем другими.
Мы можем рассматривать 9-кратный рост как утроение (затрачиваем $\ln(3)$ единиц времени), а затем снова утроение (затрачивая еще $\ln(3)$ единиц времени):
- Время роста 9x = $ \ln(9)$ = время утроиться и снова утроиться = $\ln(3) + \ln(3)$
Интересно. Любое число роста, например 20, можно рассматривать как 2-кратный рост, за которым следует 10-кратный рост. Или 4-кратный рост, за которым следует 5-кратный рост. Или 3-кратный рост, за которым следует 6,666-кратный рост. Видишь узор?
Или 4-кратный рост, за которым следует 5-кратный рост. Или 3-кратный рост, за которым следует 6,666-кратный рост. Видишь узор?
- $\ln(a*b) = \ln(a) + \ln(b)$
Логарифм a, умноженный на b = log(a) + log(b). Эта связь имеет смысл , если вы думаете о времени роста.
Если мы хотим вырасти в 30 раз, мы можем подождать $\ln(30)$ сразу или просто подождать, пока $\ln(3)$ утроится, а затем подождать, пока $\ln(10)$ вырастет в 10 раз. опять таки. Чистый эффект тот же, поэтому чистое время тоже должно быть таким же (и это так).
Как насчет деления? $\ln(5/3)$ означает: сколько времени потребуется, чтобы увеличиться в 5 раз, а затем взять 1/3 от этого?
Увеличение в 5 раз равно $\ln(5)$. Увеличение на 1/3 составляет $-\ln(3)$ единиц времени. Итак,
- $\ln(5/3) = \ln(5) – \ln(3)$
Что говорит: Увеличьте 5 раз и «вернитесь в прошлое», пока у вас не будет трети этого количества, поэтому у вас останется рост 5/3. В общем случае имеем
В общем случае имеем
- $\ln(a/b) = \ln(a) – \ln(b)$
Я надеюсь, странная логарифмическая математика начинает обретать смысл: умножение роста становится сложением времени, деление роста становится вычитанием времени. Не запоминайте правила, 9{3.4} = 30$
И интуитивно это уравнение означает «100% доход за 3,4 года — это 30-кратный рост». Мы можем рассматривать уравнение как:
Мы можем изменить «скорость» и «время», если скорость * время = 3,4. Например, предположим, что мы хотим 30-кратного роста — как долго мы будем ждать, предполагая доходность 5%?
- $\ln(30) = 3,4$
- $\text{ставка} * \text{время} = 3,4$
- $.05 * \text{время} = 3,4$
- $\text{время} = 3,4 / 0,05 = 68 \text{лет}$
Интуитивно я думаю: «$\ln(30) = 3,4$, поэтому при 100% росте потребуется 3,4 года. Если я удвою скорость роста, я сократю вдвое необходимое время».
- 100% на 3,4 года = 1,0 * 3,4 = 3,4
- 200 % на 1,7 года = 2,0 * 1,7 = 3,4 [рост 200 % означает половину времени]
- 50 % в течение 6,8 лет = 0,5 * 6,8 = 3,4 [рост 50 % означает удвоение времени]
- 5% в течение 68 лет = 0,05 * 68 = 3,4 [рост 5% означает увеличение времени в 20 раз]
Круто, да? Натуральное бревно можно использовать с любыми процентная ставка или время , пока их продукт одинаков. Вы можете менять переменные как хотите.
Вы можете менять переменные как хотите.
Удивительный пример: Правило 72
Правило 72 — это быстрый способ вычислить время, необходимое для удвоения ваших денег. Мы собираемся вывести это (ура!) И, что еще лучше, мы будем понимать это интуитивно.
Сколько времени нужно, чтобы удвоить ваши деньги при 100% годовых, начисляемых каждый год?
Ой . Мы использовали натуральный бревно для непрерывные ставки , но теперь вы просите годовых процентов? Не испортит ли это нашу формулу? Да, будет, но при разумных процентных ставках , таких как 5%, 6% или даже 15%, нет большой разницы между ежегодными начисленными процентами и полностью непрерывными процентами. Таким образом, грубая формула работает, ну, грубо, и мы притворимся, что получаем полностью непрерывный процент.
Теперь вопрос прост: как долго можно удвоить при 100% процентной ставки? ln(2) = 0,693. Требуется 0,693 единицы времени (в данном случае лет), чтобы удвоить ваши деньги с непрерывным начислением сложных процентов со ставкой 100%.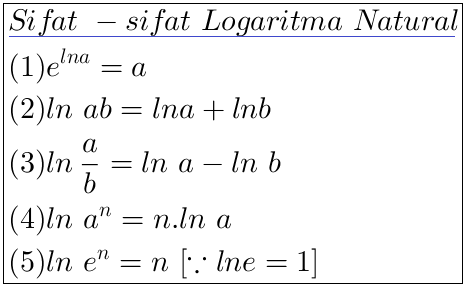
Хорошо, а что, если наша заинтересованность не равна 100 %? Что, если она составляет 5 % или 10 %?
Простой. Пока ставка * время = 0,693, мы удвоим наши деньги:
- ставка * время = 0,693 .
- время = 0,693/скорость
Итак, если бы у нас был только 10-процентный рост, удвоение заняло бы 0,693 / 0,10 или 6,93 года.
Чтобы упростить задачу, давайте умножим на 100, чтобы мы могли говорить о 10, а не о 0,10:
- время удвоения = 69,3/ставка, где скорость предполагается в процентах.
Теперь время удвоения при 5% росте составляет 69,3/5 или 13,86 лет. Однако 69,3 — не самое делимое число. Давайте выберем ближайшего соседа, 72, который можно разделить на 2, 3, 4, 6, 8 и многие другие числа.
- время удвоения = 72/скорость
это правило 72! Легко свежий.
Если вы хотите найти время утроения, вы должны использовать ln(3) ~ 109,8 и получить
- время утроения = 110 / скорость
Еще одно полезное практическое правило. Правило 72 полезно для процентных ставок, роста населения, бактериальных культур и всего, что растет в геометрической прогрессии.
Правило 72 полезно для процентных ставок, роста населения, бактериальных культур и всего, что растет в геометрической прогрессии.
Куда отсюда?
Я надеюсь, что естественный журнал имеет больше смысла — он говорит вам раз , необходимых для любого количества экспоненциального роста. Я считаю это «естественным», потому что e — это универсальная скорость роста, поэтому ln можно считать «универсальным» способом выяснить, сколько времени требуется для роста.
Когда вы видите $\ln(x)$, просто подумайте «количество времени, необходимое для роста до x». В следующей статье мы объединим e и ln, и воздух наполнится сладким ароматом математики.
Приложение: Естественный журнал E
Быстрый тест: что такое $\ln(e)$?
- Математический робот говорит: Поскольку они определены как обратные функции, ясно, что $\ln(e) = 1$
- Интуитивный человек: ln(e) — это время, необходимое для получения «e» единиц роста (около 2,718). Но e равно количеству роста после 1 единицы времени , поэтому $\ln(e) = 1$.

Думай интуитивно.
Другие сообщения из этой серии
- 90 = 1?)
- Использование логарифмов в реальном мире
- Как думать с экспонентами и логарифмами
- Сравнение дискретного и непрерывного роста
- Что на самом деле означает показатель степени?
- В: Почему е особенное? (2,718…, а не 2, 3,7 или другое число?)
Правила журнала — правила естественного журнала (правила Ln)
Правила журнала относятся к правилам логарифмирования. Эти правила выведены из правил экспоненты, поскольку логарифм — это просто другой способ записи экспоненты. Используются правила логарифмирования:
- для сжатия группы логарифмов в один логарифм
- разложить логарифм на группу логарифмов
Давайте узнаем больше о правилах ведения журналов и решим несколько примеров задач, используя правила логарифмирования.
1. | Что такое правила журнала? |
| 2. | Правила естественного бревна |
| 3. | Правило произведения логарифмов |
| 4. | Правило частных логарифмов |
| 5. | Правило степени логарифма |
| 6. | Изменение базового правила журналов |
| 7. | Часто задаваемые вопросы о правилах журнала |
Что такое правила журнала?
Правила журнала — это правила, которые используются для работы с логарифмами. Поскольку логарифм — это просто другой способ записи показателя степени, мы используем правила показателей степени для получения правил логарифмирования. В основном есть 4 важных правила ведения журнала, которые сформулированы следующим образом:
- правило продукта: log b mn = log b m + log b n
- частное правило: log b m/n = log b m — log b n
- правило мощности: log b m n = n log b m
- изменение базового правила: log a b = (log c b) / (log c a)
Следующие логарифмические правила выводятся из формулы преобразования логарифмической формы в экспоненциальную и наоборот (b x = m ⇔ log b m = x).
- б 0 = 1 ⇒ log б 1 = 0
- б 1 = б ⇒ log б б = 0
Правила логарифмирования
Наряду с этими правилами у нас есть несколько других правил логарифмирования. Все правила логарифмирования упомянуты ниже:
Далее мы увидим, как каждое из этих правил выводится с использованием правил экспоненты.
Правила натурального бревна
Натуральный логарифм — это логарифм с основанием «e». Обозначается буквой «лн». т. е. log e = ln. т. е. мы НЕ записываем основание натурального логарифма. Когда «ln» отображается автоматически, подразумевается, что его основанием является «e». Правила логарифмов одинаковы для всех логарифмов, включая натуральный логарифм. Следовательно, важные правила естественного логарифма (правила ln) таковы:
- ln (mn) = ln m + ln n
- лн (м/н) = лн м — пер н
- п.м. n = п п.м.
- ln a = (log a) / (log e)
- лн е = 1
- лн 1 = 0
Число, возведенное в правило журнала (упомянутое в таблице выше), равно b log b x = x. Эквивалентное правило для ln: e ln x = x.
Эквивалентное правило для ln: e ln x = x.
Правило произведения логарифмов
По правилу произведения логарифмов логарифм произведения двух членов равен сумме логов отдельных членов. то есть правило говорит log б мн = лог б м + лог б н. Выведем это правило.
Вывод:
Предположим, что log b m = x и log b n = y. Преобразуя каждую из них в экспоненциальную форму, мы получаем
log b m = x ⇒ m = b x … (1)
log b n = y ⇒ n = b y .. (2)
Умножьте уравнения (1) и (2),
mn = b x · b y
Используя правило умножения показателей степени,
mn = b x + y
Возврат к логарифмической форме,
log b mn = x + y
и подстановка значений x здесь
log b mn = log b m + log b n
Отсюда выводится правило произведения логарифма. Мы можем применить это правило следующими способами:
Мы можем применить это правило следующими способами:
- log (3a) = log 3 + log a .
- лог 10 = лог (5×2) = лог 5 + лог 2
- log 3 (ab) = log 3 a + log 3 b
Примечание: Правило произведения журналов ничего не говорит о журнале (m + n). Он говорит только о log (mn). log (m + n) действительно нельзя разделить на два логарифма.
Правило частных логарифмов
По правилу частных логарифмов логарифм частного двух слагаемых равен разности логарифмов отдельных слагаемых. то есть правило говорит log б мн = лог б м + лог б н. Выведем это правило.
Вывод:
Предположим, что log b m = x и log b n = y. Преобразуем их в экспоненциальные формы.
- бревно б м = х ⇒ м = б х … (1)
- log b n = y ⇒ n = b y .
 .. (2)
.. (2)
Разделив уравнения (1) и (2),
m/n = b x / b y
Используя правило возведения в частную степень,
m/n = b x — y
Преобразование этого обратно в логарифмическую форму,
log b 4 m/n = x0 — 3y подставляя 4 значения x и y возвращаются сюда,
log b m/n = log b m — log b n
Отсюда выводится правило частного логарифмирования. Мы можем применить это правило следующими способами:
- log (y/3) = log y — log 3
- лог. 25 = лог. (125/3) = лог. 125 — лог. 3
- журнал 7 (a/b) = журнал 7 а — журнал 7 б
Примечание: Правило отношения НЕ имеет никакого отношения к log (m — n).
Правило степени логарифма
Степенное правило журналов гласит, что если аргумент логарифма имеет показатель степени, то показатель степени можно поставить перед логарифмом. т. е. лог б м н = n log б м. Выведем это правило.
т. е. лог б м н = n log б м. Выведем это правило.
Вывод:
Предположим, что log b m = x. Изменение этого в экспоненциальную форму,
B x = M
Повышение обеих сторон на N,
(B x ) N = M N
по правлению мощности. nx = m n
Преобразуя это в логарифмическую форму,
log b m n = nx
Подставляя x = log b m здесь,
log b m n = n log b m
Следовательно, степень логарифмов является производной. Вот несколько применений этого правила.
- журнал 3 z = z журнал 3
- логарифм у 2 = 2 логарифм у
- логарифм 3 y x = x логарифм 3 y
Изменение базового правила журналов
Правило изменения основания журналов, как следует из названия, используется для изменения основания логарифма. Он говорит: log a b = (log c b) / (log c a). Мы можем ясно видеть, что основание в левой части правила равно «а», тогда как основания логарифмов в правой части равны «с». Теперь выведем это правило.
Он говорит: log a b = (log c b) / (log c a). Мы можем ясно видеть, что основание в левой части правила равно «а», тогда как основания логарифмов в правой части равны «с». Теперь выведем это правило.
Вывод:
Предположим, что log a b = x, log c b = y и log c а = г. Приведем эти уравнения к логарифмической форме.
- log a b = x ⇒ b = a x … (1)
- log c b = y ⇒ b = c y … (2)
- log с а = г ⇒ а = с г … (3)
Из (1) и (2),
a x = c y
Из (3), a = c z . Подставив это в приведенное выше уравнение,
(c z ) x = c y
c zx = c y
zx = y (или) x = y/z
Подставляя сюда значения x, 905 02 03:
3: a
b = (log c b) / (log c a) Отсюда выводится изменение базового правила журналов. Умножая его с обеих сторон на log c a, мы получаем другую форму изменения базового правила.
Умножая его с обеих сторон на log c a, мы получаем другую форму изменения базового правила.
бревно а б · бревно в а = бревно в b
Вот некоторые применения обеих форм этого правила:
- log 5 3 = (log 3)/(log 5)
- бревно x 4 · бревно 3 x = бревно 3 4
Правило изменения основания особенно используется, когда логарифм (с основанием, отличным от 10 и e) должен быть рассчитан с помощью калькулятора. Обратите внимание, что у нас есть только кнопки «log» и «ln» на калькуляторе. Итак, чтобы вычислить журнал с любой другой базой, скажем, журнал 5 3, кнопки с основанием 5 нет. Тогда по изменению правила основания log 5 3 = (log 3)/(log 5) и это можно легко вычислить с помощью кнопки «log» калькулятор.
Важные замечания по правилам логарифмирования
- Правила логарифмирования одинаковы как для натуральных, так и для десятичных логарифмов (log, log a и ln).
 База журнала просто переносится на каждый журнал при применении правил.
База журнала просто переносится на каждый журнал при применении правил. - log a 1 = 0 для любого основания ‘a’.
- Наиболее распространенные правила логарифмирования:
бревно б мн = бревно б м + бревно б н
бревно б м/н = бревно б м — бревно б н
лог б м n = n лог б м
☛ Связанные темы:
- Таблица журнала
- Стол Антилога
- Калькулятор журнала
- Калькулятор натурального бревна
Часто задаваемые вопросы о правилах журнала
Что такое 7 правил журнала?
Правила журнала используются для расширения или сжатия логарифмов. В таблице ниже перечислены 7 наиболее часто используемых правил ведения журналов.
| Имя правила | Правило журнала |
|---|---|
| Журнал 1 | журнал б 1 = 0 |
| Запись числа с одинаковым основанием | лог б б = 1 |
| Правило продукта | бревно б мн = бревно б м + бревно б н |
| Частное правило | бревно б м/н = бревно б м — бревно б н |
| Степенное правило логарифма | лог б м n = n лог б м |
| Изменение базы Правило | журнал б а = (лог а) / (лог б) |
| Номер увеличен до логарифмического | б журнал б х = х |
Когда использовать правила логарифмирования?
Когда нам нужно разложить логарифм на несколько логарифмов или сжать несколько логарифмов в один логарифм, мы используем правила логарифмирования .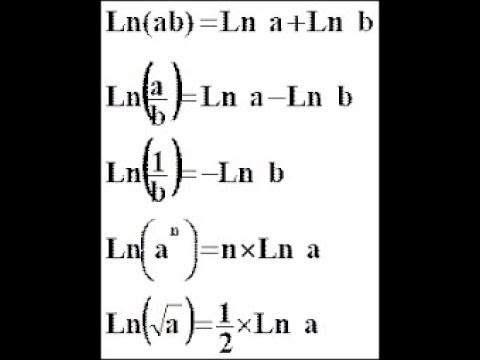 Эти правила являются производными от правил экспонент.
Эти правила являются производными от правил экспонент.
Что такое правило произведения логарифмов?
Правило произведения логарифмов: log b mn = log b m + log b n. Используя это правило, логарифм произведения можно преобразовать в сумму логарифмов. Например: log 2 (xyz) = log 2 x + log 2 y + log 2 z.
Как преобразовать отрицательный журнал в положительный?
Отрицательный журнал можно преобразовать в положительный с помощью одного из следующих правил журнала:
- Отрицательный журнал аргумента представляет собой логарифм обратной величины аргумента. т. е. -log b a = log b a -1 = log b (1/a).
- Отрицательный логарифм с основанием — это логарифм, основание которого равно величине, обратной данному основанию. т. е. -log b a = log (1/b) a.
Каковы правила Ln?
Правила «ln» относятся к натуральным логарифмам. Натуральные логарифмы — это логарифмы с основанием «е». Ниже приведены правила пер.
Натуральные логарифмы — это логарифмы с основанием «е». Ниже приведены правила пер.
- пер. 1 = 0
- лн е = 1
- ln м + ln n = ln (мн)
- ln м — ln n = ln (м/н)
- в м = м в
- е лн х = х
Что такое производные правила журнала?
Вот производные различных типов логарифмов:
- Производная ln x равна d/dx (ln x) = 1/x.
- Производная log a x, d/dx (log x) = 1/(x ln a)
Какие 4 важных правила логарифмирования?
У нас много правил логарифмирования. Среди них 4 важных правила общих журналов:
- log m + log n = log (mn)
- log m — log n = log (m/n)
- log a м = m log a
- 10 журнал х = х
В чем разница между правилами журнала и правилами естественного журнала?
На самом деле нет никакой разницы между правилами десятичных логарифмов и правилами натуральных логарифмов. Это связано с тем, что натуральный логарифм также является логарифмом (только с основанием «е»).
Это связано с тем, что натуральный логарифм также является логарифмом (только с основанием «е»).
Логарифмы и экспоненты
Одним из основных свойств чисел является то, что они могут быть выражены в экспоненциальной форме. Мы все знакомы с представлением 1000 = 10 3 или 0,001 = 10 -3 . Более общий способ заявить это свойство означает, что любое число (N) может быть выражено как основание (B) возведен в степень (x) или
В приведенных выше примерах основание равно 10. Другие примеры с использованием
основание 10, основание 2 и основание e (где e = 2,718…) приведены ниже в таблице.
1.
| Количество = 10 x | Количество = 2 x | Номер = е x | |||
. 01 01 | 10 -2 | 1 | 2 0 | .01 | е -4,605 |
| 1 | 10 0 | 2 | 2 1 | 1 | е 0 |
| 10 | 10 1 | 4 | 2 2 | 10 | е 2,303 |
| 1000 | 10 3 | 8 | 2 3 | 1000 | е 6,908 |
| 2 | 10 .301 | 2 | е . 693 693 | ||
| 4 | 10 .602 | 4 | е 1,386 | ||
| 8 | 10 .903 | 8 | е 2,079 | ||
Первые четыре записи в разделе с основанием 10 выглядят естественно, как и
записи в базе 2, но немногие студенты сразу угадали бы 0,301 как
соответствующий показатель степени для 2 = 10 х . Далее натуральная база
e (e = 2,71828..), вероятно, сначала кажется нелогичным основанием для представления
числа. Как будет показано ниже, показательные функции типа
y = ae bx очень распространены при описании физических и химических
систем, и необходимо базовое понимание этого типа функций.
Математическая формула N = B x служит основой для определение логарифмов. Логарифм числа (N) по основанию (B) определяется как (х).
логарифм (B) N = х
Обычно используются два основания, 10 и e. Сокращенные представления находятся:
логарифм по основанию 10 10 N = log 10 N = журнал NТаким образом, логарифм числа — это просто степень, в которой должно быть основание. быть поднят, чтобы дать число. В таблице 2 показаны логарифм и ln чисел в таблице 1.
и
основание e («натуральные» логарифмы) логарифм e N = пер Н
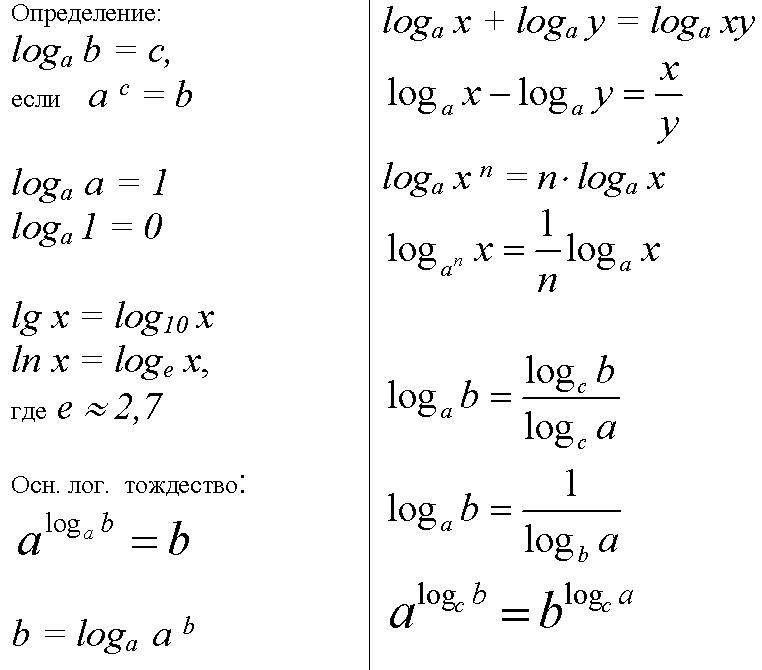 0100 0100 | ||
 00 00 | ||
ПРИМЕЧАНИЕ:
Учитываются только числа справа от десятичной точки в логарифме.
значимые фигуры. Число слева от десятичной точки просто,
по сути, говорит нам, где находится десятичная точка, и не считается
значимая фигура.
Существует несколько основных правил работы с логарифмами. Примеры даны в базе 10, но правила применимы к любой базе.
Правило 1:
журнал (a x b) = журнал a + журнал b
Примеры:
log (2000) = log (2 x 1000) = log 2 + log 1000 = 0,301 + 3 = 3.301Правило 2: журнал (а/б) = журнал а — журнал б
log (0,004) = log (4 x 0,001) = log 4 + log 0,001 = 0,602 — 3 = -2,398
Примеры:
log (2/4) = log 2 — log 4 = 0,301 — 0,602 = -0,301Правило 3: журнал (а) б = б журнал а
log (2/0,4) = log 2 — log 0,4 = log 2 — [log (4 x 0,1)] = 0,301 — [0,602 — 1] = 0,699
Примеры:
log (4) 3 = 3 log 4 = 3 x 0,602 = 1,806Правило 4: журнал (10) х = х
log (8) 1/2 = 1/2 log 8 = 1/2 x 0,903 = 0,452
Примеры:
журнал 10 -8 = -8Если кто-то знает логарифм числа и хочет найти это число, просто возводит основание в степень логарифма.
лн е 4 = 4
 Это называется взятие
антилогарифм.
Это называется взятие
антилогарифм. Примеры:
антилог. .301 = 10 .301 = 2Примечание: На большинстве калькуляторов антилогарифмы могут быть взяты
антилогарифмический 1,806 = 10 1,806 = 64
антилогарифмический -2,398 = 10 -2,398 = 0,004
против n 2,303 = е 2,303 = 10
против n 1,386 = e 1,386 = 4
Хотя логарифмы интересны и полезны сами по себе, они наибольшую применимость для нас при работе с экспоненциальными функциями.
- ИНВ + лог или ИНВ + ln
или- 10 x или e x
или- y x , где y = ОСНОВА.
Одно из очень распространенных функциональных соотношений, выявляемых экспериментально. наблюдения экспоненциальное увеличение или уменьшение. Это занимает форма выражения как
у = е х и у = е -х
В более общем виде это выглядит как
y = e ax и y = e -ax
, где a объединяет любые количества, которые можно считать
постоянна при изменении x и y. На графике эти функции
появляются, как показано на рисунке 1 (обратите внимание, что когда x = 0, y становится = 1). База
Логарифмы можно преобразовать в логарифмы по основанию 10.
На графике эти функции
появляются, как показано на рисунке 1 (обратите внимание, что когда x = 0, y становится = 1). База
Логарифмы можно преобразовать в логарифмы по основанию 10.
Рис. 1. Экспоненциальные функции
Так как очень сложно получить точную форму коэффициента
a из таких графиков становится удобнее применять логарифмы
функционировать в этой форме. Таким образом,
y = e ax становится ln y = ax; y = 10 a’x становится
журнал у = а’х
или 2,3 log y = ax. [Обратите внимание, что а’ = а/2,3]
, и график зависимости ln (или log) y от x даст прямую линию чей наклон будет «а». К этим выражениям применимы те же соображения. когда они являются прямыми линиями, как любая прямая линия.
В простом случае рассмотрим данные из табл. 3 для разложения
перекиси водорода. Показаны два способа графического отображения этих данных.
внизу: (а) концентрация в зависимости от времени в прямоугольных координатах, (б) логарифм
концентрация во времени в прямоугольных координатах. Они проиллюстрированы
на рисунках 2а-2б.
Они проиллюстрированы
на рисунках 2а-2б.
Разложение перекиси водорода | ||
| Время | Концентрация | Журнал концентрации |
Рис. 2а. Разложение перекиси водорода
2а. Разложение перекиси водорода
График зависимости концентрации от времени
Рисунок 2б. Разложение перекиси водорода
График зависимости концентрации от времени
Используете ли вы логарифмическую или экспоненциальную форму для таких отношений зависит от того, что предстоит определить. Математически экспоненциальная форма имеет определенные преимущества, а графически логарифмическая форма более информативна. Любая функциональная связь в этой форме имеет узнаваемые характеристики. которые становятся более очевидными, когда в общее выражение включается еще один символ. Таким образом,
у = у о е -ах
, где y o — константа, определяемая тем, что при x
= 0, значение e -ax = 1 и при этих условиях y = y o .
Следующие примеры иллюстрируют общие характеристики этого типа
функции. «a» — это конкретная константа в каждом примере.
- Снижение концентрации реагирующего вещества c в единицу времени t пропорционален концентрации и выражается как
- Уменьшение интенсивности падающего света I пропорционально на глубину l поглощающего материала и выражается как
- Давление атмосферы P уменьшается со скоростью, пропорциональной высота h и выражается как
c = c o e -at
, где c o – концентрация в момент времени t = 0 (в начале эксперимента).
I = I o e -al
где I o — интенсивность падающего излучения на l = 0, до прохождения через поглощающий материал.
P = P o e -ah
, где P o — давление при h = 0 на уровне моря.
- Нанесите заданные числовые значения x и y на лист миллиметровой бумаги, используя
y как вертикальная ось (ордината) и x как горизонтальная ось (абсцисса).
 Если доступна графическая программа для микрокомпьютера, она обеспечивает удобный
способ изучить график, не прибегая к бумажной копии. Экспериментально
независимое значение обычно откладывается по оси абсцисс, а экспериментально
измеряемая, зависимая, переменная по оси Y.
Если доступна графическая программа для микрокомпьютера, она обеспечивает удобный
способ изучить график, не прибегая к бумажной копии. Экспериментально
независимое значение обычно откладывается по оси абсцисс, а экспериментально
измеряемая, зависимая, переменная по оси Y. - Если полученный график показывает прямую линию, уравнение для исходного числовые значения легко определяются, так как уравнение прямой строка
y = mx + b
, где m = наклон и b = пересечение линии с осью y (при x=0).
уклон = м = подъем/спуск = 2/3
Рисунок B. Отрицательный наклон
уклон = м = подъем/спуск = -2/2 = -1
- Если график, полученный в результате шага I, не является прямой линией, вы не особенно вероятно, произойдет на уравнение путем осмотра. т.е. тот факт, что если х = 3, y = 9, (одна точка) не означает, что уравнение y = x 2 (действительно для всех точек). Один из способов заключается в преобразовании исходных данных в прямая линия. В этом курсе мы столкнемся с несколькими отношениями форма
Рассчитайте или считайте значения m и b, затем вставьте m и
значения b в уравнение y = mx + b. В результате должно получиться уравнение
ты ищешь. Чтобы еще раз проверить свою работу, попробуйте некоторые из оригинальных
данные значения для x в вашем уравнении и посмотреть, выходит ли y, как ожидалось. Уравнение линии на рис. A: y = 2x/3 + 5/3, а на рис. B:
у = -х + 5 = 5 — х.
Уравнение линии на рис. A: y = 2x/3 + 5/3, а на рис. B:
у = -х + 5 = 5 — х.
y = ae -b/T
где y — некоторое свойство системы, a и b — константы, а T это температура в Кельвинах. Все эти функции линеаризуются с помощью натуральный логарифм выражения.
ln y = ln a — b/T. График зависимости ln y от 1/T даст прямую линию с наклон -b и точка пересечения ln a.
Разница между логарифмом и Ln – определение, свойства и правила
Логарифм и Ln означают логарифм и натуральный логарифм соответственно. Логарифмы необходимы для решения уравнений, в которых неизвестная переменная появляется как показатель степени некоторой другой величины. Они важны во многих разделах математики и научных дисциплин и используются для решения задач, связанных со сложными процентами, которые широко связаны с финансами и экономикой.
Логарифмы необходимы для решения уравнений, в которых неизвестная переменная появляется как показатель степени некоторой другой величины. Они важны во многих разделах математики и научных дисциплин и используются для решения задач, связанных со сложными процентами, которые широко связаны с финансами и экономикой.
В математике логарифм может быть определен как функция, обратная возведению в степень.
Проще говоря, логарифм можно определить как степень, в которую нужно возвести число, чтобы получить любое другое число.
Он также известен как логарифм по основанию 10 или десятичный логарифм.
Общая форма логарифма может быть обозначена как:
В этой статье мы собираемся обсудить, что такое log, что такое ln в математике, правила Log и ln, разница между Log и Ln x, разница между log и natural log. и разница между логарифмом и графиком ln.
и разница между логарифмом и графиком ln.
Ниже приведены четыре основных свойства логарифма, которые помогут вам легко решать задачи, основанные на логарифмировании.
Свойства логарифма
Logb(mn) = Logb m + Logb n Это свойство логарифма означает, что умножение двух значений логарифма эквивалентно сложению отдельного логарифма. |
Logb (m/n) = Logb m — Logb n Это свойство логарифма говорит о том, что деление двух значений логарифма эквивалентно вычитанию отдельного логарифма. |
Logb (mn) = n logbm Вышеприведенное свойство известно как экспоненциальное правило логарифма. Логарифм m вместе с рациональным показателем эквивалентен показателю, умноженному на его логарифм. |
Logb m = loga m / loga При делении двух чисел по одному основанию степени вычитаются. |
Log Value from 1 to 10
Log | Value of Log |
Log 1 | 0 |
Журнал 2 | 0.3010 |
Log 3 | 0.4771 |
Log 4 | 0.6020 |
Log 5 | 0.6989 |
Log 6 | 0.7781 |
Log 7 | 0.8450 |
Log 8 | 0.9030 |
Log 9 | 0. |
Log 10 | 1 |
What is Ln in Maths?
Ln называется натуральным логарифмом. Его также называют логарифмом по основанию e. Здесь константа e обозначает число, которое является трансцендентным числом и иррациональным числом, приблизительно равным значению 2,71828182845. Натуральный логарифм (ln) может быть представлен как ln x или \[\log_{e}x\].
Давайте пройдут различные правила LN
Правило нера log деления x и y равен разности ln x и ln of y. Пример: ln(10/5) = ln(10) — ln(5) |
Правило взаимности log обратной величины x равен обратному значению ln x. 9{y})\] равно \[y \times \ln x\] Натуральный логарифм x, возведенный в степень y, равен y, умноженному на ln x. Пример: ln(4²) равно 2 * ln(4) |
Выше мы обсуждали правила log и ln.
Значения журнала от 1 до 10 до базы E приведены ниже
Таблица, показывающие значения LN от 1 до 10.
в (1) | |
в (1) | 2 |
в (1) | 7 |
в (1) | |
.0149 0 | |
In (2) | 0.6 |
In (3) | 1.098612 |
In (4) | 1.386294 |
In (5) | 1.609438 |
In (6) | 1. |
In (7) | 1.94591 |
In (8) | 2.079442 |
In (9) | 2.197225 |
In (10) | 2.302585 |
Разница между логарифмическим и линейным графиком
Эти графики покажут вам разницу между логарифмическим и линейным графиком.
(Изображения будут загружены в ближайшее время)
Давайте обсудим некоторые из ключевых различий между Log и Ln:
Чтобы решить логарифмические задачи, нужно знать разницу между логарифмом и натуральным логарифмом. Ключевое понимание экспоненциальных функций также может оказаться полезным для понимания различных концепций. Некоторые из важных различий между Log и Natural Log приведены ниже в табличной форме:
Некоторые из важных различий между Log и Natural Log приведены ниже в табличной форме:
Разница между Log и Ln x
log | LN |
LOG, как правило, относится к Logarithm в базу 10,0003 | 99999999999999999999999999999999999999999 2999999999999999999999999999999999999999999999999999999 гг. |
Это также известно как десятичный логарифм. | Также известен как натуральный логарифм. |
Общий журнал может быть представлен как log10 (x). | 9{x} = y\]|
Вопросительное утверждение для десятичного логарифма записывается как «На какое число нужно возвести 10, чтобы получить y?» | Вопросительное утверждение для натурального логарифма записывается как «На какое число мы должны возвести постоянное число Эйлера, чтобы получить y?» |
Логарифмическая функция более широко используется в физике по сравнению с ln. |

 693 / ставка
693 / ставка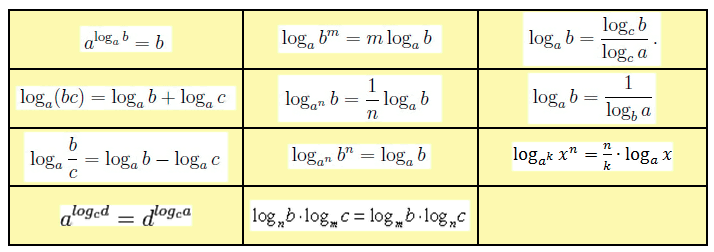

 Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.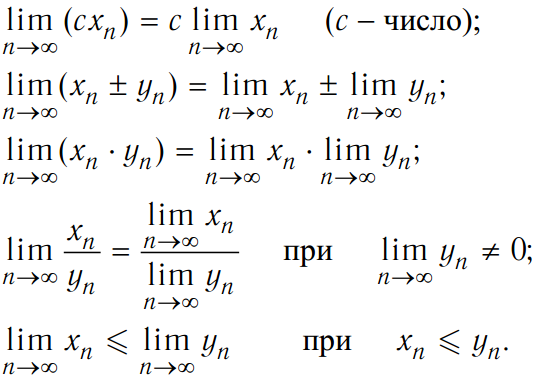
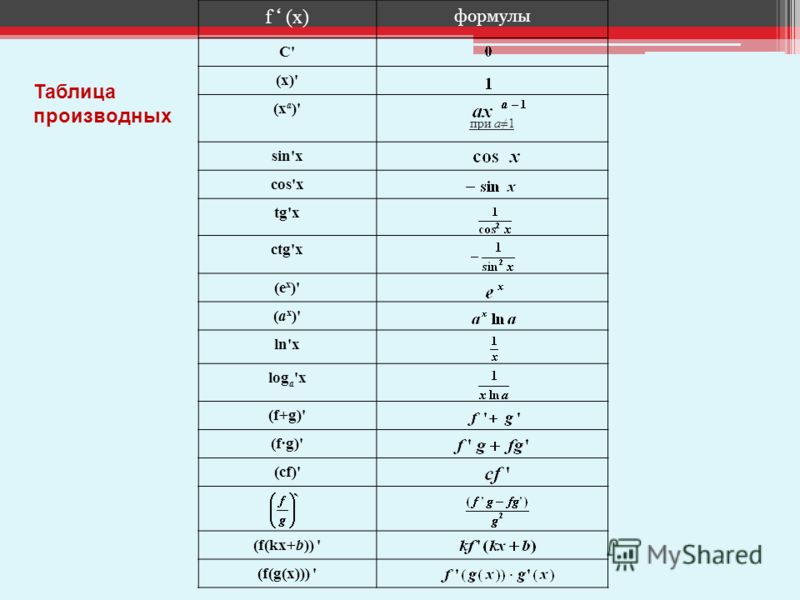 3 Двоичный логарифм
3 Двоичный логарифм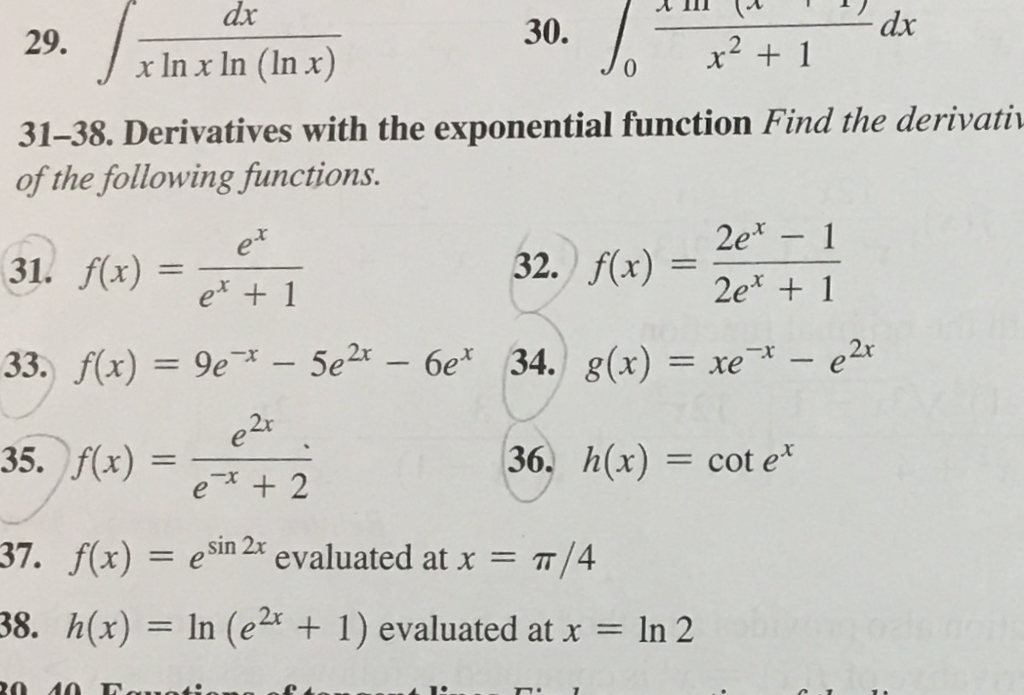 {p}) = p \ log _ {b} x. \,}
{p}) = p \ log _ {b} x. \,} {\ log _ {b} (y)} = y.}
{\ log _ {b} (y)} = y.}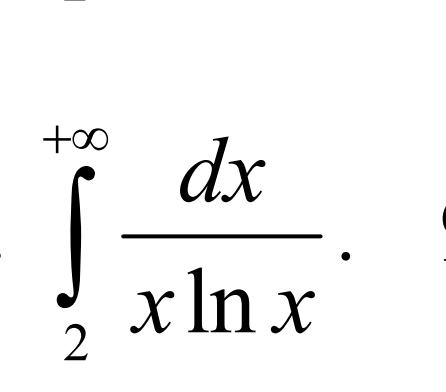 {*}}р{\ Displaystyle \ mathbb {R}}Икс↦1Икс{\ displaystyle x \ mapsto {\ frac {1} {x}}}
{*}}р{\ Displaystyle \ mathbb {R}}Икс↦1Икс{\ displaystyle x \ mapsto {\ frac {1} {x}}} {- 2} = 0,01}
{- 2} = 0,01} 1 («Колыбель логарифма») , с. 1-2.
1 («Колыбель логарифма») , с. 1-2. О. Феррье, Математика для экономистов: Анализ в экономике , т. 1, Университет Де Бека ,( ISBN 978-2-8041-4354-1 ) , стр. 275.
О. Феррье, Математика для экономистов: Анализ в экономике , т. 1, Университет Де Бека ,( ISBN 978-2-8041-4354-1 ) , стр. 275. , 1979), с. 159.
, 1979), с. 159.
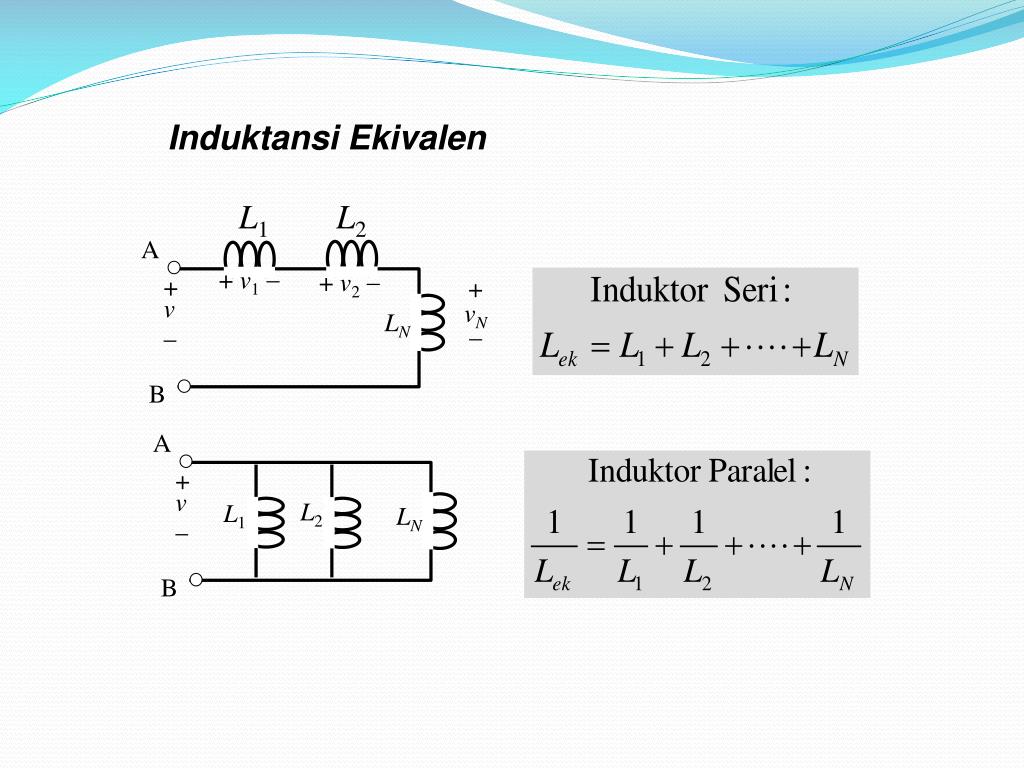
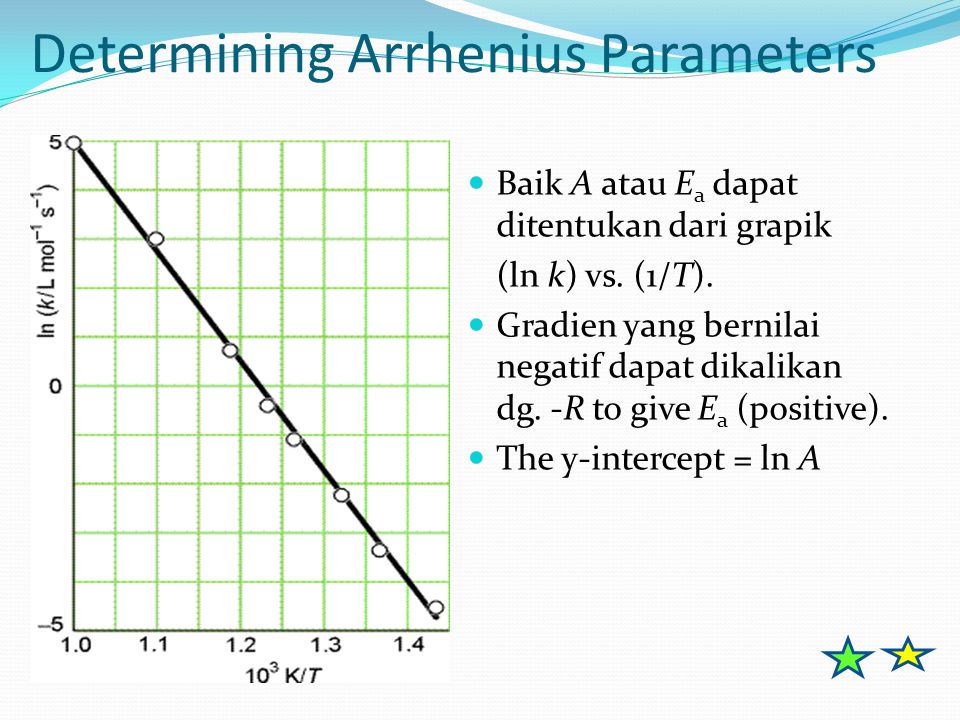 Упростите использование правил для индексов.
Упростите использование правил для индексов. 
 .. (2)
.. (2) База журнала просто переносится на каждый журнал при применении правил.
База журнала просто переносится на каждый журнал при применении правил.