Собственные значения
Собственные значения
Разложение собственного значения
Собственное значение и собственный вектор квадратной матрицы, A является, соответственно, скалярный λ и ненулевой векторный υ, которые удовлетворяют
Aυ = λυ.
С собственными значениями на диагонали диагональной матрицы Λ и соответствующие собственные вектора, формирующие столбцы матрицы V, вы имеете
AV = VΛ.
Если V несингулярен, это становится разложением собственного значения
A = VΛV–1.
Хорошим примером является матрица коэффициентов дифференциального уравнения dx/dt = A x:
A =
0 -6 -1
6 2 -16
-5 20 -10Решение этого уравнения описывается в терминах матричного экспоненциального x (t) = etAx0 . Оператор
Оператор
lambda = eig(A)
производит вектор-столбец, содержащий собственные значения
lambda =
-3.0710
-2.4645+17.6008i
-2.4645-17.6008iДействительная часть каждого из собственных значений отрицательна, таким образом, eλt нуль подходов как t увеличивается. Ненулевая мнимая часть двух из собственных значений, ±ω, вносит колебательный компонент, sin (ω t), к решению дифференциального уравнения.
С двумя выходными аргументами, eig вычисляет собственные вектора и хранит собственные значения в диагональной матрице:
[V,D] = eig(A)
V =
-0.8326 0.2003 - 0.1394i 0.2003 + 0.1394i
-0.3553 -0.2110 - 0.6447i -0.2110 + 0.6447i
-0.4248 -0.6930 -0.6930
D =
-3.0710 0 0
0 -2. 4645+17.6008i 0
0 0 -2.4645-17.6008i
4645+17.6008i 0
0 0 -2.4645-17.6008iПервый собственный вектор действителен, и другие два вектора являются сопряженными комплексными числами друг друга. Все три вектора нормированы, чтобы иметь Евклидову длину, norm(v,2), равняйтесь одному.
matrix V*D*inv(V), который может быть записан более кратко как V*D/V, в ошибке округления A. И, inv(V)*A*V, или V\A*V, в ошибке округления of D.
Несколько собственных значений
Некоторые матрицы не имеют разложения собственного вектора. Эти матрицы не являются диагонализируемыми. Например:
A = [ 1 -2 1
0 1 4
0 0 3 ]Для этой матрицы
[V,D] = eig(A)
производит
V =
1.0000 1.0000 -0.5571
0 0.0000 0.7428
0 0 0.3714
D =
1 0 0
0 1 0
0 0 3Существует двойное собственное значение в λ = 1. Первые и вторые столбцы
Первые и вторые столбцы V то же самое. Для этой матрицы не существует полный набор линейно независимых собственных векторов.
Разложение Шура
Много усовершенствованных матричных расчетов не требуют разложений собственного значения. Они базируются, вместо этого, на разложении Шура
A = U S U ′,
где U является ортогональной матрицей, и S является верхней треугольной матрицей блока с блоками 2 на 2 и 1 на 1 на диагонали. Собственные значения показаны диагональными элементами и блоками S, в то время как столбцы U обеспечивают ортогональный базис, который имеет намного лучшие числовые свойства, чем набор собственных векторов.
Например, сравните собственное значение и разложения Шура этой дефектной матрицы:
A = [ 6 12 19
-9 -20 -33
4 9 15 ];
[V,D] = eig(A)V = -0.4741 + 0.0000i -0.4082 - 0.0000i -0.4082 + 0.0000i 0.8127 + 0.0000i 0.8165 + 0.0000i 0.8165 + 0.0000i -0.3386 + 0.0000i -0.4082 + 0.0000i -0.4082 - 0.0000i D = -1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 1.0000 - 0.0000i
[U,S] = schur(A)
U =
-0.4741 0.6648 0.5774
0.8127 0.0782 0.5774
-0.3386 -0.7430 0.5774
S =
-1.0000 20.7846 -44.6948
0 1.0000 -0.6096
0 0.0000 1.0000Матричный A является дефектным, поскольку это не имеет полного набора линейно независимых собственных векторов (вторые и третьи столбцы V то же самое). С тех пор не все столбцы 1e8. Однако schur может вычислить три различных базисных вектора в U. Начиная с U является ортогональным, cond(U) = 1.
Матричный S имеет действительное собственное значение как первую запись на диагонали и повторном собственном значении, представленном нижним правым блоком 2 на 2. Собственные значения блока 2 на 2 являются также собственными значениями
Собственные значения блока 2 на 2 являются также собственными значениями A:
eig(S(2:3,2:3))
ans = 1.0000 + 0.0000i 1.0000 - 0.0000i
Смотрите также
eig | schur
Похожие темы
- Матрицы в среде MATLAB
- Факторизации
- Сингулярные значения
Mathway | Популярные задачи
Популярные задачи
Элемент. математикаОсновы алгебрыАлгебраТригонометрияОсновы мат. анализаМатематический анализКонечная математикаЛинейная алгебраХимияPhysics
| Рейтинг | Тема | Задача | Форматированная задача |
|---|---|---|---|
| 1 | Решить, используя обратную матрицу | x+2y=1 , 4x+5y=13 | , |
| 2 | Перемножить матрицы | [[1/( квадратный корень из 17),-4/( квадратный корень из 17)]][[1/( квадратный корень из 17)],[-4/( квадратный корень из 17)]] | |
| 3 | Найти область определения | x+y=3 | |
| 4 | Найти область определения | ||
| 5 | Найти область определения | y=-2x+3 | |
| 6 | Найти область определения | y=2x+1 | |
| 7 | Записать в виде векторного равенства | x=x^2+9x+3 , x=x+2 | , |
| 8 | Найти область определения | y=2x | |
| 9 | Найти область определения | y=-3x | |
| 10 | Найти область определения | y=3x-2 | |
| 11 | Найти область определения | y=4x | |
| 12 | Найти область определения | 3x+2y=6 | |
| 13 | Trovare la 5×5 Matrice Identità | 5 | |
| 14 | Trovare la 6×6 Matrice Identità | 6 | |
| 15 | Trovare la 4×4 Matrice Identità | 4 | |
| 16 | Решить, используя обратную матрицу | 2x+y=-2 , x+2y=2 | , |
| 17 | Решить, используя обратную матрицу | 4x+4=y , y=6x | , |
| 18 | Решить, используя обратную матрицу | 4x+2=5y-3 , y=3x-1 | , |
| 19 | Найти степенное множество | (3,4) | |
| 20 | Вычислить | кубический корень из 216 | |
| 21 | Найти степенное множество | (1,3) | |
| 22 | Найти область определения | 3x-2y=12 | |
| 23 | Найти область определения | y=5x+2 | |
| 24 | Найти область определения | y=2x-3 | |
| 25 | Найти область определения | y=2x-4 | |
| 26 | Найти область определения | y=2x+5 | |
| 27 | Найти область определения | y=1/2x | |
| 28 | Найти область определения | y=1/2x-3 | |
| 29 | Найти область определения | y=2/3x-2 | |
| 30 | Найти область определения | x=2y | |
| 31 | Найти область определения | x-2y=2 | |
| 32 | Найти область определения | x-2y=6 | |
| 33 | Найти область определения | 2y+x | |
| 34 | Найти область определения | 2x+y=0 | |
| 35 | Найти область определения | y=5x+6 | |
| 36 | Найти область определения | y=x+3 | |
| 37 | Solve Using a Matrix by Elimination | y=4x+3x-2 , y=6 | , |
| 38 | Проверить линейную зависимость | B={[[-10,2],[5,-2. 5]]} 5]]} | |
| 39 | Сложение | [[2,4],[6,-4]]+[[-3,-7],[20,10]] | |
| 40 | Проверить линейную зависимость | B={[[-1,2],[0,-2.5]]} | |
| 41 | Перемножить матрицы | [[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]] | |
| 42 | Найти область определения | y=5x | |
| 43 | Найти область определения | y=7x | |
| 44 | Найти область определения | y=-x-2 | |
| 45 | Найти область определения | y=x-2 | |
| 46 | Найти область определения | y=x-3 | |
| 47 | Привести матрицу к ступенчатому виду по строкам | [[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]] | |
| 48 | Записать в виде векторного равенства | x+y+z=2 , 4x+5y+z=12 , 2x=-4 | , , |
| 49 | Найти определитель | [[0,-1,a],[3,-a,1],[1,-2,3]] | |
| 50 | Найти область определения | y=-x+2 | |
| 51 | Найти определитель | [[2,5,0],[1,0,-3],[2,-1,2]] | |
| 52 | Найти определитель | [[7,5,0],[4,5,8],[0,-1,5]] | |
| 53 | Найти обратный элемент | [[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]] | |
| 54 | Найти обратный элемент | [[1,2,3],[2,5,7],[3,7,9]] | |
| 55 | Привести матрицу к ступенчатому виду по строкам | [[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]] | |
| 56 | Привести матрицу к ступенчатому виду по строкам | [[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]] | |
| 57 | Привести матрицу к ступенчатому виду по строкам | [[1,2,3],[4,5,6],[7,8,9]] | |
| 58 | Привести матрицу к ступенчатому виду по строкам | [[7,8]] | |
| 59 | Найти область определения | 2x+y=1 | |
| 60 | Записать в виде векторного равенства | 2x+y=-2 , x+2y=2 | , |
| 61 | Найти область определения | x-2y=4 | |
| 62 | Найти область определения | x-y=-1 | |
| 63 | Найти область определения | x+y=5 | |
| 64 | Найти область определения | x=-3y-8 | |
| 65 | Найти область определения | x=-2y-8 | |
| 66 | Найти область определения | x+y=6 | |
| 67 | Найти область определения | x+y=4 | |
| 68 | Найти область определения | x+2y=4 | |
| 69 | Найти область определения | x+y | |
| 70 | Найти область определения | y=7x+9 | |
| 71 | Найти область определения | y=1/2x-5 | |
| 72 | Найти область определения | y=1/2x+2 | |
| 73 | Найти область определения | y=1/2x+3 | |
| 74 | Найти область определения | x-y=-3 | |
| 75 | Найти область определения | x-y=4 | |
| 76 | Найти область определения | y=-2x | |
| 77 | Найти область определения | y=-2x+1 | |
| 78 | Найти область определения | y=2^(x+9) | |
| 79 | Найти область определения | y=10-x^2 | |
| 80 | Найти область определения | y=2x-6 | |
| 81 | Найти область определения | y=-2x-3 | |
| 82 | Найти область определения | y=3x-8 | |
| 83 | Найти область определения | y=3x | |
| 84 | Найти область определения | y=-3x+1 | |
| 85 | Найти область определения | y=4x+3 | |
| 86 | Найти область определения | y=3x-4 | |
| 87 | Найти область определения | y=4x-2 | |
| 88 | Найти область определения | y=-6x | |
| 89 | Найти область определения | y=x-4 | |
| 90 | Найти область определения | 7 корень четвертой степени из 567y^4 | |
| 91 | Найти область определения | c=5/9*(f-32) | |
| 92 | Найти область определения | f=9/5c+32 | |
| 93 | Вычислить | квадратный корень из 4 | |
| 94 | Привести матрицу к ступенчатому виду по строкам | [[-6,7],[2,6],[-4,1]] | |
| 95 | Найти собственные значения | [[2,1],[3,2]] | |
| 96 | Найти собственные значения | [[4,0,1],[2,3,2],[49,0,4]] | |
| 97 | Найти степенное множество | A=(2,3,4,5) | |
| 98 | Найти мощность | (2,1) | |
| 99 | Решить, используя обратную матрицу | -3x-4y=2 , 8y=-6x-4 | , |
| 100 | Решить, используя обратную матрицу | 2x-5y=4 , 3x-2y=-5 | , |
Собственный вектор — Википедия
Со́бственный ве́ктор — понятие в линейной алгебре, определяемое для произвольного линейного оператора как ненулевой вектор, применение к которому оператора даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение (которое может быть равно 0). Скаляр, на который умножается собственный вектор под действием оператора, называется собственным числом (или собственным значением) линейного оператора, соответствующим данному собственному вектору. Одним из представлений линейного оператора является квадратная матрица, поэтому собственные векторы и собственные значения часто определяются в контексте использования таких матриц[1][2].
Скаляр, на который умножается собственный вектор под действием оператора, называется собственным числом (или собственным значением) линейного оператора, соответствующим данному собственному вектору. Одним из представлений линейного оператора является квадратная матрица, поэтому собственные векторы и собственные значения часто определяются в контексте использования таких матриц[1][2].
Синим цветом обозначен собственный вектор. Он, в отличие от красного, при деформации (преобразовании) не изменил направление, поэтому является собственным вектором этого преобразования, соответствующим некоторому собственному значениюλ{\displaystyle \lambda } (здесь оно равно единице, так как вектор не изменил свою длину). Любой вектор, параллельный синему вектору, также будет собственным, соответствующим тому же собственному значению. Множество всех таких векторов (вместе с нулевым) образует собственное подпространство
Понятия собственного вектора и собственного числа[3] являются одними из ключевых в линейной алгебре, на их основе строится множество конструкций. Это связано с тем, что многие соотношения, связанные с линейными операторами, существенно упрощаются в системе координат, построенной на базисе из собственных векторов оператора. Множество собственных значений линейного оператора (спектр оператора) характеризует важные свойства оператора без привязки к какой-либо конкретной системе координат. По этим причинам собственные векторы имеют важное прикладное значение. Так, например, собственные векторы часто встречаются в механике, квантовой теории и так далее. В частности, оператор проекции спина на произвольную ось имеет два собственных значения и соответствующие им собственные векторы.
Это связано с тем, что многие соотношения, связанные с линейными операторами, существенно упрощаются в системе координат, построенной на базисе из собственных векторов оператора. Множество собственных значений линейного оператора (спектр оператора) характеризует важные свойства оператора без привязки к какой-либо конкретной системе координат. По этим причинам собственные векторы имеют важное прикладное значение. Так, например, собственные векторы часто встречаются в механике, квантовой теории и так далее. В частности, оператор проекции спина на произвольную ось имеет два собственных значения и соответствующие им собственные векторы.
Понятие линейного векторного пространства не ограничивается «чисто геометрическими» векторами и обобщается на разнообразные множества объектов, таких как пространства функций (в которых действуют линейные дифференциальные и интегральные операторы). Для такого рода пространств и операторов говорят о собственных функциях операторов.
Множество всех собственных векторов линейного оператора, соответствующих данному собственному числу, дополненное нулевым вектором, называется собственным подпространством[4] этого оператора.
Поиск оптимальных алгоритмов вычисления собственных значений для заданного линейного оператора является одной из важных задач вычислительной математики.
Содержание
- 1 Определения
- 2 История
- 3 Свойства собственных значений, собственных и корневых векторов и пространств
- 3.1 Общий случай
- 3.2 Конечномерные линейные пространства
- 3.3 Нормальные операторы и их подклассы
- 3.4 Положительные матрицы
- 4 Неравенства для собственных значений
- 5 Примечания
- 6 Литература
Другая трансформация Джоконды. Синий вектор меняет направление, а красный — нет. Поэтому красный является собственным вектором, а синий — нет. Так как красный вектор ни растянулся, ни сжался, его собственное значение равно, как и на картинке выше, единице. Все векторы, коллинеарные красному, тоже собственные.
Пусть L{\displaystyle L} — линейное пространство над полем K{\displaystyle K} , A:L→L{\displaystyle A\colon L\to L} — линейное преобразование.
Собственным вектором линейного преобразования A{\displaystyle A} называется такой ненулевой вектор x∈L{\displaystyle x\in L} , что для некоторого λ∈K{\displaystyle \lambda \in K}
- Ax=λx.{\displaystyle \ Ax=\lambda x.}
Собственным значением (собственным числом) линейного преобразования A{\displaystyle A} называется такое число λ∈K{\displaystyle \lambda \in K} , для которого существует собственный вектор, то есть уравнение Ax=λx{\displaystyle Ax=\lambda x} имеет ненулевое решение x∈L{\displaystyle x\in L} .
Упрощённо говоря, собственный вектор — любой ненулевой вектор x{\displaystyle x} , который отображается в коллинеарный ему вектор λx{\displaystyle \lambda x} оператором A{\displaystyle A} , а соответствующий скаляр λ{\displaystyle \lambda } называется собственным значением оператора.
Собственным подпространством (или характеристическим подпространством) линейного преобразования A{\displaystyle A} для данного собственного числа λ∈K{\displaystyle \lambda \in K} (или отвечающим этому числу) называется множество всех собственных векторов x∈L{\displaystyle x\in L} , соответствующих данному собственному числу, дополненное нулевым вектором. {\infty }V_{m,\lambda }.}
{\infty }V_{m,\lambda }.}
Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его. |
В настоящее время собственные значения обычно вводятся в контексте линейной алгебры, однако исторически они возникли при исследовании квадратичных форм и дифференциальных уравнений.
В XVIII веке Эйлер, изучая вращательное движение абсолютно твёрдого тела, обнаружил значимость главных осей, а Лагранж показал, что главные оси соответствуют собственным векторам матрицы инерции. В начале XIX века Коши использовал труды Эйлера и Лагранжа для классификации поверхностей второго порядка и обобщил результаты на высшие порядки. Коши также ввёл термин «характеристический корень» (фр. racine caractéristique) для собственного значения. Этот термин сохранился в контексте характеристического многочлена матрицы[5][6].
В начале XX века Гильберт занимался исследованием собственных значений интегральных операторов, рассматривая последние как матрицы бесконечного размера[7]. В 1904 г. для обозначения собственных значений и собственных векторов Гильберт начал использовать термины eigenvalues и eigenvectors, основанные на немецком слове eigen (собственный)[8]. Впоследствии эти термины перешли и в английский язык, заменив используемые ранее «proper value» и «proper vector»[9].
В 1904 г. для обозначения собственных значений и собственных векторов Гильберт начал использовать термины eigenvalues и eigenvectors, основанные на немецком слове eigen (собственный)[8]. Впоследствии эти термины перешли и в английский язык, заменив используемые ранее «proper value» и «proper vector»[9].
Свойства собственных значений, собственных и корневых векторов и пространствПравить
Общий случайПравить
Подпространство V⊂L{\displaystyle V\subset L} называется инвариантным подпространством линейного преобразования A{\displaystyle A} (A{\displaystyle A} -инвариантным подпространством), если:
- AV⊆V{\displaystyle AV\subseteq V} .
Собственные подпространства Eλ{\displaystyle E_{\lambda }} , корневые подпространства Vλ{\displaystyle V_{\lambda }} и подпространства Vm,λ{\displaystyle V_{m,\lambda }} линейного оператора A{\displaystyle A} являются A{\displaystyle A} -инвариантными. {2}=0} , и все векторы являются корневыми, соответствующими собственному числу 1{\displaystyle 1} , но A{\displaystyle A} имеет единственный собственный вектор (с точностью до умножения на число).
{2}=0} , и все векторы являются корневыми, соответствующими собственному числу 1{\displaystyle 1} , но A{\displaystyle A} имеет единственный собственный вектор (с точностью до умножения на число).
Для разных собственных значений корневые (и, следовательно, собственные) подпространства имеют тривиальное (нулевое) пересечение:
- Vλ⋂Vμ={0}{\displaystyle V_{\lambda }\bigcap V_{\mu }=\{0\}} если λ≠μ{\displaystyle \lambda \neq \mu } .
Метод поиска собственных значений для самосопряжённых операторов и поиска сингулярных чисел для нормального оператора даёт теорема Куранта — Фишера.
Конечномерные линейные пространстваПравить
Выбрав базис в n{\displaystyle n} -мерном линейном пространстве L{\displaystyle L} , можно сопоставить линейному преобразованию A:L→L{\displaystyle A\colon L\to L} квадратную n×n{\displaystyle n\times n} матрицу и определить для неё характеристический многочлен матрицы:
- PA(λ)=det(A−λ⋅I)=∑k=0nakλk{\displaystyle P_{A}(\lambda )=\det(A-\lambda \cdot I)=\sum \limits _{k=0}^{n}a_{k}\lambda ^{k}} .

Характеристический многочлен не зависит от базиса в L{\displaystyle L} . Его коэффициенты являются инвариантами оператора A{\displaystyle A} . В частности, a0=detA{\displaystyle a_{0}=\det \,A} , an−1=trA{\displaystyle a_{n-1}=\operatorname {tr} \,A} не зависят от выбора базиса.
Собственные значения, и только они, являются корнями характеристического многочлена матрицы. Количество различных собственных значений не может превышать размер матрицы. Если выбрать в качестве базисных векторов собственные векторы оператора, то матрица A{\displaystyle A} в таком базисе станет диагональной, причём на диагонали будут стоять собственные значения оператора. Отметим, однако, что далеко не любая матрица допускает базис из собственных векторов (общая структура описывается нормальной жордановой формой). Для положительно определённой симметричной матрицы A{\displaystyle A} процедура нахождения собственных значений и собственных векторов является не чем иным, как поиском направлений и длин полуосей соответствующего эллипса. {n}(\lambda -\lambda _{i})} ,
{n}(\lambda -\lambda _{i})} ,
где λi(i=1,…,n){\displaystyle \lambda _{i}\;(i=1,\ldots ,n)} — собственные значения; некоторые из λi{\displaystyle \lambda _{i}} могут быть равны. Кратность собственного значения λi{\displaystyle \lambda _{i}} — это число множителей, равных λ−λi,{\displaystyle \lambda -\lambda _{i},} в разложении характеристического многочлена на линейные множители (называется также алгебраическая кратность собственного значения).
Размерность корневого пространства Vλi{\displaystyle V_{\lambda _{i}}} равна кратности собственного значения.
Векторное пространство L{\displaystyle L} разлагается в прямую сумму корневых подпространств (по теореме о жордановой форме):
- L=⨁λiVλi{\displaystyle L=\bigoplus _{\lambda _{i}}V_{\lambda _{i}}}
- где суммирование производится по всем λi{\displaystyle \lambda _{i}} — собственным числам A{\displaystyle A} .
Геометрическая кратность собственного значения λi{\displaystyle \lambda _{i}} — это размерность соответствующего собственного подпространства Eλi{\displaystyle E_{\lambda _{i}}} ; геометрическая кратность собственного значения не превосходит его кратности, поскольку Eλi⊆Vλi{\displaystyle E_{\lambda _{i}}\subseteq V_{\lambda _{i}}}
Нормальные операторы и их подклассыПравить
Все корневые векторы нормального оператора являются собственными. {n}} , соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств:
{n}} , соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств:
- L=⨁λiEλi{\displaystyle L=\bigoplus _{\lambda _{i}}E_{\lambda _{i}}} ,
где суммирование производится по всем λi{\displaystyle \lambda _{i}} — собственным числам A{\displaystyle A} , а Eλi{\displaystyle E_{\lambda _{i}}} взаимно ортогональны для различных λi{\displaystyle \lambda _{i}} . Это свойство для нормального оператора над C{\displaystyle \mathbb {C} } в конечномерном случае является характеристическим: оператор нормален тогда и только тогда, когда его матрица имеет диагональный вид в каком-нибудь ортонормированном базисе.
Положительные матрицыПравить
Квадратная вещественная n×n{\displaystyle n\times n} матрица A=(aij){\displaystyle A=(a_{ij})} называется положительной, если все её элементы положительны: aij>0{\displaystyle a_{ij}>0} .
Теорема Перрона (частный случай теоремы Перрона — Фробениуса): Положительная квадратная матрица A{\displaystyle A} имеет положительное собственное значение r{\displaystyle r} , которое имеет алгебраическую кратность 1 и строго превосходит абсолютную величину любого другого собственного значения этой матрицы. Собственному значению r{\displaystyle r} соответствует собственный вектор er{\displaystyle e_{r}} , все координаты которого строго положительны. Вектор er{\displaystyle e_{r}} — единственный собственный вектор A{\displaystyle A} (с точностью до умножения на число), имеющий неотрицательные координаты.
Собственному значению r{\displaystyle r} соответствует собственный вектор er{\displaystyle e_{r}} , все координаты которого строго положительны. Вектор er{\displaystyle e_{r}} — единственный собственный вектор A{\displaystyle A} (с точностью до умножения на число), имеющий неотрицательные координаты.
Собственный вектор er{\displaystyle e_{r}} может быть вычислен посредством прямых итераций: выберем произвольный начальный вектор v0{\displaystyle v_{0}} с положительными координатами. Положим:
- vk+1=Avk‖Avk‖{\displaystyle v_{k+1}={\frac {Av_{k}}{\|Av_{k}\|}}}
Последовательность vk{\displaystyle v_{k}} сходится к нормированному собственному вектору er/‖er‖{\displaystyle e_{r}/\|e_{r}\|} .
Другая область применения метода прямых итераций — поиск собственных векторов положительно определённых симметричных операторов.
Неравенства для собственных значенийПравить
Неравенство Шура: для собственных значений λ1,…,λn{\displaystyle \lambda _{1},\dots ,\lambda _{n}} матрицы A=(aij)i,j=1,…,n{\displaystyle A=(a_{ij})_{i,j=1,\ldots ,n}} :
- ∑i=1n|λi|2⩽∑i,j=1n|aij|2=‖A‖F2{\displaystyle \sum _{i=1}^{n}|\lambda _{i}|^{2}\leqslant \sum _{i,j=1}^{n}|a_{ij}|^{2}=\|A\|_{F}^{2}} ,
причём равенство достигается тогда и только тогда, когда A{\displaystyle A} — нормальная матрица[10]. {2}} [11].
{2}} [11].
Для эрмитовых матриц A,B{\displaystyle A,B} и C=A+B{\displaystyle C=A+B} их собственные значения, упорядоченные в порядке возрастания: α1⩽…⩽αn,β1⩽…⩽βn,γ1⩽…⩽γn{\displaystyle \alpha _{1}\leqslant …\leqslant \alpha _{n},\beta _{1}\leqslant …\leqslant \beta _{n},\gamma _{1}\leqslant …\leqslant \gamma _{n}} дают: γi⩾αi+βi−j+1{\displaystyle \gamma _{i}\geqslant \alpha _{i}+\beta _{i-j+1}} при i⩾j{\displaystyle i\geqslant j} и γi⩽αi+βi−j+n{\displaystyle \gamma _{i}\leqslant \alpha _{i}+\beta _{i-j+n}} при i⩽j{\displaystyle i\leqslant j} [11].
- ↑ Herstein (1964, pp. 228,229)
- ↑ Nering (1970, p. 38)
- ↑ Иногда используются синонимичные термины: характеристический вектор и характеристическое число оператора.
- ↑ Не путать с собственным подпространством линейного векторного пространства — любым подпространством, отличным от тривиальных подпространств, то есть от самого этого пространства и от нулевого пространства.

- ↑ Kline, 1972, pp. 807–808.
- ↑ Augustin Cauchy (1839) «Mémoire sur l’intégration des équations linéaires» (Memoir on the integration of linear equations), Comptes rendus, 8 : 827—830, 845—865, 889—907, 931—937. p. 827: Архивная копия от 7 июня 2019 на Wayback Machine «On sait d’ailleurs qu’en suivant la méthode de Lagrange, on obtient pour valeur générale de la variable prinicipale une fonction dans laquelle entrent avec la variable principale les racines d’une certaine équation que j’appellerai l’équation caractéristique, le degré de cette équation étant précisément l’order de l’équation différentielle qu’il s’agit d’intégrer.»
- ↑ Kline, 1972, p. 1063.
- ↑ David Hilbert (1904).«Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. (Erste Mitteilung)» Архивная копия от 5 ноября 2018 на Wayback Machine, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, pp.
 49-91.
49-91. - ↑ Aldrich, John (2006), «Eigenvalue, eigenfunction, eigenvector, and related terms», in Jeff Miller (ed.), Earliest Known Uses of Some of the Words of Mathematics Архивная копия от 23 декабря 2017 на Wayback Machine
- ↑ Задачи и теоремы линейной алгебры, 1996, с. 206.
- ↑ 1 2 Задачи и теоремы линейной алгебры, 1996, с. 207.
- Гантмахер Ф. Р.. Теория матриц. — М.: Наука, 1966. — 576 с. — ISBN ISBN 5-9221-0524-8.
- Уилкинсон Д. Х. Алгебраическая проблема собственных значений. — М.: Наука, 1970. — 564 с. — ISBN 978-5-458-25464-9.
- Гельфанд И. М.. Лекции по линейной алгебре. — М.: Добросвет, КДУ, 2009. — 320 с. — 1000 экз. — ISBN 978-5-98227-625-4.
- Фаддеев Д. К.. Лекции по алгебре. — М.: ЁЁ Медиа, 2012. — 416 с. — ISBN 978-5-458-25543-1.

- Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — М.: Физматлит, 2009. — 512 с. — ISBN 978-5-9221-1139-3.
- Прасолов В. В. Задачи и теоремы линейной алгебры. — М.: Наука, 1996. — 304 с. — ISBN 5-02-014727-3.
- Икрамов Х. Д. Несимметричная проблема собственных значений. — М.: Наука, 1991. — 240 с. — ISBN 5-02-014462-2.
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Horn, Roger A. & Johnson, Charles F. (1985), Matrix analysis, Cambridge University Press, ISBN 0-521-30586-1
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley
- Kline, Morris (1972), Mathematical thought from ancient to modern times, Oxford University Press, ISBN 0-19-501496-0
Лекция_6_ИЭТ 2011 Собственные значения и собственные векторы матрицы
Методы
вычислений. ИЭТ. 4-й семестр. Лекция 6.
Стр. 3
ИЭТ. 4-й семестр. Лекция 6.
Стр. 3
МЕТОДЫ ВЫЧИСЛЕНИЙ
ИЭТ, 4-й семестр, 22
Лекция 6
Собственные значения и собственные векторы матрицы.
Методы решения проблемы собственных значений: степенной метод.
Пусть А — квадратная матрица порядка n.
Опр. Число называется собственным значением, а ненулевой вектор — соответствующим собственным вектором матрицы А, если они связаны между собой соотношением .
Собственные
значения матрицы и соответствующие им
собственные векторы связаны соотношением ,
где Е — единичная матрица. Это означает, что
собственный вектор — ненулевое решение
однородной линейной системы .
Решение этой однородной системы
существует тогда и только тогда, когда .
Следовательно, собственные значения
матрицы могут быть вычислены как корни
уравнения ,
а собственные векторы — как решения
соответствующих однородных систем.
Опр. Уравнение называется характеристическим уравнением матрицы, а многочлен — характеристическим многочленом; характеристический многочлен матрицы порядка n является многочленом n-й степени относительно .
Мы уже знаем, что вычисление корней многочлена — плохо обусловленная задача. Следует искать такие методы вычисления собственных значений и собственных векторов матрицы, которые не требуют вычисления корней характеристического многочлена.
Для решения многих
задач физики, механики, химии, биологии
требуется знать все собственные
значения и соответствующие собственные
векторы. Эту задачу называют полной
проблемой собственных значений. Однако в ряде случаев требуется найти
только наибольшее, наименьшее по модулю
собственное значение наиболее близкое
к некоторому заданному числу и т.п. Такие
задачи образуют частичную
проблему собственных значений. Здесь
будут рассмотрены только некоторые
методы решения частичной проблемы
собственных значений.
Обусловленность задачи вычисления собственных значений.
Опр.Матрица А называется симметричной , если Ат=А.
Пусть А — симметричная матрица, собственные значения которой и пусть А* — симметричная возмущенная матрица с собственными значениями .Собственные значения упорядочены по возрастанию. Доказано, что
,
Эти неравенства означают, что задача вычисления собственных значений симметричной матрицы хорошо обусловлена. Для несимметричных матриц дело обстоит совсем иначе. Для многих несимметричных матриц собственные значения чрезвычайно чувствительны к погрешностям элементов матрицы.
Пример плохо обусловленной задачи о собственных значениях несимметричной матрицы. Пример Дж. Уилкинсона. Рассмотрим верхнюю треугольную матрицу
.
Ее собственные
значения — корни многочлена 20-й степени,
который рассматривался в качестве
примера плохо обусловленной задачи,
т. е.
.
Если к элементу матрицы добавить малое возмущение
,
то характеристическое уравнение примет
вид:,
а собственные значения возмущенной
матрицы окажутся полностью искаженными.
е.
.
Если к элементу матрицы добавить малое возмущение
,
то характеристическое уравнение примет
вид:,
а собственные значения возмущенной
матрицы окажутся полностью искаженными.
Здесь проблема обусловленности вычисления собственных значений несимметричной матрицы не обсуждается. Отметим лишь, что рассмотренное ранее число обусловленности матрицы системы линейных уравнений никак не связано с обусловленностью задачи о собственных значениях матрицы А.
Степенной метод вычисления наибольшего по модулю
собственного значения
Пусть требуется найти наибольшее по модулю собственное значение матрицы А, причем известно, что , ; собственные значения матрицы предполагаются действительными, т.е. матрица А – симметричная. Если , то.Для несимметричных матриц возможно наличие комплексных корней с учетом кратности.
Простейший вариант степенного метода для вычисления : возьмем — произвольный начальный вектор, и построим последовательности векторов : и приближений по формулам:, ,
и при
,
причем
.
Не приводя точных условий сходимости степенного метода, покажем механизм сходимости приближенных значений наибольшего по модулю собственного значения и при этом объясним название метода.
Пусть матрица А имеет базис из собственных векторов . Выберем в качестве нулевого приближения собственного вектора такой вектор, в разложении которого по собственному базису коэффициент при отличен от нуля, , .
Тогда , т.е. получается из умножением на к+1-ю степень матрицы А (отсюда и название метода).
,
а поскольку для i =2, 3, …, m, то при , и по формуле .Разделим и числитель , и знаменатель дроби на:
при .
Докажем оценку относительной погрешности: . Т.к.
.=(*)
и т.к. положим , .
Так как для i =2, 3, …, m, то
Используя неравенство Коши-Буняковского ,имеем
. Тогда из равенства (*) и полученных оценок следует, что
. Что и требовалось докозать.
Что и требовалось докозать.
Однако, если , то при , а при , наоборот — . Для предупреждения таких случаев k—ю итерацию собственного вектора нормируют: , , , .
Заметим, что даже если первый коэффициент в разложении нулевого приближения по собственному базису окажется равным нулю, вследствие погрешностей округления он через несколько итераций станет ненулевым и итерации начнут сходиться.
Собственные значения обратной матрицы.
Пусть А — квадратная, невырожденная, симметричная матрица порядка n.
Требуется найти наименьшее по модулю собственное значение матрицы
.
Тогда, для того чтобы найти минимальное собственное значение матрицы А , ищем максимальное собственное значение обратной матрицы А-1 и .
Простота алгоритма
— основное достоинство метода. Однако
часто итерации сходятся медленно. Применяют различные модификации
степенного метода, позволяющие ускорить
сходимость, а также вычислять наименьшее
по модулю собственное значение и
соответствующий собственный вектор.
Применяют различные модификации
степенного метода, позволяющие ускорить
сходимость, а также вычислять наименьшее
по модулю собственное значение и
соответствующий собственный вектор.
Алгоритм собственных значений
В числовой анализ, одна из важнейших проблем — проектирование эффективных и стабильный алгоритмы для поиска собственные значения из матрица. Эти алгоритмы собственных значений может также найти собственные векторы.
Содержание
- 1 Собственные значения и собственные векторы
- 1.1 Нормальные, эрмитовы и вещественно-симметричные матрицы
- 2 Номер условия
- 3 Алгоритмы
- 4 Гессенберга и трехдиагональные матрицы
- 5 Итерационные алгоритмы
- 6 Прямой расчет
- 6.1 Треугольные матрицы
- 6.2 Факторизуемые полиномиальные уравнения
- 6.3 2 × 2 матрицы
- 6.4 3 × 3 матрицы
- 6.4.1 Собственные векторы нормальных матриц 3 × 3
- 7 Смотрите также
- 8 Примечания
- 9 Рекомендации
- 10 дальнейшее чтение
Собственные значения и собственные векторы
Основные статьи: Собственные значения и собственные векторы и Обобщенный собственный вектор
Учитывая п × п квадратная матрица А из настоящий или же сложный числа, собственное значение λ и связанные с ним обобщенный собственный вектор v пара, подчиняющаяся соотношению[1]
- (А−λя)kv=0,{ displaystyle left (A- lambda I right) ^ {k} { mathbf {v}} = 0,}
куда v ненулевой п × 1 вектор-столбец я это п × п единичная матрица, k положительное целое число, и оба λ и v разрешено быть сложным, даже когда А реально. Когда k = 1, вектор называется просто собственный вектор, и пара называется собственная пара. В этом случае, Аv = λv. Любое собственное значение λ из А имеет обычные[примечание 1] собственные векторы, связанные с ним, если k это наименьшее целое число такое, что (А — λя)kv = 0 для обобщенного собственного вектора v, тогда (А — λя)k-1v — обычный собственный вектор. Значение k всегда может быть меньше или равно п. Особенно, (А — λя)пv = 0 для всех обобщенных собственных векторов v связана с λ.
Когда k = 1, вектор называется просто собственный вектор, и пара называется собственная пара. В этом случае, Аv = λv. Любое собственное значение λ из А имеет обычные[примечание 1] собственные векторы, связанные с ним, если k это наименьшее целое число такое, что (А — λя)kv = 0 для обобщенного собственного вектора v, тогда (А — λя)k-1v — обычный собственный вектор. Значение k всегда может быть меньше или равно п. Особенно, (А — λя)пv = 0 для всех обобщенных собственных векторов v связана с λ.
Для каждого собственного значения λ из А, то ядро кер (А — λя) состоит из всех собственных векторов, связанных с λ (вместе с 0), называется собственное подпространство из λ, а векторное пространство кер ((А — λя)п) состоит из всех обобщенных собственных векторов и называется обобщенное собственное подпространство. { alpha _ {i}},}
{ alpha _ {i}},}
куда Det это детерминант функция, λя все различные собственные значения А и αя — соответствующие алгебраические кратности. Функция пА(z) это характеристический многочлен из А. Таким образом, алгебраическая кратность — это кратность собственного значения как нуль характеристического полинома. Поскольку любой собственный вектор также является обобщенным собственным вектором, геометрическая кратность меньше или равна алгебраической кратности. Алгебраические кратности в сумме составляют п, степень характеристического полинома. Уравнение пА(z) = 0 называется характеристическое уравнение, так как его корни — в точности собственные значения А. Посредством Теорема Кэли – Гамильтона, А сам подчиняется тому же уравнению: пА(А) = 0.[заметка 2] Как следствие, столбцы матрицы ∏я≠j(А−λяя)αя{ displaystyle textstyle prod _ {я neq j} (A- lambda _ {i} I) ^ { alpha _ {i}}} должны быть либо 0, либо обобщенными собственными векторами собственного значения λj, поскольку они уничтожаются (А−λjя)αj. { alpha _ {j}}.} Фактически, пространство столбца является обобщенным собственным подпространством λj.
{ alpha _ {j}}.} Фактически, пространство столбца является обобщенным собственным подпространством λj.
Любой набор обобщенных собственных векторов различных собственных значений линейно независим, поэтому базис для всех C п можно выбрать состоящим из обобщенных собственных векторов. В частности, эта основа {vя}п
я=1 можно выбрать и организовать так, чтобы
- если vя и vj имеют такое же собственное значение, то vk для каждого k между я и j, и
- если vя не является обычным собственным вектором, и если λя — его собственное значение, то (А — λяя )vя = vя-1 (особенно, v1 должен быть обычным собственным вектором).
Если эти базисные векторы размещены как векторы-столбцы матрицы V = [ v1v2 .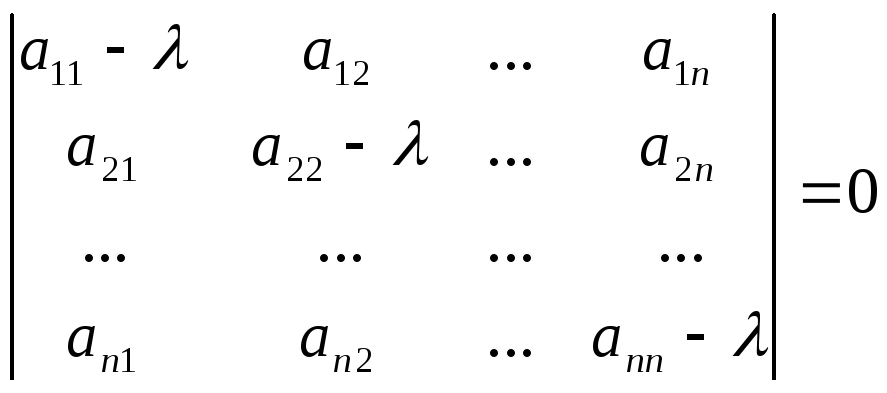 {- 1} AV = { begin {bmatrix} lambda _ {1} & beta _ {1} & 0 & ldots & 0 0 & lambda _ {2} & beta _ {2} & ldots & 0 0 & 0 & lambda _ {3} & ldots & 0 vdots & vdots & vdots & ddots & vdots 0 & 0 & 0 & ldots & lambda _ {n} end {bmatrix} },}
{- 1} AV = { begin {bmatrix} lambda _ {1} & beta _ {1} & 0 & ldots & 0 0 & lambda _ {2} & beta _ {2} & ldots & 0 0 & 0 & lambda _ {3} & ldots & 0 vdots & vdots & vdots & ddots & vdots 0 & 0 & 0 & ldots & lambda _ {n} end {bmatrix} },}
где λя собственные значения, βя = 1 если (А — λя+1)vя+1 = vя и βя = 0 иначе.
В более общем смысле, если W — любая обратимая матрица, и λ является собственным значением А с обобщенным собственным вектором v, тогда (W−1AW — λя )kW−kv = 0. Таким образом λ является собственным значением W−1AW с обобщенным собственным вектором W−kv. То есть, аналогичные матрицы имеют одинаковые собственные значения.
Нормальные, эрмитовы и вещественно-симметричные матрицы
Основные статьи: Присоединенная матрица, Нормальная матрица, и Эрмитова матрица
Сопряженным к матрице является матрица сомножителей транспонирования. Используйте другой термин. прилегающий M* сложной матрицы M является транспонированием конъюгата M: M * = M Т. Квадратная матрица А называется нормальный если он коммутирует со своим соседом: А*А = AA*. Это называется эрмитский если он равен своему сопряженному: А* = А. Все эрмитовы матрицы нормальные. Если А имеет только реальные элементы, то присоединенное — это просто транспонирование, а А является эрмитовым тогда и только тогда, когда оно симметричный. Применительно к векторам-столбцам сопряженное может использоваться для определения канонического внутреннего продукта на Cп: ш · v = ш*v. [заметка 3] Нормальные, эрмитовые и вещественно-симметричные матрицы обладают несколькими полезными свойствами:
[заметка 3] Нормальные, эрмитовые и вещественно-симметричные матрицы обладают несколькими полезными свойствами:
- Каждый обобщенный собственный вектор нормальной матрицы является обычным собственным вектором.
- Любая нормальная матрица подобна диагональной матрице, поскольку ее жорданова нормальная форма диагональна.
- Собственные векторы различных собственных значений нормальной матрицы ортогональны.
- Нулевое пространство и изображение (или пространство столбцов) нормальной матрицы ортогональны друг другу.
- Для любой нормальной матрицы А, C п имеет ортонормированный базис, состоящий из собственных векторов А. Соответствующая матрица собственных векторов есть унитарный.
- Собственные значения эрмитовой матрицы действительны, поскольку (λ — λ)v = (А* − А)v = (А − А)v = 0 для ненулевого собственного вектора v.
- Если А реально, существует ортонормированный базис для рп состоящий из собственных векторов А если и только если А симметрично.

Реальная или комплексная матрица может иметь все действительные собственные значения, не будучи эрмитовскими. Например, настоящий треугольная матрица имеет собственные значения по диагонали, но в целом не является симметричным.
Номер условия
Любую задачу числового вычисления можно рассматривать как вычисление некоторой функции ƒ для некоторого ввода Икс. В номер условия κ(ƒ, Икс) Проблема заключается в соотношении относительной ошибки на выходе функции к относительной ошибке на входе, которое зависит как от функции, так и от входа. Номер условия описывает, как растет ошибка во время расчета. Его логарифм по основанию 10 показывает, на сколько цифр точности меньше, чем было во входных данных. Номер условия — это лучший сценарий. Он отражает нестабильность, заложенную в проблему, независимо от того, как она решается. Ни один алгоритм не может дать более точных результатов, чем указано в номере условия, за исключением случая. Однако плохо спроектированный алгоритм может дать значительно худшие результаты. Например, как упоминается ниже, проблема поиска собственных значений для нормальных матриц всегда хорошо обусловлена. Однако проблема нахождения корней многочлена может быть решена. в очень плохом состоянии. Таким образом, алгоритмы собственных значений, которые работают путем нахождения корней характеристического многочлена, могут быть плохо обусловлены, даже если проблема не в этом.
Например, как упоминается ниже, проблема поиска собственных значений для нормальных матриц всегда хорошо обусловлена. Однако проблема нахождения корней многочлена может быть решена. в очень плохом состоянии. Таким образом, алгоритмы собственных значений, которые работают путем нахождения корней характеристического многочлена, могут быть плохо обусловлены, даже если проблема не в этом.
Для задачи решения линейного уравнения Аv = б куда А обратимо, число обусловленности κ(А−1, б) дан кем-то ||А||op||А−1||op, куда || ||op это норма оператора подчиняться нормальному Евклидова норма на C п. Поскольку это число не зависит от б и то же самое для А и А−1, его обычно называют просто числом условия κ(А) матрицы А. Это значение κ(А) также является абсолютным значением отношения наибольшего собственного значения А до самого маленького. Если А является унитарный, тогда ||А||op = ||А−1||op = 1, так κ(А) = 1. Для обычных матриц часто бывает сложно вычислить операторную норму. По этой причине другие матричные нормы обычно используются для оценки числа обусловленности.
Если А является унитарный, тогда ||А||op = ||А−1||op = 1, так κ(А) = 1. Для обычных матриц часто бывает сложно вычислить операторную норму. По этой причине другие матричные нормы обычно используются для оценки числа обусловленности.
Для задачи на собственные значения Бауэр и Фике доказали что если λ является собственным значением для диагонализуемый п × п матрица А с матрица собственных векторов V, то абсолютная погрешность вычисления λ ограничен произведением κ(V) и абсолютная ошибка в А.[2]Как результат, номер условия для нахождения λ является κ(λ, А) = κ(V) = ||V ||op ||V −1||op. Если А нормально, тогда V унитарен, и κ(λ, А) = 1. Таким образом, проблема собственных значений для всех нормальных матриц хорошо обусловлена.
Число обусловленности задачи нахождения собственного подпространства нормальной матрицы А соответствующему собственному значению λ было показано, что он обратно пропорционален минимальному расстоянию между λ и другие различные собственные значения А. [3] В частности, проблема собственного подпространства для нормальных матриц хорошо обусловлена изолированными собственными значениями. Когда собственные значения не изолированы, лучшее, на что можно надеяться, — это определить диапазон всех собственных векторов ближайших собственных значений.
[3] В частности, проблема собственного подпространства для нормальных матриц хорошо обусловлена изолированными собственными значениями. Когда собственные значения не изолированы, лучшее, на что можно надеяться, — это определить диапазон всех собственных векторов ближайших собственных значений.
Алгоритмы
Любой приведенный многочлен является характеристическим многочленом своего сопутствующая матрица. Таким образом, общий алгоритм поиска собственных значений может также использоваться для поиска корней многочленов. В Теорема Абеля – Руффини показывает, что любой такой алгоритм для размерностей больше 4 должен быть либо бесконечным, либо включать функции большей сложности, чем элементарные арифметические операции и дробные степени. По этой причине алгоритмы, которые точно вычисляют собственные значения за конечное число шагов, существуют только для нескольких специальных классов матриц. Для общих матриц алгоритмы итеративный, получая более приближенные решения с каждой итерацией.
Некоторые алгоритмы производят каждое собственное значение, другие — несколько или только одно. Однако даже последние алгоритмы можно использовать для нахождения всех собственных значений. Как только собственное значение λ матрицы А был идентифицирован, его можно использовать либо для направления алгоритма к другому решению в следующий раз, либо для сведения проблемы к той, которая больше не имеет λ как решение.
Перенаправление обычно выполняется смещением: заменой А с А — μя для некоторой постоянной μ. Найденное собственное значение А — μя должны быть μ добавлен обратно, чтобы получить собственное значение для А. Например, для итерация мощности, μ = λ. Степенная итерация находит наибольшее собственное значение по модулю, поэтому даже когда λ является лишь приблизительным собственным значением, степенная итерация вряд ли найдет его во второй раз. Наоборот, обратная итерация методы на основе находят наименьшее собственное значение, поэтому μ выбран далеко от λ и, надеюсь, ближе к какому-то другому собственному значению.
Уменьшение может быть достигнуто путем ограничения А в пространство столбцов матрицы А — λя, который А несёт себе. С А — λя сингулярно, пространство столбцов имеет меньшую размерность. Затем алгоритм собственных значений может быть применен к ограниченной матрице. Этот процесс можно повторять до тех пор, пока не будут найдены все собственные значения.
Если алгоритм собственных значений не создает собственные векторы, обычной практикой является использование алгоритма на основе обратной итерации с μ установить в близком приближении к собственному значению. Это быстро сведется к собственному вектору ближайшего собственного значения к μ. Для небольших матриц альтернативой является просмотр пространства столбцов произведения А — λ’я для каждого из других собственных значений λ’.
Формула для нормы составляющих единичного собственного вектора нормальных матриц была открыта Робертом Томпсоном в 1966 году и переоткрыта независимо несколькими другими. {2} = { гидроразрыва {p_ {j} ( lambda _ {i} (A))} {p ‘( lambda _ {i} (A)) }}}
{2} = { гидроразрыва {p_ {j} ( lambda _ {i} (A))} {p ‘( lambda _ {i} (A)) }}}
предполагая производную п′{ displaystyle p ‘} не равно нулю в λя(А){ Displaystyle лямбда _ {я} (А)}.
Гессенберга и трехдиагональные матрицы
Основная статья: Матрица Гессенберга
Поскольку собственные значения треугольной матрицы являются ее диагональными элементами, для общих матриц не существует конечного метода, такого как гауссовское исключение для преобразования матрицы в треугольную форму с сохранением собственных значений. Но можно достичь чего-то близкого к треугольному. An верхняя матрица Гессенберга квадратная матрица, для которой все элементы ниже субдиагональный равны нулю. Нижняя матрица Хессенберга — это матрица, для которой все элементы выше супердиагональ равны нулю. Матрицы, которые являются как верхней, так и нижней Hessenberg, являются трехдиагональный. Матрицы Хессенберга и трехдиагональные матрицы являются отправными точками для многих алгоритмов собственных значений, поскольку нулевые элементы уменьшают сложность проблемы. Для преобразования общей матрицы в матрицу Хессенберга с теми же собственными значениями обычно используются несколько методов. Если исходная матрица была симметричной или эрмитовой, то полученная матрица будет трехдиагональной.
Для преобразования общей матрицы в матрицу Хессенберга с теми же собственными значениями обычно используются несколько методов. Если исходная матрица была симметричной или эрмитовой, то полученная матрица будет трехдиагональной.
Когда нужны только собственные значения, нет необходимости вычислять матрицу подобия, поскольку преобразованная матрица имеет те же собственные значения. Если также необходимы собственные векторы, матрица подобия может потребоваться для преобразования собственных векторов матрицы Хессенберга обратно в собственные векторы исходной матрицы.
| Метод | Относится к | Производит | Стоимость без матрицы сходства | Стоимость с матрицей сходства | Описание |
|---|---|---|---|---|---|
| Преобразования домовладельцев | Общий | Hessenberg | 2п3⁄3 + О(п2)[9](стр. 474) | 4п3⁄3 + О(п2)[9](стр. 474) 474) | Отразите каждый столбец через подпространство, чтобы обнулить его нижние элементы. |
| Гивенса вращения | Общий | Hessenberg | 4п3⁄3 + О(п2)[9](p470) | Примените плоские вращения для обнуления отдельных записей. Вращения упорядочены так, чтобы последующие не заставляли нулевые записи снова становиться ненулевыми. | |
| Итерация Арнольди | Общий | Hessenberg | Выполните ортогонализацию Грама – Шмидта на подпространствах Крылова. | ||
| Алгоритм Ланцоша | Эрмитский | Трехдиагональный | Итерация Арнольди для эрмитовых матриц с сокращениями. |
Для симметричных трехдиагональных задач на собственные значения все собственные значения (без собственных векторов) могут быть вычислены численно за время O (n log (n)) с использованием пополам на характеристическом полиноме. [10]
[10]
Итерационные алгоритмы
Итерационные алгоритмы решают проблему собственных значений, создавая последовательности, сходящиеся к собственным значениям. Некоторые алгоритмы также создают последовательности векторов, которые сходятся к собственным векторам. Чаще всего последовательности собственных значений выражаются как последовательности аналогичных матриц, которые сходятся к треугольной или диагональной форме, что позволяет легко читать собственные значения. Последовательности собственных векторов выражаются в виде соответствующих матриц подобия.
| Метод | Относится к | Производит | Стоимость за шаг | Конвергенция | Описание |
|---|---|---|---|---|---|
| Итерация мощности | Общее | собственная пара с наибольшим значением | О(п2) | линейный | Многократно применяет матрицу к произвольному начальному вектору и перенормирует. |
| Обратная итерация | Общее | собственная пара со значением, ближайшим к μ | линейный | Итерация мощности для (А — μя )−1 | |
| Итерация фактора Рэлея | Эрмитский | любая собственная пара | кубический | Итерация мощности для (А — μяя )−1, куда μя для каждой итерации — это коэффициент Рэлея предыдущей итерации. | |
| Предварительно обусловленная обратная итерация[11] или же Алгоритм LOBPCG | положительно определенный настоящий симметричный | собственная пара со значением, ближайшим к μ | Обратная итерация с использованием предварительный кондиционер (приблизительная обратная А). | ||
| Метод бисекции | действительный симметричный трехдиагональный | любое собственное значение | линейный | Использует метод деления пополам найти корни характеристического многочлена, поддерживаемого последовательностью Штурма. | |
| Итерация Лагерра | действительный симметричный трехдиагональный | любое собственное значение | кубический[12] | Использует Метод Лагерра найти корни характеристического многочлена, поддерживаемого последовательностью Штурма. | |
| QR-алгоритм | Hessenberg | все собственные значения | О(п2) | кубический | Факторы А = QR, куда Q ортогонален и р является треугольным, затем применяет следующую итерацию к RQ. |
| все собственные пары | 6п3 + О(п2) | ||||
| Алгоритм Якоби на собственные значения | настоящий симметричный | все собственные значения | О(п3) | квадратичный | Использует вращения Гивенса, чтобы попытаться удалить все недиагональные записи. Это не удается, но усиливает диагональ. |
| Разделяй и властвуй | Эрмитова трехдиагональная | все собственные значения | О(п2) | Делит матрицу на подматрицы, которые диагонализируются, а затем повторно объединяются. | |
| все собственные пары | (4⁄3)п3 + О(п2) | ||||
| Гомотопический метод | действительный симметричный трехдиагональный | все собственные пары | О(п2)[13] | Строит вычислимый гомотопический путь из диагональной задачи на собственные значения. | |
| Метод свернутого спектра | настоящий симметричный | собственная пара со значением, ближайшим к μ | Предварительно обусловленная обратная итерация, примененная к (А — μя )2 | ||
| Алгоритм MRRR[14] | действительный симметричный трехдиагональный | некоторые или все собственные пары | О(п2) | «Множественные относительно надежные представления» — выполняет обратную итерацию по ЛПНПТ разложение сдвинутой матрицы. |
Прямой расчет
Хотя не существует простого алгоритма прямого вычисления собственных значений для общих матриц, существует множество специальных классов матриц, в которых собственные значения могут быть вычислены напрямую. К ним относятся:
Треугольные матрицы
Поскольку определитель треугольная матрица является произведением его диагональных элементов, если Т треугольная, то Det(λя−Т)=∏я(λ−Тяя){ displaystyle textstyle det ( lambda I-T) = prod _ {i} ( lambda -T_ {ii})}. Таким образом, собственные значения Т — его диагональные элементы.
Таким образом, собственные значения Т — его диагональные элементы.
Факторизуемые полиномиальные уравнения
Если п — любой полином и п(А) = 0, тогда собственные значения А также удовлетворяют тому же уравнению. Если п имеет известную факторизацию, то собственные значения А лежат среди его корней.
Например, проекция квадратная матрица п удовлетворение п2 = п. Корни соответствующего скалярного полиномиального уравнения, λ2 = λ, равны 0 и 1. Таким образом, любая проекция имеет собственные значения 0 и 1. Кратность 0 как собственного значения — это ничтожность из п, а кратность 1 — ранг п.
Другой пример — матрица А это удовлетворяет А2 = α2я для некоторого скаляра α. Собственные значения должны быть ± α. Операторы проекции
- п+=12(я+Аα){ displaystyle P _ {+} = { frac {1} {2}} left (I + { frac {A} { alpha}} right)}
- п−=12(я−Аα){ displaystyle P _ {-} = { frac {1} {2}} left (I — { frac {A} { alpha}} right)}
удовлетворить
- Ап+=αп+Ап−=−αп−{ displaystyle AP _ {+} = alpha P _ {+} quad AP _ {-} = — alpha P _ {-}}
и
- п+п+=п+п−п−=п−п+п−=п−п+=0.
 {2} (A) -4 { rm {det}} (A) }}} расстояние между двумя собственными значениями, легко вычислить
{2} (A) -4 { rm {det}} (A) }}} расстояние между двумя собственными значениями, легко вычислить- ∂λ∂а=12(1±а−dграммап(А)),∂λ∂б=±cграммап(А){ displaystyle { frac { partial lambda} { partial a}} = { frac {1} {2}} left (1 pm { frac {ad} {{ rm {gap}} ( A)}} right), qquad { frac { partial lambda} { partial b}} = { frac { pm c} {{ rm {gap}} (A)}}}
с аналогичными формулами для c и d. Отсюда следует, что расчет хорошо обусловлен, если собственные значения изолированы.
Собственные векторы можно найти, используя Теорема Кэли – Гамильтона. Если λ1, λ2 собственные числа, то (А — λ1я )(А — λ2я ) = (А — λ2я )(А — λ1я ) = 0, поэтому столбцы (А — λ2я ) уничтожены (А — λ1я ) наоборот. Предполагая, что ни одна из матриц не равна нулю, столбцы каждого должны включать собственные векторы для другого собственного значения.
 2 + 2 * p1 п = sqrt(p2 / 6) B = (1 / п) * (А — q * я) % I — единичная матрица р = Det(B) / 2 % В точной арифметике для симметричной матрицы -1
2 + 2 * p1 п = sqrt(p2 / 6) B = (1 / п) * (А — q * я) % I — единичная матрица р = Det(B) / 2 % В точной арифметике для симметричной матрицы -1 Еще раз, собственные векторы А можно получить, обратившись к Теорема Кэли – Гамильтона. Если α1, α2, α3 являются различными собственными значениями А, тогда (А — α1я)(А — α2я)(А — α3я) = 0. Таким образом, столбцы произведения любых двух из этих матриц будут содержать собственный вектор для третьего собственного значения. Однако если α3 = α1, тогда (А — α1я)2(А — α2я) = 0 и (А — α2я)(А — α1я)2 = 0. Таким образом обобщенный собственное подпространство α1 охватывает столбцы А — α2я в то время как обычное собственное подпространство занято столбцами (А — α1я)(А — α2я).
 {2} = { begin {bmatrix} -4 & 0 & -8 — 4 & 0 & -8 4 & 0 & 8 end {bmatrix}}, qquad (AI) (A + I) = { begin {bmatrix} 0 & 4 & 4 0 & 2 & 2 0 & -2 & -2 end {bmatrix}}}
{2} = { begin {bmatrix} -4 & 0 & -8 — 4 & 0 & -8 4 & 0 & 8 end {bmatrix}}, qquad (AI) (A + I) = { begin {bmatrix} 0 & 4 & 4 0 & 2 & 2 0 & -2 & -2 end {bmatrix}}}
Таким образом (-4, -4, 4) является собственным вектором для -1, а (4, 2, -2) является собственным вектором для 1. (2, 3, -1) и (6, 5, -3) являются обобщенными собственными векторами, связанными с 1, любой из которых может быть объединен с (-4, -4, 4) и (4, 2, -2) сформировать основу обобщенных собственных векторов А. Найденные собственные векторы при необходимости можно нормализовать.
Собственные векторы нормальных матриц 3 × 3
Если матрица 3 × 3 А{ displaystyle A} является нормальным, то перекрестное произведение можно использовать для нахождения собственных векторов. Если λ{ displaystyle lambda} является собственным значением А{ displaystyle A}, то пустое пространство А−λя{ displaystyle A- lambda I} перпендикулярно пространству столбцов, перекрестное произведение двух независимых столбцов А−λя{ displaystyle A- lambda I} будет в пустом пространстве. То есть это будет собственный вектор, связанный с λ{ displaystyle lambda}. Поскольку в этом случае пространство столбцов двумерно, собственное подпространство должно быть одномерным, поэтому любой другой собственный вектор будет параллелен ему.
То есть это будет собственный вектор, связанный с λ{ displaystyle lambda}. Поскольку в этом случае пространство столбцов двумерно, собственное подпространство должно быть одномерным, поэтому любой другой собственный вектор будет параллелен ему.
Если А−λя{ displaystyle A- lambda I} не содержит двух независимых столбцов, но не 0, перекрестное произведение можно использовать. В этом случае λ{ displaystyle lambda} является собственным значением кратности 2, поэтому любой вектор, перпендикулярный пространству столбцов, будет собственным вектором. Предполагать v{ displaystyle mathbf {v}} ненулевой столбец А−λя{ displaystyle A- lambda I}. Выберите произвольный вектор ты{ displaystyle mathbf {u}} не параллельно v{ displaystyle mathbf {v}}. потом v×ты{ displaystyle mathbf {v} times mathbf {u}} и (v×ты)×v{ Displaystyle ( mathbf {v} times mathbf {u}) times mathbf {v}} будет перпендикулярно v{ displaystyle mathbf {v}} и, таким образом, будут собственными векторами λ{ displaystyle lambda}. Смит, Оливер К. (апрель 1961 г.), «Собственные значения симметричной матрицы 3 × 3», Коммуникации ACM, 4 (4): 168, Дои:10.1145/355578.366316
Смит, Оливер К. (апрель 1961 г.), «Собственные значения симметричной матрицы 3 × 3», Коммуникации ACM, 4 (4): 168, Дои:10.1145/355578.366316
дальнейшее чтение
- Bojanczyk, Adam W .; Адам Лютоборски (январь 1991 г.). «Вычисление углов Эйлера симметричной матрицы 3×3». Журнал SIAM по матричному анализу и приложениям. 12 (1): 41–48. Дои:10.1137/0612005.
Расширенные концепции матриц — Azure Quantum
- Статья
- Чтение занимает 4 мин
В этой статье рассматриваются понятия собственных значений, собственных векторов и экспоненциалов. Эти понятия образуют базовый набор инструментов для работы с матрицами, которые используются для описания и реализации квантовых алгоритмов.
Эти понятия образуют базовый набор инструментов для работы с матрицами, которые используются для описания и реализации квантовых алгоритмов.
Собственные значения и собственные векторы
Пусть $M$ — квадратная матрица, а $v$ — вектор, который не является вектором нулевых значений (например, вектор, все значения которого равны $0$).
Вектор $v$ — собственный вектор$M$, если $Mv = cv$ для определенного числа $c$. Целое число $c$ — собственное значение, соответствующее собственному вектору $v$. Как правило, матрица $M$ может преобразовать вектор в любой другой вектор. Но собственный вектор является особым, так как он не претерпел никаких изменений, кроме умножения на число. Обратите внимание, что если $v$ — собственный вектор с собственным значением $c$, то $av$ — также собственный вектор (для любого $a$, отличного от нуля) с тем же собственным значением.
Например, для матрицы идентификации каждый вектор $v$ – собственный вектор с собственным значением $1$.
Рассмотрим другой пример — диагональная матрица$D$ содержащая значения, отличные от нуля, только по диагонали:
$$\begin{bmatrix} d_1 & 0 & 0 \\ 0 & d_2 & 0 \\ 0 & 0 & d_3 \end{bmatrix}. $$
Векторы
$$\begin{bmatrix}1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix}0 \\ 1 \\ 0\end{bmatrix}\text{и}\begin{bmatrix}0 \\ 0 \\ 1\end{bmatrix}$$
являются собственными векторами этой матрицы с собственными значениями $d_1$, $d_2$ и $d_3$ соответственно. Если $d_1$, $d_2$ и $d_3$ являются отдельными числами, то эти вектора (и кратные им) являются единственными собственными векторами матрицы $D$. В общем случае для диагональной матрицы легко определить собственные значения и собственные векторы. Собственные значения — это все числа, отображаемые по диагонали, а соответствующие собственные векторы — это векторы единиц с одной записью, равной $1$, и остальными записями, равными $ 0 $.
Обратите внимание, что в примере, приведенном выше, собственные векторы матрицы $D$ образуют базис для $3$-мерных векторов. {iBx}=\boldone \cos(x)+ iB\sin(x)$$
{iBx}=\boldone \cos(x)+ iB\sin(x)$$
. Этот прием особенно полезен, так как он позволяет вам сделать выводы об операциях матричных экспоненциалов, даже если измерение $B$ является экспоненциально большим, в особом случае, когда $B$ является одновременно унитарным и эрмитовым элементом.
собственных значений — Примеры | Как найти собственные значения матрицы?
Термины собственные значения и собственные векторы появляются при изучении линейных преобразований. Некоторые векторы меняются почти на свои масштабные коэффициенты, когда к ним применяется какое-либо линейное преобразование (матрица). Такие векторы называются собственными векторами, а соответствующие масштабные коэффициенты называются собственными значениями матрицы.
Давайте узнаем больше о собственных значениях матрицы, их свойствах и примерах.
| 1. | Что такое собственные значения матрицы? |
| 2. | Как найти собственные значения? |
3. | Собственные значения матрицы 2×2 |
| 4. | Собственные значения матрицы 3×3 |
| 5. | Свойства собственных значений |
| 6. | Применение собственных значений |
| 7. | Часто задаваемые вопросы о собственных значениях |
Что такое собственные значения матрицы?
собственных значений матрицы являются скалярами, на которые изменяются некоторые векторы (собственные векторы) при применении к ней матрицы (преобразования). Другими словами, если A — квадратная матрица порядка n x n и v — ненулевой вектор-столбец порядка n x 1 такой, что Av = λv (это означает, что произведение A и v — это всего лишь скаляр, кратный v ), тогда скаляр (действительное число) λ называется собственным значением матрицы A, которое соответствует собственному вектору v .
Слово «eigen» происходит из немецкого языка и означает «характерный», «собственный» или «собственный». Таким образом, собственные значения также известны как «характеристические значения» (или) «характеристические корни» (или) «собственные значения» и т. д. Математическое определение собственных значений показано ниже.
Как найти собственные значения?
Из определения собственных значений, если λ — собственное значение квадратной матрицы A, то
A v = λ v
Если I — единичная матрица того же порядка, что и A, то мы можем написать Приведенное выше уравнение как
A V = λ (I V ) (потому что V = I V )
A V — λ (I V ) = 0
Взятие V (I V ) = 0 0003 .
v (A — λI) = 0
Это представляет собой однородную систему линейных уравнений и имеет нетривиальное решение только тогда, когда определитель матрицы коэффициентов равен 0.
т. е. |A — λI | = 0
Это уравнение называется характеристическим уравнением (где |A — λI| называется характеристическим полиномом), и, решая его для λ, мы получаем собственные значения. Вот пошаговый процесс, используемый для нахождения собственных значений квадратной матрицы A.
- Возьмем единичную матрицу I, порядок которой такой же, как у A.
- Умножьте каждый элемент I на λ, чтобы получить λI.
- Вычтите λI из A, чтобы получить A — λI.
- Найдите его определитель.
- Установите определитель равным нулю и найдите λ.
Применим эти шаги для нахождения собственных значений матриц разных порядков.
Собственные значения матрицы 2×2
Давайте рассмотрим процесс нахождения собственных значений матрицы 2×2 на примере, где мы найдем собственные значения A = \(\begin{equation}
\left[\begin{массив}{ll}
5 и 4 \\\
1 и 2
\конец{массив}\справа]
\end{уравнение}\). Пусть λ представляет его собственное значение (значения). Единичная матрица порядка 2×2: I = \(\begin{equation}
Пусть λ представляет его собственное значение (значения). Единичная матрица порядка 2×2: I = \(\begin{equation}
\left[\begin{массив}{ll}
1 & 0 \\\
0 и 1
\конец{массив}\справа]
\end{уравнение}\). Тогда
λI = λ \(\begin{equation}
\left[\begin{массив}{ll}
1 & 0 \\\
0 и 1
\конец{массив}\справа]
\end{уравнение}\) = \(\begin{уравнение}
\left[\begin{массив}{ll}
λ&0\\
0 и λ
\конец{массив}\справа]
\end{уравнение}\)
A — λI = \(\begin{уравнение}
\left[\begin{массив}{ll}
5 и 4 \\\
1 и 2
\конец{массив}\справа]
\end{уравнение}\) — \(\begin{уравнение}
\left[\begin{массив}{ll}
λ&0\\
0 и λ
\конец{массив}\справа]
\end{уравнение}\)
= \(\begin{уравнение}
\left[\begin{массив}{ll}
5 -λ& 4 \\
1 и 2 — λ
\конец{массив}\справа]
\end{equation}\)
Его определитель равен,
|A — λI| = (5 — λ) (2 — λ) — (1)(4)
= 10 — 5λ — 2λ + λ 2 — 4
= λ 2 — 7λ + 6
Характеристическое уравнение ,
|А — λI| = 0
λ 2 — 7λ + 6 = 0
(λ — 6)(λ — 1) = 0
λ — 6 = 0; λ — 1 = 0
λ = 6; λ = 1
Таким образом, собственные значения матрицы A равны 1 и 6.
Собственные значения матрицы 3×3
Давайте просто посмотрим на результат A — λI в предыдущем разделе. Разве это не просто матрица, полученная вычитанием λ из всех диагональных элементов A? Да, поэтому мы воспользуемся этим фактом здесь и найдем собственные значения матрицы 3×3 A = \(\begin{equation}
\left[\begin{массив}{lll}
3 и 1 и 1 \
2 и 4 и 2 \
1 и 1 и 3
\конец{массив}\справа]
\end{уравнение}\).
Характеристическое уравнение:
|A — λI| = 0
\(\ начало уравнения}
\left|\begin{массив}{lll}
3 — λ&1&1\
2&4 — λ&2\
1 и 1 и 3 — λ
\конец{массив}\право|
\end{уравнение}\) = 0
(3 — λ) [(4 — λ)(3 — λ) — 2(1) ] — 1 [ 2(3 — λ) — 2(1) ] + 1 [2 (1) — 1 (4 — λ) ] = 0
(3 — λ) [12 — 4λ — 3λ + λ 2 — 2] — 6 + 2λ + 2 + 2 — 4 + λ = 0
(3 — λ) [10 — 7λ + λ 2 ] — 6 + 3λ = 0
30 — 21λ + 3λ 2 — 10λ + 7λ 2 — λ 3 — 6 + 3λ = 0
-1 3 — 6 + 3λ = 0
-1 3 — 6 + 3λ = 0
-1 3 — 6 + 3λ = 0 — λ 3 — 6. 10λ 2 — 28λ + 24 = 0
10λ 2 — 28λ + 24 = 0
Умножая обе части на -1,
λ 3 — 10λ 2 + 28λ — 24 = 0
Это кубическое уравнение. Мы найдем один из его корней методом проб и ошибок, а другой — путем синтетического деления. Методом проб и ошибок видим, что λ = 2 удовлетворяет приведенному выше уравнению (подставим и проверим, получится ли 0 = 0). Теперь, используя синтетическое деление,
Установить частное равным 0. λ = 2
Таким образом, собственные значения данной матрицы 3×3 равны 2, 2 и 6.
Свойства собственных значений
- Квадратная матрица порядка n имеет не более n собственных значений.
- Единичная матрица имеет только одно собственное значение, равное 1.
- Собственные значения треугольных матриц и диагональных матриц суть не что иное, как элементы их главной диагонали.
- Сумма собственных значений матрицы A равна сумме ее диагональных элементов.

- Произведение собственных значений матрицы A равно ее определителю.
- Собственные значения эрмитовой и симметричной матриц действительны.
- Собственные значения косоэрмитовых и кососимметричных матриц либо нули, либо чисто мнимые числа.
- Матрица и ее транспонированная матрица имеют одинаковые собственные значения.
- Если A и B — две квадратные матрицы одного порядка, то AB и BA имеют одинаковые собственные значения.
- Собственные значения ортогональной матрицы равны 1 и -1.
- Если λ является собственным значением A, то kλ является собственным значением kA, где ‘k’ является скаляром.
- Если λ является собственным значением A, то λ k является собственным значением A k .
- Если λ является собственным значением A, то 1/λ является собственным значением A -1 (если существует обратное значение A).
- Если λ является собственным значением A, то |A| / λ — собственное значение сопряженного оператора A.

Помимо этих свойств, у нас есть еще одна теорема, связанная с собственными значениями, которая называется « Теорема Кейли-Гамильтона» . В нем говорится: «Каждая квадратная матрица удовлетворяет своему характеристическому уравнению». т. е. если A — квадратная матрица, то она удовлетворяет условию |A — λI| = 0. Например, если λ 2 — 8λ + 12 = 0 — характеристическое уравнение квадратной матрицы А, тогда А 2 — 8А + 12 = 0.
Применение собственных значений
- Собственные значения используются в электрических цепях, квантовой механике, теории управления и т. д.
- Применяются в конструкции автомобильных стереосистем.
- Они также используются для проектирования мостов.
- Неудивительно, что собственные значения также используются при определении рейтинга страницы Google.
- Используются в геометрических преобразованиях.
Часто задаваемые вопросы о собственных значениях
Что такое определение собственных значений?
Собственные значения матрицы — это скаляры, на которые изменяются собственные векторы при применении к ней матрицы или преобразования. Математически, если A v = λ v , то
Математически, если A v = λ v , то
- λ называется собственным значением
- v называется соответствующим собственным вектором
Как найти собственные значения матрицы?
Чтобы найти собственные значения квадратной матрицы A:
- Найдите ее характеристическое уравнение, используя |A — λI| = 0, где I — единичная матрица того же порядка A.
- Решите это для λ, и решения дадут собственные значения.
Каковы собственные значения диагональной матрицы?
Мы знаем, что все элементы диагональной матрицы, кроме ее диагональных элементов, равны нулю. Следовательно, собственные значения диагональной матрицы — это просто ее диагональные элементы.
Как найти собственные значения и собственные векторы?
Для любой квадратной матрицы A:
- Решить |A — λI| = 0 для λ, чтобы найти собственные значения.
- Решите (A — λI) v = 0 для v , чтобы получить соответствующие собственные векторы.

Где мы можем найти калькулятор собственных значений?
Мы можем найти калькулятор собственных значений, нажав здесь. Здесь вы можете ввести любую матрицу 2×2, тогда она покажет вам собственные значения вместе с шагами.
Что такое характеристическое уравнение для нахождения собственных значений?
Если A — квадратная матрица и λ представляет ее собственные значения, то |A — λI| = 0 представляет его характеристическое уравнение, и его решение приведет к собственным значениям.
Каковы собственные значения верхнетреугольной матрицы?
Поскольку в верхней треугольной матрице все элементы под главной диагональю равны нулю, собственные значения — не что иное, как диагональные элементы матрицы.
Каковы собственные значения унитарной матрицы?
Унитарная матрица — это комплексная матрица, обратная матрица которой равна сопряженной транспонированной матрице. Собственные значения унитарной матрицы равны -1 и 1.
4.
 {2}\). 92)}\\& = 1 \pm \rho \end{align}
{2}\). 92)}\\& = 1 \pm \rho \end{align}Здесь мы возьмем следующие решения:
\( \begin{array}{ccc}\lambda_1 & = & 1+\rho \\ \lambda_2 & = & 1-\rho \end{array}\)
Далее, чтобы получить соответствующие собственные векторы, мы должны решить следующую систему уравнений:
\((\textbf{R}-\lambda\textbf {I})\textbf{e} = \mathbf{0}\)
Это произведение \(R — λ\), умноженное на I , и собственный вектор e , равный 0. Или, другими словами, , это переводится для этой конкретной проблемы в приведенном ниже выражении:
\(\left\{\left(\begin{array}{cc}1 & \rho \\ \rho & 1 \end{массив}\right)-\lambda\left(\begin{array}{cc }1 &0\\0 & 1 \end{массив}\right)\right \}\left(\begin{array}{c} e_1 \\ e_2 \end{массив}\right) = \left(\begin{ array}{c} 0 \\ 0 \end{array}\right)\)
Это упрощается следующим образом:
\(\left(\begin{array}{cc}1-\lambda & \rho \\ \rho & 1-\lambda \end{массив}\right) \left(\begin{массив}{c} e_1 \\ e_2 \end{массив}\right) = \left(\begin{массив}{c} 0 \\ 0 \конец{массив}\справа)\)
Получение системы двух уравнений с двумя неизвестными:
\(\begin{array}{lcc}(1-\lambda)e_1 + \rho e_2 & = & 0\\ \rho e_1+(1-\lambda) e_2 & = & 0 \end{массив}\)
Примечание ! Это делает , а не уникальным решением. 2_2 = 1\)) 92_1 = 1\)
2_2 = 1\)) 92_1 = 1\)
Или, другими словами:
\(e_1 = \dfrac{1}{\sqrt{2}}\)
Используя выражение для \(e_{2}\), которое мы получили выше,
\(e_2 = -\dfrac{1-\lambda}{\rho}e_1\)
получаем
\(e_2 = \dfrac{1}{\sqrt{2}}\) для \ (\lambda = 1 + \rho\) и \(e_2 = \dfrac{1}{\sqrt{2}}\) для \(\lambda = 1-\rho\)
Таким образом, два собственных вектора заданы двумя векторами, как показано ниже:
\(\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \ end{array}\right)\) для \(\lambda_1 = 1+ \rho\) и \(\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ — \frac{1}{\sqrt{2}} \end{array}\right)\) для \(\lambda_2 = 1- \rho\) 9{p}\lambda_j = \lambda_1 \times \lambda_2 \times \dots \times \lambda_p\)
Калькулятор собственных значений и векторов
Создано Bogna Szyk и Maciej Kowalski, PhD
Последнее обновление: 12 мая 2022 г.
Содержание:- Матрица 2×2
- Вычисление трассы и определителя
- Как найти собственные значения
- Калькулятор собственных значений и собственных векторов – матрицы 2×2
- Как найти собственные значения и собственные векторы матриц 3×3
- Комплексные собственные значения и собственные векторы
- Часто задаваемые вопросы
Если анализ матриц вызывает у вас головную боль, этот калькулятор собственных значений и собственных векторов является идеальным инструментом для вас. Это позволит вам найти собственные значения матрицы размера матрицы 2×2 или 3×3 и даже сэкономит ваше время, также найдя собственные векторы . В этой статье мы предоставим вам пояснения и удобные формулы, чтобы вы поняли, как работает этот калькулятор и как находить собственные значения и собственные векторы в целом.
Это позволит вам найти собственные значения матрицы размера матрицы 2×2 или 3×3 и даже сэкономит ваше время, также найдя собственные векторы . В этой статье мы предоставим вам пояснения и удобные формулы, чтобы вы поняли, как работает этот калькулятор и как находить собственные значения и собственные векторы в целом.
Начинаем прямо сейчас!
Матрица 2×2
Матрица 2×2 A имеет следующий вид:
A=[a1a2b1b2]\text{A} = \begin{bматрица} а_1 и а_2 \\ б_1 и б_2 \end{bmatrix}A=[a1b1a2b2]
, где a₁ , a₂ , b₁ и b₂ — элементы матрицы. Наш калькулятор собственных значений и собственных векторов использует приведенную выше форму, поэтому убедитесь, что вводите числа правильно — не перепутайте их!
Вычисление трассы и определителя
В случае матрицы 2×2, чтобы найти собственные векторы и собственные значения, полезно сначала получить два особых числа: трасса и определитель массива. К счастью для нас, калькулятор собственных значений и собственных векторов найдет их автоматически, и если вы хотите их увидеть, нажмите кнопку в расширенном режиме . Если вы хотите проверить, дал ли он вам правильный ответ, или просто выполнить вычисления вручную, выполните следующие действия:
К счастью для нас, калькулятор собственных значений и собственных векторов найдет их автоматически, и если вы хотите их увидеть, нажмите кнопку в расширенном режиме . Если вы хотите проверить, дал ли он вам правильный ответ, или просто выполнить вычисления вручную, выполните следующие действия:
След : след матрицы определяется как сумма элементов на главной диагонали (от левого верхнего угла к правому нижнему). Он также равен сумме собственных значений (с учетом их кратностей). В случае матрицы 2×2 это:
tr(A) = a₁ + b₂Определитель : определитель матрицы полезен во многих дальнейших операциях, например, для нахождения обратной матрицы. Для матрицы 2×2 определитель равен:
|А| = а₁b₂ - а₂b₁
Как найти собственные значения
Каждая матрица 2×2 A имеет два собственных значения: λ₁ и λ₂. Они определяются как числа, которые удовлетворяют следующему условию для ненулевого вектора-столбца v = (v₁, v₂), который мы называем собственным вектором:
Они определяются как числа, которые удовлетворяют следующему условию для ненулевого вектора-столбца v = (v₁, v₂), который мы называем собственным вектором:
A × v = λ × v
Вы также можете найти другой эквивалент вариант приведенного выше уравнения:
(A - λI)v = 0
, где I — это единичная матрица 2×2.
Зная след и определитель, найти собственные значения матрицы несложно – все, что вам нужно сделать, это ввести эти значения в следующие уравнения:
λ₁ = tr(A)/2 + √ ((tr(A)²/4 - |A|)
λ₂ = tr(A)/2 - √(tr(A)²/4 - |A|)
Некоторые матрицы имеют только одно собственное значение Примеры таких массивов включают матрицы вида:
A=[1k01]\text{A} = \begin{bматрица} 1&к\ 0 и 1 \end{bmatrix}A=[10k1]
или…
A=[k00k]\text{A} = \begin{bматрица} к & 0 \\ 0 и к \end{bmatrix}A=[k00k]
Обязательно поэкспериментируйте с нашим калькулятором, чтобы увидеть, какие матрицы имеют только одно собственное значение!
Калькулятор собственных значений и собственных векторов – матрицы 2×2
Вы также можете использовать наш калькулятор для нахождения собственных векторов . По сути, научиться находить собственные векторы сводится к непосредственному решению уравнения:
По сути, научиться находить собственные векторы сводится к непосредственному решению уравнения:
(q - λI)v = 0
Обратите внимание, что если матрица имеет только одно собственное значение, она может иметь несколько соответствующих ему собственных векторов. Например, единичная матрица:
I=[1001]\text{I} = \begin{bматрица} 1 и 0 \\ 0 и 1 \end{bmatrix}I=[1001]
…имеет только одно (двойное) собственное значение λ = 1 , но два собственных вектора: v₁ = (1,0) и v₂ = (0 ,1) .
Помните, что если вектор v является собственным вектором, то тот же вектор, умноженный на скаляр, также является собственным вектором той же матрицы. Если вы хотите упростить решение, предлагаемое нашим калькулятором, перейдите к калькулятору единичных векторов.
Как найти собственные значения и собственные векторы матриц 3×3
Теперь попробуем перевести все это на язык матриц 3×3 . Прежде всего, давайте посмотрим на пример такого объекта:
Прежде всего, давайте посмотрим на пример такого объекта:
A=[a1a2a3b1b2b3c1c2c3]\text{A} = \begin{bматрица} а_1 и а_2 и а_3 \\ б_1 & б_2 & б_3 \\ с_1 и с_2 и с_3 \end{bmatrix}A=⎣
⎡a1b1c1a2b2c2a3b3c3⎦
⎤
где для нас записи a₁ , a₂ , до c₃ — действительные числа.
В целом, большинство приведенных выше определений одинаковы для матриц 3×3. Например, след представляет собой сумму клеток на главной диагонали:
tr(A) = a₁ + b₂ + c₃
|А| = a₁×b₂×c₃ + a₂×b₃×c₁ + a₃×b₁×c₂ — a₃×b₂×c₁ — a₂×b₁×c₃ — a₁×b₃×c₂
Теперь, когда дело доходит до того, как найти собственные векторы и собственные значения, определение снова то же самое : это числа λ и векторы v , которые удовлетворяют матричному уравнению:
A × v = λ × v
, где умножение слева является матричным умножением. Однако фокус в том, что на этот раз уравнение намного сложнее . В частности, формулы выше здесь не работают.
Однако фокус в том, что на этот раз уравнение намного сложнее . В частности, формулы выше здесь не работают.
В случае матриц 2×2 все сводится к квадратичной формуле. Однако, когда массивы имеют размер 3×3, мы получаем кубическое уравнение , т. е. уравнение с переменной в третьей степени. А такие вещи не так-то просто просчитать.
К счастью, у нас есть калькулятор собственных значений и собственных векторов, который может скрыть все эти уродливые формулы и без особых усилий дать нам красивый ответ .
Но всегда ли ответ красив?
Комплексные собственные значения и собственные векторы
Квадратные и кубические уравнения иногда не имеют действительных решений . Это означает, что не существует реального числа (типа числа, которое мы выучили, когда были маленькими детьми), которое удовлетворяло бы этой формуле. Поэтому в области действительных чисел не всегда можно найти собственные значения матрицы. Однако в математике есть расширение, в котором этого никогда не может быть: каждое уравнение имеет столько решений (с учетом их кратностей) , сколько его степени .
Однако в математике есть расширение, в котором этого никогда не может быть: каждое уравнение имеет столько решений (с учетом их кратностей) , сколько его степени .
Комплексные числа, формально говоря, это пар действительных чисел . Первая из пары называется — реальная часть , а вторая — мнимая часть (ага, именно так ее назвали профессиональные математики). Второй имеет загадочное число i , которое мы определяем как квадратный корень из (-1) . Нам в школе говорили, что таких вещей не бывает, не так ли? Да, но они воображаемые .
Для нас это означает, что калькулятор всегда будет знать, как найти собственные векторы и собственные значения матрицы. Как только он это сделает, важно знать, использует ли задача, которую вы решаете , комплексные числа или только действительные . На всякий случай наш калькулятор собственных значений и собственных векторов покажет вам все значения и соответствующие им собственные векторы, будь то действительные или комплексные.
Однако, если вам нужны только настоящие, смело игнорировать все, что содержит i . Просто имейте в виду, что они существуют, хотя и являются воображаемыми.
Часто задаваемые вопросы
Как найти собственные значения и собственные векторы?
Чтобы найти собственное значение , λ и его собственный вектор v квадратной матрицы A , вам нужно: — λI с I в качестве единичной матрицы.
det(A - λI) = 0 для λ (это собственные значения). Av = λv с координатами v в качестве переменной. λ , решить систему уравнений , Av = λv . Av = λv с параметрами.
v .Как найти собственные значения матрицы 3×3?
до Найти собственные значения λ₁ , λ₂ , λ₃ из матрицы 3×3, a , вам нужно:
- 585 A , вам нужно:
- 595 . . из
A, чтобы получитьА - λI. - Запишите определитель матрицы, который равен
A - λI. - Решите кубическое уравнение, которое равно
det(A - λI) = 0, дляλ. - (не более трех) решений уравнения являются собственными значениями уравнения
A. - При необходимости перейти к найти собственные векторы собственных значений .

Как найти собственные векторы по собственным значениям?
Если у вас есть собственное значение
λквадратной матрицыA, и вы хотите найти соответствующий ему собственный векторv, вам необходимо:- как переменные (например,
v = (x,y,z)для матриц 3×3). - Запишите систему уравнений,
Av = λv(каждая координата дает одно уравнение). - Решите систему уравнений для координат
против. - Напишите решение с использованием параметров.
- Для каждого параметра его коэффициент является координатой собственного вектора .
- Сгруппируйте коэффициенты, соответствующие каждому параметру, чтобы сформировать собственный вектор,
v.
Сколько собственных значений у матрицы?
Квадратная матрица размером с
nстрок и столбцов может иметь не болееnсобственных значений . Если мы не допускаем комплексных чисел, может случиться так, что их не будет (т. Е. Когда характеристический многочлен не имеет действительных решений).
Если мы не допускаем комплексных чисел, может случиться так, что их не будет (т. Е. Когда характеристический многочлен не имеет действительных решений).Ортогональны ли собственные векторы?
В общем, нет . Если исходная матрица симметрична, то собственные векторы различных собственных значений всегда ортогональны.
Может ли 0 быть собственным значением?
Да , можно. Для этого должен существовать ненулевой вектор
v, такой чтоAv = 0(как умножение матриц).Богна Шик и Мацей Ковальски, кандидат наук
Размер матрицы
A = ⌈ a 1 a 2 ⌉ ⌊ b 1 b 2 ⌋ Первая строка
Вторая строка
Ознакомьтесь с 31 похожим калькулятором линейной алгебры 🔢
Сопряженная матрица0001
В этой главе вы узнаете о собственных значениях и собственных векторах.
 Собственные значения (также известные как характеристические корни) — это скаляры, связанные с линейными системами уравнений. Каждое собственное значение имеет соответствующий вектор, собственный вектор, связанный с ним. Собственные значения и собственные векторы играют роль во многих статистических приложениях, занимая видное место в некоторых методах декомпозиции и анализа главных компонентов (PCA).
Собственные значения (также известные как характеристические корни) — это скаляры, связанные с линейными системами уравнений. Каждое собственное значение имеет соответствующий вектор, собственный вектор, связанный с ним. Собственные значения и собственные векторы играют роль во многих статистических приложениях, занимая видное место в некоторых методах декомпозиции и анализа главных компонентов (PCA).14.1 Собственные значения
Пусть A будет квадратной матрицей \(p \times p\) и I — единичная матрица \(p \times p\). Собственные значения — это набор ненулевых скаляров \(\lambda_1,\lambda_2, \lambda_3,\ldots,\lambda_p\), которые удовлетворяют
\[ \mathrm{det}\bigg(\mathbf{A} — \lambda \mathbf{I}\bigg) = 0 \]
Рассмотрим пример,
\[ \underset{2\times 2}{\mathbf{A}} = \begin{bmatrix} -3 и 5\ 4 & -2 \\ \end{bmatrix} \]
Наша цель — найти значения \(\лямбда\), которые удовлетворяют
\[ \mathrm{det}\bigg(\begin{bmatrix} -3 и 5\ 4 & -2 \\ \end{bmatrix} — \lambda\begin{bmatrix} 1 и 0 \\ 0 и 1 \\ \end{bmatrix}\bigg) = 0 \]
Использование матричной алгебры,
\[ \начать{разделить} \mathrm{det}\bigg(\begin{bmatrix} -3 и 5\ 4 & -2 \\ \end{bmatrix} — \lambda\begin{bmatrix} 1 и 0 \\ 0 и 1 \\ \end{bmatrix}\bigg) &= 0 \\[2ex] \mathrm{det}\bigg(\begin{bmatrix} -3 и 5\ 4 & -2 \\ \end{bmatrix} — \begin{bmatrix} \лямбда & 0 \\ 0 & \лямбда\\ \end{bmatrix}\bigg) &= 0 \\[2ex] \mathrm{det}\begin{bmatrix} -3 — \лямбда&5\ 4 & -2 — \лямбда\\ \end{bmatrix} &= 0 \\[2ex] (-3 — \лямбда)(-2 — \лямбда) — 20 &= 0 \конец{разделить} \] 92-4AC}}{2А} \]
Краткий обзор в Академии Хана, если вам это нужно.

Теперь, когда у нас есть собственные значения, мы можем перепроверить, что \(\mathbf{A} — \lambda \mathbf{I}\) является сингулярным. (Я пропущу это здесь, но подставлю значения для \(\лямбда\), по одному, и убедитесь, что определитель равен нулю.) Уравнение, которое вы решили,
\[ \mathrm{det}\big(\mathbf{A} — \lambda \mathbf{I}\big)=0 \]
упоминается как характеристическое уравнение . Решение характеристического уравнения дает собственные значения. Иногда собственные значения называют характеристическими корнями матрицы 9.0057 А .
14.2 Собственные векторы
Если \(\lambda\) является собственным значением матрицы A , то можно найти вектор v (собственный вектор), который удовлетворяет
\[ \mathbf{A}\mathbf{v} = \lambda \mathbf{v} \]
В нашем предыдущем примере A было матрицей \(2\times2\), поэтому v будет вектором \(2\times1\), чтобы умножение матриц работало.

\[ \underset{2\times2}{\mathbf{A}}~\underset{2\times1}{\mathbf{v}} = \lambda \underset{2\times1}{\mathbf{v}} \]
Обратите внимание, что мы также можем переставить члены этого выражения:
\[ \начать{разделить} \mathbf{A}\mathbf{v} &= \lambda \mathbf{v} \\[2ex] \mathbf{A}\mathbf{v} — \lambda \mathbf{v} &= 0\\[2ex] \big(\mathbf{A} — \lambda \mathbf{I}\big) \mathbf{v} &= 0\\[2ex] \конец{разделить} \]
Чтобы получить ненулевое решение для v , определитель \(\mathbf{A} — \lambda \mathbf{I}\) должен быть равен нулю. Вот почему собственные значения — это \(\lambda\)-значения, которые делают это невырожденным.
14.2.1 Нахождение элементов вектора v
Мы можем использовать матричную алгебру, чтобы найти элементы вектора v , используя каждое собственное значение отдельно.
\[ \начать{разделить} \mathbf{A}\mathbf{v} &= \lambda \mathbf{v} \\[1em] \begin{bматрица} -3 и 5\ 4 & -2 \\ \end{bmatrix}\begin{bmatrix} v_1 \\ v_2 \\ \end{bmatrix} &= -7\begin{bmatrix} v_1 \\ v_2 \\ \end{bmatrix}\\[1em] \конец{разделить} \]
Получается система двух уравнений с двумя неизвестными:
\[ \начать{разделить} -3v_1 + 5v_2 &= -7v_1\ 4v_1 — 2v_2 &= -7v_2 \конец{разделить} \]
Упрощая это, мы получаем
\[ \начать{разделить} 4в_1+5в_2&=0\ 4v_1 + 5v_2 &= 0 \конец{разделить} \]
Однородная система уравнений означает, что существует бесконечное число решений.
 Общее решение здесь состоит в том, чтобы выразить одну переменную (скажем, \(v_2\)) как функцию другой.
Общее решение здесь состоит в том, чтобы выразить одну переменную (скажем, \(v_2\)) как функцию другой.\[ \начать{разделить} v_1 &= \тета \\[0.5em] v_2 &= -\frac{4}{5}\theta \конец{разделить} \] 92 &= \frac{25}{41} \\[2ex] \ тета & = \ sqrt {\ гидроразрыва {25} {41}} \\ [2ex] &=\frac{5}{\sqrt{41}} \конец{разделить} \]
Отсюда следует, что
\[ \начать{разделить} e_1 &= \frac{5}{\sqrt{41}} \\[1em] e_2 &= -\frac{4}{\sqrt{41}} \конец{разделить} \]
И нормализованный собственный вектор, соответствующий собственному значению \(-7\), равен:
\[ \mathbf{e}_1x = \begin{bmatrix}\frac{5}{\sqrt{41}} \\ -\frac{4}{\sqrt{41}}\end{bmatrix} \]
Мы могли бы проверить это, убедившись, что уравнение \(\mathbf{A}\mathbf{e}=\lambda\mathbf{e}\) выполняется:
\[ \begin{bматрица} -3 и 5\ 4 & -2 \\ \end{bmatrix}\begin{bmatrix}\frac{5}{\sqrt{41}} \\ -\frac{4}{\sqrt{41}}\end{bmatrix} = -7\begin{bmatrix} \frac{5}{\sqrt{41}} \\ -\frac{4}{\sqrt{41}}\end{bmatrix} \]
Мы можем следовать тому же процессу для второго собственного вектора, который соответствует собственному значению 2.
 Это дает собственный вектор:
Это дает собственный вектор:\[ \mathbf{e}_2 = \begin{bmatrix}\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix} \]
Что еще раз можно проверить.
14.3 Использование R для поиска собственных значений и собственных векторов
Мы можем использовать функцию
eigen()для нахождения собственных значений и собственных векторов матрицы. Синтаксис для поиска их для нашего примера матрицы A :# Создать A А = матрица ( данные = с (-3, 4, 5, -2), сейчас = 2 ) # Вычисление собственных значений и собственных векторов eigen(A)
eigen() разложение $значения [1] -7 2 $векторы [1] [2] [1,] -0,7808688 -0,7071068 [2,] 0,6246950 -0,7071068Собственные векторы для каждого из собственных значений представлены в столбцах матрицы, заданной в компоненте `\(vector\) вывода. Например, собственный вектор, связанный с собственным значением \(-7\), представлен в первом столбце матрицы, а связанный с собственным значением 2 представлен во втором столбце матрицы.

Обратите внимание, что знаки для всех элементов любого конкретного собственного вектора можно поменять местами, поскольку вектор будет представлять одно и то же векторное пространство. Таким образом, выведенный здесь второй собственный вектор имеет отрицательные значения.
Вместе собственные значения и собственные векторы составляют собственную структуру матрицы A . В нашем примере собственная структура A :
\[ \начать{разделить} \lambda_1 &= -7 \qquad &\mathbf{e}_1 = \begin{bmatrix}\frac{5}{\sqrt{41}} \\ -\frac{4}{\sqrt{41}}\end {bmatrix}\\[2ex] \lambda_2 &= 2 \qquad &\mathbf{e}_2 = \begin{bmatrix}\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix } \\[2ex] \конец{разделить} \]
Жемчужина матрицы: глубокое погружение в собственные значения и собственные векторы | Андре Йе
ИсточникСобственные значения и собственные векторы могут показаться абстрактными и далекими понятиями, но они играют неотъемлемую роль в окружающем вас мире.
 Поскольку все определяется данными, они сохраняются в матрицах. В центре матрицы — через сложности и усложнения — лежат собственные векторы и собственные значения, обеспечивающие ясность и раскрывающие природу матрицы. Понимание того, что они собой представляют, как их получить и как они применяются, является неотъемлемой частью понимания красоты матрицы и, в более широком смысле, той роли, которую данные и математика играют в мире.
Поскольку все определяется данными, они сохраняются в матрицах. В центре матрицы — через сложности и усложнения — лежат собственные векторы и собственные значения, обеспечивающие ясность и раскрывающие природу матрицы. Понимание того, что они собой представляют, как их получить и как они применяются, является неотъемлемой частью понимания красоты матрицы и, в более широком смысле, той роли, которую данные и математика играют в мире.Рассмотрим сначала двумерный вектор, который имеет два элемента, каждый из которых соответствует одной координате на двумерной плоскости. Они представляют собой перемещения от одной координаты к другой.
При умножении вектора на матрицу применяется линейное преобразование . Это приводит к растяжению (или сжатию) системы координат вдоль двух векторов. Например, матрица
[[3, 1], [1, 2]]выравнивает ось x вдоль вектора[3, 1](первый столбец) и ось y вдоль вектора[1, 2]. Визуально можно сказать, что точка (0, 1) на самом деле отображается в (1, 2), и это можно подтвердить, умножив ее на матрицу.
Визуально можно сказать, что точка (0, 1) на самом деле отображается в (1, 2), и это можно подтвердить, умножив ее на матрицу.Допустим, у нас есть вектор
[-1, -1]. После умножения на матрицу линейного преобразования он оказывается в точке[-4, -3].Промежуток вектора — это линия, которая всегда проходит через вектор. Когда вектор подвергается линейному преобразованию (умножается на матрицу), он обычно выбивается из своего диапазона.
Однако некоторые типы векторов не удаляются из своего диапазона. Это собственных векторов матрицы. Вместо этого, когда собственные векторы умножаются на матрицу, собственный вектор просто масштабируется с коэффициентом собственного значения , приземляясь где-то в другом месте их диапазона.
Собственные векторы и собственные значения запутаны — они редко бывают целыми числами и с ними легко работать.Из-за природы собственного вектора простое масштабирование базового собственного вектора в том же или прямо противоположном направлении даст еще один собственный вектор.

В трех измерениях матрица описывает преобразование трех осей — 90 446 x 90 447, 90 446 y 90 447 и 90 446 z 90 447 — соответствующих трем координатам, представляющим преобразование, которому подвергается каждая координата. Вот почему собственные векторы и собственные значения определены только для квадратных матриц; общая матрица n на n описывает преобразование n осей, каждая из которых соответствует координате с n элементами.
Чтобы найти собственный вектор матрицы, нам сначала нужно найти ее собственное значение. Из определения собственного значения мы можем построить равенство Ax = λ x , где A представляет собой матрицу, а λ представляет собой собственное значение. Это имеет смысл; умножение собственного вектора на матрицу преобразования x должно иметь тот же эффект, что и его масштабирование на собственное значение λ.
Из этого соотношения мы можем переместить оба члена в левую часть.
 Чтобы сделать выражение A — λ действительно ( A — это матрица, а λ — это число), мы умножаем λ на единичную матрицу, которая вообще не применяет никаких преобразований.
Чтобы сделать выражение A — λ действительно ( A — это матрица, а λ — это число), мы умножаем λ на единичную матрицу, которая вообще не применяет никаких преобразований.Как видно выше, существует бесконечное число тривиальных решений , или решений, которые могут быть получены простым масштабированием собственного вектора на любое число. Чтобы избавиться от тривиальных решений, воспользуемся определителем.
Определитель — это просто мера фактора, на который площадь растягивается матрицей преобразования. Рассмотрим, например, один стандартный квадрат на координатной плоскости площадью в одну квадратную единицу.
Когда пространство растягивается матрицей преобразования, новая площадь составляет четыре квадратных единицы. Поскольку площадь увеличилась в четыре раза, определитель матрицы равен четырем.
Когда определитель равен 0, площадь квадрата схлопывается до нуля, а это означает, что два вектора, описывающие расположение осей, лежат на одной линии.
 В этом случае все пространство искривлено в одну единственную линию (одномерную). Установив требование, при котором определитель должен быть равен нулю, можно отбросить пространство избыточных или тривиальных решений, что сделает уравнение гораздо более разрешимым.
В этом случае все пространство искривлено в одну единственную линию (одномерную). Установив требование, при котором определитель должен быть равен нулю, можно отбросить пространство избыточных или тривиальных решений, что сделает уравнение гораздо более разрешимым.Следовательно, для того, чтобы ранее придуманное равенство было (легко) разрешимым, сначала должно быть верным, что определитель матрицы должен быть равен нулю.
Поиск собственного значения является задачей решения квадратного уравнения. Для матриц размерности 3+ необходимо использовать другую форму формулы определителя.
В этом случае собственные значения матрицы
[[1, 4], [3, 2]]равны 5 и -2. Это означает, что при умножении собственных векторов матрицы на матрицу длина их векторов будет увеличена в 5 и -2 раза соответственно каждому из собственных векторов. Подставив обнаруженные собственные значения в наше первоначально полученное уравнение, мы можем найти собственные векторы.Собственные векторы и собственные значения действительно являются жемчужиной матрицы.
 Он воплощает дух и природу матрицы — eigen в переводе с немецкого означает «врожденный». Имея только собственные векторы и собственные значения любой матрицы, можно легко полностью восстановить исходную матрицу. Благодаря этому особому свойству собственные векторы практически гарантированно появляются везде, где есть матричная операция.
Он воплощает дух и природу матрицы — eigen в переводе с немецкого означает «врожденный». Имея только собственные векторы и собственные значения любой матрицы, можно легко полностью восстановить исходную матрицу. Благодаря этому особому свойству собственные векторы практически гарантированно появляются везде, где есть матричная операция.Возьмем, к примеру, анализ основных компонентов (PCA), распространенный метод машинного обучения без учителя, который стремится уменьшить размерность данных, сохраняя при этом ключевые статистические показатели, такие как дисперсия и среднее значение. Например, рассмотрим набор данных из 100 измерений, который PCA попытается уменьшить до двух измерений. Во-первых, алгоритм строит ковариационную матрицу, которая оценивает (в некотором смысле), насколько коррелированы две переменные. Матрица в целом определяет форму данных.
Собственные векторы ковариационной матрицы используются для переориентации данных между осями x и y вдоль линий наибольшей дисперсии.
 По сути, собственные векторы используются как снимок матрицы, который сообщает алгоритму, какие области усиливать, а какие оглушать. Бесчисленное множество других применений собственных векторов и собственных значений, от машинного обучения до топологии, используют ключевую особенность собственных векторов, заключающуюся в том, что собственные векторы предоставляют так много полезной информации о матрице, применяемой везде, от поиска линии вращения в четырехмерном кубе до сжатия многомерных изображений. Алгоритм поискового рейтинга Google. 9
По сути, собственные векторы используются как снимок матрицы, который сообщает алгоритму, какие области усиливать, а какие оглушать. Бесчисленное множество других применений собственных векторов и собственных значений, от машинного обучения до топологии, используют ключевую особенность собственных векторов, заключающуюся в том, что собственные векторы предоставляют так много полезной информации о матрице, применяемой везде, от поиска линии вращения в четырехмерном кубе до сжатия многомерных изображений. Алгоритм поискового рейтинга Google. 9собственных значений и собственных векторов
Собственные значения и собственные векторы
Определения
Если L — линейное преобразование из векторного пространства в себя, то интересует есть ли векторы v обладают тем свойством, что L( v ) кратно против . Если это так, то неоднократно применение L приведет к тому, что вектор всегда будет параллельным к против .
 Эта идея является фундаментальной
значение для приложений в физике, механике, экономике, биологии и просто
о любой другой области науки. Мы можем сформулировать это в терминах матриц
следующим образом.
Эта идея является фундаментальной
значение для приложений в физике, механике, экономике, биологии и просто
о любой другой области науки. Мы можем сформулировать это в терминах матриц
следующим образом.Определение
Пусть А быть n x n матрица. Тогда скаляр l называется собственным значением с соответствующим ненулевым собственным вектором против если
А против = л v
Пример
Для матрицы
мы можете проверить, что -1 и 4 являются собственными значениями с соответствующими собственными векторами
Уведомление что если v — собственный вектор с собственным значением l, то таково любое число, кратное v , начиная с
.A(c v ) = cA v = c(l v ) = л(с v )
Пример
единичная матрица I n имеет 1 как его единственное собственное значение.
 Все векторы являются связанными собственными векторами с
Все векторы являются связанными собственными векторами сI n v = v = (1) v
для все против .
Нахождение собственных значений и собственных векторов
Теперь мы определим, как найти собственные значения и собственные векторы для матрица. Пусть A — матрица с собственным значением l и собственный вектор v . Затем
А против = л v
подразумевает, что
A v — l v = 0
Мы хотели бы исключить и из уравнение выше (справа). Однако мы должны быть осторожны, поскольку термин A — л не имеет смысла. Вместо этого у нас есть
(А — I) v = 0
Если есть нетривиальное решение, то
det(A — lI) = 0
, и решение находится в нулевом пространстве A = lI.
Пример
Найдите собственные значения и собственные векторы числа
.
Мы есть
который имеет определитель
(3 — л)(4 — л) — 6 = л 2 — 7л + 12 — 6
= л 2 — 7л + 6 = (л — 1)(л — 6)
Так корни
л = 1 а также л = 6
Сейчас давайте найдем собственные векторы. Для л = 1, у нас есть
который имеет ссылку
А ненулевой вектор в нулевом пространстве равен
Сейчас для собственного вектора, соответствующего l = 6. У нас есть
Уведомление что вторая строка избыточна. В этот момент довольно легко увидеть что
уведомлениечто есть много вариантов для этих векторов (все кратные выше вектор). Мы сделали свой выбор в чтобы избежать дробей.
Характеристический многочлен
Мы видели, что для того, чтобы найти собственные значения, мы просто находим корни многочлен, определенный
стр.
 A (л)
= det(lI — A)
A (л)
= det(lI — A)Мы называем этот полином характеристикой . многочлен . Степень многочлена будет n где A представляет собой n x n матрица. Корнями характеристического полинома будут собственные значения. Обратите внимание, что если 0 является корнем, то
det(0I — A) = det(A) = 0
Это говорит нам, что 0 является собственным значением, если и только если det(A) = 0. Теперь мы можем добавьте еще одно утверждение к неособым эквивалентам.
Теорема
Пусть Быть п х п матрица. Затем TFAE
- А неособый.
- А x = 0 имеет только простое решение.
- А является строковым эквивалентом I.
- А x = b имеет единственное решение для всех б .
- дет(А) отличен от нуля.
- А имеет ранг n.
- А имеет недействительность 0,
- ряды А
линейно независимы.

- 595 . . из

 4645+17.6008i 0
0 0 -2.4645-17.6008i
4645+17.6008i 0
0 0 -2.4645-17.6008i 0000i 0.8165 + 0.0000i 0.8165 + 0.0000i
-0.3386 + 0.0000i -0.4082 + 0.0000i -0.4082 - 0.0000i
D =
-1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 1.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 1.0000 - 0.0000i
0000i 0.8165 + 0.0000i 0.8165 + 0.0000i
-0.3386 + 0.0000i -0.4082 + 0.0000i -0.4082 - 0.0000i
D =
-1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 1.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 1.0000 - 0.0000i

 49-91.
49-91.

 {2} (A) -4 { rm {det}} (A) }}} расстояние между двумя собственными значениями, легко вычислить
{2} (A) -4 { rm {det}} (A) }}} расстояние между двумя собственными значениями, легко вычислить 2 + 2 * p1 п = sqrt(p2 / 6) B = (1 / п) * (А — q * я) % I — единичная матрица р = Det(B) / 2 % В точной арифметике для симметричной матрицы -1
2 + 2 * p1 п = sqrt(p2 / 6) B = (1 / п) * (А — q * я) % I — единичная матрица р = Det(B) / 2 % В точной арифметике для симметричной матрицы -1  {2} = { begin {bmatrix} -4 & 0 & -8 — 4 & 0 & -8 4 & 0 & 8 end {bmatrix}}, qquad (AI) (A + I) = { begin {bmatrix} 0 & 4 & 4 0 & 2 & 2 0 & -2 & -2 end {bmatrix}}}
{2} = { begin {bmatrix} -4 & 0 & -8 — 4 & 0 & -8 4 & 0 & 8 end {bmatrix}}, qquad (AI) (A + I) = { begin {bmatrix} 0 & 4 & 4 0 & 2 & 2 0 & -2 & -2 end {bmatrix}}}



 Если мы не допускаем комплексных чисел, может случиться так, что их не будет (т. Е. Когда характеристический многочлен не имеет действительных решений).
Если мы не допускаем комплексных чисел, может случиться так, что их не будет (т. Е. Когда характеристический многочлен не имеет действительных решений). Собственные значения (также известные как характеристические корни) — это скаляры, связанные с линейными системами уравнений. Каждое собственное значение имеет соответствующий вектор, собственный вектор, связанный с ним. Собственные значения и собственные векторы играют роль во многих статистических приложениях, занимая видное место в некоторых методах декомпозиции и анализа главных компонентов (PCA).
Собственные значения (также известные как характеристические корни) — это скаляры, связанные с линейными системами уравнений. Каждое собственное значение имеет соответствующий вектор, собственный вектор, связанный с ним. Собственные значения и собственные векторы играют роль во многих статистических приложениях, занимая видное место в некоторых методах декомпозиции и анализа главных компонентов (PCA).

 Общее решение здесь состоит в том, чтобы выразить одну переменную (скажем, \(v_2\)) как функцию другой.
Общее решение здесь состоит в том, чтобы выразить одну переменную (скажем, \(v_2\)) как функцию другой. Это дает собственный вектор:
Это дает собственный вектор:
 Поскольку все определяется данными, они сохраняются в матрицах. В центре матрицы — через сложности и усложнения — лежат собственные векторы и собственные значения, обеспечивающие ясность и раскрывающие природу матрицы. Понимание того, что они собой представляют, как их получить и как они применяются, является неотъемлемой частью понимания красоты матрицы и, в более широком смысле, той роли, которую данные и математика играют в мире.
Поскольку все определяется данными, они сохраняются в матрицах. В центре матрицы — через сложности и усложнения — лежат собственные векторы и собственные значения, обеспечивающие ясность и раскрывающие природу матрицы. Понимание того, что они собой представляют, как их получить и как они применяются, является неотъемлемой частью понимания красоты матрицы и, в более широком смысле, той роли, которую данные и математика играют в мире. Визуально можно сказать, что точка (0, 1) на самом деле отображается в (1, 2), и это можно подтвердить, умножив ее на матрицу.
Визуально можно сказать, что точка (0, 1) на самом деле отображается в (1, 2), и это можно подтвердить, умножив ее на матрицу.
 Чтобы сделать выражение A — λ действительно ( A — это матрица, а λ — это число), мы умножаем λ на единичную матрицу, которая вообще не применяет никаких преобразований.
Чтобы сделать выражение A — λ действительно ( A — это матрица, а λ — это число), мы умножаем λ на единичную матрицу, которая вообще не применяет никаких преобразований.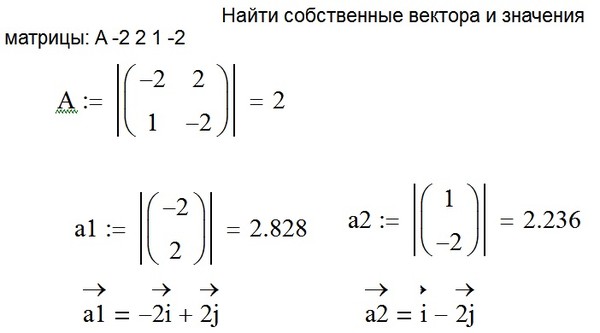 В этом случае все пространство искривлено в одну единственную линию (одномерную). Установив требование, при котором определитель должен быть равен нулю, можно отбросить пространство избыточных или тривиальных решений, что сделает уравнение гораздо более разрешимым.
В этом случае все пространство искривлено в одну единственную линию (одномерную). Установив требование, при котором определитель должен быть равен нулю, можно отбросить пространство избыточных или тривиальных решений, что сделает уравнение гораздо более разрешимым. Он воплощает дух и природу матрицы — eigen в переводе с немецкого означает «врожденный». Имея только собственные векторы и собственные значения любой матрицы, можно легко полностью восстановить исходную матрицу. Благодаря этому особому свойству собственные векторы практически гарантированно появляются везде, где есть матричная операция.
Он воплощает дух и природу матрицы — eigen в переводе с немецкого означает «врожденный». Имея только собственные векторы и собственные значения любой матрицы, можно легко полностью восстановить исходную матрицу. Благодаря этому особому свойству собственные векторы практически гарантированно появляются везде, где есть матричная операция. По сути, собственные векторы используются как снимок матрицы, который сообщает алгоритму, какие области усиливать, а какие оглушать. Бесчисленное множество других применений собственных векторов и собственных значений, от машинного обучения до топологии, используют ключевую особенность собственных векторов, заключающуюся в том, что собственные векторы предоставляют так много полезной информации о матрице, применяемой везде, от поиска линии вращения в четырехмерном кубе до сжатия многомерных изображений. Алгоритм поискового рейтинга Google. 9
По сути, собственные векторы используются как снимок матрицы, который сообщает алгоритму, какие области усиливать, а какие оглушать. Бесчисленное множество других применений собственных векторов и собственных значений, от машинного обучения до топологии, используют ключевую особенность собственных векторов, заключающуюся в том, что собственные векторы предоставляют так много полезной информации о матрице, применяемой везде, от поиска линии вращения в четырехмерном кубе до сжатия многомерных изображений. Алгоритм поискового рейтинга Google. 9 Эта идея является фундаментальной
значение для приложений в физике, механике, экономике, биологии и просто
о любой другой области науки. Мы можем сформулировать это в терминах матриц
следующим образом.
Эта идея является фундаментальной
значение для приложений в физике, механике, экономике, биологии и просто
о любой другой области науки. Мы можем сформулировать это в терминах матриц
следующим образом. Все векторы являются связанными собственными векторами с
Все векторы являются связанными собственными векторами с
 A (л)
= det(lI — A)
A (л)
= det(lI — A)