Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
3Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3. 14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
14159..— Показать, что $\log(x+1)-\log(x)0$
Задавать вопрос
спросил
Изменено 4 года назад
Просмотрено 813 раз
$\begingroup$
Покажите, что $\log(x+1)-\log(x)<\frac{1}{x}$ при $x >0$.
Мне сказали, что это очень просто, но я не знаю, как это решить. Любая помощь будет здорово.
- исчисление
- неравенство
- логарифмы
$\endgroup$
$\begingroup$
Функция $\log(1+t)$ строго вогнута, поэтому ее график остается ниже касательной в точке $0$: для любых $t\not=0$ и $t>-1$
$$\log(1+t)< t.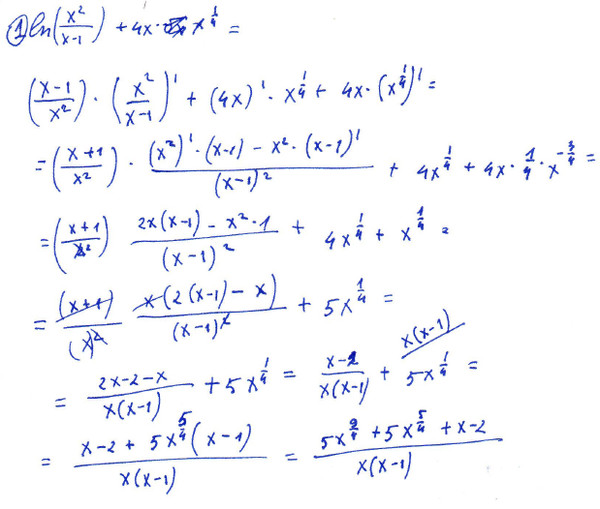
$$
Ваше неравенство эквивалентно
$$\log(x+1)-\log(x)=\log\left(1+\frac1x\right)< \frac1x.$$
$\endgroup$
2
$\begingroup$
Применить теорему о среднем значении: если $f$ дифференцируема на $]a,b[$ и непрерывна на $[a,b]$, то $$(\exists c\in]a,b[)\,f(b)-f(a)=(b-a)f'(c)$$ Так вот : $$\ln(x+1)-\ln(x)=(x+1-x)\ln'(c)=\frac1c< \frac1x$$ потому что $x+1>
Rmk : вы также можете изучить функцию $f:x\mapsto \ln(x+1)-\ln(x)-\frac1x$…
$\endgroup$
$\begingroup$
Рассмотрим $f(x)=\log\left(\frac{x+1}{x}\right)=\log\left(1+\frac{1}{x}\right)$ . Установите $u=1/x$, и тогда, сделав хорошую цифру, вы увидите, что $\log(1+u)\le u$ и все готово.
$\endgroup$
$\begingroup$
Пусть $x>0$.
$f: t\mapsto \ln(t)$ непрерывен в $[x,x+1]$ и дифференцируем в $(x,x+1)$, таким образом, согласно MVT,
9t\geq t+1$$ Итак:$$t\geq \ln{(t+1)}$$ Пусть:$t=\frac{1}{x}$ тогда:$$\ln{(1+ \frac{1}{x})}\leq \frac{1}{x}$$$\endgroup$
4реальный анализ — доказать $\log(1+x)0$
Задавать вопрос
спросил
Изменено 1 год, 6 месяцев назад 9x$ для $x\gt 0$ тогда я могу взять $\log$..
- реальный анализ
$\endgroup$
9
$\begingroup$
Пусть $$f(x) = \ln(1+x)-x\;,$$ Где $x>0$
Теперь $$\displaystyle f'(x) = \frac{1}{1 +x}-1 = -\frac{x}{1+x}<0$$ для всех $x>0$
Итак, функция $f(x)$ является строго убывающей функцией
Итак, здесь $$x> 0\Rightarrow f(x)
$\endgroup$
$\begingroup$
Пусть $f: x \mapsto x — \log (1+x)$ на $]0, +\infty[$. Так как $f'(x) = 1 — \frac{1}{1+x} > 0$ для всех $x > 0$, то $f$ строго возрастает на $]0, +\infty[$. Сможешь закончить?
$\endgroup$
$\begingroup$
Функция $\ln (1+x)$ строго вогнута на $(-1,\infty).$ Таким образом, эта функция лежит ниже любой из своих касательных в этой области (кроме точки касания). Поскольку $y=x$ — это прямая, касающаяся $y=\ln (1+x)$ в точке $(0,0),$, мы получили желаемый результат (и даже больше).
$\endgroup$
$\begingroup$
Ваше неравенство можно улучшить. $\exp(x)$ строго выпукла.