исчисление — Как доказать, что $\log(x)1$?
спросил
Изменено 11 месяцев назад
Просмотрено 21к раз
$\begingroup$
Это очень просто, но мне трудно найти способ доказать это неравенство
$\log(x) когда $x>1$ ($\log(x)$ — натуральный логарифм) Я могу думать о двух графиках, но не могу найти другой способ доказать это, и, кроме того, я не понимаю, почему это не должно выполняться, если $x<1$ Кто-нибудь может мне помочь? Заранее спасибо. $\endgroup$
$\begingroup$
Вы можете просто различать $$ f(x):=\log x-x, \quad x\geq1, $$ давая $$ f'(x)=\frac1x-1=\frac{1-x}x<0 \quad \text{for}\quad x>1 $$ с $$ f(1)=-1<0 $$ и $f$ строго убывает, то $$ f(x)<0, \quad x>1, $$ это $$ \log x -x <0, \quad x>1. $$
$\endgroup$
2
$\begingroup$
909х\ле \фрак{1}{1-х}$$Логарифмирование обеих частей $(4)$ дает желаемое неравенство
$$\log(1+x)\le x \tag 5$$
+1)$ в $(4)$ показывает
$$\log(1+z)\ge \frac{z}{z+1}$$
для $z>-1$. Собрав все вместе, мы имеем для $x>0$
$$\frac{x-1}{x}\le \log x\le x-1 $\endgroup$ 6
9{1}{\frac{1}{t}\,dt}\le 0 < x.
$\endgroup$
$\begingroup$
Я предполагаю, что вы знаете производную от $\log$.
Пусть $f(x)=\log x -x$. Затем $$f'(x) = \frac 1x -1<0\ \\forall x>1.$$ Более того, $f(1) = -1<0$. Итак, у вас есть функция, которая начинается с отрицательного значения при $x=1$, а затем уменьшается, поскольку ее производная всегда отрицательна. Это значит, что $$f(x) = \log(x) - x <0\ \\для всех x>1,$$ что вы хотели показать. 9x) > \log(x)$, так как $\log$ увеличивается. Следовательно, $x > \log(x)$ для $x\geq0$.
$\endgroup$
0
$\begingroup$
У вас даже есть $\;\log x \le x-1$, потому что $\log$ является вогнутой
функцией, а линия с уравнением $y=x-1$ является касательной к графику $\log$ в $(1,0)$.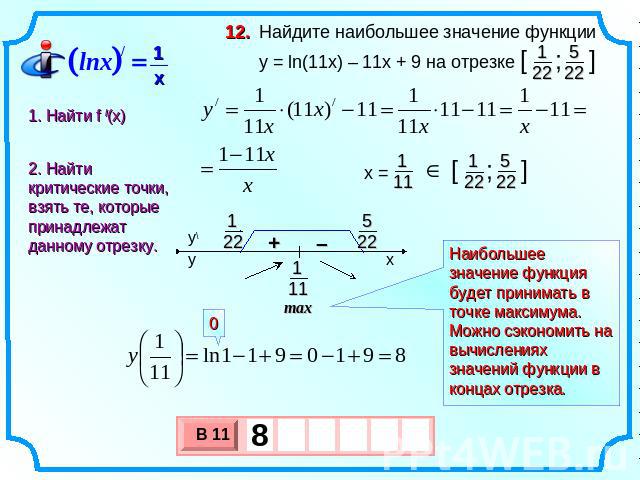
Следовательно:
$$\log x \le x-1 $\endgroup$
$\begingroup$
Определите $f(x) = \log x — x$. Теперь $f'(x) = \frac{1}{x}-1$, что отрицательно, если $x > 1$. Таким образом, $f$ строго убывает на интервале $(1, \infty)$.
Теперь, поскольку $f(1) = \log 1 — 1 = 0-1 = -1$, мы должны иметь $f(x) < -1$ на $(1, \infty)$. Таким образом, $\log x - x < -1 < 0$ на $(1, \infty)$. Отсюда следует, что $\log x < x$ при $x > 1$.
$\endgroup$
0
$\begingroup$
Когда $x=1$, $\log x=0<1=x$. Далее, для $x>1$ имеем $\frac{d}{dx}\log x=\frac{1}{x}<1=\frac{d}{dx}x$.
Это показывает, что $x$ больше $\log x$ при $x=1$ и что $x$ растет быстрее, чем $\log x$ при $x>1$. Следовательно, $x>\log x$ для $x\ge 1$.
$\endgroup$
$\begingroup$
Различные способы выполнения этого упражнения, безусловно, зависят от того, что вы хотите предположить.
+ \to \mathbb{R}$, удовлетворяющим
$$
f(xy) = f(x)+f(y) \tag{1}
$$
это немедленно дает $f(1)=0, f(x)+f(\frac1{x})=0$, поэтому $f$ является нетривиальным гомоморфизмом абелевой группы с $\exists c\dot f(c) \ne 0$ 9+$ (1) означает, что $f$ сохраняет порядок или инвертирует порядок в зависимости от знака $\log c$ и от того, $c \gt 1$. таким образом, чтобы исключить порядковые антиизоморфизмы, нам потребуется еще одно предположение, что $f((1,\infty)) \subseteq (0,\infty)$
предположим, что $f$ имеет неподвижную точку $\zeta \gt 1$. то есть точка, для которой в качестве действительных чисел $$ f(\дзета) = \дзета $$ мы покажем, что это приводит к противоречию.
поскольку $f(1)=0$ и $f$ строго монотонна и непрерывна, уравнение $f(x)=1$ имеет единственное решение, скажем, $x=e \gt 1$. 92}$, который всегда отрицателен. Это означает, что любая касательная к графику $y=\ln(x)$ будет больше или равна $\ln(x)$, причем равенство достигается только в точке касания. Тогда мы можем заключить, что касательная $x-1$ больше или равна $ln(x)$.