замена антидифференциация экспоненциальные функции логарифмические функции силовые функции
Я хочу еще немного поговорить о методе подстановки, поскольку он применяется к функциям, включающим e в x или натуральный логарифм. Но прежде всего, давайте быстро пробежимся по этим производным формулам.
Производная от e к x равна e к x, и именно здесь мы получаем интегральную формулу для e к x, верно? Все, что нам нужно сделать, это обратить это вспять. Интеграл от e к x равен e к x плюс c. И какой из них мы используем для антипроизводной? Мы всегда используем эту формулу для первообразной 1 по x, потому что областью определения этой формулы являются все действительные числа, кроме 0.
Теперь любую производную формулу можно превратить в интегральную формулу. Мы помним это. Одна из ключевых проблем с этими формулами заключается в том, что люди иногда используют их неправильно. И я хочу показать вам пример того, как это может произойти прямо сейчас. Например, интегрирование e в 3 плюс точка 4x, и это не совсем то же самое, что e в x. Но у некоторых людей может возникнуть соблазн просто сказать, ну, используя эту формулу, это будет e в 3 плюс точка 4x+c. Но я хочу показать вам, что это не так, это неправильно. Производная, вы дифференцируете ответ, вы должны получить исходную функцию, которую вы интегрировали. Таким образом, производная от этого будет такой: вы возьмете производную от е к чему угодно, и вы получите е в этой степени, е в 3 плюс 0,4x, умноженное на производную 3 плюс 0,4x, и это 0,4.
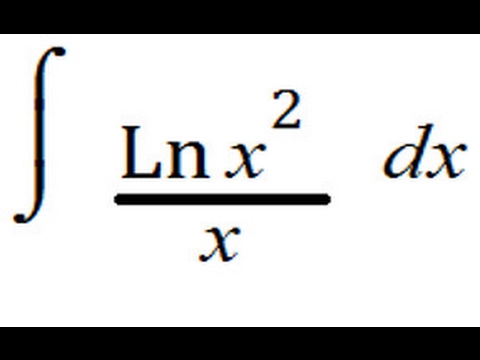Хорошо, это не то, с чего мы начали в интеграле. Так что это неправда. Итак, вы не можете просто использовать эту формулу напрямую. Здесь то же самое. Это очень похоже на ту же форму, что и 1 на x dx. У меня 1 над 2-5x dx, верно? Я могу записать это как 1 на 2-5x. И разве это не должно быть естественным логарифмом абсолютного значения 2-5x+c? Ну, ты увидишь, что это не так. Давайте продифференцируем ответ и посмотрим, получим ли мы исходную, исходную функцию снова.
Производная натурального логарифма от абсолютного значения 2-5x+c есть, ну, во-первых, производная натурального логарифма от абсолютного значения чего-то как раз из этой формулы. Верно? Это всего лишь 1 над чем-то. Но здесь нам придется использовать цепное правило. Таким образом, это 1 в 2-5 раз больше производной от 2-5x, что равно -5. А производная от +c равна 0. Хорошо. Теперь я вижу, что это не то же самое. Я начал с 1 в 2-5 раз, а закончил с 1 в 2-5 раз -5. Так что это неправильно.
Они объединяют их с помощью метода замещения. Я покажу вам это в следующих примерах.Вычислить lim x → e (ln(x)-1)/(x-e)
- Математические сомнения
- Ограничения
- Проблемы
- Логарифмические функции
$\dfrac{\log_{e}{x}-1}{x-e}$ — алгебраическая функция, в которой участвует натуральный логарифмический член. Наша задача — найти предел этой функции, когда $x$ приближается к нулю.
$\displaystyle \large \lim_{x \,\to\, e}{\normalsize \dfrac{\log_{e}{x}-1}{x-e}}$
Основные шаги для преобразования функции
Когда функция находится в логарифмической форме в пределах, вы должны учитывать свойства пределов для логарифмических функций. Давайте предпримем несколько основных шагов, чтобы преобразовать всю функцию так же, как наш стандартный результат в пределах.
Если $x \,\to\, e$, то $x-e \,\to\, 0$. Следовательно, если $x$ приближается к $e$, то $x-e$ приближается к $0$.
$ = \,\,\,$ $\displaystyle \large \lim_{x -e \,\to\, 0}{\normalsize \dfrac{\log_{e}{x}-1}{xe} }$
Теперь возьмем $x-e = u$, тогда $x = u+e$.
Теперь преобразуйте всю функцию в терминах $u$ из $x$.
$ = \,\,\,$ $\displaystyle \large \lim_{u \,\to\, 0}{\normalsize \dfrac{\log_{e}{(u+e)}-1}{ u}}$
Использовать логарифмические тождества для упрощения
Упростим выражение в числителе, используя свойства логарифмов.
$ = \,\,\,$ $\displaystyle \large \lim_{u \,\to\, 0}{\normalsize \dfrac{\log_{e}{(u+e)}-1}{ u}}$
Первый член представляет собой натуральный логарифм, а второй член представляет собой число. Если число $1$ записать в виде натурального логарифма, то члены в числителе можно объединить. Можно написать $1$ как $\ln{(e)}$ или $\log_{e}{(e)}$ в соответствии с логарифмом базового правила.
$ = \,\,\,$ $\displaystyle \large \lim_{u \,\to\, 0}{\normalsize \dfrac{\log_{e}{(u+e)}-\log_{ e}{e}}{u}}$
В числителе два натуральных логарифмических члена, и их можно объединить, используя правило частных логарифмов.
$ = \,\,\,$ $\displaystyle \large \lim_{u \,\to\, 0}{\normalsize \dfrac{\log_{e}{\Big(\dfrac{u+e} {e}\Big)}}{u}}$
Теперь продолжайте упрощать логарифмическую функцию в числителе.
$ = \,\,\,$ $\displaystyle \large \lim_{u \,\to\, 0}{\normalsize \dfrac{\log_{e}{\Big(\dfrac{u}{e }+\dfrac{e}{e}\Big)}}{u}}$
$= \,\,\,$ $\require{cancel} \displaystyle \large \lim_{u \,\to\, 0}{\normalsize \dfrac{\log_{e}{\Big(\dfrac {u}{e}+\dfrac{\cancel{e}}{\cancel{e}}\Big)}}{u}}$
$= \,\,\,$ $\displaystyle \large \ lim_{u \,\to\, 0}{\normalsize \dfrac{\log_{e}{\Big(\dfrac{u}{e}+1\Big)}}{u}}$
$= \,\,\,$ $\displaystyle \large \lim_{u \,\to\, 0}{\normalsize \dfrac{\log_{e}{\Big(1+\dfrac{u}{e}\ Big)}}{u}}$
Преобразование функции в стандартный результат
Возьмем $m = \dfrac{u}{e}$, затем $u = me$.
Если $u \,\to\, 0$, то $\dfrac{u}{e} \,\to\, \dfrac{0}{e}$. Следовательно, $\dfrac{u}{e} \,\to\, 0$, но $\dfrac{u}{e} = m$. Итак, $m\,\to\,0$. Математически получается, что если $u$ приближается к $0$, то $m$ также приближается к $0$.
Теперь преобразуйте всю предельную функцию через $m$ из $u$.
$ = \,\,\,$ $\displaystyle \large \lim_{m \,\to\, 0}{\normalsize \dfrac{\log_{e}{(1+m)}}{me} }$
Мы можем продолжить упрощение функции.