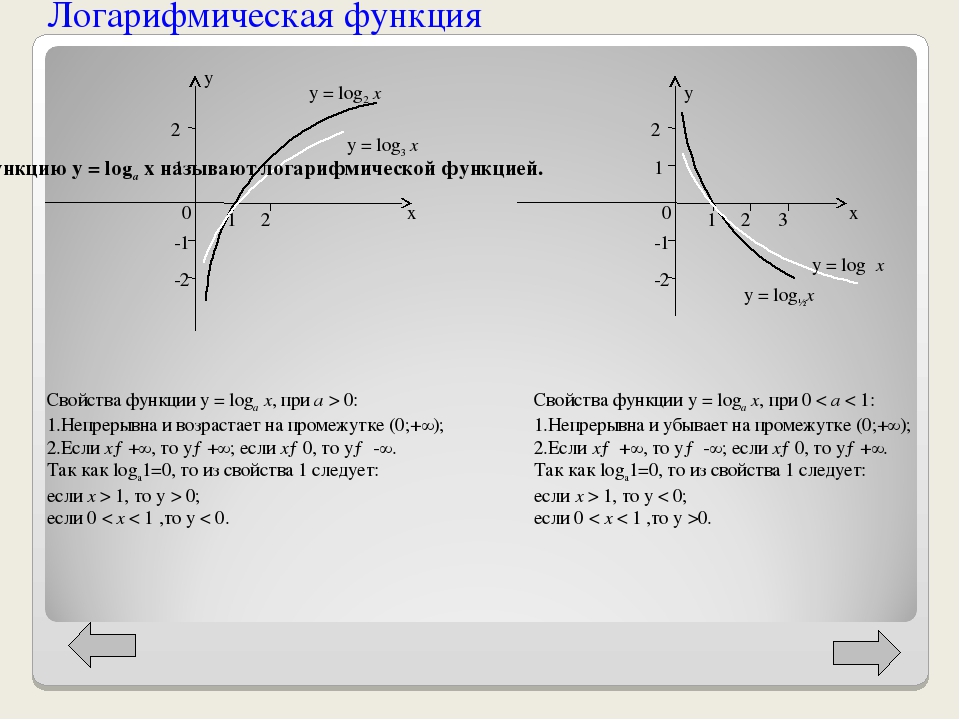
Функции и Графики — сайт по математике и не только!!! ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ Всё о Математических функциях и их графиках…
Широкое применение нашла логарифмическая функция в астрономии: Например по ней изменяется величина блеска звезд, если сравнивать характеристики блеска отмеченные глазом и с помощью приборов, то можно составить следующий график: Здесь по вертикальной оси отложим блеск звезд в единицах Гиппарха (распределение звезд по субъективным характеристикам (на глаз) на 6 групп), а на горизонтальной — показания приборов. По графику видно, что объективные и субъективные характеристики не пропорциональны, а прибор регистрирует возрастание блеска не на одну и ту же величину, а в 2,5 раза. Эта зависимость выражается логарифмической функцией.
Ещё одно применение логарифмической функции можно найти, если рассматривать логарифмическую спираль.
Спираль, по определению — это плоская линия, образованная движущейся точкой, которая удаляется по определенному закону от начала луча, равномерно вращающегося вокруг своего начала.
Например, подобно оценки блеска звезд в предыдущем пункте, оценивается громкость шума. Единицей громкости служит «бел», практически его десятая доля – децибел. Последовательные степени громкости 1 бел, 2 бела и т.д. – составляют для нашего слуха арифметическую прогрессию. Физическая сила этих шумов составляет геометрическую прогрессию со знаменателем 10. Разности громкости в 1 бел соответствует отношение силы шумов 10. Это значит, что выраженная в белах громкость шума, равна десятичному логарифму его физической силы.
Заметим, что в физике, при проведении научных, экспериментальных расчетов показательная, логарифмическая функции, экспонента и логарифмы применяются очень широко, но как правило не как описание отдельного процесса или комплекса процессов, а входят в состав сложных уравнений и систем уравнений и формул, описывающих данный процесс.
Также широкое применение нашла логарифмическая функция и 
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
09.22Другие ответы
| ||||||||||||
09.22
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Постройте график равномерного прямолинейного движения: v=5м/с и x0=2м
решите уравнение: (1/81)^cosx=9^(2sin2x) на отрезке [-2П;-П/2]
На окружности с центром в точке О по порядку отмечены 4 точки: D, H, L, P.
Найди вторую сторону получившегося четырехугольника, если угол D=90
-4корень3cos(-750градусов)
Решено
в шкафу есть 3 вертикальных ряда по4 ящикав каждом в один из ящиков в каждом ряду спрятали по одной монете.какова вероятность того что выдвинув случайным образом по одному ящику в каждом ряду можно
Пользуйтесь нашим приложением
Исследование логарифмических функций
Исследование логарифмических функций
Назначение 1
Исследование логарифмических функций
на
Кейтлин Спунер
Examine Graphing Calculator 3,5 графика
у = ln х
у = лог х
Вычислите ln e и log 10.
Также рассмотрите различные значения a и b для
у = а (ln х)
у = пер (бх)
у = а (лог х)
г = логарифм (bx)
Что такое логарифмическая функция? Как выглядит его график? О логарифмической функции говорят как о «логарифме х по основанию а». Логарифмическая функция является обратной экспоненциальной функции, поэтому можно также думать о логарифмах, используя экспоненциальную форму. это та же операция, что и мышление «а в степени у равно х». Функция десятичного логарифма, записанная как y = log x, имеет подразумеваемое основание 10. Функция натурального логарифма имеет вид y = ln x. Она равна логарифмической функции с основанием e, . Это можно представить как «е в степени у равно х».
Здесь у нас есть основные графики y = log x и y = ln x. Логарифмическая функция выделена синим цветом, а натуральная логарифмическая функция — красным.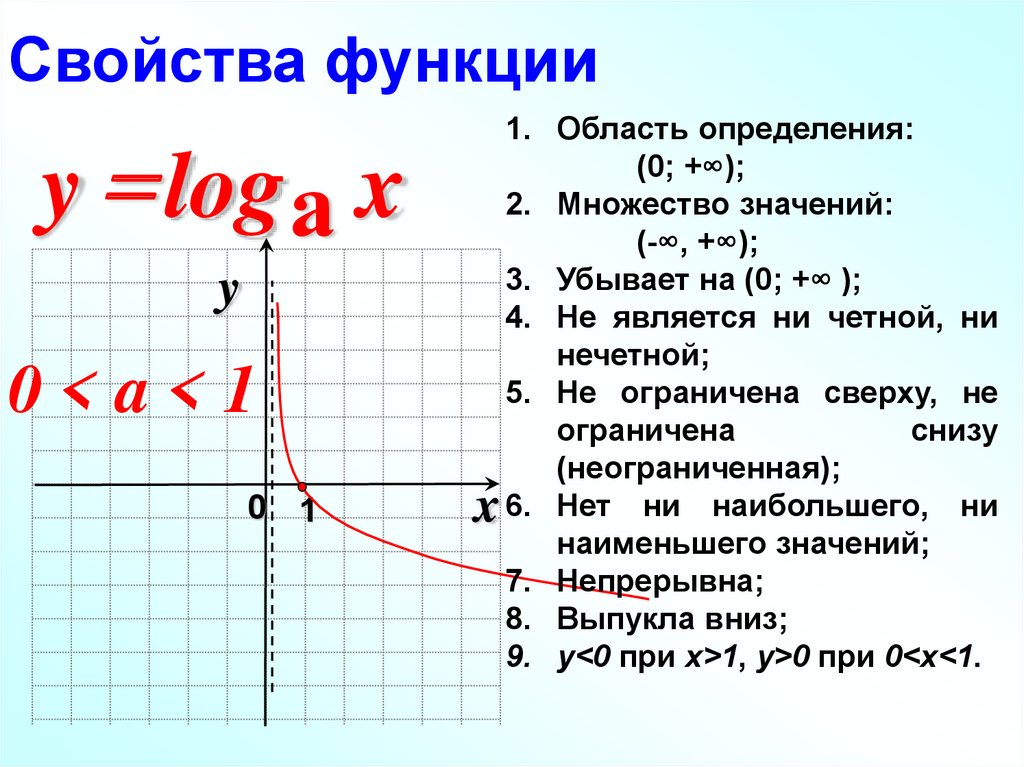
Оба графика очень похожи. У каждого есть домен всех действительных чисел больше 0, и у каждого есть диапазон всех действительных чисел. Мы видим асимптоту при x = 0, так как любое число, возведенное в очень маленькую степень, будет приближаться к 0, но на самом деле никогда не достигнет этого значения. График y = log x приближается к этой асимптоте быстрее, чем график y = ln x. Почему это происходит? Это связано с тем, что основание 10 в y = log x больше, чем e, основание y = ln x, что составляет около 2,7. Кроме того, обе функции увеличиваются во всей области их применения. График y = log x увеличивается медленнее, чем график y = ln x, поскольку основание числа 10 больше основания числа e. У каждого есть точка пересечения с точкой x = 1, и графики пересекаются в этой точке. Алгебраически любое число a, возведенное в нулевую степень, будет равно 1, поэтому логарифм любого числа при y = 0 равен единице.
Из этого анализа можно сделать вывод, что по мере увеличения основания логарифмической функции график быстрее приближается к асимптоте x = 0.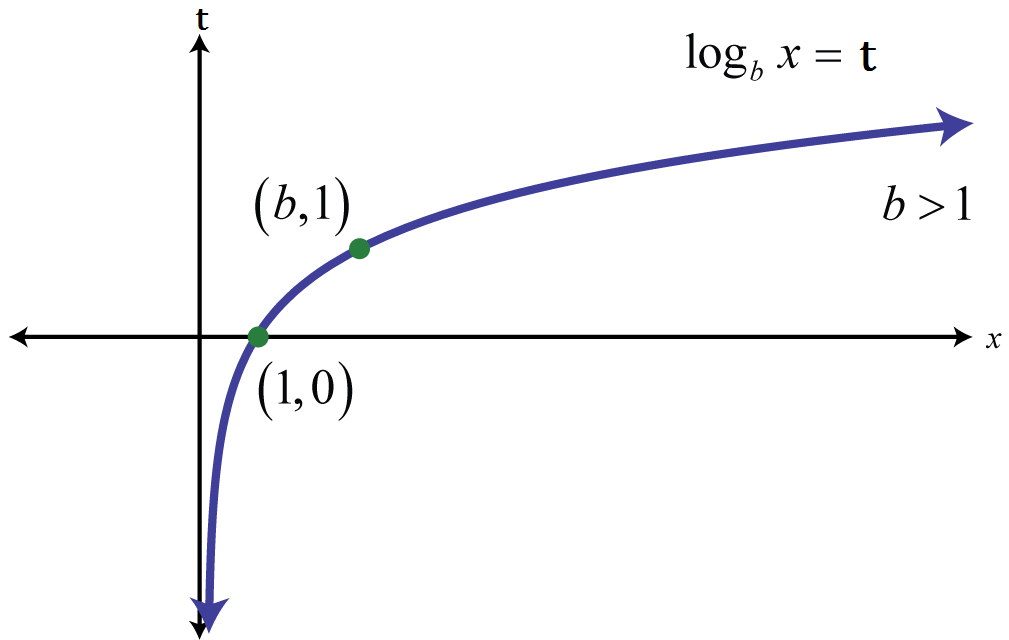
Кроме того, функция может увеличиваться медленнее по мере увеличения основания. Также можно предположить, что до тех пор, пока график не будет смещен, точка пересечения с х будет находиться в точке х = 1, а асимптота будет на линии х = 0. Продолжая это исследование, мы будем исследовать эти идеи.
Прежде чем продолжить, оценим пару значений логарифмических функций: log 10 и ln e. Во-первых, поскольку подразумеваемое основание десятичного логарифма равно 10, y = log 10 эквивалентно . Любое число в первой степени равно самому себе, поэтому y = 1. Как показано на графике y = log x выше, есть точка в (10,1), которая отражает этот результат. Далее у нас есть значение ln e. Как обсуждалось ранее, ln e = e, поэтому ln e эквивалентно . Еще раз, поскольку любое число в первой степени равно самому себе, y = 1. Следовательно, мы можем предположить, что в любом логарифме y = 1, если основание a и значение x равны.
Теперь, когда мы обсудили основные идеи графиков y = log x и y = ln x, мы рассмотрим возможность использования различных значений для изменения графиков.
Сначала мы рассмотрим y = a (log x). Как меняется график при изменении? Здесь мы видим, что по мере увеличения график y = a (log x) растет быстрее. Значения y увеличиваются с большей скоростью, поскольку каждое увеличение a умножает функцию log x на большее число. С этой большей скоростью увеличения, чем больше a, тем медленнее кажется, что график приближается к своей асимптоте при x = 0. Наконец, каждый из этих графиков имеет точку пересечения x в точке x = 1. Почему это так? Помните, что мы можем думать о логарифме, используя показатели степени, и любое число (здесь по основанию 10) в степени 0 (y = 0 на пересечении x) равно 1. Следовательно, когда y равно 0, x равно 1.
Что делать, если a — отрицательное число? Логарифмическая функция может выглядеть как график ниже. Отрицательное значение перед функцией отражает функцию по оси x, но все остальные свойства логарифмической функции сохраняются. Здесь с уменьшением а величина а увеличивается.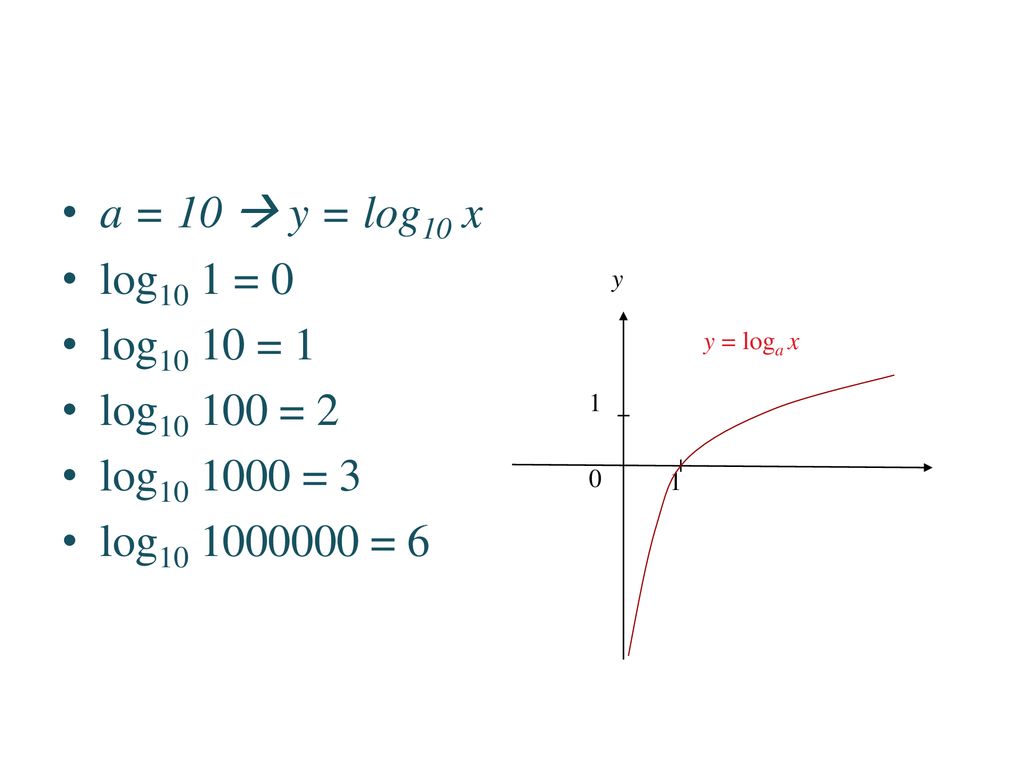
Когда это происходит, график уменьшается с большей скоростью по мере увеличения x.
Что, если мы умножим x на некоторое значение в y = log x? Здесь мы рассмотрим функцию y = log(bx). Кажется, что все графики увеличиваются с одинаковой скоростью, поэтому b по-разному влияет на график по сравнению с a на графиках выше. Кажется, что буква b перед x сдвигает график вверх, поэтому точка пересечения с x не равна 1, и возможно, что графики приближаются к асимптоте с одинаковой скоростью. Несмотря на то, что кажется, что графики растут с одинаковой скоростью, на самом деле это не так. Когда величина b больше 1, на графике происходит горизонтальное сжатие. Вот почему графики кажутся движущимися вверх. Если величина b меньше единицы, имеет место горизонтальное растяжение.
Что, если b отрицательно в уравнении y = log(bx)? Значение b имеет тот же эффект, что и выше, за исключением того, что отрицательное значение отражает график по оси Y.
Далее мы рассмотрим влияние a и b на y = ln x. Каковы ваши прогнозы относительно различий графиков y = a (ln x) и y = ln (bx) по сравнению с графиком y = ln x? Чем они будут похожи или отличаться от графиков y = a (log x) и y = log (bx) соответственно? Сначала мы рассмотрим y = a (ln x). В наших уравнениях а представлено как n, а n находится в диапазоне от -5 до 5. Влияние а на y = ln x кажется таким же, как и на y = log x. Когда a отрицательно, график отражается по оси x. По мере увеличения величины а график уменьшается с большей скоростью, если а отрицательно, или увеличивается с большей скоростью, если а положительно.
Наконец, мы рассмотрим y = ln(bx). В уравнениях b представлен как n, а n находится в диапазоне от -10 до 10. Влияние b на y = ln x аналогично влиянию b на y = log (bx). Когда b отрицательно, график отражается по оси Y.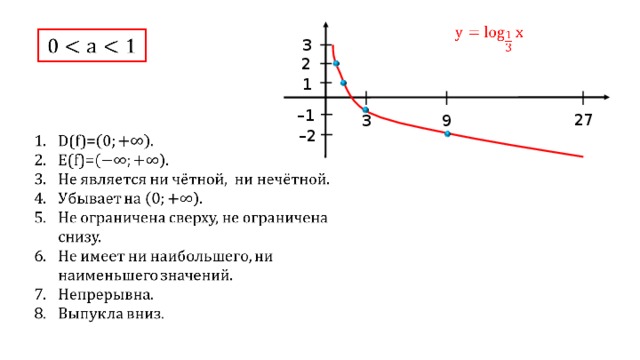
По мере увеличения величины b график, кажется, растет и увеличивается с несколько большей скоростью. Когда график y = ln (bx) имеет большее значение y, чем y = ln x, график имеет горизонтальное сжатие. Если значения y для y = ln (bx) меньше, чем для y = ln x, имеет место горизонтальное растяжение.
Вернуться на домашнюю страницу Кейтлин Спунер
7.4: Графики и свойства логарифмических функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 40182
- Рупиндер Секон и Роберта Блум
- Колледж Де Анза
Цели обучения
В этом разделе вы научитесь:
- Изучать свойства логарифмических функций.
- Изучите графики логарифмических функций.
- Изучите соотношение между графиками экспоненциальной и логарифмической функций.
Предварительные навыки 9x\) создает эту таблицу значений
\(х\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
\(f(x)\) | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 |
Поскольку логарифмическая функция является обратной экспоненциальной, \(g(x)=\log_{2}(x)\) дает таблицу значений
\(х\) | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 |
\(г(х)\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Во второй таблице обратите внимание, что
- По мере увеличения входа увеличивается выход.
- По мере увеличения ввода выход увеличивается медленнее.
- Поскольку экспоненциальная функция выводит только положительные значения, логарифм может принимать только положительные значения в качестве входных данных, поэтому область определения функции журнала равна \((0, \infty)\).
- Поскольку экспоненциальная функция может принимать все действительные числа в качестве входных данных, логарифм может иметь любое действительное число в качестве выходного, поэтому диапазоном являются все действительные числа или \((-\infty, \infty)\).
Построив график \(g(x) = \log_{2}(x)\) по точкам в таблице, обратите внимание, что по мере того, как входные значения для \(x\) приближаются к нулю, выход функции растет очень большой в отрицательном направлении, что указывает на вертикальную асимптоту в точке \(x = 0\). 9{+}, г \стрелка вправо-\infty\)
Однако, если основание \(b\) меньше 1, 0 < \(b\) < 1, тогда график выглядит следующим образом.
Это следует из логарифмического свойства взаимных оснований: \(\log _{1 / b} C=-\log _{b}(C)\)
- 9{+}, г \стрелка вправо \infty\)
- График убывающий, если 0 < \(b\) < 1
- Область определения функции: \(x\) > 0 или (0, \(\infty\))
- Диапазон функции — все действительные числа или \((-\infty, \infty)\)
При построении графика логарифмической функции в виде \(f(x) = \log_{b}(x)\) полезно помнить, что график будет проходить через точки (1, 0) и (\ (б\), 1).
Пример \(\PageIndex{1}\)
Нарисуйте каждую из следующих функций, изобразив вертикальную асимптоту, точку пересечения и точку (\(b\), 1).
- \(f(x) = \log_{2}(x)\)
- \(г(х) = \log_{5}(х)\)
- \(ч(х) = \лог(х)\)
- \(j(x) = \ln(x)\)
Решение
Все логарифмические графики в форме \(f(x) = \log_{b}(x)\) будут иметь вертикальную асимптоту на оси y и точку пересечения x на (1, 0).
x}\), with \(\bf{b>0}\)» valign=»top»>
(0,1)
(1,0)
Асимптоты 9{+}, \: у \стрелка вправо-\infty\)
Источник: материалы этого раздела учебника получены от Дэвида Липпмана и Мелони Расмуссен, Книжный магазин Open Text, Precalculus: An Investigation of Functions, «Глава 4: Экспоненциальные и логарифмические функции», лицензия Creative Commons CC BY — Лицензия SA 3.0. Материал здесь основан на материале, содержащемся в этом учебнике, но был изменен Робертой Блум, как разрешено этой лицензией.
Эта страница под названием 7.4: Графики и свойства логарифмических функций распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.