Онлайн уравнение плоскости по трем точкам: Онлайн калькулятор. Уравнение плоскости

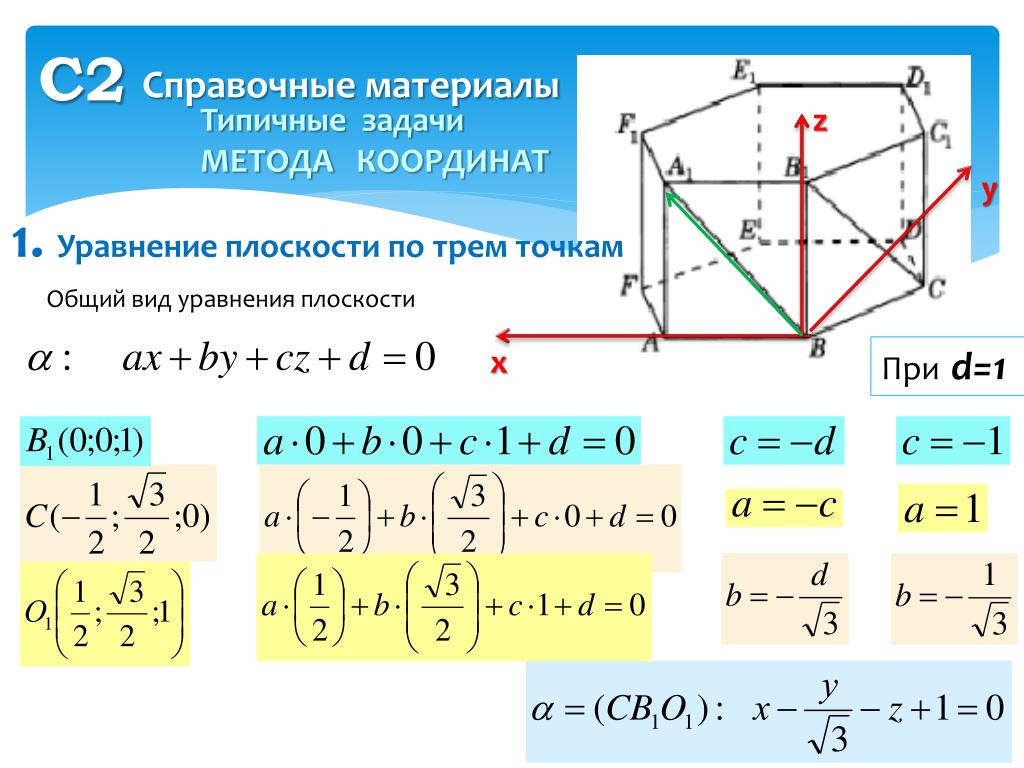
Составить уравнение плоскости онлайн

Пример решили: 22797 раз Сегодня решили: 0 раз

Введите координаты точек

x₁ y₁ z₁
x₂ y₂ z₂
x₃ y₃ z₃

Составление уравнения плоскости

Скачать решение в PDF

Порекомендуйте наш сервис друзьям

Вконтакте

Facebook

Twitter

Одноклассники

Google+

Данный онлайн-сервис поможет составить уравнение плоскости по трем координатам.

Между всеми плоскостями и линейными уравнениями первого порядка с координатами (x,y,z) существуют взаимно-однозначные соответствия: каждая плоскость описывается определённым уравнением и наоборот, каждое уравнение описывает плоскость, притом только одну.

Координаты трех точек, не лежащих на одной прямой:

$$ (x_1, \: y_1, \: z_1) \quad (x_2, \: y_2, \: z_2) \quad (x_3, \: y_3, \: z_3)$$

Изображение плоскости, построенной по трем заданным точкам:

Составим систему уравнений для плоскости, проходящей через три заданные точки:

$$ \begin{cases} A \cdot (x-x_1)+B \cdot (y-y_1)+C \cdot (z-z_1)=0 \\ A \cdot (x-x_2)+B \cdot (y-y_2)+C \cdot (z-z_2)=0 \\ A \cdot (x-x_3)+B \cdot (y-y_3)+C \cdot (z-z_3)=0 \end{cases} $$

В этой системе произвольная точка (x, y, z) удовлетворяет уравнению плоскости.
Определитель этой системы равен нулю:

$$ \begin{vmatrix} x-x_1 & x-x_2 & x-x_3 \\ y-y_1 & y-y_2 & y-y_3 \\ z-z_1 & z-z_2 & z-z_3 \end{vmatrix} = 0$$

Примеры решений

1. Дано три точки с координатами M(1;-2;0), K(2;0;-1), N(0;-1;2). Составьте уравнение плоскости, проходящей через эти точки.
   
   Посмотреть решение

   Решение:

   Общий вид уравнения плоскости A·x+B·y+C·z+D=0, чтобы его составить, необходимо найти коэффициенты A, B, C, D.

   Составим определитель, который поможет их найти:
   $$ \begin{pmatrix} x-x1 && x-x2 && x-x3 \\ y-y1 && y-y2 && y-y3 \\ z-z1 && z-z2 && z-z3 \end{pmatrix} = 0 $$

   Учитывая, что x1, x2, x3, y1, y2, y3, z1, z2, z3 – координаты точек M, K, N, подставим:

   $$ \begin{pmatrix} x-1 && x-2 && x-0 \\ y+2 && y-0 && y+1 \\ z-0 && z+1 && z-2 \end{pmatrix} = 0$$

   Решая определитель, получим: 5x-y+3z+7=0.

   Ответ:

   $$ 5x-y+3z+7=0 $$

2. Сторона основания правильной четырехугольной призмы ABCDA1B1C1D1 – квадрат со стороной 12 см. Ее высота равна 21 см. Точка М делит ребро АА1 так, что А1М= 13 см. Точка К делит ребро ВВ1 так что В1К=8 см. Составьте уравнение плоскости D1МК.
   Посмотреть решение

   Решение:

   Поместим призму в систему координат таким образом, чтобы ее начало находилось в точке А1. Тогда координаты точек, определяющих положение плоскости в пространстве, будут:

   $$ D_1(0;12;0) $$

   $$ M(0;0;13) $$

   $$ K(12;0;8) $$

   Составим определитель, позволяющий найти уравнение плоскости:

   $$ \begin{pmatrix} x-0 && x-12 && x-0 \\ y-12 && y-0 && y-13 \\ z-0 && z-0 && z-8 \end{pmatrix} = 0$$

   Расчет определителя дает результат:

   $$ 5x+13y+12z-156=0 $$ — это и есть уравнение плоскости.

   Ответ:

   $$ 5x+13y+12z-156=0 $$

Попробуйте другие сервисы

• Нахождение расстояния между двумя точками

• Составление уравнения прямой

• Нахождение расстояния от точки до плоскости

Уравнение прямой по двум точкам

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

• каноническое уравнение,
• параметрическое уравнение,
• общее уравнение прямой,
• уравнение прямой с угловым коэффициентом,
• уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Каноническое уравнение прямой на плоскости

{\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a}}

x_a и y_a — координаты первой точки A,

x_b и y_b — координаты второй точки B

Параметрическое уравнение прямой на плоскости

{\begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \end{cases}}

x_a, y_a — координаты точки, лежащей на прямой,

{l;m}

— координаты направляющего вектора прямой,

t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Каноническое уравнение прямой в пространстве

{\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a} = \dfrac{z-z_a}{z_b-z_a}}

x_a, y_a и z_a — координаты первой точки A,

x_b, y_b и z_b — координаты второй точки B

Параметрическое уравнение прямой в пространстве

{ \begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \\ z=n \cdot t + z_a \end{cases} }

x_a, y_a и z_a — координаты точки, лежащей на прямой,

{l;m;n} — координаты направляющего вектора прямой,

t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Пример нахождения уравнения прямой, проходящей через две точки

Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).

Каноническое уравнение прямой

Каноническое уравнение прямой, проходящей через две точки имеет вид {\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a}}

Подставим в формулу координаты точек A и B: {\dfrac{x-1}{3-1} = \dfrac{y-2}{8-2}}

Получаем каноническое уравнение прямой: {\dfrac{x-1}{2} = \dfrac{y-2}{4}}

Уравнение прямой с угловым коэффициентом

Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}

Параметрическое уравнение прямой

Параметрическое уравнение прямой имеет вид:

{ \begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \end{cases} }

где {x_a, y_b} — координаты точки, лежащей на прямой, {\{l;m\}} — координаты направляющего вектора прямой, t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.

Найдем координаты направляющего вектора:

\overline{AB} = \{x_b — x_a; y_b — y_a\} = \{3-1; 8-2\} = \{2; 6\}

Получаем параметрическое уравнение:

\begin{cases} x=2 t + 1 \\ y=6 t + 2 \end{cases}

Используем калькулятор для проверки полученного ответа.

linear алгебра — Общее уравнение плоскости через $3$ точек.

спросил 7 лет, 5 месяцев назад

Изменено 5 лет, 2 месяца назад

Просмотрено 7к раз

$\begingroup$

Найдите общее уравнение плоскости через точки $A(1,1,0),\, B (1,0,1),$ и $C(0,1,2)$.

Как это делается?

• линейная алгебра
• алгебра-предварительное исчисление
• геометрия
• 3d

$\endgroup$

3

$\begingroup$

Пусть общее уравнение плоскости $ax+by+cz+d = 0\;,$ Тогда уравнение плоскости проходит через точку $A(1,1,0)$, то есть $$a (x-1)+b(y-1)+c(z-0) = 0\tag1$$

Плоскость также проходит через $B(1,0,1)\;,$, поэтому положим $x =1,y=0,z=1\;,$ и получаем

$$a(1-1)+b(0-1)+c(1-0) = 0\tag2$$

Теперь плоскость также проходит через $C(0,1,2)\;, $ поэтому мы кладем $x=0,y=1,z=2\;\bf{in \; (1)\;,}$ и мы также получаем

$$a(0-1)+b(1-1)+c(2-0) = 0\tag3$$

Теперь исключаем $a,b $ и $c$ из этих $3$ уравнений получаем уравнение плоскости.

---

Мы также можем исключить $a,b$ и $c$ как

$$\displaystyle \begin{vmatrix} х-1 и у-1 и г\\ 0&-1&1\\ -1 и 0 и 2 \end{vmatrix}=0\Стрелка вправо -1\влево(y-1+z\вправо)+2(-x+1) = 0\Стрелка вправо 2x+y+z = 3$$

$\endgroup$

$\begingroup$

Уравнение плоскости при заданных $3$ точках можно найти как $B-A=(1,0,1)-(1,1,0)=(0,-1,1)$ и $C-A=(0, 1,2)-(1,1,0)=(-1,0,2)$. Теперь вы найдете векторное произведение $$(B-A)\times(C-A)=\begin{bmatrix}i & j & k \\0 & -1 & 1 \\-1 & 0 & 2 \end{bmatrix} =(-2,-1,-1)= \vec{n}$$ $i$, $j$ и $k$ — единичные векторы, направленные вдоль осей $x$, $y$ и $z$ соответственно. $\vec{n}$ известен как вектор нормали $\vec{n}$ и перпендикулярен уравнению плоскости. Теперь используйте общее векторное уравнение плоскости: $$\vec{r}\cdot\vec{n}=\vec{a}\cdot\vec{n}$$, где $\vec{r}$ — позиция вектор относительно начала координат любой точки $(x,y,z)$ на плоскости, а $\vec{a}$ — известная точка, лежащая на плоскости. Таким образом, используя $\vec{a}=A$, мы получаем $$(x,y,z)\cdot(-2,-1,-1)=(1,1,0)\cdot(-2,-1 ,-1)=-2-1+0=-3$$ В декартовых координатах это $$-2x-y-z=-3=\color{blue}{2x+y+z=3}$$ как уравнение самолета.

$\endgroup$

0

$\begingroup$

Общее уравнение для плоскости $ax+by+cz=k$

Подставьте значения для точек A, B и C, и вы получите линейную систему из трех уравнений, которую вы можете решить. Один из способов сделать это — представить систему матрицей и использовать исключение Гаусса.

Обратите внимание, что есть 4 неизвестных, поэтому нет единого решения для a, b и c, поскольку вы можете просто умножить уравнение на некоторую константу, и оно останется тем же, поэтому вы просто находите отношение a к b к c .

Также, если нет единственного решения, то есть набор решений (условиям могут удовлетворять несколько плоскостей).

$\endgroup$

4

Уравнение плоскости, проходящей через 3 точки, не лежащие на одной прямой

Плоскость представляет собой гладкую двумерную поверхность, простирающуюся бесконечно далеко. Плоскость — это двухмерное представление точки (нулевое измерение), линии (одно измерение) и трехмерного объекта. Плоскость в трехмерном пространстве имеет уравнение ax + by + cz + d = 0, где хотя бы один из коэффициентов a, b или c должен быть отличен от нуля.

Вектор — это физическая величина, для которой определены как направление, так и величина. Вектор положения в основном определяет положение конкретной точки в трехмерной декартовой системе плоскостей относительно исходной точки. Рассмотрим линию на плоскости. Эта линия имеет длину и стрелку. Здесь длина — это величина, а стрелка указывает направление. Следовательно, на плоскости линия является вектором.

Плоскости, перпендикулярные векторам и точкам

Однако для одной конкретной точки вектора существует только одна уникальная плоскость, которая проходит через нее и также перпендикулярна вектору. Вектор можно рассматривать как набор точек. Итак, для конкретного вектора существует бесконечное количество плоскостей, перпендикулярных ему.

Векторное уравнение для следующего изображения записывается так: (\[\overrightarrow{r}\] — \[\overrightarrow{r}_{0}\]). \[\overrightarrow{N}\] = 0, где \[\overrightarrow{r}\] и \[\overrightarrow{r}_{0}\] представляют векторы положения. Для этой плоскости декартово уравнение записывается как:  

\[A (x — x_{1}) + B (y — y_{1}) + C (z — z_{1}) = 0\], где A, B и C — отношения направлений.

Уравнение плоскости, проходящей через 3 точки, не лежащие на одной прямой

\[P(x_{1},y_{1},z_{1}),~Q(x_{2},y_{2},z_{2 }),~и~R(x_{3},y_{3},z_{3})\] — три неколлинеарные точки на плоскости.

Мы знаем, что: ax + by + cz + d = 0 —————(i)

Подставляя значения точек P, Q и R в уравнение (i), мы получаем следующее:

\[a(x_{1}) + b(y_{1}) + c(z_{1}) + d = 0\]

\[a(x_{2}) + b(y_{2} }) + c(z_{2}) + d = 0\]

\[a(x_{3}) + b(y_{3}) + c(z_{3}) + d = 0\]

Предположим, P = (1,0,2), Q = (2,1,1) и R = (−1,2,1)

Тогда, подставляя значения в приведенные выше уравнения, мы получаем следующее:

a(1) + b(0) + c(2) + d = 0

a(2) + b(1) + c(1) + d = 0

a(-1) + b(2) + c(1) + d = 0

Решение этих уравнений дает нам b = 3а, с = 4а и d = (-9)а. ———————(ii)

Подставив значения из (ii) в (i), мы получим следующее:

ax + by + cz + d = 0

ax + 3ay + 4az−9a

x + 3y + 4z−9

Следовательно, уравнение плоскости с тремя неколлинеарными точками P, Q и R равно x + 3y + 4z−9.

Решенные примеры

Пример 1: A (3,1,2), B (6,1,2) и C (0,2,0) — три неколлинеарные точки на плоскости. Найдите уравнение плоскости.

Решение:

Мы знаем, что: ax + by + cz + d = 0 —————(i)

Подставляя значения точек A, B и C в уравнение (i), мы получаем следующее:

a(3) + b(1) + c(2) + d = 0

a(6) + b(1) + c(2) + d = 0

a(0) + b(2) + c(0) + d = 0

Решение этих уравнений дает нам a = 0,

c =12

b, d = —2b ———————(ii)

Подставив значения из (ii) в (i), мы получим следующее:

ax + by + cz + d = 0

0x + (—by) +12bz — 2b = 0

x — y +12z —2 = 0

2x-2y + z-4 = 0

Следовательно, уравнение плоскости с тремя неколлинеарных точек A, B и C составляет

2x-2y + z-4 = 0. 

Пример 2: S (0,0,2), U (1, 0, 1) и V (3 , 1,1) — три неколлинеарные точки на плоскости.