Определители — презентация онлайн
ЛЕКЦИЯ
ТЕМА:
«ОПРЕДЕЛИТЕЛИ»
1
ПЛАН
1.
2.
3.
4.
5.
6.
Определение, порядок определителя
Миноры и алгебраические
дополнения
Свойства определителей
Вычисление определителей: итоги
Понятие обратной матрицы.
Алгоритм построения (нахождения)
обратной матрицы
Матричные выражения и матричные
уравнения
2
ИЗ ИСТОРИИ НАУКИ
Швейцарский математик Крамер (G. Cramer,
1704–1752) заложил основы теории определителей,
хотя и не предложил для них удобного
обозначения (это сделал в 1841 году А. Кэли).
В 1772 году Вандермонд (A.T. Vandermonde,
1735–1796) опубликовал обширное исследование
определителей, один из которых носит теперь его
имя.
Систематическое изложение этой теории
принадлежит Бине (J.F.M. Binet, 1786–1856) и
Коши (A.L. Cauchy, 1789–1857). Их труды по
теории определителей относятся к периоду 1812–
1815гг.
3
Габриэль Крамер
Gabriel Cramer
1704–1752
Швейцарский
математик, ученик
и друг Иоганна
Бернулли,
один из
создателей
линейной
алгебры.
4
Определитель (или детерминант) — одно из
основных понятий линейной алгебры
Это многочлен, комбинирующий элементы
квадратной матрицы таким образом, что его
значение сохраняется при транспонировании и
линейных комбинациях строк или столбцов.
ОПРЕДЕЛИТЕЛЬ ХАРАКТЕРИЗУЕТ
СОДЕРЖАНИЕ МАТРИЦЫ.
В частности, если в матрице есть линейнозависимые строки или столбцы, то определитель
равен нулю.
Определитель играет ключевую роль в решении в
общем виде систем линейных уравнений, на его
основе вводятся базовые понятия.
5
СПЕЦИАЛЬНЫЕ ВИДЫ
ОПРЕДЕЛИТЕЛЕЙ
Определитель
Вронского
(Вронскиан)
Определитель Вандермонда
Определитель Грама
Определитель Якоби (Якобиан)
Циркулянт
6
1. ОПРЕДЕЛЕНИЕ. ПОРЯДОК ОПРЕДЕЛИТЕЛЯ
Определение.
ОПРЕДЕЛИТЕЛЬ
(детерминант) n-го порядка,
составленный из элементов квадратной
матрицы (n*n) есть алгебраическая
сумма n! («эн факториал») слагаемых
или число, которое находится по
определённым правилам.
Замечание.
Квадратная матрица,
определитель которой равен нулю,
называется вырожденной (или
особенной)
7
Для обозначения определителя квадратной
матрицы используется символ:
a11 a12 … a1n
a 21 a 22 … a 2 n
A
det A
. . . .
a a … a
nn
n1 n 2
a11 a12 … a1n
a 21 a 22 … a 2 n
.
.
. .
a n1 a n 2 … a nn
т.е. элементы матрицы заключаются в прямые
вертикальные чёрточки.
Определитель матрицы А также может
обозначаться как: det(A), |А| или Δ(A).
Этот символ был введён в 19 веке английским
математиком Кэли
8
Определители второго порядка.
Определение: Определителем или
детерминантом второго порядка называется
ЧИСЛО
a11 a12
a21 a22
a11a22 a12 a21
Числа (элементы определителя)
образуют главную диагональ,
элементы определителя
побочную диагональ.
a
12
и
a
11
a21
и
a22
образуют
9
Правило: Чтобы вычислить определитель
второго порядка, надо из произведения
элементов главной диагонали вычесть
произведения элементов побочной диагонали.
Пример: Вычислить определитель
8 5
3 2
8 2 5 3 1
10
Определители третьего порядка.
Определение: Определителем или
детерминантом третьего порядка называется
ЧИСЛО
a11 a12 a13
a21 a22 a23
a31 a32 a33
a11a22a33 a12a23a31 a13a21a32 a13a22a31 a12a21a33 a11a23a32
11
ЗАМЕЧАНИЯ
1) Чтобы запомнить, какие произведения в правой
части равенства берутся со знаком «+», а какие со
знаком «-», полезно использовать следующее
правило треугольников:
12
2) Второй способ вычисления определителя
фактически совпадает с первым и
называется способом Саррюса
Суть его состоит в том, что справа от определителя
приписывают первый и второй столбец и
произведения элементов на главной диагонали и на
диагоналях, ей параллельных, берут со знаком
«плюс»,
а произведения элементов побочной диагонали и
диагоналей, ей параллельных, со знаком «минус»
13
a11 a12 a13 a11
a21 a22 a23 a21
a31 a32 a33 a31
a12
a22
a32
a11a22 a33 a12 a23a31 a13a21a32 a13a22 a31 a12 a21a33 a11a23a32
3) Определитель 4-го порядка есть алгебраическая
сумма 4!=4*3*2*1=24 слагаемых!
Как вычисляются определители, имеющие порядок
выше 3-го?
УДОБНЫМ И ЭФФЕКТИВНЫМ способом
вычисления определителей и третьего и более
высокого порядков является метод
РАЗЛОЖЕНИЯ ОПРЕДЕЛИТЕЛЯ ПО СТРОКЕ
ИЛИ СТОЛБЦУ
14
1
Пример. Вычислить определитель 4
Вычислить определитель 4
7
2 3
0
6
8
9
с помощью правила (способа)Саррюса.
Решение
1
4
7
2 3 1
2
0
6 4
0
8
9 7
8
1 0 9 ( 2) 6 ( 7) 3 4 8 3 0 ( 7) 1 6 8 ( 2) 4 9 204
15
2. МИНОРЫ И
АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
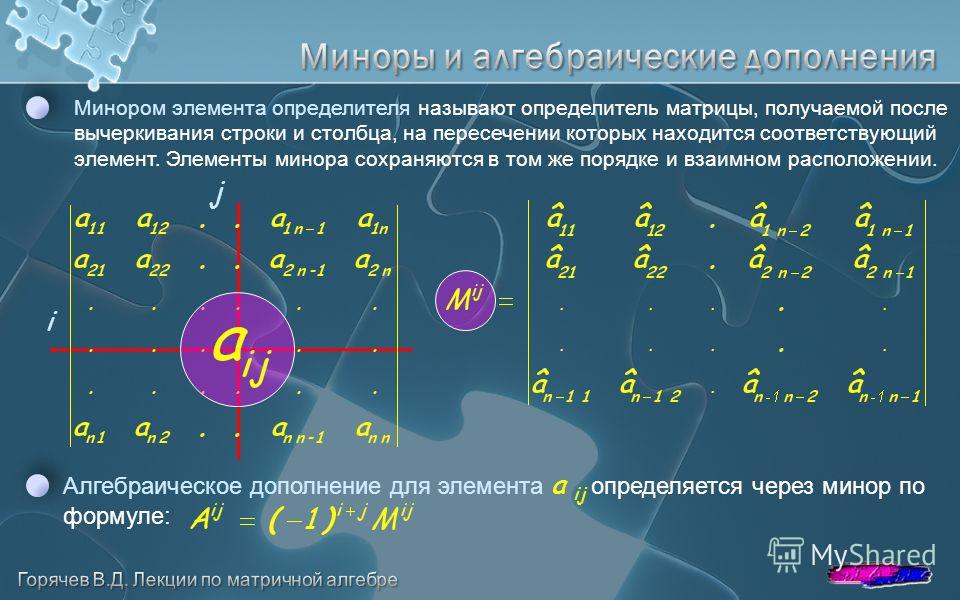
Определение: Минором M ij некоторого
элемента a ij называется определитель, который
получается из данного определителя
вычеркиванием i-ой строки и j -ого столбца, на
пересечении которых расположен этот элемент.
Пример.
1) Составить миноры M11 и M 23 определителя 3-го
порядка
a11 a12 a13
a21 a22 a23
a31 a32 a33
16
Минор элемента a11 есть ОПРЕДЕЛИТЕЛЬ 2-ГО
ПОРЯДКА, который получается путём
зачёркивания 1-й строки и 1-го столбца исходного
ОПРЕДЕЛИТЕЛЯ 3-ГО ПОРЯДКА
a11 a12 a13
a22
a21 a22 a23 M
11
a32
a31 a32 a33
a23
a33
a22a33 a23a32
Аналогично находим минор элемента
a11 a12 a13
a11
a21 a22 a23 M 23
a31
a31 a32 a33
a12
a32
a23
a11a32 a12 a31
17
2) Вычислить миноры M11 и M 23 определителя
1
3
4
0
2
1
2
3 4
Решение
M 11
1
2
3 4
M 23
1 ( 4) ( 3)( 2) 10
1
0
4
3
( 1) ( 3) 0 4 3
18
Определение: Алгебраическим дополнением Aij
какого-либо элемента a ij определителя есть
минор M ij этого элемента, взятый со знаком ( 1) i j :
Aij ( 1)
i j
M ij
Пример. Для приведенного выше определителя 3-го
Для приведенного выше определителя 3-го
порядка
1 0
2
3
4
1
2
3 4
записать и вычислить алгебраические дополнения
и A
23
A11
19
РЕШЕНИЕ
1
Дан определитель 3
4
0
2
1
2
3 4
Согласно определению находим
A11 ( 1)
1 1
A23 ( 1)
2 3
1
2
3 4
1
0
4
3
1 ( 4) ( 3)( 2) 10
( 1) ( 3) 0 4 3
1 1
A11 ( 1) M11 10 10
2 3
A23 ( 1) M 23 ( 1) 3 3
20
ЗАМЕЧАНИЕ
Алгебраическое дополнение элемента a ij
совпадает с его минором , если сумма его индексов
i+j
чётна, и является противоположным числом
к минору, если сумма его индексов нечётна
Алгебраическое дополнение используется для
вычисления определителей
21
3. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
Определитель обладает рядом свойств, которые
лежат в основе практических способов их
вычислений
Время, которое затрачивается на вычисление
определителя, зависит не только от вашего опыта,
но и ОТ ЗНАНИЙ СВОЙСТВ ОПРЕДЕЛИТЕЛЕЙ:
процесс решения вполне реально сократить до
считанных секунд, а иногда и сразу увидеть
результат!
Свойства определителей выполняются для
определителей любого порядка. Для экономии
Для экономии
времени и места рассмотрим эти свойства на
определителях второго порядка
22
1. Величина определителя не изменится, если его
строки и столбцы поменять местами:
a11 a12
a 21 a 22
a11 a 21
a12 a 22
.
Для доказательства используем определение
a11 a 21
a11a 22 a 21a12 .
a12 a 22
2. Перестановка двух столбцов или двух строк
определителя равносильна умножению его на (–1):
a11 a12
a21 a22
a12 a11
a22 a21
или
a11 a12
a21 a22
a21 a22
a11 a12
23
3. Умножение всех элементов одного столбца или
одной строки определителя на любое число
равносильно умножению определителя на это
число :
a11 a12
a11 a12
a11 a12
a11 a12
или
.
a21 a22
a21 a22
a21 a22
a21 a22
Пример.
10 4
5 2
5 2
2
2 3
2 3 (5 6) 6.
9 3
93
31
4. Если определитель имеет две одинаковые строки
или два одинаковых столбца, то он равен нулю:
a11 a12
a11 a12
a11a12 a12 a11 0, или
a11 a11
a21 a21
a11a21 a11a21 0.
24
5. Если все элементы некоторого столбца или
некоторой строки определителя равны нулю, то и
сам определитель равен нулю:
0
0
a21 a22
0 a22 0 a21 , или
a11 0
a21 0
a11 0 0 a21.
6. Если элементы двух столбцов или двух строк
определителя пропорциональны, то определитель
равен нулю
1 2
Пример.
8 8 0.
— 4 -8
25
7. Если каждый элемент некоторого столбца
(строки) определителя представляет собой сумму
двух слагаемых, то определитель может быть
представлен в виде суммы двух определителей, из
которых один в данном столбце (строке) имеет
первые из упомянутых слагаемых, а другой –
вторые. Элементы, стоящие на остальных местах, у
всех трех определителей одни и те же.
a a
‘
11
»
11
a a
‘
21
a a
‘
31
»
21
»
31
a12 a13
‘
11
a a12 a13
a22 a23 a
a32 a33
‘
21
»
11
a
a22 a23 a
a31 a32 a33
a12 a13
»
21
a22 a23
»
31
a32 a33
a
26
8. Если к элементам некоторого столбца
Если к элементам некоторого столбца
(строки) определителя прибавить
соответствующие элементы другого столбца
(строки), умноженный на любой общий
множитель , то величина определителя не
изменится.
a11 a12 a12 a13
a11 a12 a13
a21 a22 a22 a23 a21 a22 a23
a31 a32 a32 a33
a31 a32 a33
27
9. Определитель равен сумме произведений
элементов какого-нибудь столбца или строки
на их алгебраические дополнения
a11 A11 a 21 A21 a31 A31 ,
a11 A11 a12 A12 a13 A13 ,
a12 A12 a 22 A22 a32 A32 ,
a 21 A21 a 22 A22 a 23 A23 ,
a13 A13 a 23 A23 a33 A33 ,
a31 A31 a32 A32 a33 A33 .
10. Сумма произведений элементов какого-нибудь
столбца или строки определителя на
алгебраические дополнения соответствующих
элементов другого столбца или строки равна нулю
28
КАКИЕ СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
ПОЛЕЗНО ЗНАТЬ?
1) Величина определителя не меняется при
транспонировании. Свойство запоминаем.
2) Любая парная перестановка строк
(столбцов) меняет знак определителя на
противоположный. На практике лучше не
На практике лучше не
использовать
3) Из строки (столбца) определителя можно
вынести множитель (и внести его обратно).
Используем там, где это выгодно.
4) Если строки (столбцы) определителя
пропорциональны, то он равен нулю.
Определитель с нулевой строкой (столбцом)
равен нулю.
29
ПРИМЕР. ВЫЧИСЛИТЬ
ИСПОЛЬЗУЯ СВОЙСТВО
ОПРЕДЕЛИТЕЛЬ,
9.
6 -2 1
7 4 -1
-3 5 1
30
ЗОЛОТОЕ ПРАВИЛО ВЫЧИСЛЕНИЙ
ОПРЕДЕЛИТЕЛЯ
Определитель выгоднее
раскрывать по ТОЙ строке
(столбцу), где:
1) нулей побольше
2) числа поменьше
3) использовать
правило
—
знаков —
—
—
31
РЕШЕНИЕ
1. Выбираем строку или столбец: это третий
столбец
2. Записываем формулу вычисления
определителя
a13 A13 a23 A23 a33 A33
6 -2 1
1 3
7 4 — 1 ( 1) 1
-3 5 1
7
4
-3 5
( 1)
2 3
( 1)
6
-2
-3
5
( 1)
3 3
1
6 -2
7
4
(35 12) (30 6) (24 14) 47 24 38 109
32
Замечание
Можно упростить запись, если
использовать правило знаков:
6 -2 1
7 4 -1 1
-3 5 1
7
4
-3 5
( 1)
6
-2
-3
5
1
6 -2
7
4
(35 12) (30 6) (24 14) 47 24 38 109
33
4. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ (ИТОГИ)
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ (ИТОГИ)
1. Значение определителя второго порядка находим
по определению:
a11 a12
a11a22 a12 a21
a21 a22
2. Определитель третьего порядка вычисляем,
используя свойство 9, разложив данный
определитель по строке или столбцу
3. Для вычисления определителей высоких порядков
(выше третьего) используют метод ПОНИЖЕНИЯ
ПОРЯДКА
34
4. Если в определителе все числа, расположенные
ниже или выше главной диагонали, или все числа
кроме элементов главной диагонали равны нулю,
то он равен произведению элементов главной
диагонали.
Например,
1 2 3
1
0 0 1 0 0
0 4 0 3 4 0 0 4 0 24
0 0 6
2 5 6 0 0 6
1
0
2 1
6 0 12
2 0 0
35
5. ОПРЕДЕЛИТЕЛЬ РАВЕН НУЛЮ,
если две строки (столбца) определителя
пропорциональны (как частный случай –
одинаковы)
Пример.
4 2 2
2 1
5 7
1 0
3
или
4 2 2
2 1
5 7
2 1 1
1 2 2 1 1 0
3
5 7
3
6. Определитель с нулевой строкой (столбцом)
Определитель с нулевой строкой (столбцом)
равен нулю
36
5. ПОНЯТИЕ
ОБРАТНОЙ МАТРИЦЫ
Определение:
Если A – КВАДРАТНАЯ
НЕВЫРОЖДЕННАЯ МАТРИЦА, то
обратной для нее называется матрица,
обозначаемая A-1 и удовлетворяющая
условию
1
1
A A A A E
Матрицы A и A-1 называются
взаимообратными
37
Обратная
матрица определяется
единственным образом по формуле
A11
1
1
1
T
A
A
A12
det A
det A
A13
A21
A22
A23
A31
A32
A33
A11 A21 A31
T
Здесь A A12
транспонированная
A22 A32
A
A
A
23
33
13
i j
A
(
1
)
M ij
матрица алгебраических дополнений ij
соответствующих элементов исходной матрицы
38
АЛГОРИТМ ПОСТРОЕНИЯ (НАХОЖДЕНИЯ)
ОБРАТНОЙ МАТРИЦЫ
1. Убедиться, что исходная матрицы не является
вырожденной, т.е. убедиться, что det A 0
2. Найти алгебраические дополнения исходной матрицы
Aij ( 1)i j M ij
3. Составить ПРИСОЕДИНЁННУЮ матрицу, элементами
Составить ПРИСОЕДИНЁННУЮ матрицу, элементами
которой являются найденные алгебраические дополнения
A11
*
A A12
A
13
A21
A22
A23
A31
A32
A33
39
4. Записать обратную матрицу
A11
1
1
A
A12
det A
A13
A21
A22
A23
A31
A32
A33
5.
Проверить правильность решения, т.е.
убедиться, что выполняется равенство:
1
или
A A E
1
A A E
40
6. МАТРИЧНЫЕ
ВЫРАЖЕНИЯ
Матричное выражение состоит из матриц,
связанных операциями сложения, умножения,
возведения в степень, транспонирования и др.
Пример матричного выражения:
2 A B T (C D) 1 5F 3
Продумайте и запишите порядок действий над
матрицами A, B, C , D, F для нахождения
значения этого выражения
Замечание.
Если матричное выражение
имеет смысл, то результат его вычисления
является матрицей.
41
МАТРИЧНЫЕ УРАВНЕНИЯ
Матричное равенство, содержащее неизвестную
матрицу, называется матричным уравнением
Например, простейшие из них вида
A 3X B
A X B
X A B
A X 2X E
A X B C
42
ЗАМЕЧАНИЕ
Выполнены
все требования, предъявляемые
к размерам матриц, входящих в матричные
уравнения
Решить матричное уравнение – это значит
найти неизвестную матрицу
43
РАССМОТРИМ РЕШЕНИЕ МАТРИЧНОГО
УРАВНЕНИЯ ВИДА
A X B
Решение
A X B
1
1
A A X A B
1
E X A B
1
X A B
44
ПРИМЕР. РЕШИТЬ УРАВНЕНИЕ
РЕШИТЬ УРАВНЕНИЕ
2 1 1 1
X
1 3 4 3
Решение
Задано уравнение вида X A B
После умножения СПРАВА это уравнение на
1
матрицу A
получаем, что
X B A
1
2 1
1. Найдём матрицу, обратную к матрице A
1 3
по формуле
A
1 A
1
11
A
det A A12
A22
21
45
Вычислим определитель матрицы A:
2 1
2 3 ( 1) 1 7 0
det A
1 3
Найдём миноры и алгебраические дополнения
матрицы A:
M 11 3
M 12 1
M 21 1 M 22 2
Составим
A11 3 A12 1
A21 1
A22 2
обратную матрицу
1
A
1 3 1
A
7 1 2
1
46
2. Найдём неизвестную матрицу
1
X B A :
1 1 1 3 1
X
7 4 3 1 2
1 1 3 1 ( 1) 1 1 1 2 1 2 3
X
7 4 3 3 ( 1) 4 1 3 2 7 9 10
1 2 3
X
7 9 10
3. Проверка
1 2 3 2 1 1 1
7 9 10 1 3 4 3
47
1 2 2 3 1 2 ( 1) 3 3 1 1
7 9 2 10 1 9 ( 1) 10 3 4 3
1 7 7 1 1
7 28 21 4 3
1 1 1 1
верно
4 3 4 3
48
МАТЕМАТИКИ ШУТЯТ
Вычислить определитель
12. 09.2021
09.2021
49
[Править]Определение через разложение по первой строке
Схема расчета определителя матрицы .
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
Для матрицы детерминант определяется как
Для матрицы определитель задаётся рекурсивно:
, где — дополнительный минор к элементу . Эта формула называется разложением по строке.
В частности, формула вычисления определителя матрицы такова:
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
Доказательство [показать]
Также справедливо и аналогичное разложение по любой строке (столбцу):
Доказательство [показать]
Обобщением вышеуказанных
формул является разложение детерминанта
по Лапласу (
[Править]Определение через перестановки
Для матрицы справедлива формула:
,
где
— перестановка чисел
от 1 до
,
— число
инверсий в
перестановке, суммирование идёт по всем
возможным перестановкам порядка
. Таким образом, в определитель
войдёт
слагаемых,
которые также называют «членами
определителя». Важно заметить, что во
многих курсах линейной алгебры это
определение даётся как основное.
Таким образом, в определитель
войдёт
слагаемых,
которые также называют «членами
определителя». Важно заметить, что во
многих курсах линейной алгебры это
определение даётся как основное.
[Править]Альтернативные методы вычисления
где матрицы, получающиеся из исходной вычёркиванием соответствующих строк и столбцов.
[Править]Свойства определителей
Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , где и т. д. — строчки матрицы, — определитель такой матрицы.
При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:
[Править]Алгоритмическая реализация
Наивные методы для вычисления определителя могут быть основаны непосредственно на его определении, как суммы по перестановкам, или на разложении Лапласа по определителям меньшего порядка.
 Однако
такие методы очень неэффективны, так
как требуют О(n!)
операций для вычисления определителя
-го
порядка.
Однако
такие методы очень неэффективны, так
как требуют О(n!)
операций для вычисления определителя
-го
порядка.Один из более быстрых методов заключается в простой модификации метода Гаусса. Следуя методу Гаусса, произвольную матрицу можно привести к ступенчатому виду(Верхнетреугольная матрица), используя лишь две следующие операции над матрицей — перестановку двух строк и добавление к одной из строк матрицы другой строки, умноженной на произвольное число. Из свойств определителя следует, что вторая операция не изменяет определителя матрицы, а первая лишь меняет его знак на противоположный. Определитель матрицы, приведённой к ступенчатому виду, равен произведению элементов на её диагонали, так как она является треугольной, поэтому определитель исходной матрицы равен:
где
—
число перестановок строк, выполненных
алгоритмом, а
—
ступенчатая форма матрицы
,
полученная в результате работы алгоритма. Сложность этого метода, как и метода
Гаусса, составляет
.
Сложность этого метода, как и метода
Гаусса, составляет
.
Определитель можно вычислить, зная LU-разложение матрицы. Если , где и — треугольные матрицы, то . Определитель треугольной матрицы равен просто произведению её диагональных элементов.
Если доступен алгоритм, выполняющий умножение двух матриц порядка за время , где , для некоторого , то определитель матрицы порядка может быть вычислен за время .[1] В частности это означает, что, используя для умножения матриц алгоритм Копперсмита — Винограда, определитель можно вычислить за время .
Алгебраические дополнения
Алгебраическое дополнение элемента определителя — определитель где — минор элемента .
Разложение определителя
По элементам i-й строки:
По элементам j-го столбца:
Например, при n = 4 разложение по первой строке
Свойства определителя
1.
2. Если все элементы какой-нибудь строки (столбца) определителя равны нулю, то определитель равен нулю.
3. Если матрица B получена из матрицы A перестановкой двух каких-либо ее строе (столбцов), то
4. Общий множитель всех элементов произвольной строки (столбца) определителя можно вынести за знак определителя.
5. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.
6. Пусть — квадратная матрица порядка n; k — фиксированное натуральное число: — матрицы, которые получаются из A заменой ее k-й строки (столбца) соответственно строками (столбцами) Тогда
7. Определитель не меняется от прибавления к какой-либо его строке (столбцу) другой его строки (столбца), умноженной на произвольное число.
8. Если какая-либо строка (столбец) определителя есть линейная комбинация других его строк (столбцов), то определитель равен нулю.
9.
Обратная матрица
Обратной
матрицей называется
матрица, которая при умножении как
справа, так и слева на данную матрицу
дает единичную матрицу. Обозначим
обратную матрицу к матрице А через
,
тогда согласно определению получим:
Обозначим
обратную матрицу к матрице А через
,
тогда согласно определению получим:
где Е – единичная матрица. Квадратная матрица называется неособенной (невырожденной), если ее определитель не равен нулю. В противном случае она называется особенной (вырожденной) или сингулярной. Имеет место теорема: всякая неособенная матрица имеет обратную матрицу. Операция нахождения обратной матрицы называется обращением матрицы. Рассмотрим алгоритм обращения матрицы. Пусть дана неособенная матрица n-го порядка:
где Δ = det A
≠ 0.Алгебраическим дополнением элемента матрицы n -го порядка А называется взятый с определенным знаком определитель матрицы (n –1)-го порядка, полученной вычеркиванием i-ой строки и j-го столбца матрицы А:
Составим так называемую присоединенную матрицу:
где
–
алгебраические дополнения соответствующих
элементов
матрицы А. Заметим,
что алгебраические дополнения элементов
строк матрицы А размещаются
в соответствующих столбцах матрицы Ã,
то есть одновременно производится
транспонирование матрицы.
Разделив
все элементы матрицы Ã на
Δ – величину определителя матрицы А,
получим в результате обратную матрицу
:
Заметим,
что алгебраические дополнения элементов
строк матрицы А размещаются
в соответствующих столбцах матрицы Ã,
то есть одновременно производится
транспонирование матрицы.
Разделив
все элементы матрицы Ã на
Δ – величину определителя матрицы А,
получим в результате обратную матрицу
:
Отметим ряд особых свойств обратной матрицы: 1) для данной матрицы А ее обратная матрица является единственной; 2) если существует обратная матрица , то
3) транспонированная обратная матрица равна обратной матрице от данной транспонированной матрицы:
П
р и м е р . Вычислить матрицу, обратную
данной:
Вычислить матрицу, обратную
данной:
Р е ш е н и е . Определитель матрицы А равен:
Следовательно, матрица А неособенная. Присоединенная матрица Ã имеет вид:
Разделив все элементы присоединенной матрицы Ã на Δ = 1, получим обратную матрицу :
Проверим, что действительно,
Таким образом, найденная матрица является обратной для заданной матрицы А.
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
[править]Описание метода
Для системы линейных уравнений с неизвестными (над произвольным полем)
с определителем матрицы системы , отличным от нуля, решение записывается в виде
(i-ый
столбец матрицы системы заменяется
столбцом свободных членов). В другой
форме правило Крамера формулируется
так: для любых коэффициентов c
В другой
форме правило Крамера формулируется
так: для любых коэффициентов c
В этой форме формула Крамера справедлива без предположения, что отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы и , либо набор состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
[править]Пример
Система линейных уравнений:
Определители:
Решение:
Пример:
Определители:
[править]Вычислительная сложность
Метод
Крамера требует вычисления
определителей
размерности
. При использовании метода
Гаусса для
вычисления определителей, метод имеет
временную сложность порядка
,
что хуже, чем если бы метод
Гаусса напрямую
использовался для решения системы
уравнений. Поэтому метод считался
непрактичным. Однако в 2010 году было
показано, что метод Крамера может быть
реализован со сложностью
,
сравнимой со сложностью метода
Гаусса.[1]
При использовании метода
Гаусса для
вычисления определителей, метод имеет
временную сложность порядка
,
что хуже, чем если бы метод
Гаусса напрямую
использовался для решения системы
уравнений. Поэтому метод считался
непрактичным. Однако в 2010 году было
показано, что метод Крамера может быть
реализован со сложностью
,
сравнимой со сложностью метода
Гаусса.[1]
Теорема Безу. Если многочлен разделить на двучлен x — a, то в остатке получим число R, равное значению данного многочлена при x = a, т. е. R = Pn(a).
Схема сокращенного деления многочлена на двучлен. При делении многочлена , расположенного по убывающим степеням x, на двучлен x — a применяется метод сокращенного деления, называемый схемой Горнера.
Имеют
место следующие формулы для нахождения
коэффициентов частного b1, b2,
. .., bn-1 и
остатка R:
.., bn-1 и
остатка R:
Практически вычисление коэффициентов частного Qn-1(x) и остатка R проводится по следующей схеме (схеме Горнера).
Пусть требуется разделить многочлен на двучлен x — a.
Значение a двучлена, коэффициенты многочлена (bn-1, bn-2, …, b0) и остаток запишем в следующей форме:
an | an-1 | an-2 | … | a1 | a0 |
bn-1 = an | bn-2 = an-1 + abn-1 | bn-3 = an-2 + abn-2 | . | b0 = a1 + ab1 | R = a0 + ab0 |
Отсюда записываем частное
если R = 0, и результат деления
или ,
если R ≠ 0.
линейная алгебра — Идентичность определителя матрицы
Давайте сделаем шаг назад и спросим, что такое определитель и почему он полезен. Затем мы перейдем к этому конкретному свойству.
Позвольте мне представить новое произведение векторов, называемое произведением клина . Если $a, b$ — векторы, то их клин-произведение есть $a \клин b$. Результат не является вектором, но вместо этого мы интерпретируем его геометрически как ориентированную плоскость — в точности плоскость, перпендикулярную $a \times b$, на самом деле, но мы можем продолжить расклинивание — например, образуя $ a \wedge b \wedge c$, представляющий объем.
Конечно, в трехмерном пространстве есть только один объем единиц (вы могли бы назвать его $\hat x \wedge \hat y \wedge \hat z$, но позвольте мне для краткости назвать его $i$. Все другие объемы являются скалярными кратными этому объему, по крайней мере, с точки зрения величины и ориентации (вы можете подумать «ориентация?» Я утверждаю, что система координат, следующая правилу правой руки, ориентирована противоположно той, которая следует правилу левой руки, а единичные объемы, образованные заклиниванием их единичных векторов, ориентированы противоположно).По этой причине элементы объема часто называют псевдоскаляров , потому что они отличаются от скаляров только тем, что имеют ориентацию, которой нет у скаляров.
Как это относится к матрицам? Что ж, матрицы используются для представления линейных операторов над векторами, но эти операторы также могут действовать на клиновые произведения векторов или псевдоскаляров. «Матрицы», которые вы используете для представления этих расширений исходного оператора, отличаются от исходной матрицы. Мы определяем отношения по простому правилу. Если $\underline T$ — линейный оператор на векторе, то мы определяем $\underline T(a \wedge b) = \underline T(a) \wedge \underline T(b)$ и т. д. (обратите внимание, что перекрестное произведение не обладает этим прекрасным свойством, кроме поворотов).
«Матрицы», которые вы используете для представления этих расширений исходного оператора, отличаются от исходной матрицы. Мы определяем отношения по простому правилу. Если $\underline T$ — линейный оператор на векторе, то мы определяем $\underline T(a \wedge b) = \underline T(a) \wedge \underline T(b)$ и т. д. (обратите внимание, что перекрестное произведение не обладает этим прекрасным свойством, кроме поворотов).
Но опять же, мы сказали, что существует только один единичный псевдоскаляр ($i$), поэтому действие линейного оператора на $i$ должно быть некоторым скаляром, кратным $i$. То есть, если $\alpha$ является скаляром,
$$\underline T(i) = \alpha i$$
Мы определяем это число $\alpha$ как определитель, геометрически говорящий нам, как единичный объем сжимается или расширяется (или меняет ориентацию) под действием линейного оператора.
Определитель линейного оператора можно найти, записав матричное представление и соединив входящие в него векторы. Это вполне обосновано. Вам просто нужно знать, что $a \wedge b = — b \wedge a$ — векторы антикоммутируют под клином — и что клин ассоциативен. Знание этих свойств позволяет проводить расчеты с клином. 9z e_z)$$
Это вполне обосновано. Вам просто нужно знать, что $a \wedge b = — b \wedge a$ — векторы антикоммутируют под клином — и что клин ассоциативен. Знание этих свойств позволяет проводить расчеты с клином. 9z e_z)$$
Почему? Потому что $e_x \wedge e_x = 0$ всегда, поэтому, если какие-либо $e_x$ появляются в $g$ или $h$, они не имеют значения. Мы можем их игнорировать, а вместо этого находим «определитель» линейного оператора на $yz$-плоскости. Таким образом, метод разложения минорами следует за рекурсивным расширением одного вектора по линейности, чтобы свести последующие произведения клина к произведению клина («детерминанту»), которое вы, возможно, уже знаете. Метод коренится в связи между определителем и объемами, в том, что все слагаемые, составляющие определитель, должны содержать 1 и только 1 компонент некоторого вектора от каждого из координатных направлений — ни больше, ни меньше.
линейная алгебра — Как вычислить определитель матрицы всех единиц минус единица?
$\begingroup$
Как вычислить определитель следующих $n\times n$ матриц
$$\begin {bmatrix}
0 и 1 & \ldots & 1 \\
1 & 0 & \ldots & 1 \\
\vdots & \vdots & \ddots & \vdots \\
1 и 1 и . {n-1}
$$ 9{n-1}(n-1)$.
{n-1}
$$ 9{n-1}(n-1)$.
Если вы замените один столбец единицами, вы можете использовать этот результат, чтобы получить следующее. (Я вычислил это для $n=4$, но думаю, вы можете обобщить это для произвольного $n$.)
$$ \begin{vmatrix} 1 и 1 и 1 и 1 \\ 1 и 0 и 1 и 1 \\ 1 и 1 и 0 и 1 \\ 1 и 1 и 1 и 0 \\ \end{vmatrix} знак равно \begin{vmatrix} 0 и 1 и 1 и 1 \\ 1 и 0 и 1 и 1 \\ 1 и 1 и 0 и 1 \\ 1 и 1 и 1 и 0 \\ \end{vmatrix} + \begin{vmatrix} 1 и 0 и 0 и 0 \\ 1 и 0 и 1 и 1 \\ 1 и 1 и 0 и 1 \\ 1 и 1 и 1 и 0 \\ \end{vmatrix}= \begin{vmatrix} 0 и 1 и 1 и 1 \\ 1 и 0 и 1 и 1 \\ 1 и 1 и 0 и 1 \\ 1 и 1 и 1 и 0 \\ \end{vmatrix} + \begin{vmatrix} 0 и 1 и 1 \\ 1 и 0 и 1 \\ 1 и 1 и 0 \end{vmatrix} $$
Обратите внимание, что оба эти определителя относятся к типу, который вы уже рассматривали в первой части.
$\endgroup$
0
$\begingroup$
Вот подход, использующий теорему Сильвестра об определителе, которая говорит, что для любых прямоугольных матриц взаимно переставленных форм $A\in\mathrm M_{n,m}(K)$ и $B\in \mathrm M_{m,n} (K)$ один имеет $$\det(I_n+AB)=\det(I_m+BA). {п-1}.
$$
{п-1}.
$$
$\endgroup$
$\begingroup$
Обозначим через $A_n$ матрицу порядка $ n \times n $.
Вычтите каждый столбец, умноженный на $1/(n-2)$, из первого столбца. Ваш определитель тогда становится:
$ |А_n|= \влево| \начать {матрица} \frac {n-1}{n-2} & 1 & \ldots & 1 \\ 0 & 0 & \ldots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 0 и 1 и … и 0 \конец {матрица} \право| = \frac{n-1}{n-2}|A_{n-1}| $ 9п\ (1-п). \end{выравнивание}
$\endgroup$
$\begingroup$
Пусть $A_n$ обозначает матрицу $n\times n$ указанного вами вида: $0$ по диагонали и $1$ везде. Я найду $\det A_n$, вычислив собственные значения $A_n$ и перемножив их.
Сначала пусть $B_n = A_n + I_n$, так что $B_n$ состоит из всех $1$. Так как $B_n$ имеет ранг $1$, она имеет собственное значение $0$ кратности $n-1$; поскольку $\operatorname{tr} B_n = n$ и трасса представляет собой сумму собственных значений, другое собственное значение $B_n$ должно быть $n$.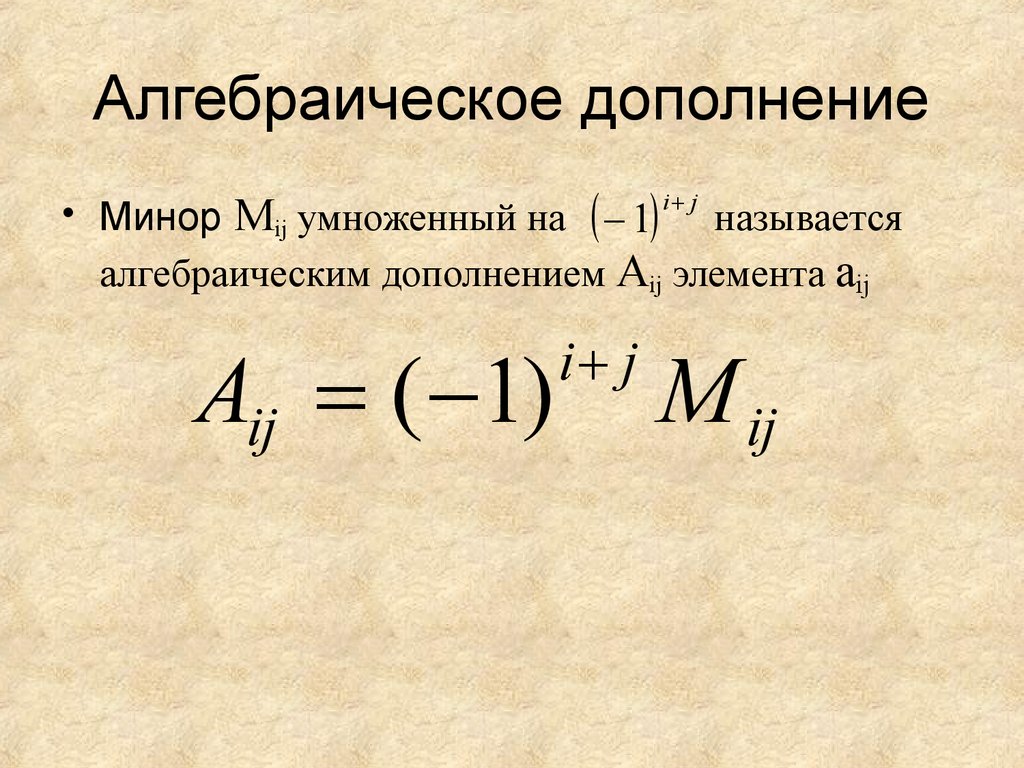

 Однако
такие методы очень неэффективны, так
как требуют О(n!)
операций для вычисления определителя
-го
порядка.
Однако
такие методы очень неэффективны, так
как требуют О(n!)
операций для вычисления определителя
-го
порядка. ..
..