Логарифм 3 по основанию 2 равен: Mathway | Популярные задачи

Содержание

Log 10 по основанию 2. Что такое логарифм? Решение логарифмов. Примеры. Свойства логарифмов

Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.

Определение логарифма

Логарифм с основанием a — это функция y(x) = log a x , обратная к показательной функции с основанием a: x(y) = a y .

Десятичный логарифм — это логарифм по основанию числа 10 : lg x ≡ log 10 x .

Натуральный логарифм — это логарифм по основанию числа e : ln x ≡ log e x .

2,718281828459045… ;
.

График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x . Слева изображены графики функции y(x) = log a x для четырех значений основания логарифма : a = 2 , a = 8 , a = 1/2 и a = 1/8 . На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0

Свойства логарифма

Область определения, множество значений, возрастание, убывание

Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.


Область определения	0	0
Область значений	— ∞	— ∞
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	x = 1	x = 1
Точки пересечения с осью ординат, x = 0	нет	нет
	+ ∞	— ∞
	— ∞	+ ∞

Частные значения

Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:

Логарифм по основанию e называется натуральным логарифмом :

Основные формулы логарифмов

Свойства логарифма, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Логарифмирование — это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.

Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.

Доказательство основных формул логарифмов

Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.

Рассмотрим свойство показательной функции
.
Тогда
.
Применим свойство показательной функции
:
.

Докажем формулу замены основания.
;
.
Полагая c = b , имеем:

Обратная функция

Обратной для логарифма по основанию a является показательная функция с показателем степени a .

Если , то

Производная логарифма

Производная логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >

Для нахождения производной логарифма, его нужно привести к основанию

e .
;
.

Интеграл

Интеграл от логарифма вычисляется интегрированием по частям : .
Итак,

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z :
.
Выразим комплексное число z через модуль r и аргумент φ :
.
Тогда, используя свойства логарифма, имеем:
.
Или

Однако, аргумент φ определен не однозначно. Если положить
, где n — целое,
то будет одним и тем же числом при различных n .

Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Что такое логарифм?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»

И для тех, кто «очень даже…»)

Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. {-5}=\)$\frac{1}{32}$

Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:

Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».

Как вычислить логарифм?

Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Например , вычислите логарифм: а) $\log_{4}{16}$ б) $\log_{3}$$\frac{1}{3}$ в) $\log_{\sqrt{5}}{1}$ г) $\log_{\sqrt{7}}{\sqrt{7}}$ д) $\log_{3}{\sqrt{3}}$

а) В какую степень надо возвести $4$, чтобы получить $16$? Очевидно во вторую. Поэтому:

$\log_{4}{16}=2$

$\log_{3}$$\frac{1}{3}$ $=-1$

в) В какую степень надо возвести $\sqrt{5}$, чтобы получить $1$? А какая степень делает любое число единицей? Ноль, конечно!

$\log_{\sqrt{5}}{1}=0$

г) В какую степень надо возвести $\sqrt{7}$, чтобы получить $\sqrt{7}$? В первую – любое число в первой степени равно самому себе.

{b}=c\) $\Leftrightarrow$ $\log_{a}{c}=b$

$\log_{4}{10}=5x-4$

Зеркально перевернем уравнение, чтобы икс был слева

$5x-4=\log_{4}{10}$

Перед нами . Перенесем $4$ вправо.

И не пугайтесь логарифма, относитесь к нему как к обычному числу.

$5x=\log_{4}{10}+4$

Поделим уравнение на 5

$x=$$\frac{\log_{4}{10}+4}{5}$

Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Ответ : $\frac{\log_{4}{10}+4}{5}$

Десятичный и натуральный логарифмы

Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы $(a>0, a\neq1)$. И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:

Натуральный логарифм: логарифм, у которого основание — число Эйлера $e$ (равное примерно $2,7182818…$), и записывается такой логарифм как $\ln{a}$.

{\log_{6}{5}}\)

Решение :

Ответ : $25$

Как число записать в виде логарифма?

Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что $\log_{2}{4}$ равен двум. Тогда можно вместо двойки писать $\log_{2}{4}$.

Но $\log_{3}{9}$ тоже равен $2$, значит, также можно записать $2=\log_{3}{9}$ . Аналогично и с $\log_{5}{25}$, и с $\log_{9}{81}$, и т.д. То есть, получается

$2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…$

Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.

Точно также и с тройкой – ее можно записать как $\log_{2}{8}$, или как $\log_{3}{27}$, или как $\log_{4}{64}$… Здесь мы как аргумент пишем основание в кубе:

$3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}. {a}}$

Пример : Найдите значение выражения $\frac{\log_{2}{14}}{1+\log_{2}{7}}$

Решение :

Ответ : $1$

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
Десятичный a, где основанием служит число 10.
Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Что такое логарифм

11 июля 2011

Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.

Мы же определим логарифм просто и наглядно. Для этого составим таблицу:

2¹	2²	2³	2⁴	2⁵	2⁶
2	4	8	16	32	64

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.

Обозначение: log_a x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.

Например, 2³ = 8 ⇒ log₂ 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2³ = 8). С тем же успехом log₂ 64 = 6, поскольку 2⁶ = 64.

Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:

2¹	2²	2³	2⁴	2⁵	2⁶
2	4	8	16	32	64
log₂ 2 = 1	log₂ 4 = 2	log₂ 8 = 3	log₂ 16 = 4	log₂ 32 = 5	log₂ 64 = 6

К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log₂ 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке [2; 3]. Потому что 2² < 5 < 2³, а чем больше степень двойки, тем больше получится число.

Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log₂ 5 = 2,32192809…
log₃ 8 = 1,89278926…
log₅ 100 = 2,86135311…

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log₂ 5, log₃ 8, log₅ 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

Как считать логарифмы

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!

Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log_a x = b ⇒ x > 0, a > 0, a ≠ 1.

Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log₂ 0,5 = −1, т.к. 0,5 = 2⁻¹.

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
Решить относительно переменной b уравнение: x = a^b;
Полученное число b будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Задача. Вычислите логарифм: log₅ 25

Представим основание и аргумент как степень пятерки: 5 = 5¹; 25 = 5²;
Составим и решим уравнение:
log₅ 25 = b ⇒ (5¹)^b = 5² ⇒ 5^b = 5² ⇒ b = 2;
Получили ответ: 2.

Задача. Вычислите логарифм:

Представим основание и аргумент как степень тройки: 3 = 3¹; 1/81 = 81⁻¹ = (3⁴)⁻¹ = 3⁻⁴;
Составим и решим уравнение:
Получили ответ: −4.

Задача. Вычислите логарифм: log₄ 64

Представим основание и аргумент как степень двойки: 4 = 2²; 64 = 2⁶;
Составим и решим уравнение:
log₄ 64 = b ⇒ (2²)^b = 2⁶ ⇒ 2^2b = 2⁶ ⇒ 2b = 6 ⇒ b = 3;
Получили ответ: 3.

Задача. Вычислите логарифм: log₁₆ 1

Представим основание и аргумент как степень двойки: 16 = 2⁴; 1 = 2⁰;
Составим и решим уравнение:
log₁₆ 1 = b ⇒ (2⁴)^b = 2⁰ ⇒ 2^4b = 2⁰ ⇒ 4b = 0 ⇒ b = 0;
Получили ответ: 0.

Задача. Вычислите логарифм: log₇ 14

Представим основание и аргумент как степень семерки: 7 = 7¹; 14 в виде степени семерки не представляется, поскольку 7¹ < 14 < 7²;
Из предыдущего пункта следует, что логарифм не считается;
Ответ — без изменений: log₇ 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.

Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2³ — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2⁴ — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3⁴ — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x. Обозначение: lg x.

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log₁₀ x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Натуральный логарифм от аргумента x — это логарифм по основанию e, т.е. степень, в которую надо возвести число e, чтобы получить число x. Обозначение: ln x.

Многие спросят: что еще за число e? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e = 2,718281828459…

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log_e x

Таким образом, ln e = 1; ln e² = 2; ln e¹⁶ = 16 — и т. д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Смотрите также:

Тест к параграфу «Что такое логарифм» (легкий)
Тест к уроку «Что такое логарифм» (средний)
Десятичные дроби
Центральные и вписанные углы в задании 6
Задача B5: вычисление площади методом обводки
Задачи B4: перевозка груза тремя фирмами

Log 3 log 12: Mathway

Содержание

ЕГЭ по математике. В 7. Логарифмические выражения.

1. Найдите значение выражения log₇ 28 – log₇ 4 = log₇ (28^{: 4) = log ₇ 7 = 1}

2. Найдите значение выражения log₅₃2 + log₅₃3 +log₅₃7= log₅₃42

3. Найдите значение выражения log₂₃²/₃+ log₂₃6 – log₂₃4 = log₂₃ 1 = 0.

4. Найдите значение выражения log₃90 – log₃ 2 – log₃5 = log₃ 9 = 2.

5. Найдите значение выражения 2log₇₂ 3 + 3log₇₂ 2 = log₇₂ 9 + log₇₂ 8 =log₇₂ 72 = 1.

6. Найдите значение выражения ^?_{log_?21 9 + log ₂₁ 49}= log₂₁ 9 + log ₂₁ 49 = log₂₁ 9 + log ₂₁ 49 = log₂₁ 441 = 2

7. Найдите значение выражения log₆5 •log₅8 + log₆27 = log₅ 8 / log₅ 6 + log₆ 27 = log₆8 + log₆ 27 = log₆ 216 = 3.

8. Найдите значение выражения 4log₇ 2 / log₇ 80 + log₈₀ 5 = 4log₈₀2 + log₈₀ 5 = log₈₀ 16_{+ log₈₀ 5_{= log₈₀ 80 = 1}}

9. Найдите значение выражения log₇(3³•7⁵) – 2 log₇ 3 – 5 = 3log₇3_{+ 5 – 2log₇3 -5 =log₇3.}

10. Найдите значение выражения log₁₅5³ + log₁₅3⁴ + log₁₅ 5⁶3⁵= log₁₅5³ + log₁₅3⁴ + log₁₅ 5⁶ + log₁₅3⁵ = log₁₅5³5⁶ + log₁₅3⁴3⁵ = log₁₅ 5⁹ + log₁₅ 3⁹ = 9(log₁₅5 + log₁₅3) = 9.

11. Найдите значение выражения log₅ ?7 + 2log₂₅ ?7 = log₅ ?7 + log₅ ?7 = log₅ 7

12. Найдите значение выражения ^?log₂48 – log₄3 = log₂?48 – log₂?3 = log₂?16 = log₂4 = 2.

13. Найдите значение выражения log₁₀₅12 + log₁₀₅5 +log₁₀₅7 – log₁₀₅4 = log₁₀₅105 = 1.

14. Найдите значение выражения2^log₁₇^375•log₅^{17 –log}₅³ = 2^log₁₇^{375 / log}₁₇^{5 –log}₅³ = 2^log₅^{375 –log}₅³ = 2^log₅¹²⁵ = 2³ =8 .

15. Найдите значение выражен ( log₃28 • log₁₅₄3 + log₁₇11 •log₁₅₄17 – log₅2 • log₁₅₄5 )² + 7 = (log₁₅₄ 28 + log₁₅₄ 11_{– log₁₅₄ 2)² + 7 = log₁₅₄² 154 + 7 = 8.}

16. Найдите значение выражения (lg900-2lg3)(ln49•log₇e + 1) = (lg 900 – lg 9)((ln 49 / ln 7) + 1) = lg100 (log₇ 49 + 1) = 2 ^. 3 = 6.

Свойства логарифмов. Готовимся к ЕГЭ

Найдите значение выражения
1
r
logab = r logab
log 5 125 log 4 16 log 5 5 log 4 4
3
3 log 5 5 2 log 4 4 3 2 ?
1
1
Запомни!
logaa = 1
2
r
logab
7
1= loga764a6
4
Найдите значение выражения
7 5
2
a
log5 4
loga b
7 4 ?
=b
r
logab = r logab
3
9
log3 4
3
2 log3 4
3
2 log3 4
log3 4 2
3
Запомни! r logab
3
log3 16
16
Найдите значение выражения
log rb = r1 logab
4
a
log 0, 25 2 log
0, 5
2
2 log 1 2 2 log 2 2 2
2
1 1
1
log 2 2
2
2
Запомни!
1
log rb = r log rb
a
a
–n
a =
n
1÷
a
Найдите значение выражения
5
r
logab = r logab
1
3
log 4 8 log 22 2 3 log 2 2
2
2
3
log rb = r1 logab
a
1
log rb = r log rb
a
a
Запомни!
r
r
logalog
b =abr logab
Найдите значение выражения
6
logab – logaс = loga b
с
log 6 270 log 6 7,5 log 6 (270 : 7,5) ?
logc b
loga b =
logc a
7
log 3 25
log
log 3 55
?
Найдите значение выражения
8
1
2
log 5 0,2 log 0,5 4 log 5 log 1 2
5
2
1
1
log 5 5 log 2 1 2 log 5 5 2 log 2 2 ?
1
r
2
logab = r logab
log rb = r1 logab
a
logaa = 1
Найдите значение выражения
9
logab logba = 1
1
log 5 7 log 7 25 log 5 7 log 7 5 2 log 5 7 log 7 5
2
?
10
log 9 8 log 9 8
log 9 8
1
?
1
log 81 8 log 92 8 1 log 8
9
2
2
1
log rb = r log rb
a
a
Найдите значение выражения
11
an :
am =
an-m
logab – logaс = loga bс
log12 432
6
log12 432
log12 3
log1 2 432 log1 2 3
6
:6
6
log12 3
6
6
log12 ( 432:3)
6
log12 144
r
6
2
log1212
logab = r logab
6
1
2 log1 2 12
6
2
Найдите значение выражения
12
logaa = 1
logab – logaс = loga b
с
(1 log 2 12)(1 log 6 12)
(log 2 2 log 2 12)(log 6 6 log 6 12)
1
1
log 2 (2 :12) log 6 (6 : 12) log 2 log 6
6
2
1
log 2 6 1 log 6 2 1 1 ( 1) log 2 6 log 6 2 ?
r
r
logalog
b =abr logab
logab logba = 1
Найдите значение выражения
13
m
n m
a = an
104 log 3
8
logaa = 1
1
8
1
1
3 104 log 3 3 104 log 3 3 ?
8
1
r
r
logalog
b =abr logab
14
log 6 13 13 log
1
1
13 6
13 6 log 13 13 ?
1
log rb = r log rb
a
a
Найдите значение выражения
15
logab + logaс = logabс
log 6 180 log 6 (36 5) log 6 36 log 6 5
2 log 6 5 2 log 6 5
2 log 6 5
2 log 6 5
1
2 log 6 5
Найдите значение выражения
logc b
loga b =
logc a
16
log 3 5
1
log 7 0,2 log 7 5 log 7 log 7 5 log 7 5 1
log 3 7
5
log 7 5 1log 7 5 0
r
r
logalog
b =abr logab
Только зная все свойства, можно научиться решать
примеры
logaa = 1
a
loga b
=b
logc b
loga b =
logc a
r
logab = r logab
logab + logaс = logabс
b
logab – logaс = loga с
log1bb
loga b =
logba
logab logba = 1
1
log rb = r log rb
a
a
Найдите значение выражения
17
log1bb
loga b =
logba
log 7 0,8
1
log 7 0,8
log 1, 25 7 log 7 0,8
log 7 1,25
log 7 1,25
1
5
4
5
log 1, 25 0,8 log 5 log 5 1log 5 1
4 4
4 5
4 4
logc b
loga b =
logc a
Найдите значение выражения
18
3
log9 16
3
log 2 16
3
19
log
2
11
3
121 log
1
log3 16
2
11
3
log3
121
1
16 2
2
log 1 11
112
2
2 2 log 11 11 2 2 1 ?
2
2
20
5
3 log5 2
5 5
3
log5 2
?
3
log3 16
2
3log3 4 ?
Найдите значение выражения
18
8
2 log8 3
log8 32
8
?
19
64
20
log8 3
8
2 log8 3
8
2
log 4 log 5 25 ?
log8
3 2 ?

Калькулятор онлайн — Решение логарифмических уравнений

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.

Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Логарифмическая функция. Логарифмы

Задача 1. Найти положительный корень уравнения x⁴ = 81

По определению арифметического корня имеем $ x = \sqrt[4]{81} = 3 $

Задача 2. Решить уравнение 3^x = 81

Запишем данное уравнение так: 3^x = 3⁴, откуда x = 4

В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том,
что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3.
Но уже, например, уравнение 3^x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень.
Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.

Уравнение a^x = b, где a > 0, $ a \neq 1 $, b > 0, имеет единственный корень. {-2} = \frac{1}{25}$$

Решить уравнение log₃(1-x) = 2

По определению логарифма 3² = 1 — x, откуда x = -8

Свойства логарифмов

При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются
различные свойства логарифмов. Рассмотрим основные из них.

Пусть а > 0, $ a \neq 1 $, b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:

1) log_a(bc) = log_ab + log_ac

2) $ \log_a \frac{b}{c} = \log_a b — \log_a c $

3) log_ab^r = r log_ab

Десятичные и натуральные логарифмы

Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора.
И в том и в другом случае находятся только десятичные или натуральные логарифмы.

Определение. {\infty} \frac{1}{n!} $$

$$ e \approx 2,7182818284 $$

Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы
чисел по любому основанию.

Для этого используется формула замены основания логарифма:

$$ \log_a b = \frac{\log_c b}{\log_c a} $$

где b > 0, a > 0, $ a \neq 1 $, c > 0, $ c \neq 1 $

Следствия из формулы замены основания логарифма.

При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:

$$ \log_a b = \frac{\lg b}{\lg a} , \;\; \log_a b = \frac{\ln b}{\ln a} $$

Логарифмическая функция, её свойства и график

В математике и её приложениях часто встречается логарифмическая функция

y = log_ax

где а — заданное число, a > 0, $ a \neq 1 $

Логарифмическая функция обладает свойствами:

1) Область определения логарифмической функции — множество всех положительных чисел.

2) Множество значений логарифмической функции — множество всех действительных чисел.

3) Логарифмическая функция не является ограниченной.

4) Логарифмическая функция y = log_ax является возрастающей на промежутке $ (0; +\infty) $, если a > 1,

и убывающей, если 0

5) Если a > 1, то функция y = log_ax принимает положительные значения при х > 1,

отрицательные при 0
Если 0 ax принимает положительные значения при 0
отрицательные при х > 1.

Ось Oy является вертикальной асимптотой графика функции y = log_ax

Отметим, что график любой логарифмической функции y = log_ax проходит через точку (1; 0).

При решении уравнений часто используется следующая теорема:

Теорема. Если log_ax₁ = log_ax₂ где a > 0, $ a \neq 1 $,
x₁ > 0, x₂ > 0, то x₁ = x₂

Логарифмическая функция y = log_ax и показательная функция y = a^x, где a > 0, $ a \neq 1 $, взаимно обратны.

Логарифмические уравнения

Решить уравнение log₂(x+1) + log₂(x+3) = 3

Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма
верно равенство

log₂((x+1)(x+3)) = 3

Из этого равенства по определению логарифма получаем

(x+1)(x+3) = 8

х² + 4х + 3 = 8, т.е. х² + 4x — 5 = 0, откуда x₁ = 1, х₂ = -5

Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.

Проверим, являются ли числа 1 и -5 корнями исходного уравнения.

Подставляя в левую часть исходного уравнения х = 1, получаем

log₂(1+1) + log₂(1+3) = log₂2 + log₂4 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.

При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т. е. х = -5 не является корнем этого
уравнения.

Ответ x = 1

Решить уравнение lg(2x² — 4x + 12) = lg x + lg(x+3)

По свойству логарифмов

lg(2x² — 4x + 12) = lg(x² + 3x)

откуда

2x² — 4x + 12 = x² + 3x

x² — 7x + 12 = 0

x₁ = 3, х₂ = 4

Проверка показывает, что оба значения х являются корнями исходного уравнения.

Ответ x₁ = 3, х₂ = 4

Решить уравнение log₄(2x — 1) • log₄x = 2 log₄(2x — 1)

Преобразуем данное уравнение:

log₄(2x — 1) • log₄x — 2 log₄(2x — 1) = 0

log₄(2х — 1) • (log₄ x — 2) = 0

Приравнивая каждый из множителей левой части уравнения к нулю, получаем:

1) log₄ (2х — 1) = 0, откуда 2х — 1 = 1, х₁ = 1

2) log₄ х — 2 = 0, откуда log₄ = 2, х₂ = 16

Проверка показывает, что оба значения х являются корнями исходного уравнения. {-5}=\)$\frac{1}{32}$

Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:

Как вычислить логарифм?

Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Например, вычислите логарифм: а) $\log_{4}{16}$ б) $\log_{3}$$\frac{1}{3}$ в) $\log_{\sqrt{5}}{1}$ г) $\log_{\sqrt{7}}{\sqrt{7}}$ д) $\log_{3}{\sqrt{3}}$

а) В какую степень надо возвести $4$, чтобы получить $16$? Очевидно во вторую. Поэтому:

$\log_{4}{16}=2$

б) В какую степень надо возвести $3$, чтобы получить $\frac{1}{3}$? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).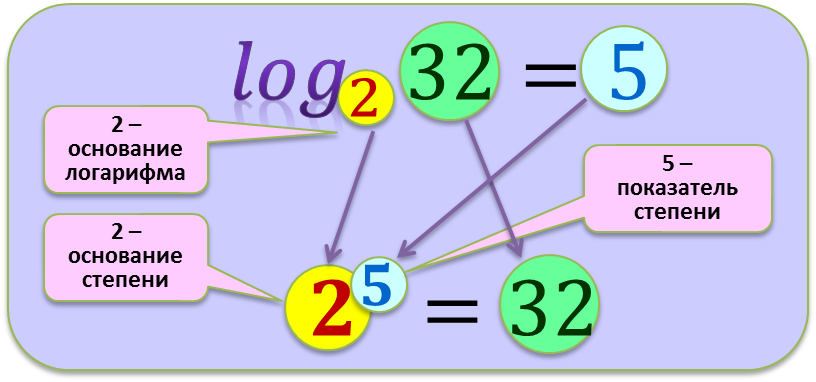

$\log_{3}$$\frac{1}{3}$$=-1$

$\log_{\sqrt{5}}{1}=0$

$\log_{\sqrt{7}}{\sqrt{7}}=1$

д) В какую степень надо возвести $3$, чтобы получить $\sqrt{3}$? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень $\frac{1}{2}$.

$\log_{3}{\sqrt{3}}=$$\frac{1}{2}$

Пример: Вычислить логарифм $\log_{4\sqrt{2}}{8}$

Решение:

$\log_{4\sqrt{2}}{8}=x$		Нам надо найти значение логарифма, обозначим его за икс. {b}=c\) $\Leftrightarrow$ $\log_{a}{c}=b$
$\log_{4}{10}=5x-4$		Зеркально перевернем уравнение, чтобы икс был слева
$5x-4=\log_{4}{10}$		Перед нами линейное уравнение. Перенесем $4$ вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу.
$5x=\log_{4}{10}+4$		Поделим уравнение на 5
$x=$$\frac{\log_{4}{10}+4}{5}$		Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Ответ: $\frac{\log_{4}{10}+4}{5}$

Десятичный и натуральный логарифмы

Натуральный логарифм: логарифм, у которого основание — число Эйлера $e$ (равное примерно $2,7182818…$), и записывается такой логарифм как $\ln{a}$.

То есть, $\ln{a}$ это то же самое, что и $\log_{e}{a}$, где $a$ — некоторое число.

Десятичный логарифм: логарифм, у которого основание равно 10, записывается $\lg{a}$.

То есть, $\lg{a}$ это то же самое, что и $\log_{10}{a}$, где $a$ — некоторое число. {2}=25\)

Ответ готов.

Ответ: $25$

Как число записать в виде логарифма?

$2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…$

$3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}…$

И с четверкой:

$4=\log_{2}{16}=\log_{3}{81}=\log_{4}{256}=\log_{5}{625}=\log_{6}{1296}=\log_{7}{2401}…$

И с минус единицей:

$-1=$ $\log_{2}$$\frac{1}{2}$$=$ $\log_{3}$$\frac{1}{3}$$=$ $\log_{4}$$\frac{1}{4}$$=$ $\log_{5}$$\frac{1}{5}$$=$ $\log_{6}$$\frac{1}{6}$$=$ $\log_{7}$$\frac{1}{7}$$…$

И с одной третьей:

$\frac{1}{3}$$=\log_{2}{\sqrt[3]{2}}=\log_{3}{\sqrt[3]{3}}=\log_{4}{\sqrt[3]{4}}=\log_{5}{\sqrt[3]{5}}=\log_{6}{\sqrt[3]{6}}=\log_{7}{\sqrt[3]{7}}…$

И так далее. {a}}\)

Пример: Найдите значение выражения $\frac{\log_{2}{14}}{1+\log_{2}{7}}$

Решение:

$\frac{\log_{2}{14}}{1+\log_{2}{7}}$$=$		Превращаем единицу в логарифм с основанием $2$: $1=\log_{2}{2}$
$=$$\frac{\log_{2}{14}}{\log_{2}{2}+\log_{2}{7}}$$=$		Теперь пользуемся свойством логарифмов: $\log_{a}{b}+\log_{a}{c}=\log_{a}{(bc)}$
$=$$\frac{\log_{2}{14}}{\log_{2}{(2\cdot7)}}$$=$$\frac{\log_{2}{14}}{\log_{2}{14}}$$=$		В числителе и знаменателе одинаковые числа – их можно сократить. {2} – 41 x + 35 right )} = w$$ подставляем w: Данное ур-ние не имеет решений, значит данное неравенство выполняется всегда или не выполняется никогда проверим подставляем произвольную точку, например x0 = 0 log(3 – 0) / 2 ———————– >= log3 – x20 – 50 + 3/ 1/ 2 log 120 – 410 + 35/ log(3) ——- >= log(6) log(35) но log(3) ——- зн. неравенство не имеет решений Найдите значение числового логарифмического выражения – как решать Формулировка задачи: Найдите значение числового логарифмического выражения. Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5 (Вычисления и преобразования). Рассмотрим, как решаются подобные задачи на логарифмы на примерах. Пример задачи 1: Найдите значение выражения log_0,310 – log_0,33 Решение: Разность логарифмов с одинаковым основанием равна логарифму частного: log_0,310 – log_0,33 = log_0,3(10/3) Возведем 10/3 в степень -1, вынесем степень из под логарифма (логарифм степени): log_0,3(10/3) = -log_0,3(3/10) = -1 Ответ: -1 Пример задачи 2: Найдите значение выражения log₇13 / log₄₉13 Решение: Преобразуем знаменатель: для этого вынесем степень основания из под логарифма: log₄₉13 = log_(7)²13 = 1/2 ⋅ log₇13 Тогда значение выражения равно: log₇13 / log₄₉13 = 2 ⋅ log₇13 / log₇13 = 2 Ответ: 2 Пример задачи 3: Найдите значение выражения 9^log₅50 / 9^log₅2 Решение: Преобразуем выражение: 9^log₅50 / 9^log₅2 = 9^{log₅50 – log₅2} Разность логарифмов с одинаковыми основаниями равна логарифму частного: log₅50 – log₅2 = log₅(50/2) = log₅25 = 2 Тогда значение выражения равно: Ответ: 81 Пример задачи 4: Найдите значение выражения 6log₇∛7 Решение: Вынесем корень за пределы логарифма: 6log₇∛7 = 6 ⋅ 1/3 ⋅ log₇7 = 2 Ответ: 2 Пример задачи 5: Найдите значение выражения log₃5 / log₃7 + log₇0,2 Решение: Преобразуем частное с помощью формулы перехода от логарифма в одном основании к логарифму при другом основании: Сумма логарифмов с одним основанием равна логарифму произведения: log₇5 + log₇0,2 = log₇1 = 0 Ответ: 0 Пример задачи 6: Найдите значение выражения log_0,83 ⋅ log₃1,25 Решение: Преобразуем второй множитель и приведем его к тому же основанию: log₃1,25 = log₃(5/4) = -log₃(4/5) = -log₃0,8 = -1 / log_0,83 И найдем значение выражения: log_0,83 ⋅ log₃1,25 = -log_0,83 / log_0,83 = -1 Ответ: -1 Пример задачи 7: Найдите значение выражения 5^log₂₅49 Решение: Вынесем степень основания логарифма за его пределы: Внесем ее обратно как логарифм корня: 1/2 ⋅ log₅49 = log₅(49)^1/2 = log₅7 И воспользуемся основным логарифмическим тождеством: Ответ: 7 Пример задачи 8: Найдите значение выражения log₄(log₂16) Решение: Вычислим значение выражения в скобках: Тогда значение выражения равно: Ответ: 1 Пример задачи 9: Найдите значение выражения log₄2 + log_0,258 Решение: Найдем значения каждой части выражения и получим результат: log₄2 =1/2 ⋅ log₂2 = 1/2 ⋅ 1 = 0,5 log_0,258 = log_1/48 = 1/2 ⋅ log_1/28 = 1/2 ⋅ log_1/22³ = 1/2 ⋅ (-3) = -1,5 Тогда значение выражения равно: log₄2 + log_0,258 = 0,5 – 1,5 = -1 Ответ: -1 Пример задачи 10: Найдите значение выражения 2^{log₂6 – 3} Решение: Разложим число на множители: 2^{log₂6 – 3} = 2^log₂6 ⋅ 2^–3 Применим основное логарифмическое тождество к первому множителю и выполним оставшиеся вычисления: 2^log₂6 ⋅ 2^-3 = 6 ⋅ 1/8 = 0,75 Ответ: 0,75 Пример задачи 11: Найдите значение выражения 7^–2log₇2 Решение: Вынесем множитель перед логарифмом в степень, чтобы избавиться от него: –2log₇2 = log₇2^–2 = log₇0,25 И применим основное логарифмическое тождество: 7^–2log₇2 = 7^log₇0,25 = 0,25 Ответ: 0,25 Пример задачи 12: Найдите значение выражения (3^log₂3)^log₃2 Решение: Если мы возведем число сначала в степень log₃2, а потом уже в степень log₂3, то сможем применить основное логарифмическое тождество: (3^log₂3)^log₃2 = (3^log₃2)^log₂3 = 2^log₂3 = 3 Ответ: 3 Пример задачи 13: Найдите значение выражения (1 – log₂12) ⋅ (1 – log₆12) Решение: Преобразуем логарифмы: log₂12 = log₂(2 ⋅ 6) = log₂2 + log₂6 = 1 + log₂6 log₆12 = log₆(2 ⋅ 6) = log₆2 + log₆6 = log₆2 + 1 Подставим полученные значения в выражение: (1 – (1 + log₂6)) ⋅ (1 – (log₆2 + 1)) = (1 – 1 – log₂6) ⋅ (1 – log₆2 – 1) = – log₂6 ⋅ (– log₆2) = log₂6 ⋅ log₆2 Преобразуем второй множитель, чтобы логарифмы имели одинаковые основания, и выполним остальные действия: log₂6 ⋅ log₆2 = log₂6 ⋅ 1/log₂6 = 1 Ответ: 1 Пример задачи 14: Найдите значение выражения log₃18 / (2 + log₃2) Решение: Преобразуем 2 в знаменателе в логарифм с основанием 3 (возведем 3 в степень 2 и получим число под логарифмом): Сумма логарифмов с одним основанием в знаменателе равна логарифму произведения: 2 + log₃2 = log₃9 + log₃2 = log₃(9 ⋅ 2) = log₃18 Осталось сократить числитель и знаменатель: Ответ: 1 Логарифмические уравнения Логарифмические уравнения. Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях «Тригонометрические уравнения», «Решение рациональных уравнений». В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты. Достаточно знать и понимать основное логарифмическое тождество, знать свойства логарифма. Обратите внимание на то, то после решения ОБЯЗАТЕЛЬНО нужно сделать проверку — подставить полученное значение в исходное уравнение и вычислить, в итоге должно получиться верное равенство. Определение: Логарифмом числа a по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a. Основное логарифмическое тождество: Например: log₃9 = 2, так как 3² = 9 Свойства логарифмов: Частные случаи логарифмов: Решим задачи. В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно. Найдите корень уравнения: log₃(4–x) = 4 Используем основное логарифмическое тождество. Так как log_ba = x b^x = a, то 3⁴ = 4 – x x = 4 – 81 x = – 77 Проверка: log₃(4–(–77)) = 4 log₃81 = 4 3⁴ = 81 Верно. Ответ: – 77 Решите самостоятельно: Найдите корень уравнения: log₂(4 – x) = 7 Посмотреть решение Найдите корень уравнения log₅(4 + x) = 2 Используем основное логарифмическое тождество. Так как log_ab = x b^x = a, то 5² = 4 + x x =5² – 4 x = 21 Проверка: log₅(4 + 21) = 2 log₅25 = 2 5² = 25 Верно. Ответ: 21 Найдите корень уравнения log₃(14 – x) = log₃5. Имеет место следующее свойство, смысл его таков: если в левой и правой частях уравнения имеем логарифмы с одинаковым основанием, то можем приравнять выражения, стоящие под знаками логарифмов. Если log_ca = log_cb, то a = b 14 – x = 5 x = 9 Сделайте проверку. Ответ: 9 Решите самостоятельно: Найдите корень уравнения log₅(5 – x) = log₅3. Посмотреть решение Найдите корень уравнения: log₄(x + 3) = log₄(4x – 15). Если log_ca = log_cb, то a = b x + 3 = 4x – 15 3x = 18 x = 6 Сделайте проверку. Ответ: 6 Найдите корень уравнения log_1/8(13 – x) = – 2. (1/8)^–2 = 13 – x 8² = 13 – x x = 13 – 64 x = – 51 Сделайте проверку. Небольшое дополнение – здесь используется свойство степени (отрицательная степень дроби). Ответ: – 51 Решите самостоятельно: Найдите корень уравнения: log_1/7(7 – x) = – 2 Посмотреть решение Найдите корень уравнения log₂(4 – x) = 2 log₂5. Преобразуем правую часть. воспользуемся свойством: log_ab^m = m∙log_ab log₂(4 – x) = log₂5² Если log_ca = log_cb, то a = b 4 – x = 5² 4 – x = 25 x = – 21 Сделайте проверку. Ответ: – 21 Решите самостоятельно: Найдите корень уравнения: log₅(5 – x) = 2 log₅3 Посмотреть решение Решите уравнение log₅(x² + 4x) = log₅(x² + 11) Если log_ca = log_cb, то a = b x² + 4x = x² + 11 4x = 11 x = 2,75 Сделайте проверку. Ответ: 2,75 Решите самостоятельно: Найдите корень уравнения log₅(x² + x) = log₅(x² + 10). Посмотреть решение Решите уравнение log₂(2 – x) = log₂(2 – 3x) +1. Необходимо с правой стороны уравнения получить выражение вида: log₂(……) Представляем 1 как логарифм с основанием 2: 1 = log₂2 Далее применяем свойство: log_с(ab) = log_сa + log_сb log₂(2 – x) = log₂(2 – 3x) + log₂2 Получаем: log₂(2 – x) = log₂ 2 (2 – 3x) Если log_ca = log_cb, то a = b, значит 2 – x = 4 – 6x 5x = 2 x = 0,4 Сделайте проверку. Ответ: 0,4 Решите самостоятельно: Найдите корень уравнения log₅(7 – x) = log₅(3 – x) +1 Посмотреть решение Решите уравнение log_х_–125 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них. Воспользуемся основным логарифмическим тождеством: (x – 1)²= 25 Далее необходимо решить квадратное уравнение. Кстати, квадратное уравнение, как вы поняли, это очень важная «буковка» в математической азбуке. К нему сводятся очень многие решения совершенно различных задач. Помнить формулы дискриминанта и корней нужно обязательно, и уметь решать такое уравнение вы должны очень быстро, периодически практикуйтесь. Конечно же, опытный глаз сразу увидит, что в нашем примере выражение, стоящее под знаком квадрата равно 5 или – 5, так как только эти два числа при возведении в квадрат дают 25, устно можно посчитать: корни равны 6 и – 4. Корень «–4» не является решением, так как основание логарифма должно быть больше нуля, а при «– 4» оно равно «–5». Решением является корень 6. Сделайте проверку. Ответ: 6. Решите самостоятельно: Решите уравнение log_x_–549 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них. Посмотреть решение Как вы убедились, никаких сложных преобразований с логарифмическими уравнениями нет. Достаточно знать свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!! С уважением, Александр Крутицких. P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях. 3
6	Решить для?	cos (x) = 1/2
7	Решить относительно x	sin (x) = — 1/2
8	Преобразование из градусов в радианы	225
9	Решить для?	cos (x) = (квадратный корень из 2) / 2
10	Решить относительно x	cos (x) = (квадратный корень из 3) / 2
11	Решить относительно x	sin (x) = (квадратный корень из 3) / 2
12	График	г (x) = 3/4 * корень пятой степени x
13	Найдите центр и радиус	х ^ 2 + у ^ 2 = 9
14	Преобразование из градусов в радианы	120 градусов
15	Преобразование из градусов в радианы	180
16	Найдите точное значение	коричневый (195)
17	Найдите степень	е (х) = 2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2
18	Решить для?	тангенс (x) = квадратный корень из 3
19	Решить для?	sin (x) = (квадратный корень из 2) / 2
20	Найдите центр и радиус	х ^ 2 + у ^ 2 = 25
21	Найдите центр и радиус	х ^ 2 + у ^ 2 = 4
22	Решить относительно x	2cos (x) -1 = 0
23	Решить относительно x	6x ^ 2 + 12x + 7 = 0
24	Найдите домен	х ^ 2
25	Найдите домен	е (х) = х ^ 2
26	Преобразование из градусов в радианы	330 градусов
27	Расширьте логарифмическое выражение	натуральный логарифм (x ^ 4 (x-4) ^ 2) / (квадратный корень из x ^ 2 + 1)
28	Упростить	((3x ^ 2) ^ 2y ^ 4) / (3y ^ 2)
29	Упростить	(csc (x) детская кроватка (x)) / (sec (x))
30	Решить для?	тангенс (х) = 0
31	Решить относительно x	х ^ 4-3x ^ 3-х ^ 2 + 3x = 0
32	Решить относительно x	cos (x) = sin (x)
33	Найдите точки пересечения по осям x и y	х ^ 2 + у ^ 2 + 6х-6у-46 = 0
34	Решить относительно x	квадратный корень из x + 30 = x
35	Упростить	детская кроватка (x) коричневый (x)
36	Найдите домен	у = х ^ 2
37	Найдите домен	квадратный корень из x ^ 2-4
38	Найдите точное значение	грех (255)
39	Оценить	, основание журнала 27 из 36
40	преобразовать из радианов в градусы	2п
41	Упростить	(F (x + h) -Fx) / час
42	Решить для?	2sin (x) ^ 2-3sin (x) + 1 = 0
43	Решить относительно x	tan (x) + квадратный корень из 3 = 0
44	Решить относительно x	sin (2x) + cos (x) = 0
45	Упростить	(1-соз (х)) (1 + соз (х))
46	Найдите домен	х ^ 4
47	Решить для?	2sin (x) + 1 = 0
48	Решить относительно x	х ^ 4-4x ^ 3-х ^ 2 + 4x = 0
49	Упростить	9 / (х ^ 2) + 9 / (х ^ 3)
50	Упростить	(детская кроватка (x)) / (csc (x))
51	Упростить	1 / (с ^ (3/5))
52	Упростить	квадратный корень из 9a ^ 3 + квадратный корень из
53	Найдите точное значение	желто-коричневый (285)
54	Найдите точное значение	cos (255)
55	Преобразовать в логарифмическую форму	12 ^ (x / 6) = 18
56	Расширьте логарифмическое выражение	(основание 27 из 36) (основание 36 из 49) (основание 49 из 81)
57	Недвижимость	х ^ 2 = 12 лет
58	Недвижимость	х ^ 2 + у ^ 2 = 25
59	График	f (x) = — натуральный логарифм x-1 + 3
60	Найдите значение, используя единичную окружность	арксин (-1/2)
61	Найдите домен	корень квадратный из 36-4x ^ 2
62	Упростить	(корень квадратный из x-5) ^ 2 + 3
63	Решить относительно x	х ^ 4-2x ^ 3-х ^ 2 + 2x = 0
64	Решить относительно x	у = (5-х) / (7х + 11)
65	Решить относительно x	х ^ 5-5x ^ 2 = 0
66	Решить относительно x	cos (2x) = (квадратный корень из 2) / 2
67	График	г = 3
68	График	f (x) = — логарифм по основанию 3 из x-1 + 3
69	Найдите корни (нули)	f (x) = 3x ^ 3-12x ^ 2-15x
70	Найдите степень	2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2
71	Решить относительно x	квадратный корень из x + 4 + квадратный корень из x-1 = 5
72	Решить для?	cos (2x) = — 1/2
73	Решить относительно x	основание журнала x 16 = 4
74	Упростить	е ^ х
75	Упростить	(соз (х)) / (1-грех (х)) + (1-грех (х)) / (соз (х))
76	Упростить	сек (x) sin (x)
77	Упростить	кубический корень из 24 кубический корень из 18
78	Найдите домен	квадратный корень из 16-x ^ 2
79	Найдите домен	квадратный корень из 1-x
80	Найдите домен	у = грех (х)
81	Упростить	корень квадратный из 25x ^ 2 + 25
82	Определить, нечетно ли, четно или нет	е (х) = х ^ 3
83	Найдите домен и диапазон	f (x) = квадратный корень из x + 3
84	Недвижимость	х ^ 2 = 4г
85	Недвижимость	(x ^ 2) / 25 + (y ^ 2) / 9 = 1
86	Найдите точное значение	cos (-210)
87	Упростить	кубический корень 54x ^ 17
88	Упростить	квадратный корень из квадратного корня 256x ^ 4
89	Найдите домен	е (х) = 3 / (х ^ 2-2x-15)
90	Найдите домен	квадратный корень из 4-x ^ 2
91	Найдите домен	квадратный корень из x ^ 2-9
92	Найдите домен	е (х) = х ^ 3
93	Решить относительно x	е ^ х-6е ^ (- х) -1 = 0
94	Решить относительно x	6 ^ (5x) = 3000
95	Решить относительно x	4cos (x-1) ^ 2 = 0
96	Решить относительно x	3x + 2 = (5x-11) / (8лет)
97	Решить для?	грех (2x) = — 1/2
98	Решить относительно x	(2x-1) / (x + 2) = 4/5
99	Решить относительно x	сек (4x) = 2
100	Решите для n	(4n + 8) / (n ^ 2 + n-72) + 8 / (n ^ 2 + n-72) = 1 / (n + 9)

Mathway | Популярные задачи

1	Упростить	корень квадратный из s корень квадратный из s ^ 7
2	Упростить	кубический корень из 8x ^ 7y ^ 9z ^ 3
3	Упростить	arccos ((квадратный корень из 3) / 2)
4	Решить для?	грех (х) = 1/2
5	Упростить	корень квадратный из s корень квадратный из s ^ 3
6	Решить для?	cos (x) = 1/2
7	Решить относительно x	sin (x) = — 1/2
8	Преобразование из градусов в радианы	225
9	Решить для?	cos (x) = (квадратный корень из 2) / 2
10	Решить относительно x	cos (x) = (квадратный корень из 3) / 2
11	Решить относительно x	sin (x) = (квадратный корень из 3) / 2
12	График	г (x) = 3/4 * корень пятой степени x
13	Найдите центр и радиус	х ^ 2 + у ^ 2 = 9
14	Преобразование из градусов в радианы	120 градусов
15	Преобразование из градусов в радианы	180
16	Найдите точное значение	коричневый (195)
17	Найдите степень	е (х) = 2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2
18	Решить для?	тангенс (x) = квадратный корень из 3
19	Решить для?	sin (x) = (квадратный корень из 2) / 2
20	Найдите центр и радиус	х ^ 2 + у ^ 2 = 25
21	Найдите центр и радиус	х ^ 2 + у ^ 2 = 4
22	Решить относительно x	2cos (x) -1 = 0
23	Решить относительно x	6x ^ 2 + 12x + 7 = 0
24	Найдите домен	х ^ 2
25	Найдите домен	е (х) = х ^ 2
26	Преобразование из градусов в радианы	330 градусов
27	Разверните логарифмическое выражение	натуральный логарифм (x ^ 4 (x-4) ^ 2) / (квадратный корень из x ^ 2 + 1)
28	Упростить	((3x ^ 2) ^ 2y ^ 4) / (3y ^ 2)
29	Упростить	(csc (x) детская кроватка (x)) / (sec (x))
30	Решить для?	тангенс (х) = 0
31	Решить относительно x	х ^ 4-3x ^ 3-х ^ 2 + 3x = 0
32	Решить относительно x	cos (x) = sin (x)
33	Найдите точки пересечения x и y	х ^ 2 + у ^ 2 + 6х-6у-46 = 0
34	Решить относительно x	квадратный корень из x + 30 = x
35	Упростить	детская кроватка (x) коричневый (x)
36	Найдите домен	у = х ^ 2
37	Найдите домен	квадратный корень из x ^ 2-4
38	Найдите точное значение	грех (255)
39	Оценить	, основание журнала 27 из 36
40	преобразовать из радианов в градусы	2п
41	Упростить	(F (x + h) -Fx) / час
42	Решить для?	2sin (x) ^ 2-3sin (x) + 1 = 0
43	Решить относительно x	tan (x) + квадратный корень из 3 = 0
44	Решить относительно x	sin (2x) + cos (x) = 0
45	Упростить	(1-соз (х)) (1 + соз (х))
46	Найдите домен	х ^ 4
47	Решить для?	2sin (x) + 1 = 0
48	Решить относительно x	х ^ 4-4x ^ 3-х ^ 2 + 4x = 0
49	Упростить	9 / (х ^ 2) + 9 / (х ^ 3)
50	Упростить	(детская кроватка (x)) / (csc (x))
51	Упростить	1 / (с ^ (3/5))
52	Упростить	квадратный корень из 9a ^ 3 + квадратный корень из
53	Найдите точное значение	желто-коричневый (285)
54	Найдите точное значение	cos (255)
55	Преобразовать в логарифмическую форму	12 ^ (x / 6) = 18
56	Разверните логарифмическое выражение	(основание 27 из 36) (основание 36 из 49) (основание 49 из 81)
57	Недвижимость	x ^ 2 = 12 лет
58	Недвижимость	х ^ 2 + у ^ 2 = 25
59	График	f (x) = — натуральный логарифм x-1 + 3
60	Найдите значение, используя единичную окружность	арксин (-1/2)
61	Найдите домен	корень квадратный из 36-4x ^ 2
62	Упростить	(корень квадратный из x-5) ^ 2 + 3
63	Решить относительно x	х ^ 4-2x ^ 3-х ^ 2 + 2x = 0
64	Решить относительно x	у = (5-х) / (7х + 11)
65	Решить относительно x	х ^ 5-5x ^ 2 = 0
66	Решить относительно x	cos (2x) = (квадратный корень из 2) / 2
67	График	г = 3
68	График	f (x) = — логарифм по основанию 3 из x-1 + 3
69	Найдите корни (нули)	f (x) = 3x ^ 3-12x ^ 2-15x
70	Найдите степень	2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2
71	Решить относительно x	квадратный корень из x + 4 + квадратный корень из x-1 = 5
72	Решить для?	cos (2x) = — 1/2
73	Решить относительно x	логарифм по основанию x 16 = 4
74	Упростить	е ^ х
75	Упростить	(соз (х)) / (1-грех (х)) + (1-грех (х)) / (соз (х))
76	Упростить	сек (x) sin (x)
77	Упростить	кубический корень из 24 кубический корень из 18
78	Найдите домен	квадратный корень из 16-x ^ 2
79	Найдите домен	квадратный корень из 1-x
80	Найдите домен	у = грех (х)
81	Упростить	квадратный корень из 25x ^ 2 + 25
82	Определить, нечетно ли, четно или нет	е (х) = х ^ 3
83	Найдите домен и диапазон	f (x) = квадратный корень из x + 3
84	Недвижимость	х ^ 2 = 4г
85	Недвижимость	(x ^ 2) / 25 + (y ^ 2) / 9 = 1
86	Найдите точное значение	cos (-210)
87	Упростить	кубический корень 54x ^ 17
88	Упростить	квадратный корень из квадратного корня 256x ^ 4
89	Найдите домен	е (х) = 3 / (х ^ 2-2x-15)
90	Найдите домен	квадратный корень из 4-x ^ 2
91	Найдите домен	квадратный корень из x ^ 2-9
92	Найдите домен	е (х) = х ^ 3
93	Решить относительно x	е ^ х-6е ^ (- х) -1 = 0
94	Решить относительно x	6 ^ (5x) = 3000
95	Решить относительно x	4cos (x-1) ^ 2 = 0
96	Решить относительно x	3x + 2 = (5x-11) / (8лет)
97	Решить для?	грех (2x) = — 1/2
98	Решить относительно x	(2x-1) / (x + 2) = 4/5
99	Решить относительно x	сек (4x) = 2
100	Решите для n	(4n + 8) / (n ^ 2 + n-72) + 8 / (n ^ 2 + n-72) = 1 / (n + 9)

Калькулятор логарифма log (x)

Калькулятор логарифма находит результат логарифмической функции (может быть назван экспонентой) из заданного основного числа и действительного числа.

Логарифм

Логарифм считается одним из основных понятий в математике.
Определений существует множество, начиная от действительно сложных и заканчивая довольно простыми.
Чтобы ответить на вопрос, что такое логарифм, давайте взглянем на таблицу ниже:

Это таблица, в которой мы можем видеть значения двух квадратов, двух кубов и так далее.
Это операция в математике, известная как возведение в степень .
Если мы посмотрим на числа в нижней строке, мы можем попытаться найти значение степени, до которого нужно возвести 2, чтобы получить это число.Например, чтобы получить 16, необходимо возвести два в четвертую степень.
А чтобы получить 64, нужно возвести два в шестую степень.

Следовательно, логарифм — это показатель степени, до которого необходимо возвести фиксированное число (которое называется основанием), чтобы получить число y.
Другими словами, логарифм можно представить в следующем виде:

журнал _b x = y

, где b — основание, x — действительное число, а y — показатель степени.

Например, 2 ³ = 8 ⇒ log ₂ 8 = 3 (логарифм 8 по основанию 2 равен 3, потому что 2 ³ = 8).
Аналогично, log ₂ 64 = 6, потому что 2 ⁶ = 64.

Следовательно, очевидно, что операция логарифмирования является обратной по отношению к возведению в степень .

2 ¹	2 ²	2 ³	2 ⁴	2 ⁵	2 ⁶
2	4	8	16	32	64
журнал ₂ 2 = 1	журнал ₂ 4 = 2	журнал ₂ 8 = 3	журнал ₂ 16 = 4	журнал ₂ 32 = 5	журнал ₂ 64 = 6

К сожалению, не все логарифмы можно так легко вычислить.Например, найти журнал ₂ 5 вряд ли возможно, просто используя наши простые вычислительные возможности.
Воспользовавшись калькулятором логарифмов, мы можем узнать, что

журнал ₂ 5 = 2,321

Есть несколько особых типов логарифмов.
Например, логарифм с основанием 2 известен как двоичный логарифм,
и он широко используется в информатике и языках программирования.
Логарифм с основанием 10 обычно называют десятичным логарифмом,
и имеет огромное количество приложений в инженерии, научных исследованиях, технологиях и т. д.Наконец, так называемый натуральный логарифм использует число e (которое приблизительно равно 2,71828) в качестве основания,
и этот вид логарифма имеет большое значение в математике, физике,
и другие точные науки.

Логарифм log _b (x) = y читается как логарифм с основанием b x равно y .
Обратите внимание, что основание журнала номер b должно быть больше 0 и не должно равняться 1.
И число (x), которое мы вычисляем log с основанием (b), должно быть положительным действительным числом.

Например, журнал 2 из 8 равен 3.

 журнал ₂ (8) = 3 (лог по основанию 2 из 8)
Экспонента равна 2 ³ = 8

Общие значения для базы журнала

Логарифмические тождества

Список логарифмических отождествлений, формул и примеров логарифмов в логарифмической форме.

Логарифм произведения

 журнал _b (x · y) = журнал _b (x) + журнал _b (y)
журнал ₂ (5 · 7) = журнал ₂ (5) + журнал ₂ (7)

Логарифм частного

 журнал _b (x / y) = журнал _b (x) - журнал _b (y)
журнал ₂ (5/7) = журнал ₂ (5) - журнал ₂ (7)

Логарифм степени

 журнал _b (x ^y) = y · log _b (x)
журнал ₂ (5 ⁷) = 7 · журнал ₂ (5)

Изменение базы

 журнал _b (x) = (журнал _k (x)) / (журнал _k (b))

Примеры натурального логарифма

ln (2) = log _e (2) = 0. 6931
ln (3) = log _e (3) = 1,0986
ln (4) = log _e (4) = 1,3862
ln (5) = log _e (5) = 1,609
ln (6) = log _e (6) = 1,7917
ln (10) = log _e (10) = 2.3025

Таблицы логарифмических значений

Список таблиц значений функций журнала в общих базовых числах.

83

1 9000 9000 12)

83

18)

200004 фунтов 4.321928

1 9000

1 9000 9000 24)

log ₂ (x)	Обозначение	Значение
log ₂ (1)	фунтов (1)	0
log ₂	(2) (2)	1
log ₂ (3)	фунтов (3)	1.584963
log ₂ (4)	фунтов (4)	2
log ₂ (5)	фунтов (5)	2.321928
фунтов (6)	2,584963
log ₂ (7)	фунтов (7)	2,807355
log ₂ (8)	фунтов 3
журнал ₂ (9)	фунтов (9)	3. 169925
log ₂ (10)	фунтов (10)	3,321928
log ₂ (11)	фунтов (11)	3.459432	фунтов (12)	3,584963
log ₂ (13)	фунтов (13)	3,70044
log ₂ (14)	фунтов 3.807355
log ₂ (15)	фунтов (15)	3.
log ₂ (16)	фунтов (16)	4
log ₂ (17)	фунтов (17)	4.087463	фунтов (18)	4.169925
log ₂ (19)	фунтов (19)	4.247928
log ₂ (20)
log ₂ (21)	фунта (21)	4.3
log ₂ (22)	фунтов (22)	4,459432
log ₂ (23)	фунтов (23)	4. 523562	4.523562	фунта (24)	4.584963

83 5)

83 84 журнал 11)

83 17)

журнал (194) 1,278754

83 83 23)

журнал ₁₀ (x)	Обозначение	Значение
журнал ₁₀ (1)	журнал (1)	0
журнал ₁₀		журнал ₁₀		журнал (2)	0.30103
журнал ₁₀ (3)	журнал (3)	0,477121
журнал ₁₀ (4)	журнал (4)	0,60206	журнал (5)	0,69897
журнал ₁₀ (6)	журнал (6)	0,778151
журнал ₁₀ (7)	журнал (7) 0,845098
лог ₁₀ (8)	лог (8)	0.
журнал ₁₀ (9)	журнал (9)	0,	3
журнал ₁₀ (10)	журнал (10)	1
журнал (11)	1. 041393
журнал ₁₀ (12)	журнал (12)	1.079181
журнал ₁₀ (13)	журнал (134) 1,113943
журнал ₁₀ (14)	журнал (14)	1.146128
журнал ₁₀ (15)	журнал (15)	1,176091
журнал ₁₀ (16)	журнал (16)	1.20412	журнал (17)	1.230449
журнал ₁₀ (18)	журнал (18)	1.255273
журнал ₁₀ (19)
журнал ₁₀ (20)	журнал (20)	1.30103
журнал ₁₀ (21)	журнал (21)	1,322219
журнал ₁₀ (22)	журнал (22)	1,342423	журнал (23)	1,361728
журнал ₁₀ (24)	журнал (24)	1,380211

000 (2) (2)

1 log 5)

130004

1 9000

1 9000 9000 17)

1 log

1 9000 9000 23)

log _e (x)	Обозначение	Значение
log _e (1)	ln (1)	0
log _e	0. 6
log _e (3)	ln (3)	1.0
log _e (4)	ln (4)	1.386294 9000 9000	ln (5)	1.609438
log _e (6)	ln (6)	1.7
log _e (7)	ln5 1.
лог _e (8)	ln (8)	2.079442
log _e (9)	ln (9)	2,1
log _e (10)	ln (10)	2.302585 9000 9000	11 log 11)	ln (11)	2.3
log _e (12)	ln (12)	2.484907
log _e (13)	ln 2,564949
лог _e (14)	ln (14)	2.639057
log _e (15)	ln (15)	2,70805
log _e (16)	ln (16)	2. 772589	2.772589	ln (17)	2.833213
log _e (18)	ln (18)	2.8
log _e (19)		ln5 2.₉
лог _e (20)	ln (20)	2.9
log _e (21)	ln (21)	3.044522
log _e (22)	ln (22)	3.0
3.0
ln (23)	3.135494
log _e (24)	ln (24)	3.178054

Калькуляторы связанной базы журналов

Калькулятор общего журнала log (x) base 10 Log10 Calculator

Common Log Calculator log (x) base 10 Log10 Calculator

Калькулятор десятичного логарифма находит результат функции логарифма по основанию 10. Вычислите по основанию 10 числа.

Примеры десятичных логарифмов

Используя логарифм идентификатора продукта, найдите общий журнал из 120:

журнал (120) = журнал (100 × 1,2)
журнал (120) = журнал (100) + журнал (1,2)
журнал (120) = 2 + 0746 = 2,0746

Использование логарифма степенного тождества для нахождения общего журнала из 10 ⁶:

журнал (10 ⁶) = 6 × журнал (10)
журнал (10 ⁶) = 6 × 1 = 6

Общий логарифм с основанием 10 Таблицы значений

Список таблиц значений функций общего журнала, логическая основа 10 чисел.

83 8)

83 14)

83 83 20)

829

83

26)

журнал (284) 1.447158

83 (

83) 32)

журнал (344) 1,531479

83 83 38)

журнал (404) 1.60206

83 44)

83 50)

журнал (524) 1,716003

83 56)

журнал (584) 1.763428

83 62)

83 68)

83 83 74)

83 83 80)

8

86)89

83 92)

83 98)

журнал ₁₀ (x)	Обозначение	Значение
журнал ₁₀ (1)	журнал (1)	0
журнал ₁₀		журнал ₁₀		журнал (2)	0,30103
журнал ₁₀ (3)	журнал (3)	0,477121
журнал ₁₀ (4)	журнал (4)		0,6011 журнал ₁₀ (5)	журнал (5)	0. 69897
журнал ₁₀ (6)	журнал (6)	0,778151
журнал ₁₀ (7)	журнал (7)	104098	журнал (8)	0,
журнал ₁₀ (9)	журнал (9)	0,	3
журнал ₁₀ (10)		журнал (10) 1
журнал ₁₀ (11)	журнал (11)	1.041393
журнал ₁₀ (12)	журнал (12)	1.079181
журнал ₁₀ (13)	журнал (13)	1113943	журнал (14)	1,146128
журнал ₁₀ (15)	журнал (15)	1,176091
журнал ₁₀ (16)	журнал (164) 1.20412
журнал ₁₀ (17)	журнал (17)	1. 230449
журнал ₁₀ (18)	журнал (18)	1.255273
журнал ₁₀ (19)	журнал (19)	1078754	журнал (20)	1,30103
журнал ₁₀ (21)	журнал (21)	1,322219
журнал ₁₀ (22)		журнал (22) 1,342423
журнал ₁₀ (23)	журнал (23)	1.361728
журнал ₁₀ (24)	журнал (24)	1,380211
журнал ₁₀ (25)	журнал (25)	1,39794
журнал (26)	1.414973
журнал ₁₀ (27)	журнал (27)	1.431364
журнал ₁₀ (28)
журнал ₁₀ (29)	журнал (29)	1. 462398
журнал ₁₀ (30)	журнал (30)	1,477121
журнал ₁₀ (31)	журнал (31)	1.4		журнал (32)	1.50515
журнал ₁₀ (33)	журнал (33)	1.518514
журнал ₁₀ (34)
журнал ₁₀ (35)	журнал (35)	1.544068
журнал ₁₀ (36)	журнал (36)	1.556303
журнал ₁₀ (37)	журнал (37)	1068202
журнал (38)	1,579784
журнал ₁₀ (39)	журнал (39)	1,5
журнал ₁₀ (40)
лог ₁₀ (41)	лог (41)	1. 612784
журнал ₁₀ (42)	журнал (42)	1,623249
журнал ₁₀ (43)	журнал (43)	10633468	журнал (44)	1,643453
журнал ₁₀ (45)	журнал (45)	1,653213
журнал ₁₀ (46)		журнал (46) 1.662758
журнал ₁₀ (47)	журнал (47)	1.672098
журнал ₁₀ (48)	журнал (48)	1,681241
журнал ₁₀ (49)	журнал (49)	10	журнал (50)	1,69897
журнал ₁₀ (51)	журнал (51)	1,70757
журнал ₁₀ (52)
журнал ₁₀ (53)	журнал (53)	1. 724276
log ₁₀ (54)	log (54)	1,732394
log ₁₀ (55)	log (55)	1040363	журнал (56)	1,748188
журнал ₁₀ (57)	журнал (57)	1,755875
журнал ₁₀ (58)
журнал ₁₀ (59)	журнал (59)	1.770852
log ₁₀ (60)	log (60)	1.778151
log ₁₀ (61)	log (61)	1,78533	журнал (62)	1,7
журнал ₁₀ (63)	журнал (63)	1,7
журнал ₁₀ (64)		журнал (644) 1.80618
лог ₁₀ (65)	лог (65)	1. 812913
журнал ₁₀ (66)	журнал (66)	1,819544
журнал ₁₀ (67)	журнал (67)	10,826075	журнал (68)	1,832509
журнал ₁₀ (69)	журнал (69)	1,838849
журнал ₁₀ (70)	журнал (704) 1.845098
лог ₁₀ (71)	лог (71)	1.851258
журнал ₁₀ (72)	журнал (72)	1.857332
журнал ₁₀ (73)	журнал (73)	1063323	журнал (74)	1,869232
журнал ₁₀ (75)	журнал (75)	1.875061
журнал ₁₀ (76)	журнал (760004) 1,880814
журнал ₁₀ (77)	журнал (77)	1. 886491
журнал ₁₀ (78)	журнал (78)	1.8
журнал ₁₀ (79)	журнал (79)	10	журнал (80)	1.
журнал ₁₀ (81)	журнал (81)	1.
журнал ₁₀ (82)	журнал (82000)		журнал (82) 1.
журнал ₁₀ (83)	журнал (83)	1.8
журнал ₁₀ (84)	журнал (84)	1.
журнал ₁₀ (85)	журнал (85)	1,₉
журнал (86)	1.
журнал ₁₀ (87)	журнал (87)	1.
журнал ₁₀ (88)	журнал (884) 1.	3
журнал ₁₀ (89)	журнал (89)	1.
журнал ₁₀ (90)	журнал (90)	1.	3
журнал ₁₀ (91)	журнал (91)	1,	1	журнал (92)	1.	8
журнал ₁₀ (93)	журнал (93)	1.	3
журнал ₁₀ (94)	журнал (94) 1.	8
журнал ₁₀ (95)	журнал (95)	1.	4
журнал ₁₀ (96)	журнал (96)	1.
журнал ₁₀ (97)	журнал (97)	1,
журнал (98)	1.9
журнал ₁₀ (99)	журнал (99)	1.9

83 500)

83 83 1700)

журнал ₁₀ (x)	Обозначение	Значение
журнал ₁₀ (100)	журнал (100)	2
журнал ₁₀		журнал (200)	2. 30103
журнал ₁₀ (300)	журнал (300)	2,477121
журнал ₁₀ (400)	журнал (400)	2,60206
журнал (500)	2.69897
журнал ₁₀ (600)	журнал (600)	2.778151
журнал ₁₀ (700)	журнал (700000)	журнал (700000) 2,845098
журнал ₁₀ (800)	журнал (800)	2.
журнал ₁₀ (900)	журнал (900)	2.	3
журнал ₁₀ (1000)	журнал (1000)	3
журнал 1100)	журнал (1100)	3.041393
журнал ₁₀ (1200)	журнал (1200)	3.079181
журнал ₁₀ (1300)	журнал 3,113943
журнал ₁₀ (1400)	журнал (1400)	3. 146128
журнал ₁₀ (1500)	журнал (1500)	3,176091
журнал ₁₀ (1600)	журнал (1600)	3.20412	журнал (1700)	3,230449
журнал ₁₀ (1800)	журнал (1800)	3.255273
журнал ₁₀ (1900)	журнал 3,278754
журнал ₁₀ (2000)	журнал (2000)	3.30103
журнал ₁₀ (2100)	журнал (2100)	3,322219
журнал ₁₀ (2200)	журнал (2200)	3,3424230003 9000 9000	3,342423000 9000 9000	3,342423000 9000 9000	2300)	журнал (2300)	3,361728
журнал ₁₀ (2400)	журнал (2400)	3.380211
журнал ₁₀ (2500)	журнал 3,39794
журнал ₁₀ (2600)	журнал (2600)	3. 414973
журнал ₁₀ (2700)	журнал (2700)	3,431364
журнал ₁₀ (2800)	журнал (2800)	3.447189

3,44718

0 2900)

000

000 3,568202

1 9000

1 9000 9000 4100)

000 9000 4300

000000

журнал (2900)	3,462398
журнал ₁₀ (3000)	журнал (3000)	3.477121
журнал ₁₀ (3100)	журнал 3.4
журнал ₁₀ (3200)	журнал (3200)	3.50515
журнал ₁₀ (3300)	журнал (3300)	3,518514
журнал ₁₀ (3400)	журнал (3400)	3,53147		3.531479 9000 9000	3500)	журнал (3500)	3,544068
журнал ₁₀ (3600)	журнал (3600)	3,556303
журнал ₁₀ (3700)
журнал ₁₀ (3800)	журнал (3800)	3. 579784
журнал ₁₀ (3900)	журнал (3900)	3,5
журнал ₁₀ (4000)	журнал (4000)	3,60203	3.60203	журнал (4100)	3,612784
журнал ₁₀ (4200)	журнал (4200)	3.623249
журнал ₁₀ (4300)	000 3.633468
журнал ₁₀ (4400)	журнал (4400)	3.643453
журнал ₁₀ (4500)	журнал (4500)	3,653213
журнал ₁₀ (4600)	журнал (4600)	3.662758
3.662758

0 4700)

000

000 9000 9000

5300)

000

000 ₁₀ (5500)

000

000 3,740363

журнал (4700)	3.672098
журнал ₁₀ (4800)	журнал (4800)	3.681241
журнал ₁₀ (4900)	000 3,6
журнал ₁₀ (5000)	журнал (5000)	3. 69897
журнал ₁₀ (5100)	журнал (5100)	3.70757
журнал ₁₀ (5200)	журнал (5200)	3,716003
3,716003
журнал (5300)	3,724276
журнал ₁₀ (5400)	журнал (5400)	3,732394
журнал ₁₀ (5500)
журнал ₁₀ (5600)	журнал (5600)	3.748188
журнал ₁₀ (5700)	журнал (5700)	3,755875
журнал ₁₀ (5800)	журнал (5800)	3.761830 00

900 5900)

6500)

0005 3.826075

4 9184 9000

000

000) 3.863323

7700)

000

8300)

000 3.₉

4 9183

8900)

9500)

000)

000

000 3.

3.761834 00	журнал (5900)	3,770852
журнал ₁₀ (6000)	журнал (6000)	3. 778151
журнал ₁₀ (6₎	журнал 3,78533
журнал ₁₀ (6200)	журнал (6200)	3.7
журнал ₁₀ (6300)	журнал (6300)	3,7
журнал ₁₀ (6400)	журнал (6400)	3,80618	3,80618 9000 9000	журнал (6500)	3.812913
журнал ₁₀ (6600)	журнал (6600)	3.819544
журнал ₁₀ (67004000)
журнал ₁₀ (6800)	журнал (6800)	3.832509
журнал ₁₀ (6900)	журнал (6900)	3.838849
журнал ₁₀ (7000)	журнал (7000)		3,8450 9000 9000 7100)	журнал (7100)	3. 851258
журнал ₁₀ (7200)	журнал (7200)	3.857332
журнал ₁₀ (7300)
журнал ₁₀ (7400)	журнал (7400)	3.869232
журнал ₁₀ (7500)	журнал (7500)	3,875061
журнал ₁₀ (7600)	журнал (7600)	3.88011
3.88011
журнал (7700)	3.886491
журнал ₁₀ (7800)	журнал (7800)	3.8
журнал ₁₀ (7900)	000 3.8
журнал ₁₀ (8000)	журнал (8000)	3.
журнал ₁₀ (8100)	журнал (8100)	3.
журнал ₁₀ (8200)	журнал (8200)	3.	3.	журнал (8300)	3.8
журнал ₁₀ (8400)	журнал (8400)	3.
журнал ₁₀ (85004000)
журнал ₁₀ (8600)	журнал (8600)	3.
журнал ₁₀ (8700)	журнал (8700)	3.
журнал ₁₀ (8800)	журнал (8800)
журнал (8900)	3.
журнал ₁₀ (9000)	журнал (9000)	3.	3
журнал ₁₀ (	) 000 000 000 3.	1
журнал ₁₀ (9200)	журнал (9200)	3.	8
журнал ₁₀ (9300)	журнал (9300)	3.	3
журнал ₁₀ (9400)	журнал (9400)	3.	8
3.	8	журнал (9500)	3.	4
журнал ₁₀ (9600)	журнал (9600)	3.
журнал ₁₀ (
журнал ₁₀ (9800)	журнал (9800)	3.9
журнал ₁₀ (9900)	журнал (9900)	3.9

8

7000)

000

000 3.

14000)

000

20000)

000

0004000 4.342423

000

32000)

000

38000)

000

000 4.60206

log ₁₀ (x)	Обозначение	Значение
log ₁₀ (1000)	log (1000)	3
log ₁₀		log (2000)	3.30103
log ₁₀ (3000)	log (3000)	3.477121
log ₁₀ (4000)	log (4000)	3. 60206
журнал ₁₀ (5000)	журнал (5000)	3.69897
журнал ₁₀ (6000)	журнал (6000)	3,778151
журнал (7000)	3.845098
журнал ₁₀ (8000)	журнал (8000)	3.
журнал ₁₀ (9000)	000)	3
журнал ₁₀ (10000)	журнал (10000)	4
журнал ₁₀ (11000)	журнал (11000)	4.041393
журнал ₁₀ (12000)	журнал (12000)	4.079181
журнал ₁₀ (13000)	журнал (13000)	4.113943
4.113943	4.113943	журнал (14000)	4.146128
журнал ₁₀ (15000)	журнал (15000)	4. 176091
журнал ₁₀ (160004000)	0004 4.20412
журнал ₁₀ (17000)	журнал (17000)	4.230449
журнал ₁₀ (18000)	журнал (18000)	4,255273
журнал ₁₀ (19000)	журнал (19000)	4,278754
4,278754	4,278754	журнал (20000)	4,30103
журнал ₁₀ (21000)	журнал (21000)	4,322219
журнал ₁₀ (22000)
журнал ₁₀ (23000)	журнал (23000)	4.361728
журнал ₁₀ (24000)	журнал (24000)	4.380211
журнал ₁₀ (25000)	журнал (25000)	4,397	4,397 26000)	журнал (26000)	4. 414973
журнал ₁₀ (27000)	журнал (27000)	4.431364
журнал ₁₀ (28000)		4.447158
журнал ₁₀ (29000)	журнал (29000)	4.462398
журнал ₁₀ (30000)	журнал (30000)	4,477121
журнал ₁₀ (31000)	журнал (31000)	4.4
4.4		журнал (32000)	4.50515
журнал ₁₀ (33000)	журнал (33000)	4.518514
журнал ₁₀ (34000) 9000 34000 9000 34000 9000 34000 9000 34000 4.531479
журнал ₁₀ (35000)	журнал (35000)	4.544068
журнал ₁₀ (36000)	журнал (36000)	4.556303
журнал ₁₀ (37000)	журнал (37000)	4. 568202 9000 9000 9000
4.568202	журнал (38000)	4.579784
журнал ₁₀ (39000)	журнал (39000)	4.5
журнал ₁₀ (40000)
журнал ₁₀ (41000)	журнал (41000)	4.612784
журнал ₁₀ (42000)	журнал (42000)	4.623249
журнал ₁₀ (43000)	журнал (43000)	4.6334 00

44000)

000

000 4.662758

50000)

000

4.6334 00	журнал (44000)	4,643453
журнал ₁₀ (45000)	журнал (45000)	4.653213
журнал ₁₀ (46000)	000)
журнал ₁₀ (47000)	журнал (47000)	4.672098
журнал ₁₀ (48000)	журнал (48000)	4,681241
журнал ₁₀ (49000)	журнал (49000)	4. 6	000	4,6
4,6	журнал (50000)	4.69897
журнал ₁₀ (51000)	журнал (51000)	4.70757
журнал ₁₀ (52000)	журнал 4,716003
журнал ₁₀ (53000)	журнал (53000)	4.724276
log ₁₀ (54000)	log (54000)	4,732394
log ₁₀ (55000)	log (55000)	4,740183

4,740183

0 56000)

000

000)

000 4.80618

68000)

000

000)

000 4.845098

000 9000

74000)

000

0004 4.880814

80000)

000

000 4.

журнал (56000)

4,748188

журнал ₁₀ (57000)

журнал (57000)

4.755875

журнал ₁₀ (58000)

000 4,763428

журнал ₁₀ (59000)

журнал (59000)

4.770852

журнал ₁₀ (60000)

журнал (60000)

778151

журнал ₁₀ (61000)

журнал (61000)

30 (61000)

журнал (61000)

85000

62000)

журнал (62000)

4,7

журнал ₁₀ (63000)

журнал (63000)

4,7

журнал ₁₀ (64000)

журнал ₁₀ (65000)

журнал (65000)

4.812913

журнал ₁₀ (66000)

журнал (66000)

4,819544

журнал ₁₀ (67000)

журнал (67000)

4.826018 00

4,826018

журнал (68000)

4.832509

журнал ₁₀ (69000)

журнал (69000)

838849

журнал ₁₀ (70000)

журнал ₁₀ (71000)

журнал (71000)

4.851258

журнал ₁₀ (72000)

журнал (72000)

4,857332

журнал ₁₀ (73000)

журнал (73000)

4,863323

4,863323 9000 9000

журнал (74000)

4,869232

журнал ₁₀ (75000)

журнал (75000)

4.875061

журнал ₁₀ (76000)

журнал ₁₀ (77000)

журнал (77000)

4.886491

журнал ₁₀ (78000)

журнал (78000)

4,8

журнал ₁₀ (79000)

журнал (79000)

4,8

0 9000

4,8

журнал (80000)

журнал ₁₀ (81000)

журнал (81000)

журнал ₁₀ (820004)

журнал ₁₀ (83000)

журнал (83000)

4.8

журнал ₁₀ (84000)

журнал (84000)

журнал ₁₀ (85000)

журнал (85000)

4.₉

0 86000)89

000

000)

000 4.

журнал (86000)

журнал ₁₀ (87000)

журнал (87000)

журнал ₁₀ (88000)

журнал ₁₀ (89000)

журнал (89000)

журнал ₁₀ ()

журнал ()

журнал ₁₀ (

)

журнал (

)

4,953

900

4,953 9000 9000

)

000

000)

000 4.

072

журнал ()	4,	8
журнал ₁₀ (	)	журнал (	)	4.	3
журнал ₁₀ (
8
журнал ₁₀ (	)	журнал (	)	4.	4
log ₁₀ (	)	log (	)	4.
log ₁₀ (	)	log (	)	4.

072

0 )

)

журнал ()	4,9
журнал ₁₀ (	журнал (	4.9

База логарифма 2 Калькулятор Log2

Калькулятор логарифма 2 находит результат функции логарифма по основанию 2.Вычислите логарифм по основанию 2 числа.

Калькулятор бревенчатой базы 2
журнал ₂
Рассчитать

журнал ₂ (x) = y

x: — действительное число, x> 0

журнал ₂ (x) = y и x = 2 ^y

База логарифмических данных 2 таблицы значений

Список журналов ₂ таблиц значений функций, база 2 чисел.

83

1 9000 9000 12)

83

18)

200004 фунтов 4.321928

1 9000

1 9000 9000 24)

000

36)

4440005 фунтов 5,459432

9004 9000 9000 9000 48)

1 9000 9000 54)

560004

1 9000

1 9000 9000 60)

624

83 829 66)

6840005 фунтов 6.087463

1 9000 9000 78)

1 9000

1 9000 9000 84)

860005

1 9000

1 9000 9000 90)

фунтов 6.523562

log ₂ (x)	Обозначение	Значение
log ₂ (1)	фунтов (1)	0
log ₂	(2) (2)	1
log ₂ (3)	фунтов (3)	1.584963
log ₂ (4)	фунтов (4)	2
log ₂ (5)	фунтов (5)	2.321928
фунтов (6)	2,584963
log ₂ (7)	фунтов (7)	2,807355
log ₂ (8)	фунтов 3
журнал ₂ (9)	фунтов (9)	3.169925
log ₂ (10)	фунтов (10)	3,321928
log ₂ (11)	фунтов (11)	3.459432	фунтов (12)	3,584963
log ₂ (13)	фунтов (13)	3,70044
log ₂ (14)	фунтов 3. 807355
log ₂ (15)	фунтов (15)	3.
log ₂ (16)	фунтов (16)	4
log ₂ (17)	фунтов (17)	4.087463	фунтов (18)	4.169925
log ₂ (19)	фунтов (19)	4.247928
log ₂ (20)
log ₂ (21)	фунта (21)	4.3
log ₂ (22)	фунта (22)	4.459432
log ₂ (23)	фунтов (23)	4.523562	4.523562	фунтов (24)	4.584963
log ₂ (25)	фунтов (25)	4.643856
log ₂ (26)	фунтов 4,70044
log ₂ (27)	фунтов (27)	4. 754888
log ₂ (28)	фунтов (28)	4.807355
log ₂ (29)	фунтов (29)	4.857 95	4.857 95	4.857 95	30)	фунтов (30)	4.
log ₂ (31)	фунтов (31)	4.
log ₂ (32)	фунтов 5
журнал ₂ (33)	фунта (33)	5.044394
log ₂ (34)	фунтов (34)	5,087463
log ₂ (35)	фунтов (35)	5.129283 8295	5.129283
фунтов (36)	5.169925
log ₂ (37)	фунтов (37)	5.209453
log ₂ (38)	фунтов 5. 247928
log ₂ (39)	фунтов (39)	5.285402
log ₂ (40)	фунтов (40)	5,321928
log ₂ (41)	фунтов (41)	552 95	552 95	552 95	552 95	42)	фунтов (42)	5,3
log ₂ (43)	фунтов (43)	5,426265
log ₂ (44)
лог ₂ (45)	фунтов (45)	5.4
log ₂ (46)	фунтов (46)	5.523562
log ₂ (47)	фунтов (47)	5.554589	фунтов (48)	5.584963
log ₂ (49)	фунтов (49)	5. 61471
log ₂ (50)	фунтов 5.643856
log ₂ (51)	фунта (51)	5.672425
log ₂ (52)	фунтов (52)	5.70044
log ₂ (53)	фунтов (53)	5.72792	фунтов (54)	5,754888
log ₂ (55)	фунтов (55)	5,78136
log ₂ (56)		5.807355
log ₂ (57)	фунта (57)	5.83289
log ₂ (58)	фунтов (58)	5,857981
log ₂ (59)	фунтов (59)	5,882643	5,882643	фунтов (60)	5.
log ₂ (61)	фунтов (61)	5.
log ₂ (62)	фунтов 5.
log ₂ (63)	фунта (63)	5.
log ₂ (64)	фунтов (64)	6
log ₂ (65)	фунтов (65)	6.022368
фунтов (66)	6.044394
log ₂ (67)	фунтов (67)	6.066089
log ₂ (68)
log ₂ (69)	фунтов (69)	6.108524
log ₂ (70)	фунтов (70)	6,129283
log ₂ (71)	фунтов (71)	0006,149747 95	000 6,149747 95	72)	фунтов (72)	6,169925
log ₂ (73)	фунтов (73)	6,189825
log ₂ (74)	фунтов 6. 209453
log ₂ (75)	фунтов (75)	6.228819
log ₂ (76)	фунтов (76)	6,247928
log ₂ (77)	фунтов (77)	6.266787	фунтов (78)	6.285402
log ₂ (79)	фунтов (79)	6.303781
log ₂ (80)	фунтов 6.321928
log ₂ (81)	фунтов (81)	6.33985
log ₂ (82)	фунтов (82)	6.357552
log ₂ (83)	фунтов (83)	6,375039	6,375039	фунтов (84)	6.3
log ₂ (85)	фунтов (85)	6.409391
log ₂ (86)	фунтов 6. 426265
log ₂ (87)	фунтов (87)	6.442943
log ₂ (88)	фунтов (88)	6.459432
log ₂ (89)	фунтов (89)	6.475733	6.475733	фунтов (90)	6.4
log ₂ (91)	фунтов (91)	6.507795
log ₂ (92)
log ₂ (93)	фунта (93)	6.539159
log ₂ (94)	фунта (94)	6.554589
log ₂ (95)	фунта (95)	000 6,56	000 6,56	000 6,56	000 96)	фунтов (96)	6.584963
log ₂ (97)	фунтов (97)	6. 5
log ₂ (98)	фунтов 6,61471
журнал ₂ (99)	фунтов (99)	6.629357
журнал ₂ (100)	фунтов (100)	6,643856

1 9000 9000 107)

000

113)

119)

121

000

log ₂ (x)	Обозначение	Значение
log ₂ (101)	фунтов (101)	6,658211
log 02 918 (102)	6,672425
log ₂ (103)	фунта (103)	6.686501
log ₂ (104)	фунтов (104)	70044
log ₂ (105)	фунтов (105)	6,714246
log ₂ (106)	фунтов (106)	6.7273	фунтов (107)	6,741467
log ₂ (108)	фунтов (108)	6,754888
log ₂ (109)			6. 768184
log ₂ (110)	фунтов (110)	6.78136
log ₂ (111)	фунта (111)	6.7
log ₂ (112)	фунта (112)	6.807355
6,807355 9000 9000	фунтов (113)	6.820179
log ₂ (114)	фунтов (114)	6.83289
log ₂ (115)	фунтов 6,84549
log ₂ (116)	фунтов (116)	6.857981
log ₂ (117)	фунтов (117)	6,870365
log ₂ (118)	фунтов (118)	6.882643 8295
фунтов (119)	6.8
log ₂ (120)	фунтов (120)	6.
log ₂ (121)	фунтов 6.
log ₂ (122)	фунта (122)	6.
log ₂ (123)	фунтов (123)	6.
log ₂ (124)	фунтов (124)	6.
6.

0 125)

1 138)

140

фунтов 7.129283

4 9293

144)

140004 7.189825

9169 150)

0004

000

фунтов (125)	6.	4
log ₂ (126)	фунтов (126)	6.
log ₂ (127)	фунтов 6.	5
log ₂ (128)	фунтов (128)	7
log ₂ (129)	фунтов (129)	7.011227
log ₂ (130)	фунтов (130)	7.022368
log ₂ (131)	фунтов (131)	7.0334000	7.0334000	7.033423	132)	фунтов (132)	7. 044394
log ₂ (133)	фунтов (133)	7.055282
log ₂ (134)			7.066089
log ₂ (135)	фунтов (135)	7.076816
log ₂ (136)	фунтов (136)	7.087463
log ₂ (137)	фунтов (137)	7.0032 95	7.0032 95	7.0032 95	фунтов (138)	7.108524
log ₂ (139)	фунтов (139)	7.118941
log ₂ (140)
log ₂ (141)	фунтов (141)	7.139551
log ₂ (142)	фунта (142)	7.149747
log ₂ (143)	фунта (143)	9,15984 9293		фунта (144)	7. 169925
log ₂ (145)	фунта (145)	7.179909
log ₂ (146)
log ₂ (147)	фунтов (147)	7.1
log ₂ (148)	фунта (148)	7.209453
log ₂ (149)	фунтов (149)
7,219169
фунтов (150)	7.228819
log ₂ (151)	фунтов (151)	7.238405
log ₂ (152)				7,247928
log ₂ (153)	фунта (153)	7.257388
log ₂ (154)	фунта (154)	7,266787
log ₂ (155)	фунтов (155)	7.276124	фунтов (155)	7. 276124

04 7.276124

900 156)

7.303781

фунтов (156)

7.285402

log ₂ (157)

фунтов (157)

7.2

log ₂ (150004)

log ₂ (159)

фунтов (159)

7.312883

лог ₂ (160)

фунта (160)

7.321928

лог ₂ (161)

фунт (161)

7.330930 00 92950

7.357552

168)

04 1704

7,409391

180)

0004 7,507795

000

186)

192)

40004 7,5

000000

198)

7.3309000 9295 900 162)	фунтов (162)	7,33985
log ₂ (163)	фунтов (163)	7,348728
log ₂ (164)
log ₂ (165)	фунтов (165)	7.366322
log ₂ (166)	фунта (166)	7.375039
log ₂ (167)	фунтов (167)

фунтов (168)	7,3
log ₂ (169)	фунтов (169)	7,400879
log ₂
log ₂ (171)	фунта (171)	7. 417853
log ₂ (172)	фунта (172)	7,426265
log ₂ (173)	фунтов (173)	7,411628
7,411628 9000 174)	фунтов (174)	7,442943
log ₂ (175)	фунтов (175)	7,451211
log ₂ (176)			7,459432
log ₂ (177)	фунтов (177)	7.467606
log ₂ (178)	фунта (178)	7,475733
log ₂ (179)	фунтов (179)
фунтов	7,411438
фунтов (180)	7,4
log ₂ (181)	фунтов (181)	7,4
log ₂ (182)
log ₂ (183)	фунта (183)	7. 5157
лог ₂ (184)	фунта (184)	7,523562
лог ₂ (185)	фунта (185)	7,531381
7,531381 9295	7,531381 9000 9294	фунтов (186)	7,539159
log ₂ (187)	фунтов (187)	7,546894
log ₂ (188)	7,554589
log ₂ (189)	фунтов (189)	7.562242
log ₂ (190)	фунтов (190)	7,569856
log ₂ (191)	фунтов (191)	7,5429 00	7,5429 9295 900	7,5429	фунтов (192)	7,584963
log ₂ (193)	фунтов (193)	7,5
log ₂ (194)

log ₂ (195)	фунтов (195)	7. 60733
log ₂ (196)	фунтов (196)	7,61471
log ₂ (197)	фунтов (197)	7.622018
7.622018
фунтов (198)	7,629357
log ₂ (199)	фунтов (199)	7,636625
log ₂ (200)			7.643856

200005

7. 686501

210)

7.72792

222)

)

00050005 7.807355

000 2,821148000 2,821148000 2,8265

000

7,84549

234)

)

0005

7,882643

000 2

000

000 2,9311000 2,9311 90000005

0 9293

252)

0005000 7.

1 9000 9000 258)

8,022368

8.055282

270)

000 8.087463

8.118941

09 282)

8.149747

4907 9295

4907

288)

8.179909

757

4757

294)

8.209453

300)

log ₂ (x)	Обозначение	Значение
log ₂ (201)	фунтов (201)	7.651052
log ₂ (202)	фунта (202)	7,658211
log ₂ (203)	фунтов (203)
lb 204)	фунтов (204)	7,672425
журнал ₂ (205)	фунтов (205)	7,67948
журнал ₂ (206)
log ₂ (207)	фунтов (207)	7.6
лог ₂ (208)	фунта (208)	7.70044
лог ₂ (209)	фунт (209)	7.70114359
фунтов (210)	7.714246
log ₂ (211)	фунтов (211)	7.721099
log ₂ (2120004)
log ₂ (213)	фунтов (213)	7.73471
log ₂ (214)	фунта (214)	7,741467
log ₂ (215)	фунтов (215)
193
193 216)	фунтов (216)	7,754888
log ₂ (217)	фунтов (217)	7.761551
log ₂5	(	) (	) (	) 7,768184
log ₂ (219)	фунтов (219)	7. 774787
log ₂ (220)	фунтов (220)	7,78136
log ₂ (221)	фунтов (221)	7.78718 9293	фунтов (222)	7.7
log ₂ (223)	фунтов (223)	7.8009
log ₂ (
log ₂ (225)	фунтов (225)	7.813781
log ₂ (226)	фунта (226)	7,820179
log ₂ (227)	фунтов (227)
228)	фунтов (228)	7,83289
log ₂ (229)	фунтов (229)	7,839204
log ₂ (2304)
log ₂ (231)	фунта (231)	7. 851749
log ₂ (232)	фунта (232)	7,857981
log ₂ (233)	фунта (233)	7.8644186 9295	7.8644186	фунтов (234)	7.870365
log ₂ (235)	фунтов (235)	7.876517
log ₂ (
log ₂ (237)	фунта (237)	7.888743
log ₂ (238)	фунтов (238)	7,8
log ₂ (239)	фунтов (239)
11967 240)	фунтов (240)	7.
log ₂ (241)	фунтов (241)	7.	9
log ₂ (242)
log ₂ (243)	фунта (243)	7.
log ₂ (244)	фунта (244)	7.
log ₂ (245)	фунтов (245)
фунтов (245)
фунтов 246)	фунтов (246)	7.
log ₂ (247)	фунтов (247)	7.	7
log ₂5 9000 (9000) 9248 7.
log ₂ (249)	фунтов (249)	7.	2
log ₂ (250)	фунта (250)	7.	4
log ₂ (251)	фунта (251)	7.	фунта (252)	7.
log ₂ (253)	фунта (253)	7.₄
log ₂ (254000)	5
log ₂ (255)	фунтов (255)	7. 9
log ₂ (256)	фунтов (256)	8
log ₂ (257)	фунтов (257)	8.005625	фунтов (258)	8.011227
log ₂ (259)	фунтов (259)	8.016808
log ₂
лог ₂ (261)	фунта (261)	8.027906
log ₂ (262)	фунтов (262)	8.033423
log ₂ (263)	фунтов (263)	8,011919 9000	8,011919 9000 264)	фунтов (264)	8,044394
log ₂ (265)	фунтов (265)	8,049849
log ₂ (	)
log ₂ (267)	фунтов (267)	8.060696
log ₂ (268)	фунта (268)	8. 066089
log ₂ (269)	фунта (269)		462	8111462
фунтов (270)	8.076816
log ₂ (271)	фунтов (271)	8.082149
log ₂ (272)
log ₂ (273)	фунтов (273)	8.0
log ₂ (274)	фунта (274)	8.0
log ₂ (275)	фунта (275)			фунтов 276)	фунтов (276)	8.108524
log ₂ (277)	фунтов (277)	8.113742
log ₂ (	)
log ₂ (279)	фунтов (279)	8.124121
log ₂ (280)	фунтов (280)	8.129283
log ₂ (281)	фунтов (281)	8. 134426 00 2
фунтов (282)	8.139551
log ₂ (283)		фунтов (283)	8.144658
log ₂ (	)
log ₂ (285)	фунтов (285)	8.154818
log ₂ (286)	фунтов (286)	8.159871
log ₂ (287)	фунтов (287)			фунтов (288)	8.169925
log ₂ (289)	фунтов (289)	8.174926
log ₂ (	)
log ₂ (291)	фунтов (291)	8.184875
log ₂ (292)	фунта (292)	8.189825
log ₂ (293)	фунта (293)
	фунтов (294)	8. 1
log ₂ (295)	фунтов (295)	8.204571
log ₂ (	)
log ₂ (297)	фунтов (297)	8.214319
log ₂ (298)	фунтов (298)	8,219169
log ₂ (299)	фунтов (299)
2	9,2114002	фунтов (300)	8,228819

Калькулятор натурального логарифма ln (x)

Калькулятор натурального логарифма ln (x) находит результат функции логарифма по основанию e , что приблизительно равно 2.718 .

Калькулятор натурального логарифма
пер.
Рассчитать

ln (x) = y

x: — действительное число, x> 0

Натуральный логарифм: ln
ln (x) = y

ln (x) эквивалентно log _e (x)

Примеры натурального логарифма

ln (2) = log _e (2) = 0,6931
ln (3) = log _e (3) = 1,0986
ln (4) = log _e (4) = 1. 3862
ln (5) = log _e (5) = 1,609
ln (6) = log _e (6) = 1,7917
ln (10) = log _e (10) = 2.3025

Таблицы значений натурального логарифма

Список таблиц значений функции журнала в экспоненциальных числах с основанием (e).

000 (2) (2)

1 log 5)

130004

1 9000

1 9000 9000 17)

1 log

1 9000 9000 23)

1 9000

1 9000 9000 29)

1 9000 9000 35)

1 9000 9000 41)

430004

1 log 47)

1 9000

1 9000 9000 53)

550004

1 log 59)

log _e (x)	Обозначение	Значение
log _e (1)	ln (1)	0
log _e	0.6
log _e (3)	ln (3)	1.0
log _e (4)	ln (4)	1.386294 9000 9000	ln (5)	1.609438
log _e (6)	ln (6)	1.7
log _e (7)	ln5 1.
лог _e (8)	ln (8)	2.079442
log _e (9)	ln (9)	2,1
log _e (10)	ln (10)	2. 302585 9000 9000	11 log 11)	ln (11)	2.3
log _e (12)	ln (12)	2.484907
log _e (13)	ln 2,564949
лог _e (14)	ln (14)	2.639057
log _e (15)	ln (15)	2,70805
log _e (16)	ln (16)	2.772589	2.772589	ln (17)	2.833213
log _e (18)	ln (18)	2.8
log _e (19)		ln5 2.₉
лог _e (20)	ln (20)	2.9
log _e (21)	ln (21)	3.044522
log _e (22)	ln (22)	3.0
3. 0
ln (23)	3.135494
log _e (24)	ln (24)	3.178054
log _e (25)	ln5 3.218876
лог _e (26)	ln (26)	3.258097
log _e (27)	ln (27)	3.2
log _e (28)	ln (28)	3.332205	3.332205	ln (29)	3.367296
log _e (30)	ln (30)	3.401197
log _e (31)	ln5 3.433987
лог _e (32)	ln (32)	3.465736
log _e (33)	ln (33)	3,4
log _e (34)	ln (34)	3,5263 3,5263	ln (35)	3. 555348
log _e (36)	ln (36)	3.583519
log _e (37)	ln5 3.610918
лог _e (38)	ln (38)	3.637586
log _e (39)	ln (39)	3.663562
log _e (40)	ln (40)	3.688879	ln (41)	3,713572
log _e (42)	ln (42)	3,73767
log _e (43)	5 3.7612
лог _e (44)	ln (44)	3.78419
log _e (45)	ln (45)	3.806662
log _e (46)	ln (46)	3.828641 9000 9000 9000	3,828641 9000 9000	ln (47)	3.850148
log _e (48)	ln (48)	3. 871201
log _e (49)			3.89182
лог _e (50)	ln (50)	3.	3
log _e (51)	ln (51)	3.6
log _e (52)	ln (52)	3.	4	3.	4	ln (53)	3.
log _e (54)	ln (54)	3.	4
log _e (55)	4.007333
лог _e (56)	ln (56)	4.025352
log _e (57)	ln (57)	4.043051
log _e (58)	ln (58)	4.060443 9000 9295	ln (59)	4.077537
log _e (60)	ln (60)	4. 0
log _e (61)	ln5 4.110874
лог _e (62)	ln (62)	4.127134
log _e (63)	ln (63)	4.143135
log _e (64)	ln (64)	4.158883

1 9000

1 9000 9000 70)

1 log 76)

1 9000 9000 82)

1 log 88)

1 9000

1 9000 9000 94)

83 100)

9000

1 log 106)

83 112)

1 log 118)

1 log 124)

126 40004 ln5 4.836282

log _e (x)	Обозначение	Значение
log _e (65)	ln (65)	4,174387
log _l	0 (66)	4.189655
log _e (67)	ln (67)	4.204693
log _e (68)	ln (68)	4,219508
log _e (69)	ln (69)	4,234107	4,234107	ln (70)	4.248495
log _e (71)	ln (71)	4,26268
log _e (72)	0004 ln (72)	4. 276666
лог _e (73)	ln (73)	4.2
log _e (74)	ln (74)	4.304065
log _e (75)	ln (75)	4.317488 95	ln (76)	4.330733
log _e (77)	ln (77)	4.343805
log _e (78)	ln5 4.356709
log _e (79)	ln (79)	4.369448
log _e (80)	ln (80)	4.382027
log _e (81)	ln (81)	4.3	ln (82)	4.406719
log _e (83)	ln (83)	4.418841
log _e (84)	ln5 4.430817
лог _e (85)	ln (85)	4. 442651
log _e (86)	ln (86)	4.454347
log _e (87)	ln (87)	4.465908 95	ln (88)	4.477337
log _e (89)	ln (89)	4.488636
log _e (90)	ln5 4.49981
лог _e (91)	ln (91)	4.51086
log _e (92)	ln (92)	4.521789
log _e (93)	ln (93)	4.532599	4.532599	ln (94)	4.543295
log _e (95)	ln (95)	4.553877
log _e (96)	ln5 4.564348
лог _e (97)	ln (97)	4.574711
log _e (98)	ln (98)	4. 584967
log _e (99)	ln (99)	4.59512	ln (100)	4.60517
log _e (101)	ln (101)	4.615121
log _e (102)		ln5 4.624973
лог _e (103)	ln (103)	4.634729
log _e (104)	ln (104)	4.644391
log _e (105)	ln (105)	4.653
ln (106)	4.663439
log _e (107)	ln (107)	4.672829
log _e (108) 084000	ln5 4.682131
лог _e (109)	ln (109)	4.6
log _e (110)	ln (110)	4.70048
log _e (111)	ln (111)	4. 70953
ln (112)	4,718499
log _e (113)	ln (113)	4,727388
log _e (114)		ln5 4,736198
лог _e (115)	ln (115)	4.744932
log _e (116)	ln (116)	4,75359
log _e (117)	ln (117)	4,762174 95	4,762174 95	4,762174 95	ln (118)	4,770685
log _e (119)	ln (119)	4,779123
log _e (120)	ln5 4,787492
лог _e (121)	ln (121)	4.7
log _e (122)	ln (122)	4.804021
log _e (123)	ln (123)	4,812184 95	ln (124)	4. 820282
log _e (125)	ln (125)	4.828314
log _e (126)
log _e (127)	ln (127)	4.844187
лог _e (128)	ln (128)	4.85203

1 log

1 9000 135)

000

log _e (x)	Обозначение	Значение
log _e (129)	ln (129)	4,859812
log _e	0 (130)	4,867534
log _e (131)	ln (131)	4,875197
log _e (132)	ln (132)	4.882802
log _e (133)	ln (133)	4.8
log _e (134)	ln (134)	4.89784		ln (135)	4.
log _e (136)	ln (136)	4.	5
log _e (137) 9000 137)		l5 4.1
лог _e (138)	ln (138)	4.₄
log _e (139)	ln (139)	4.
log _e (140)	ln (140)	4.2	4.2	141)	ln (141)	4.
log _e (142)	ln (142)	4.
log _e (143)	5
log _e (144)	ln (144)	4.
log _e (145)	ln (145)	4.
log _e (146)	ln (146)	e 00 9295 9005	4,	607

0 147)

5.003946

000

log 153)

0005

5.043425

159)

900 165)

log 171)

5. 153292

1 9000 9000 177)

5.187386

183)

000 (185)

000 5.220356

189)

ln (147)	4. 9
log _e (148)	ln (148)	4.9
log _e (14	)
лог _e (150)	ln (150)	5.010635
log _e (151)	ln (151)	5,01728
log _e (152)	ln (152)	5,023881
ln (153)	5,030438
log _e (154)	ln (154)	5,036953
log _e (155000)
лог _e (156)	ln (156)	5.049856
log _e (157)	ln (157)	5.056246
log _e (158)	ln (158)	5112595
ln (159)	5.068904
log _e (160)	ln (160)	5. 075174
log _e (161)	5.081404
лог _e (162)	ln (162)	5.087596
log _e (163)	ln (163)	5,09375
log _e (164)	ln (164)	e 9295 900	e 9295 9005	5,0	ln (165)	5.105945
log _e (166)	ln (166)	5.111988
log _e (167)		5.117994
лог _e (168)	ln (168)	5.123964
log _e (169)	ln (169)	5.129899
log _e (170)	ln (170)	5,13573000
ln (171)	5.141664
log _e (172)	ln (172)	5.147494
log _e004
лог _e (174)	ln (174)	5.159055
log _e (175)	ln (175)	5.164786
log _e (176)	ln (176)	5.170484	ln (177)	5,17615
log _e (178)	ln (178)	5,181784
log _e (17	)
лог _e (180)	ln (180)	5.1
log _e (181)	ln (181)	5,1
log _e (182)	ln (182)	5.2018400	0	ln (183)	5.209486
log _e (184)	ln (184)	5.214936
log _e (185)
лог _e (186)	ln (186)	5. 225747
log _e (187)	ln (187)	5.231109
log _e (188)	ln (188)	e 9184	005	5,231842	ln (189)	5.241747
log _e (190)	ln (190)	5.247024
log _e (191)		5.252273
log _e (192)	ln (192)	5.257495

логарифм с основанием 3 из 12? | Калькулятор Log3

Вот ответ на такие вопросы: log base 3 of 12? или что такое логарифм по основанию 3 из 12?

Воспользуйтесь нашим | Калькулятор Log3, чтобы найти логарифм любого положительного числа для любой системы счисления, которую вы вводите.

Что такое логарифм?

Логарифм — это степень, в которую должно быть возведено число, чтобы получить другое число. Другими словами, логарифм говорит нам, на сколько нужно умножить одно число, чтобы получить другое число.

Например:

Логарифм 4 по основанию 2 равен 2, потому что 2 в степени 2 равняется 4:
log ₃ 9 = 2, потому что 3 ² = 9

Это пример логарифма по основанию 3. Мы называем это логарифмом по основанию 3, потому что 3 — это число, возведенное в степень.

Чаще всего используются натуральные логарифмы и десятичные логарифмы. Для них есть специальные обозначения:

Журнал с основанием 10 записывается просто в журнал.
Натуральный логарифм записывается просто как ln.

Таким образом, одна запись log означает десятичный логарифм, а запись ln — натуральный логарифм.

Основные правила журнала

журнал _b (x · y) = журнал _b (x) + журнал _b (y)
log _b (x / y) = log _b (x) — журнал _b (y)
журнал _b (xy) = y · log _b (x)
журнал _b (x) = журнал _k (x) / журнал _k (b)

Калькулятор журнала

Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши изображение выше, выберите «Копировать адрес ссылки» и вставьте его в свой HTML-код.

Пример расчета логарифмов

Заявление об ограничении ответственности

Несмотря на то, что прилагаются все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения или за результаты, полученные в результате использования этой информации. Вся информация на этом сайте предоставляется «как есть», без каких-либо гарантий полноты, точности, своевременности или результатов, полученных в результате использования этой информации.

alexxlab

Основание логарифма 2 Калькулятор Log2

Калькулятор логарифма 2 находит результат функции логарифма по основанию 2. Вычисляет логарифм по основанию 2 числа.

Лог базы 2 Калькулятор журнал ₂

логарифм ₂ (х) = у

x: действительное число, x>0

log ₂ (x) = y и x = 2 ^y

Список журналов ₂ таблицы значений функций, журнал по основанию 2 чисел.

50505050505050505050505050505050505050505ра50505050505050150505015015050505ер.

7505050505050505050507.50505050505050505.505050505050505.5050505050505.5050505050505.50505050505057)505050505050505050505050505050505r150505050505050509815050505098) 9007

9007

9007 9003 9003 9003 9003 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9003 9003 9003 9003 797933755555555555599977980979тели.

log ₂ (x)	Notation	Value
log ₂ (1)	lb(1)	0
log ₂ (2)	lb(2)	1
log ₂ (3)	lb(3)	1.584963
log ₂ (4)	lb(4)	2
бревно ₂ (5)	фунтов(5)	2.321928
log ₂ (6)	lb(6)	2. 584963
log ₂ (7)	lb(7)	2.807355
log ₂ (8)	lb(8)	3
log ₂ (9)	lb(9)	3.169925
log ₂ (10)	lb(10)	3.321928
журнал ₂ (11)	lb(11)	3.459432
log ₂ (12)	lb(12)	3.584963
log ₂ (13)	lb(13 )	3.70044
log ₂ (14)	lb(14)	3.807355
log ₂ (15)	lb(15)	3.1
log ₂ (16)	фунтов(16)	4
log ₂ (17)	lb(17)	4.087463
log ₂ (18)	lb(18)	4. 169925
log ₂ (19)	lb(19)	4.247928
log ₂ (20)	lb(20)	4.321928
log ₂ (21)	lb(21)	4.3
журнал ₂ (22)	lb(22)	4.459432
log ₂ (23)	lb(23)	4.523562
log ₂ (24)	lb(24	4.584963
Log ₂ (25)	фунтов (25)	4,643856
(26). 2 (27)	фунтов(27)	4.754888
log ₂ (28)	lb(28)	4.807355
log ₂ (29)	lb(29)	4.857981
log ₂ (30)	lb(30)	4.1
log ₂ (31)	lb(31)	4. 6
log ₂ (32)	lb(32)	5
журнал ₂ (33)	lb(33)	5.044394
log ₂ (34)	lb(34)	5.087463
log ₂ (35)	lb(35 )	5.129283
log ₂ (36)	lb(36)	5.169925
log ₂ (37)	lb(37)	5.209453
log ₂ (38)	фунтов(38)	5.247928
log ₂ (39)	lb(39)	5.285402
log ₂ (40)	lb(40)	5.321928
log ₂ (41)	фунтов (41)	5,357552
Log ₂ (42)	фунтов (42)	5,3
_{9 2}	5.426265
журнал ₂ (44)	lb(44)	5.459432
log ₂ (45)	lb(45)	5.4
log ₂ (46)	lb( 46)	5.523562
log ₂ (47)	lb(47)	5.554589
log ₂ (48)	lb(48)	5.584963
log ₂ (49)	фунтов(49)	5.61471
LOG ₂ (50)	фунтов (50)	5,643856
_{9 2} (51). (52)	фунтов (52)	5,70044
Log ₂ (53)	фунт (53)	5,72792
2 10505050505050505050544444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444))	5. 754888
журнал ₂ (55)	lb(55)	5.78136
log ₂ (56)	lb(56)	5.807355
log ₂ (57)	lb( 57)	5.83289
log ₂ (58)	lb(58)	5.857981
log ₂ (59)	lb(59)	5.882643
log ₂ (60)	фунтов (60)	5.1
log ₂ (61)	lb(61)	5.
log ₂ (62)	lb(62)	5. 6
log ₂ (63)	фунт (63)	5,97728
Log ₂ (64)	фунт (64)	6
Log ₂ (65)		)	)	777777777777777777777 гг.	6.022368
журнал ₂ (66)	lb(66)	6. 044394
log ₂ (67)	lb(67)	6.066089
log ₂ (68)	lb(68 )	6.087463
log ₂ (69)	lb(69)	6.108524
log ₂ (70)	lb(70)	6.129283
log ₂ (71)	фунтов(71)	6.149747
log ₂ (72)	lb(72)	6.169925
log ₂ (73)	lb(73)	6.189825
log ₂ (74)	lb(74)	6.209453
log ₂ (75)	lb(75)	6.228819
log ₂ (76)	lb(76)	6.247928
журнал ₂ (77)	lb(77)	6.266787
log ₂ (78)	lb(78)	6. 285402
log ₂ (79)	lb( 79)	6.303781
log ₂ (80)	lb(80)	6.321928
log ₂ (81)	lb(81)	6.33985
log ₂ (82)	фунтов(82)	6.357552
log ₂ (83)	lb(83)	6.375039
log ₂ (84)	lb(84)	6.3
log ₂ (85)	фунтов (85)	6.409391
Log ₂ (86)	фунтов (86)	6.426265
_{2 ⁵}
9009 2 77777777.	6.442943
журнал ₂ (88)	lb(88)	6. 459432
log ₂ (89)	lb(89)	6.475733
log ₂ (90)	lb( 90)	6.4
log ₂ (91)	lb(91)	6.507795
log ₂ (92)	lb(92)	6.523562
log ₂ (93)	фунтов(93)	6.539159
log ₂ (94)	lb(94)	6.554589
log ₂ (95)	lb(95)	6.569856
log ₂ (96)	фунтов (96)	6.584963
Log ₂ (97)	фунтов (97)	6.599913
2	6.61471
журнал ₂ (99)	фунтов (99)	6. 629357
Log ₂ (100)	LB (100)	6.643856
79393
6		Notation	Value
log ₂ (101)	lb(101)	6.658211
log ₂ (102)	lb(102)	6.672425
журнал ₂ (103)	lb(103)	6.686501
log ₂ (104)	lb(104)	6.70044
log ₂ (105)	lb(105)	6.714246
log ₂ (106)	lb(106)	6.72792
log ₂ (107)	lb(107)	6. 741467
log ₂ (108)	фунтов(108)	6,754888
log ₂ (109)	lb(109)	6.768184
log ₂ (110)	lb(110)	6.78136
log ₂ (111 )	lb(111)	6.7
log ₂ (112)	lb(112)	6.807355
log ₂ (113)	lb(113)	6.820179
журнал ₂ (114)	lb(114)	6.83289
log ₂ (115)	lb(115)	6.84549
log ₂ (116)	lb(116 )	6.857981
log ₂ (117)	lb(117)	6.870365
log ₂ (118)	lb(118)	6.882643
log ₂ (119)	фунтов (119)	6. 8
log ₂ (120)	lb(120)	6.1
log ₂ (121)	lb(121)	6.
log ₂ (122)	lb(122)	6.
log ₂ (123)	lb(123)	6.	5
log ₂ (124)	lb(124 )	6. 6
log ₂ (125)	lb(125)	6.4
log ₂ (126)	lb(126)	6.97728
log ₂ (127)	lb(127)	6.988685
log ₂ (128)	lb(128)	7
log ₂ (129)	lb(129)	7.011227
бревно ₂ (130)	lb(130)	7.022368
log ₂ (131)	lb(131)	7. 033423
log ₂ (132)	lb(132)	7.044394
log ₂ (133)	фунтов (133)	7,055282
Log ₂ (134)	LB (134)	7,06109999	фунтов(135)	7,076816
log ₂ (136)	lb(136)	7.087463
log ₂ (137)	lb(137)	7.098032
log ₂ (138 )	lb(138)	7.108524
log ₂ (139)	lb(139)	7.118941
log ₂ (140)	lb(140)	7.129283
журнал ₂ (141)	lb(141)	7.139551
log ₂ (142)	lb(142)	7. 149747
log ₂ (143)	lb( 143)	7.159871
log ₂ (144)	lb(144)	7.169925
log ₂ (145)	lb(145)	7.179909
log ₂ (146)	фунтов (146)	7.189825
log ₂ (147)	lb(147)	7.199672
log ₂ (148)	lb(148)	7.209453
log ₂ (149)	lb(149)	7.219169
log ₂ (150)	lb(150)	7.228819
log ₂ (151)	lb(151)	7.238405
log ₂ (152)	lb(152)	7.247928
log ₂ (153)	lb(153)	7. 257388
log ₂ (154)	lb(154)	7.266787
log ₂ (155)	lb(155)	7.276124
log ₂ (156)	lb(156)	7.285402
бревно ₂ (157)	фунт (157)	7.2
Log ₂ (158)	фунтов (158)	7,303781
LOG 9009 2 (15 050505050505050505050505.	77777777777777777777777777777777777777777777777777778	77777777777777777777777777777777777777777.
)
log ₂ (160)	lb(160)	7.321928
log ₂ (161)	lb(161)	7.330917
log ₂ (162)	фунтов(162)	7,33985
log ₂ (163)	lb(163)	7. 348728
log ₂ (164)	lb(164)	7.357552
log ₂ ( 165)	lb(165)	7.366322
log ₂ (166)	lb(166)	7.375039
log ₂ (167)	lb(167)	7.383704
журнал ₂ (168)	lb(168)	7.3
log ₂ (169)	lb(169)	7.400879
log ₂ (170)	lb( 170)	7.409391
log ₂ (171)	lb(171)	7.417853
log ₂ (172)	lb(172)	7.426265
log ₂ (173)	фунтов (173)	7.434628
log ₂ (174)	lb(174)	7. 442943
log ₂ (175)	lb(175)	7.451211
log ₂ (176)	lb(176)	7.459432
log ₂ (177)	lb(177)	7.467606
log ₂ (178)	lb(178)	7.475733
log ₂ (179)	lb(179)	7.483816
log ₂ (180)	lb(180)	7.4
log ₂ (181)	lb(181)	7.499846
log ₂ (182)	lb(182)	7.507795
log ₂ (183)	lb(183)	7.5157
бревно ₂ (184)	lb(184)	7.523562
log ₂ (185)	lb(185)	7.531381
log ₂ (186)	lb(186)	7. 539159
log ₂ (187)	lb(187)	7.546894
log ₂ (188)	lb(188)	7.554589
log ₂ (189)	фунтов(189)	7,562242
log ₂ (190)	lb(190)	7.569856
log ₂ (191)	lb(191)	7.577429
log ₂ (192 )	lb(192)	7.584963
log ₂ (193)	lb(193)	7.5
log ₂ (194)	lb(194)	7.599913
журнал ₂ (195)	lb(195)	7.60733
log ₂ (196)	lb(196)	7.61471
log ₂ (197)	lb( 197)	7. 622052
log ₂ (198)	lb(198)	7.629357
log ₂ (199)	lb(199)	7.636625
log ₂ (200)	фунтов (200)	7.643856

89769769769769769769769800009ам.793784505050505050505.

50.700505010505050505.

5010505010505050505.101050501017. 27001010505050505.50505050505017)

log ₂ (x)	Notation	Value
log ₂ (201)	lb(201)	7.651052
log ₂ (202)	lb(202)	7.658211
log ₂ (203)	lb(203)	7.665336
log ₂ (204)	lb(204 )	7.672425
log ₂ (205)	lb(205)	7.67948
log ₂ (206)	lb(206)	7.686501
log ₂ (207)	lb(207)	7. 6
log ₂ (208)	lb(208)	7.70044
log ₂ (209)	lb(209)	7.707359
log ₂ (210)	lb(210)	7.714246
log ₂ (211)	lb(211)	7.721099
log ₂ (212)	lb(212)	7.72792
log ₂ (213)	lb(213)	7.73471
log ₂ (214)	lb(214)	7.741467
бревно ₂ (215)	lb(215)	7.748193
log ₂ (216)	lb(216)	7.754888
log ₂ (217)	lb(217)	7.761551
log ₂ (218)	lb(218)	7.768184
log ₂ (219)	lb(219)	7. 774787
log ₂ (220)	фунтов (220)	7,78136
log ₂ (221)	lb(221)	7.787903
log ₂ (222)	lb(222)	7.7
log ₂ (223 )	lb(223)	7.8009
log ₂ (224)	lb(224)	7.807355
log ₂ (225)	lb(225)	7.813781
журнал ₂ (226)	lb(226)	7.820179
log ₂ (227)	lb(227)	7.826548
log ₂ (228)	lb(228 )	7.83289
log ₂ (229)	lb(229)	7.839204
log ₂ (230)	lb(230)	7.84549
log ₂ (231)	фунтов (231)	7. 851749
log ₂ (232)	lb(232)	7.857981
log ₂ (233)	lb(233)	7.864186
log ₂ (234)	lb(234)	7.870365
log ₂ (235)	lb(235)	7.876517
log ₂ (236)	lb(236)	7,882643
Log ₂ (237)	фунтов (237)	7,888743
₂ (238)	LB (238)	7,8

lb(239)	7.
log ₂ (240)	lb(240)	7.1
log ₂ (241)	lb(241)	7.
журнал ₂ (242)	lb(242)	7.
log ₂ (243)	lb(243)	7.	3
log ₂ (244)	lb(244)	7.
log ₂ (245)	lb(245)	7.
log ₂ (246)	lb(246)	7.	5
log ₂ (247)	фунтов(247)	7,	7
log ₂ (248)	lb(248)	7. 6
log ₂ (249)	lb(249)	7.	2
log ₂ ( 250)	lb(250)	7.4
log ₂ (251)	lb(251)	7.
log ₂ (252)	lb(252)	7,97728
журнал ₂ (253)	lb(253)	7.982994
log ₂ (254)	lb(254)	7. 988685
log ₂ (255)	lb( 255)	7.9
log ₂ (256)	lb(256)	8
log ₂ (257)	lb(257)	8.005625
log ₂ (258)	фунтов (258)	8.011227
log ₂ (259)	lb(259)	8.016808
log ₂ (260)	lb(260)	8.022368
log ₂ (261)	lb(261)	8.027906
log ₂ (262)	lb(262)	8.033423
log ₂ (263)	lb(263)	8.038919
log ₂ (264)	lb(264)	8.044394
log ₂ (265)	lb(265)	8.049849
log ₂ (266)	lb(266)	8. 055282
log ₂ (267)	lb(267)	8.060696
log ₂ (268)	lb(268)	8.066089
журнал ₂ (269)	lb(269)	8.071462
log ₂ (270)	lb(270)	8.076816
log ₂ (271)	lb(271)	8.082149
log ₂ (272)	lb(272)	8.087463
log ₂ (273)	lb(273)	8.0
log ₂ (274 )	фунтов(274)	8.098032
log ₂ (275)	lb(275)	8.103288
log ₂ (276)	lb(276)	8.108524
log ₂ (277)	фунтов (277)	8. 113742
Log ₂ (278)	фунт (278)	8.118941
2 101010105050505. 50 50 50 50 50 50	8.124121
log ₂ (280)	lb(280)	8.129283
log ₂ (281)	lb(281)	8.134426
log ₂ (282)	lb(282)	8.139551
log ₂ (283)	lb(283)	8.144658
log ₂ (284)	lb(284)	8.149747
бревно ₂ (285)	lb(285)	8.154818
log ₂ (286)	lb(286)	8.159871
log ₂ (287)	lb(287)	8. 164907
log ₂ (288)	lb(288)	8.169925
log ₂ (289)	lb(289)	8.174926
log ₂ (290)	фунтов (290)	8,179909
log ₂ (291)	фунтов (291)	8.184875
Log ₂ (292)	фунтов (292)	8.18.8979777779777777777777777789877777777777777789778787898787878787878987878787878787.1878	77777777777777897777777777777777759778977. (292). 293)	lb(293)	8.1
log ₂ (294)	lb(294)	8.199672
log ₂ (295)	lb(295)	8.204571
журнал ₂ (296)	lb(296)	8.209453
log ₂ (297)	lb(297)	8. 214319
log ₂ (298)	lb( 298)	8.219169
log ₂ (299)	lb(299)	8.224002
log ₂ (300)	lb(300)	8.228819

Мэтуэй | Популярные задачи 93-8


9	Оценить	квадратный корень из 12
10	Оценить	квадратный корень из 20
11	Оценить	квадратный корень из 50	94
18	Оценить	квадратный корень из 45
19	Оценить	квадратный корень из 32
20	Оценить	квадратный корень из 18	93-8
9	Оценить	квадратный корень из 12
10	Оценить	квадратный корень из 20
11	Оценить	квадратный корень из 50	94
18	Оценить	квадратный корень из 45
19	Оценить	квадратный корень из 32
20	Оценить	квадратный корень из 18	92

Основание логарифма 2 — формула, решение, примеры

LearnPracticeDownload

Основание логарифма 2 полезно для записи экспоненциальной формы с основанием 2 в логарифмическую форму. Число 2 ⁰ = 1, 2 ¹ = 2, 2 ² = 4, 2 ³ = 8, 2 ⁴ = 16, но если у нас есть 2 ^х = 25 чтобы найти значение x, мы можем сначала записать его как логарифмическую базу 2 или $log_225 = x$ и найти значение x. Логарифмическая база 2 помогает найти экспоненциальное значение 2.

Давайте узнаем больше о логарифмическом преобразовании по основанию 2, преобразовании в экспоненциальную форму и свойствах логарифмического основания 2 с помощью примеров и часто задаваемых вопросов.

1.	Что такое логарифмическая база 2?
2.	Преобразование логарифмической базы 2 в экспоненциальную форму
3.	Свойства базы журнала 2
4.	Примеры по логарифмической базе 2
5.	Практические вопросы
6.	Часто задаваемые вопросы по базе журнала 2

Что такое логарифмическая база 2?

Логарифмическое основание 2 — это математическая форма выражения любого натурального числа в виде экспоненциальной формы по основанию 2. Экспоненциальную форму 2 ⁴ = 16 можно легко представить как логарифмическое основание 2 и записать как $log_2 16 = 4$. Лог N по основанию 2 равен выражению числа N в экспоненциальной форме с основанием 2. Далее, если нам надо найти значение k, которое представлено в выражении 2 ^k = 24. Это сложно, но можно приблизительно угадать. Здесь логарифмическая база 2 помогает найти значение k, и здесь мы имеем $log_2 24 = k$.

Каждое положительное натуральное число может быть представлено как показатель степени числа 2. Здесь в таблице ниже логарифмическая форма логарифмического основания 2 представлена в виде экспоненциальной формы по основанию 2.

Логарифмическая форма	Экспоненциальная форма 98 = 256\)

Преобразование логарифмической базы 2 в экспоненциальную форму

Логарифмическая база 2 может быть преобразована в экспоненциальную форму с 2 в качестве базы. Давайте поймем это с помощью простой формулы. Для натурального числа N его логарифм по основанию 2 равен k и записывается как $log_2N = k$, что можно записать в экспоненциальной форме как 2 ^k = N.

. пример преобразования экспоненциальной формы в логарифмическую по основанию 2. Экспоненциальное число 8 ^k = 2492, сначала нужно записать в основание 2, как (2 ³) ^k = 2492, или 2 ^3k = 2492. Это можно записать в лог в основание 2 как \ (log_22492 = 3k\). Таким образом, мы можем стремиться записать каждую экспоненциальную форму в экспоненту по основанию 2 и преобразовать ее в логарифмическую форму логарифмического основания 2.

Свойства базы бревен 2

Свойства логарифмической базы 2 аналогичны логарифмическим свойствам.

Логарифм 1 по основанию 2 всегда равен 0. $log_21 = 0$.
Журнал 2 по тому же основанию 2 равен 1.$log_22 = 1$
Сумма логарифмической базы 2 в a и логарифмической базы 2 в b может быть объединена и записана как один журнал с произведением ab. $log_2a + log_2b = log_2ab$.
Разницу между логарифмической базой 2 и а и логарифмической базой 2 и b можно объединить и записать в виде единого логарифма с разделением а/б. $log_2a — log_2b = log_2 a/b$

☛ Похожие темы

Логарифмы
Свойства логарифмов
Логарифмические функции
Логарифмическое дифференцирование

Примеры по базе данных 2

Пример 1: Найдите значение 1024 по основанию логарифма 2.
Решение:
Число 1024 легко выражается и решается с помощью логарифмического основания 2. 9{10}\)
$log_21024 = 10log_22$
$log_21024 = 10$.
Пример 2: Как мы можем представить 4 ³ = 64 в формате журнала с основанием 2?
Решение:
. Данное выражение может быть сначала экспрессировано до основания 2.
4 ³ = 64
(2 ²) ³ = 64
2 ⁶ = 64.
Теперь преобразуем экспоненциальную форму в логарифмическую.
$log_264 = 6$
Таким образом, экспоненциальная форма теперь преобразована в логарифмическую форму с основанием 2.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Забронировать бесплатный пробный урок

Практические вопросы по журналу базы 2

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по базе журналов 2

Что такое логарифмическая база 2 в алгебре?

Логарифмическая база 2 числа N в алгебре равна показателю степени 2, который дает число N. логарифмическая база 2 записывается в логарифмической форме как $log_2N = k$, и то же самое записывается в экспоненциальной форме как 2 ^k = N.

Как решить логарифмическую базу 2?

Логарифм по основанию 2 можно решить, преобразовав его в экспоненциальную форму. Основание логарифма 2 к числу N равно значению показателя степени, до которого надо возвести основание 2, чтобы получить число N.

Какая формула для логарифмической базы 2?

Логарифмическая база 2 может быть записана как $log_2N=k$, что можно записать в экспоненциальной форме как 2 ^k = N.

Что означает логарифмическая база 2?

Логарифмическая база 2 означает, что значение степени, до которого необходимо возвести логарифмическую базу 2, чтобы получить число, для которого вычисляется логарифмическая база 2.

Что такое производная от логарифмической базы 2 до x?

Производная логарифмической базы 2 по x равна 1/x.log2. Это можно представить в виде следующей формулы.

d/dx.log ₂ x= d/dx.logx/log2 = 1/x . 1/log2 = 1/xlog2

Рабочие листы по математике и
наглядный учебный план

Изменение базовой формулы или правила

Большинство правил ведения журнала я обсуждал в отдельном уроке. Тем не менее, я намеренно пропустил один, чтобы обсудить его здесь подробно. Правило журнала называется формулой изменения базы .

Если вас интересует, почему работает изменение формулы, щелкните следующую ссылку, чтобы увидеть доказательство: Доказательство свойств логарифма.

Логарифм по основанию 10 известен как десятичный логарифм , а логарифм по основанию e известен как натуральный логарифм .

Число \Large{\color{black}{e}}

Примечание: Число e является математической константой, числовое значение которой равно e \приблизительно 2,71828. Это иррациональное число, потому что его нельзя выразить как отношение двух целых чисел или как дробь. Более того, число e является основанием натурального логарифма.

Таким образом, десятичные логарифмы и натуральные логарифмы используют стандартные основания 10 и e соответственно.

десятичный логарифм записывается как \large{\color{red}\log x = {\log _ {10}}x}

натуральный логарифм записывается как \large{\color{blue}\ln x = {\log _e}x}

Прежде чем мы продолжим, я хотел бы указать на некоторые нюансы или тонкости, касающиеся математических выражений десятичного и натурального логарифмов.

Кнопки LOG и LN графического калькулятора

Большинство графических калькуляторов имеют функции или клавиши, которые непосредственно вычисляют логарифмы чисел по основанию 10 и e. Таким образом, вы увидите только две кнопки: LOG для десятичного логарифма и LN для натурального логарифма.

Очевидно, что проблема возникает, когда мы хотим вычислить логарифм числа, используя нестандартные системы счисления, такие как 2, 3, 7, 0,5 и 0,25.

Приведенные выше логарифмы используют НЕСТАНДАРТНЫЕ основания, потому что они не являются ни \large{\color{green}10}, ни числом \large{\color{green}e}.

Как продолжить ввод чисел на графическом калькуляторе? Как я упоминал ранее, большинство калькуляторов ограничено вычислением логарифмов только с основанием 10 и основанием e.

Здесь на помощь приходит Сменная Базовая Формула . Он может преобразовать логарифм с нестандартным основанием как отношение двух логарифмических операций, использующих стандартное основание либо 10, либо константу e.

Что такое формула смены основания ?

Формула изменения основания — это инструкция о том, как переписать или преобразовать заданное логарифмическое выражение как отношение или долю двух операций логарифмирования с использованием любого допустимого основания.

Это означает, что если у нас есть логарифм, использующий определенное основание, то мы можем превратить его в эквивалентное отношение или долю двух логарифмических операций, так что мы можем выбрать любое основание, которое захотим. Мы можем буквально выбрать любую базу, если она положительна, но не равна \color{red}1.

Но если мы хотим вычислить или узнать значение логарифма, мы должны выбрать по основанию 10 или по основанию e, так как большинство калькуляторов имеют эти функциональные клавиши. 9Ключ журнала 0003 [log] вычисляет десятичный логарифм, а ключ ln [ln] вычисляет натуральный логарифм (по основанию e).

Давайте разберем, как формула преобразовала исходный логарифм в эквивалентное выражение как отношение двух логарифмических операций.

Аргумент исходного логарифма становится аргументом логарифма числителя.

Основание исходного логарифма становится аргументом логарифма знаменателя.

Логарифмы в числителе и знаменателе имеют одинаковое основание. Значением основания \large\color{green}c является любое выбранное нами основание.

Примеры формулы замены основания

Первые два примера (пример № 1 и № 2) идеально подходят для учебника, потому что аргумент и основание логарифма могут быть выражены как степени обыкновенного числа ( положительное число, не равное 1), которое служит новой базой при применении правила смены базы. 9k}} \right) = k \cdot {\log _b}\left( x \right)}

\large{\color{red}{\log _b}b = 1}

полное решение.

Пример 2: Вычислить \large{\log {}_{\large{{1 \over {27}}}}\left( 9 \right)}.

Вы можете подумать, что проблема в вопросе, потому что основанием логарифма является дробь. Помните, что основание логарифма должно быть положительным, но не может равняться 1. Таким образом, основание \large{1 \over {27}} совершенно нормально. Очевидно, что это положительное число, и оно не равно 1,9.k}} \right) = k \cdot {\log _b}\left( x \right)}

\large{\color{red}{\log _b}b = 1}

Теперь ниже является полным решением.

Пример 3: Вычислить значение \large{\log {}_{\large{5}}\left({12} \right)}. Округлите ответ до ближайших тысячных .

Это уже не «хорошая» задача, потому что аргумент и основание логарифма нельзя выразить в виде степеней обычного числа. Другими словами, не существует сценария, в котором мы могли бы выразить 5 и 12 в виде экспоненциальных чисел так, чтобы они имели одно и то же основание.

Чтобы решить эту проблему, мы можем использовать правило смены основания, чтобы переписать исходный логарифм как отношение двух логарифмов по выбранному нами основанию. У нас есть два варианта: использовать base-10 или base-e. Неважно, какой из них мы выберем, потому что ответ будет таким же. Для этой задачи воспользуемся основанием 10.

Не забудьте округлить свой ответ до трех знаков после запятой, потому что нас просят округлить его до ближайшей тысячной.

Наш калькулятор должен подтвердить правильность нашего ответа.

Пример 4: Вычислить значение \large{\log {}_{\large{7}}\left({9} \right)}. Округлите ответ до сотых.

В предыдущем примере мы использовали основание 10 для вычисления логарифма. На этот раз мы будем использовать натуральное число \color{red}e в качестве основы выбора при применении формулы смены основы.

Обратите внимание, что нам не нужно записывать натуральный логарифм как \large{{{\log }_e}\left( x \right)}. Мы можем опустить этот шаг и сразу записать его как \large{\ln \left( x \right)}. Я добавил это как один из шагов ниже для ясности и акцентирования внимания.

Давайте продолжим и применим правило изменения базы для преобразования \large{\log {}_7\left( 9 \right)} как отношение или дробь двух операций натурального логарифма.

Кроме того, не забудьте округлить свой ответ до двух знаков после запятой, так как задача требует, чтобы мы выражали наш окончательный ответ в ближайших сотых.

Ваш калькулятор должен выдать результат, аналогичный приведенному ниже.

Пример 5: Изменить \large{\log {}_{\large{6}}\left( {0,1} \right)} как частное двух натуральных логарифмов. Вычислите его значение, затем округлите до десятых.

Эта задача требует от нас изменить заданный логарифм как частное натуральных логарифмов. Это означает, что у нас нет другого выбора, кроме как использовать натуральное число \large\color{red}e в качестве базы, когда мы применяем формулу замены базы. Не забывайте также, что нам говорят округлить наш ответ до ближайшей десятой (один десятичный знак).

Вот наше решение:

Наш калькулятор согласен с нашим ответом.

Пример 6: Изменить \color{blue}\large{\log \left( 7 \right)} как частное в натуральных логарифмах. Затем вычислить его значение. Округлите ответ до десятитысячных.

Я признаю, что, хотя мы можем напрямую определить значение \color{red}\log \left( 7 \right) с помощью калькулятора, так как он имеет ключ LOG , эта задача заставляет нас идти длинным путем. Не потому, что это бесполезное занятие нашего времени, но, что более важно, это возможность для нас применить наше твердое понимание или понимание формулы смены основы.

Помните, что когда вы видите логарифмическую операцию без основания, предполагается, что она имеет основание 10. Поэтому наш самый первый шаг — переписать \log \left( 7 \right) как {\log _{10} }\left( 7 \right), чтобы было намного легче увидеть, с какими числами мы имеем дело во время шага смены базы.

Это прекрасное чувство, когда калькулятор выдает значение, подтверждающее наш ответ.

Пример 7: Изменить \color{blue}\large\ln \left( {13} \right) как отношение десятичных логарифмов. Затем рассчитайте его стоимость. Округлите ответ до десятитысячных.

Как и в примере № 6, нет необходимости применять формулу изменения основания, потому что мы можем вычислить ее напрямую с помощью калькулятора. Однако цель этой задачи — продемонстрировать наше глубокое понимание десятичных и натуральных логарифмов, а также то, как правильно обращаться с формулой.

Итак, давайте преобразуем \large\ln \left( {13} \right) в логарифмическую форму , где основание равно \large\color{blue}e, таким образом, \large{\log _{\large{e }}}\влево({13}\вправо). Теперь мы используем формулу замены основания, чтобы выразить это как отношение двух десятичных логарифмов. Помните, десятичный логарифм использует основание 10.

Да! Калькулятор согласен с нашим ответом.

Полный курс алгебры

Навыки
в
A L G E B R A

Содержание | Дом

Определение

десятичные логарифмы

Три закона логарифмов

КОГДА НАМ ЗНАЕТ, например, основание 2 и показатель степени 3, мы можем вычислить 2 ³ .

2 ³ = 8.

Обратно, если нам дано основание 2 и степень 8 —

2 ^? = 8

— тогда какой показатель степени даст 8?

Этот показатель степени называется логарифмом. Мы называем показатель степени 3 логарифмом числа 8 по основанию 2. Мы пишем

3 = логарифм ₂ 8.

Основание 2 записывается как нижний индекс.

3 — это показатель степени , до которого нужно возвести 2, чтобы получить 8.

Логарифм является показателем степени.

10 ⁴ = 10 000

, затем

журнал ₁₀ 10 000 = 4.

«Логарифм 10 000 по основанию 10 равен 4».

4 — это показатель степени , до которого нужно возвести 10, чтобы получить 10 000.

«10 ⁴ = 10 000″ называется экспоненциальной формой.

«log ₁₀ 10 000 = 4″ называется логарифмической формой.

Вот определение:

log _b x = n означает b ⁿ = x .

Эта база с этим показателем степени дает x .

Пример 1. Запишите в экспоненциальной форме: log ₂ 32 = 5

Ответ . 2 ⁵ = 32

Пример 2. Запишите в логарифмической форме: 4 ⁻² =

1
16

Ответ. журнал ₄

1
16

= −2.

Задача 1. Какие числа имеют отрицательные логарифмы?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!

Правильные дроби.

Урок 20 арифметики

Пример 3. Оценить log ₈ 1.

Ответить . 8 в какой степени дает 1?

8 ⁰ = 1.

журнал ₈ 1 = 0,

Мы можем заметить, что по любому основанию логарифм 1 равен 0.

журнал _б 1 = 0

Пример 4. Оценить log ₅ 5.

Ответ . 5 с каким показателем даст 5? 5 ¹ = 5. Следовательно,

журнал ₅ 5 = 1.

В любом основании логарифм самого основания равен 1.

log _б б = 1

Пример 5. журнал ₂ 2 ^м = ?

Ответ . 2 с каким показателем будет 2 ^m ? м , очевидно.

бревно ₂ 2 ^м = м .

Следующее важное формальное правило справедливо для любого основания b :

бревно _б б ^х = х

Это правило воплощает в себе сам смысл логарифма. x — справа — показатель степени , до которого необходимо возвести основание b , чтобы получить b ^x .

Пример 6. Журнал оценки ₃

1
9

Ответ.

1
9

в каком показателе равно 3?

1
9

= 3 ⁻² .

журнал ₃

1
9

log ₃ 3 ⁻² = −2.

Сравните предыдущее правило.

Пример 7. log ₂ .25 = ?

Ответ . .25 = ¼ = 2 ⁻² . Следовательно,

log ₂ .25 = log ₂ 2 ^-2 = -2.

Пример 8. log ₃ = ?

Ответ. = 3 ^1/5 . (Определение рационального показателя.) Следовательно,

журнал ₃ = журнал ₃ 3 ^1/5 = 1/5.

Задача 2. Запишите каждое из следующих чисел в логарифмической форме.

а) б ⁿ = x .	log _b x = n .	б) 2 ³ = 8.	журнал ₂ 8 = 3.

в) 10 ² = 100.	журнал ₁₀ 100 = 2.	d) 5 ⁻² = 1/25.	log ₅ 1/25 = −2.

Задача 3. Запишите каждое из следующих чисел в экспоненциальной форме.

a) log _b x = n .	б ^н = х .	б) log ₂ 32 = 5.	2 ⁵ = 32.

в) 2 = log ₈ 64.	8 ² = 64,	г) log ₆ 1/36 = −2.	6 ⁻² = 1/36.

Проблема 4. Оцените следующее.

а) журнал ₂ 16	= 4	б) журнал ₄ 16	= 2

в) журнал ₅ 125	= 3	г) журнал ₈ 1	= 0

e) журнал ₈ 8	= 1	f) журнал ₁₀ 1	= 0

Задача 5. Какое число равно п ?

а) log ₁₀ n = 3.	1000	b) 5 = log ₂ n .	32

в) log ₂ n = 0.	1	г) 1 = логарифм ₁₀ n .	10

e) лог _n	1 16	= −2.	4	f) журнал _n	1 5	= −1.	5

ж) лог ₂	1 32	= n .	−5	h) журнал ₂	1 2	= n .	-1

Задача 6. журнал _б б ^x = х

Задача 7. Оцените следующее.

а) журнал ₉

1
9

= логарифм ₉ 9 ⁻¹ = −1

б) журнал ₉	1 81	= −2	в) журнал ₂	1 4	= −2

г) журнал ₂	1 8	= −3	e) журнал ₂	1 16	= −4

f) журнал ₁₀ . 01	= −2	g) журнал ₁₀ .001	= −3

h) журнал ₆	= 1/3

Запишите в экспоненциальной форме и примените задачу 6.

i) журнал _б

= 3/4

десятичные логарифмы

Система десятичных логарифмов имеет основание 10. Когда база не указана:

логарифм 100 = 2

, то подразумевается система десятичных логарифмов по основанию 10.

Вот степени числа 10 и их логарифмы:

Степени 10:	1 1000	1 100	1 10	1	10	100	1000	10 000

Логарифмы:	−3	−2	−1	0	1	2	3	4

Логарифмы заменяют геометрический ряд арифметическим.

Задача 8.

а) log 10 ⁵ = 5. 10 — основание.

б) log 10 ⁿ = n

в) log 58 = 1,7634. Следовательно, 10 ^1,7634 = 58

1,7634 — это десятичный логарифм числа 58. Когда 10 возводят в эту степень, получается 58.

Задача 9. log (log x ) = 1. Какое число равно x ?

Лог какого числа равен 1? Поскольку 10 — это основание, log 10 = 1,

(см. выше)

Следовательно, log (log x ) = 1 подразумевает log x = 10. И, следовательно, поскольку 10 — это основание:

х = 10 ¹⁰ = 10 000 000 000

Три закона логарифмов

1 . log _b xy = log _b x + log _b y4

» Логарифм произведения равен сумме
логарифмов каждого множителя. «

2 . журнал _б

= log _b x − log _b y

» Логарифм частного равен логарифму числителя
минус логарифм знаменателя. »

3 . журнал _б x ⁿ = n бревно _b x

» Логарифм степени x равен показателю степени , умноженному на
логарифм x . »

Для доказательства этих законов см. Тему 20 Предварительного исчисления.

Пример 9. Примените законы логарифмов к журналу

абв ²
г ³

Ответ. Согласно первым двум законам,

журнал	абв ² г ³	=	журнал ( абв ² ) − журнал д ³

		=	журнал a + журнал b + журнал c ² − журнал д ³

		=	журнал a + журнал b + 2 журнала c − 3 журнала д ,

по третьему закону.

Ответ выше показывает полные теоретические шаги. На практике, однако, нет необходимости писать строку

.
журнал абв ²
г ³ = журнал ( абв ² ) − журнал д ³ .
Студент должен иметь возможность сразу перейти на следующую строку —
журнал абв ²
г ³ = бревно а + бревно б + бревно в ² − журнал д ³
— если не до последней строки
журнал абв ²
г ³ = лог. a + лог. b + 2 лог. c — 3 лог. d .
Пример 10. Примените законы логарифмирования к log
   из ⁵ .
Ответ. журнал
   я ⁵   =  log x + log — log z ⁵
Сейчас, = y ^½ . (Урок 29.) Следовательно, согласно третьему закону,
журнал
   я ⁵   =  log x + ½ log y − 5 log z .
Пример 11.   Используйте законы логарифмов, чтобы переписать log (sin x log x )
Решение . Он имеет вид log ab . a = sin x , b = log x . Следовательно,
log (sin x log x ) = log sin x + log log x .
Пример 12.   Используйте законы логарифмирования, чтобы переписать log .
Решение .
Журнал
журнал = ( x , потому что x )

= ½ журнала ( x потому что x ), 3-й закон

= ½ (log x + log cos x ), 1-й закон.
Задача 10.   Используя законы логарифмов, перепишите следующее.
а)  лог аб
в = журнал a + журнал b — журнал c

б)  лог аб ²
в ⁴ = журнал a + 2 журнала b — 4 журнала c

в)  журнал
з    = 1/3 логарифма x + 1/2 логарифма y − логарифма z
  d) log (sin ² x log x ) = log sin ² x + log log x

= 2 log sin x + log log x
  e) журнал = логарифм (sin x cos x ) ^1/2

= ½ журнала (sin x cos x )

= ½ (log sin x + log cos x ).
Пример 13.   Дано: log 3 = 0,4771. Вычислить
.
а) журнал 3000
Раствор. Запишите 3000 в экспоненциальном представлении:
журнал 3000 = журнал (3 × 10 ³ )

= журнал 3 + журнал 10 ³

= .4771 + 3

= 3,4771
б) лог.003
   Решение. журнал 0,003 = логарифм (3 × 10 ⁻³ )

= журнал 3 + журнал 10 ⁻³

= . 4771 − 3

= −2,5229
Задача 11.   Дано: log 6 = 0,7781 Используйте законы логарифмов, чтобы оценить следующее.
а) журнал 600 = журнал (6 × 10 ² )

= журнал 6 + журнал 10 ²

= .7781 + 2

= 2,7781
б) журнал 60 = бревно (6×10)

= журнал 6 + журнал 10

= . 7781 + 1

= 1,7781
в) лог .06 = логарифмов (6 × 10 ⁻² )

= логарифм 6 + логарифм 10 ⁻²

= .7781 − 2

= −1,2219
Пример 14. Дано: log 2 = 0,3010, log 3 = 0,4771 Оценить log 18.
Решение . 18 = 2 · 3 ² . Следовательно,
журнал 18 = журнал (2 · 3 ² )

= журнал 2 + журнал 3 ²

= журнал 2 + 2 журнал 3

= . 3010 + 2(.4771)

= .3010 + .9542

= 1,2552
Задача 12.   Дано: log 2 = 0,3010 log 3 = 0,4771   log 5 = 0,6990
Используйте законы логарифмов, чтобы найти следующее.
а) журнал 6 = журнал 2 + журнал 3 = 0,7781
б) лог 15 = журнал 3 + журнал 5 = 1,1761
в) лог 4 = журнал 2 ² = 2 журнал 2 = 0,6020
г) лог 8 = журнал 2³ = 3 журнал 2 = 0,9030
д) журнал 30 = журнал 3 + журнал 10 = 1,4771
е) журнал 300 = журнал 3 + журнал 100 = 2,4771
г) log 3000 = журнал 3 + журнал 1000 = 3,4771
ч) лог 12 = журнал 3 + журнал 4 = 1,0791
  i) журнал 3
5 = журнал 3 — журнал 5 = -0,2219
к) журнал = ½ журнала 3 = 0,2386
к) лог = ½ журнала 5 = 0,3495
  л) лог  = 3
2 логарифм 3 = 0,7157
  м) лог  = 1
3 лог 2 = 0,1003
n) log = ½ (журнал 2 — журнал 3) = -0,0881
о) лог 1500 = журнал 3 + журнал 5 + журнал 100 = 3,1761
Систему натуральных логарифмов см.
No related posts.

\(\log_{4\sqrt{2}}{8}=x\)		Нам надо найти значение логарифма, обозначим его за икс. {b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
\(\log_{4}{10}=5x-4\)		Зеркально перевернем уравнение, чтобы икс был слева
\(5x-4=\log_{4}{10}\)		Перед нами линейное уравнение. Перенесем \(4\) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу.
\(5x=\log_{4}{10}+4\)		Поделим уравнение на 5
\(x=\)\(\frac{\log_{4}{10}+4}{5}\)		Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Log 10 по основанию 2. Что такое логарифм? Решение логарифмов. Примеры. Свойства логарифмов

Определение логарифма

Свойства логарифма

Область определения, множество значений, возрастание, убывание

Частные значения

Основные формулы логарифмов

Основное свойство логарифмов и его следствия

Формула замены основания

Доказательство основных формул логарифмов

Обратная функция

Производная логарифма

Интеграл

Выражения через комплексные числа

Разложение в степенной ряд

Сбор и использование персональной информации

Раскрытие информации третьим лицам

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Что такое логарифм?

Аргумент и основание логарифма

Как вычислить логарифм?

Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Десятичный и натуральный логарифмы

Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).

Как число записать в виде логарифма?

Определение в математике

Разновидности логарифмов

Правила и некоторые ограничения

Как решать логарифмы?

Уравнения и неравенства

Основные теоремы о логарифмах

Примеры задач и неравенств

Как использовать формулы логарифмов: с примерами и решениями

Задания из ЕГЭ

Что такое логарифм

Как считать логарифмы

Десятичный логарифм

Натуральный логарифм

Log 3 log 12: Mathway

ЕГЭ по математике. В 7. Логарифмические выражения.

Свойства логарифмов. Готовимся к ЕГЭ

Калькулятор онлайн — Решение логарифмических уравнений

Логарифмическая функция. Логарифмы

Свойства логарифмов

Десятичные и натуральные логарифмы

Логарифмическая функция, её свойства и график

Логарифмические уравнения

Аргумент и основание логарифма

Как вычислить логарифм?

Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Десятичный и натуральный логарифмы

Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).

Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg{a}\).

Как число записать в виде логарифма?

Найдите значение числового логарифмического выражения – как решать

Логарифмические уравнения

Основное логарифмическое тождество:

Mathway | Популярные задачи

Калькулятор логарифма log (x)

Логарифм

Общие значения для базы журнала

Логарифмические тождества

Логарифм произведения

Логарифм частного

Логарифм степени

Изменение базы

Примеры натурального логарифма

Таблицы логарифмических значений

83

83

83

83

83

83 5)

83

84 журнал 11)

83 17)

83

83 23)

Калькуляторы связанной базы журналов

50
50
50
50
50

50
50
50