Натуральный логарифм: онлайн калькулятор | BBF.RU
Логарифмирование — арифметическая операция, обратная возведению в степень. Для решения практических задач на поиск количества удвоений, утроений или удесятирений используются стандартные логарифмы. Если же требуется вычислить время, необходимое для роста до выбранного уровня, то математики используют натуральный логарифм.
Возведение в степень и логарифм
Возведение в степень представляет собой операцию повторяющегося умножения числа на само себя. Если нам требуется умножить тройку на себя 7 раз, то мы записываем это как 3 × 3 × 3 × 3 × 3 × 3 × 3. Компактная запись такого выражения выглядит как 37 — это и есть возведение в степень.
Деление — операция, обратная умножению. Если верно выражение A × B = C, то и выражение A = C / B так же верно. Такая взаимосвязь часто используется при решении линейных уравнений вида Ax + B = 0, где мы легко можем выразить неизвестное при помощи операции деления. Но что делать, если уравнение не линейное, а показательное? Например, как решить уравнение вида Ax = B. Икс — показатель степени и он нам неизвестен. Возникает задача, в какую степень требуется возвести A, чтобы получить B?
Икс — показатель степени и он нам неизвестен. Возникает задача, в какую степень требуется возвести A, чтобы получить B?
Для наглядности попробуем решить не абстрактный буквенный пример Ax = B, а числовой. Пусть есть элементарное показательное уравнение 2x = 4. В какую степень нужно возвести двойку, чтобы получить 4? Очевидно, что во вторую. Более сложное уравнение 3x = 243. Для решения такого уравнения можно постепенно умножать тройку на саму себя, пока не получим число 243. Легко подсчитать, что 3 × 3 × 3 = 27, но этого мало. Умножим еще на 3 и получим 81. Умножив еще раз мы получим искомое 243. Мы умножили 3 на себя 5 раз, следовательно, x = 5.
Ну а что делать с уравнением 2x = 5? Небольшое изменение, и элементарное уравнение превращается в практически не разрешимое вручную. Очевидно, что ответ больше 2 и меньше 3, но его точное значение мы можем узнать лишь с заданной точностью. Вот тут нам и пригодятся логарифмы. Для решения уравнения следует записать x = log2 5. Все, это и есть ответ, которого достаточно любому математику.
Все, это и есть ответ, которого достаточно любому математику.
Понятие натурального логарифма
Таким образом, логарифм log A B – это число, в которое требуется возвести A, чтобы получить B. Число A в данном случае называется основанием, которое может быть любым, однако на практике чаще всего встречаются логарифмы с основанием 10 и e. Первые соответственно называются десятичными, а вторые — натуральными. Несмотря на название, натуральный логарифм — техническая функция.
Экспонента (число е) — иррациональное число, приблизительно равное 2,718281828. Экспонента представляет собой базовое соотношение роста для любых растущих процессов. Число e – это предельная константа, ограничивающая процессы роста так же, как скорость света ограничивает передвижение объектов в пространстве. Именно операции с экспонентой дают возможность определить темпы роста в таких ситуациях, как вычисление прироста населения, процентов по банковскому депозиту или объема полураспада радиоактивного вещества. Так как любой процесс можно описать при помощи математических формул, любой рост можно выразить упрощенной формулой вида:
Так как любой процесс можно описать при помощи математических формул, любой рост можно выразить упрощенной формулой вида:
Рост = ex
Например, если мы положили $100 на банковский депозит поl 9% годовых сроком на 3 года, то прибыль будет рассчитываться как:
Конечный результат: 100e(0,09 × 3) = $130.
Это простая операция возведения числа е в степень. Если же нам требуется обратная операция, то на помощь придет натуральный логарифм. Рассмотрим пример с банковским депозитом.
Вычисление необходимой ставки
В примере выше мы вычислили прибыль, но что делать, если вы инвестор и хотите получить от вклада заданный доход? Пусть у вас есть $1 000 и вы хотите, чтобы через год на банковском депозите было уже $1 500. Какую процентную ставку должен предлагать банк для осуществления этого инвестиционного плана? Составим уравнение:
- 1000ex = 1500
- ex = 1,5
Требуется найти икс, и нам на помощь спешит натуральный логарифм. Решением данного уравнения будет x = ln1,5, но если для математика такого ответа достаточно, то инвестору придется подсчитать это значение на нашем калькуляторе. Для этого введите значение в ячейку и сделайте один клик мышью. В результате получаем 0,40. Увы, никакой банк не предложит вам депозит под 40% годовых. Но зная необходимый процент вы можете определить произведение годовой ставки на количество лет. Зная, что вам требуется получить прирост в размере 40%, вы можете выбрать несколько вариаций и положить деньги в банк:
Решением данного уравнения будет x = ln1,5, но если для математика такого ответа достаточно, то инвестору придется подсчитать это значение на нашем калькуляторе. Для этого введите значение в ячейку и сделайте один клик мышью. В результате получаем 0,40. Увы, никакой банк не предложит вам депозит под 40% годовых. Но зная необходимый процент вы можете определить произведение годовой ставки на количество лет. Зная, что вам требуется получить прирост в размере 40%, вы можете выбрать несколько вариаций и положить деньги в банк:
- под 10% годовых на 4 года;
- под 8% годовых на 5 лет;
- под 13% годовых на 3 года.
Как видите, экспонента и натуральный логарифм необходимы не только на занятиях по алгебре.
Наш онлайн-калькулятор — это быстрая и точная программа для вычисления значений натурального логарифма. Калькулятор представляет собой сборник из четырех программ для вычисления логарифмов разного типа. Для подсчетов достаточно выбрать в меню натуральный логарифм, ввести значение в ячейки и получить результат. Программа вычисляет как само значение логарифма lnx, так и возвращает величину x при известном значении логарифма.
Программа вычисляет как само значение логарифма lnx, так и возвращает величину x при известном значении логарифма.
Использование логарифмов
Логарифмы пришли в нашу жизнь в 17-м веке, когда математики впервые упорядочили знания об арифметических операциях. Логарифмические таблицы значительно упростили масштабные расчеты и позволили ученым оперировать огромными числами.
Логарифмы широко используются для отображения графиков функций, значения которых имеют огромный разброс. Например, если требуется отобразить график, в котором присутствуют значения 1, 100 и 100 000, то на помощь приходит логарифмическая шкала, в которой числа отображаются при помощи десятичных логарифмов.
Натуральный логарифм используется в основном для описания любых процессов непрерывного роста. В целом для этого используется экспоненциальная функция, но, если требуется найти неизвестный параметр, на помощь приходит натуральный логарифм.
Заключение
Логарифм — удобный математический инструмент, который используется не только в высокой математике, но и в реальной жизни. Наш онлайн-калькулятор пригодится для простых вычислений выражений, оперирующих натуральными логарифмами.
Наш онлайн-калькулятор пригодится для простых вычислений выражений, оперирующих натуральными логарифмами.
Добро пожаловать в калькулятор логарифмов онлайн. Для чего нужен этот калькулятор. Ну, в первую очередь для того, что бы свериться со своими письменными или умственными расчетами. С логарифмами (в российских школах) столкнуться можно уже в 10-том классе. И эта тема считается достаточно сложной. Решение логарифмов, особенно с большими или дробными числами, знаете ли, дело не легкое. Уж лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте основание с числом. Калькулятор логарифмов чем то, схож с калькулятором факториалов, который автоматически выдает несколько решений. Калькулятор логарифмов (вещественных) – этот калькулятор находит логарифм по заданному основанию онлайн.
Понятие вещественного логарифма: Существует множество разных определений логарифма. Сперва, неплохо было бы узнать, что логарифм — это некая алгебраическая запись, обозначенная как log a b, где а – основание, b – число. Основание, то есть «а» всегда находится внизу. Так как оно всегда возводится в степень. А теперь собственно, определение самого логарифма: Логарифмом положительного числа b по основанию a (где a>0, a≠1)называется степень, в которую нужно возвести число а, чтобы получить число b. Кстати, не только основание должно быть в положительной форме. Число(аргумент), так же должно быть положительным. В противном случае калькулятор логарифмов включит неприятную тревогу. Логарифмирование – это операция нахождения логарифма, по заданному основанию. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните:
А операция обратная логарифмированию это – Потенцирование. |
Добро пожаловать в калькулятор логарифмов онлайн. Для чего нужен этот калькулятор. Ну, в первую очередь для того, что бы свериться со своими письменными или умственными расчетами. С логарифмами (в российских школах) столкнуться можно уже в 10-том классе. И эта тема считается достаточно сложной. Решение логарифмов, особенно с большими или дробными числами, знаете ли, дело не легкое. Уж лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте основание с числом. Калькулятор логарифмов чем то, схож с калькулятором факториалов, который автоматически выдает несколько решений. Калькулятор логарифмов (вещественных) – этот калькулятор находит логарифм по заданному основанию онлайн.
Понятие вещественного логарифма: Существует множество разных определений логарифма. Сперва, неплохо было бы узнать, что логарифм — это некая алгебраическая запись, обозначенная как log a b, где а – основание, b – число. А читается эта запись так: Логарифм по основанию a числа b. Иногда используется обозначение log b .
А операция обратная логарифмированию это – Потенцирование. |
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2
Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5 , log 3 8 , log 5 100 .
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1 , т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b будет ответом.
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача.
Вычислите логарифм: log 5 25
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Получили ответ: 2.
Составим и решим уравнение:
log 5 25 = b
⇒ (5 1) b
= 5 2 ⇒ 5 b
= 5 2 ⇒ b
= 2 ;
Задача. Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Получили ответ: 3.
Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.
е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459. ..
..
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x
Таким образом, ln e = 1 ; ln e 2 = 2 ; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Логарифмирование — это операция, обратная возведению в степень. Если вы задаетесь вопросом, в какую степень нужно возвести 2, чтобы получить 10, то вам на помощь придет логарифм.
Обратная операция для возведения в степень
Возведение в степень — это повторяющееся умножение. Для возведения двойки в третью степень нам потребуется вычислить выражение 2 × 2 × 2. Обратная операция для умножения — это деление. Если верно выражение, что a × b = c, то обратное выражение b = a / c так же верно. Но как обратить возведение в степень? Задача обращения умножения имеет элегантное решение благодаря простому свойству, что a × b = b × a. Однако a b не равно b a , за исключением единственного случая, когда 2 2 = 4 2 . В выражении a b = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы.
Однако a b не равно b a , за исключением единственного случая, когда 2 2 = 4 2 . В выражении a b = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы.
Понятие логарифма
Давайте попробуем решить простое уравнение вида 2 x = 16. Это показательное уравнение, так как нам требуется отыскать показатель степени. Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4.
Теперь попробуем решить 2 x = 20. Сколько раз нужно умножить двойку на саму себя, что бы получить 20? Это сложно, ведь 2 4 = 16, а 2 5 = 32. Рассуждая логически, корень этого уравнения располагается между 4 и 5, причем ближе к 4, возможно 4,3? Математики не терпят приблизительных вычислений и хотят знать точный ответ. Для этого они и используют логарифмы, а корнем этого уравнения будет x = log2 20.
Выражение log2 20 читается как логарифм 20 по основанию 2. Это и есть ответ, которого строгим математикам достаточно. Если вы хотите выразить это число точно, то вычислите его при помощи инженерного калькулятора. В этом случае log2 20 = 4,32192809489. Это иррациональное бесконечное число, а log2 20 — его компактная запись.
Это и есть ответ, которого строгим математикам достаточно. Если вы хотите выразить это число точно, то вычислите его при помощи инженерного калькулятора. В этом случае log2 20 = 4,32192809489. Это иррациональное бесконечное число, а log2 20 — его компактная запись.
Таким элегантным способом вы можете решить любое простое показательное уравнение. Например, для уравнений:
- 4 x = 125, x = log4 125;
- 12 x = 432, x = log12 432;
- 5 x = 25, x = log5 25.
Последний ответ x = log5 25 математикам не понравится. Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 5 2 = 25. Поэтому для уравнения вида 5 x = 25, x = 2.
Десятичный логарифм
Десятичный логарифм — это функция по основанию 10. Это популярный математический инструмент, поэтому он записывается иначе. К примеру, в какую степень нужно возвести 10, чтобы получить 30? Ответом был бы log10 30, однако математики сокращают запись десятичных логарифмов и записывают его как lg30. Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно.
Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно.
Натуральный логарифм
Натуральный логарифм — это функция по основанию e. В нем нет ничего натурального, и многих неофитов такая функция попросту пугает. Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов.
В какую степень нужно возвести число e, чтобы получить 10? Ответом был бы loge 10, но математики обозначают натуральный логарифм как ln, поэтому ответ будет записан как ln10. Тоже самое с выражениями loge 35 и loge 40, верная форма записи которых – ln34 и ln40.
Антилогарифм
Антилогарифм — это число, которому соответствует значение выбранного логарифма. Простыми словами, в выражении loga b антилогарифмом считается число b a . Для десятичного логарифма lga, антилогарифм равен 10 a , а для натурального lna антилогарифм равняется e a . По сути, это тоже возведение в степень и обратная операция для логарифмирования.
По сути, это тоже возведение в степень и обратная операция для логарифмирования.
Физический смысл логарифма
Нахождение степеней — чисто математическая задача, но для чего нужны логарифмы в реальной жизни? В начале развития идеи логарифмирования данный математический инструмент использовался для сокращения объемных вычислений. Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.
Логарифмы нашли применение и в сфере изображения графических процессов. Если требуется нарисовать график функции, которая принимает значения 1, 10, 1 000 и 100 000, то маленькие значения будут невидны и визуально они сольются в точку около нуля. Для решения подобной проблемы используются десятичный логарифм, которой позволяет построить график функции, адекватно отображающий все ее значения.
Для решения подобной проблемы используются десятичный логарифм, которой позволяет построить график функции, адекватно отображающий все ее значения.
Физический же смысл логарифмирования — это описание временных процессов и изменений. Так, логарифм по основанию 2 позволяет определить, сколько требуется удвоений начального значения для достижения определенного результата. Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.
Наша программа представляет собой сборник из четырех онлайн-калькуляторов, которые позволяют вычислить логарифм по любому основанию, десятичную и натуральную логарифмическую функцию, а также десятичный антилогарифм. Для проведения вычислений вам потребуется ввести основание и число, или только число для десятичного и натурального логарифма.
Примеры из реальной жизни
Школьная задача
Как было сказано выше, иррациональные значения по типу log2 345 не требуют дополнительных преобразований, и такой ответ полностью удовлетворит учителя математики. Однако если логарифм вычисляется, вы обязаны представить его в виде целого числа. Пусть вы решили 5 примеров по алгебре, и вам требуется проверить результаты на возможность целочисленного представления. Давайте проверим их при помощи калькулятора логарифма по любому основанию:
Однако если логарифм вычисляется, вы обязаны представить его в виде целого числа. Пусть вы решили 5 примеров по алгебре, и вам требуется проверить результаты на возможность целочисленного представления. Давайте проверим их при помощи калькулятора логарифма по любому основанию:
- log7 65 — иррациональное число;
- log3 243 — целое число 5;
- log5 95 — иррациональное;
- log8 512 — целое число 3;
- log2 2046 — иррациональное.
Таким образом, значения log3 243 и log8 512 вам потребуется переписать как 5 и 3 соответственно.
Потенцирование
Потенцирование — это нахождение антилогарифма числа. Наш калькулятор позволяет найти антилогарифмы по десятичному основанию, что по смыслу означает возведение десятки в степень n. Давайте вычислим антилогарифмы для следующих значений n:
- для n = 1 antlog = 10;
- для n = 1,5 antlog = 31,623;
- для n = 2,71 antlog = 512,861.
Непрерывный рост
Натуральный логарифм позволяет описывать процессы непрерывного роста. Представим, что ВВП страны Кракожия увеличилось с 5,5 миллиардов долларов до 7,8 за 10 лет. Давайте определим ежегодный прирост ВВП в процентах при помощи калькулятора натурального логарифма. Для этого нам надо подсчитать натуральный логарифм ln(7,8/5,5), что равнозначно ln(1,418). Введем это значение в ячейку калькулятора и получим результат 0,882 или 88,2% за все время. Так как ВВП рос в течение 10 лет, то ежегодный его прирост составит 88,2 / 10 = 8,82%.
Представим, что ВВП страны Кракожия увеличилось с 5,5 миллиардов долларов до 7,8 за 10 лет. Давайте определим ежегодный прирост ВВП в процентах при помощи калькулятора натурального логарифма. Для этого нам надо подсчитать натуральный логарифм ln(7,8/5,5), что равнозначно ln(1,418). Введем это значение в ячейку калькулятора и получим результат 0,882 или 88,2% за все время. Так как ВВП рос в течение 10 лет, то ежегодный его прирост составит 88,2 / 10 = 8,82%.
Поиск количества удесятирений
Допустим, за 30 лет количество персональных компьютеров увеличилось с 250 000 до 1 миллиарда. Сколько раз количество ПК увеличивалось в 10 раз за все это время? Для подсчета такого интересного параметра нам потребуется вычислить десятичный логарифм lg(1 000 000 000 / 250 000) или lg(4 000). Выберем калькулятор десятичного логарифма и посчитаем его значение lg(4 000) = 3,60. Получается, что с течением времени количество персональных компьютеров возрастало в 10 раз каждые 8 лет и 4 месяца.
Заключение
Несмотря на сложность логарифмов и нелюбовь детей к ним в школьные годы, этот математический инструмент находит широкое применение в науке и статистике. Используйте наш сборник онлайн-калькуляторов для решения школьных заданий, а также задач из разных научных сфер.
Используйте наш сборник онлайн-калькуляторов для решения школьных заданий, а также задач из разных научных сфер.
Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Предыдущую статью о показательных уравнениях мы начали с уравнения 2x = 8. Там всё было ясно: x = 3.
А теперь рассмотрим уравнение 2x = 7.
По графику функции y = 2x мы видим, что это уравнение имеет корень, и притом единственный.
Ясно, что этот корень — не целое число (так как 22 = 4, 23 = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.
Этот корень обозначается log27 (читается: «логарифм семи по основанию два». Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log27 = 2,807354922057604107…
Итак, наше число log27 — это показатель степени, в которую надо возвести 2, чтобы получить 7.
Теперь дадим общее определение логарифма. Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).
Определение. Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b.
Иными словами,
Например:
так как
, так как
так как ;
, так как .
Логарифм с основанием 10 называется десятичным и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.
Логарифм с основанием e называется натуральным и обозначается ln.
Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log2(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.
Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.
Основные формулы
По определению, logab — это показатель степени, в которую надо возвести число a, чтобы получить число b:
| alogab=b | (1) |
Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:
logaax=x.
Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.
Логарифм произведения — это сумма логарифмов:
| loga(bc) = logab + logac. | (2) |
Логарифм частного — это разность логарифмов:
| (3) |
Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:
| (4) |
Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:
| (5) |
Формулы (4) и (5) вместе дают:
| (6) |
В частности, если m = n, мы получаем формулу:
| (7) |
Например, .
Наконец, важнейшая формула перехода к новому основанию:
| (8) |
В частности, если c = b, то logbb = 1, и тогда:
| (9) |
Приведём несколько примеров из банка заданий.
1. (применили формулу (2) суммы логарифмов).
2. (применили основное логарифмическое тождество(1))
3. (применили формулу (4).
4. (применили формулу (9), перейдя к новому основанию 0,8).
5. (применили формулу (3) разности логарифмов)
Немного истории
Теперь вы поняли, что такое логарифмы и как ими пользоваться. Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?
Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.
Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?
Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.
В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.
Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.
Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу. Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).
А затем по таблице логарифмов найти само произведение чисел b и c.
Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.
Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.
Точка росы и ее расчет – онлайн калькулятор
- Главная
- »
- Словарь терминов
- »
- Точка росы
Точка росы – значение температуры, при которой водяные пары, находящиеся в воздухе, конденсируют в росу.
Конденсат – это продукт образованный в результате перехода жидкости из газообразного состояния в жидкое.
Конденсат на стекле
Точка росы зависит от:
- Температуры;
- Относительной влажности воздуха.

Чем выше относительная влажность воздуха, тем выше значение точки росы, соответственно, чем меньше влажность, тем она ниже.
Точка росы не может превышать температуру воздуха.
При 100 %-ой влажности воздуха, точка росы будет равна температуре воздуха.
Расчет точки росы
Рассчитать температуру выпадения конденсата можно по следующей формуле:
Тр = (b*f(T, Rh))/(a-ƒ(T, Rh))
ƒ(T, Rh) = (a*T)/(b+T)+ln(Rh/100)
где:
- Тр – температура точки росы, °С;
- а (постоянная) = 17,27;
- в (постоянная) = 237,7;
- Т – температура воздуха, °С;
- Rh – относительная влажность воздуха, %;
- ln – натуральный логарифм.
Данная формула обладает погрешностью в ±0,4 °С в диапазоне:
- 0 °С < Т < 60 °С;
- 0,01 < Rh < 1,00
- 0 °С < Тр < 50 °С;
Приборы для расчета точки росы
Для определения температуры выпадения конденсата используются различные приборы:
- Психрометр – прибор, с помощью которого измеряется относительная влажность и температура воздуха.
 Он состоит из двух термометров: один – сухой, второй – с постоянным увлажнением. В ходе испарения влаги увлажненный термометр постепенно охлаждается. Чем ниже относительная влажность воздуха, тем ниже его температура. Психрометр используется в лабораторных условиях.
Он состоит из двух термометров: один – сухой, второй – с постоянным увлажнением. В ходе испарения влаги увлажненный термометр постепенно охлаждается. Чем ниже относительная влажность воздуха, тем ниже его температура. Психрометр используется в лабораторных условиях. - Портативный термогигрометр – цифровой прибор, показывающий влажность и температуру воздуха, а некоторые модели отображают и значение точки росы. Используется в строительстве для обследования зданий.
- Тепловизоры. Некоторые приборы включают в себя функцию расчета точки росы. При этом на экране тепловизора показываются зоны с температурой ниже ее значения.
Таблица вычисления точки росы
Для быстрого расчета точки росы используют таблицу ее вычисления. Зная фактическую температуру и относительную влажность воздуха, можно легко определить температуру выпадения конденсата.
Точка росы – таблица вычисления
Так, например, при температуре воздуха, равной 20°С и относительной влажности 40%, выпадение конденсата будет происходить на поверхностях с температурой 6°С и ниже.
Полная таблица
Калькулятор точки росы
Результат вычислений
Комфортные значения точки росы для человека
| Точка росы, °C | Восприятие человеком | Относительная влажность (при 32°С), % |
|---|---|---|
| более 26 | крайне высокое восприятие, смертельно опасно для больных астмой | 65 и выше |
| 24-26 | крайне некомфортное состояние | 62 |
| 21-23 | очень влажно и некомфортно | 52-60 |
| 18-20 | неприятно воспринимается большинством людей | 44-52 |
| 16-17 | комфортно для большинства, но ощущается верхний предел влажности | 37-46 |
| 13-15 | комфортно | 38-41 |
| 10-12 | очень комфортно | 31-37 |
| менее 10 | немного сухо для некоторых | 30 |
Точка росы в строительстве
Расчет точки росы имеет большое значение в строительстве. Благодаря ей, определяется:
Благодаря ей, определяется:
- Толщина и материал стен;
- Толщина, материал и место утепления;
- Система вентиляции и отопления в помещении.
Игнорирование или неправильный расчет точки росы ведет к образованию плесени и грибков. Это оказывает негативное влияние на долговечность здания, значительно сокращая срок его эксплуатации.
В оконной сфере – точка росы прямо касается проблемы выпадения конденсата на окнах. Зная ее определение, можно легко это устранить – достаточно понизить влажность воздуха либо повысить температуру поверхности стекла.
- 5
- 4
- 3
- 2
- 1
(24 голоса, в среднем: 4.9 из 5)
Интересная статья, но хотелось бы еще узнать о таком понятии как «Дефицит точки росы», что это такое и по какой формуле можно найти.
Виктор
08.01.2019
Дефицит точки росы – разность между температурой воздуха T и точкой росы.
Находится по формуле:
Тd(Δ) = T – Тd.
где:
- Td(Δ) – дефицит точки росы;
- Т – фактическая температура воздуха, °С;
- Td – температура точки росы, °С.
Чем выше значение дефицита точки росы, тем более сухой воздух, т.е. меньше относительная влажность воздуха. Так, при значении дефицита точки росы равным 0, относительная влажность воздуха равна 100%.
Сергей, менеджер
16.01.2019
Хотел бы понять как рассчитать толщину утеплителя, чтобы при утеплении изнутри конденсат не собирался на стене внутри помещения.
Юрий
15.08.2019
Юрий, для того, чтобы упростить Вам расчеты, воспользуйтесь готовым калькулятором для этих задач. Для этого пройдите по ссылке — https://www.smartcalc.ru/thermocalc?&gp=212&rt=0&ct=0&os=0&ti=20&to=-10&hi=55&ho=85
Сергей, менеджер
16.10.2019
Скажите пожалуйста, как найти влажность, если известна точка росы -20 С, температура воздуха +20 С.
Филипп
25.08. 2019
2019
Относительную влажность можно найти, через формулу определения точки росы. Зная температуру точки росы (-20С) и температуру воздуха (+20С), можно определить, с небольшой погрешностью, относительную влаэность воздуха. Она будет примерно равна 5%.
Сергей, менеджер
26.08.2019
Какова будет температура точки росы, если температура воздуха равна 18°, температура влажности равна 9°, относительная влажность 27%?
Мэри
18.02.2021
Исходя из Ваших данных, температура точки росы будет равна -1.28°C
Т.к. температура — величина отрицательная, то вместо конденсата образуется иней.
Сергей, менеджер
18.02.2021
Сергей, благодарю за ссылку на калькулятор. Абалденно помогает все разрулить правильно, благодаря ему убедился что если бы неглядя сделал утепление дома как советовали «мастера» — было бы попадалово крепкое
Рома
18.08.2021
Пожалуйста, скоро данный калькулятор будет у нас на сайте. Получли от его разработчика согласие на размещение.
Сергей, менеджер
18.08.2021
Требуется ли утепление трубы входящего воздуха бризера, находящейся внутри стены. Прямо противоположные мнения в инструкции и от установщика.
Алексей
18.09.2021
Алексей, здесь лучше обратиться к профильным специалистам. Но лучше делать как написано в инструкции, т.к. это официальный документ от производителя бризера, который проходил различные испытания перед тем как выйти в продажу.
Сергей, менеджер
18.09.2021
Здравствуйте. Ничего не понимаю в таблицах, и как высчитывать, но окна плачут, на стенах конденсат и все «цветет». Как избавиться от всего? Спасибо.
Елена
15.01.2022
Здравствуйте, если конденсат образуется и на стенах и окнах, то проблема с большой вероятностью не в окнах. Вам лучше обратится к строителям в своем регионе, которые смогут приехать и выявить причину, чтобы потом ее устранить.
Самый простой вариант — это чаще проветривать помещение, т.к. у вас большая влажность в нем. Т.к. конденсат образуется и на стенах, то значит они промерзают и их желательно утеплить снаружи дома.
Т.к. конденсат образуется и на стенах, то значит они промерзают и их желательно утеплить снаружи дома.
Но лучше обратитесь к специалистам в своем регионе.
Сергей, менеджер
16.01.2022
Добрый день! Помогите разобраться в ситуации: Температура в помещении +27 градусов, температура на улице -14 градусов, влажность в помещении 35%, температура в углах помещения +18 градусов (фасадная стена), специалист с тепловизором говорит что температура +18 ниже расчетной точки росы и в этих углах будет образовываться конденсат. Так ли это?
Геннадий
04.02.2022
Добрый день. В вашей нужно знать материал стены, есть ли утеплитель и тд., т.к. все это влияет теплопровожность. Но исходя из ваших данных, для стены из газобетонных блоков D300, толщиной 300 мм — температура точки росы будет в пределах 7-8 °С.
Результат расчета по ссылке — https://www.smartcalc.ru/thermocalc?&gp=212&rt=0&ct=0&os=0&ti=24&to=-14&hi=35&ho=85&ld0=3000&le0=1<0=0&mm0=452
Также стоит учитывать, что специалист обращал внимание на углы, возможно в местах стыков есть промерзание. Однако при температуре стены 18 °С исходя из расчетов выше — образование конденсата маловероятно. Возможно специалист оговорился и имел ввиду 8 °С — в данном случае образование конденсата вполне может быть.
Однако при температуре стены 18 °С исходя из расчетов выше — образование конденсата маловероятно. Возможно специалист оговорился и имел ввиду 8 °С — в данном случае образование конденсата вполне может быть.
P.S. Я менеджер по продажам и мой ответ не стоит расценивать как верный на 100%. Отвечая на Ваш вопрос пользовался специализированным калькулятором.
Сергей, менеджер
08.02.2022
Подскажите пожалуйста, в вакууме будет аналогичная точка росы?
Анатолий
04.05.2022
Не буду утверждать точно, но исходя из определения «Точки росы» следует, что это значение температуры, при которой водяные пары, находящиеся в воздухе, конденсируют в росу.
«Вакуум» – это пространство, свободное от вещества (см. здесь — https://ru.wikipedia.org/wiki/%D0%92%D0%B0%D0%BA%D1%83%D1%83%D0%BC). Поэтому логично предположить, что там не будет точки росы.
Сергей, менеджер
05.05.2022
Температура воздуха в помещении равна 180С, относительная влажность воздуха составляет 50%.
Определите физический дефицит насыщения влажности и точку росы.
Подскажите пожалуйста
Мирослав
29.05.2022
Мы коммерческая организация по продаже и установке окон ПВХ. К сожалению не сможем вам помочь в данном вопросе.
Сергей, менеджер
30.05.2022
Добрый день.
Подскажите, столкнулся с проблемой образования коррозии на металле. Считаю, что причина образования конденсата, но не могу определить когда это происходит. Известно, что температура воздуха 27 градусов, влажность 77%, точка росы 21 градус. До каких показателей и что должно измениться, что образовался конденсат.
Кирилл
04.08.2022
Добрый день, Кирилл. Т.к. точка росы по вашим расчетам 21 градус — это значит, что конденсат образовывается в тот момент, когда температура металла равна или ниже данного значения
Сергей, менеджер
23.08.2022
Калькулятор натурального логарифма
Создано Мирославом Йерковичем, доктором философии
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 30 июля 2022 г.
- Как использовать калькулятор натурального логарифма натуральный логарифм
- Что такого естественного в натуральном логарифме?
- График натурального логарифма
- Откуда взялось число e
- Как заработать e сумму денег
- Реальное значение ln 2 и других натуральных логарифмов
- Другие применения натурального логарифма
- Ссылки
Калькулятор натурального логарифма вычисляет логарифм по основанию известной математической константы , e, иррациональной число с приблизительным значением e = 2,71828 . Но чему равен натуральный логарифм , ln x, данного числа x? Это степень, в которую нужно возвести число e, чтобы получить заданное число x.
Как пользоваться калькулятором натурального логарифма
Как и все другие логарифмы, натуральный логарифм x возвращает степень или показатель степени, в которую нужно возвести данное основание e, чтобы получить число x. Это понятие легче понять, когда основание представляет собой целое число, например 2 или 3:
Это понятие легче понять, когда основание представляет собой целое число, например 2 или 3:
log 2 16 = 4 , поскольку 2 4 = 16
4 89044 = 5 89044 4 с 3 4 = 81 .
В случае натурального логарифма это несколько менее интуитивно понятно, потому что его основание e не является целым числом. Но, поскольку значение e находится между значениями 2 и 3, мы понимаем, что e 4 должно быть где-то между 2 4 = 16 и 3 4 = 81.
Получается, что e 4 = 54,498 . Это равенство можно выразить в виде натурального логарифма следующим образом, что можно проверить с помощью калькулятора ln:
ln 54,498 = 4 .
Вот некоторые примеры натурального логарифма :
-
ln 1 = 0так какe 0 = 1 -
ln 10 = 2,3026сe 2,3026 = 10 -
ln 20 = 2,996сe 2,996 = 20 -
ln 50 = 3,912сe 3,912 = 50 -
ln 100 = 4,605 сe 4,605 = 100.
Проверьте правильность приведенных выше результатов, используя наш калькулятор натурального логарифма и калькулятор степени. Чтобы лучше понять взаимодействие между экспоненциальной и логарифмической функциями , вы можете проверить наши экспоненциальные и логарифмические калькуляторы.
Другие способы обозначения натурального логарифма
Один из способов обозначения натурального логарифма: log e . Это то же самое, как, скажем, когда мы записываем логарифм по основанию два как log 2 .
Но гораздо более распространенным способом написания натурального логарифма является ln , что является аббревиатурой латинского выражения logarithmus naturalis, название натурального логарифма, которое было дано, когда латинский язык был еще lingua franca науки.
Существует также третий способ записи натурального логарифма: log . Однако эта запись несколько проблематична, так как ее часто ошибочно принимают за логарифм по основанию 10, хотя это синтаксис, который используют многие программные реализации натурального логарифма, поэтому будьте осторожны!
Что такого естественного в натуральном логарифме?
Почему именно ln x заслуживает того, чтобы называться естественным ? Возможно, самым важным свойством натурального логарифма является то, что он является обратной функцией экспоненциальной функции e x , единственной функцией, скорость изменения которой, или производной , снова в точности равна самой себе: (e х )' = е х .
Проще говоря, экспоненциальная функция e x управляет своей собственной скоростью изменения, что в некотором смысле делает его самодостаточным и независимым от какой-либо другой функции, определяющей способ его изменения. Именно это свойство делает как e x , так и его обратную функцию ln x естественным выбором, когда описывает многие явления реального мира .
График натурального логарифма
Другим интересным свойством натурального логарифма является то, как он меняет свои значения при увеличении аргумента x. Один из способов выразить это — сказать, что производная натурального логарифма обратно пропорциональна его значению x, которое можно записать как (ln x)' = 1/x .
Вы также можете наблюдать это свойство, взглянув на график натурального логарифма . Хотя он увеличивается с увеличением значения x, скорость роста становится все меньше и меньше по мере приближения x к все более и более высоким значениям:
Натуральный логарифмический график
Источник: Википедия Атрибуция: Elmextube (общественное достояние)
Откуда взялось число е
На первый взгляд, вы бы не сказали, что число е имеет какое-либо значение для усилий людей или природы. Но это не так! Бывает, что это число одна из самых важных констант в математике, настолько, что заслуживает собственного имени. Его называют либо числом Эйлера , либо константой Непера , в зависимости от того, кому из этих двух великих математиков хотят приписать его открытие.
Но это не так! Бывает, что это число одна из самых важных констант в математике, настолько, что заслуживает собственного имени. Его называют либо числом Эйлера , либо константой Непера , в зависимости от того, кому из этих двух великих математиков хотят приписать его открытие.
Тем не менее, кажется, что Леонард Эйлер (1707 — 1783) действительно получил больше признания, основываясь на том факте, что та самая буква, которую Эйлер использовал для обозначения этой константы, — это то, как мы обозначаем ее сегодня. Хотя Эйлер был первым, кто вычислил e со значительным числом знаков после запятой, он не был первым, кто обнаружил это : подробнее об этом читайте в следующем абзаце.
Leonhard Euler
Источник: Википедия Атрибуция: Jakob Emanuel Handmann (Общественная домена)
Как заработать на сумму денег
Swiss Matematian Jacob Bernia Bernia Berni -BerniaRou. число e при решении проблемы сложных процентов . Давайте сначала поймем идею простых процентов. Для заданной первоначальной суммы денег, скажем, 1 доллар США, вы хотите знать, сколько у вас будет по прошествии одного года, если проценты в размере 100% будут зачислены только один раз и в конце года? Ответ прост: 2 доллара.
число e при решении проблемы сложных процентов . Давайте сначала поймем идею простых процентов. Для заданной первоначальной суммы денег, скажем, 1 доллар США, вы хотите знать, сколько у вас будет по прошествии одного года, если проценты в размере 100% будут зачислены только один раз и в конце года? Ответ прост: 2 доллара.
Якоб Бернулли
Источник: Википедия Атрибуция: Никлаус Бернулли (1662-1716) (общественное достояние)
Но со сложными процентами все становится немного сложнее. Например, если один и тот же процент в размере 100 % теперь разделить на две равные части по 50 % и кредитовать дважды, 50 % в конце первых шести месяцев и еще 50 % в конце года, то окончательная доходность составит получено по формуле
1*(1 + 1/2) 2 = 2,25 долларов США.
Кроме того, если проценты в размере 100% разделить на недельные суммы, вы получите окончательный доход
1*(1 + 1/52) 52 = 2,692 долларов США.
Бернулли задал простой вопрос: что произойдет, если начисление процентов будет непрерывным ? Другими словами, какова будет конечная доходность, если процентная ставка в 100% будет разделена на бесконечные части, каждая из которых будет кредитоваться в конце бесконечно короткого периода времени? Чтобы подробнее узнать, как работают непрерывные и другие типы начисления процентов, воспользуйтесь нашим инвестиционным калькулятором.
Эта проблема непрерывных сложных процентов, сформулированная математически, сводится к задаче вычислить предел (1 + 1/n) n при приближении n к бесконечности. Оказывается, в результате получается именно число e! Кроме того, приведенное выше выражение может использоваться как способ определения e. Чтобы ответить на вопрос Бернулли: при непрерывном начислении процентов первоначальный доллар давал бы ровно е = 2,718281828 долларов США в конце года!
Реальное значение ln 2 и других натуральных логарифмов
Натуральные логарифмы проще всего вычислить: с е 1 = е .
Но, по-видимому, наиболее важным натуральным логарифмом является тот, который вычисляет значение числа между 1 и e, которое оказывается числом 2. С помощью калькулятора натурального логарифма мы получаем
ln 2 = 0,6931 .
Оказывается, что ln 2 также равно знакопеременной сумме обратных чисел всех натуральных чисел :
ln 2 = 1 – 1/2 + 1/3 – 1/4 + 1/5 – 1/ 6 + ... .
На первый взгляд кажется, что это число не имеет никакого особого значения. Но пункт 2, каким бы неясным он ни казался, фигурирует в некоторых весьма существенных и на первый взгляд не связанных с реальным миром задачах.
Например, он играет роль в формуле периода полураспада радиоактивно разлагающееся вещество , или при расчете времени, необходимого для удвоения первоначальной суммы денег, если в течение заданного времени применяется фиксированная ставка.
Итак, если у вас есть 1000 долларов США на вашем банковском счете, и банк предоставляет процентную ставку r = 7% годовых, вы можете спросить себя , сколько времени потребуется, чтобы удвоить мою первоначальную сумму? Ну, здесь в игру вступает ln 2: формула натурального логарифма, которая вычисляет необходимое время, равна (100 * ln 2)/r, что можно упростить до приблизительного значения 70/r. Помимо 70, для этой цели еще чаще используется число 72, потому что оно имеет больше делителей: проверьте калькулятор правила 72!
Помимо 70, для этой цели еще чаще используется число 72, потому что оно имеет больше делителей: проверьте калькулятор правила 72!
Таким образом, в случае r = 7% вы получите 70/7 = 10 лет как приблизительное время, необходимое для удвоения первоначальной суммы денег. Точно так же можно получить аналогичные формулы для времени, необходимого для того, чтобы начальная величина увеличилась втрое, вчетверо или в n раз при заданной фиксированной скорости роста с течением времени.
Другие применения натурального логарифма
Из предыдущего абзаца мы можем заключить, что натуральные логарифмы встречаются в каждом процессе, связанном с периодом, постоянным ростом или убыванием какого-либо измеримого явления.
Помимо уже упомянутых примеров радиоактивного распада и проблемы выхода с фиксированной процентной ставкой, натуральные логарифмы появляются при расчете роста и распада любой популяции бактерий, животных и растений , скорости распада заряженного конденсатор или изменение температуры объекта.
Ссылки
- Демистификация натурального логарифма
- Что такого «естественного» в основании натуральных логарифмов?
- Что плохого в математической константе e?
- Дэвид С. Кан: Решение проблем логарифмов и экспоненциальных функций, Дуврская книга по математике, 2015 г.
- Эдвард Каснер: Математика и воображение, Dover Books on Mathematics, 2001
Miroslav Jerkovic, PhD
Натуральный логарифм …
равно …
Посмотрите 14 похожих калькуляторов показателей степени и логарифмов0003
Калькулятор логарифма — log(x) Калькулятор
Вычисление логарифма числа по любому основанию:
Число
* Используйте e для научной записи. Например: 5e3, 4e-8, 1.45e12
Когда:
b y = x
Тогда логарифм по основанию b числа x:
log
b
367 y
Калькулятор антилогарифмического вычисления
Чтобы рассчитать log -1 (y) на калькуляторе, введите основание b (10 — значение по умолчанию, введите e вместо константы e), введите значение логарифма y и нажмите кнопку вычислить :
Результат
Когда
y = log b x
Антилогарифм (или обратный логарифм) вычисляется путем возведения основания b в логарифм y:
x = log b -1 ( y ) = b y
- Logarithm definition
- Logarithm rules
- Logarithm problems
- Complex logarithm
- Graph of log (x)
- Таблица логарифмов
- Калькулятор логарифмов
Определение логарифмов
0367 x
Затем базовая B Logarithm of x равна Y:
Log B ( x ) = Y
Например, когда:
2 4 9 = 16000 2
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 . Затем
ЗатемLog 2 (16) = 4
Logarithm в качестве обратной функции экспоненциальной функции
Функция логарифмии,
y = log B ( x 7 B ( x 0) B ( x 0) B ( x 0) — ). экспоненциальной функции,
x = b y
So if we calculate the exponential function of the logarithm of x (x>0),
f ( f -1 ( x ) ) = b log b ( x ) = x
Or if we calculate the logarithm of the exponential function of x,
f -1 ( f ( x )) = логарифм B ( B x ) = x
Натуральный логарифм (LN)
Natural Logarithm — это логарифм для базы E:
LN ( x 037703770370370377037037703770377037703770377037703770377037703770377037037703703703770370370370370370 370376). ( x )
( x )
, когда E -константа — число:
или
См.: Natural Logarithm
Обратный логарифм расчет. b в логарифм y:
x = log -1 ( Y ) = B Y
Logarithmic Function
Функция Logarithmic имеет фундаментальную форму:
777. b ( x )
Правила логарифмирования
См. Правила логарифмирования
Правило логарифмического произведения
Логарифм произведения x и логарифма представляет собой сумму x и логарифма y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
For example:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Правило логарифмического частного
Разность логарифма x и логарифма логарифма и логарифм y.
бревно б ( x / y ) = log b ( x ) — log b ( y )
For example:
log 10 (3 / 7) = log 10 (3) — log 10 (7)
Правило степени логарифма
Логарифм x, возведенный в степень y, равен y, умноженному на логарифм x.
log b ( x y ) = Y ∙ log B ( x )
Например:
Log 10 (2 8 ) = 8 ∙ 10 10 10 ). Логарифм по основанию b числа c равен 1, деленному на логарифм по основанию c числа b. Log B ( C ) = 1 / log C ( B ) Log 2 9004 (8) = 1 /404444444444 (8) = 1 /294444444 (8) = Логарифм по основанию b числа x равен логарифму по основанию с числа x, деленному на логарифм по основанию с числа b. Log B ( x ) = log C ( x ) / log C ( B 7 C ( B ) C ( B ) C . (8) в калькуляторе нам нужно изменить основание на 10: log 2 (8) = log 10 (8) / log 10 (2) См.: правило изменения основания логарифма Действительный логарифм x по основанию b, когда x<=0, не определен, когда x отрицательно или равно нулю: log B ( x ) не определен, когда x ≤ 0 См.: Журнал отрицательного числа База B Logarithm Zero не является определенным: Log 49 777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777. ) не определено Предел логарифма по основанию b числа x, когда x приближается к нулю, равен минус бесконечности: См. Логарифм по основанию b единицы равен нулю: log b (1) = 0 Например, логарифм по основанию два равен нулю: log 2 (1) = 0 См.: log of one. Например:
=
44444 (8) =.0045 (2)
Правило изменения основания логарифма

Логарифм отрицательного числа
Логарифм 0
 : log of zero
: log of zero Логарифм 1
Логарифм бесконечности
25 Предел 9 логарифм x по основанию b, когда x приближается к бесконечности, равен бесконечности:
LIM LOG B ( x ) = ∞, когда x → ∞
См.: Log of Infinity
Logarithm базы
БАБА B ( B ) = 1
Например, базовый два логарифма из двух:
Log 2 (2) = 1
Деривативная логаритм
, когда
4 7777777777777777777777 год 7777777777777777777 год 7777777777777777777 гг. х ) = журнал б ( x )
Затем производство F (x):
F ‘ ( x ) = 1 / ( x LN ( B )
9000 2
9000 2
9000 2 9000 2 9000 2
Logarithm integral
The integral of logarithm of x:
∫ log b ( x ) dx = x ∙ ( log b ( x ) — 1/лн( б ) ) + C
.
 ) + C
) + C . z:
z = относительно iθ = x + iy
Комплексный логарифм будет (n = …-2,-1,0,1,2,…):
Log z = ln( r ) + I ( θ +2Nπ ) = LN (√ ( x 2 + Y 2 )) + I · ARCT (9036.103INT (
0). и ответыЗадача №1
Найти x для
log 2 ( x ) + log 2 ( x -3) = 2
Решение:
Использование правила продукта:
Log 2 ( x ∙ ( x -3) = 2
Изменение формы логарифма в соответствии с логарифтом Определение:
67. x ∙ ∙ ∙ 77770. ( x -3) = 2 2
или
x 2 -3 x -4 = 0
Решение. [3±√(9+16) ] / 2 = [3±5] / 2 = 4,-1
Поскольку логарифм не определен для отрицательных чисел, ответ:
x = 4
Задача № 2
Найти X для
Log 3 ( x +2) — log 3 ( x ) = 2 9003
5.
 правило частного:
правило частного:log 3 (( x +2) / x ) = 2
Изменение логарифмической формы в соответствии с определением логарифма:
( x 7 ) /
+ 3 3 2
или
x +2 = 9 x
или
8 x = 2
или
x = 0,25
График из лога
Logarithms table
| x | log 10 x | log 2 x | log e x | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | undefined | undefined | undefined | |||||||||||
| 0 + | — ∞ | — ∞ | — ∞ | |||||||||||
| 0.0001 | -4 | -13.287712 | -9.210340 | |||||||||||
| 0.001 | -3 | -9.965784 | -6.5 | |||||||||||
0. 01 01 | -2 | -6.643856 | -4.605170 | |||||||||||
| 0.1 | -1 | -3.321928 | -2.302585 | |||||||||||
| 1 | 0 | 0 | 0 | |||||||||||
| 2 | 0.301030 | 1 | 0.693147 | |||||||||||
| 3 | 0.477121 | 1.584963 | 1.098612 | |||||||||||
| 4 | 0.602060 | 2 | 1.386294 | |||||||||||
| 5 | 0.698970 | 2.321928 | 1.609438 | |||||||||||
| 6 | 0.778151 | 2.584963 | 1.7 | |||||||||||
| 7 | 0.845098 | 2.807355 | 1.945910 | |||||||||||
| 8 | 0.0 | 3 | 2.079442 | |||||||||||
| 9 | 0.954243 | 3.169925 | 2.197225 | |||||||||||
| 10 | 1 | 3.321928 | 2. 302585 302585 | |||||||||||
| 20 | 1.301030 | 4.321928 | 2.995732 | |||||||||||
| 30 | 1.477121 | 4.1 | 3.401197 | |||||||||||
| 40 | 1.602060 | 5.321928 | 3.688879 | |||||||||||
| 50 | 1.698970 | 5.643856 | 3. | |||||||||||
| 60 | 1.778151 | 5.1 | 4.094345 | |||||||||||
| 70 | 1,845098 | 6.129283 | 1,845098 | 6.129283 | 1,845098 | 6.129283 | 1,845098 | 6.129283 | 1,845098 | 6.129283 | 1,845098 | 6.129283 | 1163 | 4.248495 |
| 80 | 1.0 | 6.321928 | 4.382027 | |||||||||||
| 90 | 1.954243 | 6.4 | 4.499810 | |||||||||||
| 100 | 2 | 6.643856 | 4.605170 | |||||||||||
| 200 | 2. 301030 301030 | 7.643856 | 5.298317 | |||||||||||
| 300 | 2.477121 | 8.228819 | 5.703782 | |||||||||||
| 400 | 2.602060 | 8.643856 | 5.9 | |||||||||||
| 500 | 2.698970 | 8.965784 | 6.214608 | |||||||||||
| 600 | 2.778151 | 9.228819 | 6.396930 | |||||||||||
| 700 | 2.845098 | 9.451211 | 6.551080 | |||||||||||
| 800 | 2.0 | 9.643856 | 6.684612 | |||||||||||
| 900 | 2.954243 | 9.813781 | 6.802395 | |||||||||||
| 1000 | 3 | 9.965784 | 6.5 | |||||||||||
| 10000 | 4 | 13.287712 | 9.210340 |
Logarithm calculator »
Logarithm — log(x) »
В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и преподавателей, дизайнеров и просто для всех.
Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация пароля или калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook). Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Ниже перечислены наиболее часто используемые многими пользователями по всему миру.
- Бесплатные онлайн-калькуляторы и инструменты
- Калькуляторы часовых поясов/часов/дат
- Бесплатные онлайн-калькуляторы перевода единиц
- Бесплатные онлайн-инструменты для веб-дизайна
- Бесплатные онлайн-инструменты для электричества и электроники
- Математика 1 Инструменты Онлайн-инструменты
И мы все еще разрабатываем больше. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Калькулятор логарифмов — логарифм и антилогарифм (натуральный, по основанию e, 2, 10)
Да – это интеллектуальный калькулятор логарифмов, который помогает вычислять логарифмические и обратные логарифмические по любой системе счисления. Итак, начнем с термина «логарифм».
С точки зрения математики, логарифмическая (логарифмическая) операция называется операцией, обратной возведению в степень, что означает, что (логарифмическое число) — это показатель степени, до которого было возведено другое фиксированное число, известное как «основание», для получения числа . Однако вы можете выполнять любые вычисления логарифмов с помощью калькулятора логарифмов. В частности, логарифм числа x по основанию b — это показатель степени, в которую нужно возвести b, чтобы получить x. Другими словами, логарифм y по основанию b является решением y данного уравнения:
= x
И для любых x и b есть:
x =
Логарифмические правила:Логарифмическое произведение:
(x*y =) (x*y)
Правило коэффициента логарифма:
(x/y) = (x) — (y)
Правило мощности логарифма:
) = y*(x)
(c) = 1/(b) Правило изменения основания логарифма: (x) = (x)/ (b) При использовании вышеупомянутого логарифмического калькулятора вам просто нужно ввести «основание» 10 для десятичного логарифма, 2 для двоичного логарифма и оставить базовое поле пустым для вычисления натурального логарифма. Логарифмическая форма или калькулятор логарифмов — важный инструмент, который помогает вычислить любой тип логарифма действительного числа по любому основанию. Примечание. Функция «Журнал» на научном или графическом/научном калькуляторе — это клавиша, которая позволяет пользователю выполнять вычисление логарифмов. Логарифмы — это способы, помогающие определить, какие показатели степени нужно умножать на определенное число. Как правило, функция журнала на большинстве калькуляторов работает одинаково! Вы должны выразить члены в десятичных логарифмах, отношение представлено как log mn = log m + log n. Например: Выражение 100 × 1000: Однако его можно вычислить, найдя логарифмы 100 (2) и 1000 (3), тогда вам следует сложить логарифмы вместе (5), сразу после этого нужно посмотреть его антилогарифм (100 000) в таблице. Предположим, что необходимо вычислить log2 числа «12», то есть log2 (12). Чтобы вычислить логарифм по основанию 2 числа (y), вы должны разделить логарифм y на логарифм 2. В математическом выражении log10(x) эквивалентно log(10,x). Логарифм по основанию (10) выражается для всех комплексных аргументов x ≠ 0. log10(x) , здесь необходимо переписать логарифмы по основанию 10 в математических терминах натурального логарифма i:e log10(x) = ln (х)/ln(10) . В соответствии с термином логарифма антилогарифм называется обратной функцией логарифма, поэтому log(b) x = y. Вы можете записать это в экспоненциальной записи, так что антилогарифм (b) y = x подразумевает = x. Например: Если лог 39.2 = 1.5933, то антилог 1.5933 = 39.2 Если вы хотите определить лог по произвольной базе, то вы должны придерживаться следующих правил: logₐ(x) = ln(x) / ln(a) logₐ(x) = lg( x) / lg(a) Кроме того, для его расчета можно использовать приведенный выше калькулятор журнала с основанием 10 или калькулятор натурального журнала! Калькулятор логарифмических уравнений будет учитываться для понимания запросов (образование K-12) или для понимания концепции показателей и журналов. Также вы можете использовать этот инструмент исчисления, алгебры, вероятности и многих других областей науки и жизни. Logarithmantilog . Где, Вычисление Antilog: y = 10 x Где, — Руководство Автор: Корин Б. Аренас и глобальные темпы экономического роста, то вы попали в нужное место. Расчет очень больших сумм может быть медленным и запутанным. Но с помощью логарифмов (log) и антилогарифмов (antilog) вычисления можно упростить. Читайте дальше, чтобы узнать больше о log и antilog, о том, как они работают, и почему это важные математические концепции. Логарифм — это степень, в которую число (называемое основанием ) должно быть умножено само на себя, чтобы получить данное число. Проще говоря, логарифм решает задачу: Сколько раз нужно умножить на , чтобы получить еще одно число y ? Логарифм подсчитывает, сколько раз нужно умножить один и тот же множитель, чтобы получить заданное число. Бревно было изобретено в 16 -м -м веке шотландским математиком, физиком и астрономом Джоном Нейпиром в качестве инструмента для расчетов. Он написал книгу Mirifici Logarithmorum Canonis Descriptio с таблицами и числами, в которых обсуждаются натуральные логарифмы, заложив основу для его основной концепции. Нейпир ввел термин логарифм от греческого слова logos , что означает «отношение или пропорция», и arithmos , что означает «число». В сочетании это буквально означает «число отношения». Натуральный логарифм числа — это его логарифм по основанию константы e , где e приблизительно равно 2,718281828459. Уравнение записывается как log e (x) . Если логарифм не указывает основание , как в этом примере: log(1000) , он известен как десятичный логарифм , который использует основание 10 . log(1000) , он известен как десятичный логарифм , который использует по основанию 10 . Как только вы начнете считать цифры миллионами, миллиардами и триллионами, это может стать довольно утомительным. Касается ли это подсчета больших денег, роста населения или преодоления больших расстояний, журнал может работать на вас. Он может упростить большие суммы, которые включают длинные и запутанные уравнения, облегчая их понимание. Вот стандартное уравнение для log: Где, Чтобы понять, как работает эта концепция, вот пример с меньшим числом: log 2 (32) = y 32. Следовательно, в этом примере: Логарифм 32 по основанию 2 равен 5, или логарифм 2 по основанию 32 равен 5. Кроме того, log — это обратная функция возведения в степень, где математическая операция записывается как млрд . b — это основание, которое умножается в соответствии со степенью n, то есть количеством раз, когда оно умножается на себя. Что это значит? Журнал числа равен степени , на которую умножается основание b для получения заданного числа. Чтобы дать вам лучшее представление, обратитесь к приведенному ниже примеру уравнения журнала вместе с его экспоненциальным уравнением. Теперь попробуем с большим числом. log b (x) = y  такие науки, как физика и химия. Люди, которые относятся к области науки или техники, часто используют калькулятор логарифмической базы для выполнения расчетов логарифмической базы
такие науки, как физика и химия. Люди, которые относятся к области науки или техники, часто используют калькулятор логарифмической базы для выполнения расчетов логарифмической базы Проще говоря, этот качественный инструмент работает как решатель логов, чтобы понять, как решать логарифмы любого числа. Кроме того, вы можете вычислить обратный логарифм, используя этот калькулятор обратного логарифма для действительного числа по отношению к заданным или натуральным базовым значениям.
Проще говоря, этот качественный инструмент работает как решатель логов, чтобы понять, как решать логарифмы любого числа. Кроме того, вы можете вычислить обратный логарифм, используя этот калькулятор обратного логарифма для действительного числа по отношению к заданным или натуральным базовым значениям.
Вычисления против логарифмов дел:  Этот калькулятор расширяющихся логарифмов эффективно работает для нахождения логарифма или антилогарифма любого числа по заданному основанию. 92 = 64.
Этот калькулятор расширяющихся логарифмов эффективно работает для нахождения логарифма или антилогарифма любого числа по заданному основанию. 92 = 64.
Примеры преобразования между логами и антилогами: 9-3 Как вычислить логарифм с произвольным основанием?  Например: y = log 15(8) становится 15y = 8
Например: y = log 15(8) становится 15y = 8 Рассчитайте Logarithm & обратный логарифм
Калькулятор журнала
Anti-Log Calculator
Математические формулы
 б у = х.
б у = х. Логарифмы и антилогарифмы: как это работает и их значение
Что такое логарифм?

Кто это придумал?
2 Типы логарифмов

Как используется журнал?
log b (x) = y
Вопрос: Сколько двоек нужно умножить, чтобы получить 32?
b = 2, x = 32
Ответ: 2 x 2 x 2 x 2 x 2 = 32
Ответ: log 2 (32) = 5
Вопрос: Сколько десятков надо умножить, чтобы получить 150 000 000 000?
b = 10, x = 150,000,000,000
log(150,000,000,000) = y
y = 11. 17609125
17609125
log(150,000,000,000) = 11.17609125
This is solved by using the логарифмическая функция в научном калькуляторе. Или воспользуйтесь калькулятором на этой странице, чтобы получить ответ.
Как антилогарифм связан с логарифмом?
Затем номер журнала может быть возвращен к исходному номеру. Это можно сделать с помощью антилогарифм (антилогарифм). Таким образом, антилогарифм — это обратная функция логарифма. Аналогично, антилогарифмические функции для возводят в степень упрощенное логарифмическое значение.
Чтобы вычислить антилогарифм числа y, вы должны возвести основание логарифма b (обычно 10, иногда константу e) в степень, которая даст число y.
Вот уравнение для антилогарифма с основанием 10:
10 x = y
Где x — показатель степени, а y — антилогарифмическое значение.
Например, если мы возьмем это уравнение, log(5) = x, его антилогарифм будет 10x = 5.
- Log: log(5) = 0,698970004336019
- Антилог: 10 0,698970004336019 = 5
Теперь попробуем с большим числом.
Если мы возьмем log(150 000 000 000) = x, его антилогарифм будет 10x = 150 000 000 000.
- Лог: лог 10 (150 000 000 000) = 11,17609125
- Антилог: 10 11.17609125 = 150 000 000 000
Важность и практическое применение
До изобретения калькуляторов логарифмы использовались для упрощения вычислений в различных областях знаний, таких как навигация, геодезия, астрономия, а позже и инженерия.
Представьте, что вы плывете в глуши 16 века. В то время навигаторы полагались на положение звезд и механизм секстанта, чтобы определить их точное местоположение. Без современных технологий, помогающих вычислять большие расстояния, вы можете использовать логарифм для упрощения вычислений. Точность важна, иначе вы рискуете провести больше дней в море со скудными припасами. Чем меньше уравнений, тем меньше места для ошибки.
Чем меньше уравнений, тем меньше места для ошибки.
А как насчет других практических применений? Live Science утверждает, что логарифмы связывают геометрические прогрессии с арифметическими. Если вы когда-нибудь замечали повторяющиеся формы и узоры в природе, архитектуре и искусстве, эти образования обладают собственными логарифмическими значениями.
Сегодня знания о том, как работают эти шаблоны, влияют на то, как человечество строит и проектирует дома, здания и городские ландшафты.
Логарифмы также используются для выражения степени и интенсивности определенных шкал. Помимо больших расстояний и высоких скоростей, он измеряет и другие параметры, такие как:
- Сила звука
- Звуковая частота
- Сила урагана
- Сила землетрясений
- Коррозионный уровень кислот
- Твердость минералов
- Яркость звезд
Возьмем для примера децибелы. Чтобы громкоговорители стали громче на 10 децибел, необходимо подать в 10 раз больше мощности. При увеличении его до +20 дБ потребуется в 100 раз больше мощности, а при +30 дБ потребуется мощность в 1000 раз.
При увеличении его до +20 дБ потребуется в 100 раз больше мощности, а при +30 дБ потребуется мощность в 1000 раз.
Более того, интенсивность звука увеличивается арифметически. Он также изменяется пропорционально логарифму звуковой волны, которая развивается геометрически.
Ниже приведена таблица из Live Science, в которой перечислены различные логарифмические шкалы с соответствующими им линейными шкалами.
In Measuring Rates and Ranks
По словам Калида Азада, преподавателя математики из BetterExplained.com, логарифмы — это то, как мы определяем, насколько быстро что-то растет.
Простые логарифмы в основном описывают числа с точки зрения их степеней 10. Когда дело доходит до процентной ставки, логарифмом является рост инвестиций .
При определении темпов роста ВВП страны аналитики рассматривают ВВП в последующие годы. Они берут ВВП предыдущего года и ВВП следующего года, а затем вычисляют логарифм, чтобы найти расчетный темп роста.
Поисковые системы используют график ссылок для оценки важности, надежности и авторитетности документов в Интернете. Google PageRank стал важным этапом эволюции в поиске, который повысил релевантность поиска и помог Google увеличить долю рынка поиска.
Согласно Азаду, по шкале от 1 до 10 целевая страница с PageRank 2 в 10 раз популярнее, чем страница с PageRank 1. Если сайт имеет PageRank 5, а сайт конкурента PageRank равен 9, тогда разница составляет на 4 порядка .
порядок величины означает примерно 10-кратную разницу, или ранжирование на 1 цифру больше по сравнению с другим. В этом случае сайт с PageRank 9 на 100 000 000 популярнее, чем сайт с PageRank 1.
Практический результат
Лог и антилогарифм — важные вычислительные методы, позволяющие упростить большие суммы. Упрощение сокращает процесс вычислений и упрощает их понимание. Это помогает уменьшить место для ошибки.
Кроме того, использование логарифма обеспечивает измеримые масштабы для оценки природных явлений, таких как интенсивность землетрясений, сила ураганов и яркость звезд. С точки зрения финансов логарифмы позволяют точно определить процентные ставки и темпы экономического роста.
С точки зрения финансов логарифмы позволяют точно определить процентные ставки и темпы экономического роста.
Практически используется во многих областях. Большие значения, которые зависят от точности измерения, выигрывают от использования логарифмических вычислений.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающих экономические тенденции, их влияние на население, а также то, как помочь потребителям принимать более разумные финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам.
Использование законов естественного бревна — Криста Кинг Математика
Логарифмические законы эквивалентно применимы к натуральным логарифмам
Все эти правила, которые мы только что изучили для манипулирования логарифмами, применимы и к натуральным логарифмам.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Общее правило для бревен
9x=y???,соответствующее логарифмическое уравнение: ???\ln{(y)}=x???,
и наоборот.
Правило продукта
Правило продукта для журналов:
???\log_a(xy)=\log_ax+\log_ay???
В натуральных логарифмах это же правило
???\ln(xy)=\ln{x}+\ln{y}???
Общее правило бревен и правило продукта для натуральных бревен
Пройти курс
Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого. 🙂
Учить больше
Как добавить натуральные бревна
Пример
Упростите выражение.
???\ln{64}+\ln{16}???
Во-первых, мы можем использовать правило произведения.
???\ln(xy)=\ln{x}+\ln{y}???
???\ln(64 \cdot 16)???
???\ln(1,024)???
Отсюда мы можем использовать калькулятор, чтобы найти приблизительное значение этого натурального бревна. 9x???, а затем берем лог (в базу ???a???) результата, возвращаемся к нашей исходной точке (???x???). Это означает, что наше уравнение упрощается до
???x=\ln{1,024}???
???х\ок6.9315???
Частное правило
Частное правило для журналов:
???\log_a\left(\frac{x}{y}\right)=\log_ax-\log_ay???
С точки зрения натуральных логарифмов, это же правило
???\ln\left(\frac{x}{y}\right)=\ln{x}-\ln{y}???
Как и со всеми правилами журнала, помните, что мы можем использовать это уравнение в любом направлении. Если мы начнем с чего-то, что соответствует выражению из левой части уравнения, мы можем переписать его как правую часть уравнения или наоборот.
Пример
Запишите выражение в виде одного логарифма.
???\ln{32}-\ln{8}???
Используя правило отношения для натуральных бревен,
???\ln\left(\frac{x}{y}\right)=\ln{x}-\ln{y}???
мы можем переписать выражение как один логарифм.
???\ln{\frac{32}{8}}???
???\ln{4}???
Мы можем оставить логарифм таким образом, как точное значение, или мы можем использовать калькулятор, чтобы найти приблизительное значение.
???\ln{4}\приблизительно1.3863??? 96)}???
???6\ln{2}???
Правила произведения, частного и степени для логарифмов, а также общее правило для логарифмов можно использовать вместе в любой комбинации для решения задач с натуральными логарифмами.
Комбинирование правил натурального логарифма
Правила произведения, частного и степени для логарифмов, а также общее правило для логарифмов можно использовать вместе в любой комбинации для решения задач с натуральными логарифмами.
Специальные значения для натуральных логарифмов
Мы рассмотрим графики экспоненциальной и логарифмической функций в следующих нескольких уроках, а пока давайте взглянем на график функции натурального логарифма, ??? \лн{х}???:
Обратите внимание, как график резко падает вниз по мере приближения к ???x=0??? справа (по мере того, как положительные значения ???x??? все ближе и ближе к ???0???). Это показывает, что значение естественной логарифмической функции равно ???-\infty??? как ???x\to0??? справа, и что естественная логарифмическая функция не определена при ???x=0???. 90=1???, получаем ???1=x???.
Это показывает, что значение естественной логарифмической функции равно ???-\infty??? как ???x\to0??? справа, и что естественная логарифмическая функция не определена при ???x=0???. 90=1???, получаем ???1=x???.
Таким образом, основываясь на его графике, мы можем сказать, что для натурального журнала есть несколько ключевых значений:
???\ln{0}=\text{undefined}???
???\ln{1}=0???
???\ln{\infty}=\infty???
Получить доступ к полному курсу Алгебра 2
Начать
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 2, алгебра II, натуральные журналы, законы натуральных журналов, ln, ln(x), законы ln, законы ln(x), логарифмические законы, натуральные логарифмы
0 лайковКалькулятор логарифмических функций — MathCracker.
 com
comАлгебра Решатели
Инструкции: Используйте этот пошаговый калькулятор логарифмической функции, чтобы найти логарифмическую функцию, которая проходит через две заданные точки на плоскости XY. Вам нужно указать точки \((t_1, y_1)\) и \((t_2, y_2)\), и этот калькулятор оценит соответствующую экспоненциальную функцию и предоставит ее график.
Тип \(t_1\) (одно числовое выражение) =
Тип \(y_1\) (одно числовое выражение) =
Тип \(t_2\) (одно числовое выражение) =
Тип \(y_2\) ( Одно числовое выражение) =
Список точек для оценки (необязательно. Разделенные запятой или пробелом) =
Разделенные запятой или пробелом) =
Основная цель этого калькулятора — оценить параметры \(A_0\) и \(k\) для логарифмической функции \(f(t)\), которая определяется как:
\[f(t) = A_0 \ln(k t)\]
Параметры должны быть такими, чтобы логарифмическая функция проходила через две заданные точки \((t_1, y_1)\) и \((t_2, y_2)\).
Как оценить логарифмическую функцию по двум точкам?
Алгебраически говоря, вам нужно решить следующую систему уравнений, чтобы найти параметры \(A_0\) и \(k\):
\[y_1 = A_0 \ln(k t_1)\] \[y_2 = A_0 \ln(k t_2)\]
Решая эту систему для неизвестных \(A_0\) и \(k\), мы можем найти уникальные решения, пока \(t_1 = \not t_2\).
Действительно, вычитая обе части уравнений:
\[\displaystyle y_1 — y_2 = A_0 \left( \ln(k t_1) — \ln(k t_2) \right)\] \[\displaystyle \Rightarrow \, y_1 — y_2 = A_0 \ln \left(\displaystyle\frac{k t_1}{k t_2}\right) \] \[\displaystyle \Rightarrow \, y_1 — y_2 = A_0 \ln \left(\displaystyle\frac{t_1}{t_2}\right) \] \[ \Rightarrow \, A_0 = \displaystyle \frac{y_1 — y_2}{\ln(t_1) — \ln(t_2)} \] 9{\ гидроразрыва {y_1} {A_0}}} {t_1} \]
и там мы нашли \(k\) как функцию \(A_0\), которая уже определена и известна.
Как вычислить экспоненциальную функцию?
Если вместо логарифмической функции вас интересует экспоненциальное поведение, то вам, вероятно, следует использовать эту
калькулятор экспоненциальной функции
, который следует той же логике оценки параметров, чтобы заставить функцию проходить через две заданные точки.

 К примеру, вам нужно найти log 2 8 (логарифм 8-ми по основанию 2 или логарифм по основанию 2 числа 8, не пугайтесь разного произношения). Итак, вводим 2 в поле «введите основание», а 8 вводим в поле «введите число». После чего нажимаем «найти логарифм» или enter. Далее калькулятор логарифмов логарифмирует заданное выражение и выводит на ваши экраны такой результат.
К примеру, вам нужно найти log 2 8 (логарифм 8-ми по основанию 2 или логарифм по основанию 2 числа 8, не пугайтесь разного произношения). Итак, вводим 2 в поле «введите основание», а 8 вводим в поле «введите число». После чего нажимаем «найти логарифм» или enter. Далее калькулятор логарифмов логарифмирует заданное выражение и выводит на ваши экраны такой результат.

 Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .
Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .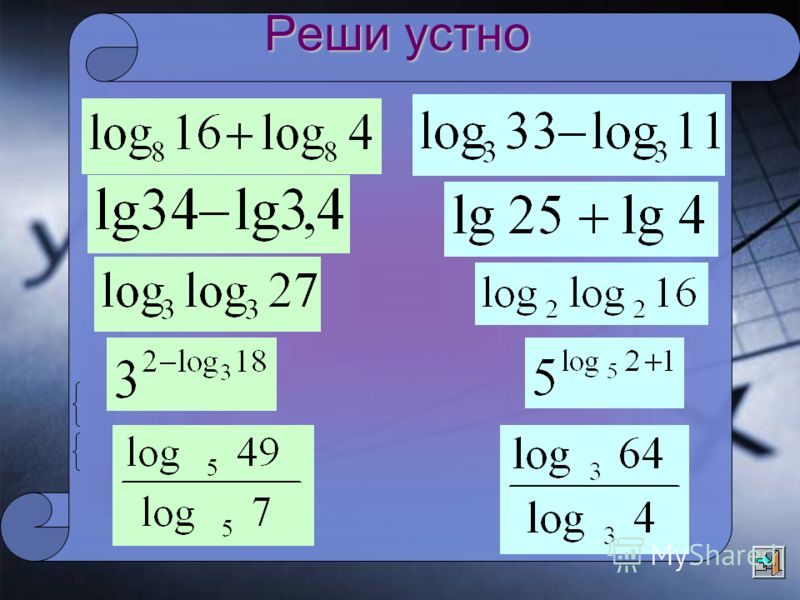

 Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.
Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.

 72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x.
72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x. Такой вариант подсчета создан на основе двух математических фактов:
Такой вариант подсчета создан на основе двух математических фактов:
 Позже диалог возобновился, но уже между Эйлером и Даламбером.
Позже диалог возобновился, но уже между Эйлером и Даламбером.

 Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 5 2 = 25. Поэтому для уравнения вида 5 x = 25, x = 2.
Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 5 2 = 25. Поэтому для уравнения вида 5 x = 25, x = 2.
 С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.
С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде. Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.
Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.

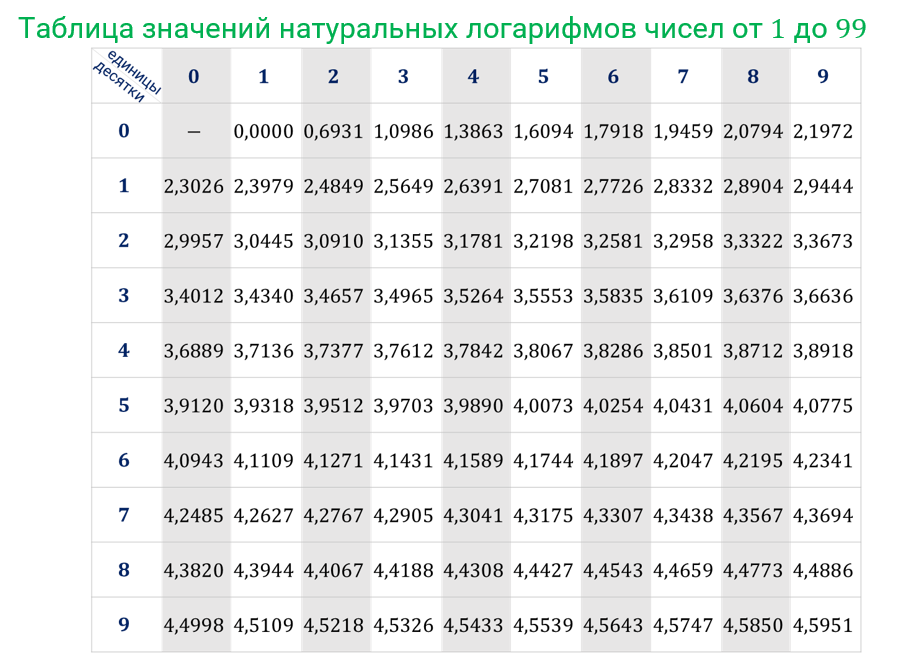 Например, для вычисления десятичного логарифма для 900 введите в поле поискового запроса lg 900 и сразу (даже без нажатия кнопки) получите 2.95424251.
Например, для вычисления десятичного логарифма для 900 введите в поле поискового запроса lg 900 и сразу (даже без нажатия кнопки) получите 2.95424251.
 В качестве нижнего предела можно взять . Затем рассчитайте ожидаемый объем прибыли, который вы хотели бы получить на продаваемый товар. Ее верхний предел будет органичен покупательной способностью товара и его конкурентными свойствами. Максимальную скидку можно рассчитать следующим образом: (прибыль – (прибыль х минимальный объем продаж / ожидаемый объем) / цена единицы продукции.
В качестве нижнего предела можно взять . Затем рассчитайте ожидаемый объем прибыли, который вы хотели бы получить на продаваемый товар. Ее верхний предел будет органичен покупательной способностью товара и его конкурентными свойствами. Максимальную скидку можно рассчитать следующим образом: (прибыль – (прибыль х минимальный объем продаж / ожидаемый объем) / цена единицы продукции. Подобными скидками пользуются супермаркеты для того, чтобы разгрузить работу магазина в вечерние часы и выходные дни. В данном случае размер скидки определяется размером упущенной выгоды при неудовлетворении покупательского спроса в часы пик.
Подобными скидками пользуются супермаркеты для того, чтобы разгрузить работу магазина в вечерние часы и выходные дни. В данном случае размер скидки определяется размером упущенной выгоды при неудовлетворении покупательского спроса в часы пик. 5}{5}….$
5}{5}….$ Ряды для log(l — x) используют те же численные члены, но все их знаки — отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными.
Ряды для log(l — x) используют те же численные члены, но все их знаки — отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными. Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой.
Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой. Log 9 есть удвоенной log 3 потому что 9 = 32. Наконец, log 10 есть log 2+ log 5.
Log 9 есть удвоенной log 3 потому что 9 = 32. Наконец, log 10 есть log 2+ log 5.  Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln.
Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln. Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, xy. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора.
Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, xy. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора. Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро.
Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро.  Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4.
Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4.