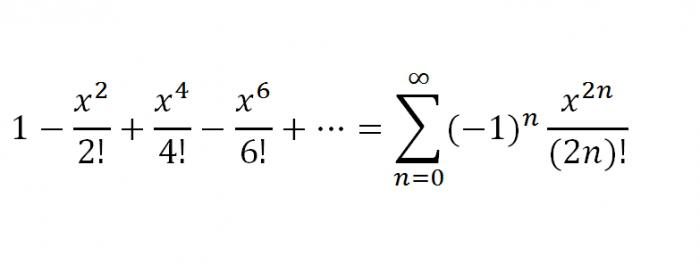Логарифм ряд тейлора: {\displaystyle \ln(1+x)={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\dots ={\cfrac {x}{1-0\cdot x+{\cfrac {1^{2}x}{2-1\cdot x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}}

51. Ряд Маклорена …

Ряды Маклорена некоторых функций

Экспонента:

Натуральный логарифм:

для всех

Биномиальное разложение:

для всех и всех комплексных где

В частности:

Квадратный корень:

для всех

для всех | x | < 1

Конечный геометрический ряд:

для всех

Тригонометрические функции:

для всех где B2n — Числа Бернулли

для всех

для всех

для всех

Гиперболические функции:

для всех

для всех

для всех

52. Ряд Тейлора…

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

Определение

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд

называется рядом Тейлора функции f в точке a.

Свойства

Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a.

Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности a. Например, Коши предложил такой пример:

У этой функции все коэффициенты ряда Тейлора равны нулю.

Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Теорема:

• Пусть функция f(x) имеет n + 1 производную в некоторой окрестности точки a, U(a,ε)

• Пусть

• Пусть p — произвольное положительное число,

тогда: точка при x < a или при x > a:

Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).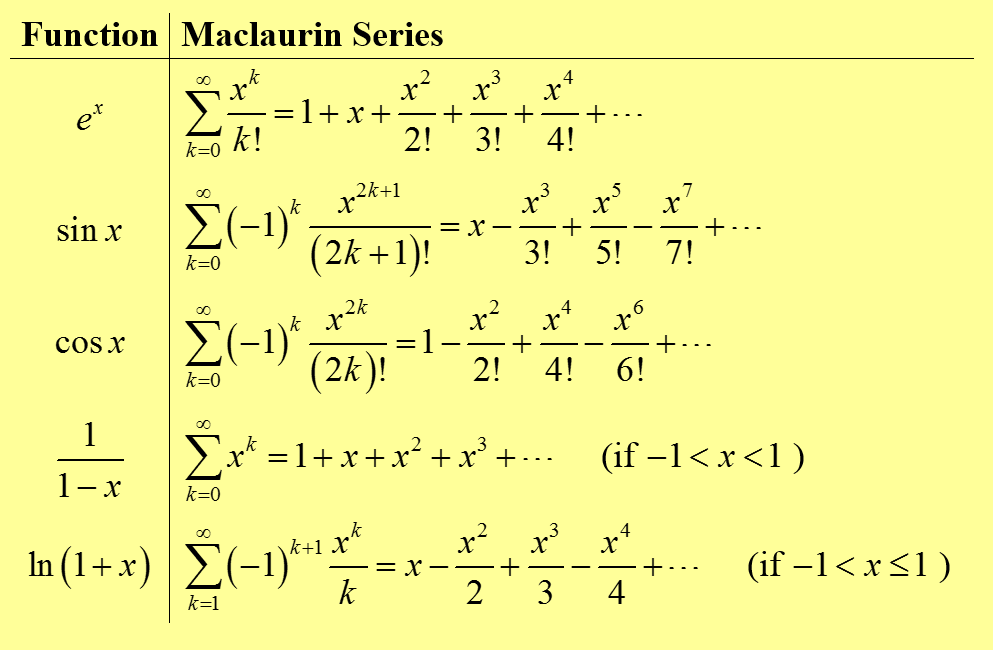

Различные формы остаточного члена

В форме Лагранжа:

В форме Коши:

Ослабим предположения:

Пусть функция f(x) имеет n − 1 производную в некоторой окрестности точки a

И n производную в самой точке a, тогда:

— остаточный член в асимптотической форме (в форме Пеано, в локальной форме)

53.Применение рядов для приближенного вычисления определенных интегралов

Вычислить определённый интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд, и затем проинтегрировать его почленно.

Так как , то для требуемой точности достаточно первых пяти членов полученного ряда:

Самый натуральный логарифм / Хабр

devpony

16 янв 2014 в 12:56

Время на прочтение 2 мин

Количество просмотров

24K

Ненормальное программирование *C++ *Математика *

Recovery mode

Из песочницы

Вдохновившись постом про вычисление pi, решил вычислить подобным образом число e. По пути получилась функция натурального логарифма.

Собственно,

#include <iostream>
#define I r=
#define l ;
#define o
#define x if(1+(d*2)*(1/(__*2))<=k)d++;
#define e p+=d;d=1;
#define h _++;
#define s __++;
double ln(double k){double p=0,n,y,r,d,_=0,__=0;
I 3.30 l o o o o o o
I 3.25 l o o o o o o
I 3.20 l o o o o o o
I 3.15 l o o o o o o
I 3.10 l o o o o o o
I 3.05 l o o o o o o
I 3.00 l o o o o o o
I 2.95 l o o o o o o
I 2.90 l o o o o o o
I 2.85 l o o o o o o
I 2.80 l o o o o o o
I 2.75 l o o o o o o o
I 2.70 l o o o o o o o
I 2.65 l o o o o o o o
I 2.60 l o o o o o o o 
I 2.55 l o o o o o o o
I 2.50 l o o o o o o o
I 2.45 l o o o o o o o
I 2.40 l o o o o o o o o
I 2.35 l o o o o o o o o 
I 2.30 l o o o o o o o o
I 2.25 l o o o o o o o o
I 2.20 l o o o o o o o o
I 2.15 l o o o o o o o o
I 2.10 l o o o o o o o o
I 2.05 l o o o o o o o o
I 2.00 l o o o o o o o o
I 1.95 l o o o o o o o o o
I 1.90 l o o o o o o o o o
I 1.85 l o o o o o o o o o
I 1.
  80 l o o o o o o o o o
I 1.75 l o o o o o o o o o
I 1.70 l o o o o o o o o o 
I 1.65 l o o o o o o o o o
I 1.60 l o o o o o o o o o
I 1.55 l o o o o o o o o o o
I 1.50 l o o o o o o o o o o
I 1.45 l o o o o o o o o o o
I 1.40 l o o o o o o o o o o
I 1.35 l o o o o o o o o o o o
I 1.30 l o o o o o o o o o o o
I 1.25 l o o o o o o o o o o o
I 1.20 l o o o o o o o o o o o o
I 1.15 l o o o o o o o o o o o o
I 1.10 l o o o o o o o o o o o o
I 1.05 l o o s s s s s s s s s s o
I 1.00 l o o h h h h h h h h h h  o
I 0.95 l o o h h h h h h h h h h e o
I 0.90 l o o h h h h h h h h h h e  o
I 0.85 l o o h h h h h h h h h h e x o
I 0.80 l o o h h h h h h h h h h e x x o
I 0.75 l o o h h h h h h h h h h e x x x o
I 0.70 l o o h h h h h h h h h h e x x x x o
I 0.65 l o o h h h h h h h h h h e x x x x x o
I 0.60 l o o h h h h h h h h h h e x x x x x x o
I 0.55 l o o h h h h h h h h h h e x x x x x x x x o
I 0.50 l o o h h h h h h h h h h e x x x x x x x x x x o
I 0.45 l o o h h h h h h h h h h e x x x x x x x x x x x x x x o
I 0.  40 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x o
I 0.35 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x o
I 0.30 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x o
I 0.25 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.20 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.15 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.10 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x e return p/_;
//          0                   +1                   +2                   +3                   +4                   +5
}

Принцип прост — натуральный логарифм от a есть площадь под графиком 1/x от единицы до a.

Соответственно, чем точнее нарисован график, тем точнее будут вычисления.

Немного о построении графика. Символами s обозначается единичный отрезок, h — квадрат единичной площади, e — функция f(x)=1, x — площадь под графиком 1/x на отрезке (1, +inf).
Имея функцию натурального логарифма и зная, что ln(e)=1 найти теперь e перебором не составляет труда.

for(double i = 0; i <= 3; i += 0.01)
	if (ln(i) > 0.98)
	{
		std::cout << i << std::endl;
		break;
	}

Некоторые результаты:

Выражение	Значение	Истинное значение
ln(2)	0.721053	0.69315
ln(2.7)	1	0.99325
ln(3)	1.09474	1.09861
ln(4)	1.35263	1.38629
ln(5)	1.54211	1.60943
e	2.7	2.718281828

Ссылка на полный код.

Теги:

• c++
• e
• логарифм

Хабы:

• Ненормальное программирование
• C++
• Математика

{n+1}}{n+1}$.

NB : Со свойствами степенного ряда требуется четыре линии…

Разложение $\log{x}$ в ряд Тейлора для получения бесконечной последовательности для $\log{2}$

спросил 6 лет, 5 месяцев назад

Изменено 11 месяцев назад

Просмотрено 15 тысяч раз

$\begingroup$

Итак, я знаю, что $\log{2} = 1 — 1/2 + 1/3 — 1/4 + 1/5 …$

Я попытался получить этот результат, используя разложение в ряд Тейлора на $ \log{x}$ около $1$, я думал, что если в расширении используется бесконечно много терминов, то как только я подставлю $2$, я получу упомянутый ряд.