24.2. Равномерная сходимость функциональных рядов
Функциональный ряд (24.1) называется равномерно сходящимся в некотором промежутке, если, каково бы ни былоСуществует такое, не зависящее от Что приДля всехИз данного промежутка выполняется неравенство
Где- остаток ряда, определяемый формулой (24.3).
Теорема 24.1 (признак Вейерштрасса). Функциональный ряд (24.1) сходится абсолютно и равномерно в некотором промежутке, если существует сходящийся числовой ряд с положительными членами
(24.4)
Такой, что
(24.5)
Для всех х из данного промежутка
Ряд (24.4) в этом случае называется мажорантным рядом для ряда (24.1). Свойства функциональных рядов выражаются следующими теоремами. Теорема 24.2. Сумма равномерно сходящегося ряда функций, непрерывных в замкнутом промежуткеЕсть функция, непрерывная в данном промежутке.
Теорема 24.3. Если члены сходящегося ряда (24.1) имеют непрерывные производные приИ рядСходится равномерно в замкнутом промежутке, то ряд (24.
(24.6)
Теорема 24.4. Если члены ряда (24.1) непрерывны приИ ряд этот
Сходится равномерно в замкнутом промежутке, то его можно интегрировать почленно в данном промежутке:
Теорема 24.5. Если ряд (24.1) сходится равномерно в некоторой области, и каждый член ряда имеет конечный предел, где- точка сгуще
Ния данной области, то к пределу можно перейти почленно, т. е.
Пример 24.4. Исследовать, равномерно ли сходится ряд
Так какДля всехТо, т. е. каждый
Член данного ряда не превышает соответствующего члена сходящегося числового ряда
(геометрический ряд,I. Последний ряд является мажорантным для
Данного ряда. В соответствии с признаком Вейернпрасса заключаем, что данный ряд сходится абсолютно и равномерно для всех*, т. е. на всей действительной оси.
Пример 24.5. Доказать, что сумма рядаявляется непре
Рывной функцией при всех х.
Прежде всего каждый член данного рядаЕсть
Функция, непрерывная при всех х. Ряд сходится равномерно при всех х, поскольку
Ряд сходится равномерно при всех х, поскольку
И для данного ряда существует мажорантный ряд-
Сходящийся числовой ряд с положительными членами (ряд Дирихле;).
Согласно теореме 24.2, сумма данного ряда есть функция, непрерывная при всех х (как сумма равномерно сходящегося ряда непрерывных функций).
Пример 24.6. Можно ли почленно дифференцировать ряд
В области его сходимости?
Каждый член данного ряда есть функция, дифференцируемая
При всех х, причем
Составим ряд производныхКаждый член нового ряда —
Непрерывная функцияТак как
, то для него существует мажорантный ряд
Следовательно, ряд производных равномерно сходится при всех х, поэтому, согласно теореме 24.3, исходный ряд можно дифференцировать почленно. По формуле (24.6) получаем
Этот ряд сходится равномерно при всех х, ибо для него существует мажорантный ряд(так как). Каждый член ряда
Есть функция дифференцируемая, причем
Ряд производныхРасходится в каждой точке, ибо ни в
Одной точке не выполняется необходимый признак сходимости (общий член к нулю не стремится). Следовательно, исходный ряд почленно дифференцировать нельзя.
Следовательно, исходный ряд почленно дифференцировать нельзя.
Пример 24.8. Можно ли почленно интегрировать ряд
Каждый член данного рядаЕсть функция, непрерывная для
Всех х, ряд сходится равномерно на всей числовой оси. Действительно, так как для всех х выполняется неравенство, то для данного ряда сущест
Вует мажорантный ряд
Таким образом, согласно теореме 24.4, данный ряд можно интегрировать по любому промежутку из его области сходимости, в частности по промежутку . Интегрируя, получаем
| < Предыдущая | Следующая > |
|---|
16.1 Равномерная сходимость — ПриМат
Определение. Пусть на множестве $E$ задана последовательность функций $f_{n}\left(n=1,2…\right)$, сходящаяся на $E$ поточечно к функции $f$. Говорят, что последовательность {$f_{n}$} сходится равномерно к функции $f$ на множестве $E$, если для любого $\varepsilon > 0$ найдется такой номер $N$, зависящий только от $\varepsilon$ (и не зависящий от $x$), что для каждого $n \geq N$ справедливо неравенство $\mid f_{n}\left(x\right)- f\left(x\right)\mid < \varepsilon$.
Определение поточечной сходимости на множестве $E$ в кванторах можно записать следующим образом:
$$ \forall x \in E \; \forall\varepsilon > 0 \; \exists N = N\left(\varepsilon,x\right) : \forall n \geq N \mid f_{n}\left(x\right)- f\left(x\right)\mid < \varepsilon, $$ а равномерной сходимости — так: $$ \forall \varepsilon > 0 \; \exists N = N\left(\varepsilon\right) : \forall n \geq N \; \forall x \in E \mid f_{n}\left(x\right)- f\left(x\right)\mid < \varepsilon.$$ В определении поточечной сходимости номер $N$ зависит, вообще говоря, от $\varepsilon$ и от $x$, а в определении равномерной сходимости $N$ зависит только от $\varepsilon$ и не зависит от $x$. Иначе говоря, поточечная сходимость будет равномерной, если для заданного $\varepsilon > 0 $ номер $N$ можно подобрать так, чтобы он был пригоден сразу для всех $x \in E$.
Теперь видно, что свойство равномерной сходимости не слабее, чем свойство поточечной сходимости, т. е. из равномерной сходимости следует поточечная сходимость. {n}} < \varepsilon$ при $0 <\varepsilon< 1$ не может выполняться сразу для всех $x \in \mathbb{R}$, каким бы большим номер $n$ мы ни взяли. Таким образом, $r_{n}(x)\rightarrow 0 \; (n \rightarrow \infty)$, но неравномерно. Следовательно, данный ряд сходится на $\mathbb{R}$ неравномерно.
{n}} < \varepsilon$ при $0 <\varepsilon< 1$ не может выполняться сразу для всех $x \in \mathbb{R}$, каким бы большим номер $n$ мы ни взяли. Таким образом, $r_{n}(x)\rightarrow 0 \; (n \rightarrow \infty)$, но неравномерно. Следовательно, данный ряд сходится на $\mathbb{R}$ неравномерно.
Ряд (16.2) сходится равномерно на множестве $E$, если $\lim_{n\to\infty} \mu_{n} = 0.$
Действительно, если $\mu_{n}\rightarrow 0 \; (n \rightarrow \infty)$, то для любого $\varepsilon > 0$ найдется такой номер $N$, что для всех $n \geq N$ справедливо неравенство $\mu_{n} < \varepsilon$, т.е. для всех $x \in E$ справедливо неравенство $\mid r_{n}(x)\mid < \varepsilon$, а значит ряд (16.2) сходится равномерно. Обратно, если $r_{n}(x)$ равномерно сходится к нулю, то для всех $x \in E$ справедливо неравенство $\mid r_{n}(x)\mid < \varepsilon$. Поэтому и $\mu_{n} = \sup_{x\in E} \mid r_{n}(x)\mid \leq \varepsilon$, т.е. $\mu_{n} \rightarrow 0$ при $n \rightarrow \infty$.
Пример 3. {2}+n+1}\leq \frac{1}{n+1}$. Таким образом, $\mu_{n}\leq \frac{1}{n+1} \rightarrow 0 \; \; (n\rightarrow \infty)$, и, следовательно, данный ряд сходится равномерно на $\mathbb{R}$.
{2}+n+1}\leq \frac{1}{n+1}$. Таким образом, $\mu_{n}\leq \frac{1}{n+1} \rightarrow 0 \; \; (n\rightarrow \infty)$, и, следовательно, данный ряд сходится равномерно на $\mathbb{R}$.
Теорема(критерий Коши равномерной сходимости последовательности). Для того чтобы последовательность функций {$f_{n}$} равномерно сходилась на множестве $E$ к некоторой функции, необходимо и достаточно, чтобы для любого $\varepsilon > 0$ существовал такой номер $N$, зависящий только от $\varepsilon$, что для любых $n,m \geq N$ и для любого $x \in E$ было выполнено неравенство $\mid f_n(x)-f_m(x)\mid < \varepsilon$.
Необходимость. Пусть последовательность {$f_n$} сходится к $f$ равномерно на $E$. Зададим $\varepsilon > 0 $. Тогда найдется такой номер $N$, что для все $n\geq N$ и для всех $x \in E$ справедливо неравенство $\mid f_n(x) — f(x)\mid < \frac{\varepsilon}{2}$. Если возьмем произвольные, $n,m \geq N$, то для любого $x \in E$ получим $$\mid f_n(x) — f_m(x)\mid \leq \mid f_n(x) — f(x)\mid + \mid f_m(x) — f(x)\mid < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon,$$ т.
Достаточность. Пусть выполнено условие Коши. Зафиксируем $x \in E$ и получим числовую последовательность {$f_n(x)$}, которая, согласно условию Коши, является фундаментальной и, следовательно, сходящейся. Обозначим ее предел через $f(x)$. Так как $x \ in E$ произвольное, то, проделав эту операцию для все $x \in E$, получим функцию $f(x)$. Покажем, что последовательность {$f_n(x)$} стремится к $f(x)$ равномерно на $E$. Зададим $\varepsilon > 0$. Тогда найдется такой номер $N$, что для всех $n,m\geq N$ и для любого $x \in E$ справедливо неравенство $\mid f_n(x)-f_m(x)\mid < \varepsilon$. Зафиксируем $n \geq N, x \in E$ и устремим $m\rightarrow \infty$. Тогда получим $\mid f_n(x)-f(x)\mid \leq \varepsilon.$ Это неравенство выполнено для любого $n \geq N$ и для всех $x \in E$, а это и означает, что последовательность {$f_n$} сходится к $f$ равномерно на $E$.
Доказанную теорему можно переформулировать для рядов следующим образом.
Теорема(критерий Коши равномерной сходимости ряда). {+\infty} = \frac{\sin nx}{n}$ .
{+\infty} = \frac{\sin nx}{n}$ .
Решение
На данном отрезке частичные суммы вспомогательного ряда не будут ограничены. Применим критерий Коши. Выберем $m=2n, x_0 = \frac{1}{n}$, тогда $$ \mid \frac{\sin \frac{n+1}{n}}{n+1} + … + \frac{\sin 2}{2n}\mid \geq \frac{\sin 1}{n+1} + … + \frac{\sin 1}{2n} \geq \frac{1}{2}\sin 1 = \varepsilon_0.$$ Для ряда выполнился критерий Коши, следовательно, ряд не сходится равномерно.
[свернуть]
Пройдите этот тест, чтобы проверить свои знания по только что прочитанной теме. |
Тер-Крикоров А.М., Шабунин М.И. Курс Математического Анализа. 1997; с исправлениями 2001. ФИЗМАТЛИТ, 2001, стр. 384 — 407.
В.И.Коляда, А.А.Кореновский. Курс лекций по математическому анализу Т.2. Одесса, «Астропринт», 2010, стр. 32-41.
Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления» ФИЗМАТЛИТ, 1964 т.2, стр. 376-386.
Страница не найдена | CUHK Математика
- Главная
- Страница не найдена
×
Предупреждающее сообщение
В вашем поиске использовано слишком много выражений И/ИЛИ. В этот поиск были включены только первые 7 терминов.
В этот поиск были включены только первые 7 терминов.×
Сообщение об ошибке
Запрашиваемая вами страница не существует. Для вашего удобства был выполнен поиск по запросу курс ИЛИ конструктор ИЛИ 1718 ИЛИ math3060a ИЛИ заметки ИЛИ 203 ИЛИ 20униформа ИЛИ 20конвергенция ИЛИ 202018 ИЛИ pdf .Конференция
https://www.math.cuhk.edu.hk/research/conferenceMATh2010G — Университетская математика — 2014/15
https://www.math.cuhk.edu.hk/course/1415/math2010g
Курс Имя: Университет Преподаватель математики: Доктор … Пожалуйста, проверьте ссылку GeoGebra ниже. (16/3) Лекция отмечает 10 выпущен ( 20/3 ) Задание 4 выпущено, срок сдачи 2 апр. Общий …Лекция 7
https://www.math.cuhk.edu.hk/community-outreach/new-wave-mathematics/lecture-7
. ..
地點:香港中文大學逸夫書院文瀾堂 LG 203 室
語言:粵語
…
..
地點:香港中文大學逸夫書院文瀾堂 LG 203 室
語言:粵語
…MATh3060A — Математический анализ II — 2017/18
https://www.math.cuhk.edu.hk/course/1718/math3060a
Курс Название: Математический анализ II Преподаватель: Проф. Кай Сенг ЧОУ Курс Год: 2017/18 Срок: 2 …MATh3060A — Математический анализ II — 2014/15
https://www.math.cuhk.edu.hk/course/1415/math3060a
Курс Название: Математический анализ II Преподаватель: Проф. Чи Вай ЛЕУН Курс Год: 2014/15 Срок: 2 математика3060а …MATh3060A — Математический анализ II — 2019/20
https://www.math.cuhk.edu.hk/course/1920/math3060a
Курс Название: Математический анализ II Преподаватель: Доктор Леунг Фу ЧЕНГ Курс Год: 2019/20 Срок: 2 …MATh3060A — Математический анализ II — 2018/19
https://www. math.cuhk.edu.hk/course/1819/math3060a
math.cuhk.edu.hk/course/1819/math3060a
Курс Название: Математический анализ II Преподаватель: Проф. Кай Сенг ЧОУ Курс Год: 2018/19 Срок: 2 …MATh3060A — Математический анализ II — 2016/17
https://www.math.cuhk.edu.hk/course/1617/math3060a
Курс Название: Математический анализ II Преподаватель: профессор Кай Сенг ЧОУ Курс Год: 2016/17 Срок: 2 …MATh3060A — Математический анализ II — 2021/22
https://www.math.cuhk.edu.hk/course/2122/math3060a
Курс Название: Математический анализ II Преподаватель: Доктор Леунг Фу ЧЕНГ Курс Год: 2021/22 Срок: 2 …MATh3060A — Математический анализ II — 2022/23
https://www.math.cuhk.edu.hk/course/2223/math3060a
Курс Название: Математический анализ II Преподаватель: д-р Леунг Фу ЧЕНГ Курс Год: 2022/23 Срок: 2 . ..
..
Равномерная сходимость | Brilliant Math & Science Wiki
Огнен Вукадин и Кристофер Уильямс внес
Содержание
- Определение и основные свойства
- Равномерная сходимость и непрерывность
9{\infty}{fn}n=1∞ вещественнозначных функций на множестве XXX, fn:X→R f_n : X\to \mathbb{R} fn:X→R, считается равным равномерно сходящейся на XXX к предельной функции f:X→Rf:X\to \mathbb{R}f:X→R, если для каждого ϵ>0\epsilon > 0 ϵ>0 существует N∈NN\in \ mathbb{N}N∈N такое, что
∣f(x)−fn(x)∣<ϵ |f(x) - f_n(x)|< \epsilon ∣f(x)−fn(x)∣<ϵ
выполняется для всех n≥Nn\geq Nn≥N и x∈Xx\in Xx∈X.
Важнейшее условие, отличающее равномерную сходимость от поточечной сходимости последовательности функций, состоит в том, что число NNN в определении зависит только от ϵ\epsilonϵ, а не от xxx.
 Отсюда следует, что каждая равномерно сходящаяся последовательность функций сходится поточечно к одной и той же предельной функции, поэтому равномерная сходимость сильнее, чем поточечная сходимость.
Отсюда следует, что каждая равномерно сходящаяся последовательность функций сходится поточечно к одной и той же предельной функции, поэтому равномерная сходимость сильнее, чем поточечная сходимость.Определение равномерной сходимости эквивалентно требованию, чтобы
limn→∞supx∈X∣f(x)−fn(x)∣=0. \displaystyle\lim_{n\to \infty} \displaystyle\sup_{x\in X} |f(x) — f_n(x)| = 0 . n→∞limx∈Xsup∣f(x)−fn(x)∣=0.
Если мы обозначим через ∣∣g∣∣∞:=supx∈X∣g(x)∣||g||_{\infty}:= \displaystyle\sup_{x\in X}|g( x)|∣∣g∣∣∞:=x∈Xsup∣g(x)∣ верхняя норма функции g:X→Rg:X\to \mathbb{R}g:X→R, последняя условие становится
limn→∞∣∣f−fn∣∣∞=0. \displaystyle\lim_{n\to \infty} ||f-f_n||_{\infty} = 0 .n→∞lim∣∣f−fn∣∣∞=0. 9nfn(x)=xn — последовательность функций [0,1]→R[0,1]\to \mathbb{R}[0,1]→R. Затем limn→∞fn(x)={0,x∈[0,1)1,x=1 \displaystyle\lim_{n\to \infty} f_n(x) = \begin{case} 0, & х\в [0,1) \\ 1, х = 1 \\ \end{cases}n→∞limfn(x)={0,1,x∈[0,1)x=1
, поэтому последовательность {fn}\{f_n\}{fn} сходится поточечно к функции f(x)={0,x∈[0,1)1,x=1f(x) = \begin{cases} 0, & х\в [0,1) \\ 1, х = 1 \\ \end{cases}f(x)={0,1,x∈[0,1)x=1Однако при заданном ϵ>0\epsilon > 0ϵ>0 для x∈[0,1)x\in[0,1)x∈[0,1) мы имеем ∣fn(x)−f(x)∣=∣xn∣<ϵ ⟺ 0≤x<ϵ1n<1|f_n(x) - f(x)| = |х^п| < \epsilon \iff 0\leq x < \epsilon^{\frac{1}{n}}< 1∣fn(x)−f(x)∣=∣xn∣<ϵ⟺0≤x<ϵn1 <1 поэтому не может существовать N∈NN\in \mathbb{N}N∈N, для которого оценка будет выполняться равномерно (т.
 n|∣xn∣ произвольно близко к 1). Это позволяет быстрее сделать вывод о неравномерности сходимости, поскольку limn→∞∣∣f−fn∣∣∞=1≠0\displaystyle\lim_{n\to \infty} ||f-f_n|| _{\infty} = 1 \neq 0n→∞lim∣∣f−fn∣∣∞=1=0.
9{\infty}{fn}n=1∞ является монотонным, показывает, что непрерывность предельной функции влечет за собой равномерную сходимость.
n|∣xn∣ произвольно близко к 1). Это позволяет быстрее сделать вывод о неравномерности сходимости, поскольку limn→∞∣∣f−fn∣∣∞=1≠0\displaystyle\lim_{n\to \infty} ||f-f_n|| _{\infty} = 1 \neq 0n→∞lim∣∣f−fn∣∣∞=1=0.
9{\infty}{fn}n=1∞ является монотонным, показывает, что непрерывность предельной функции влечет за собой равномерную сходимость.Дзета-функция Римана непрерывна на (1,∞)(1,\infty)(1,∞)
ζ(x)\zeta(x)ζ(x) — равномерно сходящийся предел своих частичных сумм на каждом [a,∞)[a,\infty)[a,∞), a>1a>1a>1, которые являются непрерывными функциями. Следовательно, по Единой предельной теореме ζ(x)\zeta(x)ζ(x) непрерывна при каждом a>1a>1a>1.
Рассмотрим функции fn:[0,∞]→Rf_n: [0,\infty]\to \mathbb{R}fn:[0,∞]→R, определенные как fn(x):=min{ n,x}f_n(x):= min\{n,x\}fn(x):=min{n,x}. Для каждого x∈[0,∞]x\in [0, \infty]x∈[0,∞] существует натуральное число N∈NN\in \mathbb{N}N∈N такое, что fn(x)= xf_n(x)=xfn(x)=x для каждого n≥Nn\geq Nn≥N (возьмем N>xN>xN>x).
 Отсюда следует, что поточечным пределом {fn}\{f_n\}{fn} является функция f:[0,∞]f:[0,\infty]f:[0,∞], заданная выражением f(x) =xf(x)=xf(x)=x. Все функции fnf_nfn являются ограниченными функциями (0≤fn(x)≤n ∀x∈[0,∞]0\leq f_n(x)\leq n \ \forall x\in[0,\infty]0≤fn (x)≤n ∀x∈[0,∞]), но предельная функция fff неограничена. В случае равномерной сходимости ограниченных функций предельная функция снова ограничена: 9{\infty}{fn}n=1∞ — индикаторная функция Q∩[0,1]\mathbb{Q}\cap [0,1]Q∩[0,1], которая, как известно, неинтегрируемые по Риману.
Отсюда следует, что поточечным пределом {fn}\{f_n\}{fn} является функция f:[0,∞]f:[0,\infty]f:[0,∞], заданная выражением f(x) =xf(x)=xf(x)=x. Все функции fnf_nfn являются ограниченными функциями (0≤fn(x)≤n ∀x∈[0,∞]0\leq f_n(x)\leq n \ \forall x\in[0,\infty]0≤fn (x)≤n ∀x∈[0,∞]), но предельная функция fff неограничена. В случае равномерной сходимости ограниченных функций предельная функция снова ограничена: 9{\infty}{fn}n=1∞ — индикаторная функция Q∩[0,1]\mathbb{Q}\cap [0,1]Q∩[0,1], которая, как известно, неинтегрируемые по Риману.В приведенном выше примере поточечный предел интегрируемых по Риману функций оказался неинтегрируемым по Риману. В предположении равномерной сходимости справедлива следующая теорема:
Равномерная сходимость и интегрируемость по Риману
Пусть fn:[a,b]→Rf_n:[a,b]\to \mathbb{R}fn:[a,b]→R — последовательность интегрируемых по Риману функций на [a,b][a, b][a,b], сходящиеся равномерно к f:[a,b]→Rf:[a,b]\to \mathbb{R}f:[a,b]→R.


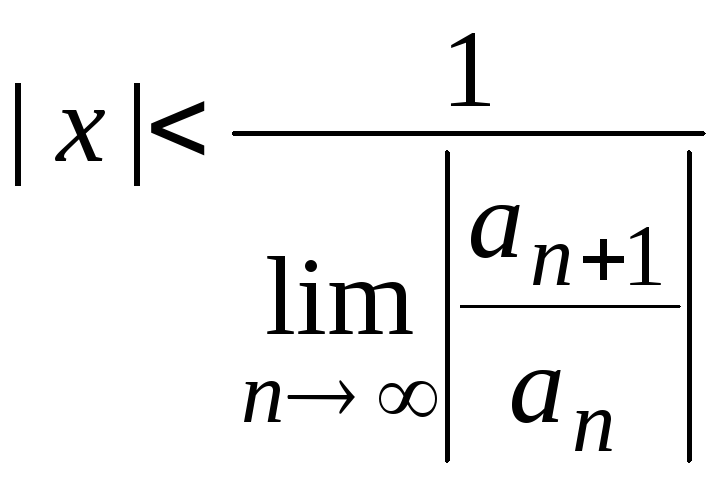 ..
地點:香港中文大學逸夫書院文瀾堂 LG 203 室
語言:粵語
…
..
地點:香港中文大學逸夫書院文瀾堂 LG 203 室
語言:粵語
… math.cuhk.edu.hk/course/1819/math3060a
math.cuhk.edu.hk/course/1819/math3060a  ..
.. Отсюда следует, что каждая равномерно сходящаяся последовательность функций сходится поточечно к одной и той же предельной функции, поэтому равномерная сходимость сильнее, чем поточечная сходимость.
Отсюда следует, что каждая равномерно сходящаяся последовательность функций сходится поточечно к одной и той же предельной функции, поэтому равномерная сходимость сильнее, чем поточечная сходимость. n|∣xn∣ произвольно близко к 1). Это позволяет быстрее сделать вывод о неравномерности сходимости, поскольку limn→∞∣∣f−fn∣∣∞=1≠0\displaystyle\lim_{n\to \infty} ||f-f_n|| _{\infty} = 1 \neq 0n→∞lim∣∣f−fn∣∣∞=1=0.
9{\infty}{fn}n=1∞ является монотонным, показывает, что непрерывность предельной функции влечет за собой равномерную сходимость.
n|∣xn∣ произвольно близко к 1). Это позволяет быстрее сделать вывод о неравномерности сходимости, поскольку limn→∞∣∣f−fn∣∣∞=1≠0\displaystyle\lim_{n\to \infty} ||f-f_n|| _{\infty} = 1 \neq 0n→∞lim∣∣f−fn∣∣∞=1=0.
9{\infty}{fn}n=1∞ является монотонным, показывает, что непрерывность предельной функции влечет за собой равномерную сходимость. Отсюда следует, что поточечным пределом {fn}\{f_n\}{fn} является функция f:[0,∞]f:[0,\infty]f:[0,∞], заданная выражением f(x) =xf(x)=xf(x)=x. Все функции fnf_nfn являются ограниченными функциями (0≤fn(x)≤n ∀x∈[0,∞]0\leq f_n(x)\leq n \ \forall x\in[0,\infty]0≤fn (x)≤n ∀x∈[0,∞]), но предельная функция fff неограничена. В случае равномерной сходимости ограниченных функций предельная функция снова ограничена: 9{\infty}{fn}n=1∞ — индикаторная функция Q∩[0,1]\mathbb{Q}\cap [0,1]Q∩[0,1], которая, как известно, неинтегрируемые по Риману.
Отсюда следует, что поточечным пределом {fn}\{f_n\}{fn} является функция f:[0,∞]f:[0,\infty]f:[0,∞], заданная выражением f(x) =xf(x)=xf(x)=x. Все функции fnf_nfn являются ограниченными функциями (0≤fn(x)≤n ∀x∈[0,∞]0\leq f_n(x)\leq n \ \forall x\in[0,\infty]0≤fn (x)≤n ∀x∈[0,∞]), но предельная функция fff неограничена. В случае равномерной сходимости ограниченных функций предельная функция снова ограничена: 9{\infty}{fn}n=1∞ — индикаторная функция Q∩[0,1]\mathbb{Q}\cap [0,1]Q∩[0,1], которая, как известно, неинтегрируемые по Риману.