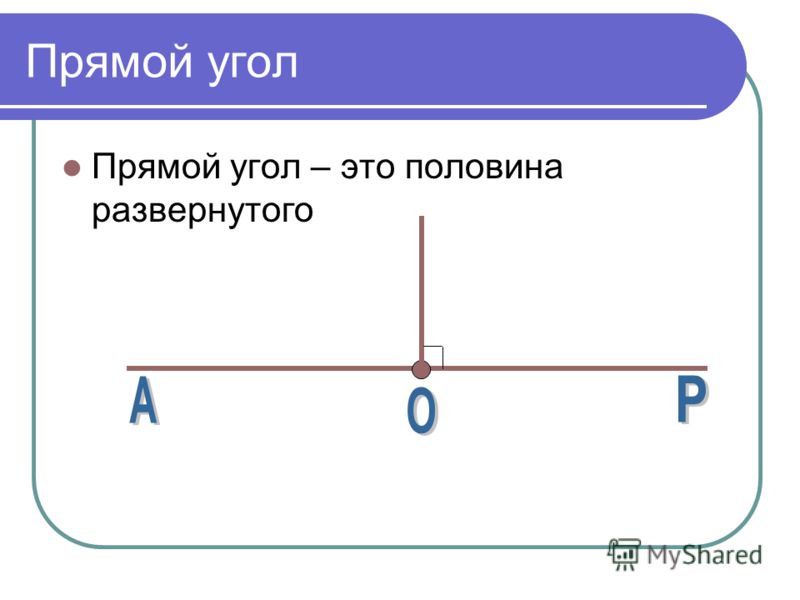
Урок по наглядной геометрии «Острый, прямой, тупой, развернутый углы»
Цели: закрепить с детьми строение угла (вершина, две стороны), уточнить название углов в зависимости от размера, развивать пространственное мышление, воображение.
Оборудование: карандаши, линейки, рабочая тетрадь, модель прямого угла, демонстрационный угольник, карточки с заданием, рисунок парусника, квадраты из цветной бумаги.
Ход урока
1. Организационный момент
– Проверьте готовность к уроку.
2. Введение в тему урока
1. Вступительное слово учителя
– Сегодня у нас с вами необычный урок. Мы отправимся в путешествие по стране Геометрии. А вместе с нами отправится в путешествие наша хорошая знакомая – Точка.
3. Актуализация опорных знаний
– Готовы вы путешествовать?
– Итак, жила в стране Геометрии очень
любознательная Точка.
Однажды она получила
приглашение в гости. А вот к кому в гости мы
отправимся вместе с Точкой, попробуем
догадаться, выполнив графический диктант.
1. Графический диктант
– Пропустите клетку вниз и на пересечении клеточек поставьте точку. Готовы?
1 клетка вправо, 2 – вниз, 2 – вправо, 2 – вверх, 1 – вправо, 6 – вниз, 4 – влево, 1 – вверх, 3 – вправо, 2 – вверх, 3 – влево, 3 – вверх.
– Закрасьте внутреннюю поверхность. Что
получилось? (Буква “У”.)
– Догадались, кто же позвал нас в гости?
– Действительно, это углы. Что же такое “угол”? (Два
луча, выходящие из одной точки.)
2. Повторение пройденного
– Путь у нас с вами не близкий. И, возможно,
маленькой Точке понадобится наша помощь.
– Посмотрите, не успели мы отправиться, как путь
нашей Точке преградил непроходимый лес. Назвав
правильно все геометрические фигуры, мы
расчистим путь нашей Точке.
Рис. 1
– Выпишите в тетрадь только названия лучей. Что
получилось?
– С нашей помощью Точка преодолела первое
препятствие и направилась далее.
Рис. 2
– Спустившись с пригорка, Точка увидела озеро. К нему вели две дороги. Задумалась Точка, по какой же из них ей идти, чтобы добраться до озера быстрее? Давайте ей поможем. Как вы считаете, какая самая короткая дорога? Почему? (Самый короткий путь – по прямой.)
– Как называются другие геометрические фигуры? (Ломаная незамкнутая, кривая незамкнутая, кривая замкнутая.)
– Добралась Точка до озера. Но как же перебраться на другой берег? Озеро-то большое, да глубокое. И тут в зарослях камыша Точка обнаружила парусник. Но сесть на него и перебраться можно лишь при условии, что вы назовёте и покажете все виды углов.
Рис.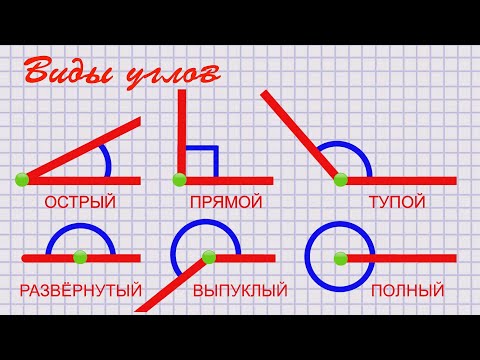
3
4. Работа по теме урока
1. Определение углов с помощью угольника
– Молодцы, ребята, помогли переправиться через
реку.
– Перед нами 4 домика. В них живут 4 брата-угла.
Назовём их.
– Что вы знаете об остром угле? (Он меньше
прямого.)
– Что вы знаете о тупом угле? (Он больше прямого.)
– Что вы знаете о развёрнутом угле? (Его стороны
лежат на одной прямой.)
– Нам нужен помощник, который поможет нам
определить точно, в каком домике какой угол
живёт. Но помощник этот очень гордый и не
общается с теми, кто не знает, как его зовут.
– Поэтому, чтобы узнать его имя, нужно решить
примеры.
| 55 – 50 + 8 | О | 12 10 13 0 6 27 35 12 |
| 11 – 6 + 30 | И | У Г О Л Ь Н И К |
| 9 + 7 – 10 | Ь | |
| 62 – 2 + 10 | У | |
| 14 – 7 + 20 | Н | |
| 8 + 8 – 6 | Г | |
| 78 – 70 + 4 | К | |
| 34 – 30 – 4 |
– Как же зовут нашего помощника? (Угольник.
)
– Определим с его помощью, где чей домик.
Вспомните, как это делается методом наложения.
Рис. 4
– Где в жизни мы встречаемся с прямыми углами? С острыми? С тупыми? С развёрнутыми?
2. Физкультминутка
– Покажем с помощью рук все виды углов – прямой, острый, тупой, развёрнутый.
3. Практическая работа по карточкам
– Наши хозяева – углы предлагают нам поиграть
с ними в прятки. Найдите их на карточках с помощью
модели прямого угла и подпишите.
– Проверим, что же у вас получилось.
Рис. 5
4. Работа в тетради
– А теперь наша Точка хочет поиграть с углами в прятки.
– Отметьте в тетради точку О – вершину угла и нашу точку – назовём её К. Постройте угол АОВ так, чтобы точка К лежала внутри угла АОВ. Кто покажет на доске, как это сделать?
– Отметьте ещё раз в тетрадях точку О – вершину
угла и точку К.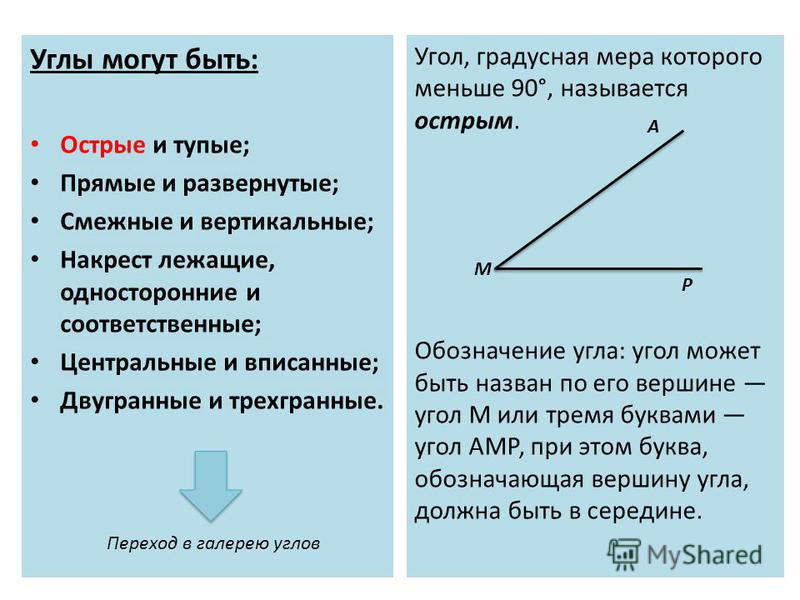
Постройте угол АОВ так, чтобы
точка К лежала вне угла АОВ. Покажем на доске.
– Постройте в тетрадях прямой угол СОД. Как это можно сделать без угольника? (по клеточкам)
– Проведите луч ОМ так, чтобы он лежал внутри угла СОД. Что скажете об угле МОД? (он острый) Почему?
– Постройте ещё раз угол СОД. Проведите луч О N так, чтобы он лежал вне угла СОД.
– Что скажете об угле NОД? (Он тупой.)
– Почему? (Ответы учащихся.)
5. Оригами “Кошка”
– А теперь я предлагаю сделать подарок нашим хозяевам – углам – оригами “Кошку”.
– Что за фигура из цветной бумаги лежит у вас на партах? Что вы знаете о квадрате? (Стороны равны, углы прямые.)
– Сложите квадрат по диагонали. Какой угол получился в основании? (Прямой.) Справа и слева? (Острые.)
Рис. 6
– Дорисуйте мордочку.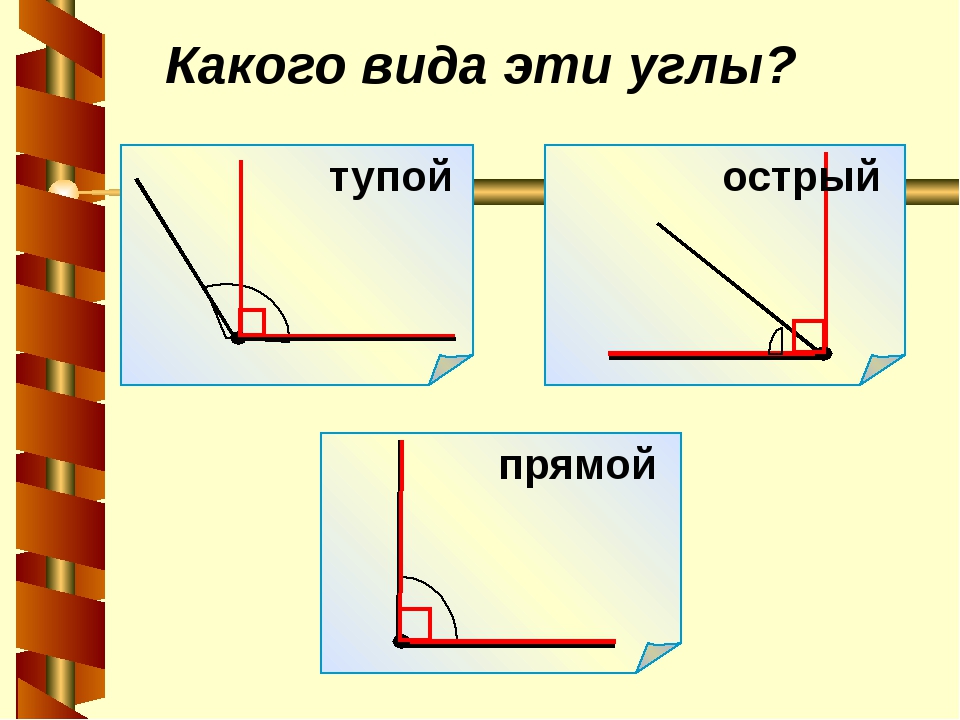
6. Итог урока
– Пора возвращаться домой. Вам понравилось
наше путешествие?
– У кого сегодня мы были в гостях? Что мы о них
знаем?
Конспект урока математики в 5 классе по теме «Угол. Прямой, острый, тупой и развёрнутый углы. Измерение углов»
5 класс Математика Урок №51
Тема: Угол. Прямой, острый, тупой и развёрнутый углы. Измерение углов.
Тип: урок изучения нового материла.
Цель: ввести понятие угла, величины угла и видов углов; знакомство с инструментами измерения углов.
Задачи:
Образовательные: научиться выполнять измерение углов, работать с чертёжными инструментами, определять виды углов.
Развивающие: развитие мыслительной деятельности; привитие интереса к предмету.
Воспитательные: воспитывать нравственные качеств личности, таких как ответственность, аккуратность, дисциплинированность.
Автор разработки: Попов Дмитрий Сергеевич.
ХОД УРОКА
I. Организационный момент
— Добрый день, 5 класс! Приятно видеть ваше присутствие на уроке математики. Давайте проверим вашу готовность к уроку! У вас на партах должны лежать ручка, карандаш, транспортир, тетрадь и учебник.
II. Постановка темы и целей урока
— Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия», – сказал в своё время французский архитектор Ле Корбюзье, и трудно с ним не согласиться. Геометрические фигуры постоянно встречаются в творениях природы и человека.
Сегодня мы рассмотрим ещё одну геометрическую фигуру – угол, разберём его виды и опишем процесс построения и измерения углов.
III. Изучение нового материала
Откройте ваши тетради, запишите дату и тему урока.
Учитель одновременно с учениками делает запись на доске:
17 ноября
Классная работа
Тема: Угол.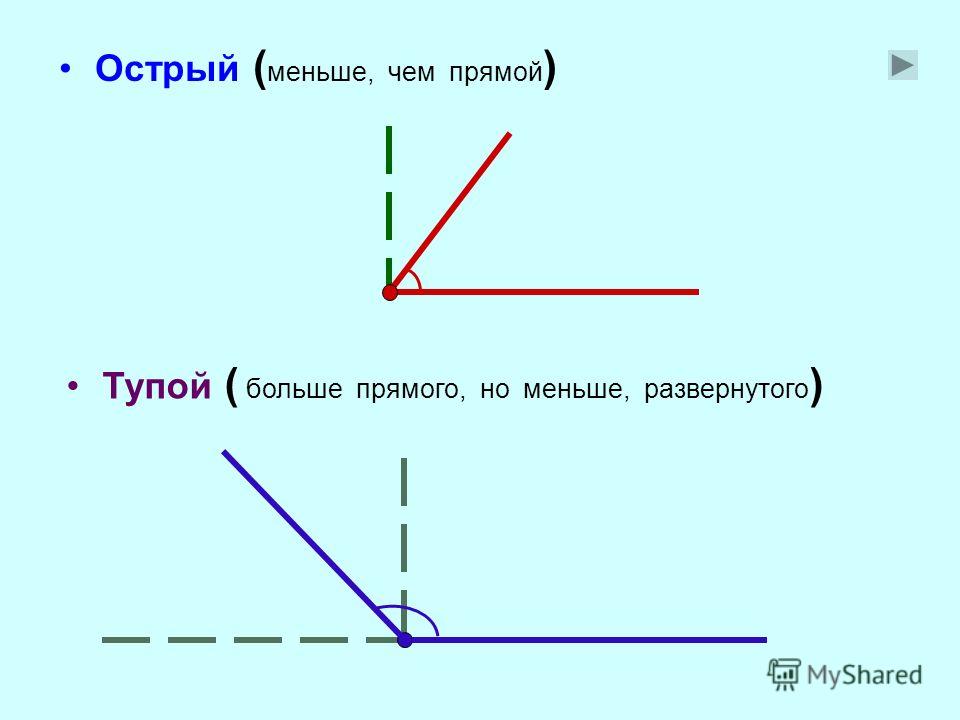
Прямой, острый, тупой и развёрнутый углы. Измерение углов.
— Для начала определим, что называют углом.
— Запишите определение:
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Построим угол. Для этого отметим на плоскости точку В и проведём два луча – АВ и ВС. Получим геометрическую фигуру, образованную точкой В и двумя лучами, исходящими из этой точки. Такую геометрическую фигуру и называют углом.
А С
В
Лучи АВ и ВС называют сторонами угла, точку В – общее начало этих лучей – называют вершиной угла.
Обозначается угол чаще всего тремя буквами. Например, ∠КОМ или ∠МОК. В середине пишется буква, которой обозначена вершина угла. Также угол можно обозначать и одной буквой, поставленной у вершины угла. Например, ∠О.
Начертим два луча, исходящих из точки В и принадлежащих одной прямой.
Лучи АВ и ВС вместе с точкой В дополняют друг друга до прямой – это дополнительные лучи.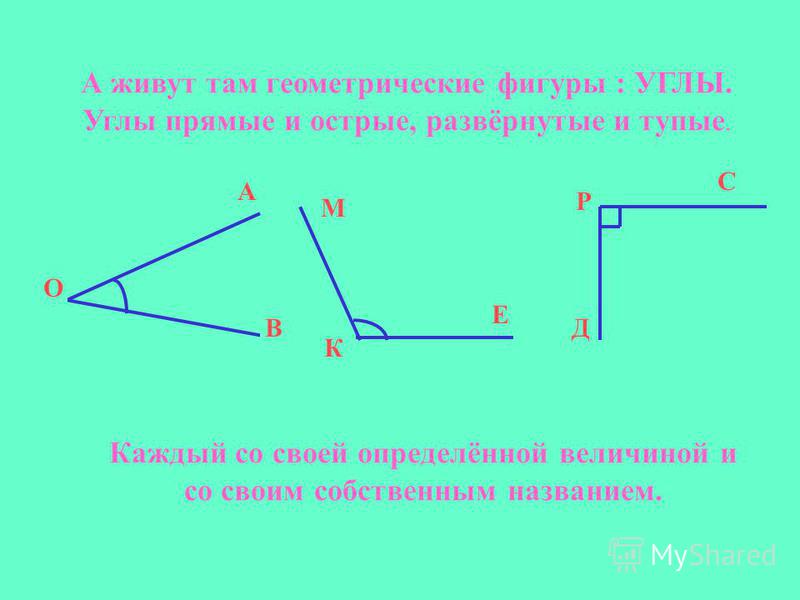
Угол называют развёрнутым, если его стороны являются дополнительными лучами.
Угол АВС – развёрнутый.
А В С
Построим развёрнутый угол АОВ и полуокружность с центром в точке О. Полуокружность разделим на 180 равных частей. Если построим углы с вершиной в точке О, стороны которых проходят через точки деления полуокружности, то таких углов будет 180. Один такой угол будет составлять часть развёрнутого угла.
Меру угла, составляющего часть развёрнутого угла, принимают за единицу измерения углов и называют градусом. Обозначают: 1º.
Г радусной мерой угла называют число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Например, градусная мера угла КOВ равна 25 градусам, так как в нём единица измерения градус содержится двадцать пять раз. Записывают: ∠КОВ = 25º.
Стоит отметить, что для более точного измерения угла используют доли градуса:
минуты, которые обозначают одной чёрточкой сверху над цифрой справа;
секунды, которые обозначаются двумя чёрточками над цифрой справа.
В одном градусе содержится 60 минут, а в одной минуте – 60 секунд.
Например, если угол А равен 10 градусам 5 минутам, записывают: ∠А = 10º5′.
Градусная мера развёрнутого угла равна 180º.
Для измерения углов в градусах пользуются прибором, который называется транспортиром. На транспортире имеется шкала – полуокружность, разделённая на 180 равных частей. На линейке транспортира чёрточкой отмечен центр полуокружности транспортира.
Чтобы найти градусную меру угла, например, угла АВС, нужно совместить центр транспортира с вершиной угла, в данном случае точкой В; расположить линейку транспортира так, чтобы одна из сторон угла прошла через начало отсчёта шкалы транспортира – ноль градусов (в данном случае сторона АВ), и найти на шкале транспортира деление, через которое проходит другая сторона угла – в данном случае сторона ВС.
Углы с равными градусными мерами равны. Из двух углов больше тот, который имеет большую градусную меру; а меньше тот, который имеет меньшую градусную меру.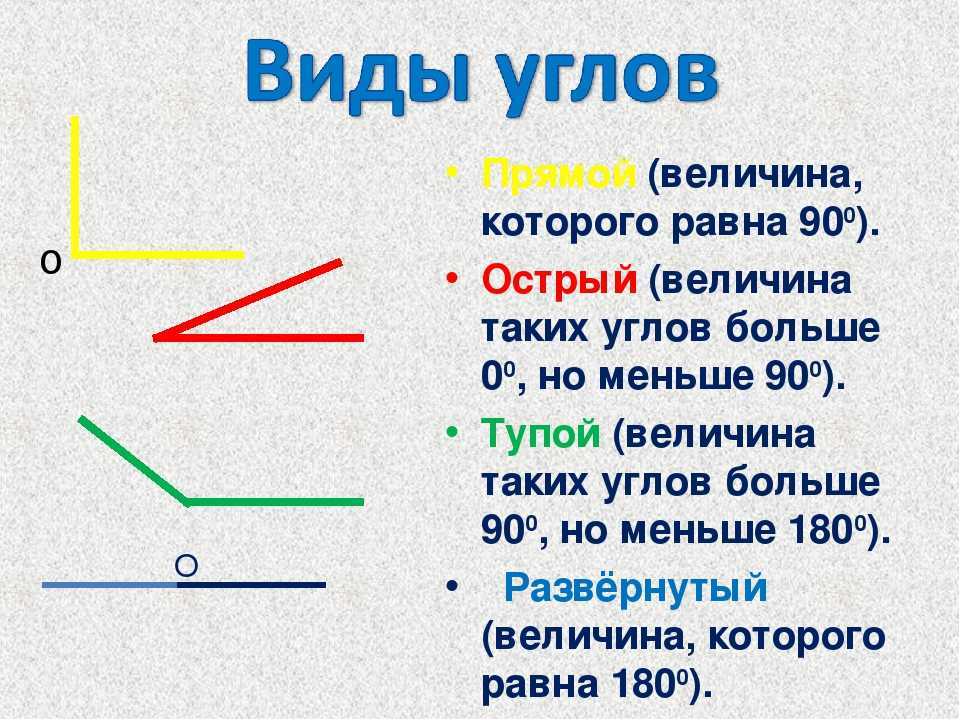
Углы можно сравнить также наложением. Если при этом они совпадают, то равны.
Ну, а теперь приступим к изучению видов углов.
Помимо развёрнутого, углы можно разделить на следующие виды: прямой, острый и тупой.
Угол называют прямым, если его градусная мера равна 90º.
Острым – если его градусная мера меньше 90º.
Тупым – если его градусная мера больше 90º и меньше 180º.
IV. Решение упражнений
На уроке устно выполняются №419-422.
Письменно выполняются №424, 427, 428, 432 (а), 430 (1 столбик), 431 (1 столбик), 435, 437.
V. Закрепление изученного материала
Учитель выдаёт карточки, а ученики выполняют самостоятельную работу.
Самостоятельная работа по теме | |
1. 2. За какое время минутная стрелка повернётся на угол в 90°? 3. В какое время из перечисленного угол между часовой и минутной стрелками наибольший? 4. Выполните сложение 9°42՛ + 26°23՛. 5. Луч ОС делит прямой ∠АОВ так, что ∠АОС на 34° больше ∠ВОС. Найдите величину ∠ВОС. | 1. Какая из данных величин соответствует острому углу. 2. За какое время минутная стрелка повернётся на угол в 120°? 3. В какое время из перечисленного угол между часовой и минутной стрелками наименьший? 4. Выполните сложение 49°31՛ + 18°47՛. 5. Луч КМ делит прямой ∠АКО так, что ∠АКМ на 15° меньше ∠ОКМ. Найдите величину ∠ОКМ. |
Какая из данных величин соответствует тупому углу.
Самостоятельная работа выполняется на отдельных листочках.
VI. Анонс домашнего задания
Прочитать пункт 2.6.
Решить №423, 429, 430 (2-ой столбик), 431 (2-ой столбик).
VII. Подведение итогов урока
Учитель выставляет оценки за урок.
Произвольный тупой угол. Прямой, тупой, острый и развитый угол. Смотреть что такое «Острый угол» в других словарях
В этой статье мы всесторонне разберем одну из основных геометрических фигур — угол. Начнем со вспомогательных понятий и определений, которые приведут нас к определению угла. После этого приводим принятые способы обозначения углов. Далее мы подробно разберемся с процессом измерения углов. В заключение покажем, как можно разметить углы на чертеже. Всю теорию мы снабдили необходимыми рисунками и графическими иллюстрациями для лучшего запоминания материала.
Навигация по страницам.
Определение угла.
Угол — одна из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур, как точка, прямая и плоскость. Поэтому, прежде чем знакомиться с определением угла, рекомендуем освежить теорию из разделов и .
Итак, начнем с понятий точка, прямая на плоскости и плоскость.
Сначала дадим определение луча.
Пусть дана некоторая прямая на плоскости. Обозначим его буквой а. Пусть O — некоторая точка прямой a . Точка О делит прямую а на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Также можно услышать, что луч называется полупрямой .
Для краткости и удобства введены следующие обозначения лучей: луч обозначается либо строчной латинской буквой (например, луч p или луч k), либо двумя большими латинскими буквами, первая из которых соответствует начало луча, а второй обозначает некоторую точку этого луча (например, луч ОА или луч CD).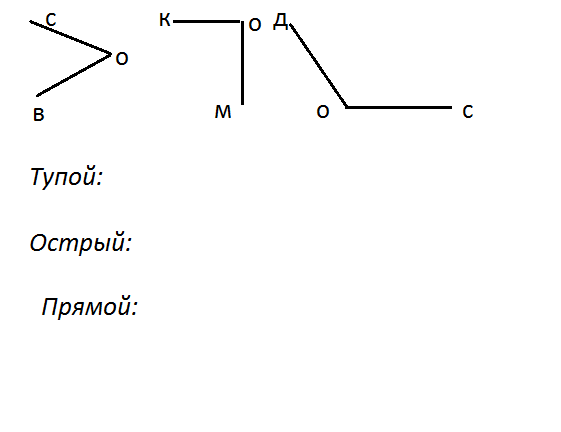
Покажем изображение и обозначение лучей на рисунке.
Теперь мы можем дать первое определение угла.
Определение.
Впрыск — это плоская геометрическая фигура(то есть целиком лежащая в определенной плоскости), которая составлена из двух несовпадающих лучей, имеющих общее начало. Каждый из лучей называется угловой стороной , общее начало сторон угла называется верхним углом .
Стороны угла могут образовывать прямую линию. Этот угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то угол называется развернутым .
Предлагаем вашему вниманию графическую иллюстрацию развернутого угла.
Символ угла используется для обозначения угла. Если стороны угла обозначаются строчными латинскими буквами (например, одна сторона угла k, а другая h), то для обозначения этого угла после значка угла пишутся буквы, соответствующие сторонам ряд, и порядок записи значения не имеет (то есть или).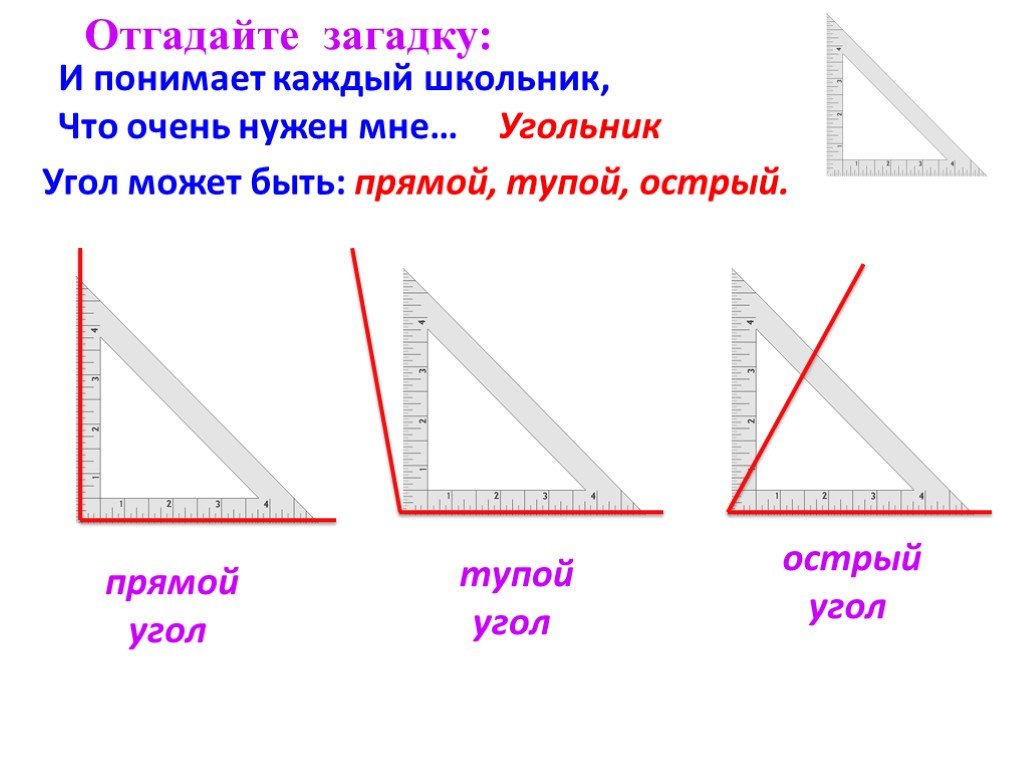
Любой угол делит плоскость на две части. При этом, если угол не развернут, то одна часть плоскости называется внутренним угловым участком , а другая наружным угловым участком . На следующем изображении показано, какая часть плоскости соответствует внутренней части угла, а какая — внешней.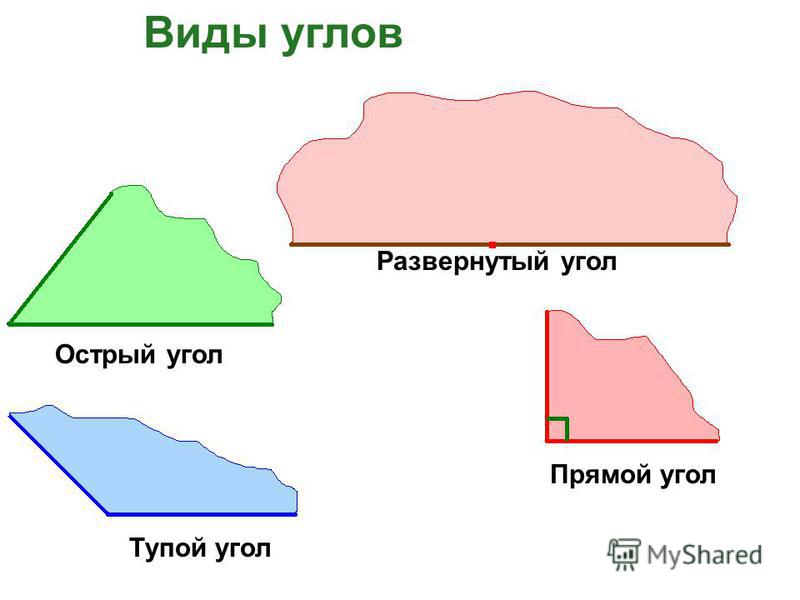
Любая из двух частей, на которые сплющенный угол делит плоскость, может считаться внутренней областью сплющенного угла.
Определение внутренней части угла приводит нас ко второму определению угла.
Определение.
Впрыск — это геометрическая фигура, которая составлена из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Следует отметить, что второе определение угла более строгое, чем первое, так как содержит больше условий. Однако не следует отбрасывать первое определение угла и не следует рассматривать первое и второе определения угла отдельно. Поясним этот момент. Когда речь идет об угле как геометрической фигуре, то под углом понимается фигура, составленная из двух лучей, имеющих общее начало. Если возникает необходимость производить с этим углом какие-либо действия (например, измерение угла), то под углом следует понимать уже два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличие как внутренней, так и внешней области угла ).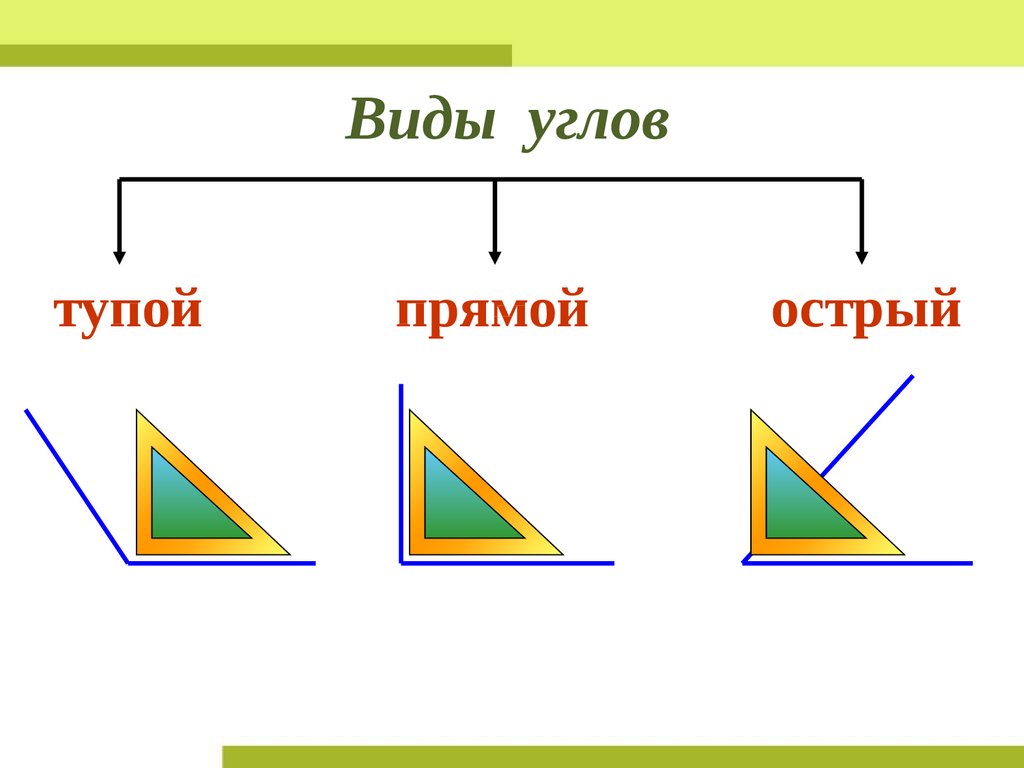
Дадим больше определений смежных и вертикальных углов.
Определение.
Смежные углы — это два угла, у которых одна сторона общая, а две другие образуют прямой угол.
Из определения следует, что смежные углы дополняют друг друга с точностью до прямого угла.
Определение.
Вертикальные углы — это два угла, в которых стороны одного угла являются продолжениями сторон другого.
На рисунке показаны вертикальные углы.
Очевидно, две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае с неравными углами поясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно наложить друг на друга.
Даны два угла. Приведем рассуждение, которое поможет нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, мы всегда можем сопоставить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла.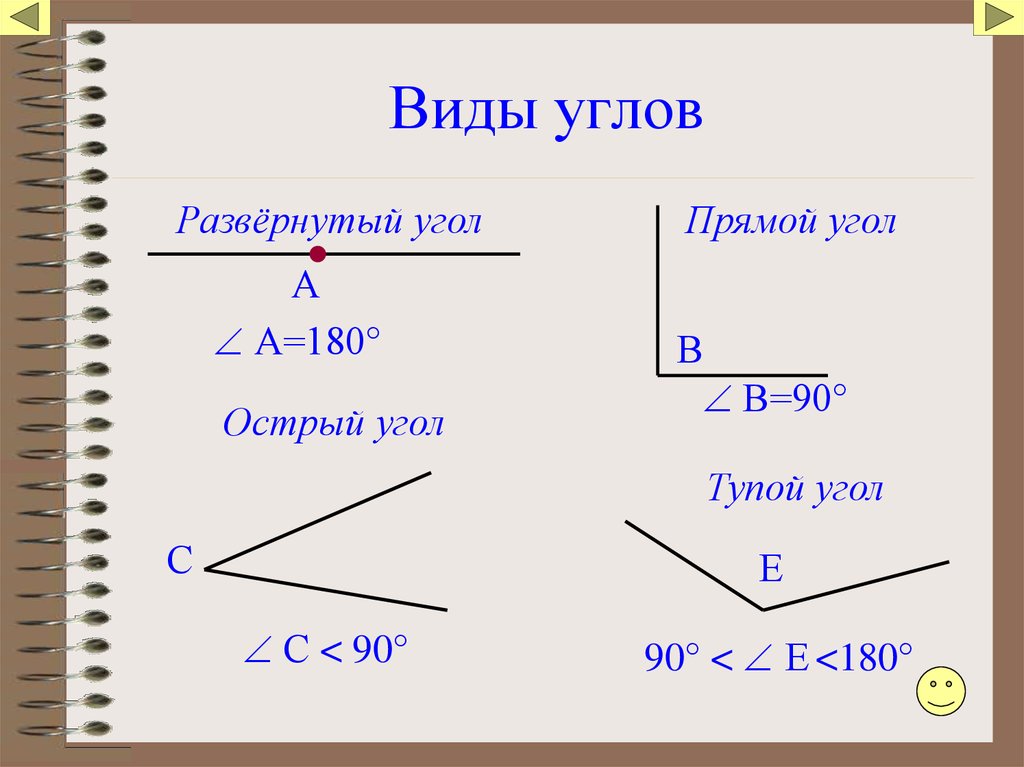
Соединим сторону первого угла с той стороной второго угла так, чтобы остальные стороны углов оказались по ту же сторону от прямой, на которой лежат объединенные стороны углов. Тогда, если две другие стороны углов совмещены, то углы называются равно .
Если две другие стороны углов не совпадают, то углы называются неравными , а меньшим угол считается частью другого ( большой угол который полностью содержит другой угол) .
Очевидно, что два прямых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение угла.
Измерение угла основано на сравнении измеренного угла с углом, принятым за единицу измерения. Процесс измерения углов выглядит так: начиная с одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют одиночными углами, плотно укладывая их один к другому. При этом запоминается количество укладываемых углов, что дает меру измеренного угла.
Фактически любой угол можно принять за единицу измерения углов.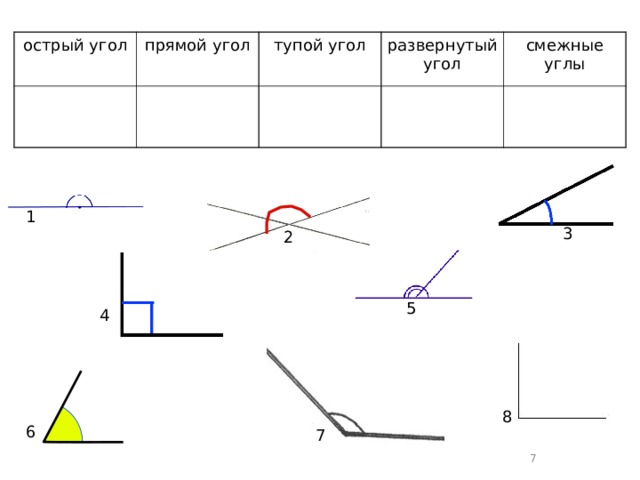
Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градусов .
Определение.
один градус угол равен сто восьмидесятой части выпрямленного угла.
Степень обозначается символом «», следовательно, одна степень обозначается как.
Таким образом, в развернутом угле мы можем уместить 180 углов в один градус. Это будет похоже на половину круглого пирога, разрезанного на 180 равных частей. Очень важно: «кусочки пирога» плотно подогнаны друг к другу (то есть стороны углов выровнены), причем сторона первого угла выровнена с одной стороной сглаженного угла, а сторона последнего единичного угла совпал с другой стороной сплющенного угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемый угол, пока не будет полностью покрыта внутренняя площадь измеряемого угла.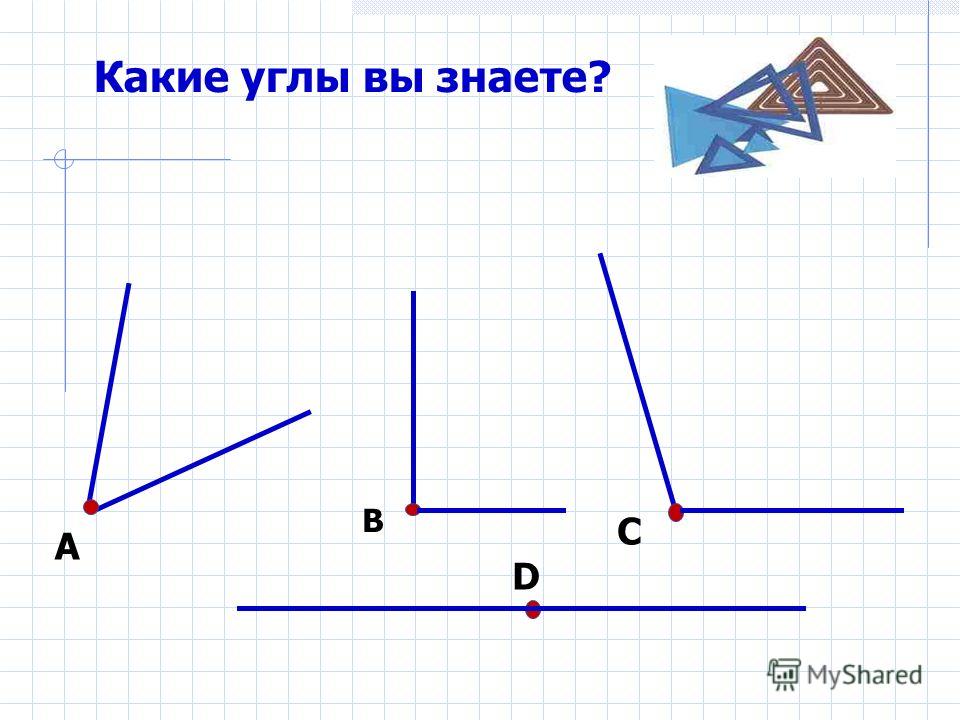
Как мы уже видели, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть прямого угла) и ровно 90 раз (половина прямого угла).
Для измерения углов меньше одного градуса (или иной единицы измерения углов) и в случаях, когда угол не может быть измерен целым числом градусов (принятых единиц измерения), необходимо использовать части градуса ( частей принятых единиц измерения). Отдельные части степени получили специальные названия. Наиболее распространены так называемые минуты и секунды.
Определение.
Минута — это одна шестидесятая градуса.
Определение.
Секунда — это одна шестидесятая минуты.
Другими словами, в минуте шестьдесят секунд, а в градусе шестьдесят минут (3600 секунд). Символ «» используется для обозначения минут, а символ «» — для обозначения секунд (не путать со знаками производной и второй производной).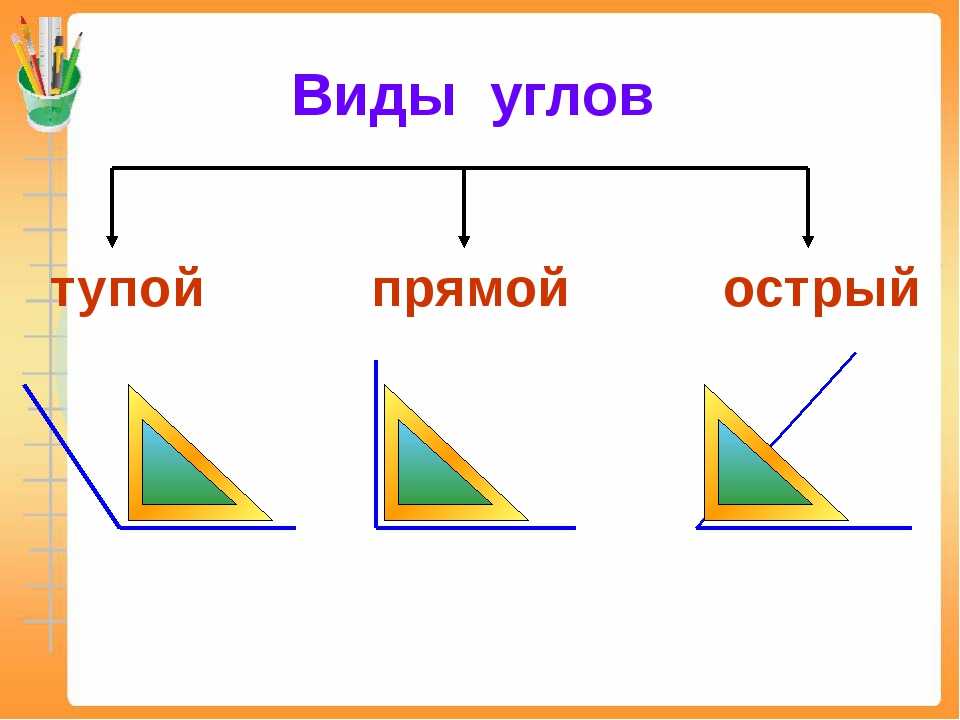
Тогда с введенными определениями и обозначениями имеем , а угол, в который укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусная мера угла называется положительным числом, которое показывает, сколько раз градус и его части входят в данный угол.
Например, градусная мера выпрямленного угла равна сто восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, самый известный из них транспортир.
Если известны и обозначение угла (например, ), и его градусная мера (пусть 110), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии углы с произвольным градусной мерой считаются, их называют). Угол в девяносто градусов имеет особое название, он называется прямым углом .
Угол меньше 90 градусов называется острым углом . Угол больше девяноста градусов называется тупой угол . Так, мера острого угла в градусах выражается числом из интервала (0, 90), мера тупого угла — числом из интервала (90, 180), прямой угол равен девяносто. градусов. Мы даем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, состоящего из нескольких углов равна сумме градусных мер составляющих углов. На рисунке ниже показан угол AOB, который состоит из углов AOC, COD и DOB, а .
Таким образом, сумма смежных углов составляет сто восемьдесят градусов , так как они образуют прямой угол.
Из этого утверждения следует, что . Действительно, если углы AOB и COD вертикальны, то углы AOB и BOC смежные и углы COD и BOC тоже смежные, поэтому справедливы равенства и, из которых следует равенство.
Наряду с градусом удобную единицу измерения углов называют радиан . Радианная мера широко используется в тригонометрии. Давайте определим радиан.
Определение.
Один радиан угла — это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Приведем графическую иллюстрацию угла в один радиан. На чертеже длина радиуса ОА (как и радиуса ОВ) равна длине дуги АВ, поэтому по определению угол АОВ равен одному радиану.
Аббревиатура «рад» используется для обозначения радианов. Например, запись 5 рад означает 5 радиан. Однако на письме обозначение «рад» часто опускается. Например, когда написано, что угол равен пи, это означает пи рад.
Отдельно следует отметить, что значение угла, выраженное в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом, и дуга окружности с центром в вершине данного угла подобны друг другу.
Измерение углов в радианах можно производить так же, как и измерение углов в градусах: узнать, сколько раз угол в один радиан (и его части) входит в данный угол.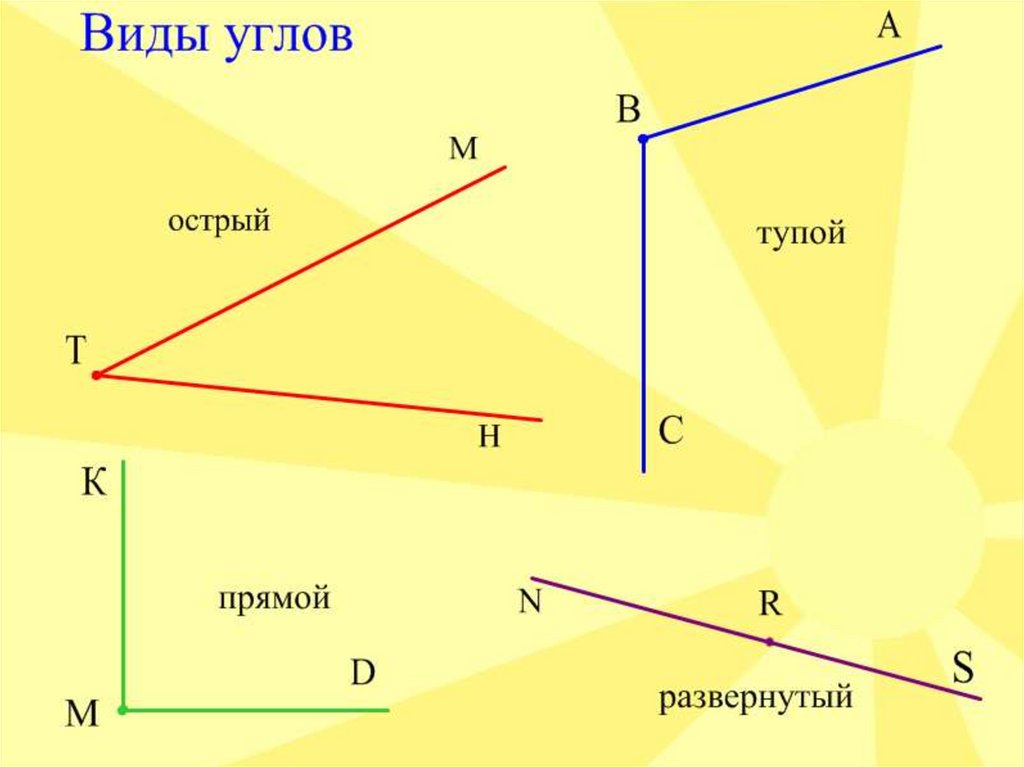
А можно вычислить длину дуги соответствующего центрального угла, а затем разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся градусы и радианы, так как предстоит выполнить довольно большую часть. В данной статье устанавливается связь между степенью и радианной мерой угла, а также приводятся примеры перевода градусов в радианы и наоборот.
Обозначение углов на чертеже.
На чертежах для удобства и наглядности углы можно обозначать дугами, которые обычно проводят во внутренней области угла от одной стороны угла к другой. Равноугольные обозначают одинаковое количество дуг, неравные углы — разное количество дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла к другой.
Если на чертеже приходится обозначать множество различных углов (обычно больше трех), то при обозначении углов, помимо обычных дуг, допустимо использовать дуги какого-либо специального вида.
Например, можно изобразить зубчатые дуги или что-то подобное.
Следует отметить, что не следует увлекаться обозначением углов на чертежах и не загромождать чертежи. Мы рекомендуем отмечать только те углы, которые необходимы в процессе решения или доказательства.
Библиография.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Е.Г., Юдина И.И. Геометрия. 7 — 9 классы: учебник для общеобразовательных учреждений.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Угол – геометрическая фигура, состоящая из двух разных лучей, исходящих из одной точки. В этом случае эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На картинке виден угол с вершиной в точке О , а стороны к А м .
Точки A и C отмечены на сторонах угла.
Этот угол можно обозначить как угол АОС. Посередине должно быть название точки, в которой находится вершина угла. Существуют и другие обозначения, угол О или угол км. В геометрии вместо слова угол часто пишется специальный значок.
Угол повернутый и неповоротный
Если обе стороны угла лежат на одной прямой, то такой угол называется развернуто угол. То есть одна сторона угла является продолжением другой стороны угла. На рисунке ниже показан угол О.
Следует отметить, что любой угол делит плоскость на две части. Если угол не расширен, то одна из частей называется внутренней областью угла, а другая — внешней областью этого угла. На рисунке ниже показан несплющенный угол и отмечены внешняя и внутренняя области этого угла.
В случае развернутого угла любая из двух частей, на которые он делит плоскость, может считаться внешней областью угла. Мы можем говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может быть на одной из его сторон, а может лежать внутри угла (во внутренней области).
На рисунке ниже точка A лежит вне угла O, точка B лежит на одной стороне угла, а точка C лежит внутри угла.
Измерение углов
Для измерения углов существует устройство, называемое транспортиром. Единицей угла является градусов . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Острый угол – это угол, градусная мера которого не превышает 90 градусов.
Прямой угол — это угол, мера которого равна 90 градусам.
Тупой угол – это угол, градусная мера которого больше 90 градусов. Острый угол — это угол меньше 90°. Тупой угол – это угол больше 90°, но меньше 180°. Прямой угол это угол = 90°.
20. Какие углы называются смежными? Какова их сумма?
Смежные углы — два угла с общей вершиной, одна из сторон которых общая, а остальные стороны лежат на одной прямой (не совпадают). Сумма смежных углов равна 180°.
Или
Два угла называются смежными , если у них одна сторона общая, а другие стороны являются дополнительными лучами. сумма смежных углов равна 180°. Каждый из этих углов дополняет другой до полного угла.
21. Какие углы называются вертикальными? Какое у них имущество?
Вертикальные углы — два угла, стороны одного из которых являются продолжением сторон другого. Вертикальные углы равны. (Углами называются вертикальные , образованные пересекающимися прямыми и не примыкающие друг к другу, т. е. не имеющие общей стороны, но вертикальные углы имеют вершину в одной точке. Вертикальные углы равны между собой).
22. Какие прямые называются перпендикулярными? Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла. Или Перпендикулярные линии — это линии, пересекающиеся под углом 90 градусов. Или Две прямые, образующие при пересечении прямые углы, называются перпендикулярными.
23. Объясните, что отрезком называется перпендикуляр, проведенный из данной точки к данной прямой. Что является основанием перпендикуляра? — отрезок, перпендикулярный данному, имеющий один конец в точке их пересечения. Этот конец отрезка называется основанием перпендикуляра. Перпендикулярно этой прямой перпендикулярно данной прямой отрезок, один из концов которого находится в точке их пересечения. Конечная точка отрезка на данной линии называется основанием перпендикуляра.
24. Что такое теорема и доказательство теоремы? В математике утверждение, справедливость которого устанавливается рассуждениями, называется теоремой, а само рассуждение называется доказательством теоремы.
Теорема — утверждение, для которого в рассматриваемой теории имеется доказательство (проще говоря, вывод). В отличие от теорем аксиомами называются утверждения, которые в рамках той или иной теории принимаются за истинные без каких-либо доказательств или обоснований.
Доказательство — это утверждение, объясняющее теорему. Теорема — гипотеза, которую нужно доказать; Гипотезу всегда нужно доказывать. Proof — аргументов, подтверждающих справедливость, правильность теоремы.
Начнем с определения угла. Во-первых, он во-вторых, образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которая называется вершиной угла. На основании этих признаков можно дать определение: угол – это геометрическая фигура, состоящая из двух лучей (сторон), выходящих из одной точки (вершины).
Они классифицируются по степеням, по расположению относительно друг друга и относительно окружности. Начнем с видов уголков по их размеру.
Есть несколько разновидностей. Рассмотрим подробнее каждый тип.
Основных видов углов всего четыре — прямой, тупой, острый и развитый угол.
Прямой
Выглядит так:
Его градусная мера всегда 90°, другими словами, прямой угол равен 90 градусов.
Они есть только у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Выглядит так:
Градусная мера всегда больше 90 градусов, но меньше 180 градусов. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, в многоугольниках.
Пряный
Это выглядит так:
Градусная мера острого угла всегда меньше 90°. Встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
развернутый
Расширенный угол выглядит так:
В полигонах не встречается, но не менее важен, чем все остальные. Прямой угол – это геометрическая фигура, градусная мера которой всегда равна 180º. Вы можете построить его, проведя один или несколько лучей от его вершины в любом направлении.
Есть несколько других второстепенных типов углов. В школах их не изучают, но знать хотя бы об их существовании необходимо. Второстепенных типов углов всего пять:
1.
Ноль
Выглядит это так:
Само название угла уже говорит о его величине. Его внутренняя площадь равна 0 o, а стороны лежат друг над другом, как показано на рисунке.
2. Косой
Косой может быть и прямым, и тупым, и острым, и с развитым углом. Главное ее условие – она не должна быть равна 0 o, 90 o, 180 o, 270 o.
3. Выпуклые
Выпуклыми являются нулевые, прямые, тупые, острые и развитые углы. Как вы уже поняли, градусная мера выпуклого угла составляет от 0° до 180°.
4. Невыпуклые
Невыпуклыми являются углы с градусной мерой от 181° до 359° включительно.
5. Полный
Полный угол составляет 360 градусов.
Это все виды уголков в зависимости от их размера. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительный
Это два острых угла, образующих одну прямую, т.е. их сумма равна 90°.
2.
Родственные
Смежные углы образуются, если провести луч в любом направлении через развернутую, точнее, через ее вершину. Их сумма равна 180 o.
3. Вертикальный
Вертикальные углы образуются при пересечении двух прямых. Их степенные меры равны.
Теперь перейдем к видам углов, расположенных относительно окружности. Их всего две: центральная и вписанная.
1. Центральный
Центральный угол – это угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, опирающейся на стороны.
2. Вписанный
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Его градусная мера равна половине дуги, на которую он опирается.
Все дело в углах. Теперь вы знаете, что кроме самых известных — острых, тупых, прямых и развернутых — в геометрии существует множество других их видов.
Примеры острых, тупых, прямых и плоских углов
Встреча двух линий или лучей всегда приводит к образованию угла .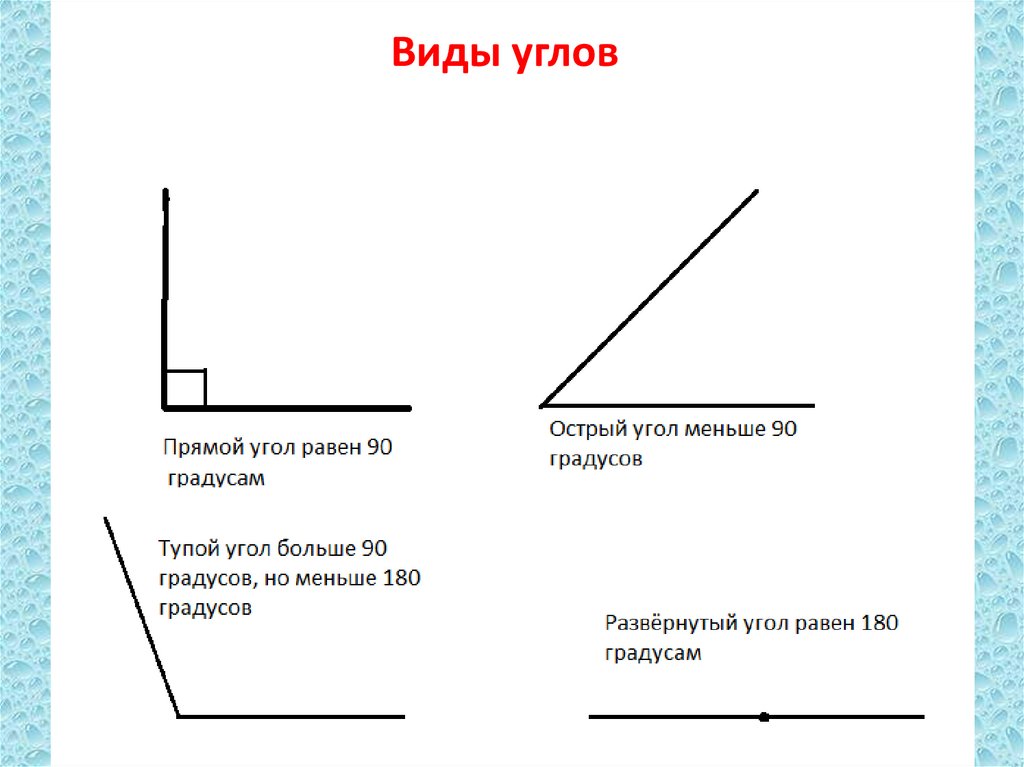
Вообще говоря, мы говорим об углах для обозначения плоской тригонометрии, то есть той, которая соответствует встрече между лучами, которые не имеют криволинейной формы, а представляют собой линию. Например: полит угол, тупой угол, прямой угол .
Точка, где соприкасаются два луча, называется вершиной , и именно здесь начинается угол: это сущность, которая не имеет физического разграничения, но существует, начиная с вершины и до тех пор, пока два луча не закончатся или не изменятся форма.
Обычно стремятся установить отношения сходства или различия между углами. Когда два угла имеют общую вершину и сторону, их называют в ряду , а когда они имеют общую вершину, но стороны продолжаются в противоположном направлении (то есть вершина общая, но угол образован с другой стороны) называются противоположностями по вершине: противолежащие вершине углы всегда имеют одинаковую амплитуду, и тогда они порождают две пары углов равной амплитуды.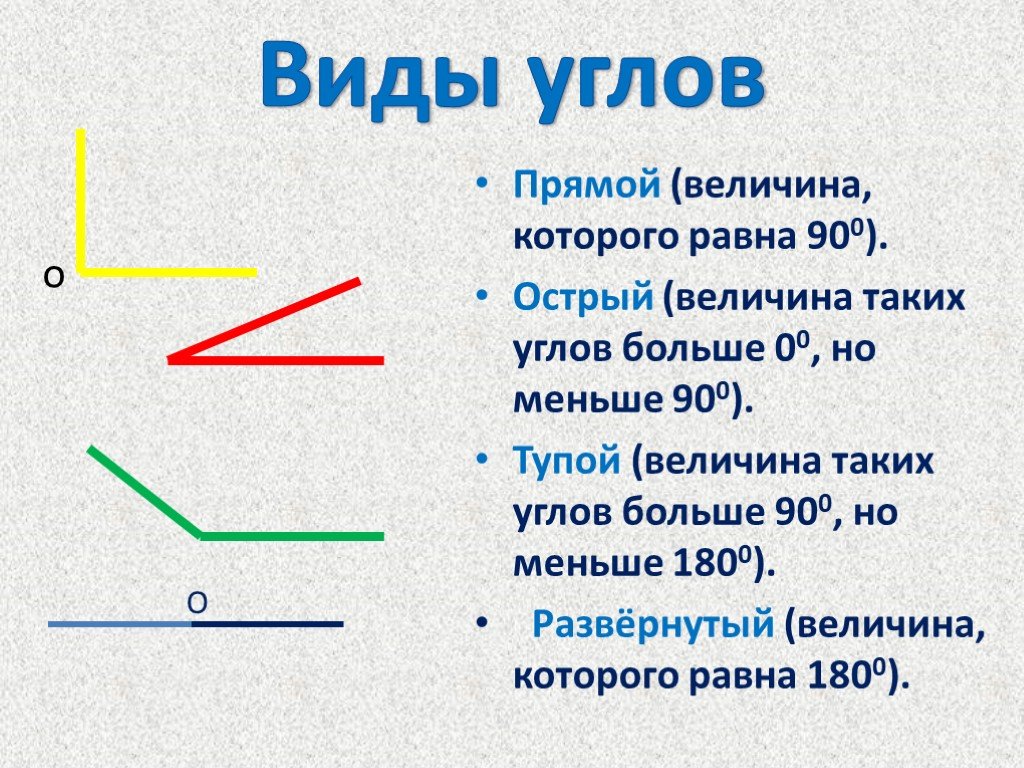
Это происходит потому, что угол не может иметь бесконечную амплитуду, но в лучшем случае это будет угол полного поворота, 360 ° (градусов) , 400 g (градов) или 2π радиан. Углы, которые в сумме дают полный оборот, называются дополнительными, а те, которые образуют четверть оборота, называются дополнительными.
Вопрос об амплитудах углов является математической основой тригонометрии, и он всегда был необходим в деле математических приложений действительности: все, что имеет отношение к архитектурным и инженерным конструкциям, использует этот тип процедуры. Элементарным инструментом для измерения амплитуды угла является конвейер , который понимает не весь оборот, а только его половину.
Вы используете измерение градусов , поэтому максимальное значение, которое вы можете зафиксировать, составляет 180 °. Способ использования инструмента заключается в том, чтобы поместить прямую сторону транспортира на одну сторону угла и проверить значение угла другой стороны в соответствии со шкалой транспортира.
Таким будет угол, независимо от длины сторон. По ширине сторон появляется наиболее распространенная классификация измерения угла.
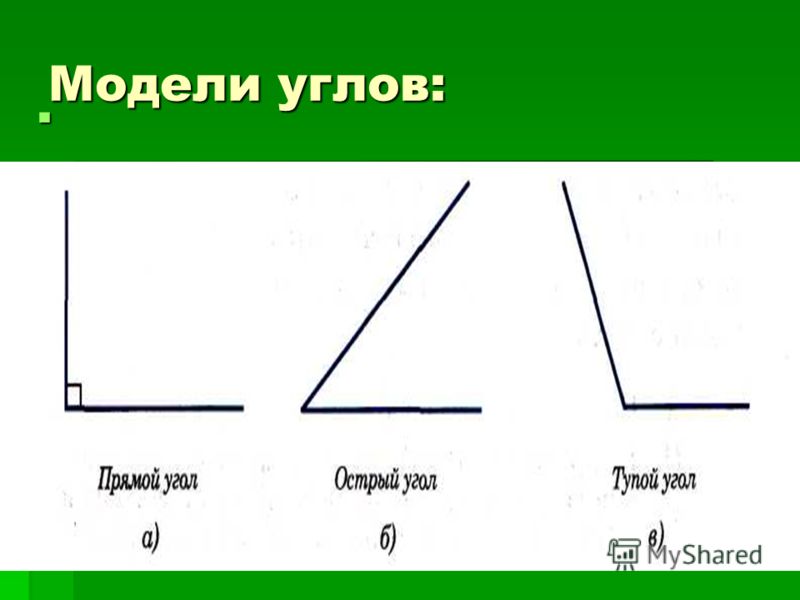
Примеры острых, тупых, прямых и прямых углов
- Острые углы. Это те, у которых амплитуда меньше 90°, то есть четверть оборота. Равносторонние треугольники (те, у которых все стороны равны) всегда состоят из трех углов по 60°, то есть трех острых углов.
- Тупые углы. Это те, амплитуда которых больше 90°, но меньше 180°. Если какой-либо из двух лучей выйдет за пределы вершины, то он будет сопровождаться острым и даст начало 180°. Если два луча длиннее вершины, через вершину будет две пары противоположных углов, что в сумме даст 360°.
- Углы прямые. Это те, которые измеряют ровно 90°. Символика, которая обычно используется для выражения этого, представляет собой угол в форме квадрата, а не круга. У всех квадратов и прямоугольников таких углов четыре, поэтому внутри они в сумме составляют 360°.
